|
|
Contents Introduction Overview of Deterministic algorithm Overview of Monte Carlo algorithm Scenes used for comparison Accuracy analysis Results obtained Conclusion Acknowledgments |
|
|
|
Contents Introduction Overview of Deterministic algorithm Overview of Monte Carlo algorithm Scenes used for comparison Accuracy analysis Results obtained Conclusion Acknowledgments |
|
We analyzed luminance in several points on a cube face. These points constitute the uniform 5x5 grid on the whole face. Due to symmetry there are only 6 different points (Figure 2). Below "semi-theoretical" luminance values for these points are presented. They are computed in the following way. At first we run the Monte Carlo simulation to get a luminance distribution in cube faces. Then illuminance of each point was computed by the direct integration of the energy transfer equation. This equation is equivalent to the rendering equation [Kaj86], for our case it can be written as:
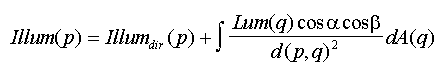
where
| Illum(p) | unknown illuminance at some point p; |
Illumdir(p) |
direct illuminance at p (computed analytically); |
| Lum(q) | luminance at point q; |
| spans over all surfaces in scene; | |
| angles between the surface normals at points p and q and segment connecting points p and q; | |
| d(p, q) | ordinary (Euclidean) distance between p and q; |
| dA(q) | differential area element at point q. |
A special trick was used to avoid singularity of this integral at points D, E, and F lying on cube edges.
| Point | Lum.nit | Comment |
| A | 892.8 | Face center |
| B | 768.7 | |
| C | 686.6 | |
| D | 565.1 | Middle of edge |
| E | 522.4 | |
| F | 388.4 | Cube corner |
Table 1. Theoretical luminance values for cube.
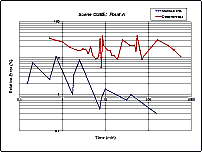
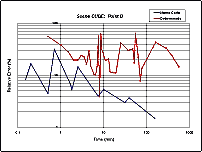
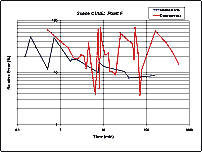
In graphs (Figure 3) we present accuracy (relative error is drawn along Y-axis) achieved as it depends on time spent. The graphs for the three points are presented: A (the most convenient), D, and F (the most inconvenient).
 |
 |
 |
| Figure 3a (800x600, 10K) |
Figure 3b (800x600, 12K) |
Figure 3c (800x600, 12K) |
It should be mentioned that we try to vary both main parameters influencing accuracy (and running time), namely, a size of triangles (by specifying different levels of "initial subdivision") and a length of a Monte Carlo simulation run (for the deterministic algorithm - a number of iterations and a threshold value). The graphs presented correspond to the best results obtained by each method for different combinations of control parameters.
The results are summarized in the table below (Table 2(a, b)). We used several Specter runs for different parameters. We varied a subdivision of a cube face and a requested accuracy of SPECTER simulation. A face subdivision determines how accurate the "ideal i-map" (the piece-wise linear luminance distribution which SPECTER results approach as time passes) can be. A subdivision denoted as, say, 10x10 means that each face is subdivided into grid of 10x10 = 100 squares each subdivided into 2 triangles that totals in 100*2*6 = 1200 triangles for the whole cube.
The column "Accuracy requested" in the Monte Carlo table contains values of the final error estimate; SPECTER simulation stops after reaching this value. The Deterministic algorithm in TBT presents 5 predetermined levels of accuracy (differing by values of several control parameters) denoted as "Draft", "Standard", "Fine", "Super", and "Supersuper" (super2).
The relative error column gives the relative deviation of the simulation results in a particular point from the theoretical value presented in Table 1.
| subdivision | accuracy requested |
time (min) |
rel. error at points | ||
| A | D | F | |||
| 10 x 10 | 8% | 0.15 | 2.0% | 8.4% | 20.7% |
| 4% | 0.5 | 2.6% | 5.7% | 11.6% | |
| 2% | 1.7 | 1.0% | 6.5% | 16.2% | |
| 1% | 8 | 0.8% | 4.3% | 15.8% | |
| 20 x 20 | 16% | 0.2 | 7.4% | 16.8% | 48.8% |
| 8% | 0.5 | 4.5% | 4.5% | 23.1% | |
| 4% | 1.8 | 3.4% | 5.3% | 18.1% | |
| 2% | 7.4 | 0.4% | 4.0% | 10.1% | |
| 1% | 31 | 0.7% | 3.0% | 10.5% | |
| 40 x 40 | 16% | 0.7 | 10.9% | 31.6% | 46.4% |
| 8% | 2.5 | 8.8% | 14.6% | 17.5% | |
| 4% | 10 | 1.4% | 5.4% | 13.3% | |
| 2% | 39 | 1.0% | 3.7% | 7.9% | |
| 1% | 156 | 0.3% | 1.5% | 8.8% | |
Table 2 (a). Results of accuracy analysis for the CUBE scene. Monte Carlo results.
| subdivision | accuracy requested |
Num. of iterat. |
time (min) |
rel. error at points | ||
| A | D | F | ||||
| 10 x 10 | Draft | 1 | 0.5 | 34.8% | 55.9% | 66.2% |
| 2 | 1.0 | 27.5% | 38.3% | 39.5% | ||
| 3 | 1.5 | 19.5% | 29.6% | 32.6% | ||
| Standard | 1 | 1.0 | 36.2% | 56.7% | 67.4% | |
| 2 | 1.5 | 29.2% | 39.7% | 42.1% | ||
| 3 | 3.0 | 17.7% | 24.1% | 21.9% | ||
| Fine | 1 | 1.0 | 35.5% | 54.4% | 66.7% | |
| 2 | 2.0 | 28.4% | 38.6% | 39.5% | ||
| 3 | 3.5 | 17.1% | 22.6% | 20.8% | ||
| Super | 1 | 1.0 | 33.9% | 51.1% | 65.0% | |
| 2 | 1.5 | 22.0% | 29.6% | 30.1% | ||
| 3 | 2.5 | 15.9% | 19.6% | 18.3% | ||
| 4 | 6.5 | 9.6% | 10.3% | 3.8% | ||
| Super2 | 1 | 1.0 | 31.6% | 48.5% | 62.4% | |
| 2 | 2.5 | 18.3% | 23.8% | 24.8% | ||
| 3 | 4.0 | 13.3% | 16.1% | 11.9% | ||
| 4 | 6.0 | 9.5% | 10.3% | 5.6% | ||
| 5 | 8.0 | 5.5% | 3.9% | 5.0% | 20 x 20 | Draft | 1 | 1.0 | 32.2% | 53.7% | 63.1% |
| 2 | 1.5 | 21.1% | 28.0% | 32.0% | ||
| 3 | 2.0 | 16.9% | 19.6% | 19.2% | ||
| Standard | 1 | 1.0 | 31.7% | 54.2% | 65.0% | |
| 2 | 2.5 | 20.2% | 28.8% | 38.0% | ||
| 3 | 5.0 | 11.9% | 14.8% | 16.9% | ||
| Fine | 1 | 2.5 | 31.8% | 54.4% | 64.9% | |
| 2 | 4.5 | 20.0% | 28.7% | 36.6% | ||
| 3 | 7.0 | 11.6% | 14.7% | 16.8% | ||
| Super | 1 | 3.0 | 32.5% | 56.4% | 66.8% | |
| 2 | 9.0 | 22.5% | 31.6% | 41.6% | ||
| 3 | 13 | 16.0% | 20.7% | 23.6% | ||
| 4 | 19 | 9.3% | 11.1% | 9.1% | ||
| Super2 | 1 | 8.5 | 39.6% | 62.8% | 72.0% | |
| 2 | 25 | 31.7% | 42.4% | 57.1% | ||
| 3 | 48 | 22.1% | 32.2% | 35.6% | ||
| 4 | 64 | 16.1% | 21.9% | 23.4% | ||
| 5 | 78 | 11.1% | 13.6% | 11.3% | ||
| 40 x 40 | Draft | 1 | 2.0 | 32.3% | 54.6% | 64.2% |
| 2 | 8.0 | 20.9% | 28.2% | 37.6% | ||
| 3 | 11 | 16.6% | 19.2% | 21.7% | ||
| Standard | 1 | 2.0 | 31.9% | 54.1% | 63.9% | |
| 2 | 6.0 | 20.3% | 26.9% | 34.8% | ||
| 3 | 14 | 11.9% | 11.7% | 10.7% | ||
| Fine | 1 | 4.0 | 31.7% | 53.9% | 63.6% | |
| 2 | 11 | 20.1% | 26.6% | 34.6% | ||
| 3 | 16 | 11.7% | 11.3% | 10.4% | ||
| Super | 1 | 7.5 | 32.7% | 56.5% | 65.5% | |
| 2 | 37 | 22.2% | 30.2% | 41.8% | ||
| 3 | 52 | 15.7% | 17.3% | 17.8% | ||
| 4 | 71 | 8.9% | 7.8% | 3.7% | ||
| Super2 | 1 | 55 | 39.6% | 64.0% | 72.6% | |
| 2 | 162 | 31.6% | 42.9% | 63.4% | ||
| 3 | 286 | 22.1% | 33.2% | 37.6% | ||
| 4 | 397 | 16.2% | 23.2% | 25.5% | ||
| 5 | 566 | 11.1% | 14.6% | 14.7% | ||
Table 2 (b). Results of accuracy analysis for the CUBE scene. Deterministic results.
Note, that the most accurate results of the deterministic method were obtained for the most crude subdivision (10x10). The result for point F (face corner) is even more accurate than the best Monte Carlo result. It may be explained by a compensation of the discretization error and the convergence error. The discretization error is always positive in point F because any averaged luminance value will be greater than actual luminance in F - the global minimum of luminance over the whole cube surface. On the other hand, the convergence error in the deterministic algorithm is always negative - the deterministic algorithm approaches its limit from below. This is not the case for the Monte Carlo algorithm. Consequently, we observe a good compensation for luck of the deterministic algorithm, while in the Monte Carlo case looking at the last lines for each subdivision we see a decreasing (with subdivision) discretization error added with a more or less constant and not small in this case convergence error. To conclude, these unexpectedly good results of deterministic algorithm should be considered as an occasional luck.
For realistic scenes we don't try to vary an initial subdivision taking into account that we anyhow compare only the convergence error, while the discretization error (that depends on an initial subdivision) should be the same (or very close) for both methods. So, the only control parameter is a length of a Monte Carlo run or a number of deterministic iterations. The graphs included in figures presenting images of realistic scenes show accuracy (a relative distance from reference solution) versus time spent.
For the deterministic algorithm we use the 5 predetermined accuracy levels ("Draft", "Standard", "Fine", "Super", "Supersuper") and take only the final results of a simulation not including results of intermediate iterations (as opposed to CUBE) with one exception: we included (under the mark "Draft1") results after the first iteration of the deterministic algorithm with the "Draft" setting of control parameters; this is the fastest result of the deterministic algorithm. In the table below deterministic results are numbered in the following manner:
| Det. No | Accuracy level |
| 0 | Draft1 |
| 1 | Draft |
| 2 | Standard |
| 3 | Fine |
| 4 | Super |
| 5 | Supersuper |
Table 3. Correspondence of accuracy level and image number for deterministic data.
To make possible a comparison of Monte Carlo and Deterministic results obtained in equal time intervals we prepare a series of Monte Carlo results that take (approximately) the same processor time as Deterministic results. They are demonstrated in parallel with the deterministic ones in corresponding figures. However, sometimes two consecutive deterministic results need almost the same execution time. In such case we provide only Monte Carlo image for both of them. Also for some scenes the Monte Carlo algorithm can generate a reasonable image spending less time than the first deterministic image (Draft1) needs. In such cases we included this Monte Carlo image under number 0, while Monte Carlo images that spent the same time as some deterministic are numbered from 1.
We have prepared a separate comparison page for each of the five scenes. Each page contains a series of parallel images and a graph with accuracy / time results.
| Comparison results | ||||
| APART2 | DREAM0 | FLOWER | CG | HONSHA |
Below the accuracy data are presented in the tabular form (Tables 4-8). For each of the two algorithms the columns mean:
N - number. For the deterministic algorithm it corresponds to the interreflection accuracy level requested (see Table 3).
Time - time for the global illumination computation (including the direct phase). We exclude time spent for rendering (image preparation). Time values are measured on Convex SPP 1000 computer.
Accuracy - relative average difference between a reference data (the most precise result) and a current result. It is computed as explained in ch. Accuracy analysis . The result of the last Monte Carlo run was used as reference data. Accordingly, accuracy of these reference data is extrapolated value (see ch. Accuracy analysis). Such values are marked by character "~" to emphasize that they are less reliable.
The above description relates to two columns: "Realistic accuracy" for the deterministic algorithm and "Accuracy" for the Monte Carlo one.Optimistic accur. - Optimistic accuracy estimate for Deterministic results as explained in ch. Accuracy analysis.
Average lumin. - Average (quadratic) value of luminance in the visible part of a scene. These values are included to illustrate different character of convergence of deterministic and Monte Carlo algorithms.
| Deterministic | Monte Carlo | |||||||
| N | Time h:mm |
Realistic Accuracy % vs MC(3) |
Optimistic Accuracy % vs DT(5) |
Average lumin |
N | Time h:mm |
Accuracy % vs MC(3) |
Average lumin |
| 0 | 0:09 | 2.28% | 8.30 | |||||
| 0 | 0:46 | 46.95% | 33.65% | 3.69 | 1 | 0:41 | 1.04% | 8.34 |
| 1 | 1:05 | 37.15% | 19.10% | 4.30 | ||||
| 2 | 1:49 | 32.06% | 13.41% | 4.89 | 2 | 1:37 | 0.78% | 8.33 |
| 3 | 2:08 | 30.80% | 13.41% | 5.19 | ||||
| 4 | 5:20 | 26.17% | 6.90% | 5.46 | ||||
| 5 | 7:55 | 21.98% | --- | 5.46 | 3 | 7:05 | ~0.37% | 8.33 |
Table 4. Results of accuracy analysis for realistic scenes. Scene: APART2.
| Deterministic | Monte Carlo | |||||||
| N | Time h:mm |
Realistic Accuracy % vs MC(3) |
Optimistic Accuracy % vs DT(5) |
Average lumin |
N | Time h:mm |
Accuracy % vs MC(3) |
Average lumin |
| 0 | 0:26 | 1.96% | 11.18 | |||||
| 0 | 1:50 | 25.01% | 18.11% | 7.81 | 1 | 1:43 | 1.31% | 11.19 |
| 1 | 2:40 | 18.30% | 9.66% | 8.95 | 2 | 2:00 | 1.15% | 11.19 |
| 2 | 4:05 | 15.12% | 5.57% | 9.49 | 3 | 3:53 | 0.98% | 11.19 |
| 3 | 4:45 | 14.81% | 6.03% | 9.39 | ||||
| 4 | 7:03 | 12.21% | 2.06% | 9.89 | 4 | 6:54 | ~0.65% | 11.19 |
| 5 | 11:56 | 10.91% | --- | 10.12 | ||||
Table 5. Results of accuracy analysis for realistic scenes. Scene: DREAM0.
| Deterministic | Monte Carlo | |||||||
| N | Time h:mm |
Realistic Accuracy % vs MC(3) |
Optimistic Accuracy % vs DT(5) |
Average lumin |
N | Time h:mm |
Accuracy % vs MC(3) |
Average lumin |
| 0 | 00:44 | 4.95% | 19.76 | |||||
| 0 | 02:07 | 9.39% | 4.83% | 15.68 | 1 | 01:59 | 1.62% | 19.57 |
| 1 | 02:15 | 9.19% | 4.59% | 15.73 | 2 | 02:07 | 1.54% | 19.56 |
| 2 | 03:39 | 07.45% | 2.78% | 16.43 | 3 | 03:37 | 1.10% | 19.55 |
| 3 | 7:36 | 6.08% | 1.40% | 16.99 | 4 | 07:27 | 0.78% | 19.49 |
| 4 | 26:27 | 5.39% | 0.61% | 17.27 | 5 | 24:22 | 0.44% | 19.53 |
| 5 | 1:23:13 | 4.85% | --- | 17.50 | 6 | 1:16:31 | ~0.24% | 19.53 |
Table 6. Results of accuracy analysis for realistic scenes. Scene: FLOWER .
| Deterministic | Monte Carlo | |||||||
| N | Time h:mm |
Realistic Accuracy % vs MC(3) |
Optimistic Accuracy % vs DT(5) |
Average lumin |
N | Time h:mm |
Accuracy % vs MC(3) |
Average lumin |
| 0 | 0:08 | 2.27% | 12.26 | |||||
| 0 | 0:46 | 4.30% | 2.52% | 10.21 | 1 | 0:39 | 1.04% | 12.25 |
| 1 | 1:33 | 3.12% | 1.30% | 10.89 | 2 | 1:17 | 0.77% | 12.25 |
| 2 | 2:55 | 2.77% | 1.13% | 11.10 | ||||
| 3 | 3:38 | 2.73% | 1.17% | 11.16 | ||||
| 4 | 9:15 | 2.37% | --- | 11.40 | 3 | 7:45 | ~0.37% | 12.25 |
| 5 | n/a | |||||||
Table 7. Results of accuracy analysis for realistic scenes. Scene: CG.
The last, "Supersuper" result for the deterministic algorithm was not computed for scene CG as it takes too much time (more than 24 h).
| Deterministic | Monte Carlo | |||||||
| N | Time h:mm |
Realistic Accuracy % vs MC(3) |
Optimistic Accuracy % vs DT(5) |
Average lumin |
N | Time h:mm |
Accuracy % vs MC(3) |
Average lumin |
| 0 | 3:10 | 11.16% | 7.67% | 16.77 | 1 | 2:54 | 0.46% | 20.40 |
| 1 | 3:27 | 10.32% | 6.84% | 17.17 | ||||
| 2 | ||||||||
| 3 | 5:00 | 7.54% | 4.00% | 18.06 | 2 | 4:17 | 0.42% | 20.41 |
| 4 | 8:30 | 6.33% | 2.52% | 18.43 | 3 | 6:28 | ~0.34% | 20.41 |
| 5 | 18:10 | 4.15% | --- | 19.18 | ||||
Table 8. Results of accuracy analysis for realistic scenes. Scene: HONSHA.
Comparing these data we can conclude that the Monte Carlo algorithm is considerably better in all cases. Even the optimistic accuracy estimate of Deterministic algorithm runs much above accuracy graph for the Monte Carlo images. However, we should accept this conclusion with some care. Indeed, it relates to the objective measure of accuracy as root mean square difference from "real" data. If we are interested in accurate optical simulation and would like to get some digital result (say, efficiency coefficient of some optical system) then our measure is probably appropriate. Such situation is typical for tasks of technical device design.
But TBT has other area of application - image generation (for presentation of designed building, say). In such case an accurate calculation of luminance / illuminance values may be of less importance, while it is more important to produce a "nice looking" and "truth-like" image. These criteria are subjective, we can not measure them quantitatively. To estimate a visual quality of resultant images we can only look at them.
Let's look at the two images of the FLOWER scene having the same accuracy estimate (about 5%): the first computed by the deterministic algorithm, the second - by Monte Carlo. It is clearly seen that they have quite different character of errors: the Monte Carlo image exhibits a high level of random noise, uncorrelated errors in neighboring areas; the deterministic image exhibits a constant (more or less uniform) underestimate of the indirect illumination (the image is darker than the accurate image ( MC6 )). This character of the deterministic algorithm can be seen from the "Average lumin." column of the resultant tables. For the deterministic algorithm average luminance monotonically increases with time approaching the final value while for Monte Carlo it oscillates irregularly around the final value (and is much closer to it).
In other words, the deterministic image is more smooth than the equally accurate Monte Carlo one and this results in more "nice looking" of the former.
But, it should be taken into account that the image MC0 was computed by the Monte Carlo algorithm in less than 1 min while DT5 (by the deterministic algorithm) took more than an hour. It is more reasonable is to compare images calculated by both algorithms in the same time. Figures present such series.
The first pair of images (about 2 minutes) can be estimated as having a low quality: the deterministic image is too dark while the Monte Carlo one contains a noticeable random noise. Next pairs are better. However, even in the last pair (1h20m) we can notice a difference between the Monte Carlo and deterministic images: a color of walls in the Monte Carlo image has green shade (caused by light reflected by the plant) while in the Deterministic image the walls are almost gray. This is probably because the plant consists of small triangles each of which is considered unimportant by the deterministic algorithm and thus ignored. But there is a lot of them making in total a considerable secondary light. In this situation we observe a bias introduced by deterministic acceleration scheme - ignorance of unimportant (low energy) emitters.
Let's look now at the DREAM0 images. Here we can see an illustration for the "plane reflector" problem mentioned in sec. 3.2. At any of the deterministic images we can see a bright trapezoid on the left wall that is produced by light (from some hidden source) reflected in the back window. The Monte Carlo images don't contain this trapezoid. Instead at its place we can see a very fuzzy (almost indistinguishable) bright spot.
The reason is the following. The deterministic algorithm creates a virtual light source (VLS) - reflection of real one and then treats the illumination by this VLS as the direct illumination. But, as is explained in sec. 2.3, the direct illumination is calculated more accurately than the indirect (secondary) one because it is computed in each point separately while the secondary illuminance is interpolated from i-maps. We can say that the direct component of illuminance is computed without the discretization error.
In contrary, the Monte Carlo algorithm treats specularly reflected light in the same way as refracted of diffusely scattered light and includes it in a secondary i-map. Therefore its distribution is subject to the discretization error that is visible as a fuzzy boundary in Monte Carlo images (it can be done less fuzzy with more fine triangular mesh subdivision).
Another scene where a Monte Carlo image is injured by this effect is APART2 (a fixture shadow on the ceiling is cast by reflected light).
So, for these two scenes our "realistic" accuracy estimates are not actually realistic and it is better to base the comparison on the "optimistic" accuracy estimate for the deterministic algorithm.
On the other hand, the scene FLOWER is free of this effect (it does not contain specular surfaces). The scenes CG and HONSHA contain specular surfaces, however, we had to switch off the virtual emitters method in the deterministic algorithm because it is a high memory-consuming method and these scenes can not be processed with virtual emitters on.
These effect is a drawback of the considered implementation of the Monte Carlo global illumination analysis algorithm; it could beneficially apply the "virtual emitters" method in cases when deterministic algorithm applies it thus eliminating the mentioned possibility to be beaten by the Deterministic algorithm.
|
|
Contents Introduction Overview of Deterministic algorithm Overview of Monte Carlo algorithm Scenes used for comparison Accuracy analysis Results obtained Conclusion Acknowledgments |
|

|
|
| Copyright 1996 Andrei Khodulev. | [Home] |