Comparison of two Methods of Global Illumination Analysis

Andrei Khodulev

Prev Contents    Introduction    Overview of Deterministic algorithm    Overview of Monte Carlo algorithm    Scenes used for comparison    Accuracy analysis    Results obtained    Conclusion    Acknowledgments Next

5. ACCURACY ANALYSIS

The main characteristic of the two algorithms being compared is a dependence of the achievable accuracy level on the running time. Below our approach to measuring accuracy of simulation is discussed.

We measure inaccuracy by the distance of our result (luminance distribution) from some reference data that are considered to be accurate (at least much more accurate then an estimated result). All the three components of this procedure (the luminance distribution, the distance, and the reference data) are explained below.

Luminance distribution

We don't use for comparison the luminance distribution in the whole scene (we have not a convenient way in TBT to extract this distribution). Instead we set some viewer (a camera) to observe a part of a scene and compare luminance distributions as seen by the camera. TBT has capability to generate (in addition to an ordinary image seen by camera) a file with objective physical luminance values (measured in nit), or illuminance values (lux) in each pixel of the image. We use these luminance files and compare them by means of a simple additional program.

Measure of distance

Our measure of distance between two luminance distributions is essentially the ordinary L2 distance [Edw65] (normalized by dividing by N - a total number of pixels). Namely, having two distributions fi and gi (i=1,...,N means pixel number) we define the distance between them as

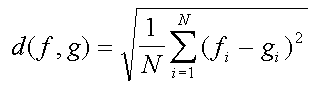
d(f,g) = \sqrt{1/N * \sum_{i=1}^N (f_i - g_i)^2}

This is the absolute distance (measured in nit). However, the relative distance (in percent of the average luminance of an image) is more clear for human, so we present results in the relative form:

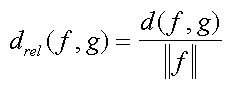
d_rel(f,g) = d(f,g) / |f|

where f is considered as a reference image, g - as compared with;

|f| = d(f, 0) - is (quadratic) mean luminance of f;

0 stands for the constantly zero luminance distribution.

A different approach is used for the simple CUBE scene. Here we don't use average quantities, we simply compare luminance values at the individual characteristic points.

Reference data

For the simple CUBE scene we have the theoretical values to be used as reference data. They are values of luminance at some characteristic points (a face center, the middle of a cube edge, a cube corner, etc.; in principle, we can compute luminance at an arbitrary point on the cube surface). Difference of our simulation results and these theoretical values includes both mentioned in sec. 3.1 kinds of errors: the discretization error and the convergence one.

Of course, no theoretical values are present for realistic scenes, so there is a problem of choosing a reference solution. We'd like to have as reference the absolutely precise data; as it is impossible, we need a reference solution to be at least much more accurate than any solution we compare with it. We used as such solution results of a rather long run of the Monte Carlo method. As the results of the experiments with the simple scene show, the Monte Carlo results actually approach the exact values; moreover, we can even estimate the accuracy of our reference data by some heuristic procedure.

The procedure is based on the observation that the actual error of our output luminance data (measured as an average over the entire image) is not necessarily equal to the error reported by the Monte Carlo simulation algorithm (estimated as an average over the entire scene); nevertheless, we can expect that it is PROPORTIONAL to the estimate. So, we can establish a proportionality factor based on less accurate results (and simultaneously check that the proportionality really takes place). Then we can extrapolate this proportionality to the reference result and deduce its "actual" error (defined as a distance to the absolutely accurate solution) from the error estimate report produced by the Monte Carlo algorithm. Of course, such error estimate is less reliable compared with the estimate based on the direct comparison, however, the points corresponding to reference data reasonably fit in accuracy / time dependence graphs (presented in the next chapter).

The reference data obtained in the described way include a discretization error. This fact has some consequences:

(1) The distance we measure estimates only the convergence error; our procedure does not allow to estimate the discretization error.

(2) For the comparison to be fair we need that i-maps in both methods use exactly the same set of triangles (so that the discretization error will be the same). To achieve this we need to switch off adaptive triangle subdivision during the indirect phase in the deterministic algorithm.

Realistic and optimistic estimates

Nevertheless, usage of the Monte Carlo solution as reference data for estimation of the deterministic algorithm might be considered unfair for the deterministic algorithm. While we detected a better convergence of the Monte Carlo solutions to our reference data (see the next chapter) one might try to explain a high "error" of deterministic solutions by some incorrectness in the Monte Carlo reference data, so that the deterministic method could, in principle, converge to the correct result that is different from the result produced by Monte Carlo. Such case takes place in presence of plane reflectors in a scene, it is explained in the next chapter where we analyze results for particular scenes.

To accomplish the comparison regardless of such doubts we provide another, "self-contained" estimate of deterministic convergence. Namely, we produce an "optimistic" error estimate of a deterministic solution as a distance of this solution to the most accurate (last) DETERMINISTIC solution (this is not applicable to the last solution itself, of course). We can assume that deterministic solutions approach the limit monotonically increasing; therefore, a distance from any solution to a more accurate one is UNDERESTIMATE of the error of the first solution. For this reason we call such estimate "optimistic".

To summarize, we provide one accuracy estimate of a Monte Carlo solution. It measures distance from a solution to the Monte Carlo limit that it would reach in infinite time. For a deterministic solution we provide two estimates:

  1. The distance from a solution to the same Monte Carlo limit.
  2. The distance from a solution to the last deterministic solution.

Assuming that there are no inaccuracies in generation of the Monte Carlo reference data we can take (1) as a realistic error estimate for a deterministic solution. However, for those who doubt, we provide also the optimistic error estimate (2) that doesn't refer to Monte Carlo at all. If it happens that even the optimistic error estimate of a Deterministic solution is larger than error of a Monte Carlo solution produced in the same time then we can for sure conclude that the Monte Carlo method is preferable from the viewpoint of the accuracy / time criterion.

Prev Contents    Introduction    Overview of Deterministic algorithm    Overview of Monte Carlo algorithm    Scenes used for comparison    Accuracy analysis    Results obtained    Conclusion    Acknowledgments Next
Copyright 1996 Andrei Khodulev. [Home]