Аннотация
Работа посвящена исследованию такой актуальной проблемы современности как устойчивое развитие.
Исследование данного понятия проводится на основе модели Форрестера. Устойчивое развитие
предлагается понимать как режим стабилизации основных материальных характеристик мировой
системы. Показывается, что устойчивое развитие мировой системы, исследуемой в модели
Форрестера, можно наблюдать лишь при выполнении ряда определенных модификаций и достаточно
жестких мер. Наряду с нахождением стационарных решений модифицированной модели проводится их
теоретическое исследование.
Abstract
The work is devoted to research such present-day problem as sustainable development.
Investigation of that conception is realized on basis of Forrester's model. It is suggested
to understand sustainable development as stable regime of the main world system material
indicators. It is shown that sustainable development of world system investigated in
Forrester's model can be observed if a set of certain modifications and sufficiently strict
measures will accomplished. Besides finding of stationary decisions in modified model their
theoretical research is realized.
Исторический экскурс
В 1968 г. по инициативе Аурелио Печчеи [1, 2]
(общественного деятеля и бизнесмена, тогда входившего в руководство фирмы
"Оливетти") был создан Римский клуб – неправительственная организация
ученых, предпринимателей, общественных деятелей. Клуб был создан с целью
анализа и поиска решений глобальных проблем. С самого начала существования
Клуба его задачей стало привлечение внимание широкой общественности к накопившимся
глобальным проблемам. Довольно быстро члены Клуба осознали, что наилучшей
формой достижения подобной цели было бы создание и использование математических
моделей. Это позволило бы, с их точки зрения, представить существующие проблемы
в наиболее объективном ракурсе и поставить их в центр внимания всего общества.
В июне 1970 г. на заседании в Берне Римский клуб
предложил профессору МТИ, руководителю группы системной динамики Дж. Форрестеру
разработать модель глобального развития. Уже через 4 недели тот представил примитивную
модель, грубо имитирующую основные процессы мировой системы. Эта модель
получила название "Мир-1". Последующая доработка и отладка привела к
появлению так называемой модели "Мир-2". Именно ее мы и рассмотрим
подробнее. Описание самой модели, анализ полученных результатов и выводы были
опубликованы в книге "Мировая динамика" [3], увидевшей свет в 1971 г.
Кратко изложим саму модель.
Модель Форрестера построена на основании принципов системной динамики – метода изучения
сложных систем с нелинейными обратными связями, который до этого сам Форрестер
со своими сотрудниками разрабатывал с конца 50-х годов. Аналитические основы
построения модели, предназначенной для имитации мировых процессов, были рассмотрены
в его предыдущих работах, посвященных изучению промышленных и урбанизированных
систем [4]. Качественный скачок заключался лишь в том, чтобы перейти от подобных
микросистем к глобальной макросистеме.
Метод системной динамики предполагает, что для
основных фазовых переменных (так называемых системных
уровней) пишутся дифференциальные уравнения одного и того же типа:
 , ,
где y+ –
положительный темп скорости переменной y, включающий в себя все
факторы, вызывающие рост переменной y; y––
отрицательный темп скорости, включающий в себя все факторы, вызывающие убывание
переменной y.
Предполагается, что эти темпы расщепляются на
произведение функций, зависящих только от "факторов" – комбинаций
основных переменных, т.е., в свою очередь, самих являющихся функциями системных
уровней: y± = g(y1, y2,…, yn) = f(F1, F2,…, Fk) = f1(F1) f2(F2) … fk(Fk), где 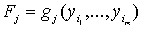 – факторы,
причем m = m(j) < n, k = k(j) < n (число уровней). Т.е. факторов
меньше, чем основных переменных, и каждый фактор зависит не от всех системных
уровней, а только от какой-то их части. Это позволяет упростить задачу моделирования. – факторы,
причем m = m(j) < n, k = k(j) < n (число уровней). Т.е. факторов
меньше, чем основных переменных, и каждый фактор зависит не от всех системных
уровней, а только от какой-то их части. Это позволяет упростить задачу моделирования.
Непосредственно моделирование мировой динамики
проводилось Форрестером поэтапно. Основные этапы таковы.
1. Концептуализация
– выделение главного. На этом этапе выделялись наиболее существенные, на взгляд
Форрестера, мировые процессы, такие как: 1) быстрый рост населения; 2)
индустриализация и связанный с ней промышленный рост; 3) нехватка пищи; 4) рост
отходов производства; 5) нехватка ресурсов.
Отсюда основные переменные (системные уровни):
1)
население P;
2)
основные фонды K;
3)
доля фондов в сельском хозяйстве (т.е. в отрасли
обеспечения пищей) X;
4)
уровень загрязнения (или просто загрязнение) Z;
5)
количество невозобновляемых (невосстановимых) природных
ресурсов R.
А также факторы, через которые и осуществляется
взаимовлияние переменных при построении дифференциальных уравнений:
·
относительная численность населения PP (население, нормированное на его численность в
1970 году);
·
удельный капитал KP;
·
материальный уровень жизни C;
·
относительный уровень питания (количество пищи
на человека) F;
·
нормированная величина удельного капитала в
сельском хозяйстве XP;
·
относительное загрязнение ZS;
·
доля остающихся ресурсов RR.
Помимо перечисленных переменных, Форрестер ввел еще
понятие о "качестве жизни" Q. Этот фактор является
своего рода мерой функционирования исследуемой системы, т.е. носит характер
индикатора. Зависит этот индикатор от четырех факторов PP,
C, F, ZS:
Q = QC QF QP QZ. В целом он не играет существенной роли в
модели, поэтому, в дальнейшем не рассматривается.
Скажем несколько слов по поводу единиц измерения
основных переменных. Население естественно оценивать числом людей, доля фондов
в сельском хозяйстве – безразмерная величина между 0 и 1. Выбор единиц для
фондов, загрязнения и ресурсов осуществлялся привязкой к базовому году.
Единицей капитала считается условная величина – капитал, приходящийся на душу
населения в 1970 г.; единицей ресурсов считается их годовое потребление в 1970
г.; за единицу загрязнения принимается условная величина – загрязнение, приходящееся
на одного человека в 1970 году.
2. Составление
уравнений. Для системных уровней пишется система дифференциальных
уравнений, которая в упрощенном виде записывается так:
 , (1) , (1)
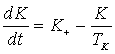 , (2) , (2)
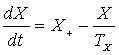 , (3) , (3)
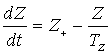 , (4) , (4)
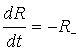 , (5) , (5)
где B = B(C, F, PP, ZS) = cB·BC(C)·BF(F)·BP(PP)·BZ(ZS) – темп рождаемости,
D = D(C, F, PP, ZS) = cD·DC(C)·DF(F)·DP(PP)·DZ(ZS) – темп смертности,
K+ = K+(P, C) =
P·KC(C) –
скорость производства основных фондов,
X+ = X+(F, Q) =
XF(F)·XQ(Q) / TX – прирост доли
сельскохозяйственных фондов,
Z+ = Z+(P, KP) = P·ZK(KP) – скорость генерации загрязнения,
TZ = TZ(ZS) – характерное время естественного разложения
загрязнения,
R- = R-(P, C) =
P·RC(C) –
скорость потребления ресурсов.
Уравнения для вспомогательных
переменных:
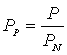 – относительная
плотность населения – относительная
плотность населения
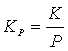 – удельный капитал – удельный капитал
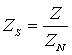 – относительное
загрязнение – относительное
загрязнение
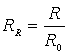 – доля оставшихся
ресурсов – доля оставшихся
ресурсов
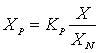 – относительная
величина сельскохозяйственных фондов – относительная
величина сельскохозяйственных фондов
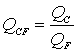 – относительное
качество жизни – относительное
качество жизни
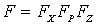 – уровень питания – уровень питания
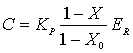 – материальный уровень
жизни – материальный уровень
жизни
Все обозначенные выше буквы с подстрочными символами (BC, BF, KC и т.д.) суть таблицы с линейной интерполяцией
(так называемые множители). Эти
таблицы строились (задавались) либо экспертами в данной области, либо – если
экспертов не было – самим Форрестером (в качестве примеров см. рис. 1 и
2).
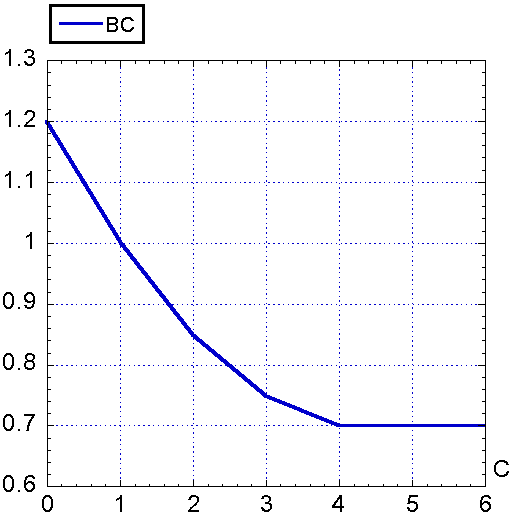
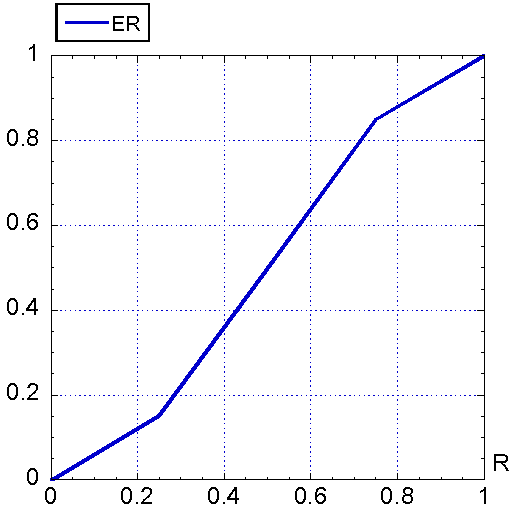
Рис. 1.
Множитель BC(C)
Рис. 2.
Множитель ER(R)
Константы:
cB
= 0,04 – нормальный темп рождаемости,
cD
= 0,028 – нормальный темп смертности,
cK
= 0,05 – нормальный темп фондообразования,
TK
= 40 лет – постоянная износа основных фондов,
TX
= 15 лет – время выбытия доли сельскохозяйственных фондов,
tN
= 1970 – базовый год,
PN
= 3,6·109 – численность населения в 1970 г.,
XN
= 0,3 – нормальная часть фондов в сельском хозяйстве,
ZN
= 3,6·109 – стандартное загрязнение, численно совпадающее с PN.
Начальные данные:
t0
= 1900, P0
= 1,65·109, K0 = 0,4·109, X0 = 0,2, Z0 = 0,2·109, R0 =9·1011
(значение было взято, исходя из предположения, что ресурсов при скорости их
потребления как в 1970 г. должно хватить на 250 лет).
Расчеты по своей модели Форрестер проводил для
временного интервала с 1900 по 2100 г.г. С 1900 г. по 1970 г. – главным
образом, для того, чтобы "отладить" (настроить) параметры модели на
известных данных, а с 1970 г.
– уже как чисто прогнозные. Иными словами, параметры модели (в частности, cB, cD, cK ), начальные данные и отчасти табличные функции
подбирались, чтобы динамика системы совпала по возможности с реальной мировой
динамикой на интервале от 1900 до 1970 г.г., а дальше система пускалась, так сказать,
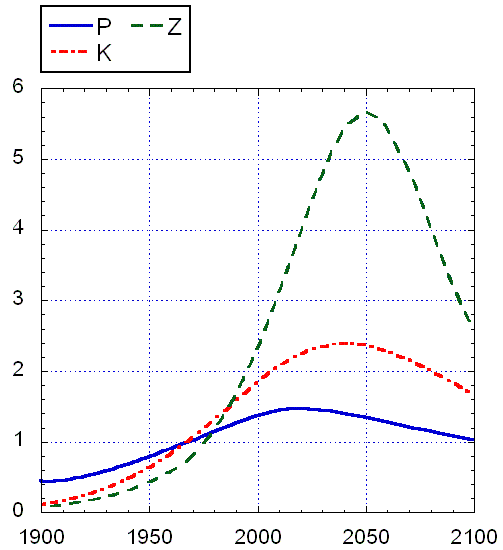
"в свободное плавание". В результате этого расчета получилась картина
развития, представленная на рис. 3.
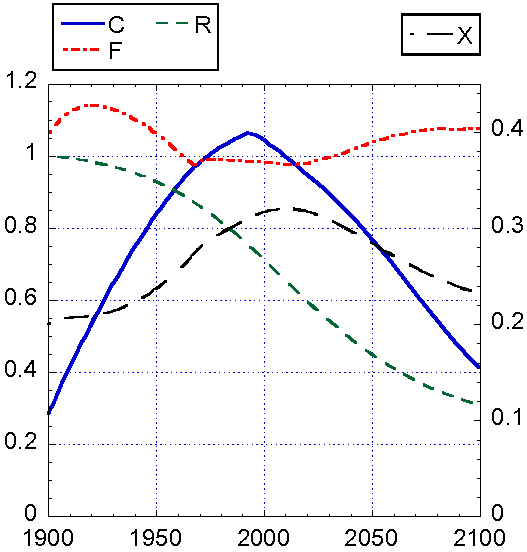
а)
б)
Рис. 3. Модель
Форрестера в первоначальном виде: кризис ввиду истощения ресурсов. Сначала падает
материальный уровень жизни, потом численность населения и капитал. Кризис наступает
примерно к 2020-30 г.г. Все величины представлены в условных единицах (т.е.
реально показаны не P, K, Z,
R а PP,K/PN, ZS,
RR соответственно). На рисунке б) графики представлены в
двух масштабах: один показан на левой оси ординат, второй – на правой оси.
Т.е., такие переменные, как уровень питания F, уровень жизни C и количество ресурсов R меняются от 0 до 1.2, а доля фондов в сельском
хозяйстве – от 0 до 0.45.
Видно, что после периода монотонного роста численность
населения с 2025 г. начинает уменьшаться, причем за 75 лет сокращается в
полтора раза, т.е. почти на 2 млрд. человек. Невозобновляемых природных
ресурсов к 2100 году остается меньше ⅓ начальных запасов (т.е. R0), уровень загрязнения к 2050 г. в несколько раз
превышает стандартный уровень ZN, а затем
начинает падать, что является следствием общего упадка промышленности и
сокращения численности населения. Материальный уровень жизни (или просто
уровень жизни) достигает максимума примерно в 2000 г., а затем падает.
Относительный уровень питания после 1970 г. незначительно уменьшается примерно
до 2015 г., затем вырастает из-за того, что падает население, хотя в целом
ведет себя весьма стабильно – это связано главным образом с заложенным в модель
механизмом распределения инвестиций по отраслям. Как только сокращаются
ресурсы, резко падает численность населения и промышленное производство.
Заметим, что о технологиях и их развитии Форрестер
ничего не говорит и в свою модель явным образом не вводит, пожалуй, это одно из
основных упущений его работы. Здесь позиция исследователя такова: зафиксируем
наши возможности (технологический уровень) на данном этапе и экстраполируем современные
тенденции в части потребления ресурсов, роста загрязнения, выбытия плодородных
земель, демографической динамики. Понятно, к чему такое приведет. С другой
стороны, тем самым Форрестер показал необходимость развития нужных технологий,
решающих тот круг задач, который рассматривается в модели.
Форрестер пробовал изменять по очереди параметры
модели в разумных пределах (такие, как запасы ресурсов, их потребление на душу
населения, продуктивность сельского хозяйства и т.п.); в результате несколько
менялись величина и время наступления спада, но общая картина упадка (типа
представленной на рис. 3) сохранилась.
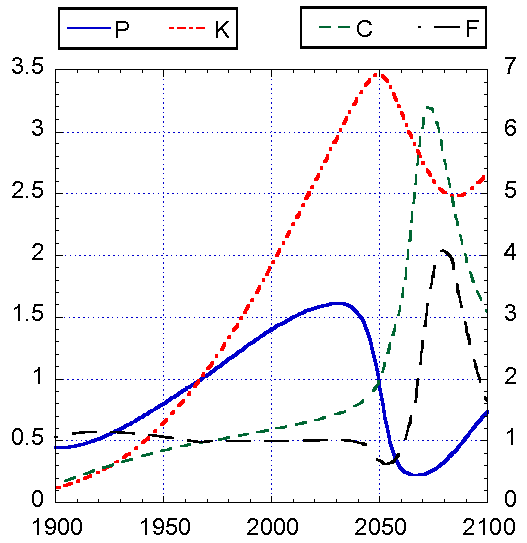
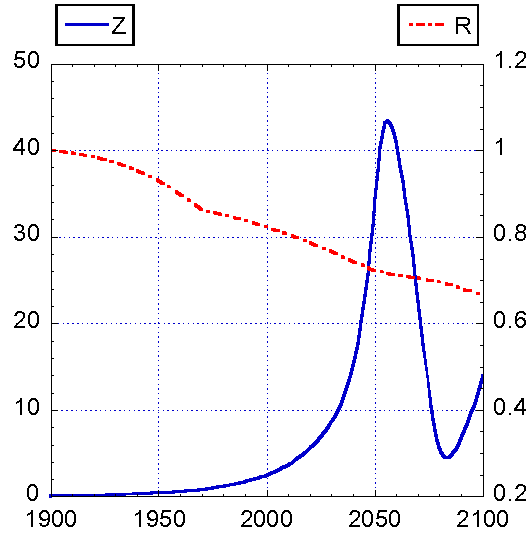
а)
б)
Рис. 4. Результаты
модели Форрестера в предположении о снижении в 1970 году скорости потребления
ресурсов в 4 раза, что могло быть вызвано, к примеру, экономией. Это вызывает
кризис загрязнений. Население резко уменьшается в несколько раз, также быстро
падают фонды, рост уровня питания и уровня жизни просто означает, что
оставшийся капитал используется остальной частью населения (такое может быть
справедливо в предположении, что все "вредные" производства находятся
в густонаселенных отсталых странах, а население, активно использующее капитал,
проживает в других странах).
В частности, на рис. 4 приведен расчет в случае,
когда в 1970 г. происходит уменьшение скорости потребления ресурсов в 4 раза,
т.е. в соответствующем уравнении (5) в правой части появляется коэффициент
0,25. Иначе говоря, предполагается, что технологии обеспечивают тот же уровень
жизни при меньшем истощении расходуемых невосполнимых ресурсов. Такое предположение
приводит к кризису, связанного с загрязнением. Из-за того, что потребление ресурсов
сократилось, их количество довольно велико для того, чтобы успели сильно
вырасти численность населения, материальный уровень жизни и фонды, что приводит
к резкому росту загрязнения. Максимум загрязнения к 2060 г. в 40 с лишним раз
превышает стандартный уровень. Население достигает своей максимальной
численности в 2030 г., а затем в течение 20-летнего периода резко падает до
шестой части этого наибольшего значения.
Необходимо сказать, что в задачу Дж. Форрестера
при построении модели не входило точное предсказание количественных
характеристик мировой системы, но скорее выявление общих качественных тенденций
динамики основных переменных, анализ чувствительности результатов по отношению
к различным заложенным в модель предположениям (сам Форрестер изначально считал
"Мир-2" просто рабочей моделью, помогающей лучше освоить предмет
системной динамики). Для достижения этой цели существенным является не столько
точное количественное определение всех параметров модели, сколько правильный
учет причинно-следственных связей системы.
Следует обратить внимание на то, что численные
результаты модели по населению вступают в противоречие с реальными данными о
том, как на самом деле росло население Земли за последние 30 лет. Так,
например, в 2000 г. реальная численность населения была чуть больше 6 млрд.
чел., в то время как модель "Мир-2" предсказывала 5 млрд. (см.
рис. 3). Это дает повод усомниться в численном, количественном
соответствии модели и реальности, но такая цель и не преследовалась автором
модели. Здесь куда важнее качественная сторона результатов, т.е. вид динамики
переменных, поскольку не вполне ясно в какой мере будут соотноситься модель и
реальность в будущем. Может оказаться, кроме того, что реальная динамика более
сжата или, наоборот, растянута по времени, т.е. условные годы – временные шаги
модели – могут соответствовать месяцам или, наоборот, десятилетиям в
реальности. Для целей глобальной модели и то, и другое не столь существенно по
сравнению с поведением переменных системы. И если удается это поведение хоть
как-то предсказать, можно считать, что модель строилась не зря. С этой точки
зрения вопрос о справедливости прогноза мировой динамики, данный в модели, до
сих пор остается открытым (еще не прошли сроки, позволяющие судить, оправдался
ли сделанный прогноз).
Результаты (в трактовке самого Форрестера и следующих
за ним исследователей) показали неизбежность кризиса, связанного с истощением
ресурсов и ростом загрязнения (рис. 3, 4), если сохранятся современные
тенденции и не будет предпринято никаких мер для обеспечения бескризисного
развития.
Единственный способ избежать кризиса, связанного, как
считал Форрестер, с экспоненциальным ростом, – переход к глобальному
равновесию, когда переменные системы выходят на стационарные значения и не
меняются. Подчеркнем, кризиса в рамках данной модели, а не в реальности.
Соответствие модели действительности – отдельная проблема, которая здесь в
полном объеме не рассматривается. Не касаясь вопроса, насколько вообще реальна
концепция "нулевого роста", приписываемая Форрестеру (а потом и всему
Римскому клубу), обратим внимание лишь на то, что осуществить такую
стабилизацию в рамках модели невозможно, поскольку ресурсы могут только убывать
и, следовательно, не могут стабилизироваться. Сам Форрестер это прекрасно
понимал и в своей книге писал, что без регенерации отходов и применения
заменителей истощение природных ресурсов рано или поздно вызовет кризис в
моделируемой системе [3].
Тем не менее, для остальных переменных можно добиться
выхода на стационар в течение рассматриваемого Форрестером промежутка времени
(с 1970 по 2100 г.г., после чего снова начинается деградация системы), что он и
продемонстрировал (см. рис. 5), видоизменив модель и введя следующие
ограничения (начиная с 1970 г.):
1)
темп потребления ресурсов уменьшен вчетверо по
сравнению с 1970г.
2)
генерация загрязнения уменьшена вдвое
3)
фондообразование уменьшена на 40%
4)
производство продуктов питания уменьшено на 20%
5)
темп рождаемости уменьшен на 30%
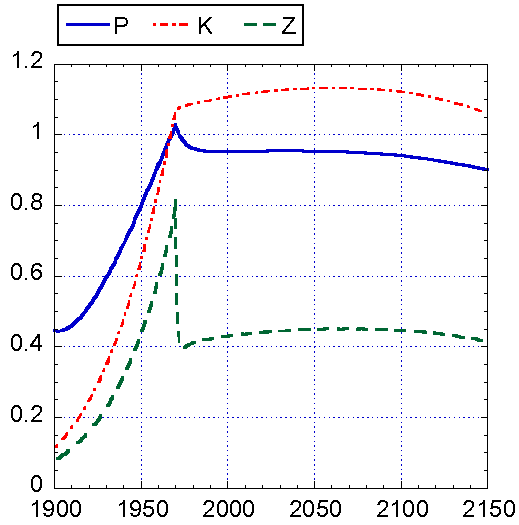
а)
б)
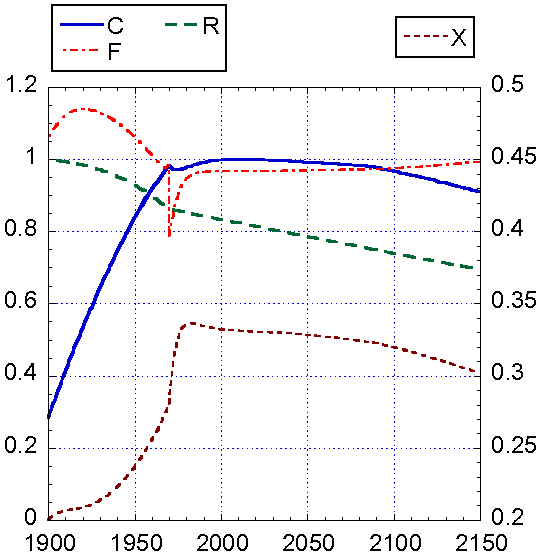
Рис. 5. Модель
Форрестера при условиях 1-5. Основные параметры стабилизируются до конца XXI века, после чего истощение ресурсов все-таки вызывает
кризис. Чтобы это проиллюстрировать, динамика переменных показана до
2150 г.
Общий вывод, который можно сделать на основании модели
"Мир-2", таков. Модель Форрестера – простая, ясная и полезная модель,
иллюстрирует интересный подход к моделированию сложных нелинейных систем.
Задуманная как учебный пример применения метода системной динамики, она стала
неким образцом для последующих работ, привлекла внимание к проблеме мировой
динамики, дала толчок к проведению других исследований, что привело к появлению
целого направления, получившего название глобального моделирования.
Вместе с тем нельзя не упомянуть и о недостатках модели: не учитывается много важных
факторов, явным минусом также является затрудненная идентификация модели,
некоторые зависимости носят непроверяемый фантастический характер, метод
построения модели не во всем адекватен, рекомендации Форрестера по
предотвращению кризиса нереалистичны.
После Форрестера разработка новой глобальной модели
была осуществлена его учеником Д. Медоузом, построившим более подробную
модель "Мир-3", являющуюся в некотором смысле продолжением работы
Форрестера. Результаты его исследований стали широко известны после выхода в
свет в 1972 г. книги "Пределы роста", которая стала первым
официальным докладом, подготовленного по инициативе Римского клуба. Как и
"Мир-2", модель Медоуза основывается на методе системной динамики, в
ней тоже 5 основных секторов (демографии, капитала, сельского хозяйства,
загрязнения, невозобновляемых ресурсов), только переменных не по одной на
каждый сектор, как было у Форрестера, а больше (за исключением загрязнения и
ресурсов). То есть была проведена дезагрегация переменных, кроме того были
сделаны и другие небольшие изменения-усложнения. Как и у Форрестера,
интегрирование системы уравнений проводилось на участке с 1900 г. по 2100 г. Расчеты
по модели показали, что ее поведение качественно очень похоже на поведение
модели "Мир-2". Оказалось, что здесь также неизбежна катастрофа по
причине истощения ресурсов и чрезмерного роста загрязнения.
К сожалению, несмотря на большую детализацию и
кажущуюся поэтому большую объективность по сравнению с моделью
Форрестера, модель "Мир-3", как нам представляется, является еще
более некорректной чем "Мир-2". Сам Медоуз признавал, что обладал
всего лишь 0,1% необходимой информации, остальное, по-видимому, он придумал
сам. Поэтому, наверное, некоторые зависимости (табличные функции) получились
просто неверными. Излишнее усложнение модели привело к тому, что ее
идентификация еще более затруднилась (ввиду того, что количество параметров
модели выросло почти в три раза). То, что результаты в целом совпали, связано
было именно с тем, что костяк модели остался прежним (т.е. такой же, как и в
модели Форрестера), главным образом, это касается уравнений для ресурсов и
загрязнения. А раз так, то и получается тот же эффект. Иначе говоря, достоинств
значительно не прибавилось, а вот минусов стало гораздо больше, поэтому усложнение,
проведенное Медоузом, представляется с этой точки зрения (полученные результаты
по отношению к затраченным усилиям) неоправданным.
По тому же пути усложнений и детализации моделей
двигались и последующие исследователи. Среди прочих работ по глобальному
моделированию выделяются работы Месаровича – Пестеля, Эрреры, Кайя – Судзуки,
Линнемана, Робертса, В.Леонтьева [2, 6], в Советском Союзе модели создавались
коллективами ВНИИСИ и ВЦ АН СССР.
В подавляющем большинстве случаев эти модели очень
"раздуты", количество переменных и параметров в них исчисляется
сотнями или даже тысячами. Такие сверхсложные модели неудовлетворительны: их
трудно верифицировать, поскольку жизнь не стоит на месте, а мы имеем дело с
необратимо развивающейся сложной системой; в них трудно понять, какие факторы
являются определяющими, а какие сопутствующими; есть опасность подмены
понимания вычислениями.
Успехи, достигнутые в этом направлении, более чем
скромны: только одному коллективу во главе с академиком Н.Н. Моисеевым
удалось произвести воздействие на массовое сознание и на политиков, сравнимое с
тем, какое произвели первые глобальные модели. Именно, речь идет о
моделировании "ядерной зимы". Результаты, полученные группой Н.Н.
Моисеева, оказали огромное влияние на нашу жизнь, да и продолжают оказывать,
продемонстрировав невозможность глобальной ядерной войны и, тем самым, очертив
границы дозволенного человеку. Других глобальных моделей, которые давали бы
такой же понятный и наглядный результат, по-видимому, не построено (либо они
широко не известны).
В 70-е и отчасти в 80-е г.г. XX века исследователи полагали, что достаточно
учесть как можно больше факторов, чтобы адекватно описать реальное поведение
мировой системы. Они не учли при этом трудности идентификации больших моделей,
поскольку в большинстве случаев известны не количественные характеристики
протекающих процессов, но лишь качественное поведение. "Глобальное
моделирование" показало серьезную ограниченность существующих методов
прогноза мировой динамики. Оказалось, что задачи, которые ставились при
построении большинства моделей, не могли быть решены применяемыми средствами в
силу общей ограниченности знания, носящей зачастую принципиальный характер.
Поэтому большинство проведенных исследований зашло в тупик и не оправдало
возлагавшихся на них надежд.
В исследованиях мировой динамики, видимо, стоит
опираться, прежде всего, на наглядные и простые базовые модели. К сожалению,
таких моделей не очень много и модель Форрестера – одна из них.
Глобальные модели и устойчивое развитие
Модели Форрестера и Медоуза привлекли внимание мировой
общественности и научного сообщества к глобальным проблемам. Хотя в истории
человечества не было недостатка в проблемах различной степени сложности и драматизма,
но никогда еще не намечалось эпохи, когда бы проблемы одна другой масштабнее и
труднее возникали почти в одно и то же время перед человечеством в целом, да
еще с такой категоричностью, которая ставит общество на грань гибели в случае
недостаточно точного и правильного ответа на этот исторический вызов. Впервые в
истории все человеческой общество оказалось перед выбором пути развития и,
пожалуй, самое необычное в сложившейся ситуации то, что "оценивать"
правильность выбора будут не столько сами люди, сколько окружающая их природная
среда и биосфера в целом. От этого выбора будет зависеть существование самого
человечества, на карту поставлена жизнь всей мировой цивилизации и человека как
вида.
Решение этих проблем требует решительного пересмотра
существовавшей до сих пор парадигмы развития мирового сообщества. По общему
признанию, человечеству необходим новый путь развития, поскольку существующий
завел в тупик, поэтому складывается впечатление, что многие нынешние мировоззренческие
ценности, ориентиры, порожденные и взятые человечеством у Западной цивилизации,
перестали быть адекватными при попытке справиться с растущими трудностями.
На роль такой новой парадигмы претендует идея
"устойчивого развития" (от англ. sustainable development, которое
буквально переводится как согласованное, самоподдерживающее развитие), впервые
озвученная в 1986г. Гру Харлем Брундтланд в докладе "Наше общее
будущее". Именно с этого момента в средствах массовой информации начал употребляться
термин "sustainable development", под которым стали понимать такую
модель развития, при которой достигается удовлетворение жизненных потребностей
нынешнего поколения людей без уменьшения такой возможности для будущих
поколений. Она получила поддержку в 1992г. на конференции ООН в Рио-де-Жанейро,
где была принята Декларация по окружающей среде и развитию – декларация необходимых
мер для проведения в жизнь стратегии устойчивого развития, основные идеи
которой таковы.
·
Люди имеют право на здоровую и плодотворную
жизнь в гармонии с природой.
·
Сегодняшнее развитие не должно осуществляться во
вред интересам развития и охране окружающей среды на благо нынешнего и будущих
поколений.
·
Для достижения устойчивого развития защита
окружающей среды должна составлять неотъемлемую часть процесса развития и не
может рассматриваться в отрыве от него.
·
Искоренение нищеты и неравенства в уровне жизни
в различных частях мира необходимо для обеспечения устойчивого роста и
удовлетворения потребностей большинства населения.
·
Государства сотрудничают в целях сохранения,
защиты и восстановления целостности экосистемы Земли. Развитые страны признают
ответственность, которую они несут в контексте международных усилий по обеспечению
устойчивого развития с учетом стресса, который создают их общества для
глобальной окружающей среды, технологий и финансовых ресурсов, которыми они
обладают.
·
Государства должны ограничить и ликвидировать
нежизнеспособные модели производства и потребления и поощрять соответствующую
демографическую политику.
·
Экологические вопросы решаются наиболее
эффективным образом при участии всех заинтересованных граждан. Государства
развивают и поощряют информированность и участие населения путем предоставления
широкого доступа к экологической информации.
·
Государства должны сотрудничать в деле создания
открытой международной экономической системы, которая приведет к экономическому
росту и устойчивому развитию во всех странах.
·
Устойчивое развитие требует более глубокого
научного понимания проблем. Государствам следует делиться знаниями и новыми
технологиями для достижения целей устойчивости.
·
Война неизбежно оказывает разрушительное
воздействие на процесс устойчивого развития. Поэтому государства должны уважать
международное право, обеспечивающее защиту окружающей среды во время вооруженных
конфликтов, и должны сотрудничать в деле его дальнейшего развития.
Несмотря на принятие концепции устойчивого развития,
тем не менее, нельзя не отметить, что "... анализ даже научных публикаций
показывает, что ясности в понимании самого понятия не прибавилось. Можно
сказать, что идет ожесточенная борьба за выгодное каждому участнику этих
научных и не очень научных дискуссий понимание этого термина. Суть проблемы
заключается в том, что за этими двумя словами скрываются колоссальные
материальные и финансовые интересы, которые и формируют различные в своих целях
концепции устойчивого развития. В то же время существует ядро идей, которое признается
всеми участвующими в общественном дискурсе сторонами, и которое было бы правильно
называть парадигмой устойчивого развития" [7, с. 7].
Одним из последствий таких дискуссий стало принятие
положения о том, что каждое государство должно разрабатывать собственную
национальную концепцию устойчивого развития и стратегии перехода к нему.
Наибольший интерес представляет возможная национальная концепция США (на
основании материалов Президентского совета по устойчивому развитию), поскольку
это пока единственная на сегодняшний день сверхдержава, во многом определяющая
будущее мировой цивилизации. Следовательно, любая стратегическая инициатива,
исходящая из Вашингтона, должна рассматриваться предельно внимательно.
Если кратко суммировать основные положения данной
концепции и "Повестки на XXI
век", то получатся следующие условия устойчивого развития:
1.
скорейшая стабилизация численности населения планеты;
2.
отказ от излишеств в потреблении, т.е. его сокращение;
3.
минимизация удельных расходов сырья и энергии во всех
видах производства и замена невозобновимого сырья на возобновимое везде, где
это возможно;
4.
недопущение роста загрязнений, переход к более чистому
промышленному производству;
5.
широкое вовлечение науки в решение вставших проблем
(создание необходимых технологий).
Сравнение условий 1, 3, 4 с условиями глобального
равновесия в модели Форрестера показывает, что, в общем и целом, это
совпадающие понятия и в модели Форрестера устойчивое развитие может быть
реализовано в виде стационарного (или близкого к нему, если вдруг окажется, что
технологии будущего позволят экономический рост при стабилизации остальных
переменных) решения. По упоминавшимся ранее причинам в классической модели
такой режим оказывается невозможным, поэтому необходимо модифицирование модели
Форрестера.
Одна из таких модификаций была осуществлена в работах
коллектива исследователей под руководством В.А. Егорова [5, 6]. В своих
исследованиях они занимались вопросом введения управляющих воздействий в
глобальные модели "Мир-2" и "Мир-3" с целью предотвращения
глобального кризиса. Для этого предлагается воздействовать на такие факторы как
материальный уровень жизни C, относительное
загрязнение ZS, уровень питания F путем распределения капиталовложений в предположении (при
условии того), что:
1) разработана и внедрена в промышленность технология
утилизации и/или восстановления ресурсов;
2) создана промышленная отрасль по искусственной
очистке загрязнения;
3) можно изменять инвестиции в сельскохозяйственные
фонды.
Тогда можно направлять капитал во вновь созданные
отрасли и на изменение доли фондов в сельском хозяйстве. На языке уравнений это
означает следующее.
В правую часть уравнения для ресурсов (5) добавляется
слагаемое 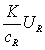 , где UR –
доля капитала, идущая на восстановление ресурсов, cR – стоимость восстановления единицы ресурса, т.е.: , где UR –
доля капитала, идущая на восстановление ресурсов, cR – стоимость восстановления единицы ресурса, т.е.:
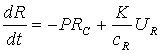 (6) (6)
В правую часть уравнения для загрязнения (4)
добавляется отрицательный член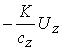 , где UZ –
доля капитала, направляемая на борьбу с загрязнением, cZ – стоимость очистки единицы загрязнения, т.е.: , где UZ –
доля капитала, направляемая на борьбу с загрязнением, cZ – стоимость очистки единицы загрязнения, т.е.:
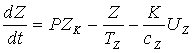 . (7) . (7)
В правую часть уравнения для доли сельского хозяйства
(3) вводится управляющее воздействие в виде множителя (1+UX),
тогда:
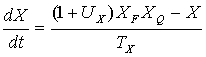 . (8) . (8)
Кроме того, материальный уровень жизни вычисляется по
новой формуле, учитывающей введенное распределение капитала:
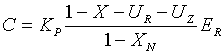 . (9) . (9)
Указанные величины UR, UZ и UX представляют собой функции времени и, будучи определены,
задают некоторый сценарий развития системы. Далее решалась по существу задача
оптимального управления: задавался критерий и искались управления, доставляющие
максимум выбранного критерия. В.А. Егоров с коллегами показал, что
подбором критерия и приближенным решением получающейся вариационной задачи
можно добиться динамики, при которой в модели не будет "кризиса по
Форрестеру" на достаточно продолжительном временном интервале (до конца XXI века).
К сожалению, наряду с достоинствами, в работах В.А.
Егорова и его группы есть ряд положений, вызывающих серьезные вопросы.
Перечислим их.
Прежде всего, вызывает сомнения возможность постановки
задачи оптимального управления для мировой системы. Очень точно управлять
можно, зная какие факторы и процессы главные, а какие несущественны не только в
настоящий момент, но и в будущем, иначе может оказаться, что программа
управления не доставит максимум критерия, а наоборот ухудшит ситуацию. К
сожалению, в силу быстрых изменений в мире подобное управление не может
гарантировать устойчивость системы.
Затем, не вполне понятно, зачем вводить управление для
доли сельского хозяйства. Какая именно проблема решается таким способом, если
основная проблема в модели Форрестера – исчерпание ресурсов и большой рост
загрязнений? Подобная модификация представляется излишней.
Ну, и, наконец, последнее замечание. Большие сомнения
вызывают проделанные расчеты и полученные на их основании результаты, так как
выполнены они были не совсем для модели Форрестера, поскольку В.А. Егоров
вместо относительного загрязнения использовал понятие удельного, т.е.
отнесенного на численность населения: 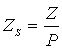 . Это предположение не очень логично: получается, что
загрязнение делится на всех жителей, и чем больше население, тем меньшее
влияние оказывает загрязнение на систему (поскольку оно действует только через
переменную ZS). У самого Форрестера
в модели другая логика: загрязнение влияет на систему как абсолютная, а не
удельная величина, но измерять его можно в относительных единицах, тем самым
приводя все табличные функции к унифицированному виду и более или менее единому
масштабу. . Это предположение не очень логично: получается, что
загрязнение делится на всех жителей, и чем больше население, тем меньшее
влияние оказывает загрязнение на систему (поскольку оно действует только через
переменную ZS). У самого Форрестера
в модели другая логика: загрязнение влияет на систему как абсолютная, а не
удельная величина, но измерять его можно в относительных единицах, тем самым
приводя все табличные функции к унифицированному виду и более или менее единому
масштабу.
От этого нововведения меняются (и весьма заметно)
численные результаты модели. Так, например, максимум загрязнения в модели
Форрестера достигает примерно 20·109, а при такой модификации около
12.5·109 (условных единиц), т.е. отличие более чем в полтора раза.
Также по этой причине этими исследователями были получены неверные результаты
при исследовании стационарных решений модифицированной модели.
Из современных исследователей модификациями моделей
"Мир-2" и "Мир-3" занимается в Институте
социально-политических исследований группа под руководством В.М. Матросова
[8, 9]. Ими была осуществлена серьезная модификация модели Форрестера в
трактовке В.А. Егорова. В частности, были введены такие факторы как биомасса
растительности Земли, научно-технический прогресс, политическая
напряженность. В отличие от В.А. Егорова, они ничего не оптимизировали,
а включили управления в систему уравнений, жестко задав закон их изменения и
связав с прочими факторами. В рамках полученной модели удалось найти
стационарные решения и показать их устойчивость.
Здесь минусом является сложность модификаций, заслоняющая
существо дела. Тем более что нет общепринятой точки зрения на взаимосвязь таких
величин, как научно-технический прогресс и политическая напряженность с другими
переменными. А существо, при всех модификациях, то же, что и в модели
Форрестера: без "планетосбергающих" технологий кризис неизбежен.
Плюсом же является отказ от оптимизации, т.е. в
каком-то смысле упрощение концепции управления посредством обычно
функциональной обратной связи (носящей "подстраиваемый" характер),
что при надлежащем выборе функции может придать структурную устойчивость
мировой системы, а также при возникновении новых факторов развития гарантировать
минимальное ухудшение, возникающее при этом. Эти соображения позволяют произвести
еще одну модификацию модели Форрестера (более простую и, как кажется, более
корректную, чем предыдущие).
Модифицированная модель Форрестера. Исследование стационарных
решений
Как и В.А. Егоров, будем считать, что часть
капитала направляется на восстановление ресурсов (или их вторичную переработку)
и на борьбу с загрязнением. Соответственно вместо уравнений (4) и (5) имеем (7)
и (6) соответственно. В отличие от работ В.А. Егорова, не проводилось
модификации сельскохозяйственного блока, так как это не влияет на существование
стационарных решений и потому на выбранном уровне описания является излишним,
т.е. уравнение (3) остается в силе. Материальный уровень жизни вычисляется по
формуле (9).
Остальные определения, соотношения и уравнения модели
Форрестера сохраняются, поэтому при Ui ≡ 0, i = R, Z данная модель совпадает с моделью
(1)–(5). Функции UR, UZ
в отличие от упоминавшихся работ В.А. Егорова и его соавторов не являются
произвольными функциями времени, но определяются через основные переменные
модели. Поскольку они по своему смыслу подобны X, считалось,
что для них справедливы по аналогии с (3) уравнения:
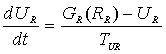 , (10) , (10)
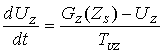 , (11) , (11)
где GR, GZ – инвестиции (с точностью до множителей TUR, TUZ) в соответствующие
отрасли индустрии по восстановлению ресурсов и очистке загрязнений, TUR, TUZ – время
выбытия части фондов в данных отраслях (отражая тот факт, что фонды не
создаются и не исчезают мгновенно). Они считались константами одного порядка с TX, т.е. 10-15 лет. Предполагалось, что новые отрасли
не созданы до 2000 г., т.е. при t < t' = 2000 GR = 0, GZ
= 0.
Немаловажным является вопрос о "качестве"
получающихся стационаров, поэтому к искомым стационарным решениям предъявлялся
ряд "желательных" требований: 1) Z ≤ Zmax; 2) R ≥ Rmin; 3) C ≥ Cmin; 4) F ≥ Fmin,
где Zmax – максимально допустимый уровень Z, а Rmin, Cmin, Fmin –
минимально допустимые уровни R, C, F. Наиболее типичные значения, использовавшиеся при расчетах,
такие: Rmin = 0.5R0
(где R0 = R(1900) – начальный запас
ресурсов), Cmin = 0.5, Fmin = 0.9, (ZS)max = 10. Выбор подобных
значений обусловлен прежде всего тем, что при них указанные величины через
табличные функции начинают качественно влиять на остальные переменные и
динамику системы в целом.
Наша задача состоит в том, чтобы указать вид
функциональной зависимости GR(R) и GZ(Z), гарантирующих нужные
стационары модифицированной системы, т.е. удовлетворяющие перечисленным выше
требованиям. Поэтому сначала было исследовано, при каких значениях параметров cR, cZ, GR, GZ (или, что
то же, UR, UZ)
стационарные решения вообще существуют (см. рис. 6).
Вещественные части всех собственных значений системы,
линеаризованной в окрестности каждого из найденных решений, оказались
отрицательными, из чего можно сделать вывод об устойчивости всех найденных
стационаров.
_CR=0.3_CZ=0.4.GIF)
Рис. 6. Область
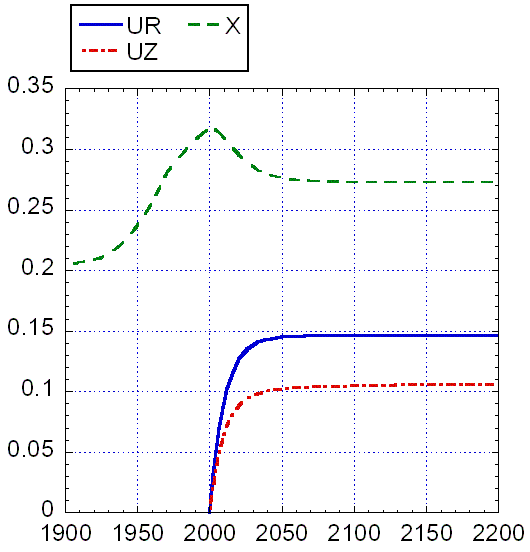
допустимых значений (UR, UZ)
при cR = 0.3, cZ = 0.4.
Сплошная линия соответствует границе области допустимых значений, на ней
стационары перестают существовать. На левой части границы (от UR = 0
до UR = 0.115) Z ≤ 0, на правой (от UR = 0.115
до UR = 0.164 ) R ≥ 1 (в условных единицах по отношению
к R0, т.е. фактически RR). Левый пунктир (UR = 0.136) соответствует C = 0.5,
правый (UR = 0.15) – Z = 10 (точнее говоря, при UR > 0.15
Z > 10,
но само значение UR = 0.15 области принадлежит). Таким образом,
"хорошие" решения находятся в области, ограниченной двумя пунктирами,
осью UZ = 0 и сплошной кривой.
_CR=0.3_CZ=0.4.GIF)
Рис. 7.
Зависимость UR* от R* при
фиксированном UZ*. Заметно, что кривая имеет две точки излома, что
связано, по всей видимости, с характером зависимости ER(R) (см.
рис. 2). Как видно, с ростом UZ* кривая UR*(R*)
смещается вправо.
_CR=0.3_CZ=0.4.GIF)
Рис. 8.
Зависимость UZ* от Z* при
фиксированном UR*, как видно, с ростом UR* сдвигается вправо. При этом зависимость носит
практически линейный характер. На кривой "Envelope" выполняется условие R = 1, таким образом, она ограничивает допустимые
"хорошие" решения. Также видно, что данная кривая по характеру
поведения близка к гиперболе, и ее можно приблизить, например, следующим образом:
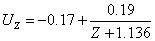 . .
Как следует из анализа картины стационаров,
стационарное значение UR* должно находиться
в диапазоне значений [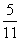 сR; 0.5cR], при этом UR* с ростом R*
(при фиксированном UZ*) также
растет (см. рис. 7), поэтому имеет смысл взять в качестве GR(R) убывающую (чтобы решение заведомо существовало по теореме
Больцано–Коши и вычислительный процесс сходился к нему) функцию, на отрезке
[0.5, 1] попадающую в указанный выше достаточно узкий интервал. Таким свойством
обладают гиперболы и показательные функции, поэтому можно положить GR(R) = α + β∙exp(-RR),
при этом α ≈ (0.45±0.05)cR, β ≈ (0.05±0.05)cR. Аналогично, UZ*
с ростом Z* (при фиксированном UR*) убывает практически линейным
образом (см. рис. 8), поэтому GZ(Z) удобно взять возрастающей и линейной, поскольку больше
никаких ограничений нет: GZ(Z) = γZ, при этом γ< 4cZ/cR. сR; 0.5cR], при этом UR* с ростом R*
(при фиксированном UZ*) также
растет (см. рис. 7), поэтому имеет смысл взять в качестве GR(R) убывающую (чтобы решение заведомо существовало по теореме
Больцано–Коши и вычислительный процесс сходился к нему) функцию, на отрезке
[0.5, 1] попадающую в указанный выше достаточно узкий интервал. Таким свойством
обладают гиперболы и показательные функции, поэтому можно положить GR(R) = α + β∙exp(-RR),
при этом α ≈ (0.45±0.05)cR, β ≈ (0.05±0.05)cR. Аналогично, UZ*
с ростом Z* (при фиксированном UR*) убывает практически линейным
образом (см. рис. 8), поэтому GZ(Z) удобно взять возрастающей и линейной, поскольку больше
никаких ограничений нет: GZ(Z) = γZ, при этом γ< 4cZ/cR.
Интегрирование динамической системы велось с
1900 г. по 2200 г. Считалось, что восстановление ресурсов не заходит
столь далеко, что дает их больше, чем природа, т.е. выполнено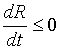 , и, следовательно, R(t) < R(t') при t > t' = 2000, что необходимо учитывать
при настройке параметров α, β, γ. Расчеты показали, что существуют такие параметры α, β, γ, при
которых модель допускает стационарные решения (см. рис. 9–12), при этом выход
на стационарный режим успевает произойти до 2150г. , и, следовательно, R(t) < R(t') при t > t' = 2000, что необходимо учитывать
при настройке параметров α, β, γ. Расчеты показали, что существуют такие параметры α, β, γ, при
которых модель допускает стационарные решения (см. рис. 9–12), при этом выход
на стационарный режим успевает произойти до 2150г.
Эти результаты были получены при cR = 0.3, cZ = 0.4 (поскольку эти значения фигурировали
в работах В.А. Егорова). Было проведено исследование и при других коэффициентах
(рис. 10, 11). Как видно, более существенное влияние оказывает подорожание
восстановления ресурсов, чем очистки загрязнения.
Также выяснилось, что стационары существуют не при
всех значениях данных параметров, поскольку есть ограничение сверху, налагаемое
коэффициентом cR: при cR > 0.7 стационарных
режимов со сформулированными желательными требованиями нет (при t' = 2000). Коэффициент сZ практически не влияет на
данную качественную картину (сравн. рис. 9 и 11).
Анализ рис. 6 приводит к любопытному выводу:
существуют "хорошие" стационарные решения при GZ =
0, т.е. в отсутствие очистки загрязнений. Этот эффект справедлив не при всех
значениях параметров, так, при малых значениях коэффициента cR (меньше 0.04) без очистки загрязнений нужных
стационаров нет.
Рис. 12 иллюстрирует влияние времени t' на картинку стационарных решений, видно, что Z* выше, а R* ниже, чем
на рис. 9, что и понятно, поскольку мы условились считать R* < R(t'). Следовательно, должен
существовать "критический" момент t'cr,
после которого "хорошие" стационары получить невозможно никакими
усилиями. Простейшие оценки (исходя из минимально возможного значения R* при C* = 0.5 и динамики R(t) в первоначальной, немодифицированной,
модели Форрестера – см. рис. 3) дают в качестве такого момента
2038-39 годы. А если еще учесть время на создание новых фондов, которое примерно
соответствует TUR и TUZ, т.е. 10 лет, то получим t'cr ≈ 2030 г.
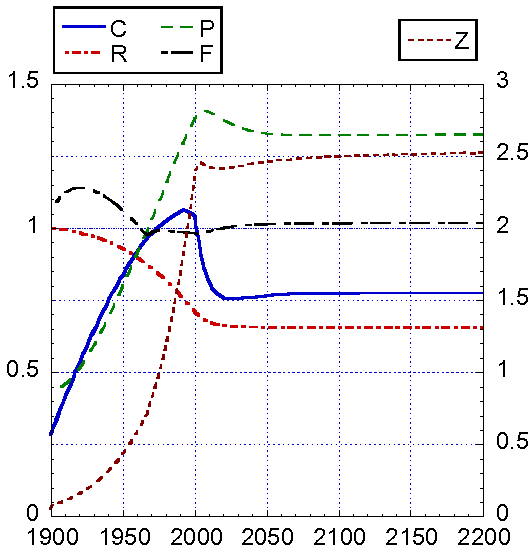
а)
б)
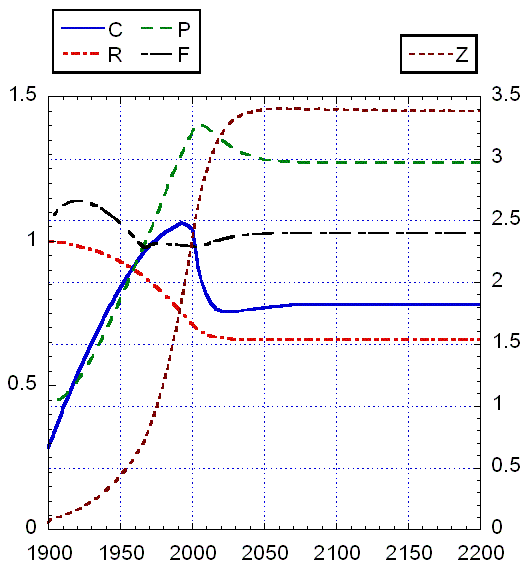
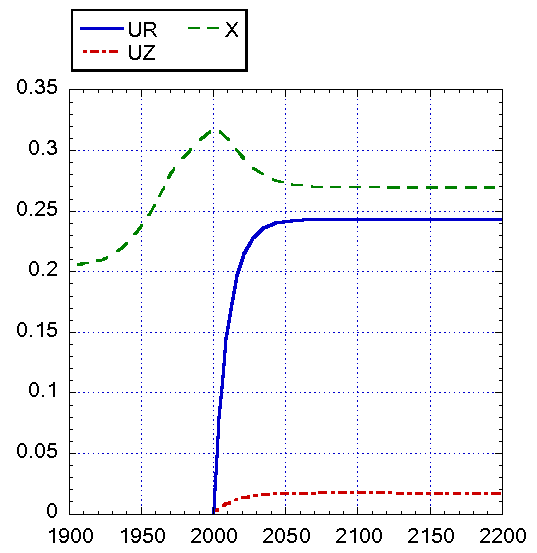
Рис. 9. Результаты
интегрирования модифицированной модели Форрестера при cR = 0.3, cZ = 0.4: а)
основные характеристики, б) доли фондов в новых отраслях и с/х. Начало
функционирования новых отраслей 2000 г. Время запаздывания TUR = TUZ = 10
лет. Параметры инвестиций в новые отрасли: a=0.135, β=0.018,
γ=0.04. На рисунке а) графики
представлены в двух масштабах: один показан слева от картинки, второй – справа.
а)
б)
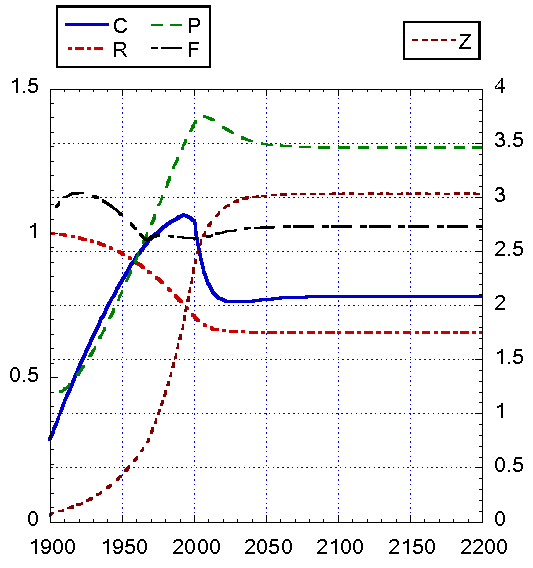
Рис. 10.
Результаты интегрирования модифицированной динамической системы при cR = 0.5, cZ = 0.4.
Начало функционирования новых отраслей 2000 г. Время запаздывания TUR = TUZ = 10
лет. Функции инвестиций в новые отрасли GR = 0.238 + 0.01exp(-RR), GZ = 0.005·ZS. Видно, что стационарное значение Z выше по
сравнению с предыдущим рисунком. Стационарное значение UR* близко к 0.25, т.е. 0.5cR, UZ* близко к нулю.
а)
б)
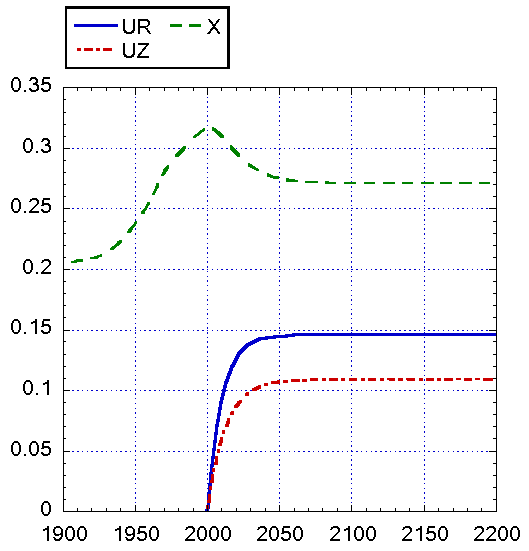
Рис. 11.
Результаты интегрирования динамической системы (1), (2), (3), (6), (7), (10),
(11) при cR = 0.3, cZ = 0.8.
Начало функционирования новых отраслей t' = 2000 г. Время запаздывания TUR = TUZ = 10
лет. Функции инвестиций в новые отрасли GR
= 0.137 + 0.017exp(-RR), GZ = 0.036∙ZS. По сравнению с рис. 9 стационарное значение
загрязнения выше, в остальном динамика системы близка к представленной на
рис. 9.
а)
б)
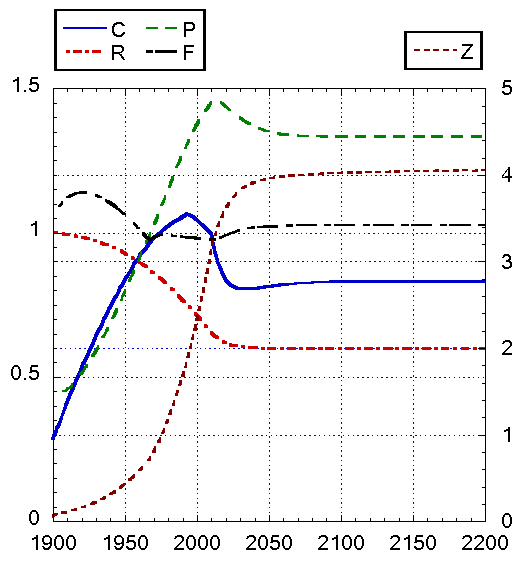
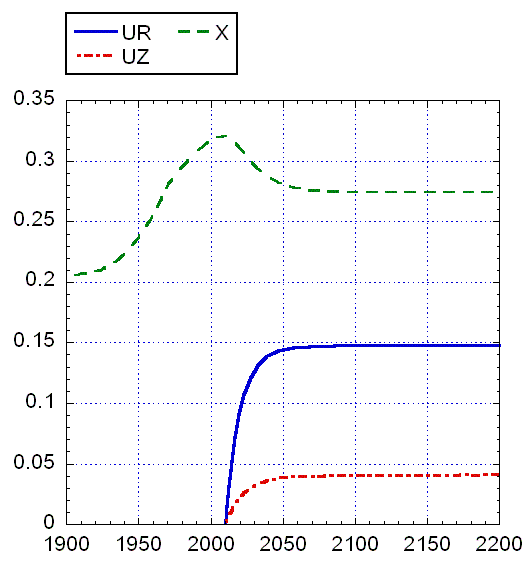
Рис. 12. Результаты интегрирования модифицированной
динамической системы при cR = 0.3, cZ = 0.4. Начало
функционирования новых отраслей t' = 2010 г. Время запаздывания TUR = TUZ = 10
лет. Функции инвестиций в новые отрасли GR = 0.141 + 0.011exp(-RR), GZ = 0.01∙ZS. Стационарное значение Z* выше по сравнению с предыдущими рисунками, UR* примерно как на рис. 9, 11, а UZ* – ниже.
Заключение
Проведенные исследования показали, что решающее
значение для достижения стационарного режима имеет введение восстановления
ресурсов и искусственной очистки загрязнения. Как показывают расчеты, не всегда
достаточно введения одного лишь восстановления ресурсов (без которого просто не
может быть стационарных режимов); чтобы достичь глобального равновесия, нужна
непременно очистка загрязнений. Также выяснено, в каких пределах должны
находиться параметры вновь введенных факторов, чтобы обеспечить выход системы
на указанное равновесие.
Таким образом, установлены минимальные требования к
существованию стационарных решений модифицированной модели мировой динамики,
что может позволить применить их на практике, поскольку, чем меньше требований
предъявляет теория, тем проще осуществить эти требования на практике.
В заключение считаю необходимым отметить, что появление этой работы во
многом связано с инициативой профессора В.А. Егорова вернуться к анализу
классических моделей мировой динамики и с этих позиций осмыслить проблемы
устойчивого развития.
Литература
1. Печчеи А.
Человеческие качества. – М.: Прогресс, 1980.
2. О проектах "Римского
клуба". / Препринт комитета по системному анализу при Президиуме АН СССР.
– М.: ВНИИСИ, 1977.
3. Форрестер Дж.
Мировая динамика. – М.: Наука, 1978.
4. Форрестер Дж. Основы кибернетики предприятия. – М.: Прогресс, 1971.
5. Геловани В.А., Егоров
В.А., Митрофанов В.Б., Пионтковский А.А. Решение одной задачи управления
для глобальной динамической модели Форрестера. – препринт ИПМ АН СССР, 1974,
№56.
6. Егоров В.А.,
Каллистов Ю.Н., Митрофанов В.Б., Пионтковский А.А. Математические модели
глобального развития. – Л.: Гидрометеоиздат, 1980.
7. Левашов В.К. Устойчивое развитие общества: парадигма, модели,
стратегия. – М.: Academia,
2001.
8. В.М. Матросов,
И.В. Матросов Глобальное моделирование с учетом динамики биомассы и
сценарии устойчивого развития. / Новая парадигма развития России (Комплексные
исследования проблем устойчивого развития). – М.: Academia, МГУК, 1999, с. 18-24.
9. К.В. Матросова
Устойчивое развитие в модифицированной математической модели "Мировая
динамика". / Новая парадигма развития России (Комплексные исследования
проблем устойчивого развития). – М.: Academia, МГУК, 1999, с. 344-353.
|