Low
Energy Trajectories for the Moon-to-Earth Space Flight
V. V. Ivashkin
Keldysh Institute of Applied Mathematics, Miusskaya Sq. 4,
Abstract
The Moon-to-Earth low energy trajectories of “detour” type are found and studied in frame of the Moon-Earth-Sun-particle system. These trajectories use a passive flight to the Earth from an initial elliptic selenocentric orbit with a high aposelenium and differ from usual ones of direct flight to the Earth using an initial hyperbolic selenocentric orbit. A numerical analysis and a qualitative theoretical one are performed for these trajectories. The Earth perturbation increases the particle selenocentric energy from a negative value first to zero and then to a positive one and therefore leads to a passive escape of the particle motion from the Moon attraction near the translunar libration point L2. This results in the particle flight to a distance of about 1.5 million km from the Earth where the Sun gravitation decreases the particle orbit perigee distance to a small value that leads to the particle approach the Earth vicinity in about 100 days of the flight. A set of the Moon-to-Earth “detour” trajectories for the flight to the geocentric altitude of
Key Words: lunar trajectories, Moon-Earth flight, gravitational escape, gravitational perturbations,
“detour” lunar flights
1. Introduction
Investigations of space trajectories for flights from the near-Moon vicinity to the Earth are important for both Celestial Mechanics and Astronautics. Usual trajectories (see, e.g., Egorov and Gusev 1980) for the Moon-to-Earth direct space flights within the Earth’s sphere of influence with respect to the Sun are well studied. In this case, perturbations caused by the Sun are small, and the model of the restricted three-body problem (Moon-Earth with a particle of negligible mass) is used in fact. Trajectories of this type were used for space flights from the Moon in both the

Figure 1. The XY geocentric view for the Moon-to-Earth trajectory of detour flight.
2. Moon-to-Earth detour trajectories
2.1 Algorithm of Calculations
As a result of the analysis and with taking into account the experience of the Earth-to-Moon trajectories studies (Ivashkin 2002, 2003, 2004a), a numerical algorithm has been developed that has allowed us to find a family of detour trajectories for space flights to the Earth from elliptic orbits of the lunar satellite. These trajectories correspond to the spacecraft start from both the Moon's surface and the low orbit of the lunar satellite for several positions of the Moon on its orbit. The spacecraft trajectories have been determined by integration using the method described in (Stepan’yants and L’vov 2000) of the equations for the particle motion. These equations are written in the Cartesian nonrotating geocentric-equatorial coordinate system OXYZ in the attraction field of the Earth (with taking into account its main harmonic c20), the Moon, and the Sun with the high-precision determination of the Moon and Sun coordinates, which is based on the DE403 JPL ephemerides. The particle motion in the selenocentric coordinate system MXYZ is also determined.
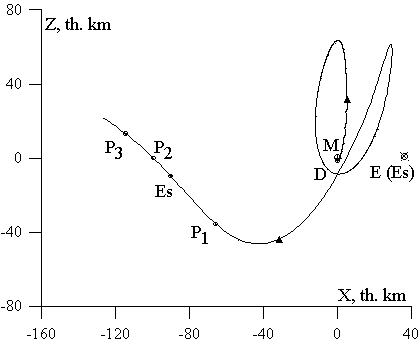
Figure 2. The XZ selenocentric view for the Moon-to-Earth trajectory of detour type at initial part of the flight.
2.2 Some Numerical Characteristics of the Moon-to-Earth Detour Flights
Characteristics of a typical detour trajectory are presented in Figures 1-3. The solid curve in Figure 1 presents geocentric motion of a spacecraft, and the dot-and-dash line shows the lunar orbit M. At the point D, the spacecraft flies away from the Moon on May 11, 2001 (for the position of the Moon near the apogee), from the perilune of an initial elliptic orbit with the perilune altitude Hp0 =
![]() (1)
(1)
occur. In Eqn. 1 V and r are the selenocentric velocity of the particle and its distance from the Moon, respectively, ![]() is semimajor axis of the particle orbit, and mM (» 4902 km3 s-2) is the lunar gravitational parameter. At the point P1 in the space flight time Dt » 19 days, the energy is Es » - 0.031 km3 s-2,
is semimajor axis of the particle orbit, and mM (» 4902 km3 s-2) is the lunar gravitational parameter. At the point P1 in the space flight time Dt » 19 days, the energy is Es » - 0.031 km3 s-2, ![]() » 79×103 km, and r » 76×103 km. At the point Es for Dt » 20.6 days and r » 91.85×103 km in the region of the translunar libration point L2, there is the escape from the lunar attraction, i.e., Es = 0 here, and the orbit is parabolic with the zero velocity “at infinity”, V¥ = 0. Further, the particle moves from the Moon along a hyperbola. At the point P2 for Dt » 21.1 days and r » 101×103 km, the energy is Es » 0.011 km2 s-2, V¥ =
» 79×103 km, and r » 76×103 km. At the point Es for Dt » 20.6 days and r » 91.85×103 km in the region of the translunar libration point L2, there is the escape from the lunar attraction, i.e., Es = 0 here, and the orbit is parabolic with the zero velocity “at infinity”, V¥ = 0. Further, the particle moves from the Moon along a hyperbola. At the point P2 for Dt » 21.1 days and r » 101×103 km, the energy is Es » 0.011 km2 s-2, V¥ =
Figures 2 and 3 show the evolution of the spacecraft detour motion with respect to the Moon at the initial part of the space flight where there is the escape from the lunar attraction. Figure 2 gives selenocentric trajectory in the XZ plane. The point E (Es) determines the direction to the Earth at the moment of the escape from the lunar gravitational attraction. Figure 3 gives the selenocentric energy constant 2Es versus the time for the initial part D P1 Es P2 P3 of the motion with escape from the lunar attraction. Here and below, on Figure 5, the time t is counted off from the Julian date 2451898.5, that is 20.12.2000.0.
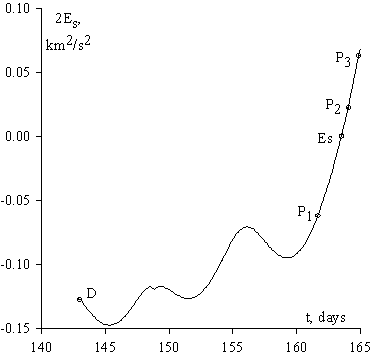
Figure 3. Selenocentric energy versus the time for initial part of the Moon-to-Earth detour flight with escape from the lunar attraction.
The initial (at the point D) velocity of spacecraft is ![]() »
» ![]() 1633 m s-1 using a velocity impulse (a high thrust), the velocity increment is DV0 »
1633 m s-1 using a velocity impulse (a high thrust), the velocity increment is DV0 » ![]() of about
of about
For a case when spacecraft leaves the Moon surface, the detour trajectory (with a0 =
If initial semimajor axis a0 is less, the decreasing dV0 of the velocity impulse for the detour flight relative to the direct one is more. Figure 4 gives this deceasing dV0 versus the initial semimajor axis a0 of detour flight for two values of the velocity at “infinity” V¥=Vinf for direct flight: V¥=0.8 km/s (approximately, for optimal direct flight from the Moon apogee) and V¥=0.9 km/s (approximately, for optimal direct flight from the Moon perigee). The lines H0=100 km correspond to the spacecraft start from the satellite orbit perilune with altitude H0=100 km. The lines H0=0 correspond to the spacecraft start from the Moon surface. Possible values of the initial semimajor axis a0 for the detour flight are given below, in item 3.
Remark. Of course, these “detour” trajectories can be applied for the flight from a low-Moon orbit using an electric-jet engine with a low thrust, too.

Figure 4. Decreasing of the velocity impulse for the Moon-Earth detour flight relative to the direct flight depending on the initial semimajor axis.
3. Earth’s gravity effect on the particle escape
We now qualitatively analyze the gravitational effects on the formation of the detour trajectory. First, we estimate an increase DEs = - Es0 of selenocentric energy (1) from the negative value Es0 for the initial elliptic orbit to the zero energy which can be caused by the Earth gravity during the particle selenocentric motion on the arc D Es from the initial state D to the escape point Es. On the base of the orbit evolution theory (Lidov 1961, 1962) and assuming that the particle’s selenocentric orbit eccentricity is es » 1, the mean energy is Es » - DEs/2, and taking into account the change in the Moon-Earth direction, we obtain (Ivashkin 2002, 2003, 2004a):
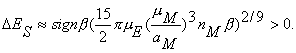 (2)
(2)
In Eqn. 2: value ![]() is the Earth's gravitational parameter, value
is the Earth's gravitational parameter, value ![]() is the semimajor axis of the Moon's orbit, value
is the semimajor axis of the Moon's orbit, value ![]() is the angular velocity of its orbital motion,
is the angular velocity of its orbital motion,
![]() (3)
(3)
here angle g is the slope of the radius vector rB for an external body (for the Earth, in this case) to the plane of the particle orbit, and a is the angle between the projection of the radius vector rB onto this plane and the direction to the orbit perilune. For DEs >0, it is necessary to have sin2a>0, 0<a<p/2 or p<a<3p/2. Estimation by Eqns 2-3 gives DEs= - Es0 » 0.096 km2 s-2, a0 »

Figure 5.
Minimal value of initial semimajor axis depending on the time of start from
near-Moon elliptic selenocentric orbit for the Moon-to-Earth detour
trajectories.
We can see that, if the orientation of the particle initial orbit relative to the Earth is suitable and its negative energy is large enough, the Earth's gravitation provides a sufficient increase in the particle orbital energy and allows its passive escape from the lunar attraction.
4. Earth’s gravity effect on the particle acceleration to hyperbolic selenocentric motion
Now we approximately analyze the acceleration of the particle motion with respect to the Moon from the zero energy to a positive one for a hyperbolic trajectory with velocity at “infinity” ![]() which is equal to about 0.15 – 0.25 km/s on the subsequent short arc Es P2 P3 (even on the somewhat larger arc P1 Es P2 P3 from the energy Es < 0). This acceleration is qualitatively described by approximate model of the one-dimensional rectilinear particle’s motion with the Earth, placed on the same line at a distance rM beyond the Moon (Ivashkin 2002, 2003, 2004a), see Figure 6.
which is equal to about 0.15 – 0.25 km/s on the subsequent short arc Es P2 P3 (even on the somewhat larger arc P1 Es P2 P3 from the energy Es < 0). This acceleration is qualitatively described by approximate model of the one-dimensional rectilinear particle’s motion with the Earth, placed on the same line at a distance rM beyond the Moon (Ivashkin 2002, 2003, 2004a), see Figure 6.
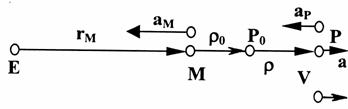
Figure
In this case dr/dt > 0, i.e., the particle moves away from the Moon. The Earth's perturbation daE = mE/rM2 - mE /(rM + r)2 > 0, it accelerates the particle motion. For this model, assuming that, approximately, rM = const, we can integrate the equations for the perturbed motion of the particle:
![]() (4)
(4)
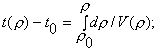 (5)
(5)
![]()
![]() (6)
(6)
inversely:
![]() (7)
(7)
where
![]() (8)
(8)
Example. Let for the presented trajectory at the point Es of the gravitational escape the selenocentric energy be Es = E0 = 0, r = r0 = ![]() = 0.15 km/s (point P2), r » 120.4×103 km for
= 0.15 km/s (point P2), r » 120.4×103 km for ![]() = 0.25 km/s (point P3), and r » 55×103 km for Es = - 0.031 km2/s2 (point P1). We can see the qualitative correspondence with the numerical results presented above, especially for Es > 0.
= 0.25 km/s (point P3), and r » 55×103 km for Es = - 0.031 km2/s2 (point P1). We can see the qualitative correspondence with the numerical results presented above, especially for Es > 0.
Thus, for the given class of the Moon-to-Earth detour space flights, the Earth's gravitation in the region of the translunar libration point L2 allows increasing the selenocentric energy of the particle motion from the zero value to the positive one for a hyperbolic trajectory. If the selenocentric hyperbolic velocity V¥ of the particle is directed along the Moon velocity, the geocentric energy and the apogee distance will be increased and the particle runs away from the Moon orbit and from the Earth, at a large geocentric distance.
5. Sun’s gravity effect on decrease of the particle orbit perigee distance
Next, we estimate the effect of the Sun gravitation on the variation Drp of the particle orbit perigee distance rp on the final arc P3 F of the space flight. We use the theory (Lidov 1961, 1962) of the orbit evolution for one orbital revolution of a planet’s (the Earth’, here) satellite due to an external body’s (the Sun’s, now) gravity perturbation assuming the Earth-Sun direction to be constant. Since the final geocentric distance rpf for the particle orbit perigee is very small (rpf = rp0 + Drp » 0), we assume that eccentricity e » 1 and take for rp its mean value rp = (2rpf - Drp)/2» - Drp/2. Thus, we have:
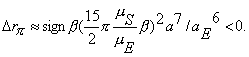 (9)
(9)
Here, mS is the gravitational parameter of the Sun, aE and a are the semimajor axes for the Earth's orbit and for the particle geocentric orbit, the value b is determined by Eqn. 3 with the Sun as the external body. For Drp < 0, it follows from Eqns. 9, 3 that sin2a<0, p/2<a<p or 3p/2<a<2p. Then, we estimate the desired value of the semimajor axis for the spacecraft orbit as
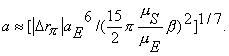 (10)
(10)
For estimation, we have assumed that Drp = – 500×103 km and b = – 0.5. Then, according to Eqn. 10, the semimajor axis of the particle geocentric orbit at the final part of the flight is a » 870×103 km and its apogee distance is ra » 1500×103 km. If we take into account that the Earth-Sun direction is not constant in time, this changes the result only slightly. Thus, if the orientation of the particle orbit with regards to the Sun is suitable enough and the orbit apogee distance is large enough (of about 1.5×106 km), the particle perigee distance decreases from about the lunar-orbit radius to almost zero. This allows the particle’s passive approach the Earth.
6. Conclusions
Reviewing the results of our analysis, we can see that gravitational perturbations of the Earth and the Sun make it possible for the particle beginning its motion from the selenocentric elliptic orbit to escape the motion from the lunar attraction, to transfer it to the Moon-to-Earth detour trajectory, and then to approach the Earth. This leads to noticeable decrease in the energy consumption for the Moon-to-Earth space flights. Such a conclusion is confirmed by both the numerical calculations of relevant trajectories and their theoretical analysis.
Acknowledgements
The author would like to emphasize that this study is the development of the previous analysis of the Earth-to-Moon space flight trajectories (Ivashkin 2002, 2003, 2004a), which was initiated and supported by the GMV SA (Madrid, Prof. J.J. Martínez Garcia, Dr. M. Bellό Mora, Dr. E. Revilla Pedreira, Dr. M. Martínez, and L.A. Mayo Muñiz). The presentation is supported by the ICEUM-6 Organizing Committee, by the Keldysh Institute of Applied Mathematics (
References
Belbruno E A and Miller J K 1993 Sun-Perturbed Earth-to-Moon Transfer with Ballistic Capture; Journal of Guidance, Control and Dynamics 16 No. 4 pp. 770-775.
Bellό Mora M, Graziani F, et al.
Egorov V A and Gusev L I 1980 Dynamics of the Earth-to-Moon Space flights (
Gatland K 1982 The Illustrated Encyclopedia of Space Technology (
Hiroshi Yamakawa, Jun’ichiro
Ivashkin V V 2002 On Trajectories of the Earth-Moon Flight of a Particle with its Temporary Capture by the Moon; Doklady Physics, Mechanics 47 No. 11 pp. 825-827.
Ivashkin V V 2003 On the Earth-to-Moon Trajectories with Temporary Capture of a Particle by the Moon: Presented at the 54th International Astronautical Congress, held in
Ivashkin V V 2004a On
Trajectories for the Earth-to-Moon Flight with Capture by the Moon;
Proceedings of the International
Lunar Conference 2003 / International Lunar Exploration Working Group 5 –
ILC2003/ILEWG 5, held November 16-22,
Ivashkin V V 2004b On
Particle’s Trajectories of Moon-to-Earth Space Flights with the Gravitational
Escape from the Lunar Attraction; Doklady Physics, Mechanics 49
No. 9 pp. 539-542.
Ivashkin V V 2004c On the
Moon-to-Earth Trajectories with Gravitational Escape from the Moon Attraction:
Presented at the 18th International Symposium of Space Flight
Dynamics, held in
Koon W S, Lo M W, Marsden J E, et al. 2001 Low Energy Transfer to the Moon; Celestial Mechanics and Dynamical Astronomy (Kluwer Academic Publishers, Netherlands) 81 pp. 63-73.
Lidov M L 1961 Evolution of the Planets
Artificial Satellites Orbits under Effect of the Outer Bodies Gravity
Perturbations; Artificial Satellites of the Earth (
Lidov M L 1962 The Evolution of Orbits of
Artificial Satellites of Planets under the Action of Gravitational
Perturbations of External Bodies; Planet. Space Sci (Pergamon Press Ltd.
Printed in
Stepan’yants V A and L’vov D V 2000
Effective Algorithm for the Motion Differential Equations System Solving; Mathematical
Modeling (
Sternfeld A 1934 Sur les trajectories permettant d’un
corps attractit central à partir d’une orbite keplérienne
donnée; Comptes rendus de l’Acad. des Sciences (
Sternfeld A 1937 Introduction to
Cosmonautics (
Sternfeld A 1956 Artificial Satellites
of the Earth (