Содержание

Введение

1.   Иерархия структур нуклеиновых кислот.

2.   Элементы вторичной структуры.

3.   Способы описания вторичной структуры.

4.   Стерическое условие и псевдоузлы.

5.   Граф межструктурных переходов.

6.   Модель свободной энергии вторичной структуры РНК.

7.   Модель процесса структурообразования.

8.   Простейшая модель биополимера.

9.   Пространственная структура.

10.   Определение пространственной формы шпилечной петли

11.   Определение формы многозвенных петель

12.   Оценка числа стеблей.

13.   Оценка числа структур.

14.   Оценка вычислительной сложности задачи.

15.   Вычислительные эксперименты на параллельных системах.

16.   Примеры структур тРНК.

Литература

Введение

Изучение методами математического моделирования процессов структурообразования биологических макромолекул, белков, рибонуклеиновых (РНК) и дезоксирибонуклеиновых (ДНК) кислот  является в настоящее время интенсивно развивающейся областью молекулярной биологии. Белки и нуклеиновые кислоты представляют собой одномерные полимерные нити, свернутые в некий пространственный клубок. Белок представляет собой полиамин – линейную цепочку аминокислотных остатков. Нуклеиновая кислота представляет собой полинуклеотид – линейную цепочку нуклеокислотных остатков. Нуклеиновые кислоты делятся на два типа – рибонуклеиновые кислоты (РНК)  и дезоксирибонуклеиновые кислоты (ДНК). В состав РНК входит рибоза, а в состав ДНК дезоксирибоза. Хранение генетической информации происходит в виде ДНК, а ее использование в виде РНК. Фундаментальность проблемы структурообразования определяется тем, что основные процессы функционирования живой клетки определяются в первую очередь пространственной формой (структурой) этих макромолекул.

Многолетний опыт математического моделирования сложных космологических систем (звездные системы, протопланетные облака) позволил организовать исследования процессов структурообразования макромолекул рибонуклеиновых кислот. Принципиально новым в нашем подходе является моделирование не только структурообразования как отдельного явления, но процесса рождения макромолекулы в целом. Это включает в себя и моделирование механизма возникновения и роста молекулярной цепи во взаимодействии с механизмами стуктурообразования. Усложнение модели позволяет получать более точное описание поведения молекулярного комплекса, но требует достаточно большого объема вычислений. Ранее нами были проведены исследования процесса структуризации молекул РНК длиной до 150 нуклеотидов, что позволило высказать гипотезу о прерывистости процесса транскрипции [1]. Представляются новые результаты исследования процессов структурообразования макромолекул РНК. 

Применение многопроцессорного вычислительного комплекса МВС-1000 позволило провести серию вычислений для существенно более длинных молекул РНК – ферментов, длина которых превышает несколько сотен нуклеотидов. Полученные результаты не только подтверждают гипотезу о прерывистости процесса удлинения молекулярной цепи, но и позволяют сделать оценку периода этого процесса.

В настоящее время завершен первый этап исследований, проведенный на основе разработанного специального алгоритма. Этот алгоритм позволил достичь среднего времени расчета процесса образования вторичной структуры РНК на два порядка меньшего, чем при традиционном подходе, применявшемся за рубежом. Стало возможным проведение серии численных экспериментов для опубликованных международных каталогов генов РНК.

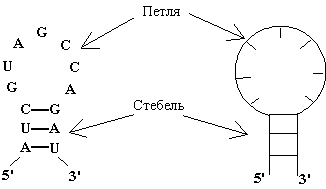
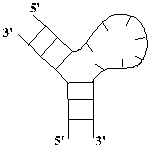
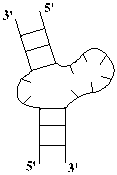
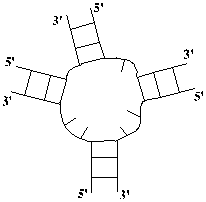
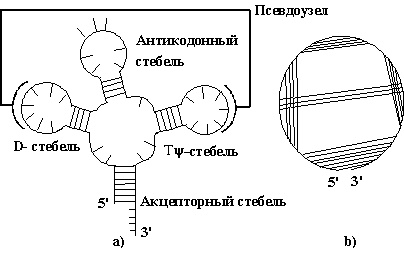
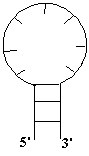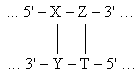В основе большинства компьютерных методов определения пространственных структур биомолекул лежит поиск глобальных или  локальных мимнимумов свободной энергии биомолекулы. Главные трудности, с которыми здесь приходится сталкиваться – это большой объем вычислений, резко растущий с размером молекулы, и большое количество локальных  минимумов, среди которых нужно выбрать минимум, соответствующий реальной пространственной структуре молекулы. Наш подход состоит в  развитии и использовании моделей процессов последовательного возникновения и роста биомолекул в живой клетке (трансляция, репликация,      транскрипция). Это, с одной стороны, приводит к значительному понижению  числа возникающих локально устойчивых конфигураций биомолекулы. C другой стороны, оказалось, что данные модели допускают эффективное распараллеливание вычислительных процессов, происходящих в них, и это позволяет достигать разумного вычислительного времени при использовании современных параллельных вычислительных систем.

Пространственная структура молекулы строится в два этапа. Сначала  определяется ее вторичная структура, а затем третичная. Нами были предложены принципиально новые подходы к решению указанных задач. Основная идея определения вторичной структуры заключается в моделировании последовательного процесса ее формирования в ходе постепенного роста молекулярной цепи. По мере роста молекулы строится цепочка межструктурных переходов от состояния, когда вторичная структура еще отсутствует, к состоянию, когда молекула обладает полной локально устойчивой вторичной структурой. Во время каждого межструктурного перехода происходит локальная минимизация свободной энергии молекулы Последовательность этих переходов определяется тем, каким образом образуется молекулярная цепь РНК в ходе транскрипционного процесса. Подход этот был назван последовательным. Его применение дало заметное повышение качества предсказания вторичных структур РНК и позволило выдвинуть гипотезу о прерывистом характере транскрипции.

1.     Иерархия структур нуклеиновых кислот.

С точки зрения наиболее энергетически сильных связей структуру молекулы РНК (ДНК) можно описывать иерархически. Это, прежде всего, первичная структура молекулы, описывающая ее как цепочку нуклеотидов, последовательно соединенных наиболее сильными фосфодиэфирными связями. Некоторые нуклеотиды в этой цепочке связаны попарно Уотсон-Криковскими связями, которые также достаточно сильны. Структура этих связей называется вторичной структурой РНК (ДНК). В силу конечности множества возможных Уотсон-Криковских связей число вторичных структур, которые может принимать данная молекула РНК (ДНК), конечно, но весьма значительно. Определение реальной вторичной структуры РНК (ДНК) по ее известной первичной структуре также является важной фундаментальной проблемой молекулярной биологии. Под третичной структурой молекулы РНК (ДНК) понимается пространственная форма, которую принимает ее молекулярная цепочка в пространстве под воздействием Уотсон-Криковских и других более слабых потенциалов. Четвертичной структурой называется форма молекулы, которую она приобретает, связываясь в комплекс с другими биомолекулами. Первичная структура у молекулы РНК одна, а потенциально возможных вторичных (третичных, четвертичных) структур много.

2.     Элементы вторичной структуры.

С точки зрения вторичной структуры все нуклеотиды в молекуле можно разбить на два класса: спаренные (т.е. образующие Уотсон-Криковскую связь с каким-либо другим нуклеотидом) и свободные (неспаренные).  Формально, вторичная структура РНК – это описание всех спаренных и свободных оснований в молекулярной цепи.

Пронумеруем последовательно нуклеотиды в молекулярной цепи, начиная от 5’ конца, так, что нуклеотид, присоединяющийся к растущей цепи позже, имеет больший номер. Отрезок  свободных оснований в молекулярной цепи называется однонитевым. Отрезки  и  спаренных оснований так, что  спарен с ,  с ,…,  с , образуют двухнитевый, или двуспиральный, участок во вторичной структуре РНК. Однонитевые участки (и семейства таких участков) называются петлями, а двухнитевые – стеблями. Стебель можно представить себе как участок винтовой лестницы, где ступеньки – это поперечные, Уотсон-Криковские связи. Длиной стебля называется число пар оснований в нём: . Таким образом, вторичная структура РНК – это совокупность стеблей и петель.

Рис. 2.1. Однонитевый (петля) и двухнитевый (стебель) элементы вторичной структуры РНК.

Типы петель во вторичной структуре. Петлей называется замкнутая последовательность однонитевых участков РНК, концы которых соединены Уотсон-Криковскими вторичными связями. При этом начало каждого следующего участка соединено с концом предыдущего, а конец последнего участка соединен с началом первого. Однонитевые участки, входящие в состав петли, называются ее ветвями, или звеньями. Длиной петли называется число свободных нуклеотидов, входящих в ее состав.  Выделяют следующие типы петель.

a) Шпилечная петля                                        b) Боковая петля

c) Внутренняя петля                                   d) Многозвенная петля

Рис 2.2. Типы петель (однонитевых участков вторичной структуры).

·        Шпилечная петля: соединяет первую и вторую нить в одном стебле. Это простейшая однозвенная петля (она состоит из одного однонитевого участка). Считается, что шпилечная петля всегда содержит не менее трех нуклеотидов.

·        Боковая петля: содержит два однонитевых участка, один из которых вырожден – имеет нулевую длину (не содержит ни одного несвязанного нуклеотида). Длина же второго участка называется длиной боковой петли.

·        Внутренняя петля: содержит два однонитевых  участка. Длины этих участков являются параметрами, определяющими петлю.

·        Многозвенная петля: содержит несколько однонитевых участков. Число этих участков и их длины являются параметрами, определяющими петлю.

3.     Способы описания вторичной структуры.

Существует несколько способов описания вторичных структур РНК. Мы опишем два основных.

·        Геометрический способ – молекулярная цепь располагается на плоскости так, чтобы стебли образовывали прямоугольные “лесенки”, а петли – замкнутые контуры (как на Рис 2.2, 3.1). Такой способ дает некоторое представление о реальной геометрии структуры молекулы.

·        Представление на окружности – молекулярная цепь располагается на плоскости по окружности, так что движению от 5’ конца к 3’  концу соответствует движение против часовой стрелки. Уотсон-Криковские связи при этом изображаются хордами  окружности. Если никакие две хорды не пересекаются, то говорят, что выполняется стерическое правило.

Рис 3.1. Представление вторичной структуры тРНК геометрически (a) и на окружности (b). Для такой структуры стерическое правило выполнено.

·        Скобочный способ: вторичная структура представляется в виде последовательности нулей, открывающих и закрывающих скобок. Нуль ставится в позиции, где отсутствует Уотсон-Криковская связь. Открывающая скобка ставится, если нуклеотид связан с нуклеотидом, имеющим больший номер. Закрывающая скобка ставится, если нуклеотид связан с нуклеотидом, имеющим меньший номер. Такое представление возможно только в том случае, когда выполнено стерическое правило. Для структуры Рис.3 скобочное представление имеет следующий вид:

   (((((((00((((0000000))))((((0000000))))0(((((0000000)))))00)))))))0000

·        Представление в виде графика: вторичная структура представляется в виде кусочно-линейной функции F(x) одного переменного, определенной на отрезке , где N – число нуклеотидов в цепи РНК. Такое представление возможно только в том случае, когда выполнено стерическое правило. Структура представляется в скобочной форме. Функция определяется следующим образом. Пусть i – номер нуклеотида, а B(i) – скобочное описание (т.е. B(i) – это ‘(', ’)’, или '0') .  Пусть . Тогда

F(0) = 0

F(x) = F(i – 1)                          при B(i) = 0

F(x) = F(i – 1) +  (x – i + 1)      при B(i) = ‘(‘

F(x) = F(i – 1) –  (x – i + 1)      при B(i) = ‘)‘

т.е. функция постоянна при отсутствии Утсон-Криковских связей и возрастает или убывает со скоростью 1 при их наличии.

Рис 3.2. Представление структуры Рис. 3.4 в виде графика.

Представив вторичную структуру в виде функции, ее можно анализировать и сравнивать с другими вторичными структурами, используя, например, ее частотный спектр.

·        Представление в виде матрицы инцидентности: пусть молекулярная цепь состоит из N нуклеотидов. Матрица инцидентности – это матрица  размером  такая, что , если нуклеотиды i и j соединены Уотсон-Криковской связью, и  в противном случае.

·        В виде клики графа стеблей. Рассмотрим множество всех стеблей, возможных для данной молекулы РНК. Два стебля назовем совместимыми, если они оба одновременно могут существовать в какой-либо вторичной структуре. Введем граф стеблей. Вершинами этого графа являются все стебли, возможные для данной молекулы РНК. Две вершины графа соединены, если соответствующие им стебли совместимы. Пусть у нас есть какая-либо вторичная структура. Выделим из графа стеблей подграф, состоящий из вершин, соответствующих всем стеблям, присутствующим в данной вторичной структуре. Все эти стебли совместимы, поэтому в выделенном подграфе все вершины попарно соединены между собой, т.е. подграф является полным (или кликой). Обратно, если мы выделим какую-либо клику из графа стеблей, то ей однозначно соответствует некоторая вторичная структура. Таким образом, множества вторичных структур и клик графа стеблей равномощны.

4.     Стерическое условие и псевдоузлы.

Если в представлении вторичной структуры на окружности никакие две хорды не пересекаются, то говорят, что выполняется стерическое условие. Перенумеруем все нуклеотиды в молекулярной цепи, начиная с 1. Две пары нуклеотидов (p₁, p₂) и (q₁, q₂) стерически совместимы, если их связи не “перекрещиваются”, т.е. выполнено одно из условий:

либо [p₁, p₂] Í [q₁, q₂],

либо [q₁, q₂] Í [p₁, p₂],   

либо [p₁, p₂] Ç [q₁, q₂] = Æ,

где [n, m] – это целочисленный отрезок от n до m. Два стебля стерически совместимы, если совместимы любые две составляющие их Уотсон-Криковские пары.

          Если стерическое правило не выполнено, то вторичная структура содержит псевдоузлы.

В описываемой модели предполагается, что псевдоузлы во вторичной структуре отсутствуют.

Рис. 4.1. Псевдоузел.

Рис. 4.2. Вторичная структура тРНК может содержать один псевдоузел.

5.     Граф межструктурных переходов.

            Помимо поиска вторичной структуры исходя из условия минимизации свободной энергии, часто используется последовательный подход, при котором вторичная структура РНК постепенно «выращивается»  путем добавления к ней или удаления из нее некоторых групп вторичных связей. При этом происходит цепочка переходов от одной вторичной структуры к другой. Процесс начинается с пустой структуры, в которой вторичные связи отсутствуют, и завершается вторичной структурой, для которой выполняются некоторые условия локального минимума свободной энергии. В ходе одного межструктурного перехода могут или добавиться, или удалиться все связи какого-либо одного стебля (он называется активным).  Другие виды переходов не рассматриваются.

          Множество допустимых стеблей данной вторичной структуры составляют стебли, которые могут быть активными. Множеству допустимых стеблей соответствует множество допустимых переходов от данной структуры к другим. Состав множества допустимых стеблей зависит от конкретной модели процесса структурообразования. В простейшей модели это множество состоит из всех стеблей.

          Для данной молекулы РНК определим граф межструктурных переходов. Его вершинами являются всевозможные вторичные структуры, а ребрами – допустимые межструктурные переходы. Этот граф является направленным.  Каждому ребру графа соответствует энергия перехода: это приращение свободной энергии новой вторичной структуры по отношению к старой.

          Процесс роста вторичной структуры представляет собой путь на графе межструктурных переходов.

          В общем случае путь перехода от одной вторичной структуры к другой не единственен.

Вероятностный конечный автомат. Имея граф межструктурных переходов, можно построить вероятностный конечный автомат, реализующий процесс роста вторичной структуры.

Обозначим за G(S) свободную энергию структуры S. Пусть    – энергия перехода от структуры  к структуре , где k  – это номер (индекс) стебля, которому соответствует переход. В соответствии со статистикой Гиббса вероятность такого перехода среди других возможных переходов равна

                                                                                                             _(5.1)

где k – постоянная Больцмана, T – температура, c – нормировочный коэффициент. Видно, что вероятность перехода тем больше, чем меньше его свободная энергия. Приписав каждому возможному межструктурному переходу такую вероятность, мы получим конечный автомат. Запустив его из вершины, соответствующей пустой структуре, мы получим процесс образования вторичной структуры.

Детерминированный конечный автомат. Положив вероятность межструктурного перехода равной единице для перехода с минимальной свободной энергией, если она отрицательна, и равной нулю для всех остальных переходов, мы получим детерминированный конечный автомат. Для такого автомата процесс образования вторичной структуры заканчивается в вершине, в которой вероятности всех переходов равны нулю. Это означает, что данной вершине соответствует локальный минимум свободной энергии (на множестве допустимых переходов).

6.     Модель свободной энергии вторичной структуры РНК.

          Свободная энергия вторичной структуры РНК вычисляется как сумма свободных энергий ее элементов – стеблей и петель. Единицей измерения свободной энергии принято считать килокалорию на моль – [ккал/моль].

          Свободная энергия стебля вычисляется как сумма энергий его элементарных ячеек. Элементарная ячейка – это пара соседних Уотсон-Криковских связей.

Рис. 6.1. Стебель и одна его элементарная ячейка.

Энергия элементарной ячейки складывается из энергии ее нижней (первой) Уотсон-Криковской связи и специального добавка, который носит название энергии стэкинг-взаимодействия. Энергия стэкинг-взаимодействия – это энергия перекрестного взаимодействия нуклеотидов верхней и нижней Уотсон-Криковской пары.

          Всего существует 10 различных типов элементарных ячеек. Их энергии даются в специальных таблицах, полученных экспериментально.

Рис. 6.2. Обозначения нуклеотидных пар «XY – ZT» в элементарной ячейке.

Таблица 6.1. Свободная энергия элементарных ячеек (в килокалориях на моль).

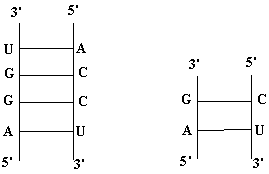
          Асимметрия стэкинг-взаимодейчствия.  Из таблицы видно, что энергии ячееек

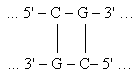 и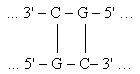 

(т.е. CG-GC и GC-CG) существенно различны (-2.4 и –3.4), хотя ячейки отличаются друг от друга только направлениями нитей. Это дает нам пример того, что стэкинг-взаимодействие существенно зависит от ориентации нитей двойной спирали.

          Свободная энергия петли. Энергия петли более точно называется энергией инициации петли. Она зависит от типа петли и от ее длины. Длиной петли называется число неспаренных нуклеотидов в ее однонитевых участках. Энергии коротких петель (до 10 нуклеотидов) даются в специальных таблицах, полученных экспериментально. Энергия более длинных петель определяется по формуле

                                                                 (6.1)

где a и b – константы, а N – число нуклеотидов в петле (длина петли). Эту оценку можно получить из формулы Гиббса (5.1) следующим образом (для простоты мы рассмотрим только шпилечную петлю).

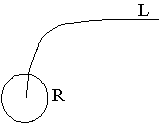
Рис. 6.3. Молекулярная нить длины и сфера Утсон-Криковского взаимодействия эффективного радиуса .

          Пусть петля имеет физическую длину L=mN (где m - коэффициент пропорциональности). Зафиксируем один конец петли. Тогда второй конец может находиться в точках шара объемом . Обозначим за эффективный радиус сферы Уотсон-Криковского взаимодействия. Тогда  – ее объем. Вероятность попадания свободного конца петли в эту сферу можно оценить как . Из формулы Гиббса (4.1) имеем 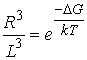. Прологарифмировав это равенство, получим искомый закон изменения свободной энергии петли в зависимости от ее длины.

Энергия инициации петли. Свободная энергия петель часто называется энергией их инициации. Следует отметить, что, как правило, она положительна, т.е. сами по себе петли неустойчивы и существуют только за счет отрицательной энергии стеблей, на которые они опираются.

7.     Модель процесса структурообразования.

          Наш подход состоит в математическом моделировании двух основных черт транскрипционного процесса: последовательного роста молекулярной цепи РНК в ходе транскрипции и постепенного последовательного формирования ее вторичной и третичной структуры.

В основу модели образования вторичной структуры РНК положено взаимодействие двух основных процессов, влияющих на структурообразование. Первый, элонгация, это последовательный рост молекулярной цепи в ходе транскрипции. Второй, структуризация, есть последовательное возникновение и формирование вторичной структуры РНК на том участке ее молекулярной цепи, который уже образовался к данному времени. Структурные перестройки при этом обеспечивают локальную минимизацию свободной энергии сформировавшегося участка молекулы. Оба этих процесса рассматриваются как дискретные. Молекулярная цепь удлиняется на целое число нуклеотидов, вторичная структура изменяется путем возникновения или разрыва целого числа вторичных связей. Отметим, что основным параметром в такой модели является относительная скорость элонгации T, определяемая как отношение скорости роста молекулярной цепи к скорости структурообразования (параметр структуризации). В рамках нашей модели параметр T можно рассматривать как количество новых нуклеотидов, на которое удлинится молекулярная цепь РНК за то время, пока на старом ее участке будет происходить формирование и стабилизация вторичной структуры.

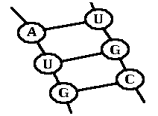
Длина стебля = 1                                  Длина стебля = 3

Рис. 7.1. Стебли являются элементарными блоками, из которых строится вторичная структура РНК.

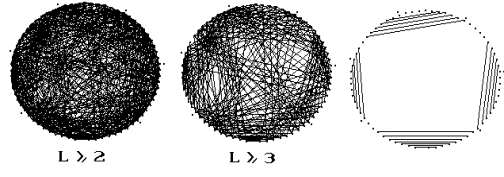
а)                                               б)                                              в)

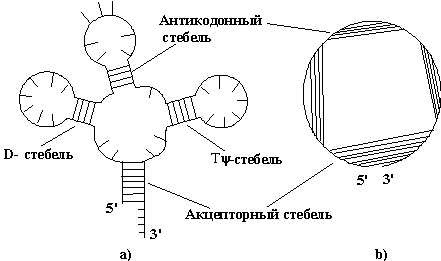
Рис.7.2. Транспортные РНК. Конкурирующие стебли длины L для аспарагиновой тРНК человека (а-б) и ее естественная вторичная структура - клеверный лист (в).

Рис.7.3. Точность описания структуры падает при увеличении минимально допустимой длины стеблей L (приведены средние значения для  транспопртных РНК).

Рис. 7.4. Разнообразие структурных элементов резко растет при увеличении точности описания вторичной структуры, т.е. при уменьшении минимально допустимой длины стеблей L.

Взаимодействие между указанными процессами моделируется в простейшей форме. Считается, что фазы роста молекулярной цепи и структуризации разделены во времени и циклически повторяются одна за другой. Скорости обоих процессов полагаются постоянными и не зависящими от нуклеотидного состава молекулярной цепи РНК, от сложности образующейся структуры и других обстоятельств. При таких допущениях модель роста вторичной структуры РНК в ходе транскрипции выглядит следующим образом.

Процесс описывается как пошаговый. На каждом шаге сначала происходит структуризация, при которой вторичная струкутура РНК формируется в пределах того участка молекулярной цепи, который уже образовался к данному шагу процесса. После образования и стабилизации вторичной структуры происходит удлинение молекулярной цепи на постоянное число нуклеотидов, равное параметру структуризации процесса . После этого происходит переход к следующему шагу процесса. Процесс заканчивается после того, как молекулярная цепь вырастет полностью и структура полностью сформируется.

Известно, что некоторые молекулы РНК могут образовываться в составе более длинного транскрипта, включающего их. Чтобы отразить этот факт в модели, используется еще один параметр  - начальная длина молекулярной цепи. Это число нуклеотидов молекулярной цепи, уже образовавшихся к началу первого шага процесса.

Таким образом, на шаге процесса с номером  молекулярная цепь содержит  нуклеотидов. На последнем шаге процесса величина  ограничивается полной длиной молекулярной цепи, обозначаемой . Поскольку оба параметра процесса,  и , целочисленные, то, исходя из физического смысла, мы имеем , . Если , то полное развитие процесса происходит уже на первом шаге и результат совпадает с результатом для случая . Поэтому поведение процесса образования вторичной структуры РНК моделируеися в области ,  на дискретной решетке ;

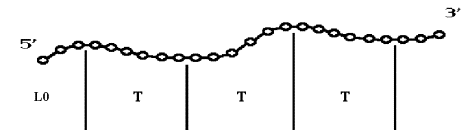
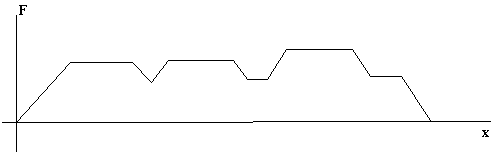
Рис. 7.5. Процесс сворачивания РНК во вторичную структуру: Последовательный, пошаговый, с локальной минимизацией свободной энергии на каждом шаге. Начинаясь с  нуклеотидов, длина цепи РНК увеличивается каждый раз на T, до тех пор, пока не будет достигнут конец цепи. Основные параметры процесса: a) набор термодинамических параметров – модель свободной энергии; b)  –  длина начального участка цепи РНК на первом шаге ; c)  (период структуризации) – длина участка, добавляемого к растущей цепи РНК на каждом шаге.

Опишем теперь более подробно, как моделируется структуризация, т.е. процесс формирования вторичной структуры РНК на том ее участке, который уже образовался. Это тоже пошаговый процесс. К началу структуризации молкулярная цепь может уже обладать вторичной структурой, возникшей на предыдущих шагах основного процесса. В нашей модели структура наращивается путем добавления к ней элементарных структурных элементов - стеблей. Стебель – это двуспиральный участок вторичной структуры, состоящий из комплементарно спаренных оснований без пропусков. При добавлении к структуре нового стебля, в ней возникают новые вторичные связи и могут разрываться старые. Модель структуризации включает в себя правила формирования множества допустимых стеблей и правила определения межструктурного перехода. В наиболее широком варианте множество допустимых стеблей включат в себя все стебли, оба спаренных участка которых находятся в пределах той части молекулярной цепи, которая имеется к данному моменту времени. В этом случае возможно не только наращивание вторичной структуры (т.е. возникновение новых вторичных связей), но и ее перестройка, т.е. разрушение старых связей, препятствующих возникновению новых. В более узком варианте множество допустимых стеблей содержит только стебли, наращивающие структуру без необходимости разрыва старых связей. В этом случае вторичная структура формируется без перестроек. Заметим, что множество допустимых стеблей можно рассматривать как вариант множества допустимых межструктурных переходов. В настоящей работе мы будем рассматривать только модель процесса с разрешением любых структурных перестроек.

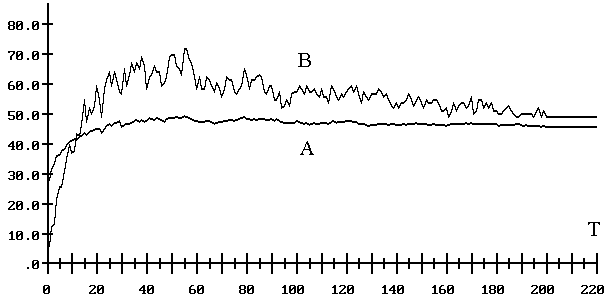
Рис. 7.6. Расчет вторичной структуры 106 молекул РНК-ферментов. Качество предсказания в зависимости от скорости приращения молекулярной цепи.  Плавный график (A) – это средний процент правильно предсказанных связей вторичной структуры. Прерывистый график (B) – это средняя доля молекул, у которых вычисленная вторичная структура не менее чем на 50% совпадает с натуральной. В дапазоне скорости роста молекулярной цепи от 20 до 60 нуклеотидов за раз набдюдается заметный рост качества предсказания вторичной структуры.

Как уже упоминалось, структуризация моделируется как пошаговый процесс. На каждом ее шаге формируется множество допустимых стеблей. Затем выбирается такой стебель, добавление которого к структуре даст наибольшее понижение ее свободной энергии. Этот стебель добавляется к структуре, после чего повторяется следующий шаг структуризации. Процесс кончается после того, как структура стабилизируется. Это означает, что множество тех допустимых стеблей, добавление которых способно понизить свободную энергию структуры, пусто. Иначе говоря, процесс кончается, когда мы попадаем в точку локального минимума свободной энергии вторичной структуры на множестве допустимых межструктурных переходов. 

После окончания процесса структуризации молекулярная цепь удлинняется и цикл шагов основного процесса повторяется.

8.     Простейшая модель биополимера.

          Будем называть биополимер однородным, если он состоит из одинаковых элементов, и нейтральным, если эти элементы не взаимодействуют друг с другом (кроме полимерной связи соседних элементов). В этом разделе мы покажем, что простейшей моделью однородного нейтрального биополимера является винтовая линия (спираль). При этом мы рассмотрим самый простейший идеальный случай, который никогда не достигается в реальности. Мы будем считать, что молекула биополимера «висит» в абсолютно пустом пространстве при отсутствии внешних сил. Допустим, что биополимер состоит из последовательности совершенно одинаковых элементов. Будем моделировать элемент твёрдым телом. Поскольку все элементы одинаковые, то каждый следующий элемент прикрепляется к предыдущему совершенно одинаковым образом.  Формально это описывается следующим образом. К элементу привязывается сопутствующая система координат. Положение и ориентация сопутствующей системы полностью определяет положение элемента в пространстве. Обозначим  начало сопутствующей системы элемента  в абсолютной системе координат. Рассмотрим ломаную линию , ,…, ,…, вершины которой расположены в началах сопутствующих систем элементов биополимера. Утверждение, которое мы хотим доказать, состоит в следующем.

          Утверждение. Возможны только три случая

a)     Точки , ,…, ,… лежат на некоторой прямой, разбивая её на одинаковые отрезки.

b)    Точки , ,…, ,… лежат на некоторой окружности, разбивая её на одинаковые дуги.

c)     Точки , ,…, ,… лежат на некоторой винтовой линии, разбивая её на одинаковые сегменты.

Доказательство. Пусть к элементу A прикреплён следующий элемент B. Тогда сопутствующая система B получается из A сдвигом и ортогональным преобразованием. По теореме Шаля ортогональное преобразование представляет собой поворот вокруг некоторой оси (проходящей через начало системы B). Поскольку элементы одинаковы, то вектора сдвигов и поворотов в их сопутствующих системах одинаковы.  В абсолютном пространстве вектор сдвига уже может меняться при переходе от одного элемента к другому. А вот вектор поворота постоянен и в абсолютном пространстве. В самом деле, при вращении системы координат вокруг какой-либо оси проекции её направляющего вектора на оси координат не меняются. Поэтому координаты вектора поворота последующего элемента в системе текущего элемента совпадают с его координатами в системе предыдущего элемента. По той же причине проекция вектора сдвига на вектор поворота в абсолютном пространстве постоянна. Вектор поворота в абсолютной системе координат обозначим  , а угол поворота .

Если поворот нулевой, то мы получаем случай a). Каждая следующая точка  получается из предыдущей сдвигом на постоянный вектор.

Пусть поворот ненулевой, но вектор поворота ортогонален вектору сдвига. В этом случае все вектора сдвига и, следовательно, точки  будут лежать в плоскости, проходящей через  и ортогональной вектору поворота. Поскольку длины векторов сдвига одинаковы и эти вектора поворачиваются на один и тот же угол, то мы получаем случай b).

Рассмотрим теперь общий случай. Фактически нам достаточно доказать, что в абсолютном пространстве найдутся ось, V параллельная вектору поворота , и вектор W, параллельный оси V, такие, что для любого i отрезок  получается из отрезка  поворотом вокруг оси V на постоянный угол  и сдвигом на вектор W. Заметим, что поскольку вектор W параллелен оси V, то порядок сдвигов и поворотов несущественен.

          Возьмём какую-либо плоскость , ортогональную вектору поворота  . Спроектируем нашу ломаную на эту плоскость. В качестве вектора W возьмём проекцию вектора сдвига на вектор поворота  в абсолютном пространстве. Поскольку она постоянна, то проекция ломаной , ,…, ,… на плоскость  состоит из одинаковых отрезков, повёрнутых на постоянный угол  друг относительно друга. Значит, точки проекции ломаной лежат на некоторой окружности и ось V проходит через её центр и параллельна вектору поворота .

          Доказательство завершено.

          Полученный в данном разделе результат качественно можно трактовать следующим образом. Биополимерам, состоящим из однородных элементов, должно быть свойственно образовывать спиральные структуры. Как мы увидим далее, это действительно имеет место как для белков, так и для нуклеиновых кислот.

Рис. 9.1. Тонкий упругий стержень в свободном состоянии.

9.     Пространственная структура.

Математическая модель двуспиральной молекулы ДНК на основе тонкого упругого прямолинейного однородного симметричного стержня стала уже классическим средством для изучения ее пространственных форм [8]. В работе [4]  была предложена математическая модель пространственной структуры молекулы РНК, в которой молекулярная цепь рассматривается как тонкий упругий стержень, имеющий в свободном состоянии форму винтовой линии. (Свободное состояние означает отсутствие действия на стержень каких-либо внешних сил и моментов.)

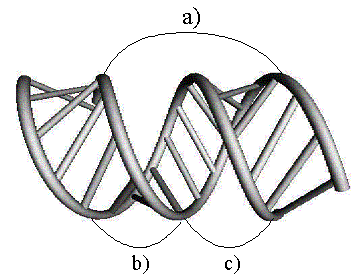
Рис. 9.2. Двойная спираль в A-форме;

a) шаг витка b) малая бороздка, c) большая бороздка.

С шагом, равным длине одного нуклеотида, в стержень вделаны жесткие перемычки, равные по длине половине Уотсон-Криковской связи. В простейшей модели параметры винтовой линии и ориентация перемычек выбираются так, что два свободных стержня одинаковой длины, будучи правильно расположены, образуют двойную спираль в A-форме.

Пространственная структура молекулы собирается из стеблей и петель в соответствии с заданной вторичной структурой.  Каждая петля состоит из семейства тонких упругих стержней со взаимно согласованными краевыми условиями равновесия. В соответствии с краевыми условиями концы стержней ориентируются так же, как концы нитей в стебле А-формы РНК.

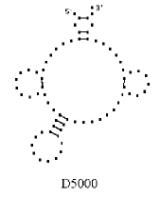
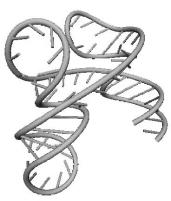
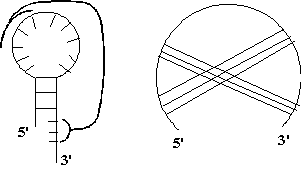
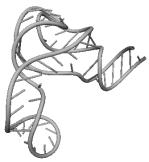
Рис. 9.3. Пример построенной третичной структуры транспортной РНК 

Аспарагиновой кислоты Asterina Pectini.

Пространственная структура молекулы строится в два этапа. Сначала  определяется ее вторичная структура, а затем третичная.

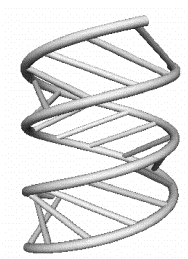
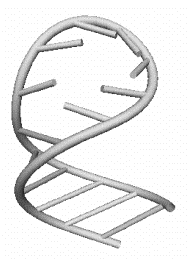
a)                                                                            b)

Рис 9.4. Элементы третичной структуры РНК: a) стебель; b) шпилечная петля

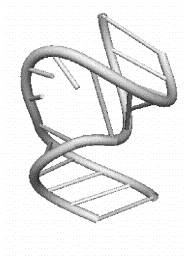
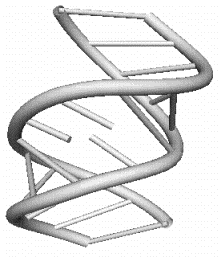
c)                                                                                  d)

Рис 9.4.  Элементы третичной структуры РНК: c) боковая петля; d) внутренняя петля

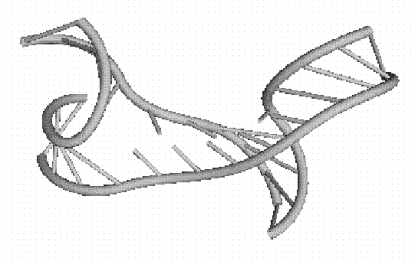
e)

Рис 9.4. Элементы третичной структуры РНК: e) многозвенная петля.

При построении третичной структуры молекулярная цепь рассматривается как тонкий упругий стержень с поперечными стяжками, соответствующими вторичной структуре. При соответствующем выборе параметров стержня его пространственная форма  приближенно описывает пространственную структуру молекулы РНК. В нашей работе используется одна из наиболее простых моделей описания пространственных структур молекул РНК - непрерывная модель. В данной модели молекула РНК описывается как упругий стержень с абсолютно твердыми поперечными связями. Пространственная структура молекулы собирается из базовых элементов, каждый из которых является замкнутым контуром, состоящим из семейства упругих стержней, последовательно соединенных между собой жесткими перемычками. Определение статически устойчивой пространственной формы базовых элементов сводится к решению системы краевых задач, каждая из которых состоит в определении конфигурации тонкого упругого стержня, удовлетворяющей геометрическим условиям на его концах.

Пространственная форма стержня определяется на основе уравнений равновесия. Они включают в себя 6 параметров: A, B, C – два главных изгибных и один крутильный коэффициенты упругости стержня; , ,  – геометрические параметры стержня в свободном состоянии (кривизна-кручение в проекции на главные оси тензора упругости).

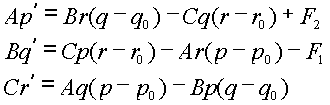
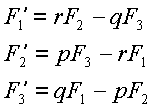
В положении равновесия достигает экстремума упругая энергия

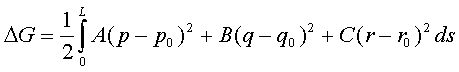
10.             Определение пространственной формы шпилечной петли

          Тонкий упругий стержень, моделирующий шпилечную петлю, является гладким продолжением одной из нитей двуспирального участка и гладко же переходит другим концом в другую его нить. Поэтому начальное положение и ориентация стержня совпадают с конечным положением и ориентацией первой нити двуспирального участка, а конечное положение и ориентация с начальным положением и ориентацией второй нити. Параметры двуспирального участка в наших экспериментах совпадали с параметрами A-формы двойной спирали.

На Рис. 10.1. показана постановка краевой задачи для шпилечной петли. Поясним обозначения.  есть радиус-вектор осевой линии стержня, параметризованный ее длиной , , i=1,2,3 –  направляющие главных осей тензора упругости.

,   ,   ,   ,   ,  

Угол – это угол поворота главных осей тензора упругости относительно осей естественного трехгранника Френе.

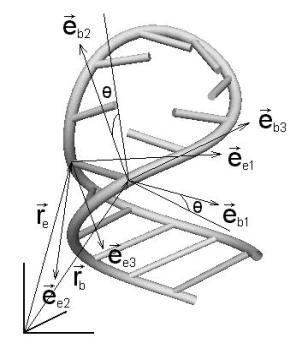
Рис.10.1. Задание краевых условий (для шпилечной петли). Пространственная структура собирается из стеблей и петель в соответствии с заданной вторичной структурой.  Каждая петля состоит из семейства тонких упругих стержней со взаимно согласованными краевыми условиями равновесия. В соответствии с краевыми условиями концы стержней ориентируются так же, как концы нитей в стебле А-формы РНК.

11.             Определение формы многозвенных петель

          Многозвенная петля описывается как равновесная форма нескольких участков тонкого упругого стержня, соединенных твердыми перемычками, моделирующими Уотсон-Криковские связи. В предыдущем разделе был описан процесс вычисления начальных условий уравнений равновесия каждого следующего участка по финальным значениям соответствующих величин для предыдущего участка упругого стержня. Это позволяет поставить краевую задачу для многозвенной петли подобно тому, как она ставилась для однозвенной шпилечной петли.

          Пусть в многозвенной петле всего n однонитевых участков, длины которых обозначаются . При построении пространственной формы приходится отыскивать форму многозвенного стержня, для которого заданы положение и ориентация на левом конце первого участка и на правом конце последнего участка, а силы и моменты на левом конце неизвестны. Их приходится определять в ходе решения краевой задачи. Более точно – краевые условия означают задание следующих величин:

,  ,                                 (11.1)

, ,                         

(верхний индекс здесь – это номер однонитевого участка). А решение краевой задачи означает правильный выбор величин

,  

Пространственная форма молекулы, рассчитанная на основе наших моделей, воспроизводит топологию пространственной структуры, полученной  методами рентгеноструктурного  анализа. Предлагаемый подход позволяет вычислять пространственные структуры молекул РНК, для которых не проводился рентгеноструктурный анализ.

12.             Оценка числа стеблей.

Попробуем оценить, каково количество стеблей, которые могут возникать в молекулярной цепи, первичная структура которой (т.е. нуклеотидный состав) случайна. Обозначим  – среднее число стеблей длины  при случайном выборе молекулярной цепи, состоящей изнуклеотидов.

Оценим сначала количество стеблей длины 1, т.е стеблей, содержащих только одну Уотсон-Криковскую связь. Если не учитывать правило комплементарности, то связь, входящая в стебель, может соединять любую пару нуклеотидов в цепи, а число пар – это .  Введем теперь в рассмотрение правило комплементарности нуклеотидов. Пусть на левом конце связи, входящей в стебель, оказался какой-то нуклеотид . Нуклеотид на правом конце может оказаться любым. В сооответствии с правилом комплементарности, вероятность того, что этот (случайный) нуклеотид будет комплементарен нуклеотиду _, равна . Поэтому среднее число стеблей длины 1 в случайной молекулярной цепи длины  оценивается как

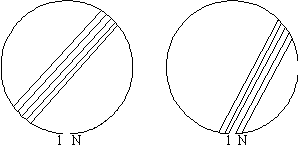
          Рассмотрим теперь общий случай. Расположим нуклеотиды молекулярной цепи последовательно на окружности.

a)                                                                                                               b)

Рис 12.1. Стебель длины   – это семейство  параллельных, идущих подряд хорд (a). Если в семейство входят две хорды с концами в точках  и , то это два стебля меньшей длины.

При таком описании, стебель – это семейство  параллельных хорд, концы которых сдвинуты на один нуклеотид по отношению к соседним хордам (см. Рис 12.1. a). Оценим число таких семейств. Самый левый нуклеотид стебля может занимать  положений на окружности. Допустим, что мы зафиксировали левый конец стебля в нуклеотиде , тогда нуклеотиды m, m+1,…, m+n–1 будут заняты и на окружности останется  свободных нуклеотидов (сложение здесь и ниже производится по модулю N). Если правый конец стебля помещен в нуклеотид j, то нуклеотиды j, ,…,  будут заняты. Поскольку левые и правые концы связей стебля не должны попадать в одни и те же позиции, то для правого конца стебля остается  возможных положений. Это , ,…, . Таким образом, всего имеется  семейств параллельных хорд, но эту величину надо еще уменьшить вдвое, поскольку каждое семейство участвовало в нашем подсчете дважды – мы можем назвать левой стороной семейства хорд любую из его двух сторон. Итак, всего мы можем получить

семейств n параллельных хорд, концы которых сдвинуты на один нуклеотид по отношению к соседним хордам.

          Найденная величина r включает в себя не только семейства хорд, описывающих стебли длины n, но и неправильные семейства, т.е семейства, описывающие два стебля меньшей длины (см. Рис 12.1. b). Это семейства, содержащие две хорды с концами в точках  и N. Левый конец таких семейств может занимать  положение, располагаясь в позициях N, ,…, . Правый конец семейства (как и в общем случае) может занимать  положений. И всего (с учетом двукратного участия семейств хорд в нашем рассмотрении) мы получим

неправильных семейств хорд.

          Вычитая неправильные семейства из общего количества, получим,  что общее количество правильных семейств хорд равно . Учитывая, что вероятность комплементарности оснований во всех n связях стебля равна , получим следующую оценку среднего числа стеблей длины n в молекулярной цепи из N случайно выбранных нуклеотидов:

          Можно оценить и общее количество стеблей любой возможной длины. Обозначим эту величину . Она равна сумме  по всем возможным n. С одной стороны  не меньше, чем . С другой стороны , а . Поэтому суммирование величин  по всем возможным n даст величину меньшую, чем .

Таким образом, скорость роста общего количества стеблей  при увеличении длины молекулярной цепи  имеет порядок не меньше и не больше .

13.             Оценка числа структур.

Попробуем оценить, каково количество вторичных структур, которые могут возникать в молекулярной цепи, первичная структура которой (т.е. нуклеотидный состав) случайна.

Будем называть длиной структуры количество Уотсон-Криковских связей в ней. Будем рассматривать только структуры, удовлетворяющие стерическому условию. Обозначим  – среднее число структур длины  при случайном выборе молекулярной цепи, состоящей изнуклеотидов.

Количество структур длины 1 равно числу стеблей, содержащих только одну Уотсон-Криковскую связь:

Рассмотрим теперь структуру длины n. В ней какие-то  нуклеотидов попарно связаны Уотсон-Криковскими связями. Всего возможно  различных выборов  нуклеотидов.  После того, как нуклеотиды выбраны, вторичная структура определяется системой связей между ними. Перенумеруем выбранные нуклеотиды последовательно от 1 до  и расположим их в вершинах правильного -угольника. Соединим связанные нуклеотиды диагоналями.  Каждой вторичной структуре взаимно однозначно соответствует набор из  непересекающихся диагоналей. 

Обозначим  число различных расположений  непересекающихся диагоналей в правильном -угольнике. Тогда (с учетом того, что вероятность комплементарности выбранных нуклеотидов равна ) имеем

Поскольку , то

                    ,

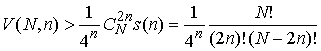причём степень полинома от , стоящего а правой части, равна . Отсюда можно сделать два вывода:

·        С ростом молекулярной цепи количество возможных вторичных структур, состоящих из  Уотсон-Криковских связей, растет как .

·        С ростом молекулярной цепи количество всех возможных вторичных структур растет быстрее чем любой полином (иначе говоря скорость роста количества вторичных структур больше полиномиальной).

Несложно убедиться, что , , . Однако общая формула для  неизвестна.

Рис. 13.1. Пять вариантов вторичной структуры с тремя связями ().

Рассмотрев структуры, у которых связаны нуклеотиды 1 и 2, а также структуры, у которых связаны нуклеотиды 2 и 3, несложно убедиться, что . Отсюда получаем, что . Следовательно, для среднего числа структур длины  при случайном выборе молекулярной цепи, состоящей из  нуклеотидов, верна оценка

14.             Оценка вычислительной сложности задачи.

В ходе транскрипции молекулярная цепь РНК последовательно удлиняется с некоторой скоростью. При этом на участке уже выросшей цепи могут образовываться водородные связи между комплементарными нуклеотидами. Совокупность этих связей называется вторичной структурой молекулы. Она, в свою очередь, определяет энергетически более слабые пространственные изгибы молекулярной цепи. В ходе роста молекулярной  цепи могут возникать новые вторичные связи или уже имеющиеся вторичные связи могут разрываться и замещаться энергетически более выгодными  комбинациями других вторичных связей (перестройка структуры). Поскольку   число возможных вторичных структур конечно (имеет порядок куба от числа нуклеотидов в молекулярной цепи), то процесс формирования или перестройки вторичной структуры молекулы дискретен и эквивалентен переходу от одной вершины графа возможных вторичных структур к другой.  Множество допустимых переходов определяется моделью процесса. В нашем случае допускаются только локальные переходы, в ходе которых в структуре могут возникать новые элементарные подструктуры, т.н. стебли. Любая вторичная структура может быть описана семейством неперекрывающихся стеблей. Число возможных стеблей имеет порядок 0.1 от квадрата числа  нуклеотидов в молекулярной цепи. Такой же порядок имеет и число допустимых переходов между соседними вершинами графа допустимых вторичных структур. Отметим, что длина цепи РНК может варьироваться от десятков до десятков тысяч нуклеотидов. Основное время вычислительного процесса при компьютерном моделировании расходуется на выбор ребра перехода от текущей вершины графа вторичных структур к следующей, обеспечивающего минимизацию свободной энергии структуры на множестве допустимых переходов. Этот же этап вычислительного процесса наиболее просто перелагается на параллельные вычислительные устройства. Оценим эффективность такого распареллеливания. Общее время, затрачиваемое одним процессором на поиск стебля, добавление которого к имеющейся структуре понижает свободную энергию молекулы наибольшим образом, оценивается как

,

где  – время вычисления свободной энергии новой структуры,  - число допустимых переходов (стеблей). Величина  линейно растет с длиной молекулярной цепи, а , как уже говорилось - квадратично, поэтому , где  - число нуклеотидов в молекулярной цепи, а  -  коэффициент пропорциональности. Если использовать вычислительную систему с  процессорами, то время вычислений сократится в  раз, но возникнут потери, связанные с пересылкой данных между процессорами. Пересылаемая информация  - это текущая вторичная структура (она имеет порядок ) и выбранный стебель из -ой части допустимых стеблей (объем этой информации примерно постоянен).

Таким образом, общее время вычислений в параллельном случае можно оценить как  

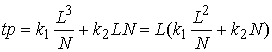
Нетрудно видеть, что эта величина имеет минимум по N, равный , и достигающийся при 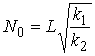. Это означает, что с ростом числа процессоров на параллельной системе можно понизить время вычислений с  до , при этом оптимальное число процессоров имеет порядок .

Рассмотрим теперь реальную ситуацию, когда у нас есть ограниченное число процессоров (N), но мы работаем со все более длинными молекулами. В этом случае эффективность распаралеливания (оцениваемая как ) меняется следующим образом:

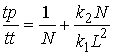
Ясно, что с ростом длины молекулярной цепи () эффективность стремится к , т.е. к максимально теоретически возможной. Следовательно, в случае нашей задачи на паралельных системах выгодно моделировать структурообразование длинных молекул, что коррелирует с тем фактом, что  структура именно длинных молекул наболее тяжело раскрывается другими методами.

15.             Вычислительные эксперименты на параллельных системах.

Выше мы   показали, что вычислительная сложность моделирования процесса образования вторичных структур РНК при заданных параметрах процесса   имеет кубический рост в зависимости от  длины молекулы.  При этом квадрат  времени раходуется на вычисления свбодной энергии переходов от текущей  структуры к потенциально возможным перестроенным структурам. В то же  время особый интерес представляет изучение структурообразования длинных молекул. Заметим,  что расчеты энергии структурных переходов могут вестись независмо друг от друга. Это определяет перспективность использования многопроцессорных систем для данного круга задач.

В 1995 году нами был разработан программный комплекс GEN, который   позволяет проводить исследования процессов образования вторичной  структуры РНК на многопроцессорном комплексе МВС-100. Он позволяет  исследовать характеристики этого процесса для заданного семейства   молекул. Распараллеливание процесса молелирования происходит на уровне расчета энергий возможных межструктурных переходов. Количество таких   переходов для молекул длиной до 100 нуклеотидов имеет порядок нескольких тысяч. Для молекул до 500 нуклеотидов – несколько десятков тысяч. А для длины 1000 - 2000 – порядка сотен тысяч - миллиона. Это позволяет эффективно использовать  возможности многопроцессорного комплекса.

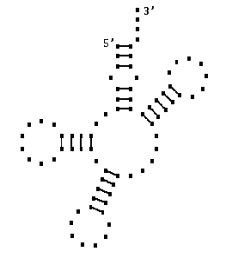
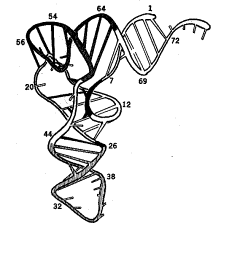
a)                                                                                                                                                    b)

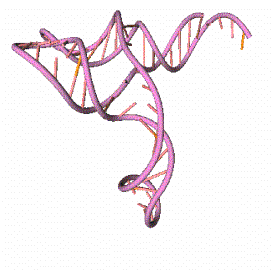
c)

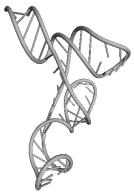
Рис. 15.1. Пример  пространственной структуры молекулы РНК, полученной методами математического моделирования. Пространственная структура молекулы тРНК Phenilalanine Yeast.  a) Вторичная структура, b) Рентгенострукутрный анализ [5].  c) Компьютерные вычисления.

В 1995-97 годах на программном комплексе GEN были исследованы  процессы структурообразования для интересных классов молекул РНК - транспортных (тРНК), рибосомальных (5S РНК), а также недавно  открытых  молекул-ферментов - рибонуклеаза P-РНК [6]. Длина этих молекул составляет  300 – 400 нуклеотидов. В семейство входит семь экземпляров молекул. Общее время расчета составило 317 часов, при этом число процессоров, участвующих в расчете, менялось в зависмости от аппаратных ресурсов, которые предоставлялись программе - от одного до 32. Заметим,  что примерное время такого расчета с использованием только одного процессора составило бы несколько тысч часов.

Эксперименты с комплексом GEN показали высокую эффективость    использования многопроцессорных методов вычислений в задачах исследования структурообразования биологических макроморлекул.  Оказалось, что для молекул длиной до 500 нуклеотидов эффективность распараллеливания составляет 60 - 70%.  В настоящее время начаты работы  по развитию следующего варианта комплекса GEN с целью увеличить возможную длину иссследумых молекул до 3000 нуклеотидов. При исследовании молекул такой  длины  эффективность  параллельной работы процессоров должна составить 90%  и выше.

В 1997-2000 годах комплекс GEN был развит, и на его основе был создан комплекс GEN-2, который позволяет исследовать характеристики структурообразования молекул РНК длиной до 3000 нуклеотидов. В настоящее время комплекс GEN-2 прошел проверку и на нем проводятся  исследования процесса структурообразования молекул из класса рибосомальных субъединиц 16S PHK. Средняя длина таких молекул составляет 2000 нуклеотидов.

16.             Примеры структур тРНК.

В данном разделе приводятся примеры третичных структур транспортных РНК, полученных методами, описанными в данной работе.

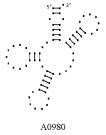
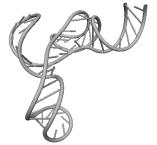
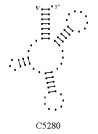
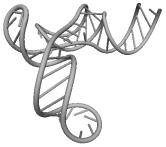
UGC THERMOPROT. TENAX                           GCA RAT

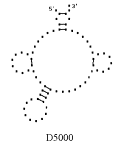
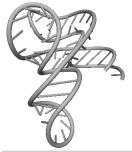
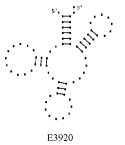
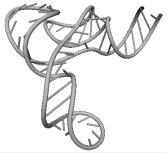
                      GUC ASTERINA PECTINI.                     UUC NICOTIANA TABACUM 

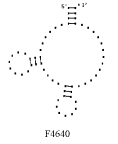
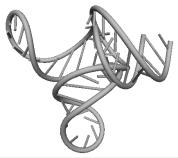
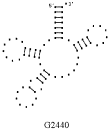
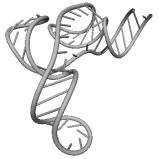
GAA ASCARIS SUUM                          UCC CHLAMYDOMO. REINH.

GUG SACCHAROMYCES CER.                          GAU ASCARIS SUUM

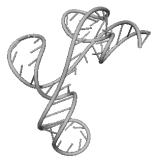
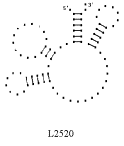
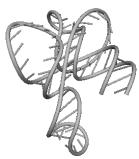
CUU TRYPANOSOMA BRUCEI                          UAG EUGLENA GRACILIS

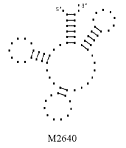
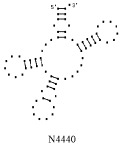
CAU HORDEUM VULGARE                        GUU TRITICUM AESTIVUM

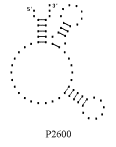
GGG MARCHANTIA POLYM.                                              UUG HUMAN

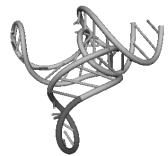
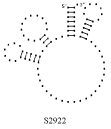
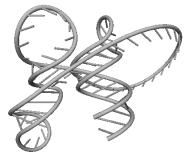
ACG CAENORHABDI. ELEG.                           UGA NICOTIANA TABACUM

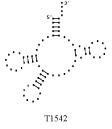
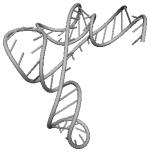
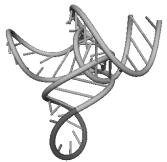
UGU BACILLUS SUBTILIS                       UAC ASCARIS SUUM

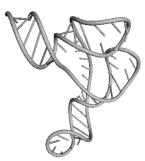
CCA SACCHAROMYCES CER.                   CAU TETRAHYMENA PYRIF.

          Вторичные структуры молекул были взяты из [7]. Молекулы выбирались случайным образом – по одной для каждой аминокислоты.

Литература

1.         Энеев Т.М., Козлов Н.Н., Кугушев Е.И. Процессы структуризации биомолекул. Результаты математического  моделирования. Препринт ИПМ им. М.В. Келдыша РАН, N 69, 1995, с. 22.

2.         Козлов Н.Н., Кугушев Е.И., Энеев Т.М.  Структурообразующие характеристики транскрипционного процесса. Математическое моделирование т.10, N 6, с.3-19, 1998.

3.         Козлов Н.Н., Кугушев Е.И., Энеев Т.М. Параллельные вычисления при решении некоторых задач астрофизики и молекулярной биологии. Математическое моделирование т.12, N 7, с.65-70, 2000.

4.         Кугушев Е.И., Старостин Е.Л.,  Пирогова Е.Е. Математическая модель образования трехмерной структуры РНК. Препринт ИПМ им. М.В. Келдыша РАН, N 77, 1997, с. 24

5.         Kim S.H., Suddath F.L., Qugley G.J., McPherson A., Sussman J.L., Wang A.H.J., Seeman N.C., Rich A. (1974) Three-Dimensional Tertiary Structure of Yeast Phenylalanine Transfer RNA. Science, 185, N 4149, 435-440.

6.         S.-Y.  Lee  and  M.  Zuker,  Jorn. of Biomol. Struct. and Dynamics. v.8, N5, 1991 pp. 1027- 1044.

7.         Sprinzl M., Dank N., Nock S., Schon A. Compilation of tRNA sequnces and sequences of tRNA genes. // Nucleic  Acids Res., 1991, v. 19, suppl., p. 2127-2171.

8.         Benham C.J. Geometry and mechanics of DNA superhelicity. Biopolymers, 1983,  v. 22, N 11, pp 2477-2495.