Содержание

5.2.3.2. Функции редукции

К функциям редукции относятся функции SUM (сумма), MULT (произведение), MAX (максимум), MIN (минимум). Результат вычисления этих функций имеет тип DOUBLE. Обращение к этим функциям имеет вид:

name-function ( ( name-domain ) arithm-expression ).

Область определяет множество точек области, в которых необходимо вычислить функцию, арифметическое выражение - множество значений, к которым применяется функция.

Пусть необходимо вычислить

Фрагмент этого вычисления на языке Норма:

Grid: (Oi: (I=I1..N) ; Oj: (J=1..M) ).

VARIABLE A DEFINED ON Grid.

VARIABLE V,W DEFINED ON Oi. VARIABLE X DEFINED ON Oj.

FOR Oi ASSUME V = W + SUM( ( OJ ) A*X) .

Пример использования вложенных функций редукции:

SurfaceMax:

(Left: (Three:(IV=1..3) ; A:(J=1..2*M);B:(I=1..2*N) );

Right: ( ( IK=1..9) ; (W=1..2*M) ; BNU:(NU=1..2*N) ) ).

SUMPOL:( (W=1..2*M) ;BNU).

ThreeAB:(Three;A;B). OLINE:(LINE=1..3).

VARIABLE VV,V DEFINED ON ThreeAB DOUBLE.

VARIABLE S DEFINED ON SurfaceMax DOUBLE.

FOR ThreeAB ASSUME

VV=SUM( (SUMPOL) SUM((OLINE)

V[IV=LINE] (V[IV=1] *S[IK=LINE]+V[IV=2]*S[IK=LINE+3]+V[IV=3]*S[IK=LINE+6]) ) ) .

Для редукционных функций справедливо правило локализации индексов: область, указанная в качестве аргумента функции редукции, вводит свою систему индексов, область действия которой - арифметическое выражение, заданное в качестве второго аргумента функции редукции. Это означает, что индексы, используемые в арифметическом выражении, можно разделить на два типа: "внутренние", то есть совпадающие с индексами области редукции и определяемые ими, и "внешние", то есть не совпадающие с индексами области редукции, и определяемые внешними областями (например, областями других функций редукции или оператора ASSUME). Множество значений "внутренних" индексов полностью определяется областью, заданной в качестве аргумента функции редукции. Множество значений "внешних" индексов определяется внешними по отношению к функции редукции областями.

Например, оператор

FOR Oik ASSUME X=(i+k) / SUM( (Oij5) B*C).

описывает запрос на вычисление

при наличии описаний :

Oij5 : ((i=1..5) ; (j=1..5)). Oik: (i=1..10) ; (k=1..10)).

Oijk: (Oij:((i=1..15) ; (j=1..15)) ;(k=1..15)).

VARIABLE B DEFINED ON Oijk. VARIABLE C DEFINED ON Oij.

VARIABLE X DEFINED ON Oik.

Если внешняя область условная, то условие действует на все внешние индексы арифметического выражения, стоящего под знаком функции редукции. Например, формула

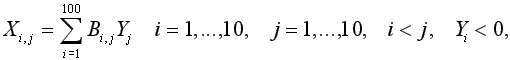
задающая вычисление

..............

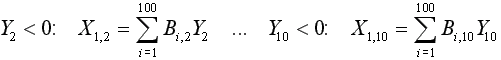
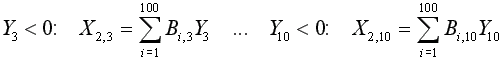
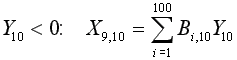
может быть записана следующим образом:

Oij: (Oi: (i=1..10); Oj: (1..10)) . OiLTj:Oij / i<j.

OiLTjYLTO, OiLTjYGEO:OiLTj / Y<0.

Oi100: (i=1..100). Oij100: (Oi100;Oj).

VARIABLE B DEFINED ON Oij100. VARIABLE X DEFINED ON Oij.

VARIABLE Y DEFINED ON Oj.

FOR OiLTjYLTO ASSUME X=SUM( ( Oi100) B*Y).

В языке Норма запрещены рекурсивные вычисления переменных, используемых в левой части оператора ASSUME и в то же время в аримфетическом выражении в функции редукции. Например, формула

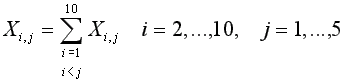
не может быть записана одним оператором ASSUME вида

FOR Oij ASSUME X = SUM ((Oij1)X).

Содержание