Measuring the Dynamics of Artificial Evolution^[1]

Mikhail S. Burtsev

Keldysh Institute of Applied Mathematics, 4 Miusskaya sq., Moscow RU-125047, Russia

mbur@narod.ru

http://www.keldysh.ru/pages/mrbur-web/

Abstract. This paper presents results of measuring evolution in a simple ALife system. Interpretation of these results is based on the notion of dynamical systems. This approach enables the discovery of periods of high evolutionary activity, which can be treated as evolutionary transitions. Attempts were also made to locate possible cycles of trajectory in the genome phase space, and it was concluded that there were no such cycles. These results demonstrate the usefulness of a dynamical systems approach in analyzing the dynamics of artificial evolution and provide suggestions for further development.

1 Introduction

When studying artificial life models, we wish to know the key features of an evolutionary process, such as its activity and stability, diversity and complexity. Measuring these features in ALife models is often complicated due to the nature of the models and the evolutionary processes themselves.

There are no direct ways to measure the fitness of an agent, a subpopulation or a whole population, and therefore no obvious way to measure how progressive an evolutionary run was. At present, measuring adaptation and fitness is one of the main issues in evolutionary theory and artificial life.

Another problem is the genotype-phenotype mapping. The diversity and complexity of the genotype are not strictly linked to the diversity and complexity of the phenotype and its behavior. It is also difficult to link elements at the level of the genotype of an agent with the acts at the behavioral level and, finally, with the consequences for survival.

In this paper we treat a simple ALife model as a dynamical system and measure its most evident characteristics, without reference to fitness.

2 Measuring Evolution

There is no explicitly defined fitness in artificial life simulations, so adaptive fitness is estimated indirectly, using various criteria. One possible criterion is to consider larger population size as indicating higher fitness of agents in the population. But competition between agents and arms races could reduce population size while agents co-adapt and become more fit.

Another indication of evolutionary activity is the speed of replication. Although a higher speed of replication for the given genotype gives it an evolutionary advantage, there is a tradeoff with the resulting disadvantages of overpopulation and overspecialization. E.g., there may be a scarcity of vital resources and decreased tolerance to environmental perturbations. Thus we must be careful of the limitations of these straightforward criteria.

Probably the most popular method for quantifying adaptive evolution in the ALife community is an evolutionary activity statistic proposed by Bedau and Packard [1,2]. The main assumption of this approach is that if a component of an evolutionary system persists, it is adaptive. One complication in applying this statistic at the genotype level is the possibility of hitchhiking. The authors suggest creating a "shadow" model to screen out neutral mutations: the shadow model is the same model, but without selection. With the aid of the shadow model, we can normalize evolutionary activities in the model and remove neutral components. However, it is not obvious for the approach, how to choose components to measure, whether they be parts of the genotype, phenotype, the agents' actions or the species. For example, if the behavior of an agent is dependant on a nonlinear interaction of genotype components, it is difficult to quantify the influence of the component on the behavior. In spite of these difficulties, the evolutionary activity statistic is a powerful method for estimating evolutionary processes, and it has been successfully applied in a number of studies [3,4].

Adami [5] proposed measuring evolution in artificial systems in terms of the complexity of an agent.  In some ALife models, e.g. Avida [6], we can easily calculate the entropy per-site of an agent's genome; this measure can give some interesting insights into the dynamics of the system. Another measure based on complexity was introduced by Nehaniv [7]. This measure, called "exhibited evolvability", is proportional to the rate of increase of complexity in a population. The original measure of complexity was presented by Nehaniv and Rhodes [8] earlier.

Several additional measures were developed by Cliff and Miller [9] to evaluate adaptive progress in cases in which fitness interdependence of co-evolving species changes the fitness landscape itself over time. E.g., the evolutionary arms races (the "Red Queen effect") mentioned in the beginning of this section.

A lot of work has been done in the area of GA [10-15] to analyze the solution space as a dynamical system, but little has been done in the field of artificial life. It is difficult to find an appropriate measure of fitness in the latter case because fitness is not defined explicitly and the models are quite complex.

In this paper I use a dynamical systems approach to quantify some aspects of the evolutionary dynamics of a system, without reference to the notion of fitness.

If we consider the population in an artificial life simulation as a dynamical system we could try to answer the following questions:

1.   How is the speed of the system movement in the phase space changing?

2.   How stable is the trajectory of the system?

3.   Does the system persist in an attractor state, or undergo transition?

4.   If the system persists in an attractor state, is the attractor a stable point or a limit cycle?

5.   How deep and how neutral is the basin of attraction?

6.   What are the control parameters of the system? Which parameters have the greatest effect on the system dynamics?

Questions 1-4 are related to evolutionary transitions and stasis, questions 5-6 to neutrality and possibilities for diversification. This paper does not answer all these questions, but rather describes an approach that enables measurement of evolutionary activity of an Alife model as a dynamical system. The following section provides a description of the ALife model, and the subsequent section presents the results for a particular simulation.

3 The Model

The model belongs to a classic set of ALife models [16-19] with simple agents in a simple world. The model was developed to study the evolution of kin selection, but is used here as a testbed.

The world in the model is a two dimensional grid which is closed to form a torus divided into knots on the grid. The world contains two kinds of objects: agents and grass, where grass is an energy resource for agents. The number of agents in any knot is unlimited, but at most one patch of grass can exist in any knot at a given point in time. Patches of grass appear randomly and are uniformly distributed on the torus.

Each agent observes part of the local environment and performs certain actions. Specifically, each agent is oriented in space and has a field of vision. The field of vision consists of four knots: the knot the agent is in, the one in front of the agent, and the ones on the left and on the right.

Agents live in discrete time. Each agent executes one of seven actions during each time step: to rest, to eat, to turn to the left/right, to move forward to the next knot, to divide, or to fight.

When an agent rests, it changes nothing in the environment. If there is a grass patch in a knot with an agent and the agent executes the "eat" action, the patch disappears. If the agent divides, an offspring is created and placed in the knot. At any given time step, if there are other agents in the knot, the agent can interact with any of them. The agent can “fight” a randomly chosen agent in the knot.

Each agent has a limited capacity to store the energy resource internally. When an agent performs an action, its internal energy resource decreases. If the agent executes the action "eat" and there is grass in the knot, the energy resource of the agent increases. When the agent produces offspring, the parent spends some amount of energy and gives half of the rest to the newborn. If the internal energy resource goes to zero, the agent dies.

The behavior of each agent is governed by simple control system, which connects inputs to outputs: the output vector O is calculated by multiplying the input vector I by a matrix of weights W. Components of W are integers in the range [-W_max,W_max].

.

(1)

The number of outputs of the agent’s control system equals the number of actions an agent can perform; at each step, the agent performs the action associated with the maximum output value.

The weights of the control system are coded in the genome of the agent.

The genome of the agent S consists of three chromosomes S = (B, W, M). The first chromosome codes the presence or the absence of individual inputs and outputs; the second one codes the weights of the control system transformation; the third chromosome codes the marker of the agent.

If the agent executes the action "divide", an offspring appears. The genome of the offspring is a copy of its parent’s genome, modified as follows:

1.   for every gene corresponding to the weight of the control system, add a small random value uniformly distributed on the interval [-p_w, p_w], where p_w is mutation intensity;

2.   with a small probability p_b , change each bit for the presence of input or output;

3.   for every gene corresponding to the marker, add a small random value uniformly distributed on the interval [-p_m, p_m], where p_m is the mutation intensity of the marker.

4 Experiment

The simulation was run with a grid size 30 x 30 and an initial population of 200 agents. To speed up program execution, the weights of the W matrix took integer values in the range [-1000,1000] and the mutation intensity p_w was set to 50.

Each agent's generation g_i, i.e. the number of ancestors, was traced. The change of the average number of generations  in the population over time is presented in Fig. 1b. The graph can be approximated by a few lines with different slopes. If we do this, we can segment the evolution of the system into several "epochs" with different and almost constant rates of evolutionary activity within epoch. Then the rate of average generation growth  (Fig. 1c) could be treated as an evolutionary (or generational) rate, i.e., the rate of generation of new solutions:

.

(2)

If we use dynamical systems approach, we could represent each agent as point in a genome phase space, and the evolution of whole population could be represented as the movement of a cloud of points.

To see how the system moves in the genome phase space, one can calculate the centroid of the population C by averaging the weights over all agents and then plotting (Fig. 1d) the Euclidean distance covered by the centroid during the given time step :

,	(3)
,	(4)

where i = weight number and N = population size.

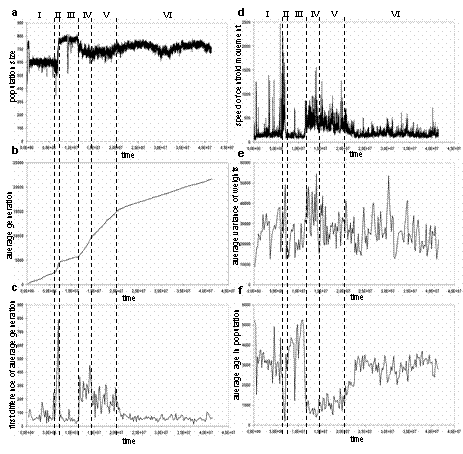
Fig. 1. Population size (a), average number of generations (b), first differences of average number of generations (c), speed of movement of the population centroid in the genome space (d), average variance of weights (e), average age of agents in the population (f).

This measure reflects the integral displacement of the system in the genome phase space during defined time intervals. The plot shows that the speed of the system's movement was higher during epochs II, IV and V than during the relatively stable epochs I, III and VI. If we consider the relatively stable states of the second set of epochs to be attractors, then the states of the more active first set of epochs are transitions between attractors. In the context of this model, we interpret epochs II, IV and V as evolutionary transitions.

The average variance of weights in the population (Fig. 1e) can serve as an indicator of diversity in the population. Although the average variance of genes weakly correlates with jumps in phase space (peaks in Fig. 1f), it is hard to hypothesize how this variance of genes is connected with evolutionary processes in our model.

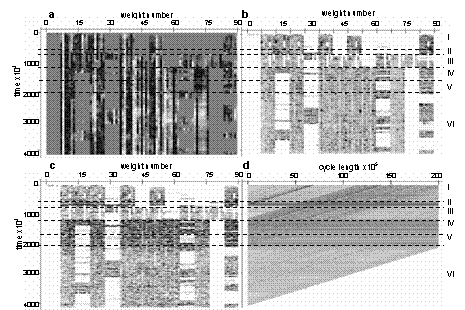
Fig. 2. Centroid weights bitmap (a) [high negative values shown in black, high positive in white, midrange in grey], weights variance bitmap (b) [here and following plots, zero shown in white and positive values in black], first differences of centroid weights bitmap (c) and distances in phase space for different cycles (d)

At the level of particular weights, evolution can be represented with the aid of bitmaps (Fig. 2). The first bitmap reflects the dynamics of the weights of the population centroid (Fig. 2a). On the bitmap, the weights are grouped by input; we see that incidents of appearance and disappearance of inputs often took place near the edges between epochs.

The complete meaning of the bitmap of the weights variance over the time (Fig. 2b) is not clear. However some vertical stripes are more uniform and brighter, i.e. have low constant variance, and perhaps the associated weights are more important for survival of agents.

The Figure 2c is a detailed analog of Figure 1e. Here the first differences of the centroid weights are plotted. The bitmap shows that during evolutionary transitions (epochs II, IV and V), the system is changing rapidly in most dimensions.

The last bitmap was created to find cycles of the population centroid trajectory in the genome phase space. (A similar approach was proposed in [9].) Such a plot can be used to help identify periodic movements of the centroid in the phase space, since the plot identifies when the system approaches a future point. The bitmap consists of vertical lines, each line for a given cycle length L. The level of gray corresponds to the Euclidean distance between the current position of the population centroid and the position after a cycle of length L:

.

(5)

If there are cycles in the phase space, they should appear as light vertical bands on the bitmap. There are no such bands in Figure 2d, but there are dark horizontal lines concentrated inside epochs II and IV. When the system is situated at the points in its phase space corresponding to the dark lines it is equidistant from all preceding and following points. So we can infer that during evolutionary transitions, the population centroid can jump quite far from the areas where it usually persists, and never return to these points.

5 Conclusions

The evolutionary dynamics of a system can be represented by the movement of the system in a phase space, using a dynamical systems approach. Applying this approach to a simple ALife model, we identified epochs in the life of the system, which we characterized as periods of evolutionary transitions and periods of smooth development. During evolutionary transitions, the system moved rapidly in the genome phase space; we found no cycles in the trajectory of the system.

The notion of splitting the evolution of the system into epochs presented here is consistent with the notion of "epochal evolution" proposed in [20]. Epochal evolution assumes existence of subbasins of attraction in the genome phase space; these are connected by portals. The population moves from one subbasin to another by tunneling through portals. By analogy, rapid movement of the system studied here corresponds to tunneling, and slow movement corresponds to persistence in a subbasin. Further investigation might include analyses of the behavior of the system in a phenotype space, as well as analyses of relationships between the behavior at the phenotype level and at the genotype level.

Acknowledgments

Thanks to Vladimir Red'ko for long and fruitful collaboration. Without his support this work would hardly be possible. Also I would like to express appreciation to Konstantin Anokhin, Peter Turchin and Joseph Spinden for careful reviewing of this paper, and, of course, to Joseph Spinden and Gary Schiltz for correcting my English.

References

1.  Bedau, M. A., and Packard, N. H.: Measurement of evolutionary activity, teleology, and life. In: C. G. Langton, C. Taylor, J. D. Farmer, and S. Rasmussen, (eds.): Proceedings of Artificial Life II, Addison-Wesley, Redwood City, CA, (1992), 431-461

2.  Bedau, M. A., Snyder, E., and Packard, N. H.: A classification of long-term evolutionary dynamics. In: C. Adami, R. Belew, H. Kitano, and C. Taylor, (eds.): Proceedings of Artificial Life VI, Los Angeles, MIT Press, Cambridge, MA, (1998), 228-237

3.  Channon, A. D.: Passing the ALife test: Activity statistics classify evolution in Geb as unbounded. In: J. Kelemen, P. Sosik (eds.): Advances in Artificial Life, Proceedings of 6th European Conference (ECAL 2001), Prague, Czech Republic, Springer, (2001)

4.  Pachepsky, E., Taylor, T., Jones, S.: Mutualism promotes diversity and stability in a simple artificial ecosystem. Artificial Life, Vol. 8(1). MIT Press, (2002), 5-24

5.  Adami, C., Ofria, C., Collier, T. C.: Evolution of biological complexity. Proc. Nat. Acad. Sci. 97, (2000), 4463-4468

6.  Adami, C.: Introduction to Artificial Life. Springer, New York, (1998)

7.  Nehaniv, C. L.: Measuring evolvability as the rate of complexity increase. In: C. C. Maley and E. Boudreau, (eds.): Artificial Life VII Workshop Proceedings, (2000), 55-57

8.  Nehaniv, C. L. and Rhodes, J. L., The evolution and understanding of biological complexity from an algebraic perspective. Artificial Life, 6(1). MIT Press, (2000), 45-67

9.   Cliff, D., Miller, G. F.: Tracking the Red Queen: Measurements of adaptive progress in co-evolutionary simulations. In: F. Moran, A. Moreno, J. J. Merelo and P. Cachon (eds): Advances in Artificial Life, Proceedings of the Third European Conference on Artificial Life (ECAL95), Lecture Notes in Artificial Intelligence 929, Springer Verlag, (1995) 200-218

10.  van Nimwegen, E., Crutchfield, J. P., Mitchell, M.: Statistical Dynamics of the Royal Road Genetic Algorithm. Theoretical Computer Science, 229, (1999)

11.  Nix, A. E., Vose, M. D.: Modeling genetic algorithms with Markov chains. Annals of Mathematics and Artificial Intelligence, 5, (1991)

12.  Vose, M. D., Liepins, G. E.: Punctuated equilibria in genetic search. Complex Systems, 5, (1991)

13.  Prugel-Bennett, A., Shapiro, J. L.: Analysis of genetic algorithms using statistical mechanics. Physical Review Letters, 72(9), (1994) 1305-1309

14.  Prugel-Bennett, A., Shapiro, J. L.: The dynamics of a genetic algorithm in simple random Ising systems. Physica D, 104 (1), (1997), 75-114

15.  Rattray, M., Shapiro, J. L.: The dynamics of a genetic algorithm for a simple learning problem. J. of Phys. A, 29(23), (1996), 7451-7473

16.  Riziki, M.M., Conrad, M.: Computing the Theory of Evolution. Physica D, 22, (1986), 83-99

17.  Packard, N.: Intrinsic adaptation in a simple model for evolution. In: C.G. Langton (ed.): Artificial life, Redwood City, Addison-Wesley, CA, (1989), 141-155

18.  Ackley, D., Littman, M.: Interactions between learning and evolution. In: Langton, C. G., Taylor, C., Farmer, J. D., and Rasmussen, S. (eds.): Artificial Life II. Addison-Wesley, (1992), 487-509

19.  Yaeger, L.: Computational Genetics, Physiology, Learning, Vision, and Behavior or PolyWord: Life in a New Context. In Langton, C. G. (ed.): Artificial Life III. Addison-Wesley, (1994), 263-298

20.  Crutchfield, J. P.: When Evolution is Revolution – Origins of Innovation. In James P. Crutchfield, J. P. and Schuster, P. (eds.): Evolutionary Dynamics: Exploring the Interplay of Selection, Accident, Neutrality, and Function. Oxford University Press, (2002), 101-134