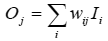Artificial Life Meets Anthropology: A Case of Aggression in Primitive Societies^[1]

Mikhail S. Burtsev

Keldysh Institute of Applied Mathematics, 4 Miusskaya sq., Moscow RU-125047, Russia

mbur@narod.ru

http://www.keldysh.ru/pages/mrbur-web/

Abstract. One of the greatest challenges in the modern biological and social sciences has been to understand the evolution of altruistic and cooperative behaviors. General outlines of the answer to this puzzle are currently emerging as a result of developments in the evolutionary theories of multilevel selection, cultural group selection, and strong reciprocity. In spite of the progress in theory there is shortage of studies devoted to the connection of theoretical results to the real social systems. This paper presents the model of cooperation which is based on assumptions of heritable markers, constrained resource, and local interactions. Verification of model’s predictions with the real data on aggression in archaic egalitarian societies has demonstrated that initial modeling assumptions are acceptable as major factors of social evolution for these societies.

1 Introduction

Many different forms of social organization are found in both historical and contemporary societies, such as kin-groups, bands, tribes, chiefdoms, and states. The question of how these modes of collective action emerge and persist is an important theoretical topic in anthropology, sociology, political science, and history. One influential theory explaining how societies form is the social contract theory, as formulated, for example, by Thomas Hobbes in his work Leviathan (1651). Hobbes' main idea is that people submit to the authority of the sovereign, who enforces the social rules, thereby maintaining peace and social stability. The main problem with this theory is that of contract enforcement. Different versions of social contract theory provide their own mechanisms of enforcement, but none of them solve the so called free-rider problem [1].

An alternative view on the emergence of societies is provided by the theories of social evolution. Pioneered in the works of evolutionary biologists [2,3], these theories have been applied to the study of human cooperation and is undergoing intensive development today. Of particular relevance are the theories of multilevel selection [4] and cultural group selection [5]. A series of mathematical models explore how human cooperation can arise [6]. These models are based on the hypotheses of kin and group selection, biased cultural transmission, and perhaps nonrandom (directed) variation. Other models studied the interplay between different kinds of reciprocity and punishment and its consequences for the evolution of cooperation [8]. The authors coined the term "strong reciprocity", which refers to the phenomenon that some people have predisposition for altruistic cooperation and altruistic punishment (norm enforcement). Bowles, Gintis and others showed that a small fraction of agents characterized by strong reciprocity could drive the whole population to a cooperative equilibrium. Important results on the evolution of cooperation in the spatially distributed and structured populations were also obtained by Axelrod et al. [8,9]. Finally, it was shown that cooperation could originate in the population of agents with arbitrary tags in the absence of reciprocity [10].

The main tool used today in the field of the evolution of cooperation is game theory. It can be purely analytical game-theoretic models, or agent-based simulations [11]. This theoretical approach yields clear-cut results, but the simple structure of payoffs and a small fixed set of strategies, imposed by investigators, in some cases may be an unrealistic assumption. It is possible to design a much harder test for the theories of social evolution. One such approach, adopted in this paper, is provided by the agent-based evolutionary models in which strategies of agents are not predetermined by researcher but emerge from elementary actions of agents.

The study of cooperation and artificial life are mostly theoretical endeavors: few are grounded with real data. Among them are outstanding examples such as a study of cultural group selection in New Guinea [12] and the simulation of Kayenta Anasazi historical dynamics in Long House Valley [13]. The first study resulted in estimation of cultural change rate. It was argued that significant change of cultural traits under group selection takes from 500 to 1000 years and therefore the more rapid social transformations should be driven by other factors. The results of the second study demonstrated that with the aid of a multi-agent computational model the main features of the history of prehistoric inhabitants of Long House Valley, located in the Black Mesa area of northeastern Arizona (USA) can be closely reproduced. Among these features were population ebb and flow, changing spatial settlement patterns, and eventual rapid decline. The agents in the model were monoagriculturalists, who decide both where to situate their fields and where to locate their settlements.

Filling the gap between the theory and computer modeling on the one hand and objective world on the other is one of the actual tasks of artificial life research. This paper presents an attempt to test predictions generated by rather simple artificial life model of cooperation with the real data. The next section provides description of the model and is followed by a presentation of model’s predictions and discussion of their correspondence to the real social systems. The final section is an outline of some conclusions.

2 The Model

The main modeling assumptions were as follows:

·     Evolution. The strategies in the population evolve through reproduction of agents by the means of mutation and selection.

·     Markers. Individual markers provide a potential tool for agents to differentiate in-group versus out-group members.

·     Local interactions. All agents interact locally, as in real social networks.

·     Limited resources. Agents have limited resources, which serves as a factor of selection in the artificial environment.

The world in the model is a two dimensional closed grid, which forms a torus. There are agents and patches of resource in the world. Only one patch of resource can exist in any cell at a given moment of time, but the number of agents in any cell is unlimited. Patches of resource appear randomly at a constant rate and are uniformly distributed in the space.

An agent can observe its local environment and perform certain actions. The agent is oriented in space and has a field of vision. The field of vision consists of four cells: the cell the agent currently occupies, and the adjacent cells directly to the left, front, and right relative to the orientation of the agent. The agent lives in a discrete time. The agent executes one of seven actions during each time step: rest, consume a resource, turn to the left/right, move forward to the next cell, divide, or fight.

When an agent rests, she changes nothing in the environment. If there is a resource patch in the cell with an agent and she executes the "consume" action, the patch disappears. If the agent divides, an offspring is created and placed in the cell. Each time step before the action is calculated for the given agent one of the other agents in the cell is chosen randomly for potential interaction. The agent can “fight” this chosen one.

Each agent stores a finite amount of resource on which to live. When the agent performs any action, its internal resource decreases. If the agent executes the action "to consume" and there is resource in the cell, the internal resource of the agent increases. When the agent produces offspring, the parent spends some amount of resources in this process and gives half of the rest to the newborn. After executing the "fight" action, the agent takes some amount of resource from the victim. If the internal resource goes to zero, the agent dies.

Each agent has external phenotype that is coded by a vector of integer values (markers). These markers are inherited with mutations by offspring. Thus the Euclidian distance between markers of two agents gives measure of their kinship.

Behavior of the agent is governed by a simple control system. In this system each output associated with a certain action is connected with each input, which is associated with a certain sensory input from environment or internal state of the agent. The control system is a linear system, which is functioning similarly to a feed-forward neural network with no hidden layer. To calculate the output vector O of values, the input vector I should be multiplied by a matrix of weights W. Values of W are integers in the range [‑W_max,W_max].

(1)

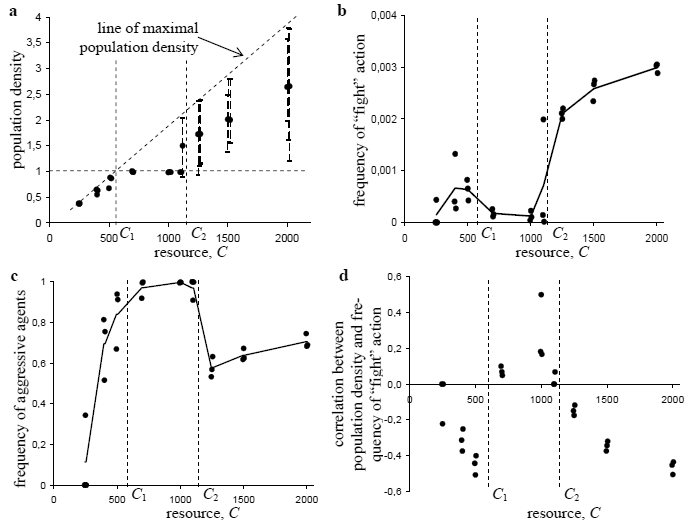
At each time step, the agent performs the action associated with the maximum output value.

The input vector I is filled with information about presence of resource and other agents in the field of vision, level of internal resource and Euclidean distance between marker vectors of current agent and its partner for potential interaction.

The weights of the control system are coded in the genome of the agent.

The genome of the agent S consists of three chromosomes S = (B, W, M). The first chromosome is the bit string which codes the presence or absence of individual sensory inputs and actions; the second one is the vector of integers which codes the weights of the control system transformation and the third chromosome, also vector of integers, codes the kinship marker of the agent.

If the agent executes the action "divide", its offspring appears. The genome of the offspring is constructed with the aid of the following evolutionary algorithm:

1.   for every gene corresponding to the weight of the control system, add a small random integer value uniformly distributed on the interval [-p_w, p_w], where p_w is mutation intensity;

2.   with a small probability p_b, change each bit for the presence of sensory input or action;

3.   for every gene corresponding to the kinship marker, add a small random integer value uniformly distributed on the interval [-p_m; p_m], where p_m is the mutation intensity of the marker.

More details on the implementation of the model could be found in [14].

3 Results and Discussion

The model described in the previous section lacks mechanisms for complex social interactions thus the simulation results are not applicable to just any complex society. But it is reasonable to conjecture that modeling assumptions (see the beginning of the previous section) hold for the archaic egalitarian societies such as communities of hunter-gatherers and primitive agriculturalists. This section is devoted to testing this hypothesis.

One of the largest domains in the area of ethnographic, anthropological, and cross-cultural studies of primitive societies is committed to the research on interrelations of resources availability, aggression, and population pressure [15-22]. So it can provide us with a variety of theories to compare and with data on the real societies to verify predictions of the simulations.

Below the agent from the model will be treated as a community of hunter-gatherers (a band) or primitive agriculturalists. In egalitarian societies, a community consisting of few nuclear or one extended family behaves like autonomous entity [23]. Members of community move, settle, and fight together. It is assumed that internal resource of an agent (from the model) corresponds to the human resource of community (its size). These assumptions allow us to grasp the following features of primitive societies in the model.

1.   Capturing enemies. For primitive societies it was a common practice that captured during an attack men were used as slaves, women as wives and children were adopted [19,20]. In the model when one agent fights another agent the former captures some amount of internal resource of the latter.

2.   Evolution is based on already obtained adaptation. If one accepts that prehistoric humans evolved pre-adaptations for hunting and gathering in small bands (“tribal social instincts” hypothesis [24]) it should be expected that development of more complex social organization will be based on and constrained by this pre-adaptations. This “tribal social instincts” hypothesis is manifested in the model as a limitation of the capacity of agent’s internal resource. In other words it is assumed that a community exists as stable social entity if its size is under some threshold (maximal size of a band).

The evolution of cooperation in the model is based on the presence of phenotypic markers. The model marker of an agent is inherited in the same manner as a strategy of its behavior. Therefore agents with similar markers will have similar behavior and it is reasonable to think of ability of agents to differentiate each other markers in the model as ability of actors in the real social systems to perceive common descent or cultural markers.

Two measures were introduced to estimate an aggression level in the model.

1.   Frequency of execution of the “fight” action in a population.

2.   Frequency of aggressive agents in a population. Here an aggressive agent is an agent which can potentially fight other agent at the cell where it is situated. Every agent in a population was tested with a fixed set of most frequent alternatives of interactions (similar vs. different marker, low vs. high internal resource) and if in any situation an agent has performed a “fight” action it was treated as “aggressive”.

As it was mentioned in the beginning of this section a large body of research on aggression in primitive societies is devoted to the study of dependence of aggression level and population density on variation in resource supply. Resources available to community in primitive societies are generally dependent on ecological conditions and on level of resources extraction technology. In the model bundles of resource which an agent can consume appears in every cell of environment with some constant probability. In a series of simulations amount of a resource in a bundle C was varied in one order of magnitude. The range of variance in amount of resource in a bundle was set in a way that for smallest values it was insufficient for agent survival without them moving out of cell. At highest values of resource supply allowed survival of few agents in one cell. As a result the simulations with low resource supply correspond to hunter-gatherers in poor ecological conditions and the simulations with high resource supply to primitive agriculturalists and hunter-gatherers with rich resource base.

The dependence of population density on an amount of a resource in a bundle C breaks on three parts (see fig. 1a). When resource supply is insufficient to support survival of one agent in the cell C < C₁ population density reaches maximum for the given value of the C. If resource base is sufficient for survival of one agent in the cell but not two C₁ ≤ C < C₂ then the number of agents per cell does not depend on C and equals 1. In this case every cell is usually occupied by only one agent which prefers don’t move. If there is other agent in the cell then the dominant strategy to escape the cell in the case of small distance between marker-vectors and fight in opposite. For the C ≥ C₂ there is no dominant strategy in a population. The model demonstrates complex interplay of mixture of cooperative and non-cooperative predator and prey strategies which results in oscillation of population density.

Applying the two measures of aggression—proposed above—to the simulation results gives dependencies which are presented on the figures 1b and 1c. Predictions of the model can be summarized as follows.

1.   In the condition of poor resource base (C < C₁), a portion of aggressive agents and a frequency of acts of aggression should grow with increase of resource supply.

2.   At intermediate resource supply (C₁ ≤ C < C₂), almost every agent should be able to fight (fig. 1c) but frequency of actually performed aggressive actions is very low (fig. 1b).

3.   In the case of rich resources (C > C₂), both amounts of aggressive agents and acts of aggressions should increase as supply rises.

Modern anthropology suggests that for primitive societies a general tendency is an increase of aggression with an enhancement of environmental conditions [16,17,21,22]. Simulation results fit this tendency for the ranges of poor (C < C₁) and rich (C > C₂) resource base (see fig. 1b and fig. 1c). But for the intermediate values of resource supply (C₁ ≤ C < C₂) it looks like that simulations contradict anthropological theory. On the other hand data about four Kalahari Bushmen groups which were provided in the influential work of Cashdan [17] shows exception from the general theory. Among these four groups, !Ko, G/wi, Nharo, and !Kung, the first lived in the poorest ecological conditions and the last in the best but the !Ko demonstrated the most territorial and aggressive behavior and the !Kung were looked the most peaceful.

Fig. 1. Dependence of population density (a), frequency of “fight” action (b), frequency of aggressive agents (c), and correlation between population density and frequency of “fight” action (d) on resource supply. Dots correspond to the values for different simulation runs; solid lines connect averages.

If one tries to align the data from Cashdan [17] with the simulations results it is reasonable to consider resource supply of the !Ko as falling in the range C < C₁ and resource supply of the !Kung in the range C₁ ≤ C < C₂. In this case the model predicts a higher aggression rates for the !Ko and a lower for the !Kung (fig. 1b). So the model’s prediction matches the data in this case. Another prediction of the model requires the !Kung to be ready to perform violent act at any moment (fig. 1c). The !Kung are hunting with bow and poisoned arrows, so there are no technical problems for the !Kung bushman to kill another man. Moreover the !Kung have norms prescribing circumstances in which one !Kung is allowed to kill another one. For example, the bushman who finds a hive obtains rights on the honey from that hive. The owner of a hive is allowed to kill anybody who attempts to take honey from the hive without permission. Such features of the !Kung bushmen as low level of observable aggression and high potential for producing violent acts fit surprisingly the second prediction form the list above. The contradiction between the actual and potential aggression is not unique for the !Kung; a similar pattern can be found among Australian’s aboriginals. Aboriginals from the Western Desert have ecological conditions similar to the !Kung. These aboriginals demonstrate low level of violence as the !Kung do but have institutes of socialization for aggression such as ritual fights and formation of secret groups of avengers, etc [21,22].

The Malthusian suggestion that population pressure should lead to war is commonly accepted in current anthropology for the case of preindustrial stateless societies [22]. Recent developments in the modeling of warfare in primitive agricultural societies are based on the approaches of population dynamics [26] and also consider population density as the major determinant positively affecting the level of warfare. The straight Malthusian approach predicts positive correlation between population density and frequency of warfare. The models of Turchin and Korotaev [26] give a weak negative correlation. Correlations between population densities and frequency of “fight” actions in the population for the simulations with the artificial life model are given on the figure 1d.

A cross-cultural test has been completed to compare all three predictions. As the source of data on real societies a Standard Cross-Cultural Sample database [27] was used. The correlations between density of population and few internal warfare variables were calculated for the societies with low level of political integration and extensive agriculture as subsistence technology. The results of cross-cultural test are presented in the table 1.

The results presented in the table 1 are in agreement with results of similar analyses provided in [22]. The analysis reveals rather strong negative correlation between variables “Density of Population” and “Frequency of Intercommunity Armed Conflict” r = -0,489 , p = 0,046. Societies with extensive agriculture correspond to the simulated populations with rich resource supply (C > C₂). Simulation results for the highest value of resource (fig. 1d, C = 2000) give the closest match to the data. The pure Malthusian approach and the models of Turchin and Korotaev are not supported by data.

In addition to the population pressure one more factor believed to affect warfare is predictability of resources. Embers [28-30] showed that resource problems, particularly those created by unpredictable weather or pest disasters strongly predict warfare frequency (for direct archaeological evidence on unpredictable resource fluctuations as a major factor of warfare frequency see, e.g., [31,32]). Multivariate analyses for nonstate societies gave standardized coefficient of r = 0,631 (p < 0.001, one tail) for natural disasters as predictor of warfare ([29] p. 254). Furthermore, the correlation between the presence of unpredictable natural disasters destroying food supplies and warfare frequency has turned out to be stronger than the one attested for more than a dozen various warfare frequency factors tested by the Embers.

Table 1. The results of cross-cultural test^[2] (data for the test are taken from a Standard Cross-Cultural Sample database [27]).

	“Density of Population” v156
Name of variable and its number in Standard Cross-Cultural Sample [27]	r	p*
“Frequency of Intercommunity Armed Conflict” v693	-0,489	0,046
“Frequency of Violent Conflict Between Groups within Local Communities” v1750	-0,230	0,375
“Frequency of Violent Conflict Involving at Least One Local Community” v1758	-0,208	0,408

^*A correlation is significant if p < 0,05.

Table 2. Two measures of aggression for the high and low predictability of resources in the model.

	case 1	case 2	case 3	average
high predictability of resources
Frequency of execution of the “fight” action in a population.	0,000686	0,000807	0,000791	0,000761
Frequency of aggressive agents in a population.	0,119	0,176	0,172	0,156
low predictability of resources
Frequency of execution of the “fight” action in a population.	0,00234	0,00267	0,00274	0,00258
Frequency of aggressive agents in a population.	0,617	0,672	0,625	0,638

 

To test if the model could grasp this phenomenon, two series of simulations were performed [33]. They differ in amount of resources in a patch and frequency of patch appearance. For the first series, the frequency of resource appearance was ten times greater than for the second, but amount of resources in a patch was ten times smaller than for the second. So, for both cases total amount of resources which could be collected by agent during given period of time was equal, but the probability (and, hence, predictability) of obtaining a single portion of resource for the first series was ten times greater than for the second.

As shown in table 2 measures of aggression proposed above drop in almost three times for simulations with high predictability of resources with respect to low predictability. So the model is deemed to have passed in the third test as well.

4 Conclusion

The artificial life model of evolution of cooperation—based on assumptions of heritable markers, constrained resource, and local interactions—demonstrates surprising fit to some features of real social systems. The model captures a general trend of increasing of the aggression level with a rising resource supply in primitive societies but grasps also some exceptions such as a case of !Ko and !Kung in Kalahari desert which demonstrates reverse interdependence between resource base and aggression. At some level of resources in environment, the model predicts mismatch between levels of actually manifested aggression and the propensity to perform violent acts. This prediction finds support in the behavior of !Kung bushmen and aboriginals of Western Desert of Australia. The correlation between population density and frequency of fight action for the case of rich resources in the model is similar to the analogous correlation extracted from ethnographic database. Finally, impact of resource predictability on internal warfare observed for real societies is correctly replicated in the model’s behavior. All this allows us to consider that initial modeling assumptions are acceptable as major factors of social evolution in archaic egalitarian societies.

Acknowledgements

Thanks to Peter Turchin who fed me with the idea to model cooperation, Daria Khaltourina for the introduction to the cross-cultural method and discussion of modeling assumptions, Andrey Korotayev for the idea to study how aggression in the model depends on the resource predictability. I deeply acknowledge the anonymous reviewers for their suggestions and comments.

References

1. Kraus J.S. The Limits of Hobbesian Contractarianism. – Cambridge: Cambridge University Press, 1993.

2. Hamilton W.D. Innate social aptitudes of man: An approach from evolutionary genetics / In: Biosocial Anthropology, ed. R. Fox, p.115–132. New York: Wiley, 1975.

3. Wilson E.O. Sociobiology: The new synthesis. – Cambridge: Belknap Press, 1975.

4. Sober E., Wilson D.S. Unto Others: The Evolution and Psychology of Unselfish Behavior. – Cambridge: Harvard University Press, 1998

5. Richerson P.J., Boyd, R. Not By Genes Alone: How Culture Transformed Human Evolution. – Chicago: University of Chicago Press, 2005.

6. Boyd R., Richerson, P.J. The Origin and Evolution of Cultures. – Oxford: Oxford University Press, 2005.

7. Bowles S., Gintis H. The evolution of strong reciprocity: cooperation in heterogeneous populations // Theoretical Population Biology V.65, p.17-28, 2004.

8. Axelrod R. The evolution of cooperation. – New York: Basic Books, 1984.

9. Cohen M.D., Riolo R L. Axelrod R. The role of social structure in the maintenance of cooperative regimes // Rationality Soc. V.13, p.5-32, 2001.

10. Riolo R., Cohen M.D., Axelrod R. Evolution of cooperation without reciprocity // Nature V.414, p.441–443, 2001.

11. Epstein J.M., Axtell R.L. Growing artificial societies: Social science from the bottom up. – MA: MIT Press, 1996.

12. Soltis J., Boyd R., Richerson P.J. Can group-functional behaviors evolve by cultural group selection? An empirical test // Current Anthropology V.36, p.437-94, 1995.

13. Gumerman G.J., Swedlund A.C., Dean J.S., Epstein J.M. The Evolution of Social Behavior in the Prehistoric American Southwest // Artificial Life V.9, p.435–444, 2003.

14. Burtsev M.S. Tracking the Trajectories of evolution // Artificial Life V.10, p.397-411, 2004.

15. Vayda A.P. Warfare in Ecological Perspective // Annual Review of Ecology and Systematics, V.5, p.183-193, 1974.

16. Dyson-Hudson R., Smith E.A. Human territoriality: An Ecological Reassessment // American Anthropologist V.10, p.21-41, 1978.

17. Cashdan E. Territoriality among Human Foragers: Ecological Models and an Application to Four Bushman Groups // Current Anthropology V.24, N1, p.47-55, 1983.

18. Ember C.R., Ember M. War, Socialization and Interpersonal Violence: A Cross-Cultural Study // The Journal of Conflict Resolution V.38, N4, p.620-646, 1994.

19. Shnirelman V.A. The roots of war and peace. War and Peace in the Early History of Humankind, V.1. – Moscow: IEA RAS, 1994. (In Russian)

20. Otterbein K.F. Killing of Captured Enemies: A Cross-cultural Study // Current Anthropology V.44, N3, p.439-443, 2000.

21. Kazankov A.A. Factors of Intercommunity Aggression In Archaic Societies: Hunter-Gatherers of the Semi-Arid Zones. – Moscow: IA RAS, 2002. (In Russian)

22. Nolan P.D. Toward an Ecological-Evolutionary Theory of the Incidence of Warfare in Preindustrial Societies // Sociological Theory V.21, N1, p.18-30, 2003.

23. Kabo V.R. Primitive Preagricultural Community. – Moscow: Nauka, 1986. (In Russian)

24. Richerson P.J., Boyd R., Henrich J. The Cultural Evolution of Human Cooperation // The Genetic and Cultural Evolution of Cooperation, P. Hammerstein ed., p.357–388. Cambridge MA: MIT Press, 2003.

25. Terry M. War of the Warramullas. – Adelaide: Rigby, 1974.

26. Turchin P., Korotayev A. Population Dynamics and Internal Warfare: a Reconsideration // submitted to American Anthropologist.

27. Standard Cross-Cultural Sample Variables (Edited by William T. Divale, Daria Khaltourina and Andrey Korotayev) // World Cultures V.13, 2002.

28. Ember M. Statistical evidence for an ecological explanation of warfare // American Anthropologist V.84, p.645-649, 1982.

29. Ember C.R., Ember M. Resource Unpredictability, Mistrust, and War: A Cross-Cultural Study // Journal of Conflict Resolution V.36, p.242-262, 1992.

30. Shankman P. Culture contact, cultural ecology, and Dani warfare // Man V.26 p.299-321, 1991.

31. Kang B.W A Reconsideration of Population Pressure and Warfare: A Prehistoric Korean Case // Current Anthropology, V.41, p.873–881, 2000.

32. Lekson S.H. War in the Southwest, War in the World // American Antiquity V.67, p.607-624, 2002.

33. Burtsev M.S., Korotaev A.V. An Evolutionary Agent-Based Model of Pre-State Warfare Patterns: Cross-Cultural Tests // submitted to World Cultures.