Г л а в а  4

МНОГОВАРИАНТНОСТЬ

      Конфигурационные построения, разбиравшиеся в предшествующих главах, могут использоваться практически всюду, где требуется разработка достаточно сложных программ. Область применения вариантного программирования, о котором пойдет речь в данной главе, также весьма широка. (Достаточно вспомнить вариантные фрагменты, настраивающие приложение на ту или иную вычислительную платформу, — с ними, вероятно, многим доводилось иметь дело.) Но относительный вес манипуляций над вариантами в общем объеме работ зачастую оказывается не таким уж заметным, из-за чего потребности в рациональном их оформлении отодвигаются на задний план.
      Существует, однако, важный класс задач, для которого эффективное обеспечение многовариантности совершенно необходимо, более того, оно превращается в центральную проблему организации программирования. Этот класс задач — вычислительный эксперимент.

4.1. Вычислительный эксперимент

      Вычислительный эксперимент — метод изучения устройств или физических процессов с помощью математического моделирования. Он предполагает, что вслед за построением математической модели проводится ее численное исследование, позволяющее «проиграть» поведение исследуемого объекта в различных условиях или в различных модификациях [Самарский, 1979; Горбунов-Посадов, 1990].
      Численное исследование модели дает возможность определять разнообразные характеристики процессов, оптимизировать конструкции или режимы функционирования проектируемых устройств. Более того, случается, что в ходе вычислительного эксперимента исследователь неожиданно открывает новые процессы и свойства, о которых ему ранее ничего не было известно.

      4.1.1. Сфера применения. Вычислительный эксперимент занимает промежуточное положение между натурным экспериментом и аналитическим исследованием.
      Натурный (физический) эксперимент при надлежащей постановке может, вообще говоря, дать исчерпывающие и надежные результаты. И все же во многих случаях предпочтение отдается вычислительному эксперименту.
      Дело в том, что в вычислительном эксперименте в роли опытной установки выступает не конкретное физическое устройство, а программа. Ее построение и последующие модификации, как правило, требуют существенно меньших затрат, чем подобные манипуляции над реальным объектом.
      Кроме того, в опытной установке нередко просто невозможно бывает воссоздать некоторые критические режимы или экстремальные условия. Поэтому математическое моделирование может оказаться практически единственно возможным способом исследования.
      При аналитическом подходе так же, как и в вычислительном эксперименте, строится математическая модель. Но исследуется эта модель исключительно посредством аналитических выкладок, без привлечения каких-либо численных методов. Если аналитических выкладок оказывается достаточно, то данный подход приводит к строгому точному решению.
      Однако на практике, как это ни парадоксально, аналитическому подходу обычно отводится роль инструмента для (сравнительно быстрого) получения грубых оценок. Объясняется это тем, что аналитическими выкладками удается ограничиться только для несложных, сильно упрощенных моделей реальных процессов. Получаемое тут строгое аналитическое решение на самом деле в силу исходного огрубления модели оказывается весьма далеким от совершенства. Напротив, численные методы, применяемые в вычислительном эксперименте, дают возможность изучать более сложные модели, достаточно полно и точно отражающие исследуемые процессы.
      Отмеченные достоинства вычислительного эксперимента вывели его в число основных методов исследования таких крупных физических и инженерно-технических проблем, как задачи ядерной энергетики, освоения космического пространства и др. Программные комплексы, обслуживающие вычислительный эксперимент, объемны и сложны, в их создание вовлечен многочисленный отряд программистов. Поэтому особую актуальность приобретает изучение возникающих здесь конфигурационных построений, которые, как будет видно из дальнейшего изложения, постоянно находятся в центре внимания участников такого рода разработок.

      4.1.2. Цикл вычислительного эксперимента. В цикле вычислительного эксперимента можно выделить следующие этапы (рис. 4.1).

 
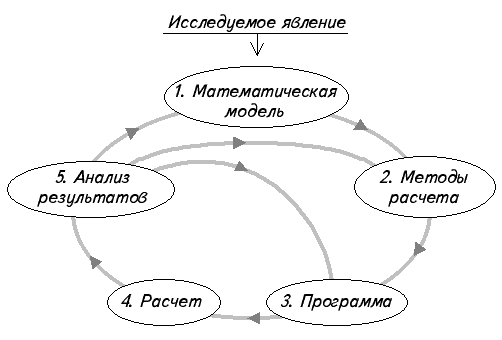
Рис. 4.1.  Этапы вычислительного эксперимента

      Э т а п  1.   Построение математической модели (составление уравнений, описывающих исследуемое явление).
      Э т а п  2.   Выбор численных методов расчета (построение дискретной модели, аппроксимирующей исходную математическую задачу, построение разностной схемы, разработка вычислительного алгоритма и т. д.).
      Э т а п  3.   Создание программы, реализующей вычислительный алгоритм.
      Э т а п  4.   Проведение расчетов и обработка полученной информации.
      Э т а п  5.   Анализ результатов расчетов, сравнение (если это возможно) с натурным экспериментом.

      Обычно на последнем (5-м) этапе исследователь приходит к заключению о том, что необходимо внести определенные изменения в решения, принятые на этапах 1, 2 или 3.
      Так, может выясниться, что построенная модель недостаточно хорошо отражает особенности исследуемого явления. В этом случае модель корректируется, вносятся соответствующие поправки в численные методы и реализующие их программы и выполняется новый расчет. Тем самым цикл вычислительного эксперимента воспроизводится в полном объеме.
      При анализе результатов могут быть выявлены какие-либо недостатки используемых численных методов, связанные, в частности, с соображениями точности или эффективности. Изменение методов влечет за собой изменение соответствующих программ и т. д. Иначе говоря, цикл повторяется в несколько сокращенном виде (этапы 2–5).
      Наконец, может оказаться неудачным некоторое программное решение, например выбранный способ работы с внешней памятью. Пересмотр таких решений приводит к повторению этапов 3–5.

      4.1.3. Особенности программирования. Разумеется, циклы, подобные циклу вычислительного эксперимента, возникают практически в любом мало-мальски сложном программном проекте. Самая первая версия программы обычно чем-нибудь не удовлетворяет разработчика или заказчика, и приходится уточнять постановку задачи, улучшать отдельные алгоритмы и т. д. Однако в большинстве случаев достаточно бывает выполнить несколько циклов, требующих сравнительно небольших усилий, и программа обретает желаемый вид.
      Совершенно иначе обстоит дело в вычислительном эксперименте. Здесь программа мыслится как экспериментальная установка, от первых опытов с которой вряд ли следует ожидать сколько-нибудь интересных результатов. Данные первых опытов послужат всего-навсего отправной точкой длительного процесса изменений и усовершенствований установки, который только и способен привести к достаточно обоснованным заключениям об исследуемом объекте.
      Таким образом, появление первоначальной версии программы лишь в самых общих чертах намечает направление исследований. Основная же работа по программированию еще впереди — она связана с многократными модификациями программы, отражающими эволюцию математической модели и методов ее расчета. Число циклов вычислительного эксперимента, каждый из которых сопряжен с модификацией расчетной программы, нередко достигает десятков тысяч. Поэтому рациональная организация таких модификаций — ключ к эффективному программированию данного класса задач.
      Продолжая параллель с натурным экспериментом, можно заметить, что там обычно не спешат выбрасывать на свалку отдельные узлы, изъятые или замененные в экспериментальной установке при проведении очередного опыта: они еще не раз могут пригодиться впоследствии. Аналогично и решения (а вместе с ними и соответствующие им фрагменты программ), пересматриваемые на очередном цикле вычислительного эксперимента, как правило, не отбрасываются и могут использоваться затем для других расчетов. Например, метод, оказавшийся непригодным для одной модели, вполне может подойти для расчета следующей модели и т. д.
      Итак, главное направление деятельности программиста, занятого вычислительным экспериментом, — не создание новых, а развитие существующих программ. Это развитие осуществляется, как правило, не за счет замены имеющихся модулей их более совершенными версиями, а за счет расширения: включения в программный фонд все новых и новых модулей, отражающих различные решения, принимаемые в ходе эксперимента.
      Накапливаемые модули могут затем комбинироваться в самых разнообразных сочетаниях, позволяя тем самым провести достаточно систематическое и глубокое исследование. Потребность в подобных манипуляциях над модулями регулярно возникает в связи с тем, что исследователь постоянно конструирует новые варианты модели, сочетающие в себе те или иные выполнявшиеся когда-либо изменения или уточнения. Таким образом, интересующая нас многовариантность программ вычислительного эксперимента является закономерным следствием изначальной многовариантности модели.
      Сложность реализуемых математических моделей, а также необходимость хранения многочисленных вариантных модулей приводят к тому, что характерные размеры программного фонда вычислительного эксперимента оказываются довольно внушительными. Число участвующих в расчетах модулей здесь нередко достигает нескольких тысяч, а суммарная длина текстов программ — сотен тысяч строк.
      Организовать эффективное функционирование и развитие столь обширного, сложного и специфичного программного хозяйства очень нелегко. Тем не менее жизнь показала, что все возникающие здесь трудности вполне преодолимы — методом вычислительного эксперимента были успешно решены многие важные практические задачи. История программирования задач вычислительного эксперимента насчитывает свыше трех десятилетий, и за это время накоплен весьма значительный опыт, позволяющий говорить о существовании определенной технологии работы с многовариантными программами. Эта технология оказалась достаточно надежной и эффективной; именно добротностью применявшейся технологии объясняется жизнестойкость известных программных реализаций вычислительного эксперимента.
      В задачах вычислительного эксперимента в полной мере проявляются практически все специфические особенности многовариантных программ. В то же время вычислительный эксперимент является наиболее крупным потребителем технологии многовариантности. Поэтому выражения «программирование задач вычислительного эксперимента» и «создание многовариантных программ» иногда будут использоваться как синонимы.