Томография

Основные сведения
Рассмотрим принцип обратной задачи томографии на примере типичной постановки задачи современного дистанционного зондирования атмосферы. На искусственном спутнике Земли (ИСЗ), движущемся по околоземной орбите, расположен передатчик электромагнитного излучения, а на поверхности Земли находится один или множество приёмников, которые осуществляют измерения (например, амплитуды, фазы или доплеровского смещения частоты волны). Будем далее считать, что они фиксируют доплеровское смещение частоты (точнее, временную разность фаз). Поскольку сигнал проходит в пространстве между спутником и приёмником путь в атмосфере, то в измеряемом параметре сигнала содержится информация о показателе преломления атмосферы вдоль траектории луча (определяемом в каждой точке луча локальными свойствами атмосферной среды). Соотношение между измеряемым параметром DF и интересующей характеристикой атмосферы N_e выражается в приближении геометрической оптики линейным интегралом вдоль луча:
(1)
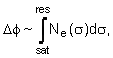
который предполагается отрезком прямой. 
Обратная задача томографии состоит в том, чтобы по набору измерений каждого приёмника в каждый момент времени измерений восстановить функцию пространственных переменных (N_e)^ij в некоторых узлах сетки, которой покрывается атмосфера. Для окончательной формулировки вычислительной задачи необходимо записать (1) в дискретном виде. Для этого производится разбиение ионосферы на конечные элементы (например, прямоугольные). В результате этого (подробнее см. ниже) получается разностный аналог задачи
(2) D
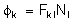
в котором в индексе l объединены индексы сетки i,j.
Решая систему линейных уравнений (2) можно реконструировать поле интересующего нас атмосферного параметра.

Геометрия задачи
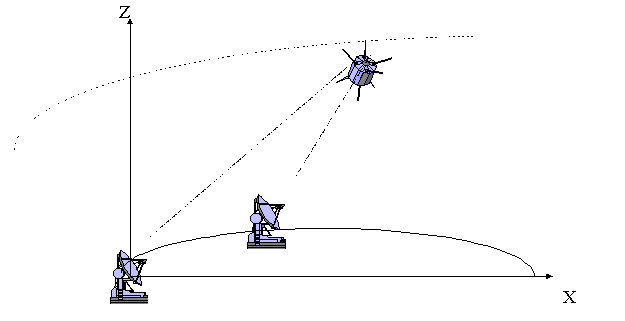
Обратимся к построению математической модели томографии ионосферы. Рассмотрим следующую схему эксперимента. В плоскости пролёта спутника на поверхности Земли расположено M_R радиоприёмников. Будем использовать не прямоугольную систему координат XZ, а более естественную для сферически-симметричной Земли ортогональную систему, в которой координатами являются криволинейное расстояние по поверхности Земли и высота над поверхностью Земли.  Начало координат свяжем, ради определённости, с положением ИСЗ в момент старта зондирования, а атмосферу будем считать расположенной в промежутке высот H_DхH_U. Координаты орбиты спутника в каждый момент времени считаются заданными. Будем считать, что орбита ИСЗ – круговая. Каждый радиоприёмник фиксирует всего M_T измерений в моменты времени t=t_S, s=0...M_T-1.

Прямая задача
Фаза радиоволны в a-й точке приёма на Земле выражается интегралом от электронной концентрации вдоль луча (1). Траекторию луча при высоких частотах зондирования на УКВ (для длин волн около метра) можно положить отрезком прямой. Существенно, что в криволинейных координатах луч перестаёт быть прямым. Поэтому для решения прямой задачи используется численное интегрирование по формулам (1). Далее, поскольку фактически измеряется не фаза (1), а разность фаз, то также численно считается производная (1) по времени (зависимость от времени описывается параметрически изменением траектории луча). В результате для каждого положения ИСЗ можно рассчитать доплеровское смещение частоты, «измеряемое» каждым приёмником. 

Обратная задача 
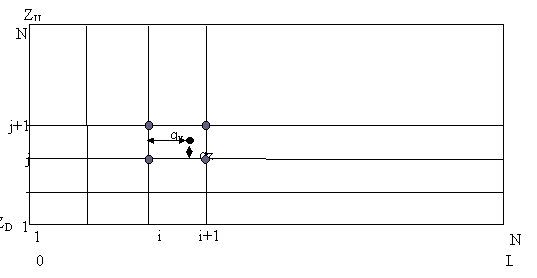
Имея набор измерений DF_K (всего их M=M_TM_R), можно поставить задачу восстановления поля показателя преломления атмосферы n(x,z). Для этого атмосфера при организации вычислений разбивается на (N_X-1)(N_Z-1) прямоугольных клеток, в N=N_XN_Z точках пересечения (узлах) которых показатель преломления n_L=n_ij (i=1... N_X, j=1...N_Z) подлежит реконструкции. (Для упрощения выкладок индексы удобно перенумеровать). Покажем, как формируется матрица обратной задачи (2) (в качестве правых частей линейной системы (2), берутся, разумеется, вычисленные в ходе решения прямой задачи значения доплеровского смещения).
Итак, подлежат реконструкции электронные плотности в узлах сетки. Для того, чтобы определить электронную концентрацию n(x,z) в остальных точках используем кусочно-планарную интерполяцию по четырём точкам:
, (4)
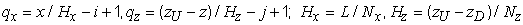где (5)

Аппроксимация (4) выполнена в каждой клетке для i=1...N_X -1, j= 1...N_Z -1. Можно видеть, что в таком случае выражение вектора измерений через искомый вектор восстанавливаемого параметра будет линейным:
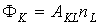(6) 
Дифференцирование оператора по времени даёт явный вид матрицы системы (2). В программе Tomography Calculator, которую Вы найдете на дистрибутивном диске с нашим курсом, предусмотрена также возможность построения матрицы задачи как с помощью худшей (кусочно-постоянной), так и лучшей (кусочно-биквадратичной) аппроксимации. 

Алгоритмы решения системы (2), по преимуществу, итерационные, ввиду большой размерности задачи.