В работе проведен анализ структуры течения в горизонтальном слое жидкости с неоднородными свойствами. Исследованы среды с нелинейной теплопроводностью, зависящей от температуры, и среды с внутренними источниками тепла. Во всех рассмотренных случаях устанавливался профиль температуры, при котором слой неустойчиво стратифицирован и основной перепад температуры приходился на тонкий верхний подслой. Получено многомасштабное течение, структура которого исследовалась методами вычислительной гомологии и методами на основе теории динамических систем. Рассматривался диапазон значений числа Прандтля от $0,5$ до $10$. Изучено, как свойства среды влияют на структуру движения жидкости.
Ключевые слова: многомасштабная конвекция, математическое моделирование, вычислительная гомология, аттрактор.
Abstract
Olga Vladimirovna Shcheritsa, Olga Semenovna Mazhorova, Oleg Alexandrovich Shatrov
Investigation of the multiscale flow structure in a horizontal fluid layer with inhomogeneous properties
The paper provides the study of the flow structure in a horizontal fluid layer with variable thermal diffusivity or with internal heat generation. The media properties are set up to produce a thin boundary sublayer convectively much more unstable than the bulk of the layer. The obtained multiscale flow was studied by computational homology methods and methods based on the theory of dynamical systems. The flows were investigated for the Prandtl number in the range $[0,5,\,10]$. The effect of medium properties on the structure of the fluid motion was studied.
Key words: multiscale convection, mathematical modeling, computational homology, attractor
Работа выполнена при поддержке гранта РФФИ 18-01-00436.
- Введение
- Постановка задачи
- Результаты расчетов
- Нелинейная теплопроводность
- Внутренние источники тепла
- Структура течения в зависимости от значения числа $Pr$
- Заключение
- Список литературы
Введение
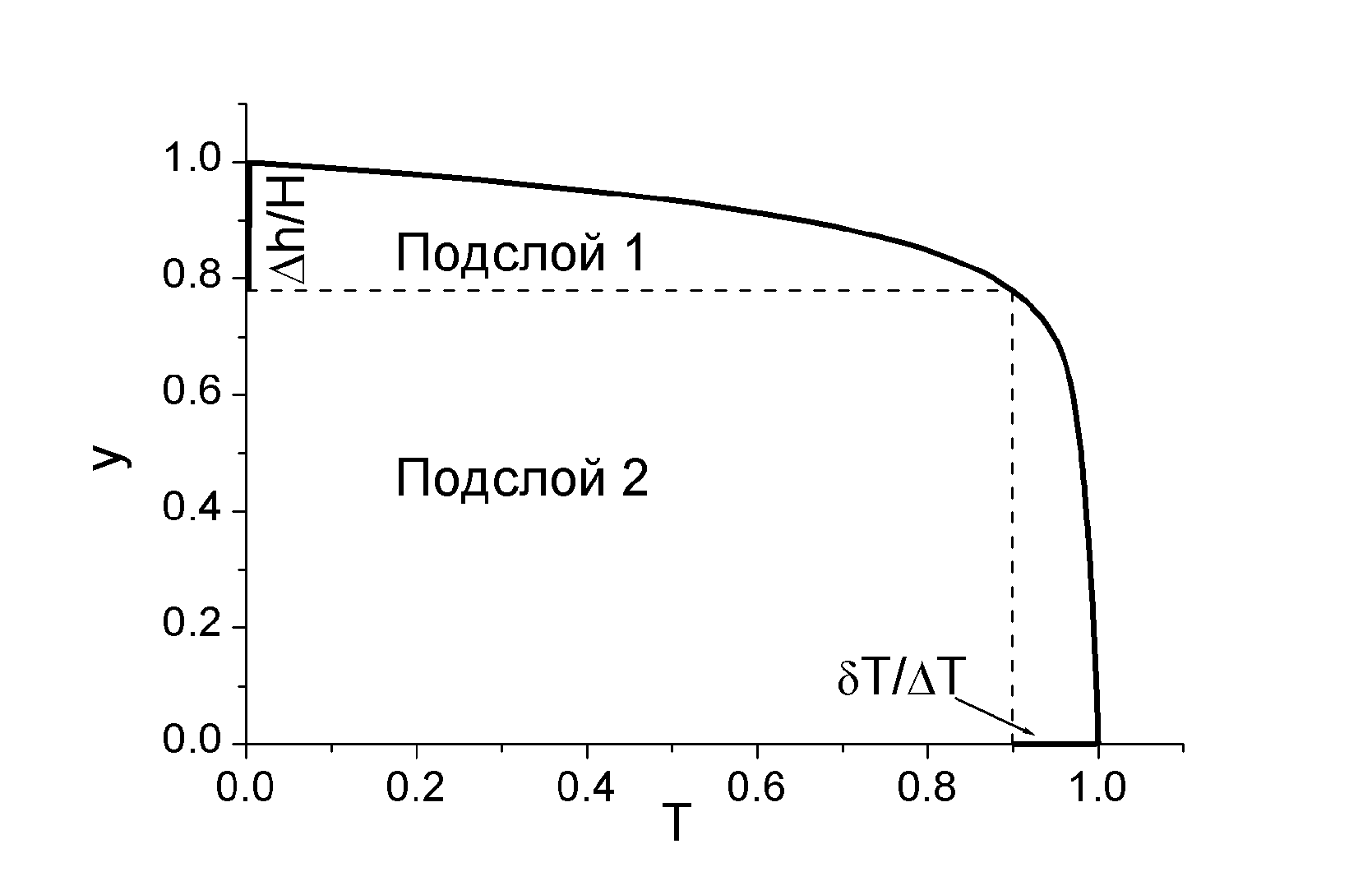
В данной работе рассматривается класс течений, в которых исходный статический профиль температуры имеет следующий вид: большая часть слоя практически равномерно прогрета. Температура изменяется на величину $\delta T,$ малую по сравнению с полным перепадом температуры $\Delta T$, а основное изменение температуры приходится на тонкий подслой вблизи верхней границы, толщина которого $\Delta h$ составляет малую часть полной толщины слоя $H$. При этом весь слой стратифицирован неустойчиво (см. рис. ). Такое распределение температуры наблюдается в мантии Земли, конвективной зоне Солнца и других астрофизических объектах. Формирование требуемого статического профиля осуществляется двумя способами: за счет нелинейного коэффициента теплопроводности, зависящего от температуры, как это было сделано в работах [, , ], или за счет специального распределения источников тепла, зависящего от температуры среды. Рассматривались течения при высокой надкритичности и различных значений числа Прандтля. Данная работа является продолжением работы [], посвященной исследованию многомасштабной конвекции.
Авторы выражают благодарность д.ф.-м.н А.В. Гетлингу за предложенную постановку задачи о конвекции в слое жидкости с переменной температуропроводностью.
Постановка задачи
Рассмотрим конвективное движение в горизонтальном слое жидкости. Прямоугольная область $\Omega=[0,\,L]\times[0,\,H]$, $L>>H$ заполнена вязкой несжимаемой жидкостью. Нижняя и верхняя границы поддерживаются при постоянной температуре, $T_{bot}=1$ и $T_{top}=0$ соответственно. Боковые стенки теплоизолированы. Основу математической модели составляют уравнения движения вязкой несжимаемой жидкости и уравнение конвективной теплопроводности [], записанные в безразмерном виде в переменных "функция тока-вихрь":
Здесь $x$, $y$ — декартовы координаты, $t$ — время, $ \omega $ — вихрь, $\psi$ — функция тока, $ v_x $ и $ v_y $ — компоненты вектора скорости, $Gr=\cfrac{g\beta H^3\Delta T}{\nu^2}$ — число Грасгофа, $ g $ — модуль ускорения свободного падения, $e_y$ — единичный вектор, направленный вертикально вверх, $\beta$ — коэффициент теплового расширения, $\nu$ — кинематическая вязкость, $T$ — температура, $\kappa{(T)} $ — коэффициент температуропроводности, $Q{(T)} $ — функция источника тепла, $Pr$ — число Прандтля, в случае нелинейной теплопроводности число Прандтля определялось по теплопроводности, соответствующей верхней границе области.Неявная консервативная разностная схема для задачи \eqref{sist:1}-\eqref{sist:4_1} была построена методом конечных объемов на разнесенных сетках с использованием переинтерполяций Аракавы [, ]. Полученная система сеточных уравнений решалась с помощью стандартной процедуры расщепления по физическим процессам []. Сначала из уравнений Навье-Стокса \eqref{sist:1}-\eqref{sist:4} с помощью матричного алгоритма [, , ] вычислялось поле скоростей, затем из уравнения теплопроводности \eqref{sist:4_1} определялось распределение температуры в слое.
В работе рассмотрено две задачи:
- задача с нелинейной теплопроводностью. $\kappa{(T)}=1+\alpha T+\beta T^n$, $Q{(T)}=0$;
- задача с внутренними источниками тепла. $\kappa{(T)}=1$, $Q{(T)}\ne0$.
Температурный профиль, приведенный на рисунке , является решением стационарной задачи теплопроводности с коэффициентом $\kappa\left(T\right)=1+\alpha T+\beta T^n$ и может быть представлен в виде неявно заданной функции []:
В то же время функция \eqref{profil} является решением задачи
где источник тепла В работах [, , ] использовали параметры $\alpha=10$, $\beta=600$, $n=10$, которые в дальнейшем будем называть параметрами I, соответствующее им распределение источника тепла $Q(T)$ приведено на рисунке , максимальное значение источника при температуре в диапазоне от $0$ до $1$ равно $3655,8,$ минимальное — $0,0966$. Резкое изменение величины источника приходится на достаточно узкий диапазон $T\in[0,99, \,1]$.
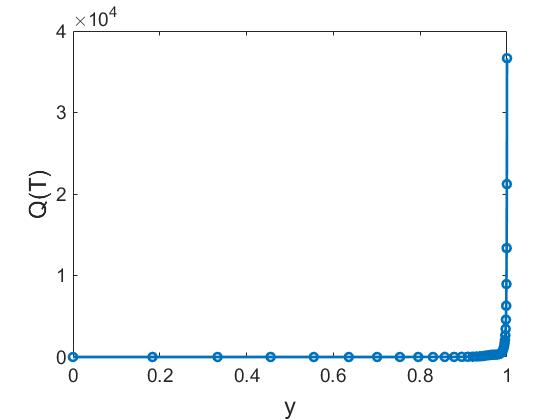
(a) |
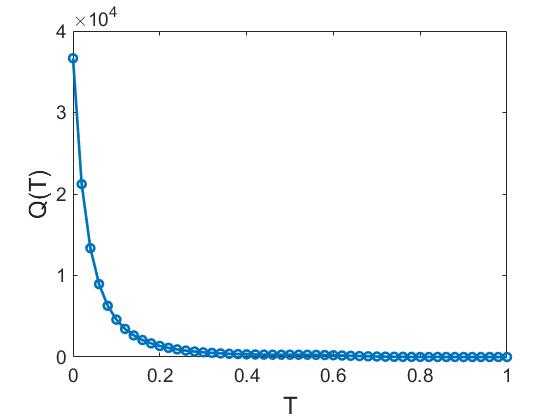
(б) |
Рассмотрим набор параметров II: $\alpha=1$, $\beta=200$, $n=10$. Соответствующий профиль температуры и распределение источников приведены на рисунках и соответственно. Статические профили температуры для параметров I и II практически совпадают, при этом источники $Q(T)$ отличаются. При параметрах II распределение источников изменяется в диапазоне от $0,0940$ до $452,0259$, при этом максимум достигается при температуре $T=0,54$.
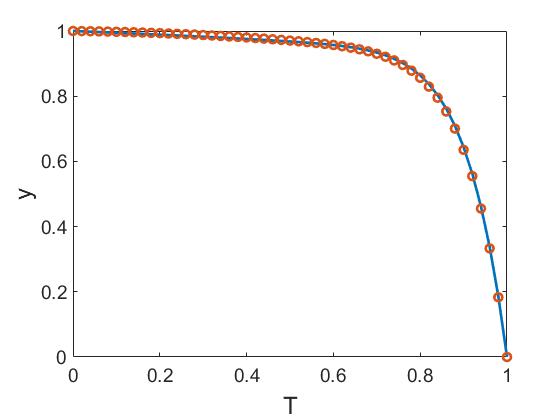
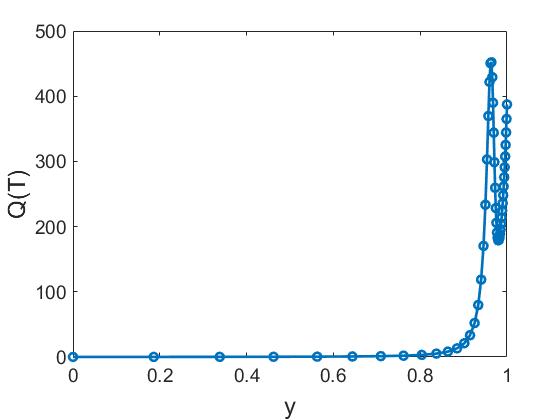
(a) |
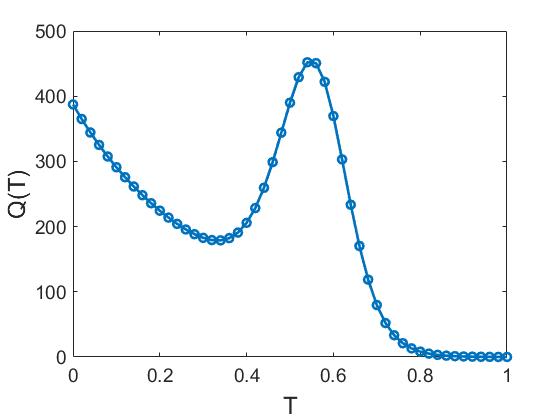
(б) |
Рассмотрим прямоугольную область с жесткими границами: $\psi=0$, $\cfrac{\partial \psi}{\partial n}=0$, где $n$ — внешняя нормаль.
Результаты расчетов
Расчеты проводились в области $[0,\,15]\times[0,\,1]$ для значения числа Прандтля $Pr\in[0,5,\,10]$ и числа Рэлея $Ra=120 Ra_{cr}$, где $Ra_{cr}$ — критическое число Рэлея. Значения критического числа Рэлея приведены в таблице . Использовались пространственные сетки с числом узлов по горизонтали $N_x=1024$, по вертикали $N_y=50$ и шагом по времени $\tau=0,01$.
| $\kappa(T)$ | $Q(T)$ | |
| Параметры I | $5\cdot 10^5$ | $ 1,5\cdot 10^4$ | Параметры II | $5,75\cdot 10^5$ | $1,75\cdot 10^{4}$ |
Расчеты проводились с помощью параллельного комплекса программ, разработанного авторами для вычислительного кластера K100, установленного в ИПМ им. М.В. Келдыша РАН.
Нелинейная теплопроводность
На рисунке приведены структуры течения в слое жидкости с температуропроводностью, зависящей от температуры. Течение начинало развиваться в тонком слое вблизи верхней границы, затем холодные струи пробивали всю толщину слоя, практически до самого дна, вовлекая весь слой в движение. Возникали валиковые структуры, размер которых сравним с высотой всей области, между этими валами вблизи горизонтальных границ области наблюдались мелкомасштабные структуры (рис. а, б). Такая же структура течения была зарегистрирована в работах [, ], но при более низкой надкритичности ($Ra=10Ra_{cr}$).

(b)

(c)

(d)

Течения, приведенные на рисунке , имеют один и тот же статический профиль и одинаковую надкритичность. В случае параметров I в области длиной $L=15$ разместилось 12 крупномасштабных структур, при параметрах II — $17$. На рисунке изображена часть расчетной области. В обоих случаях установилось периодическое течение с постоянным числом крупномасштабных структур.
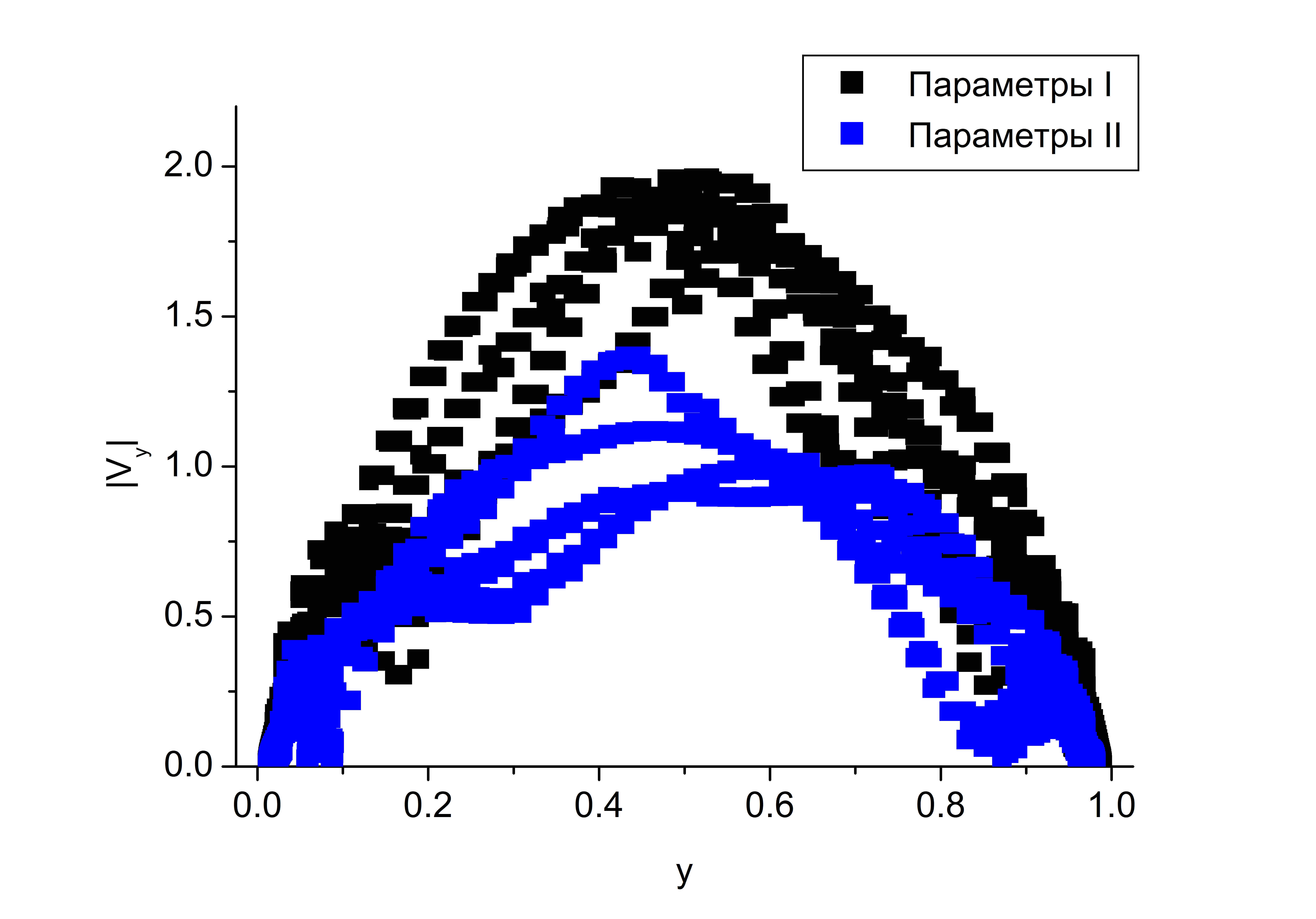
Рассмотрим траектории движения частиц (риc. ). В фазовом пространстве $(y,V_y)$ траектории образуют циклы: большой цикл соответствует крупномасштабным структурам, пара небольших вблизи горизонтальных границ ($y=0,\,1$) — мелкому масштабу (риc. b). Заметим, что при параметрах II, восходящая скорость в $1,8$ раз больше, чем при параметрах I, нисходящая — в $1,4$ раза больше. Мелкомасштабные структуры вблизи дна ($y=0$) при параметрах I практически в два раза крупнее, чем при параметрах II (риc. c).
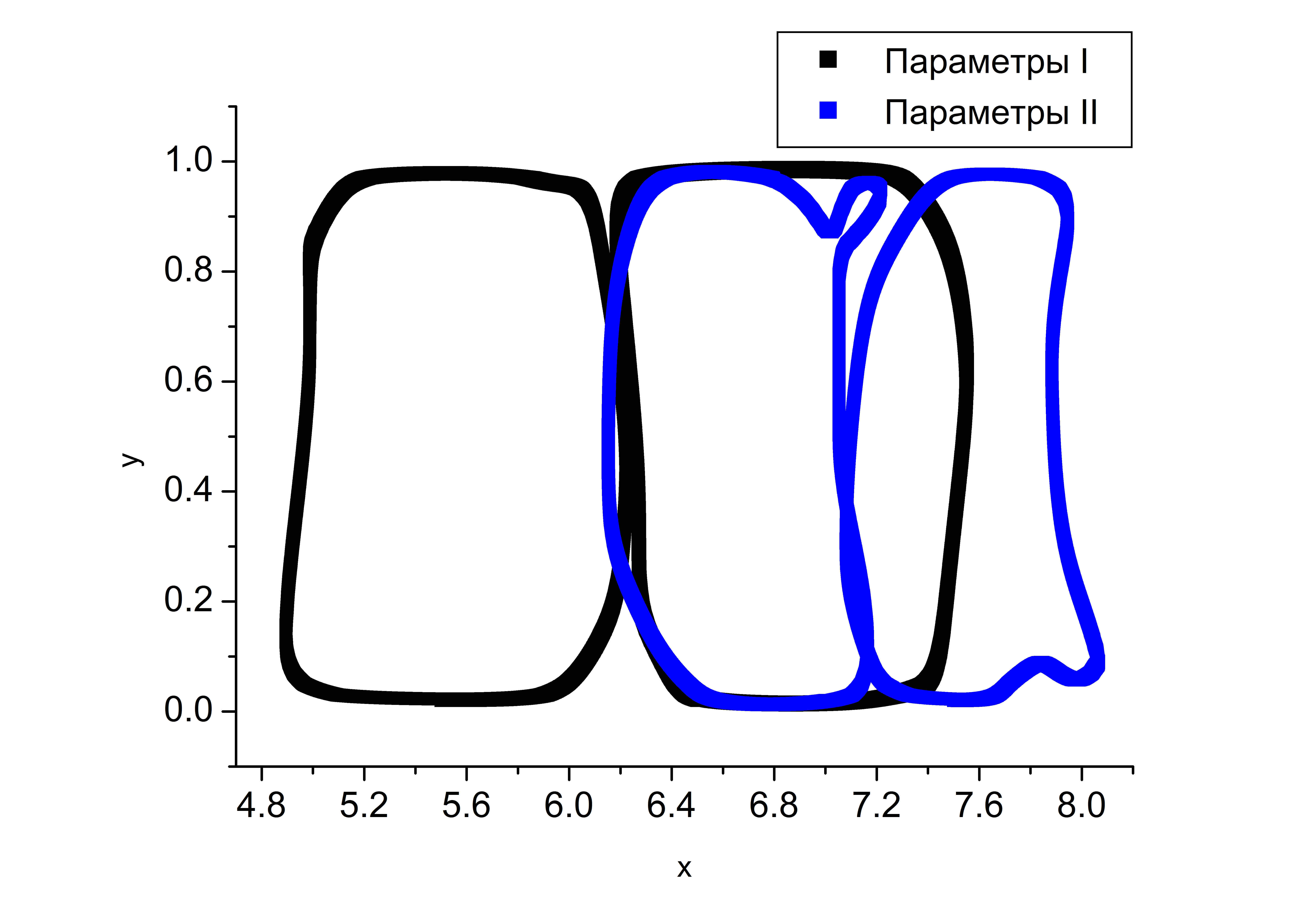
(a) |
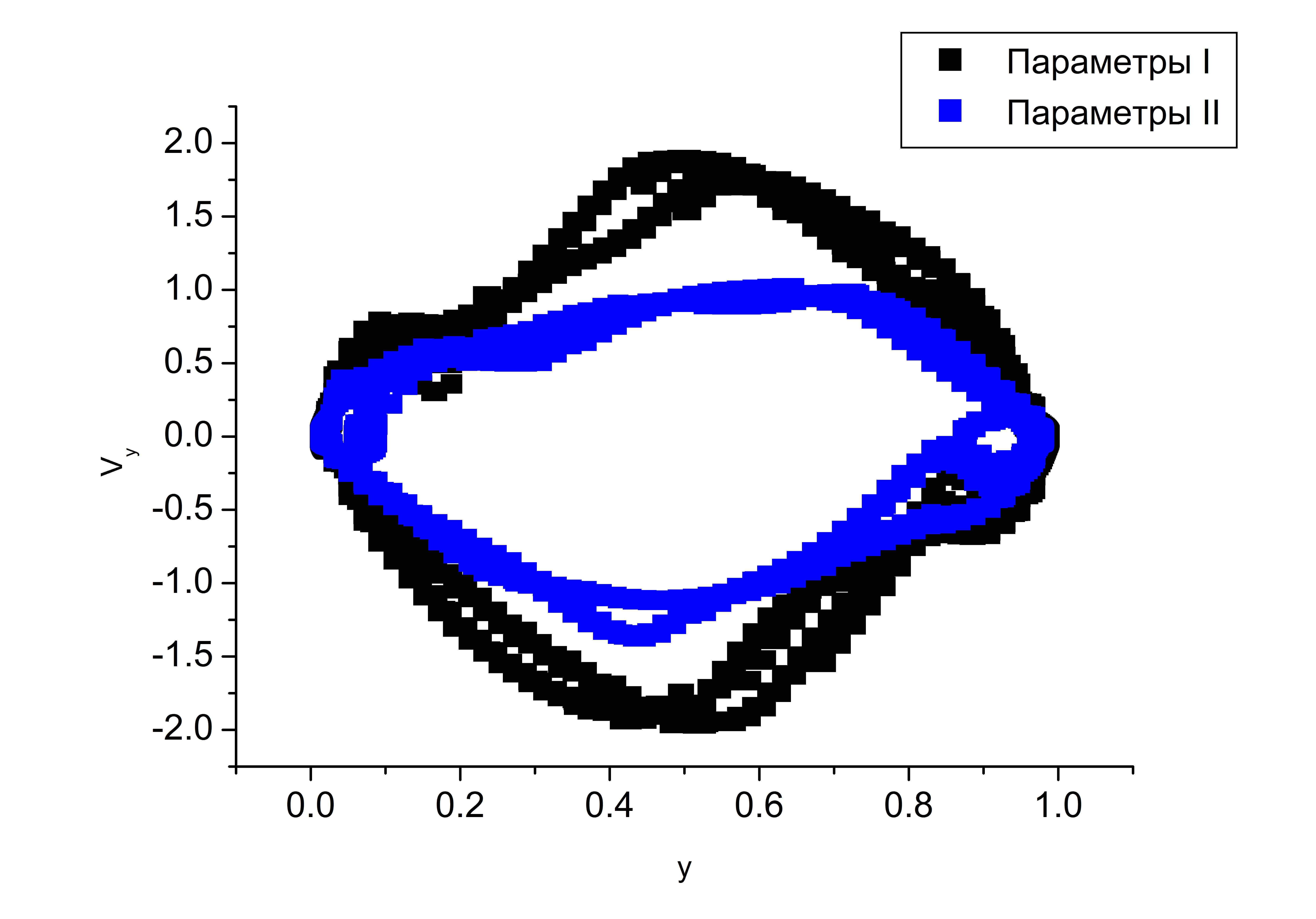
(b) |
(c) |
Внутренние источники тепла
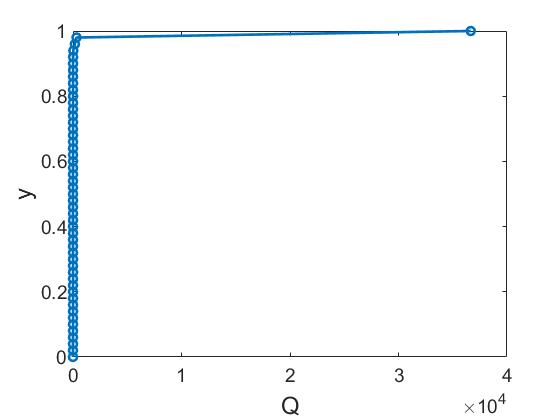
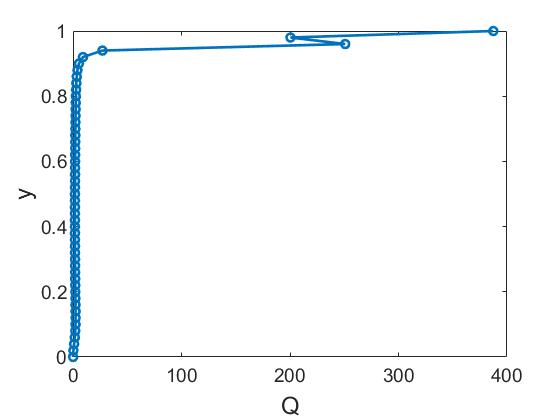
На рисунке приведены структуры течения в слое жидкости с внутренними источниками тепла. Течение развивалось так же, как и в случае нелинейной теплопроводности. При параметрах I и II установилось течение с двадцатью двумя крупными валами практически одного размера. В поле температуры можно наблюдать замкнутые изолинии. В установившемся течении источник действует только вблизи верхней горизонтальной границы (рис. ).

(b)

(c)

(d)

(a) |
(b) |
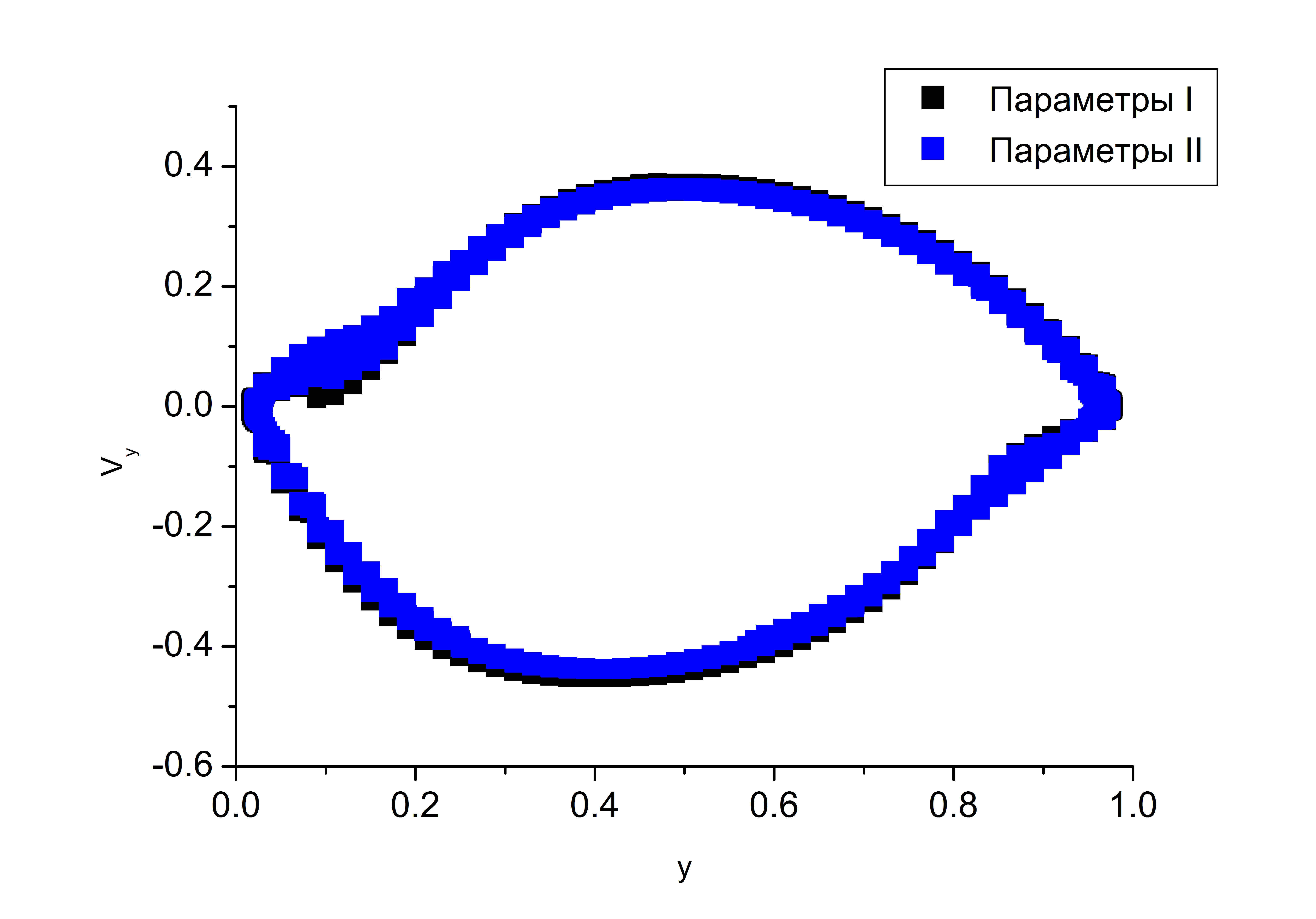
Анализ траекторий движения частиц показал, что крупномасштабные структуры~при параметрах I, и II, имеют не только одинаковые размеры, но и скорости изменяются в одинаковом диапазоне (рис. a). Это объясняется тем, что в результате установившегося распределения температуры источник действует только в верхней части слоя (рис. ). Структуры отличаются только диапазоном изменения температуры. При параметрах I $T\in[0.342,\,0.955],$ при параметрах II — $T\in[0,539,\,0,930]$ (рис. b).
(a) |
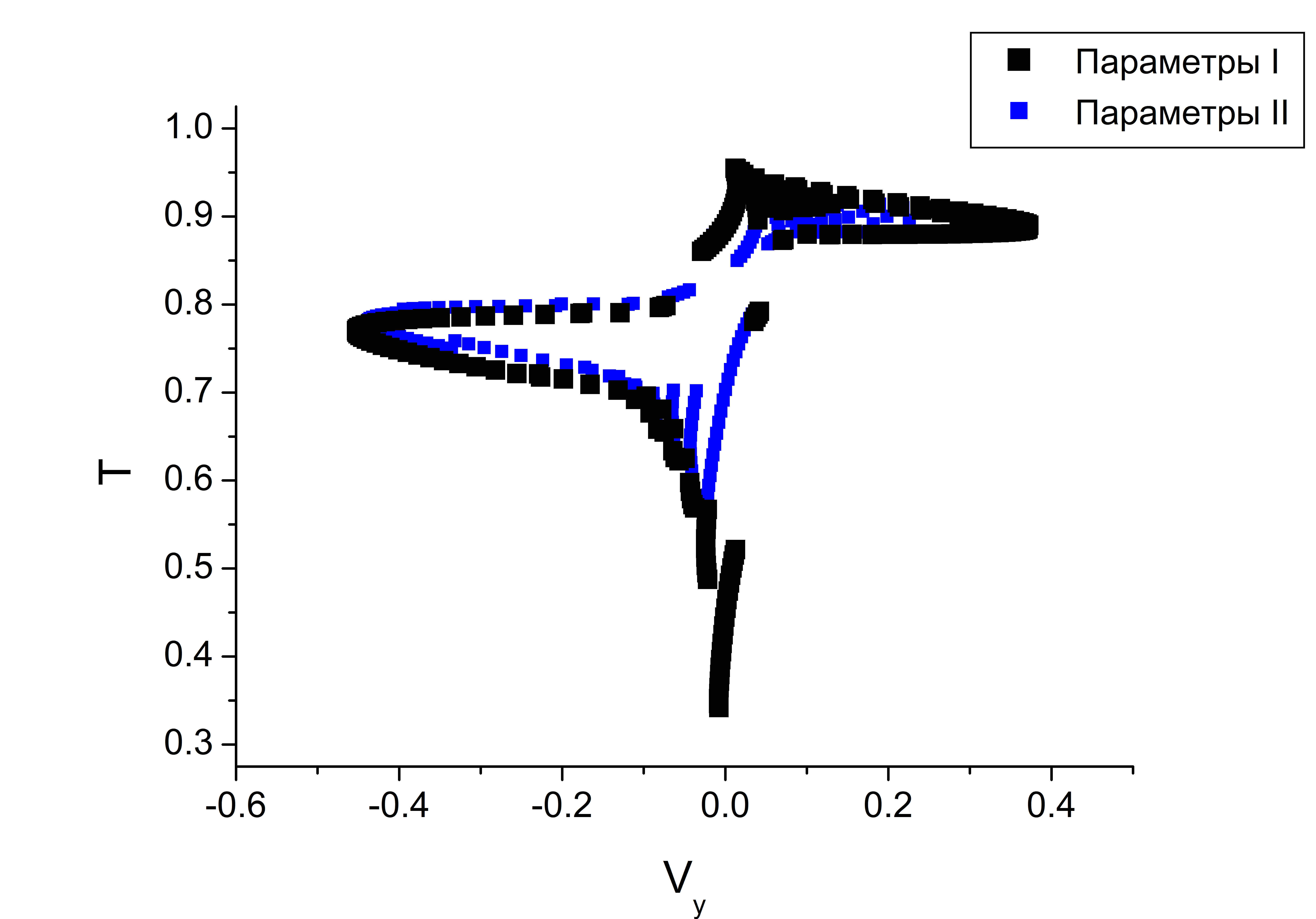
(b) |
Структура течения в зависимости от значения числа $Pr$
В случае нелинейной теплопроводности с ростом значения числа Прандтля размер крупномасштабных структур уменьшается (см. рис. ).

(b)

(c)

(d)

(e)

(f)


(b)

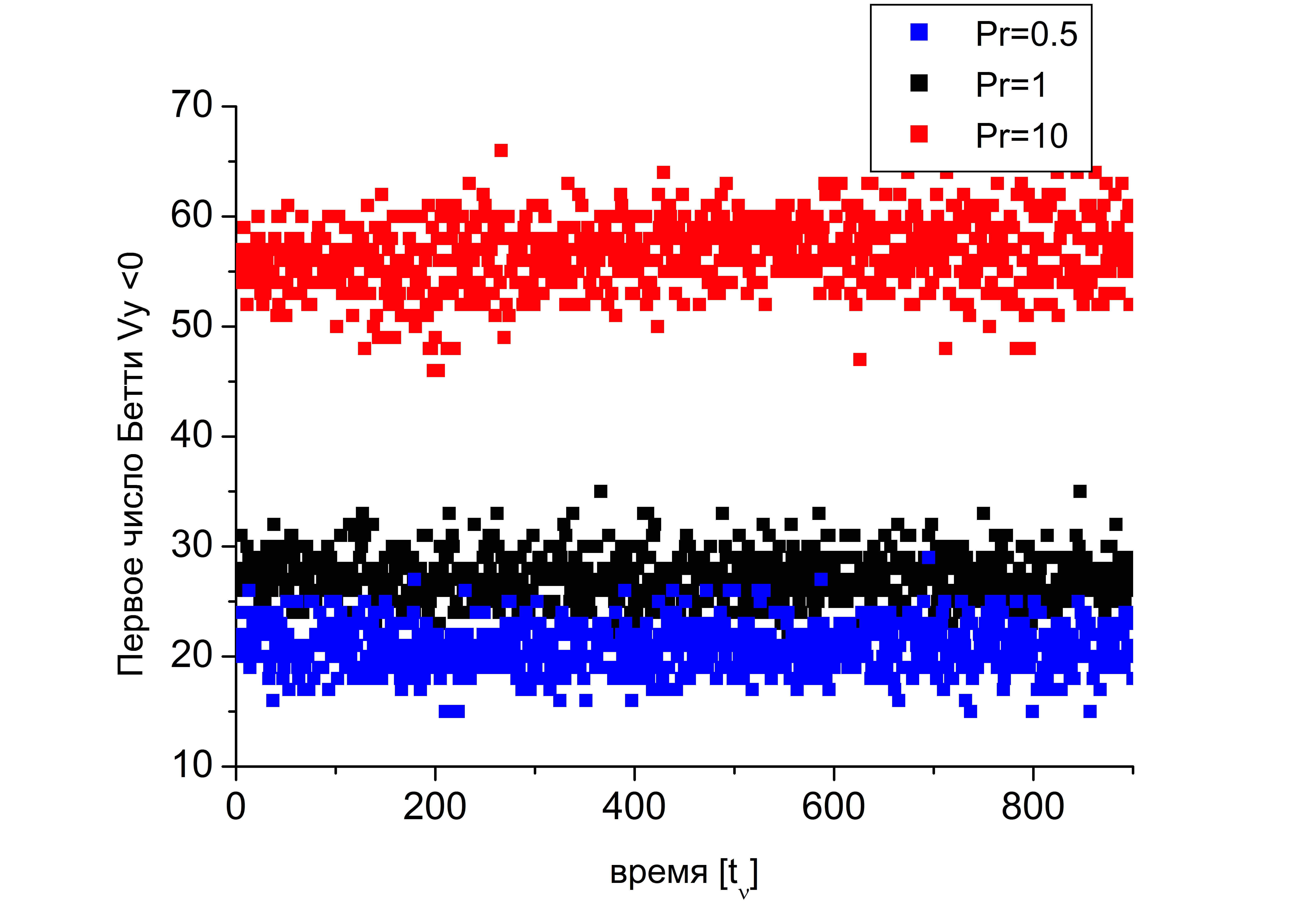
(a) |
(b) |
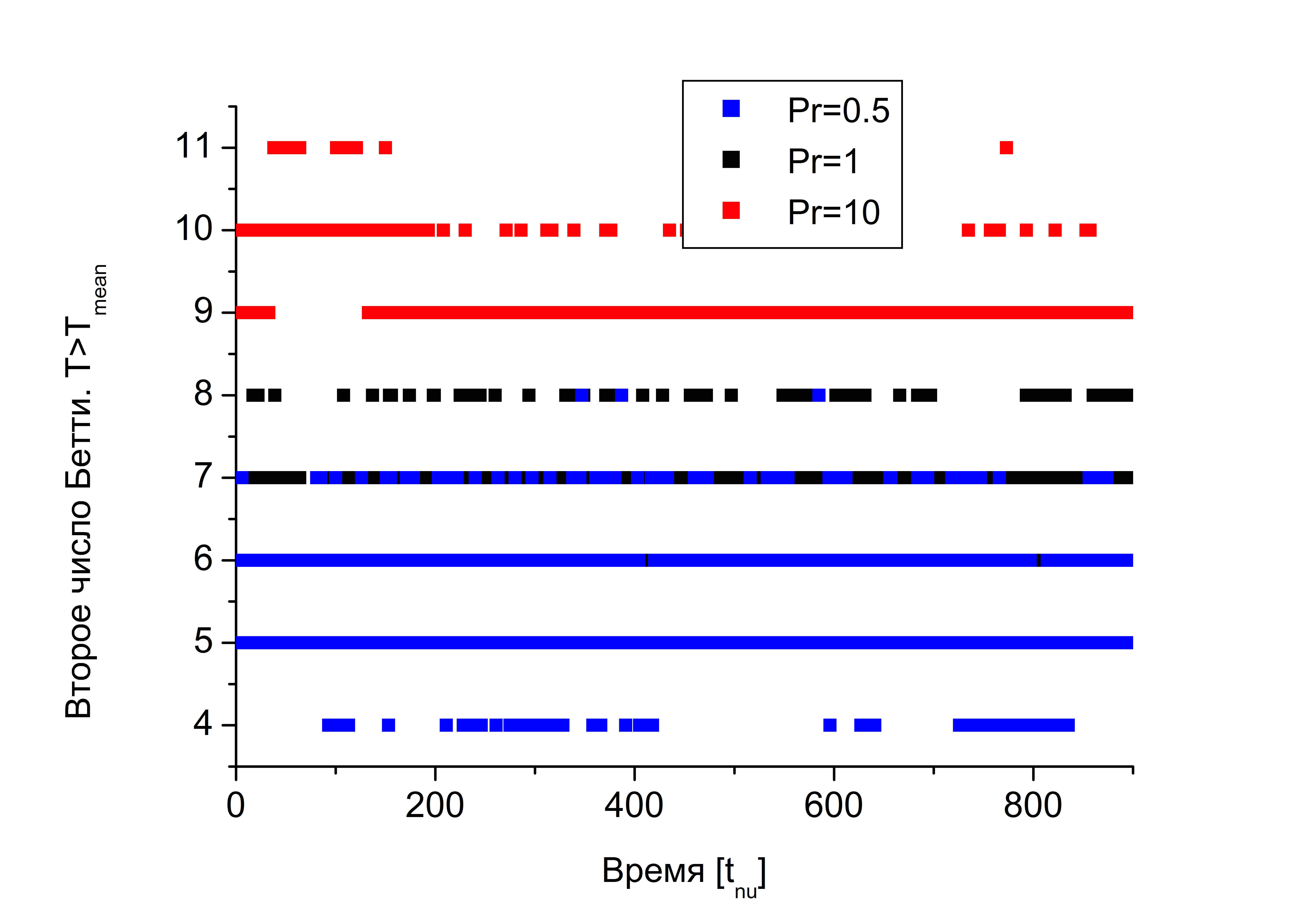
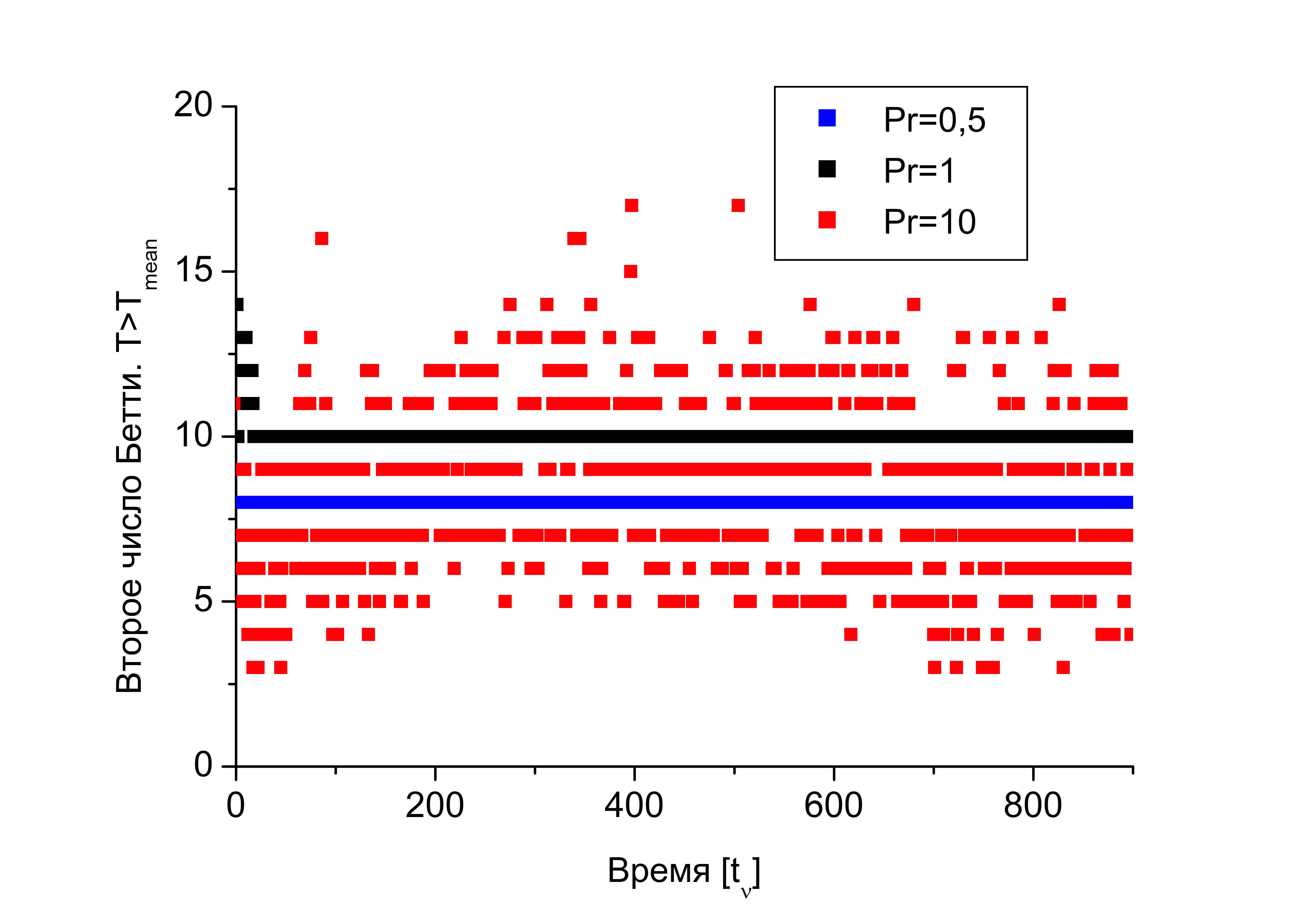
С помощью анализа поля температуры можно оценить количество крупных структур в области. Выделим топологическое пространство, состоящее из точек, в которых температура выше средней температуры в горизонтальном сечении . На рисунке b. приведены значения второго числа Бетти для разных значений числа Прандтля. Вторые числа Бетти — это количество отверстий, то есть это области более холодные. Сравнение данных рисунков b и показывает, что второе число Бетти совпадает с количеством крупных структур в течении.
На рисунке приведены структуры течения, возникающие для различных значений числа Прандтля в задаче с внутренними источниками тепла. При больших значениях Прандтля течение не вышло на квазистационарный режим, мелкомасштабные структуры перемещаются вдоль горизонтальных границ и кажется, что они проскальзывают вниз вместе с мощными нисходящими струями. На рисунке приведены результаты исследования методами вычислительной гомологии. С ростом значения числа Прандтля крупномасштабные структуры увеличиваются в размере. Когда ширина валов становится значительно больше высоты вала, течение теряет свою строгую регулярность, выхода на стационар не происходит. Крупные структуры имеют разные размеры ( c, f). На рисунках приведены соответствующие распределения температуры. При $Pr=10$ наблюдается много мелкомасштабных структур вблизи горизонтальных границ, что и отразилось в большом изменении значений чисел Бетти (см. рис. ). В каждой маленькой структуре есть и нисходящий поток, и восходящий, есть область с температурой выше и ниже средней температуры горизонтального сечения. Представление методами гомологии в случае $Pr=10$ позволяет говорить о том, что мелких структур много, течение далеко от регулярной структуры. Более интересные результаты дает анализ траекторий движения частиц.

(b)

(c)

(d)

(e)

(f)

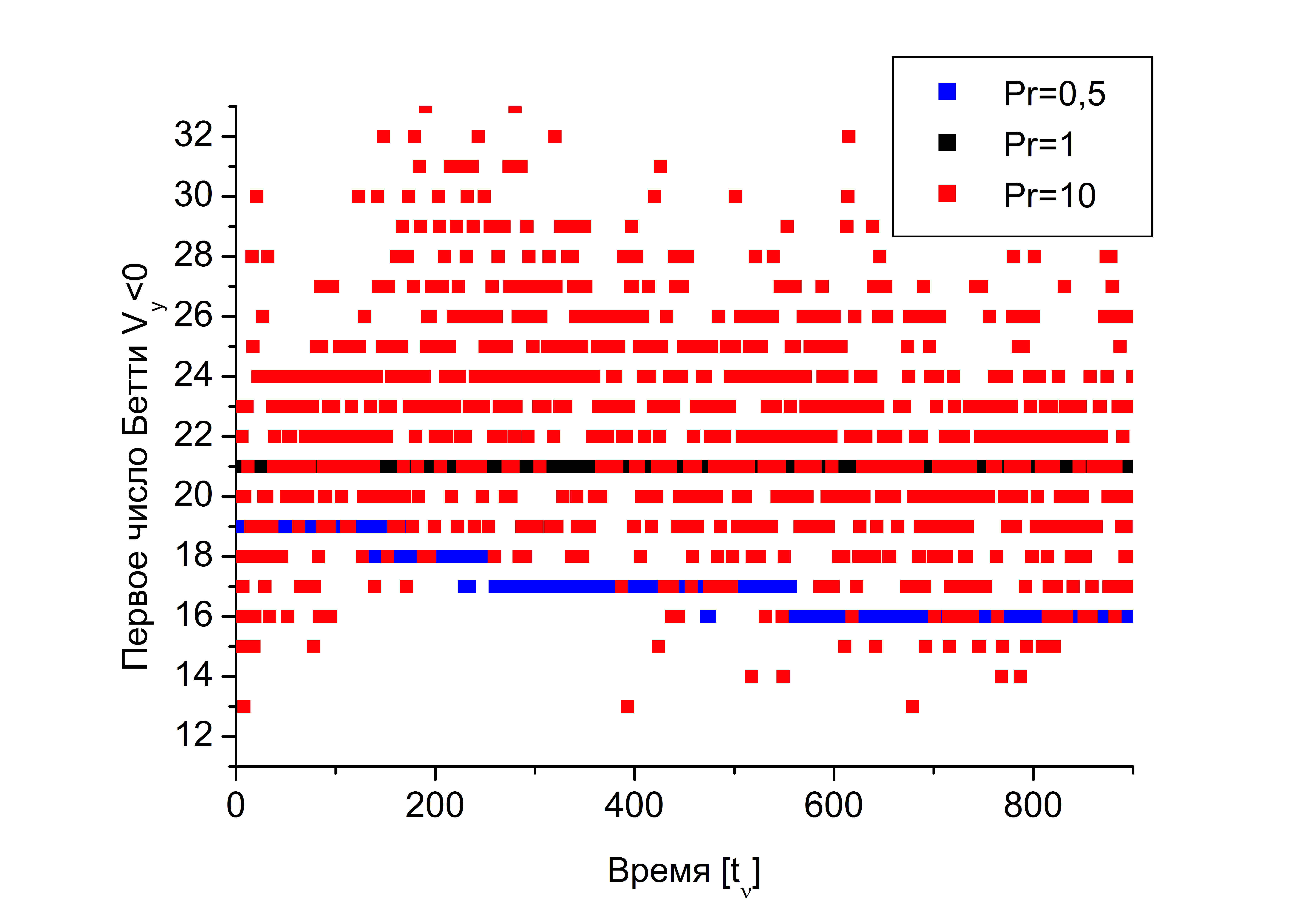
(a) |
(b) |

(b)

(c)

(d)

(e)

(f)

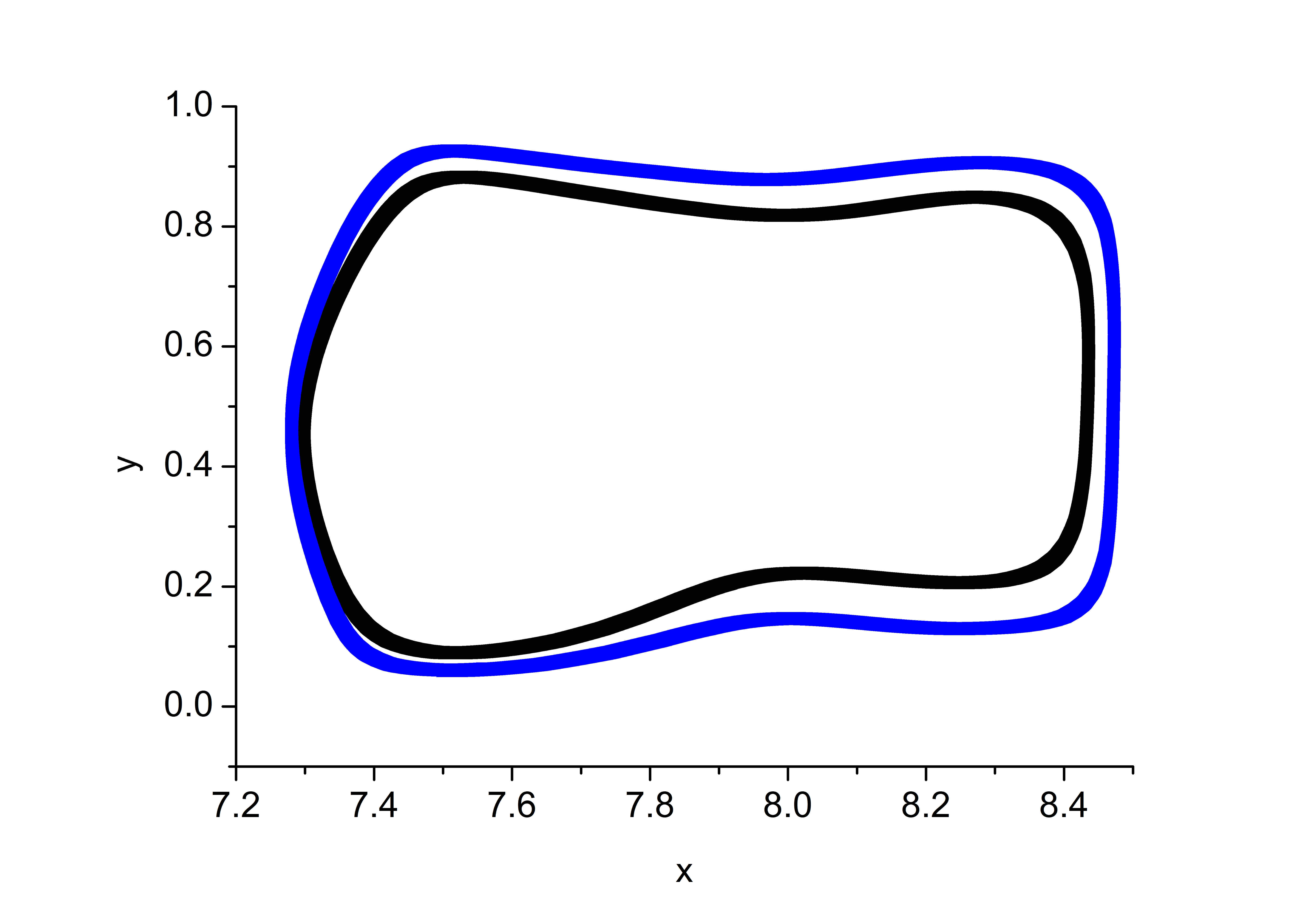
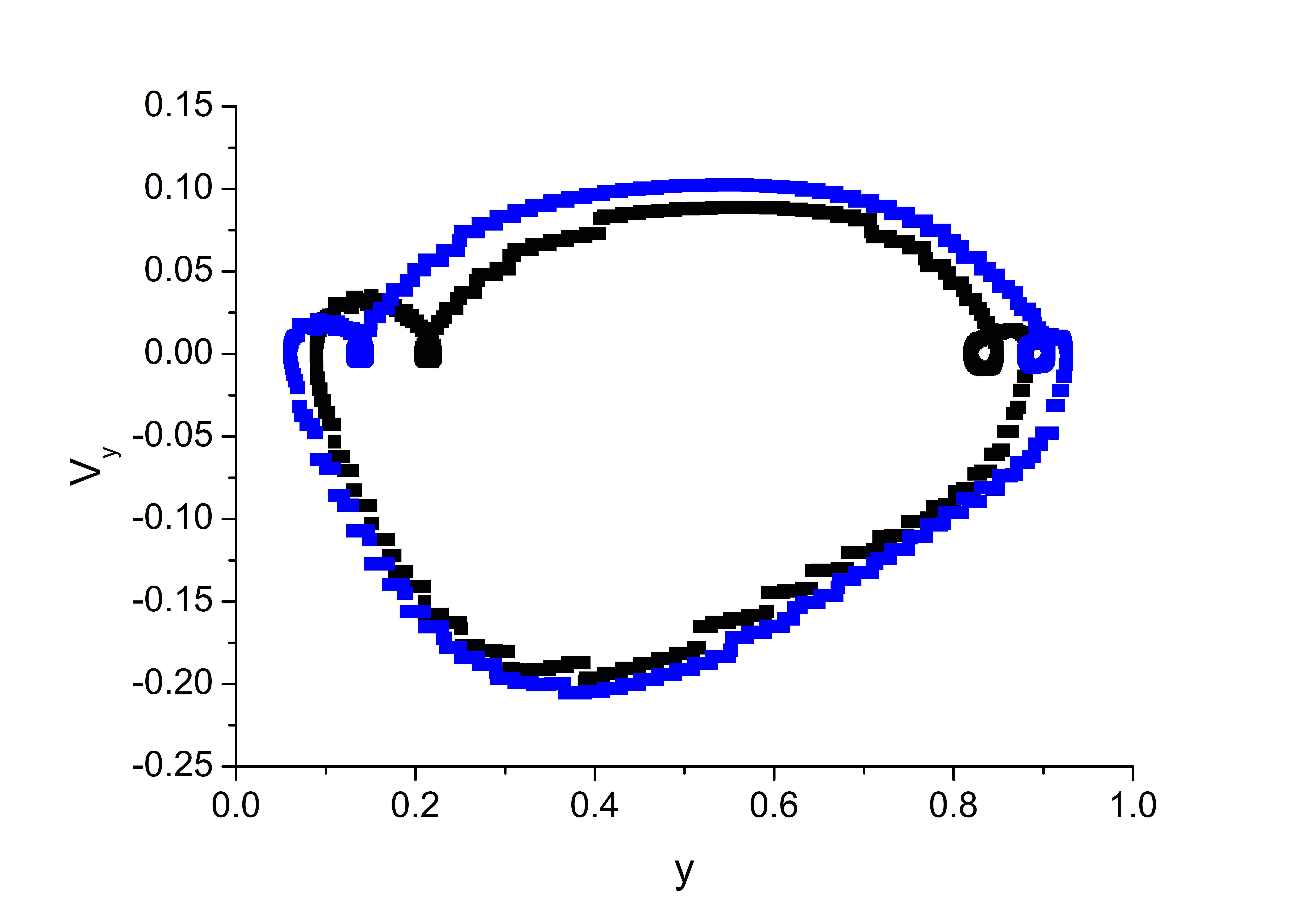
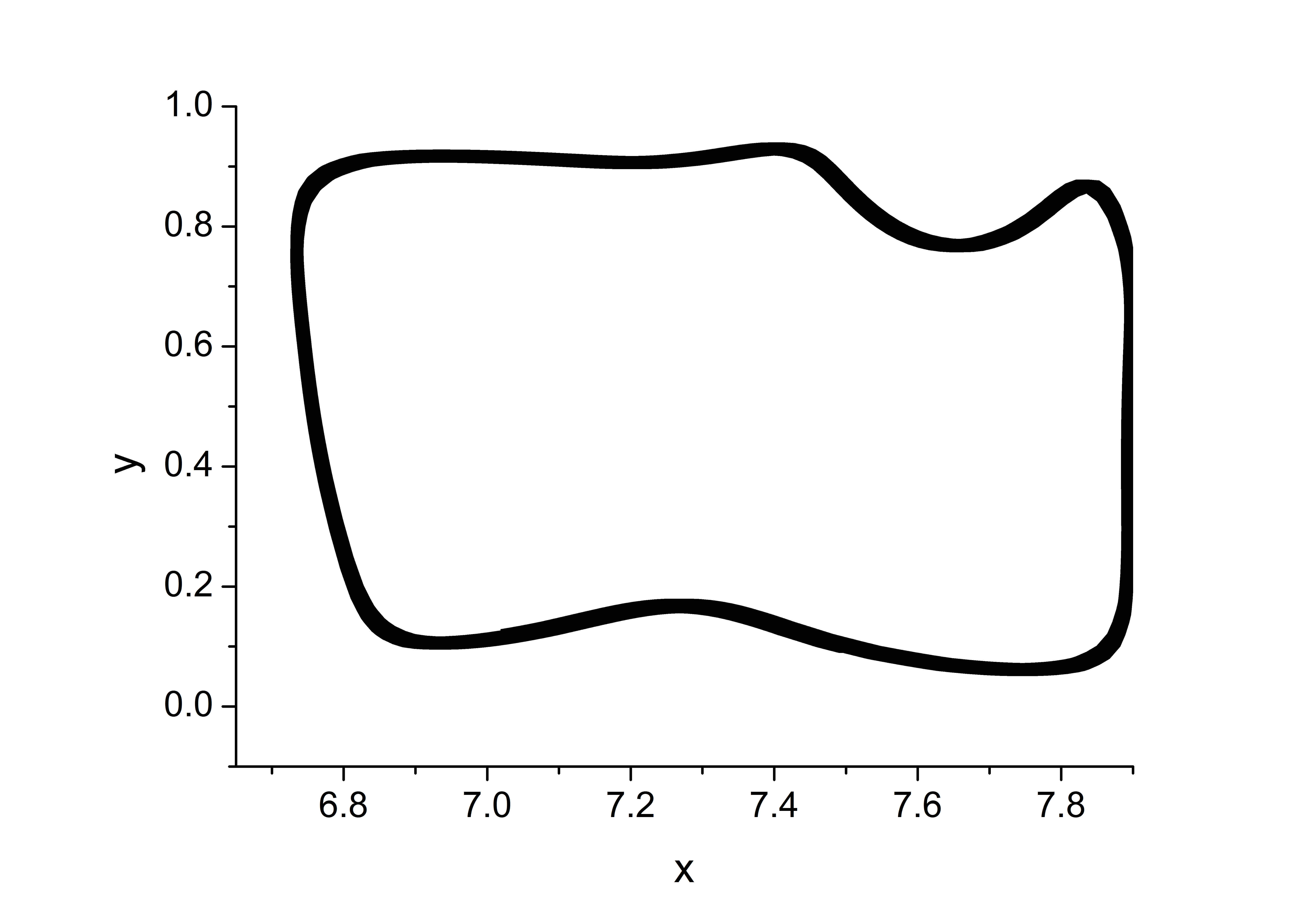
На рисунках , приведены траектории движения частиц в течении при $Pr=10$ и параметра I и II. Траектория обходит одну из крупных валиковых структур в течении. Верхняя и нижняя ее границы имеют волнистую форму, что подтверждает тот факт, что вблизи верхней и нижней границы, вдоль крупных структур перемещаются мелкомасштабные структуры, которые заметны на рисунках c, f. Траектории в фазовом пространстве $(y,\,V_y)$ образуют крупный цикл, размер которого сравним с высотой области, и малые циклы вблизи горизонтальных границ. В случае параметров I аттрактор похож на аналогичный аттрактор для задачи с нелинейной теплопроводностью (рис. b). При параметрах II вблизи верхней границы наблюдается два маленьких вихря (рис. с). Их появление можно объяснить структурой распределения источника, которое устанавливается, когда весь слой жидкости прогревается (рис. b). Появление таких мелких масштабов, один над другим, и создает иллюзию, что структуры проскальзывают вниз. Нам не удалось зарегистрировать такое движение. Мелкомасштабные структуры локализованы вблизи горизонтальных границ. Вблизи верхней границы они могут располагаться в два ряда, это подтверждается большим диапазоном изменения чисел Бетти (рис. ). Толщина слоев, в которых локализуются эти структуры, определяется распределением внутренних источников.
(a) |
(b) |
(a) |
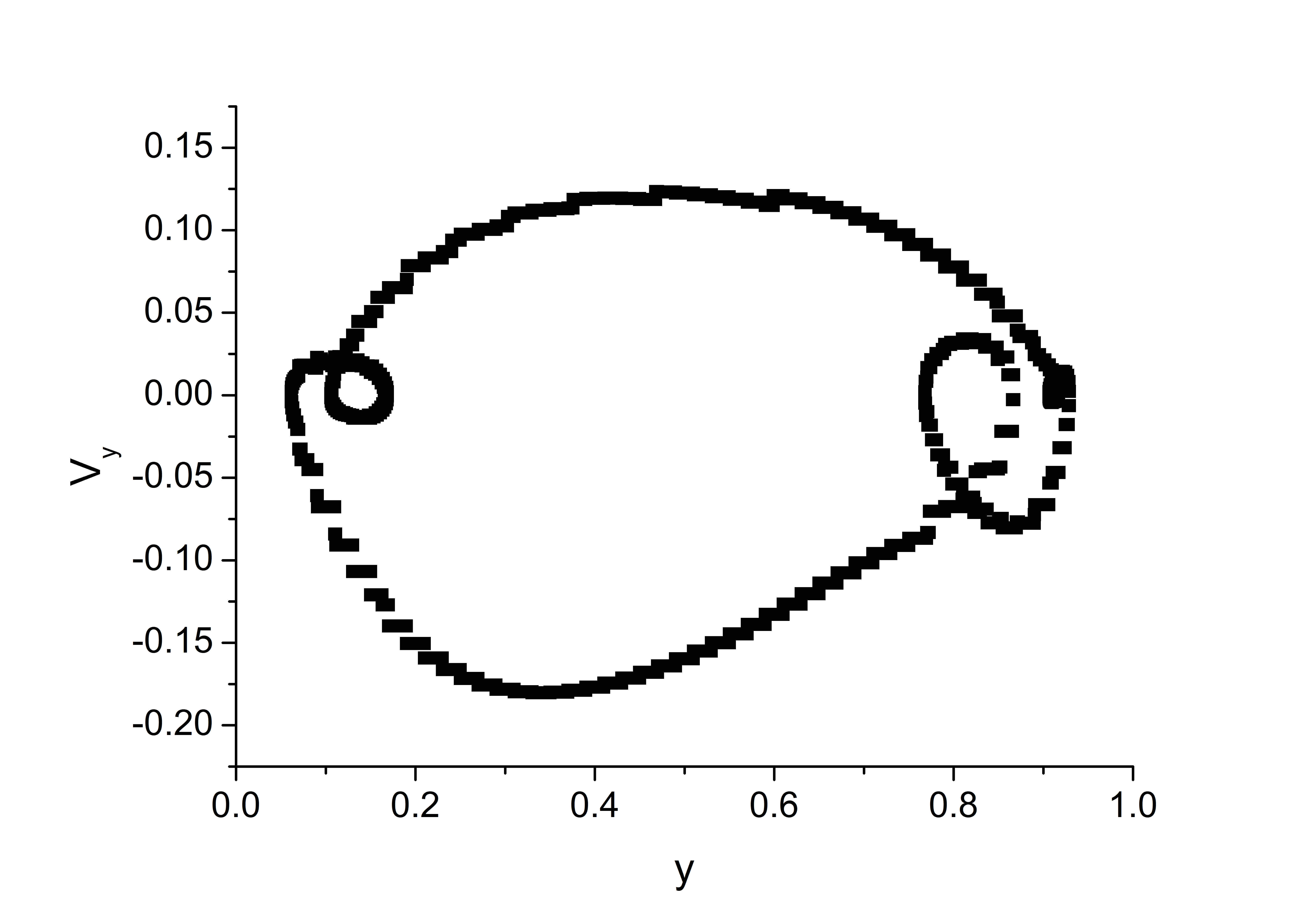
(b) |
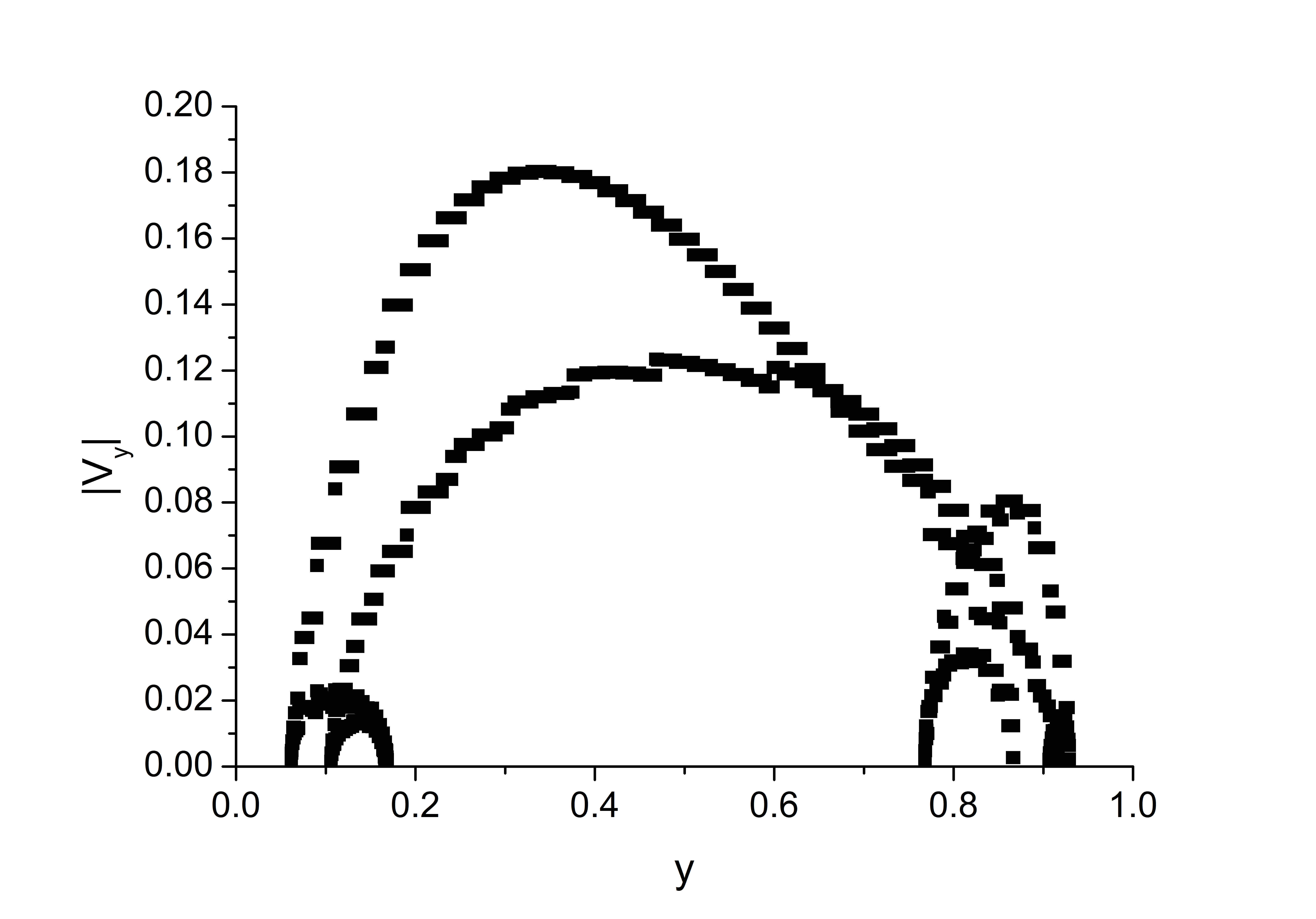
(c) |
Заключение
В работе проведен анализ структуры течения в горизонтальном слое жидкости с неоднородными свойствами. Рассмотрены две задачи: в одной задаче теплопроводность зависела от температуры, в другой — при постоянной температуропроводности были заданы внутренние источники тепла, зависящие от температуры. В обоих случаях устанавливался один и тот же статический профиль температуры, при котором весь слой неустойчиво стратифицирован и основной перепад температуры находится в тонком верхнем подслое. Рассматривалась высокая надкритичность ($Ra=120Ra_{cr}$), значение числа Прандтля варьировалось от $0,5$ до $10$, в случае нелинейной теплопроводности число Прандтля определялось по теплопроводности на верхней границе области. В расчетах наблюдалось многомасштабное течение. Крупномасштабные структуры по высоте сравнимы с толщиной слоя, мелкомасштабные локализованы вблизи горизонтальных границ. Если течение выходит на стационар, то мелкомасштабные структуры локализуются между крупными структурами и не перемещаются по области. С ростом значения числа Прандтля размер структур уменьшается, нисходящие потоки становятся уже. В задаче с внутренними источниками тепла при $Pr=10$ течение теряет регулярную структуру. Крупномасштабные структуры имеют разную ширину, превосходящую толщину слоя. Между горизонтальными границами и крупномасштабными структурами постоянно перемещаются мелкомасштабные. Методы вычислительной гомологии позволяют оценить количество мелкомасштабых структур. Анализ аттракторов (представления траекторий в различных фазовых пространствах) дает оценку размеров структур, диапазонов изменения температуры и скорости внутри этих структур. При одном и том же статическом профиле аттрактор в фазовом пространстве $(y,\,V_y)$ качественно имеет одинаковую структуру: один цикл, размеры которого сравнимы с толщиной области, и маленькие циклы вблизи горизонтальных границ. При этом размеры этих маленьких циклов, мелкомасштабных структур, определяются свойствами среды, коэффициентом теплопроводности или распределением источников тепла в зависимости от задачи.
-
Getling A.V., Mazhorova O.S., Shcheritsa O.V.
Effects of variable thermal diffusivity on the structure of convection.
Physics Letters A. 2018. Vol. 382. P. 639–645.
CrossRef Google Scholar -
Getling A.V., Mazhorova O.S., Shcheritsa O.V.
Concerning the multiscale structure of solar convection.
Geomagnetism and Aeronomy. 2013. Vol. 53, no. 7. Pp. 904–908.
CrossRef Google Scholar -
Щерица О.В., Мажорова О.С.
Методы исследования конвективных течений со сложной структурой.
Препринты ИПМ им. М.В.Келдыша. 2018. № 241. 33 с.
CrossRef Google Scholar -
Пасконов В.М., Полежаев В.И., Чудов Л.А.
Численное моделирование процессов тепло - и массообмена.
Москва: Наука, 1984.
Google Scholar -
Мажорова О.С.
Разностные методы решения уравнения динамики вязкой жидкости.
Энциклопедия низкотемпературной плазмы. Том VII-I. Математичекое моделирование в низкотемпературной плазме. Часть 2. Под ред. Попова Ю.П. М.: Янус-К. 2008. 333 c. -
Роуч, П.
Вычислительная гидродинамика.
Москва: Мир. 1980.
Google Scholar -
Ковеня В.М., Яненко Н.Н.
Метод расщепления в задачах газовой динамики.
Отв. ред. Ю.И. Шокин. Новосибирск: Наука, Сибирское отделение. 1981. 304 с.
Google Scholar -
Мажорова О.С., Попов Ю.П.
Матричный итерационный метод численного решения двумерных уравнений Навье - Стокса.
ДАН СССР. 1981. Т. 259. №3. С. 535 - 540.
Google Scholar -
Мажорова О.С., Попов Ю.П.
О методах численного решения уравнений Навье - Стокса.
Журнал вычислительной математики и математической физики. 1980. Т. 20. №4. С. 1005 - 1020.
Google Scholar -
Мажорова О.С., Попов Ю.П., Похилко В.И.
Матричный алгоритм численного решения нестационарных задач концентрационной конвекции для многокомпонентных сред.
В сб. Математическое моделирование. Получение монокристаллов и полупроводниковых структур. Под ред. Самарского А.А., Попова Ю.П., Мажоровой О.С.". Москва: Наука". 1986. C. 19-31.
Google Scholar -
Gameiro Marcio, Pilarczyk Pawel.
Automatic Homology Computation with Application to Pattern Classification
RIMS Kokyuroku Bessatsu. 2007. Vol. B3. Pp. 1 – 10.
Google Scholar -
Krishan Kapilanjan, Kurtuldu Huseyin, Schatz Michael F.
Homology and symmetry breaking in Rayleigh-Benard convection: Experiments and simulations.
Physics of Fluids. 2007. no. 17105.
CrossRef Google Scholar -
Marcio Gameiro, Konstantin Mischaikow, William Kalies
Topological characterization of spatial-temporal chaos.
Physical review. 2004. no. 035203(R).
CrossRef Google Scholar -
Emran Mohammad S., Schumacher Jorg.
Large-scale mean patterns in turbulent convection.
Journal of Fluid Mechanics. 2015. Vol. 776. P. 96–108.
CrossRef Google Scholar -
Kramar Miroslav, Levanger Rachel, Tithof Jeffrey et al.
Analysis of Kolmogorov flow and Rayleigh–Benard convection using persistent homology.
Physica D. 2016. Vol. 334. P. 82–98. CrossRef Google Scholar -
Grindrod P., Harrington H.A., Otter N., Porter M.A.
A roadmap for the computation of persistent homology.
arXiv:1506.08903. 2015. 45 p.
CrossRef Google Scholar -
CHomP, Computational Homology Project.
http://chomp.rutgers.edu.
