Аннотация
В работе описан подход к моделированию взаимодействия освещения с тонким красящим слоем.
Задача была поставлена для генерации изображений слоя чернил, исходя из внутренней структуры слоя и формы красящих частиц.
В отличие от обычных красок слой чернил характеризуется высокими объемными концентрациями частиц.
Лучевой подход или лучевое уравнение переноса практически не применимы для решения этой задачи.
Поэтому был выбран путь непосредственного решения волновых уравнений, естественно, при некоторых ограничениях и упрощениях.
В данной работе описана математическая постановка задачи и проблема генерации явной геометрии красящего слоя.
Abstract
One approach to the problem of ligting simulation inside of ink or paint layer is described.
The problem arose in the task of rendering of ink basing on information about shape of ink pigments and layer structure.
High pigment volume concentration characterizes ink layer structure. Ray tracing or LTE are hardly applicable here.
Therefore it was decided to solve it as a diffraction problem basing on wave optics methods.
The mathematical task formulation and problem of generation of explicit ink layer geometry is considered in the article.
Содержание. 3
1. Введение. 4
2. Физическая модель и
математическая постановка задачи рассеяния. 11
2.1. Волновое уравнение
Гельмгольца. 12
2.2. Граничные условия на верхней
и нижней поверхностях красящего слоя 12
2.3. Расчетная область и
граничные условия на боковых границах. 13
3. Генератор геометрии красящего
слоя. 16
3.1. Генерация геометрии
красящего слоя. 16
3.2. Форма пигментных частиц. 18
3.3. Взаимодействие между
частицами. 19
3.4. Движение частиц. 21
3.5. Описание алгоритма генерации
геометрии слоя. 22
4. Заключение. 25
Список литературы. 26
1. Введение.
В последние годы в литературе по компьютерной графике опубликовано
большое количество работ по моделированию различных красящих субстанций [1, 2].
Подавляющее число таких работ базируется или на методах геометрической оптики, или
использует компромиссное приближение известное как лучевое уравнение переноса.
Оба подхода и геометрическая оптика, и метод уравнения переноса имеют одно
существенное ограничение: в них используется предположение о возможности
расчета рассеяния и (или) поглощения на отдельной неоднородности красящей
среды. Во многих случаях такое предположение, требующее чтобы расстояние между
отдельными неоднородностями было бы много больше длины волны излучения, вполне
оправдано. Однако в случае, когда расстояние между неоднородностями или их
характерный размер меньше или порядка длины волны, применимость таких методов
вызывает сомнение.
Поскольку уравнение переноса является в значительной степени
феноменологическим уравнением, то вполне возможно, что и в случаях, когда
характерные размеры красящей среды сравнимы с длиной световой волны, уравнение
переноса не теряет своей применимости при соответствующем выборе
дифференциального сечения рассеяния (фазовой функции) и сечения поглощения.
Однако расчет этих величин требует значительных аналитических и численных
затрат и едва-ли возможен в общем случае.
В случае стохастических сред возможным способом расчета является решение
уравнения Бете-Солпитера [3], которое часто пытаются применить в квантовой
электродинамике и квантовой теории многих тел. Однако, как и в этих двух
разделах физики, в оптике решение уравнение Бете-Солпитера и сопряженного с ним
уравнения Дайсона возможно только при очень сильных упрощениях, которые делают
результаты решения практически бесполезными в оптике. Тем не менее, некоторые
авторы утверждают, что способны решать такие уравнения и приводят в своих
работах результаты [4]. Однако при детальном анализе оказывается, что все
опять-таки сводится к хорошо известному уравнению переноса и не менее хорошо известной
индикатрисе рассеяния Хеньи-Гринстайна, а декларации авторов о решении
уравнений Дайсона и Бете-Солпитера оказываются несостоятельными.
В настоящей работе рассматривается красящий слой, состощий из малых
частиц пигмента с размерами ~ 100÷500 нанометров при объемной
концентрации пигмента, доходящей до 50%. Малые размеры частиц, высокая
концентрация и малая толщина слоя (~ 1 микрона) не позволяют пременять
уравнение переноса. Поэтому был выбран путь непосредственного решения волновых
уравнений, естественно, при некоторых ограничениях и упрощениях.
Основное упрощение касается самого использованного волнового уравнения.
Точные уравнения, описывающие распространения света, хорошо известны - это
уравнения Максвелла [5]. При характерных размерах неоднородностей среды,
многократно превышающих атомные размеры, возможно применение так называемых
макроскопических уравнений Максвелла, когда свойства сред описываются
соответствующими диэлектрической и магнитной проницаемостями. Возможно, что диэлектрическая проницаемость является
комплексной. Как правило, в оптике, в частности, в нашем случае, магнитная
проницаемость равна 1. Существует небольшое число точных аналитических решений
макроскопических уравнений. Все они получены для простых пространственных
геометрий с высокой симметрией. Тем не менее, даже в случае очень высокой
симметрии, например, рассеяние плоской линейно поляризованной волны на
диэлектрической сфере (теория Ми), конечный ответ представляется в виде
бесконечного ряда, содержащего специальные функции математической физики. В
нашем случае со сложной пространственной геометрией аналитическое решение
невозможно и может быть получено только с помощью применения численной
процедуры.
Характерной особенностью макроскопических уравнений Максвелла являются
возможные разрывы нормальных компонент электрического и магнитного полей на
поверхностях разрывов проницаемостей. В связи с этим аккуратная численная
процедура должна учитывать такие разрывы путем применения специализированных
или достаточно частых пространственных сеток. Точный учет разрывов возможен
только в случае очень простых пространственных геометрий, когда поверхности
разрывов совпадают с поверхностями сетки. В случае стохастических сред с
большим числом неоднородностей расчет на подобных сетках практически невозможен
из-за необходимого огромного объема оперативной памяти и времени вычислений.
Часто в электромагнитных расчетах для таких сред прибегают к различного
рода упрощениям, например, реальное разрывное распределение диэлектрической
проницаемости заменяют на непрерывное сглаженное. Погрешность, вносимая этими
упрощениями, заранее (а зачастую и после вычислений) неизвестна. И хотя, на наш
взгляд, применение уравнений Максвелла все же предпочтительнее, нами в качестве
волнового уравнения было выбрано так называемое скалярное приближение,
уравнение Гельмгольца [5].
Скалярное приближение широко применяется в оптике при расчетах
распространения неполяризованного излучения. Оно не учитывает поляризацию
электромагнитного излучения, и приближенно можно считать, что оно соответствует
электромагнитному излучению, поляризованному в плоскости раздела разных сред. В
случае простых геометрий различие между результатами точных электромагнитных и
скалярных расчетов может быть заметным. Однако в случае стохастичесхих сред,
когда сильное, в значительной степени изотропное, рассеяние приводит к
деполяризации излучения, применение скалярного приближения вполне оправдано.
Как правило, в таких случаях все существенные волновые эффекты скалярное
приближение описывает достаточно хорошо.
Следует отметить одно важное преимущество скалярных расчетов перед
точными электродинамическими. В отличие от уравнений Максвелла решение
скалярного уравнения непрерывно вместе с его первыми частными производными. Эта
непрерывность существенно снижает требование к размерам используемой
пространственной сетки и времени вычислений. Кроме этого, геометрия
рассеивающего объекта входит в численную процедуру просто через значения
диэлектрической проницаемости в узлах сетки. Скалярное приближение оперирует
всего с одним комплексным полем вместо 5-6 полей в электромагнитном случае, что
позволяет проводить вычисления на отдельных компьютерах с вполне доступным
размером оперативной памяти (8Гб и менее), совсем не используя параллельные
вычисления.
Условно методы решения волновых задач можно разделить на две большие
группы: стационарные и зависящие от времени. Первый подход является подходом
классической теории рассеяния, когда рассеивающий объект освещается плоской
монохроматической волной. Ко второй группе можно, например, отнести методы
семейства Finite Difference Time Domain FDTD [6], которые моделируют рассеяние
квазимонохроматических импульсов конечной длительности. Методы обеих групп
имеют как свои достоинства, так и свои недостатки.
Нестационарные подходы наиболее применимы для расчета рассеяния коротких
импульсов излучения (максимально до нескольких тысяч периодов световых
колебаний) на объектах с “упорядоченной” геометрией. Несомненными достоинствами
таких методов являются
·
относительная
простота реализации, в которой используются явные конечно-разностные схемы
расчета, хотя и на достаточно сложных пространственных сетках,
·
возможность
расчетов для рассеивающих объектов с достаточно сильной частотной дисперсией
“за один проход”
·
относительно
несложное распараллеливание вычислений на большое число компьютеров.
К недостаткам следует отнести значительную необходимую оперативную память
и большую (априори неизвестную) длительность падающего импульса для достижения
удовлетворительной точности вычисления угловых распределений в дальней зоне.
В настоящем случае наиболее применимы подходы, использующие стационарное
освещение. В реальности объектом, воспринимающим освещение, является
человеческий глаз или иной регистрирующий прибор с характерным временем регистрации,
значительно превосходящим период световых колебаний. Основным достоинством
использованного стационарного подхода является простая постановка граничных
условий в явном виде. Кроме этого, более просто, чем в нестационарном случае,
осуществляется контроль достигнутой точности, поскольку ищется установившееся
решение.
К недостаткам следует отнести более сложную явно-неявную вычислительную
схему и, вследствие этого, более трудоемкое распараллеливание. Однако следует
отметить, что для вычисления усредненных по ансамблю угловых распределений
необходимо проводить вычисления для большого числа (десятки, а иногда и сотни)
вариантов случайной геометрии красящего слоя. В этом случае возможно проведение
одного варианта на одном компьютере с объемом памяти 8 Гб и менее. А потом
делается усреднение вариантов. Таким образом, достигается простое,
естественное, но достаточно эффективное, распараллеливание вычислений.
Важное упрощение задачи касается ее геометрии. В реальности освещение
всегда происходит некогерентным светом (случай лазерного освещения здесь не
рассматривается), поэтому и некогерентность освещения и стохастичность
геометрии в результате дают усредненную картину угловых распределений. При
освещении слоя когерентным светом усреднение может быть достигнуто только за
счет стохастичности структуры красящего слоя. Для этого расчет должен
использовать очень большой участок поверхности слоя, что не оправдано с точки
зрения объема оперативной памяти и времени расчета.
Вместо использования больших фрагментов был использован другой подход.
Рассеяние вычислялось для бесконечного плоского красящего слоя, составленного
из одного элементарного фрагмента размерами ~10 x 10 микрон, а затем периодически
повторенного в двух измерениях. Использование периодических структур – это
прием, достаточно часто применяемый в оптических расчетах [7]. В таком случае
угловые распределения рассеянного света в дальней зоне содержат конечное
дискретное число направлений. Интенсивность луча (мощность, переносимая в
данном направлении) является случайной величиной и в достаточной степени
зависит от геометрии элементарного фрагмента. Чтобы получить гладкие угловые
распределения, необходимо произвести расчеты для различных (случайных, но
подчиняющихся одной и той же статистике) реализаций элементарного фрагмента, а
затем усреднить результаты по ансамблю таких реализаций. Нетрудно видеть, что
подобная процедура эквивалентна усреднению по ансамблю, применяемому в
статистической физике, и достаточно точно отражает реальную картину рассеяния
на красящем слое.
В компьютерной графике свойства поверхностей описываются с помощью
соответствующих угловых распределений интенсивности или яркости отраженного
света – двунаравленной функцией отражения (ДФО). В данном случае расчеты
проводятся для монохроматического освещения. Поскольку излучение с разными
длинами волн взаимно некогерентно, то построение спектральных ДФО никаких
трудностей не вызывает. Как уже было сказано, при расчетах для периодического
слоя угловые распределения имеют дискретную угловую структуру. Полное
количество направлений и их плотность определяются размерами элементарного
фрагмента. Использованные размеры позволяют без особых проблем получить гладкие
угловые распределения для всех существенных направлений. Более того, поскольку
согласно постановке нашей задачи красящий слой располагался на подложке
(бумага) с Ламбертовским оражением, задача получения ДФО для системы слой +
бумага имеет даже более простое решение.
Уже упоминалось, что красящий слой, как правило, имеет стохастическую
структуру, в которой объемная концентрация зерен пигмента (распределенных
случайно по объему слоя) может составлять 50% и более. Экспериментальное
измерение реальной геометрии слоя практически невыполнимо. Поэтому возникает
необходимость генерации такой геометрии с помощью численной процедуры. Для
одинаковых шарообразных частиц и объемной концентрации < 30% генерация
достаточно проста и может быть осуществлена случайным разбрасыванием центров
частиц по объему элементарного фрагмента, исключая выход за поверхности фрагмента
и пересечения между частицами.
В данной работе использовались частицы более сложной формы, приближенной
к реальным формам красящих пигментов в чернилах цветных принтеров. Аксиально-симметричная форма таких частиц может быть приближена с
помощью нескольких жестко связанных шаров с возможными пересечениями различного
радиуса. Кроме этого, предполагалось, что протяженные частицы в красящем слое,
могут быть полностью или частично ориентированы. Геометрии слоя частиц должна
также удовлетворять условию, что зерна пигмента не должны выходить за
поверхности элементарного фрагмента и пересекаться между собой. Для генерации
геометрии с подобными свойствами была применена численная процедура,
аналогичная процедуре “молекулярной динамики”. Необходимая ориентация частиц
достигалась за счет наложения “магнитного” поля той или иной напряженности.
Таким образом, вся задача моделирования свелась к решению трех
самостоятельных задач:
1.
Решение
задачи дифракции на тонком периодическом красящем слое с явным распределением
коэффициента преломления конечно-разностными методами.
2.
Генерация
геометрии фрагмента красящего слоя, состоящего из частиц заданных форм и
размеров и вычисление распределения коэффициента преломления на используемой
пространственной сетке.
3.
Вычисление
ДФО красящего слоя, расположенного на Ламбертовской подложке исходя из
результатов решения задачи дифракции.
Ограниченный объем публикации не позволяет нам подробно описать решения
всех задач. В данной работе будет рассмотрена генерация фрагмента красящего слоя
и постановка задачи рассеяния. Остальные задачи и решения будут опубликованы
позднее.
Геометрия и использованная система координат
представлены на рисунке 1. Красящий слой представлен в виде синей пластины,
параллельной плоскости Oxy. Падающая
волна показана красными стрелками;
направление падения лежит в плоскости Oxz.
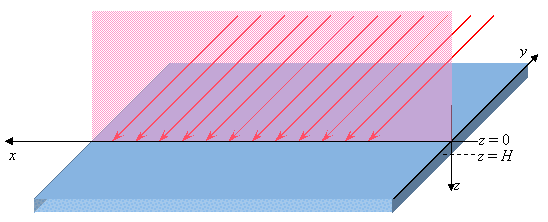
Рис. 1.
Красящий слой представлен в виде пластины, параллельной плоскости Oxy. Падающая волна показана стрелками; направление падения
лежит в плоскости Oxz.
Рассматривается стационарный режим, когда красящий слой освещается
падающей монохроматической волной. В этом случае временная зависимость всех
полей имеет гармонический вид: 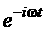 и
может быть исключена из волнового уравнения. Поэтому волновое уравнение
становится уравнением Гельмгольца: и
может быть исключена из волнового уравнения. Поэтому волновое уравнение
становится уравнением Гельмгольца:
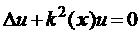 (1.1)
(1.1)
где k(x) = η(x)k0 – есть локальное волновое число, k0 – волновое число в вакууме и η – локальный показатель преломления.
В нашем случае показатель преломления различен в ваккуме, частицах пигмента и в
объемлющей среде.
Формально необходимо проинтегрировать уравнение Гельмгольца (1.1) во всей
области, включая красящий слой и вакуум по обе стороны от него. Естественно,
прямой подход, который использует дискретизированное поле во всей расчетной
области, невозможен. Вместо этого мы разделим все пространство на три части:
вакуум выше красящего слоя, сам слой и вакуум ниже слоя. В полупространствах
заполненных вакуумом выше и ниже слоя показатель преломления постоянен, а
уравнение (1.1) имеет хорошо известные аналитические решения. Таким образом,
нет необходимости оперировать с полем выше и ниже слоя на пространственной
разностной сетке. Для поля внутри красящего слоя аналитическое решение не
существует, поэтому решение находится с помощью численной процедуры.
Решение дифракционной задачи должно быть найдено в трех разных областях.
На границах этих областей, т.е. на границах вакуум-красящий слой, должны быть
заданы условия сшивки для искомого решения. Для уравнения (1.1) условия
сопряжения имеют следующий вид: поле u вместе с его нормальной производной
должно быть непрерывно на границах:
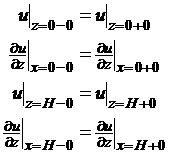 (1.2)
(1.2)
Условий (1.2) еще недостаточно. Поскольку (1.1) есть уравнение второго
порядка, то на границах каждой области необходимы два граничных условия.
Однако, для заполненных вакуумом полупространств формулы (1.2) задают граничные
условия только на границах слоя. Недостающие условия, называемые условиями
излучения, задаются на других “поверхностях” полупространств, т.е. на
бесконечности. Эти условия утверждают:
·
Решение ограничено на бесконечности.
·
Все компоненты поля, описывающие приходящие волны (за
исключением падающей волны в верхнем полупространстве) исчезают на
бесконечности.
Естественно, численная процедура не может использовать бесконечную
расчетную область. Существуют две возможности: первая, мы можем работать с
конечным фрагментом красящего слоя (как показано на рис. 2.); вторая, мы можем использовать
бесконечный красящий слой, состоящий из периодически повторяющегося
элементарного фрагмента (пример приведен на рис. 3).
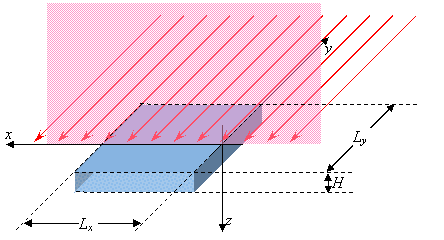
Рис. 2. Рассеяние
конечным фрагментом красящего слоя (параллельным плоскости Oxy).
Падающая волна показана красными стрелками; направление падения – в плоскости Oxz.
Первый подход физически оправдан, поскольку в любом эксперименте площадь
красящего слоя ограничена. В этом случае на всех внешних границах конечного
фрагмента должны быть заданы условия сопряжения, к которым добавляются условия
излучения на бесконечности во всем пространстве, окружающем фрагмент слоя.
Постановка граничных условий для этого варианта сопряжена со значительными
вычислительными трудностями.
Второй подход состоит в использовании бесконечного красящего слоя,
состоящего из элементарного фрагмента (имеющего форму параллелепипеда),
повторяющегося периодически в двух измерениях (рис. 3). Такой подход широко
используется в дифракционных задачах [7].
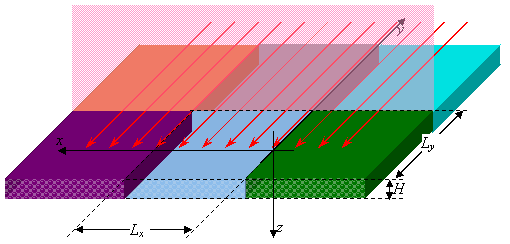
Рис. 3. Бесконечный
красящий слой, образованный элементарным фрагментом, периодически повторяющимся
в двух измерениях. Показаны несколько соседних периодов, выделенных различными
цветами.
Все “плитки” (элементарные фрагменты) одинаковы. Из непрерывности
следует, что поле на левой вертикальной границе зеленой плитки равно полю на
правой границе синей плитки. И так на всех вертикальных границах. В случае
нормального падения (вдоль оси Oz) освещающее поле и поле внутри каждой плитки, а также рассеянное
поле для каждой плитки будут одинаковы. Таким образом, полное поле будет
периодическим в двух измерениях. Отсюда получаем периодические граничные
условия на вертикальных границах между плитками:
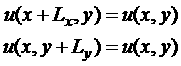 (1.3) (1.3)
В случае наклонного падения поле уже не одинаково для всех плиток.
Освещающее поле на поверхности красящего слоя имеет вид:
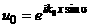
где k0 – волновое число в вакууме, σ – угол падения (угол между
направлением освещения и нормалью к красящему слою). Поле для двух соседних
периодов отличается множителем 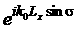 . Если
выполняется следующее соотношение (здесь и далее λ – длина волны в вакууме) . Если
выполняется следующее соотношение (здесь и далее λ – длина волны в вакууме)
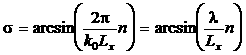 , ,
то поле будет
одним и тем же для всех периодов, и мы опять можем применять периодические
граничные условия (1.3).
Для фрагмента с периодом порядка 100 длин волн “сетка” подобных направлений
достаточна для задания всех необходимых направлений падения с приемлемой
точностью.
Для других углов падения поле уже не будет периодическим, а граничные
условия принимают вид:
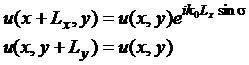 (1.3’) (1.3’)
В таком
случае решение дифракционной задачи удобно искать в представлении Блоха:
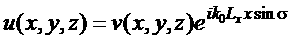
здесь v – периодическая функция. Представление Блоха широко
применяется в методах, основанных на преобразовании Фурье [7].
3.1.
Генерация геометрии красящего слоя.
Дифракционный расчет рассеяния света красящим слоем предполагает задание
геометрии такого слоя в явном виде. Мы проанализировали структуры реальных
красящих слоев, состоящих из прозрачного связующего вещества, наполненного
зернами пигмента различной формы. Зерна пигментов в объеме слоя, как правило,
располагаются однородно и хаотически. Однако возможны случаи, когда зерна имеют
преимущественную ориентацию или образуют конгломераты (агглютинация).
Поверхность красящего слоя может быть плоской, так как при высыхании
краски действуют силы поверхностного натяжения связующего вещества. При
значительных концентрациях пигмента сил поверхностного натяжения недостаточно
для формирования плоской поверхности и часть частиц “выступает” из слоя,
образуя поверхность с микрорельефом. Наличие микрорельефа приводит к
возникновению дополнительного рассеяния.
Генерация геометрии для небольших концентраций пигментных зерен
достаточно проста. Она может быть осуществлена последовательным случайным
разбрасыванием центров и ориентаций частиц по объему фрагмента слоя. При этом
если новая добавляемая к ансамблю частица пересекается с уже существующими
частицами или выходит за границы фрагмента, то такая частица отбрасываетсяся, и
происходит случайное разыгрывание следующей частицы. Процедура заканчивается,
когда фрагмент слоя наполняется необходимым числом частиц.
В случае очень тонких красящих слоев (толщина ~1 микрона) объемная
концентрация зерен пигмента может достигать значительной величины ~ 30% и
более. При таких концентрациях случайное разбрасывание не дает необходимого
результата и следует применять более сложную процедуру, например, подобную
методу молекулярной динамики.
Использованный подход можно описать следующим образом. Сначала в
расчетной области случайно разбрасывается необходимое число частиц, которые
могут пересекаться между собой. Затем между частицами вводится упругое
взаимодействие, в нашем случае чисто отталкивательное, которое приводит к
возникновению сил между пересекающимися частицами или при пересечении частицей
границы области. Под действием сил частицы могут перемещаться (и вращаться), и
таким образом пересечения между частицами и частиц с границами устраняются.
Когда все нежелательные пересечения устранены процедура заканчивается. Для
придания ансамблю частиц предпочтительной ориентации может быть введено
дополнительное взаимодействие, аналогичное взаимодействию магнитного момента
частицы с внешним магнитным полем. При этом степень ориентированности ансамбля
частиц регулируется с помощью величины такого поля.
Перемещение частиц под воздействием сил можно находить различными
методами, например, методами спуска, минимизируя энергию взаимодействия всего
ансамбля. В случае очень большого числа частиц и высоких концентраций можно
использовать динамические подходы (интегрирование соответствующих уравнений
движения). Если используется динамика второго порядка (уравнения Ньютона), то
необходимо ввести массы частиц и вязкость (силы, зависящие от скорости). Методы
второго порядка предпочтительны в случае концентраций, близких к предельным.
В данной работе мы использовали динамику первого порядка. Это означает,
что частицы не обладают инерцией, и движение частицы мгновенно прекращается как
только исчезает действующая на нее сила. В таком случае нет необходимости
вводить массы частиц. Нетрудно видеть, что настоящий подход практически
эквивалентен минимизации энергии ансамбля взаимодействующих частиц методом
наискорейшего спуска.
После того как геометрия красящего слоя получена, вычисление
распределения коэффициента преломления на пространственной сетке (исходные
данные для задачи дифракции) не вызывает никаких затруднений. Отметим, что в
нашем случае, красящий слой может состоять из зерен различных пигментов
различной формы.
.
Анализ красящих слоев показал, что с достаточной точностью в качестве
пигментных зерен можно использовать аксиально-симметричные частицы. Такие
частицы могут быть аппроксимированы некоторым количеством жестко соединенных
между собой шаров. Например, цилиндрическая частица может быть аппроксимирована
несколькими одинаковыми шарами с центрами, расположенными на оси цилиндра.
Точность аппроксимации будет зависеть от количества шаров и расстояний между их
центрами. Примеры возможных частиц, построенных из шаров, приведены на рис. 4.

Рис.
4. Примеры используемых частиц.
В расчетах частица задается координатами ее центра, ориентацией оси
симметрии частицы, числом составляющих частицу шаров, радиусами этих шаров и
расстоянием от центра каждого шара до центра частицы. Нетрудно видеть, что
используемая аппроксимация частиц шарами позволяет конструировать частицы самой
разнообразной формы. Естественно, время расчета геометрии сильно зависит как от
числа частиц, так и от точности задания частиц (числа шаров, необходимого для
задания частицы).
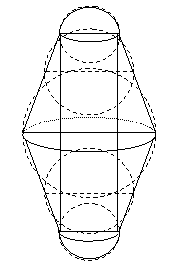
Рис.
5. Частица “рисовое зерно”.
Наш анализ показал, что во многих случаях форма частиц пигмента близка к
форме рисового зерна. Поэтому, наряду с возможностью использовать частицы
различной формы, мы для удобства расчетов, также использовали частицу именно
такой формы (размеры частицы могут быть переменными). Схема частицы в форме
рисового зерна приведена на рис. 5.
Сила взаимодействия между пересекающимися частицами вычисляется как сумма
всех сил для пересекающихся шаров, из которых частицы состоят (естественно,
шары, составляющие одну частицу, не взаимодействуют между собой). Сила
взаимодействия между пересекающимися шарами зависит от величины этого
пересечения L (рис. 6):
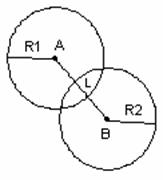
Рис.
6. Пересечение шаров. L=R1+R2-AB.
Конкретный вид силы взаимодействия может быть выбран в достаточно широком
диапазоне. Как правило, сила взаимодействия максимальна при совмещении центров
шаров и становится равной нулю для L<0. В том случае, когда данный шар
пересекается с несколькими шарами, действующая на него сила определяется как
векторная сумма всех сил (рис. 7).
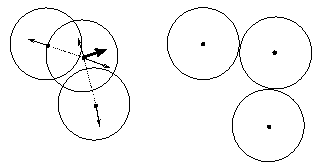
Рис.
7. Пример взаимодействия трех шаров.
Если частица состоит более чем из одного шара, кроме перемещения
необходимо определить возможные вращения оси симметрии частицы. При этом для
каждой протяженной частицы определяется ее “центр масс” (например,
геометрический центр частицы), и вычисляется действующий на частицу вращающий
момент:
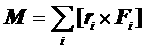 , ,
где 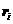 – вектор, соединяющий
центр частицы и центр ее i-го шара, – вектор, соединяющий
центр частицы и центр ее i-го шара,
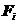 – сила, действующая на
центр i-го шара. – сила, действующая на
центр i-го шара.
Точные уравнения, описывающие движение i-ой частицы имеют следующий вид:
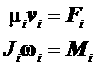
где 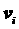 – скорость центра частицы, – скорость центра частицы,
 – вектор угловой скорости вращения оси
симметрии частицы. – вектор угловой скорости вращения оси
симметрии частицы.
Величины μ и J могут быть названы коэффициентами
трансляционной и вращательной вязкости. В данной задаче нет необходимости
интегрировать уравнения движения с высокой точностью, поскольку конечным результатом
является ансамбль непересекающихся частиц, а не точные траектории движения.
Поэтому возможно применение простейшего метода интегрирования дифференциальных
уравнений – метода Эйлера [8].
В процессе интегрирования уравнений движения очень важную роль играет
выбор шага интегрирования. Малый шаг интегрирования обеспечивает достаточную
точность вычислений, но увеличивает длительность расчетов. Слишком большой шаг
интегрирования приводит к заметным ошибкам, в результате ухудшается сходимость
решения, возможен переход в режим осциллирующего поведения, и даже потеря
сходимости.
Обычный способ состоит в том, чтобы выбрать величину шага интегрирования,
для которой изменения правых частей динамических уравнений будут невелики. В
нашем случае, когда силы взаимодействия зависят от расстояний между
отталкивающимися шарами, такое условие сводится к малости перемещений шаров по
сравнению с их радиусами за один шаг интегрирования. В настоящей работе выбор
оптимального шага был произведен экспериментально, учитывая результаты
достаточно большого числа пробных расчетов. Эти расчеты показали, что следует
использовать шаг интегрирования, при котором максимальные смещения не
превосходят ~ 0.2 от характерного радиуса шаров, составляющих частицы пигмента.
На рис. 8 показан случай движения трех частиц (каждая состоит из трех
одинаковых шаров), пересекающихся в начальный момент. Для наглядности показан
случай двумерного движения (вращение осей симметрии частиц происходит в
плоскости рисунка). Окончательные перемещения частиц изображены с помощью синих
стрелок.
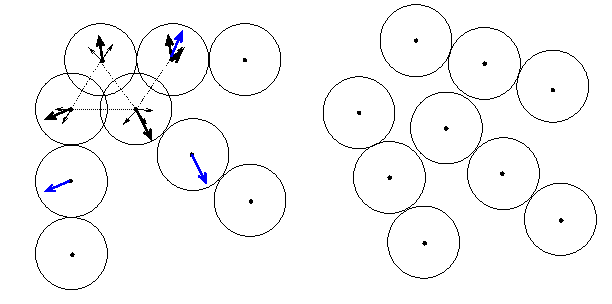
Рис.
8. Двумерное движение трих одинаковых частиц.
3.5. Описание алгоритма генерации
геометрии слоя.
Вычисление геометрии слоя состоит из нескольких последовательных итераций
(число итераций определяется заранее). Каждая итерация стартует с ансамбля,
состоящего из некоторого числа непересекающихся частиц, находящихся в
неподвижном состоянии (в самом начале расчета частиц нет совсем). Итерации
состоят из следующих шагов.
1.
Добавление
к ансамблю новых частиц. Новые частицы распределены случайно (координаты
центров и ориентация оси симметрии). Количество добавляемых частиц определено
заранее и зависит от объемных концентраций частиц различных видов, используемых
в вычислениях. Все вновь добавленные частицы записываются в текущий список
движущихся частиц. Список движущихся частиц должен содержать частицы, которые
могут пересекаться с другими частицами или с границами расчетной области.
Поскольку перед началом каждой итерации все пересечения устранены, то в текущий
список добавляются только новые частицы.
2.
Вокселизация.
Чтобы ускорить вычисления производится “вокселизация” расчетной области, т. е.
вся расчетная область разбивается на одинаковые элементарные подобласти
(вокселы). Размеры вокселей выбираются большими, чем максимальный размер
частицы. Вокселизация частиц состоит в определении соответствующего воксела для
каждой частицы. При рациональном выборе размеров вокселей возможно
взаимодействовие только между частицами, расположенными в соседних вокселах.
Использование вокселизации позволяет существенно ускорить перебор возможных пар
взаимодействующих частиц при вычислении сил и вращающих моментов.
3.
Вычисление
сил и вращающих моментов. Для каждой частицы из текущего списка движущихся
частиц вычисляются силы и моменты, возникающие при возможном пересечении со
всеми остальными частицами. Естественно, что для перебора всех
взаимодействующих пар достаточно перебрать только частицы из текущего списка,
т. к. частицы вне этого списка на предыдущем шаге ни с чем не взаимодействовали
(покоились). Потенциальные взаимодействующие частицы определяются, используя
вокселизацию из п. 2. Силы и моменты, действующие на каждую взаимодействующую
частицу, суммируются, а сама частица добавляется в новый список движущихся частиц.
Перебор взаимодействующих пар выполнен так, чтобы избежать двойного учета
взаимодействий.
4.
Взаимодействие
с границами области. Если частица пытается выйти за границу расчетной области,
на нее начинает действовать упругая возвращающая сила, аналогичная силе между
пересекающимися частицами. Возвращающая сила направлена по нормали к границе,
ее величина растет по мере удаления частицы от допустимого объема области.
Вычисленные силы добавляются к силам, вычисленным в п. 3. Все частицы, вышедшие
за границы, добавляются в новый список движущихся частиц.
5.
Перемещения
и вращения. С помощью вычисленных сил и вращающих моментов определяется шаг
интегрирования. Затем происходит перемещение и вращение частиц.
6.
Модификация
текущего списка движущихся частиц. Вычисленный новый список движущихся частиц
переписывается в текущий список. После этого новый список очищается.
7.
Если
пересечения не устранены и число шагов интегрирования не превышает заранее
заданный лимит, то происходит переход к п. 2. В противном случае переход к п.
1.
Итерации прекращаются, когда достигается необходимая объемная
концентрация пигментаов.
Естественно, настоящий алгоритм имеет ограничения по объемной
концентрации. Однако, для реальных концентраций пигмента, например для
шарообразных частиц при объемной концентрации пигмента < 60%, результаты
работы генератора геометрий вполне удовлетворительные.
Мы провели достаточно большое количество расчетов и вычислили необходимые
статистические характеристики распределений частиц, полученных с помощью
генератора геометрий. Все расчеты дали вполне удовлетворительные результаты, а
статистические характеристики распределений находились в допустимых пределах.
В данной работе было приведено начало описания оригинального подхода к
моделированию взаимодействия освещения с тонким красящим слоем. Задача была
поставлена для генерации изображений слоя чернил, исходя из внутренней
структуры слоя и формы красящих частиц. В отличие от автомобильных красок,
рассмотренных авторами в более ранних работах, слой чернил характеризуется
высокими объемными концентрациями частиц. Лучевой подход или лучевое уравнение
переноса практически не применимы для решения этой задачи. Поэтому был выбран
путь непосредственного решения волновых уравнений, естественно, при некоторых ограничениях
и упрощениях.
Задача естественно разделяется на три составляющие: генерация явной
геметрии частиц и структуры слоя чернил, решения задачи дифракции для
конкретной геометрии чернильного слоя и генерация визуального представления
слоя. Для большинства сложных материалов их визуальное предсталение может быть
описано с помощью двунаправленной функции отражения (ДФО) в общей, табулярной
форме. Поэтому третья составляющая нашей задачи сводится к генерации ДФО из
набора решений задачи дифракции, рассчитанных для различных явных геометрий
красящего слоя.
Так как это первая работа, описывающая наш подход, в нее были включены
только описание математической постановки задачи дифракции и описание
алгоритмов генерации явной геометрии красящего слоя. Предполагается остальные
части работы опубликовать в дальнейшем.
Электронная версия статьи с цветными иллюстрациями размещена по адресу
http://www.keldysh.ru/pages/cgraph/publications/cgd_publ.htm.
[1] Ershov, S., Kolchin, K.,
Myszkowski, K., Rendering pearlescent appearance based on paint-composition
modeling. Computer Graphics Forum, Vol. 20, No 3, 2001, pp. 227-238.
[2] Durikovic, R., Kolchin, K.,
Ershov, S., Rendering of Japanese artcraft. In Proceeding of the EUROGRAPHICS,
short presentations, 2002, pp. 131-138.
[3] Рытов, С.М., Кравцов, Ю.А., Татарский, В.И., Введение в
статистическую радиофизику. Ч.2. Случайные поля — М.:Наука, 1978
[4] Kuz’min, V.L., Meglinskii, I.V.,
Numerical Simulation of Coherent Effects under Conditions of Multiple
Scattering. Optics and Spectroscopy, Vol. 97, No. 1, 2004, pp. 100-106.
[5] Кошляков Н.С., Глинер Э.Б. Смирнов М.М. Уравнения в частных
производных математической физики. М.: Высшая школа, 1970.
[6] Yee, K.S.: "Numerical solution of initial
boundary value problems involving Maxwell’s equations in isotropic media."
IEEE Transactions on Antennas and Propagation, Vol. 14, No. 3, 1966, pp.
302-307.
[7] Исимару И., Распространение и рассеяние волн в случайно- неоднородных средах. М.: Мир, 1981.
[8] Эльсгольц, Л.Э.,Дифференциальные
уравнения и вариационное исчисление. М.: Наука, 1969.
|