Определение параметров вращательного движения КА «Монитор-Э» по телеметрическим данным о токе солнечных батарей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||
Система уравнений вращательного движения КА образована
динамическими уравнениями Эйлера для компонент угловой скорости и кинематическими
соотношениями Пуассона для элементов первой и третьей строк матрицы ![]() . В уравнениях Эйлера учитываются гравитационный и восстанавливающий
аэродинамический моменты. Уравнения вращательного движения имеют вид
. В уравнениях Эйлера учитываются гравитационный и восстанавливающий
аэродинамический моменты. Уравнения вращательного движения имеют вид
|
|
(1) |
Здесь
![]() и
и ![]() – соответственно
компоненты векторов абсолютной угловой скорости КА и скорости его центра масс
относительно поверхности Земли в системе
– соответственно
компоненты векторов абсолютной угловой скорости КА и скорости его центра масс
относительно поверхности Земли в системе ![]() ;
; ![]() – среднее орбитальное
движение КА;
– среднее орбитальное
движение КА; ![]() – моменты инерции КА относительно осей
– моменты инерции КА относительно осей ![]() ,
, ![]() – плотность атмосферы
в точке
– плотность атмосферы
в точке ![]() ;
; ![]() – параметры
аэродинамического момента. Плотность атмосферы рассчитывается согласно модели
[1].
– параметры
аэродинамического момента. Плотность атмосферы рассчитывается согласно модели
[1].
Переменные ![]() и
и ![]() связаны между собой
условиями ортогональности матрицы
связаны между собой
условиями ортогональности матрицы ![]() . Поэтому начальные условия для них выражаются через углы
. Поэтому начальные условия для них выражаются через углы ![]() ,
, ![]() и
и ![]() . При интегрировании уравнений (1) вторая строка матрицы
. При интегрировании уравнений (1) вторая строка матрицы ![]() вычисляется как
векторное произведение ее третьей и первой строк.
вычисляется как
векторное произведение ее третьей и первой строк.
2. Метод
определения вращательного движения КА.
Решения уравнений (1), аппроксимирующие фактическое вращательное движение КА, выбираются
из условия наилучшего сглаживания с их помощью телеметрических данных о токе,
снимаемом с солнечных батарей (СБ). В процессе обработки этих данных, помимо
начальных условий движения КА, уточняются и параметры ![]() ,
, ![]() ,
, ![]()
![]() .
.
Ток, вырабатываемый СБ, примерно пропорционален
косинусу угла падения солнечных лучей на их светочувствительную поверхность.
Последняя расположена в плоскости, неподвижной относительно системы ![]() . Нормаль
. Нормаль ![]() к светочувствительной
стороне СБ задается двумя углами: углом
к светочувствительной
стороне СБ задается двумя углами: углом ![]() между вектором
между вектором ![]() и его проекцией на плоскость
и его проекцией на плоскость
![]()
![]() и углом
и углом ![]() между осью
между осью ![]() и проекцией
и проекцией ![]() на плоскость
на плоскость ![]()
![]() . Направление отсчёта
. Направление отсчёта ![]() согласовано с
направлением оси
согласовано с
направлением оси ![]() . Компоненты
. Компоненты ![]() в системе
в системе ![]() вычисляются по
формулам:
вычисляются по
формулам: ![]() ,
, ![]() ,
, ![]() . Орт
. Орт ![]() направления
«Земля-Солнце» задается в орбитальной системе координат компонентами
направления
«Земля-Солнце» задается в орбитальной системе координат компонентами ![]()
![]() , которые рассчитываются по приближенным формулам [2] и
элементам кеплеровой орбиты КА. Упомянутый косинус и снимаемый с СБ ток
задаются формулами
, которые рассчитываются по приближенным формулам [2] и
элементам кеплеровой орбиты КА. Упомянутый косинус и снимаемый с СБ ток
задаются формулами
|
|
(2) |
Здесь ![]() – ток, вырабатываемый
СБ на орбите Земли при перпендикулярном падении солнечных лучей на их
плоскость,
– ток, вырабатываемый
СБ на орбите Земли при перпендикулярном падении солнечных лучей на их
плоскость, ![]() А.
А.
На самом деле расчёт тока более сложен и требует
знания труднодоступной дополнительной информации, но и упрощённые формулы (2)
позволяют получить приемлемые результаты. Эти формулы можно ещё более упростить,
если учесть, что в те моменты времени, когда телеметрические значения тока
превышали некоторый положительный предел ![]() , заведомо выполнялось условие
, заведомо выполнялось условие ![]() . Для таких моментов расчётные значения тока можно находить
по формуле
. Для таких моментов расчётные значения тока можно находить
по формуле ![]() . При обработке полученных данных принималось
. При обработке полученных данных принималось ![]() А.
А.
Телеметрическая информация о токе,
снимаемом с батарей, представляет собой последовательность чисел
|
|
(3) |
Здесь
![]() – приближённое
значение тока в момент времени
– приближённое
значение тока в момент времени ![]() ,
, ![]() . Разности
. Разности ![]() , как правило, не превышают нескольких секунд. В обработку
включаются отрезки данных, длина которых
, как правило, не превышают нескольких секунд. В обработку
включаются отрезки данных, длина которых ![]() составляет от 20 до 40
минут.
составляет от 20 до 40
минут.
Обработка данных (3) выполняется
методом наименьших квадратов. Пусть ошибки в значениях ![]() независимы и имеют
одинаковое нормальное распределение с нулевым средним значением и стандартным
отклонением
независимы и имеют
одинаковое нормальное распределение с нулевым средним значением и стандартным
отклонением ![]() . Значение
. Значение ![]() неизвестно. На
решениях уравнений движения, заданных на отрезке
неизвестно. На
решениях уравнений движения, заданных на отрезке ![]() , определим функционал
, определим функционал
|
|
(4) |
Аппроксимацией
фактического движения КА на этом отрезке будем считать решение, доставляющее
такому функционалу минимум. Минимизация ![]() проводится по начальным
значениям параметров движения КА в точке
проводится по начальным
значениям параметров движения КА в точке ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() и параметрам
и параметрам ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Для простоты письма объединим все уточняемые величины в
один вектор
. Для простоты письма объединим все уточняемые величины в
один вектор ![]() и будем рассматривать
функционал (4) как функцию
и будем рассматривать
функционал (4) как функцию ![]() . Тогда
. Тогда ![]() – искомая оценка вектора
– искомая оценка вектора
![]() .
.
Минимизация функционала (4) выполнялась
в два этапа: сначала методом случайного поиска находилось грубое приближение ![]() , которое затем уточнялось методом Левенберга-Марквардта.
, которое затем уточнялось методом Левенберга-Марквардта.
3.
Реализация метода Левенберга-Марквардта. Применение этого метода в задачах определения вращательного движения
спутников по данным измерений бортовых датчиков описано в [3, 4]. Метод является одним из вариантов
метода Гаусса-Ньютона. На каждой итерации этого метода поправка ![]() , уточняющая имеющееся приближённое значение
, уточняющая имеющееся приближённое значение ![]() , определяется системой
, определяется системой
|
|
(5) |
Здесь ![]() – матрица нормальных
уравнений,
– матрица нормальных
уравнений, ![]() – положительный параметр,
– положительный параметр,
![]() – единичная матрица
порядка 13,
– единичная матрица
порядка 13, ![]() – символ Леви-Чивиты,
– символ Леви-Чивиты, ![]() – псевдопроизводные [3], служащие для
представления истинных производных
– псевдопроизводные [3], служащие для
представления истинных производных ![]() при
при ![]() . Значения
. Значения ![]()
![]() определяются в процессе
интегрирования уравнений
определяются в процессе
интегрирования уравнений
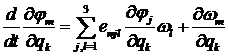
совместно
с уравнениями (1) и уравнениями в вариациях относительно ![]() . Ненулевые начальные условия
. Ненулевые начальные условия ![]() и
и ![]() имеют вид
имеют вид
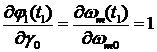 ,
, 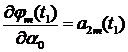 ,
, 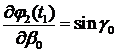 ,
, 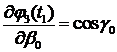 .
.
Ненулевые
производные ![]() в уравнениях (5) определяются следующим
формулами:
в уравнениях (5) определяются следующим
формулами:
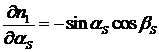 ,
,  ,
,
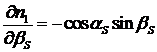 ,
, 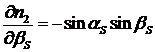 ,
, 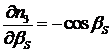 .
.
Точность аппроксимации данных (3) и разброс в
определении компонент ![]() будем характеризовать,
следуя методу наименьших квадратов, соответствующими стандартными отклонениями.
Стандартное отклонение
будем характеризовать,
следуя методу наименьших квадратов, соответствующими стандартными отклонениями.
Стандартное отклонение ![]() ошибок в значениях
ошибок в значениях ![]() находится по формуле
находится по формуле
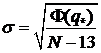 ,
,
стандартные
отклонения компонент вектора ![]() равны квадратным
корням из соответствующих диагональных элементов матрицы
равны квадратным
корням из соответствующих диагональных элементов матрицы ![]() . Ниже стандартные отклонения величин
. Ниже стандартные отклонения величин ![]() ,
, ![]() ,
, ![]() и т. п. будем
обозначать
и т. п. будем
обозначать ![]() ,
, ![]() ,
, ![]() .
.
Чтобы в результате минимизации
функционала (4) значения параметров ![]() ,
, ![]() ,
, ![]() лежали в разумных с
физической точки зрения пределах, в этот функционал вводились дополнительные слагаемые
лежали в разумных с
физической точки зрения пределах, в этот функционал вводились дополнительные слагаемые
![]() .
.
Здесь
![]() и
и ![]() – положительные числа,
– положительные числа, ![]() и
и ![]() – проектные значения
параметров
– проектные значения
параметров ![]() и
и ![]() . В расчётах принимались
. В расчётах принимались ![]() ,
, ![]() ,
, ![]() . Такая замена функционала учитывает априорную информацию об
уточняемых параметрах и регуляризует задачу поиска минимума
. Такая замена функционала учитывает априорную информацию об
уточняемых параметрах и регуляризует задачу поиска минимума ![]() . Ниже, при вычислении стандартных отклонений использовано
новое выражение для функционала.
. Ниже, при вычислении стандартных отклонений использовано
новое выражение для функционала.
4. Поиск
начального приближения. Чтобы
алгоритм минимизации Левенберга-Марквардта был надёжен, необходимо иметь
достаточно точное начальное приближение точки минимума. Для этого использовался
метод случайного поиска с обучением [5].
Начальные значения уточняемых параметров для процедуры
случайного поиска находились из анализа имеющейся телеметрической информации и
конструкторской документации на КА. Анализ основывался на следующих соображениях
(рис. 1). Пусть угловое положение КА в орбитальной системе координат в
начальный момент времени определяется углами ![]() ,
, ![]() и
и ![]() . Начальный угол
. Начальный угол ![]() между направлением на
Солнце и нормалью к рабочей поверхности СБ приближённо находится из соотношения
между направлением на
Солнце и нормалью к рабочей поверхности СБ приближённо находится из соотношения
![]() . Из всех возможных комбинаций углов
. Из всех возможных комбинаций углов ![]() ,
, ![]() и
и ![]() имеет смысл выбирать
варианты, обеспечивающие найденное значение
имеет смысл выбирать
варианты, обеспечивающие найденное значение ![]() . Очевидно, что угол
. Очевидно, что угол ![]() не изменится при
повороте системы
не изменится при
повороте системы ![]() на произвольные углы
вокруг орта
на произвольные углы
вокруг орта ![]() направления на Солнце
(угол
направления на Солнце
(угол ![]() ) и вокруг орта
) и вокруг орта ![]() нормали к рабочей поверхности
СБ (угол
нормали к рабочей поверхности
СБ (угол ![]() ).
).
Направление ![]() в орбитальной системе
в орбитальной системе ![]() будем задавать двумя
углами: углом
будем задавать двумя
углами: углом ![]() между
между ![]() и плоскостью орбиты, и углом
и плоскостью орбиты, и углом ![]() между проекцией
между проекцией ![]() на плоскость орбиты и
осью
на плоскость орбиты и
осью ![]() . Направление отсчёта
. Направление отсчёта ![]() согласовано с осью
согласовано с осью ![]() . Углы
. Углы ![]() и
и ![]() считаем постоянными в
пределах рассматриваемых участков движения КА.
считаем постоянными в
пределах рассматриваемых участков движения КА.
Определить значение ![]() для КА, повёрнутого на
произвольные углы
для КА, повёрнутого на
произвольные углы ![]() (вокруг орта
(вокруг орта ![]() ) и затем
) и затем ![]() (вокруг орта
(вокруг орта ![]() ), можно по формулам
), можно по формулам
|
|
(6) |
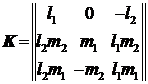 ,
, 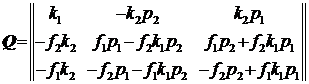 ,
, 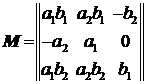 ,
,
|
|
|
|
Здесь
матрица ![]() определяется
положением Солнца в орбитальной системе координат в начальный момент времени,
матрица
определяется
положением Солнца в орбитальной системе координат в начальный момент времени,
матрица ![]() определяется положением
определяется положением
![]() в системе координат
в системе координат ![]() (раздел 2),
(раздел 2), ![]() – матрица последовательных
поворотов КА: вокруг орта
– матрица последовательных
поворотов КА: вокруг орта ![]() на угол
на угол ![]() и затем вокруг орта
и затем вокруг орта ![]() на угол
на угол ![]() . Элементы матрицы
. Элементы матрицы ![]() зависят также от начального
угла
зависят также от начального
угла ![]() между ортами
между ортами ![]() и
и ![]() .
.
Соотношение (6) позволяет выразить углы ![]() ,
, ![]() и
и ![]() в функции углов
в функции углов ![]() и
и ![]() . Эти углы (
. Эти углы (![]() и
и ![]() ) использовались в процедуре случайного поиска для задания начальной
ориентации КА. Кроме того, для удобства выбора начального значения и
последующего контроля величины угловой скорости КА, компоненты
) использовались в процедуре случайного поиска для задания начальной
ориентации КА. Кроме того, для удобства выбора начального значения и
последующего контроля величины угловой скорости КА, компоненты ![]() (
(![]() ) вектора
) вектора ![]() были заменены величинами
были заменены величинами ![]() ,
, ![]() ,
, ![]() .
.
С учётом вышеизложенного, в процедуре случайного
поиска вместо вектора ![]() использовался новый
вектор
использовался новый
вектор ![]() , имеющий 12 компонент:
, имеющий 12 компонент: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Алгоритм случайного поиска с обучением [5] состоит в
построении последовательности векторов ![]() и
и ![]() по следующему правилу.
На первом шаге в качестве
по следующему правилу.
На первом шаге в качестве ![]() берётся произвольно, и
принимается
берётся произвольно, и
принимается ![]() . На каждом последующем шаге вычисляются векторы
. На каждом последующем шаге вычисляются векторы
|
|
(7) |
где
![]() и
и ![]() – положительные числа,
– положительные числа,
![]() – случайный вектор, равномерно распределённый на поверхности
единичной сферы в
– случайный вектор, равномерно распределённый на поверхности
единичной сферы в ![]() .
.
Если ![]() , то в качестве новых значений векторов
, то в качестве новых значений векторов ![]() и
и ![]() берутся векторы
берутся векторы ![]() и
и ![]() ,
, ![]() . При
. При ![]() выбирается новое значение
случайного вектора
выбирается новое значение
случайного вектора ![]() и вычисления по
формулам (7) повторяются снова. Если число неудачных проб на данном шаге
превысит заданны порог
и вычисления по
формулам (7) повторяются снова. Если число неудачных проб на данном шаге
превысит заданны порог ![]() , то параметр
, то параметр ![]() уменьшается в два
раза. Процесс продолжается до тех пор, пока
уменьшается в два
раза. Процесс продолжается до тех пор, пока ![]() . Элемент обучения вносит вектор
. Элемент обучения вносит вектор ![]() . Процесс характеризуется параметрами
. Процесс характеризуется параметрами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , а также начальным значением вектора
, а также начальным значением вектора ![]() на первом шаге поиска.
В расчётах, как правило, принималось
на первом шаге поиска.
В расчётах, как правило, принималось ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
После окончания случайного поиска по найденным
компонентам вектора ![]() определяется начальное
приближение вектора
определяется начальное
приближение вектора ![]() для вычислений методом
Левенберга-Марквардта.
для вычислений методом
Левенберга-Марквардта.
5. Результаты определения вращательного движения КА. Определение фактического движения КА относительно центра
масс по данным (3) было выполнено на 12 интервалах времени. Основные
характеристики этих интервалов приведены в табл. 1. Здесь для каждого интервала
указаны: дата и декретное московское время первого измерения ![]() , длина интервала
, длина интервала ![]() , число
, число ![]() включённых в обработку
измерений. Полученные результаты представлены в табл. 2, 3 и на рис. 2¸15. В таблицах приведены результаты минимизации функционала
(4) на интервалах из табл. 1. Здесь указаны значения некоторых компонент
вектора
включённых в обработку
измерений. Полученные результаты представлены в табл. 2, 3 и на рис. 2¸15. В таблицах приведены результаты минимизации функционала
(4) на интервалах из табл. 1. Здесь указаны значения некоторых компонент
вектора ![]() , стандартные отклонения этих компонент и стандартное отклонение
, стандартные отклонения этих компонент и стандартное отклонение
![]() ошибок данных (4).
Параметры
ошибок данных (4).
Параметры ![]() ,
, ![]() ,
, ![]() и
и ![]() были определены со
значительной погрешностью, поэтому в таблицах не приводятся. Погрешность определения
начального углового положения КА на интервалах
были определены со
значительной погрешностью, поэтому в таблицах не приводятся. Погрешность определения
начального углового положения КА на интервалах ![]() характеризуется
значениями
характеризуется
значениями ![]() , на интервалах 7¸12 – значениями
, на интервалах 7¸12 – значениями ![]() , причем доминируют значения, близкие верхним границам.
Стандартные отклонения параметров
, причем доминируют значения, близкие верхним границам.
Стандартные отклонения параметров ![]() лежала в пределах от
0.01 до 1.5. Большая погрешность определения угловых параметров
лежала в пределах от
0.01 до 1.5. Большая погрешность определения угловых параметров ![]() ,
, ![]() ,
, ![]() вызвана, по-видимому,
неблагоприятным расположением векторов
вызвана, по-видимому,
неблагоприятным расположением векторов ![]() и
и ![]() , а параметров
, а параметров ![]() – слабым влиянием
аэродинамического момента на вращательное движение КА.
– слабым влиянием
аэродинамического момента на вращательное движение КА.
Анализ графиков найденных угловых скоростей КА
показывает, что вращательное движение КА на интервалах 1¸6 близко к регулярной прецессии Эйлера с преимущественным
вращательным движением КА вокруг оси ![]() . На интервалах 7¸12 характер движения КА более сложный, однако преимущественное
вращение спутник также совершает вокруг оси
. На интервалах 7¸12 характер движения КА более сложный, однако преимущественное
вращение спутник также совершает вокруг оси ![]() .
.
Для визуализации
вращательного движения КА можно использовать графики углов ![]() ,
, ![]() ,
, ![]() . Однако в данном случае такое описание вращательного
движения КА не обладает наглядностью. Если спутник совершает движение, близкое
к регулярной прецессии Эйлера, то наибольший интерес представляет движение оси
собственного вращения КА. С учетом этого обстоятельства вращательное движение
КА будем представлять следующим образом.
. Однако в данном случае такое описание вращательного
движения КА не обладает наглядностью. Если спутник совершает движение, близкое
к регулярной прецессии Эйлера, то наибольший интерес представляет движение оси
собственного вращения КА. С учетом этого обстоятельства вращательное движение
КА будем представлять следующим образом.
Введём инерциальную
систему координат ![]() , совпадающую с орбитальной системой, фиксированной на момент
прохождения КА через восходящий узел орбиты. Вращение КА представим в виде
суперпозиции сравнительно медленного движения вектора
, совпадающую с орбитальной системой, фиксированной на момент
прохождения КА через восходящий узел орбиты. Вращение КА представим в виде
суперпозиции сравнительно медленного движения вектора ![]() кинетического момента
спутника в его движении относительно центра масс и регулярной прецессии КА
вокруг этого вектора. Положение вектора
кинетического момента
спутника в его движении относительно центра масс и регулярной прецессии КА
вокруг этого вектора. Положение вектора ![]() в системе
в системе ![]() будем задавать двумя
углами: углом
будем задавать двумя
углами: углом ![]() между
между ![]() и плоскостью орбиты, и
углом
и плоскостью орбиты, и
углом ![]() между проекцией
между проекцией ![]() на плоскость орбиты
осью
на плоскость орбиты
осью ![]() (рис. 2). Угол
(рис. 2). Угол ![]() будем считать положительным,
если проекция
будем считать положительным,
если проекция ![]() на ось
на ось ![]() положительна.
Направление отсчёта
положительна.
Направление отсчёта ![]() согласовано с осью
согласовано с осью ![]() .
.
Аналогичным образом
углы ![]() и
и ![]() задают в системе
задают в системе ![]() положение вектора
положение вектора ![]() (рис. 2). Угол между
векторами
(рис. 2). Угол между
векторами ![]() и
и ![]() обозначим
обозначим ![]() .
.
Анализ результатов
определения движения КА показал, что на интервале 1 ![]() и
и ![]() , на интервалах 2¸6
, на интервалах 2¸6 ![]() и
и ![]() . Эти величины существенно меньше угловой скорости движения
КА вокруг
. Эти величины существенно меньше угловой скорости движения
КА вокруг ![]() , равной на интервалах
, равной на интервалах ![]() примерно
примерно ![]() °/с. На интервалах 7¸12
°/с. На интервалах 7¸12 ![]() и
и ![]() , а угловая скорость КА равна
, а угловая скорость КА равна ![]() °/с.
°/с.
Для наглядного представления движения КА вокруг
вектора ![]() , будем рисовать проекции годографа орта оси
, будем рисовать проекции годографа орта оси ![]() – оси собственного
вращения КА – на координатные плоскости системы
– оси собственного
вращения КА – на координатные плоскости системы ![]() , связанной с этим вектором [6]. Система
, связанной с этим вектором [6]. Система ![]() определяется следующим
образом (рис. 3). Ось
определяется следующим
образом (рис. 3). Ось ![]() направлена вдоль
направлена вдоль ![]() ; ось
; ось ![]() лежит в плоскости
лежит в плоскости ![]() , перпендикулярна
, перпендикулярна ![]() и образует тупой угол
с осью
и образует тупой угол
с осью ![]() ; ось
; ось ![]() дополняет систему до
правой. Помимо проекций годографа орта оси
дополняет систему до
правой. Помимо проекций годографа орта оси ![]() движение КА будем
характеризовать углом нутации
движение КА будем
характеризовать углом нутации ![]() , который эта ось образует с вектором
, который эта ось образует с вектором ![]() .
.
Учитывая характер движения КА на рассматриваемых
интервалах, это движение можно характеризовать усреднёнными величинами
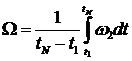 ,
, 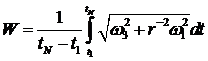 .
.
При
отсутствии внешних механических моментов угловые скорости КА-твёрдого тела относительно
главных центральных осей инерции будут определяться по соотношениям ![]() ,
, ![]() ,
, ![]() , где
, где ![]() ,
, ![]() – постоянные величины,
– постоянные величины,
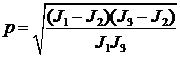 ,
, 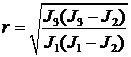 .
.
Средние
квадратические отклонения
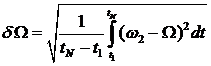 ,
, 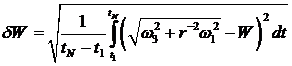
характеризуют
близость движения КА к регулярной прецессии с параметрами ![]() и
и ![]() . В рассматриваемом случае
. В рассматриваемом случае ![]() ,
, ![]() .
.
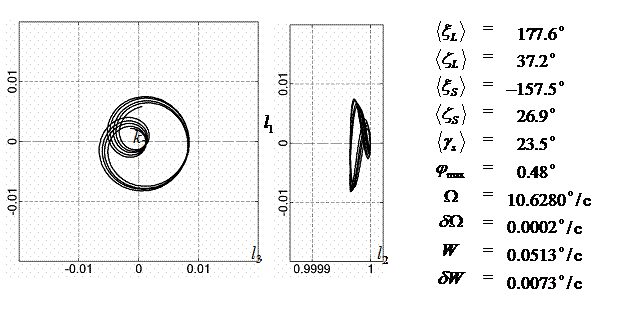
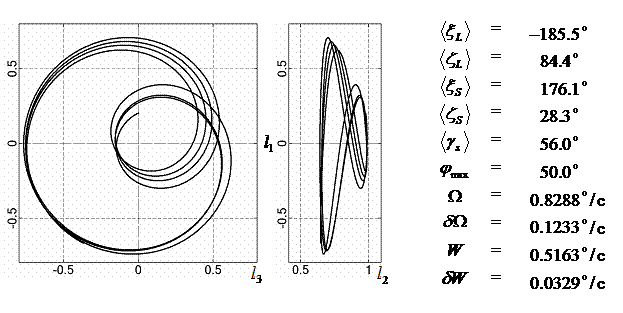
В табл. 4 приведены некоторые параметры вращательного
движения КА для рассмотренных интервалов. Вращательное движение КА
характеризуется здесь параметрами ![]() ,
, ![]() ,
, ![]() и
и ![]() , а также максимальным значением угла
, а также максимальным значением угла ![]() на интервале –
параметром
на интервале –
параметром ![]() . Движение векторов
. Движение векторов ![]() и
и ![]() происходило медленно и
характеризуется усреднёнными значениями
происходило медленно и
характеризуется усреднёнными значениями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Усреднение выполнялось по формулам, приведённым для
параметров
. Усреднение выполнялось по формулам, приведённым для
параметров ![]() и
и ![]() .
.
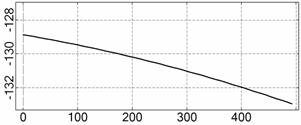
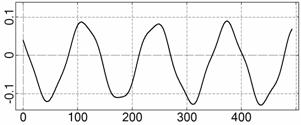
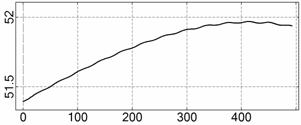
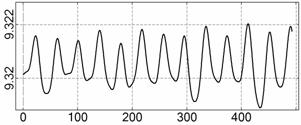
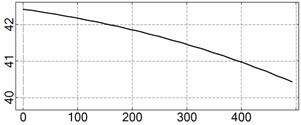
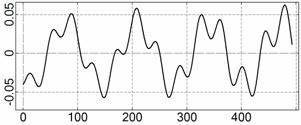
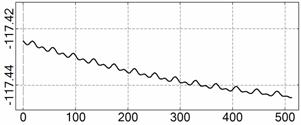
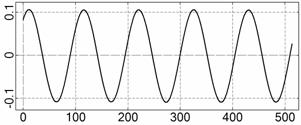
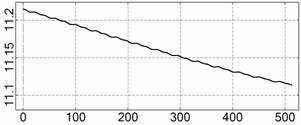
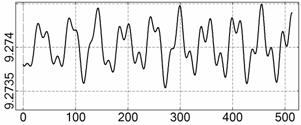
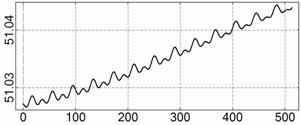
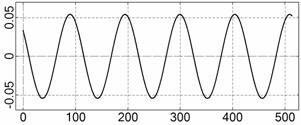
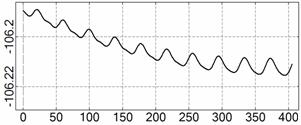
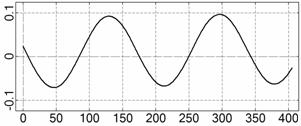
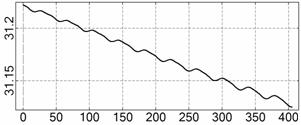
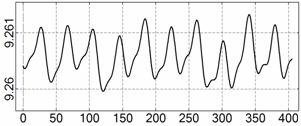
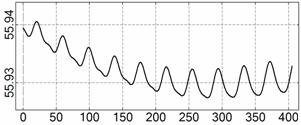
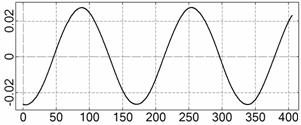
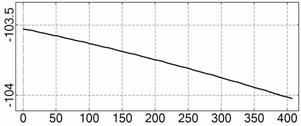
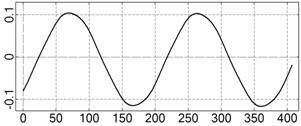
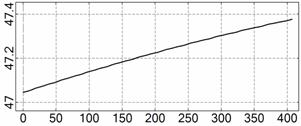
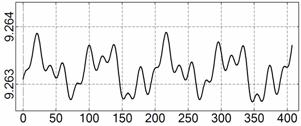
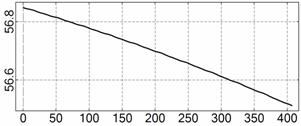
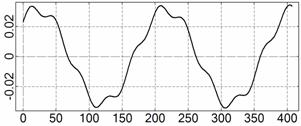
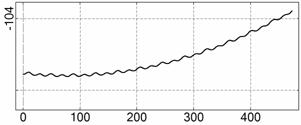
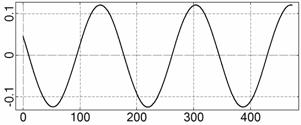
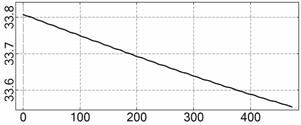
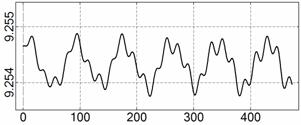
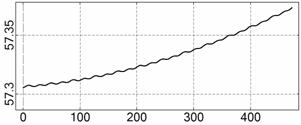
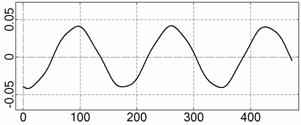
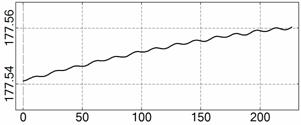
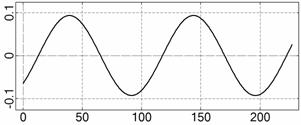
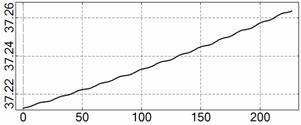
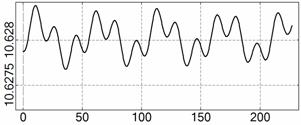
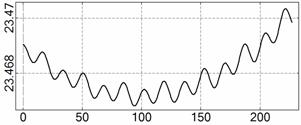
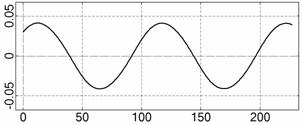
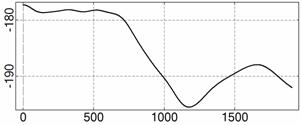
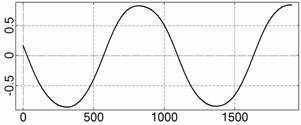
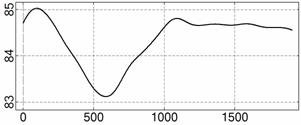
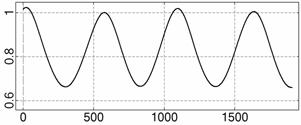
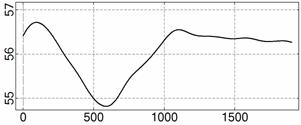
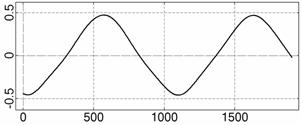
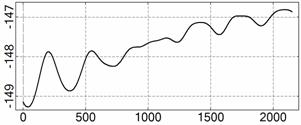
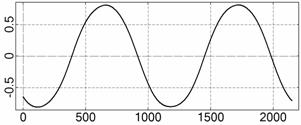
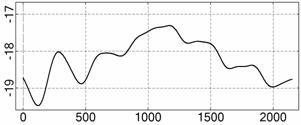
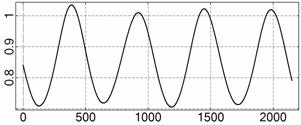
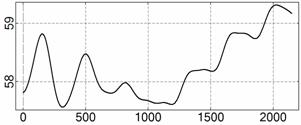
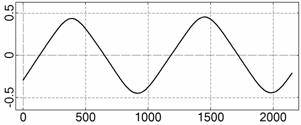
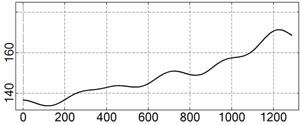
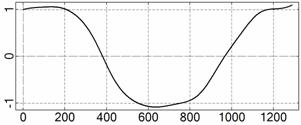
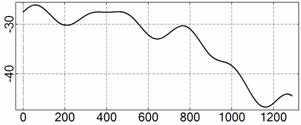
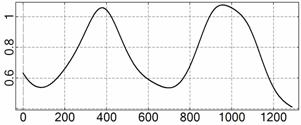
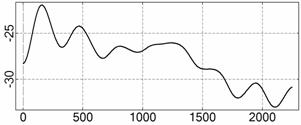
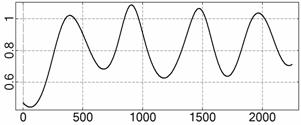
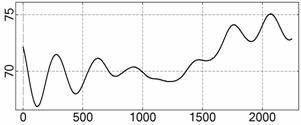
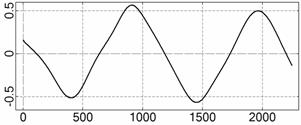
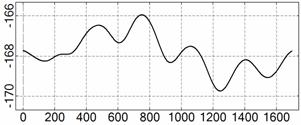
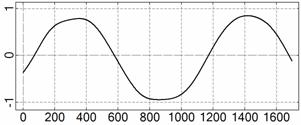
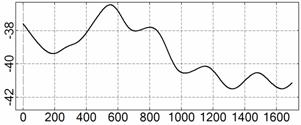
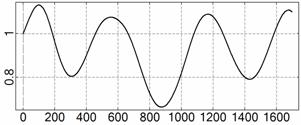
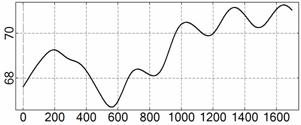
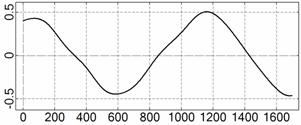
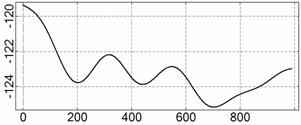
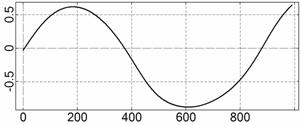
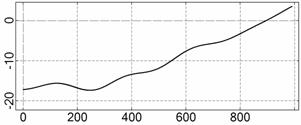
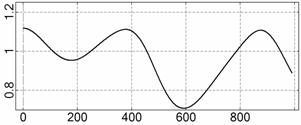
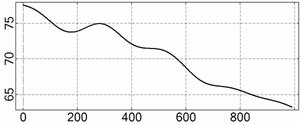
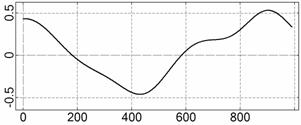
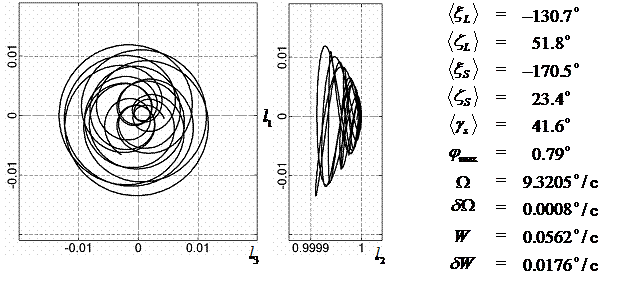
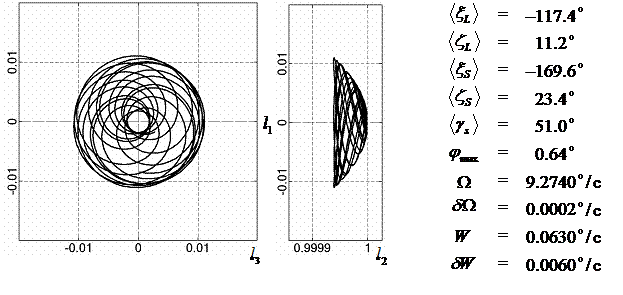
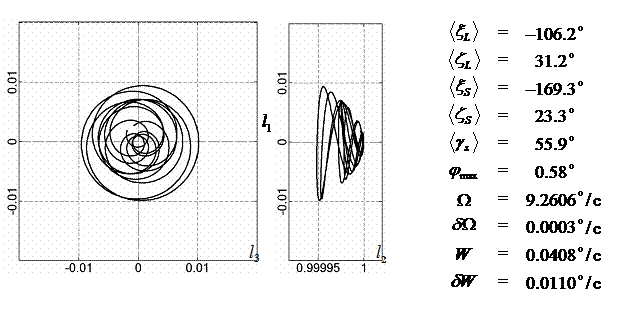
На рис. 4 – 15 представлена реконструкция
вращательного движения КА на этих интервалах. Эти рисунки иллюстрируют решения
уравнений вращательного движения КА, доставляющие минимум функционалу (4). Все
рисунки скомпонованы одинаково и содержат проекции годографа орта ![]() на плоскости системы
на плоскости системы ![]() , графики углов
, графики углов ![]() и
и ![]() , графики угловых скоростей КА
, графики угловых скоростей КА ![]() ,
, ![]() ,
, ![]() и графики расчетного
тока СБ
и графики расчетного
тока СБ ![]() . Маркерами рядом с графиками
. Маркерами рядом с графиками ![]() указаны данные
измерений
указаны данные
измерений ![]() . Все графики построены на соответствующих отрезках
. Все графики построены на соответствующих отрезках ![]() ; началом отсчета времени служит точка
; началом отсчета времени служит точка ![]() . Угловые величины выражены в градусах, угловые скорости – в
град./с, ток – в амперах.
. Угловые величины выражены в градусах, угловые скорости – в
град./с, ток – в амперах.
Исследуемые
интервалы движения КА, можно разделить на интервалы быстрого движения КА
(интервалы 1¸6, рис. 4 – 9) и
медленного движения (интервалы 7¸12, рис. 10 – 15). На быстрых интервалах движение КА
представляет собой регулярную прецессию Эйлера с преимущественным вращением
вокруг оси ![]() . Кинетический момент КА на разных интервалах находился как
вблизи орбитальной плоскости, так и далеко от последней. Скорость движения
вектора кинетического момента была значительно меньше скорости движения КА. На
более медленных интервалах движение КА носило более сложный характер, хотя
проекции оси
. Кинетический момент КА на разных интервалах находился как
вблизи орбитальной плоскости, так и далеко от последней. Скорость движения
вектора кинетического момента была значительно меньше скорости движения КА. На
более медленных интервалах движение КА носило более сложный характер, хотя
проекции оси ![]() на направление вектора
на направление вектора
![]() сохраняли свой знак.
Как и следовало ожидать, в случае более медленного вращательного движения КА и
более сложного изменения во времени тока, снимаемого с СБ, движение
определялось лучше, чем в случае быстрого вращения КА вокруг оси
сохраняли свой знак.
Как и следовало ожидать, в случае более медленного вращательного движения КА и
более сложного изменения во времени тока, снимаемого с СБ, движение
определялось лучше, чем в случае быстрого вращения КА вокруг оси ![]() . Эта ситуация является общей, хотя возможны исключения.
Примером может служить случай, когда коллинеарны или достаточно близки по
направлению вектор нормали к СБ, ось вращения КА и вектор, направленный на
Солнце.
. Эта ситуация является общей, хотя возможны исключения.
Примером может служить случай, когда коллинеарны или достаточно близки по
направлению вектор нормали к СБ, ось вращения КА и вектор, направленный на
Солнце.
Данная работа выполнена в рамках проекта РФФИ
08-01-00467.
Литература.
|
[1] |
Модель верхней атмосферы для баллистических
расчётов. ГОСТ 22721-77. М., Изд-во стандартов, 1978. |
|
[2] |
Меес Ж. Астрономические формулы для калькуляторов.
М., Мир, 1988. |
|
[3] |
В.А. Сарычев, В.В. Сазонов, М.Ю. Беляев, Н.И.
Ефимов. Повышение точности определения вращательного движения орбитальных
станций «Салют-6» и «Салют-7» по данным измерений. Космические исследования,
1991, т.29, с. 375 – 389. |
|
[4] |
Сарычев
В.А., Беляев М.Ю., Сазонов В.В., Тян Т.Н. Определение движения орбитальных
станций «Салют-6» и «Салют-7» относительно центра масс в режиме медленной
закрутки по данным измерений. Космические исследования. 1988, т. 24, N 3, с. 337 – 344. |
|
[5] |
Л.А. Растригин. Статистические методы поиска.
Москва, Наука, 1968. |
|
[6] |
Белецкий
В.В., Движение искусственного спутника относительно центра масс. Москва,
Наука, 1965. |
Таблица 1. Интервалы определения вращательного движения
КА.
|
Интервал |
дата, д. м. г. |
ч : мин : с |
|
|
|
1 |
24.10.2006 |
06:35:46 |
493 |
330 |
|
2 |
26.10.2006 |
12:33:34 |
514 |
391 |
|
3 |
27.10.2006 |
07:40:12 |
406 |
319 |
|
4 |
27.10.2006 |
10:49:50 |
408 |
321 |
|
5 |
27.10.2006 |
12:24:00 |
473 |
362 |
|
6 |
22.12.2006 |
13:54:56 |
228 |
501 |
|
7 |
20.03.2007 |
16:17:43 |
1905 |
183 |
|
8 |
20.03.2007 |
17:50:01 |
2151 |
216 |
|
9 |
20.03.2007 |
20:29:51 |
1289 |
124 |
|
10 |
21.03.2007 |
09:18:21 |
2249 |
200 |
|
11 |
21.03.2007 |
19:22:08 |
1699 |
189 |
|
12 |
21.03.2007 |
22:24:02 |
991 |
96 |
Таблица 2. Результаты минимизации.
|
Инт. |
|
|
|
|
|
|
|
|
1 |
1.6763 |
0.0007 |
0.0020 |
0.1627 |
0.0002 |
-0.0007 |
0.0007 |
|
2 |
1.1657 |
0.0014 |
0.0010 |
0.1619 |
0.00004 |
0.0006 |
0.0006 |
|
3 |
0.9081 |
0.0004 |
0.0015 |
0.1616 |
0.00005 |
-0.0005 |
0.0002 |
|
4 |
1.0366 |
-0.0014 |
0.0016 |
0.1617 |
0.0002 |
0.0004 |
0.0004 |
|
5 |
1.0489 |
0.0008 |
0.0014 |
0.1615 |
0.00004 |
-0.0007 |
0.0003 |
|
6 |
0.5705 |
-0.0011 |
0.0006 |
0.1855 |
0.0001 |
0.0005 |
0.0003 |
|
7 |
1.2287 |
0.0030 |
0.0003 |
0.0177 |
0.0001 |
-0.0077 |
0.0002 |
|
8 |
1.2536 |
-0.0112 |
0.0004 |
0.0147 |
0.0002 |
-0.0051 |
0.0002 |
|
9 |
1.4877 |
0.0175 |
0.0006 |
0.0111 |
0.0008 |
0.0040 |
0.0009 |
|
10 |
1.6085 |
0.0190 |
0.0004 |
0.0082 |
0.0006 |
0.0028 |
0.0006 |
|
11 |
1.4798 |
-0.0064 |
0.0004 |
0.0174 |
0.0002 |
0.0070 |
0.0002 |
|
12 |
1.9865 |
-0.0007 |
0.010 |
0.0195 |
0.0005 |
0.0075 |
0.0015 |
Таблица 3. Результаты минимизации.
|
Инт. |
|
|
|
|
|
|
|
|
|
1 |
3.2973 |
0.53 |
0.7329 |
0.041 |
2.0099 |
0.036 |
-0.0620 |
0.25 |
|
2 |
3.0459 |
0.37 |
0.7332 |
0.030 |
1.9486 |
0.063 |
-0.2037 |
0.12 |
|
3 |
3.0524 |
0.29 |
0.6980 |
0.028 |
1.9687 |
0.0071 |
0.0058 |
0.12 |
|
4 |
3.0623 |
0.33 |
0.6924 |
0.032 |
1.9658 |
0.020 |
0.0685 |
0.10 |
|
5 |
3.0675 |
0.33 |
0.6992 |
0.031 |
1.9534 |
0.025 |
-0.1203 |
0.081 |
|
6 |
3.0896 |
0.57 |
0.7231 |
0.048 |
1.9500 |
0.081 |
-0.1594 |
0.16 |
|
7 |
2.8499 |
0.11 |
0.7289 |
0.0094 |
2.0762 |
0.0061 |
-0.0059 |
0.0040 |
|
8 |
2.7101 |
0.084 |
0.7120 |
0.0082 |
2.0493 |
0.0048 |
-0.0114 |
0.0072 |
|
9 |
3.1803 |
0.23 |
0.8201 |
0.019 |
2.3926 |
0.024 |
-0.0173 |
0.0095 |
|
10 |
2.5848 |
0.075 |
0.7051 |
0.0073 |
1.9518 |
0.018 |
-0.0289 |
0.0075 |
|
11 |
2.4625 |
0.063 |
0.6720 |
0.0076 |
1.5088 |
0.019 |
0.0228 |
0.0037 |
|
12 |
3.6879 |
0.50 |
0.7535 |
0.030 |
2.1576 |
0.50 |
-0.0059 |
0.046 |
Таблица 4. Параметры движения КА.
|
Инт. |
|
|
|
|
|
|
|
|
|
|
|
1 |
-130.7 |
51.8 |
-170.5 |
23.4 |
41.6 |
9.32 |
0.0008 |
0.056 |
0.018 |
0.79 |
|
2 |
-117.4 |
11.2 |
-169.6 |
23.4 |
51.0 |
9.27 |
0.0002 |
0.063 |
0.006 |
0.64 |
|
3 |
-106.2 |
31.2 |
-169.3 |
23.3 |
55.9 |
9.26 |
0.0003 |
0.041 |
0.011 |
0.58 |
|
4 |
-103.8 |
47.2 |
-169.3 |
23.3 |
56.7 |
9.26 |
0.0003 |
0.054 |
0.015 |
0.71 |
|
5 |
-104 |
33.7 |
-169.3 |
23.3 |
57.3 |
9.25 |
0.0003 |
0.062 |
0.014 |
0.75 |
|
6 |
177.6 |
37.2 |
-157.5 |
26.9 |
23.5 |
10.63 |
0.0002 |
0.051 |
0.007 |
0.48 |
|
7 |
-185.5 |
84.4 |
176.1 |
28.3 |
56.0 |
0.83 |
0.12 |
0.516 |
0.033 |
50.0 |
|
8 |
-147.7 |
-18.2 |
176.1 |
28.3 |
58.2 |
0.86 |
0.11 |
0.495 |
0.032 |
46.6 |
|
9 |
148.9 |
-33.5 |
176.1 |
28.3 |
68.0 |
0.75 |
0.20 |
0.655 |
0.082 |
67.1 |
|
10 |
130.5 |
-27.7 |
175.8 |
28.2 |
70.9 |
0.81 |
0.17 |
0.591 |
0.047 |
65.6 |
|
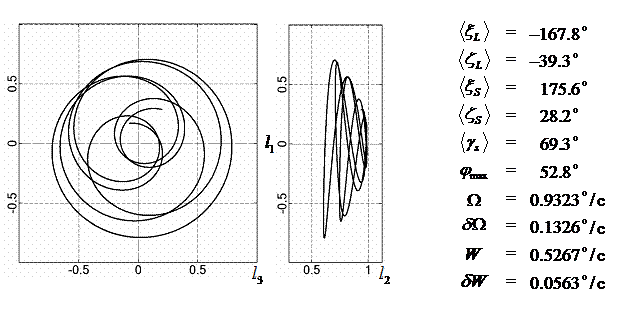
11 |
-167.8 |
-39.3 |
175.6 |
28.2 |
69.3 |
0.93 |
0.13 |
0.527 |
0.056 |
52.8 |
|
12 |
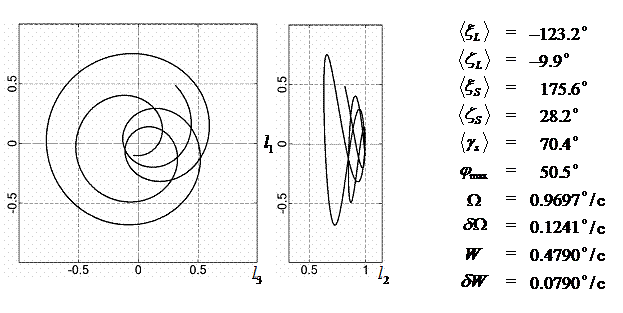
-123.2 |
-9.9 |
175.6 |
28.2 |
70.4 |
0.97 |
0.12 |
0.479 |
0.079 |
50.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
t, c
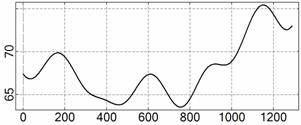
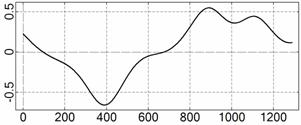
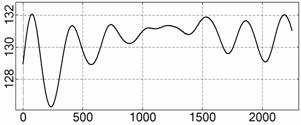
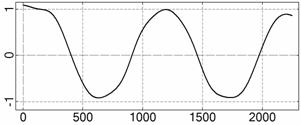
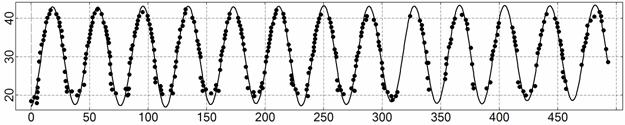
Рис. 4. Интервал 1, момент ![]() соответствует 06:35:46
ДМВ 24.10.2006.
соответствует 06:35:46
ДМВ 24.10.2006.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
t, c
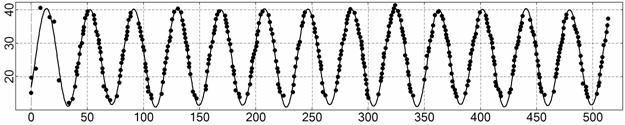
Рис. 5. Интервал 2, момент ![]() соответствует 12:33:34
ДМВ 26.10.2006.
соответствует 12:33:34
ДМВ 26.10.2006.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
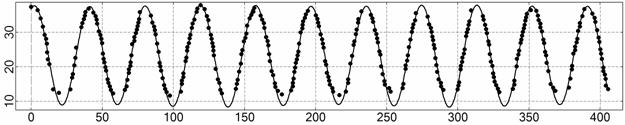
t, c
Рис. 6. Интервал 3, момент ![]() соответствует 07:40:12
ДМВ 27.10.2006.
соответствует 07:40:12
ДМВ 27.10.2006.
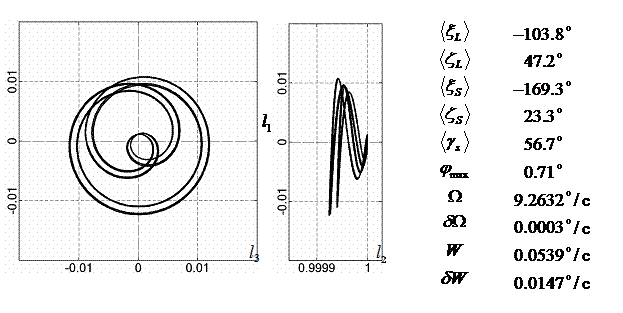
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
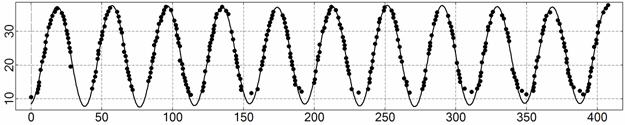
t, c
Рис. 7. Интервал 4, момент ![]() соответствует 10:49:50
ДМВ 27.10.2006.
соответствует 10:49:50
ДМВ 27.10.2006.
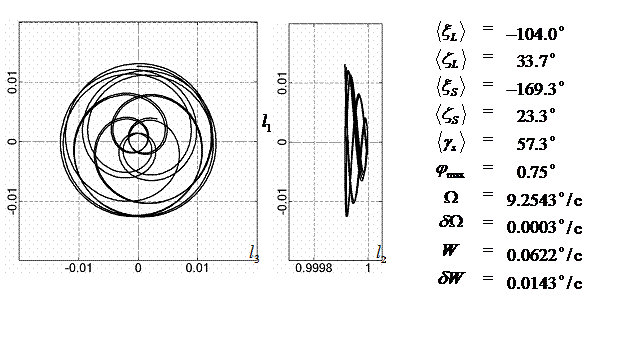
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
t, c
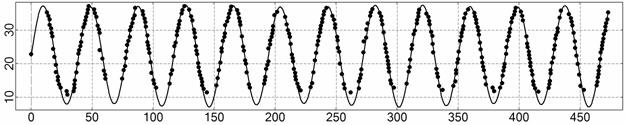
 Рис. 8. Интервал 5, момент
Рис. 8. Интервал 5, момент ![]() соответствует 12:24:00
ДМВ 27.10.2006.
соответствует 12:24:00
ДМВ 27.10.2006.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
t, c
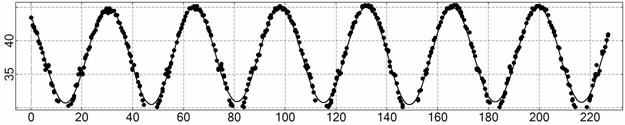
Рис. 9. Интервал 6, момент ![]() соответствует 13:54:56
ДМВ 22.12.2006.
соответствует 13:54:56
ДМВ 22.12.2006.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
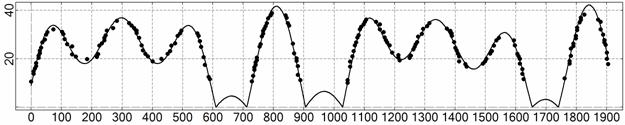
t, c
Рис. 10. Интервал 7, момент ![]() соответствует 16:17:43
ДМВ 20.03.2007.
соответствует 16:17:43
ДМВ 20.03.2007.
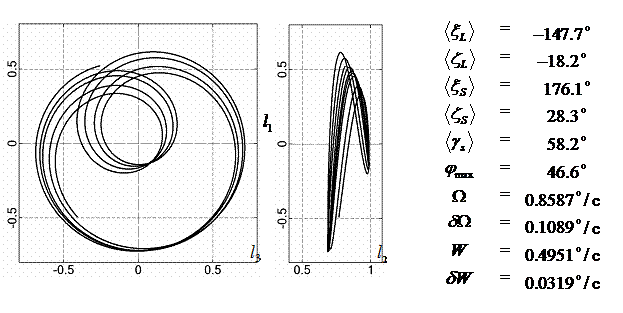
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
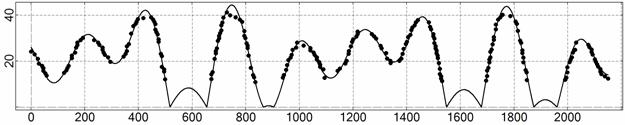
t, c
Рис. 11. Интервал 8, момент ![]() соответствует 17:50:01
ДМВ 20.03.2007.
соответствует 17:50:01
ДМВ 20.03.2007.
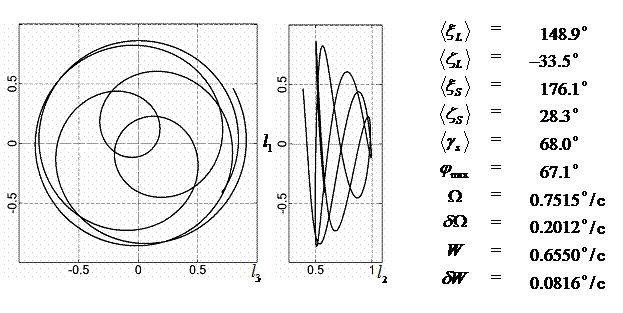
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
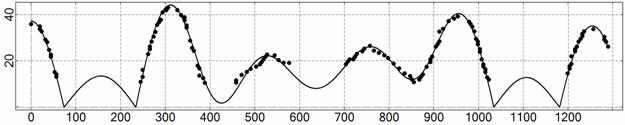
t, c
Рис. 12. Интервал 9, момент ![]() соответствует 20:29:51 ДМВ
20.03.2007.
соответствует 20:29:51 ДМВ
20.03.2007.
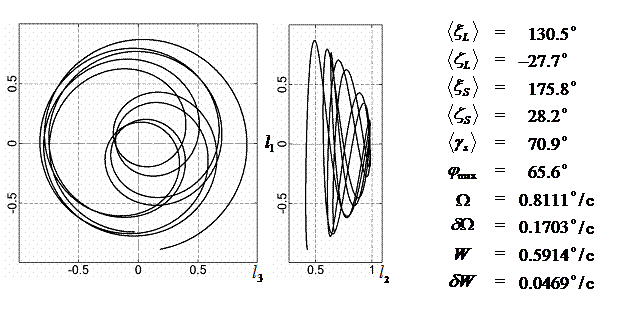
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
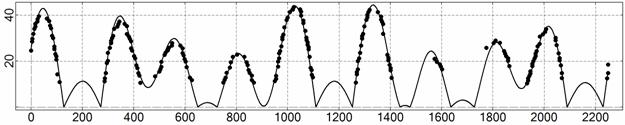
t, c
Рис. 13. Интервал 10, момент ![]() соответствует 09:18:21
ДМВ 1.03.2007.
соответствует 09:18:21
ДМВ 1.03.2007.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
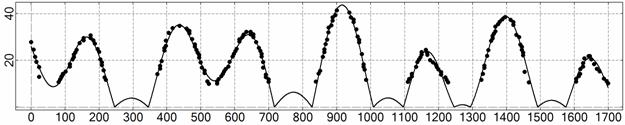
t, c
Рис. 14. Интервал 11, момент ![]() соответствует 19:22:08
ДМВ 21.03.2007.
соответствует 19:22:08
ДМВ 21.03.2007.
|
|
|
|
|
|
|
|
|
|
|
|
![]() , A
, A
t, c
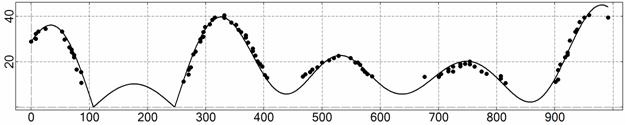
Рис. 15. Интервал 12, момент ![]() соответствует 22:24:02
ДМВ 21.03.2007.
соответствует 22:24:02
ДМВ 21.03.2007.
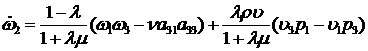 ,
,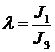 ,
,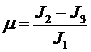 ,
,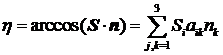 ,
,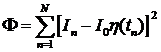 .
.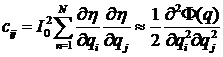 ,
,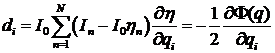 ,
,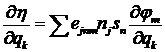
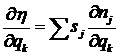
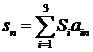 .
.