Аннотация
Квазиравновесная эволюция плазмы токамака с учетом диффузии магнитного поля в резистивной плазме и токов
, наведенных в окружающих плазму пассивных проводниках и катушках полоидального поля, описывается следующей системой нелинейных
дифференциальных уравнений: двумерным уравнением равновесия плазмы со свободной границей, одномерным уравнением диффузии магнитного
поля и уравнениями цепей для наведенных токов. Система дифференциальных уравнений, дополненная начальными и краевыми условиями,
аппроксимируется конечно-разностной схемой и решается итерационными методами. Приводятся примеры расчетов.
Abstract
Quasi-equilibrium evolution of tokamak plasma with taking into account the magnetic field diffusion in a resistive plasma
and eddy currents in poloidal field coils and passive conductors is described by a set of nonlinear equations: 2D free boundary plasma
equilibrium equation, 1D magnetic field diffusion equation and circuit equations for eddy currents. The set of differential
equations with initial and boundary conditions is approximated by a finite-difference scheme. The discrete problem is solved
using iterative methods. The results of simulations are presented.
Содержание:
1. Введение
…………………………………………. 4
2. Модель и
основные уравнения…………………. 5
3. Вычислительный алгоритм……………………. 8
4.
Примеры расчетов………………………………. 9
5.
Литература……………………………………….. 21
1. Введение
Аксиально-симметричное
равновесие плазмы токамака описывается двумерным нелинейным дифференциальным
уравнением Грэда-Шафранова [1,2]. В токамаках перенос энергии и частиц вдоль
силовых магнитных линий происходит намного быстрее, чем поперек. В
предположении, что топология вложенных магнитных поверхностей в плазме не
нарушается в ходе эволюции плазмы, процесс диффузии магнитного поля может быть
описан с помощью одномерного дифференциального уравнения для тороидального и
полоидального потоков магнитного поля.
Таким образом, в
теоретических исследованиях удержания плазмы в токамаках большое распространение
и развитие получило использование математических моделей (т.н. полуторамерные
коды для расчета квазиравновесной эволюции плазмы), в которых равновесие
плазменного шнура описывается в двумерном приближении, а диффузия магнитного
поля в плазме в одномерном приближении, но самосогласованно с конкретной формой
найденных из решения двумерной задачи равновесия магнитных поверхностей.
Квазиравновесные эволюционные коды устроены
таким образом, что на каждом временном шаге решается двумерная задача
равновесия самосогласованно с одномерными транспортными уравнениями, уравнением
диффузии магнитного поля и уравнением цепей для наведенных вихревых токов.
Исторически первыми в таких кодах в качестве равновесного солвера
использовались коды расчета равновесия с предписанной границей плазмы, такие
как POLAR [3], SPIDER [4], CAXE 5].
В качестве примера такого рода эволюционных кодов можно назвать коды ASTRA [6], BALDUR [7].
Однако для самосогласованного (с точки
зрения определения неизвестных формы и положения плазмы) расчета эволюции на каждом временном шаге необходимо решать
задачу равновесия плазмы с неизвестной свободной границей во внешних магнитных
полях, изменяющихся за счет эволюции токов и напряжений в обмотках управляющих
катушек полоидального поля, в вакуумной камере и проводниках пассивной
стабилизации. Эта группа моделей в разных приближениях используется для
самосогласованного моделирования сценариев плазмы в существующих токамаках. В
большинстве кодов этой группы уравнение равновесия решается методом конечных
разностей на фиксированной пространственной сетке (R,Z), в результате чего находится функция полоидального
потока Y(R,Z) и строятся магнитные поверхности – линии уровня этой
функцииY(R,Z)=const.
Интегрированием вдоль этих уровней получаются метрические коэффициенты для
усредненных по движущимся магнитным поверхностям транспортных уравнений.
На сегодняшний день можно выделить несколько кодов
второй группы, которые в той или иной мере приспособлены для решения задач,
связанных с моделированием эволюции плазмы в токамаках. Это коды ДИНА[8], PET[9], CORSICA[10] и TSC[11], в которых, кроме решения уравнения равновесия со
свободной границей, представлен весь набор транспортных уравнений, включающих в
себя диффузию магнитного потока, балансы энергии и частиц. Существует ряд задач в эволюции плазмы, такие
как, быстрое перемещение горячей плазмы как по горизонтали, так и по вертикали,
срезание плазмы лимитером при отказе системы управления, образование внешних
транспортных барьеров и большой величины бутстреп-тока, когда сильно затруднено
моделирование поведения плазмы с использованием стандартных методов для решения
уравнения равновесия со свободной границей на прямоугольной сетке. В таких
задачах локальная величина плотности тока может на порядки превышать его среднее
значение, что требует других более точных адаптационных методов решения. Одним
из наиболее приспособленных для такого рода задач методом является метод
адаптированных к магнитным поверхностям сеток, реализованный в коде SPIDER[12]. В этой
работе дается описание квазиравновесного эволюционного кода SPIDER со свободной границей плазмы токамака с учетом
диффузии магнитного поля.
2. Модель и основные уравнения
Модель и основные уравнения
Квазиравновесная
эволюция плазмы токамака с учетом диффузии магнитного поля в резистивной плазме
и токов, наведенных в окружающих плазму пассивных проводниках и катушках полоидального
поля, описывается двумерной задачей равновесия со свободной границей
совместно с одномерной задачей для
диффузии магнитного поля и уравнениями цепей для определения наведенных токов.
Эта система дифференциальных уравнений аппроксимируется конечно-разностной
схемой и решается при помощи итерационных методов при заданных начальных и
граничных условиях.
В предположении вложенности магнитных
поверхностей равновесие плазмы может быть описано с помощью следующего набора
потоковых функций:
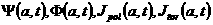 , ,
где Ψ –
полоидальный поток магнитного поля, Φ
– тороидальный поток, 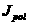 –полоидальный ток, –полоидальный ток,  – тороидальный ток, 0≤ a(R,Z) ≤1 –
метка магнитной поверхности – неизвестная функция цилиндрических координат (R,Z) , t - время. – тороидальный ток, 0≤ a(R,Z) ≤1 –
метка магнитной поверхности – неизвестная функция цилиндрических координат (R,Z) , t - время.
Катушки полоидального поля и окружающие плазму пассивные
проводящие структуры аппроксимируются
конечными наборами филаментов.
Предполагается, что в процессе эволюции в каждый
момент времени выполняется уравнение равновесия плазмы со свободной границей:
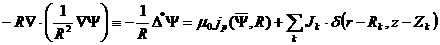 , (2.1) , (2.1)
 . .
Здесь и далее  - внешний по отношению к магнитной поверхности полоидальный
поток, деленный на - внешний по отношению к магнитной поверхности полоидальный
поток, деленный на  , ,
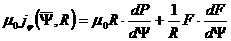 , , 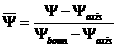 , ,
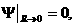 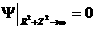 , , 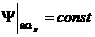 , ,
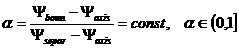 . .
Здесь  - свободная граница
плазмы, которая должна быть найдена, - свободная граница
плазмы, которая должна быть найдена,  - заданный профиль
давления; - заданный профиль
давления;  - величина
полоидального потока на магнитной оси; - величина
полоидального потока на магнитной оси; 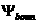 - величина
полоидального потока на границе плазмы; - величина
полоидального потока на границе плазмы; 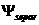 - величина
полоидального потока на ближайшей к плазме сепаратрисе магнитного поля,; - величина
полоидального потока на ближайшей к плазме сепаратрисе магнитного поля,; 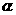 - входной параметр задачи равновесия, задающий близость
границы плазмы к сепаратрисе ( - входной параметр задачи равновесия, задающий близость
границы плазмы к сепаратрисе (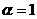 соответствует границе
плазмы, совпадающей с сепаратриссой); соответствует границе
плазмы, совпадающей с сепаратриссой); 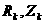 - координаты
филаментов с токами вне плазмы; - координаты
филаментов с токами вне плазмы; 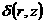 - дельта функция Дирака, - дельта функция Дирака, 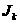 - величины токов в
филаментах, удовлетворяющие уравнению цепей: - величины токов в
филаментах, удовлетворяющие уравнению цепей:
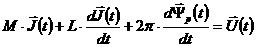  , (2.2) , (2.2)
где
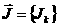 - вектор неизвестных
токов в филаментах, которые аппроксимируют окружающие плазму проводники; - вектор неизвестных
токов в филаментах, которые аппроксимируют окружающие плазму проводники; 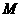 - матрица
сопротивлений для филаментов (диагональная в нашем случае); - матрица
сопротивлений для филаментов (диагональная в нашем случае); 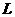 - матрица
индуктивности; - матрица
индуктивности; 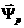 - вектор значений
полоидального потока, создаваемого плазмой в точках филаментов; - вектор значений
полоидального потока, создаваемого плазмой в точках филаментов; 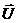 - вектор напряжений на
активных катушках, управляющих положением, формой и другими параметрами плазмы. - вектор напряжений на
активных катушках, управляющих положением, формой и другими параметрами плазмы.
Ключевым моментом квазиравновесной
эволюции с учетом диффузии магнитного поля является точное решение уравнения
диффузии магнитного поля при фиксированной границе плазмы. Напишем проекцию закона
Ома на направление равновесного магнитного поля 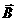 : :
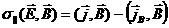 , ,
где 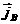 - плотность неиндуктивного тока в плазме (например, бутстреп-тока), - плотность неиндуктивного тока в плазме (например, бутстреп-тока),
 - проводимость плазмы
в направлении магнитного поля. Это уравнение, будучи осредненным по магнитным
поверхностям, с учётом уравнения
индукции - проводимость плазмы
в направлении магнитного поля. Это уравнение, будучи осредненным по магнитным
поверхностям, с учётом уравнения
индукции
 , ,
приводит
к одномерному уравнению взаимной диффузии полоидального и тороидального потоков
магнитного поля [13]:
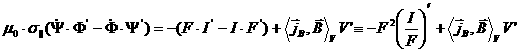 , (2.3) , (2.3)
где 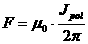 , , 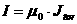 , , 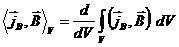 - осреднение по объёму
между двумя магнитными поверхностями, - осреднение по объёму
между двумя магнитными поверхностями, 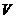 - объем внутри
магнитной поверхности, - объем внутри
магнитной поверхности, 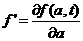 , , 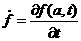 - обозначения
производных по потоковой переменной a(R,Z) и по
времени. - обозначения
производных по потоковой переменной a(R,Z) и по
времени.
При заданной фиксированной границы плазмы уравнение
равновесия Грэда-Шафранова:
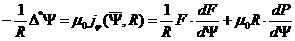 (2.4) (2.4)
должно
быть решено совместно с уравнением диффузии
(2.3).
Уравнение
равновесия (2.4), осредненное по магнитным поверхностям приводит к уравнению Крускала-Калсруда:
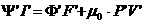 . (2.5) . (2.5)
Для осесимметричной плазмы токамака выполнены
следующие соотношения между токами и потоками:
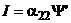 , , 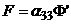 , (2.6) , (2.6)
где
коэффициенты 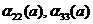 определяются
геометрией магнитных поверхностей и выбором метки магнитных поверхностей a. определяются
геометрией магнитных поверхностей и выбором метки магнитных поверхностей a.
Соотношения (2.6), (2.3) и (2.5) приводят
к следующей системе двух нелинейных уравнений для потоков Ψ и Φ:
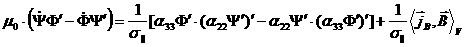 , (2.7) , (2.7)
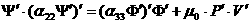 . (2.8) . (2.8)
Условия для системы (2.7)-(2.8) на магнитной оси:
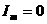 , , 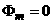 , , 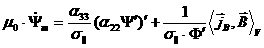 (2.9) (2.9)
следуют
из определения тороидального потока и тороидального тока, отсчитываемых от
магнитной оси. На границе плазмы
естественно задать тороидальное магнитное поле через потоковую функцию
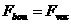 (2.10) (2.10)
и
полоидальный поток 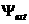 , которые определяются внешними проводниками и не
зависят от плазмы. , которые определяются внешними проводниками и не
зависят от плазмы.
В силу
соотношения на границе плазмы:
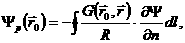
и с
учётом соотношения 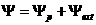 имеем: имеем:
 , (2.11) , (2.11)
что дает граничное условие для  , где , где  - функция Грина для
оператора Грэда-Шафранова (2.1), - функция Грина для
оператора Грэда-Шафранова (2.1), 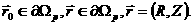
3. Вычислительный
алгоритм
Описанная выше задача диффузии магнитного поля в
случае фиксированной границы плазмы решается по следующему алгоритму: на каждом
временном шаге выполняется одна итерация Пикара по нелинейности в правой части
уравнения Грэда-Шафранова (2.4). При
этом радиально-кольцевая расчетная сетка адаптируется к магнитным поверхностям
внутри плазмы на каждом шаге итерационного процесса. Это дает геометрические
параметры α22 , α33 (2.6), S(a) и V(a) – площадь
тороидального сечения и объем внутри магнитной поверхности. Предполагая
фиксированную геометрию магнитных поверхностей,
решаем систему уравнений (2.7), (2.8)
для того, чтобы получить новое приближение для потоковой функции 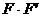 , входящей в правую часть уравнения равновесия. Такой
итерационный процесс продолжается до достижения заданной точности. Нелинейные
уравнения (2.7), (2.8) решаются при
помощи метода Ньютона путем линеаризации системы уравнений в предположении , входящей в правую часть уравнения равновесия. Такой
итерационный процесс продолжается до достижения заданной точности. Нелинейные
уравнения (2.7), (2.8) решаются при
помощи метода Ньютона путем линеаризации системы уравнений в предположении 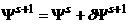 , , 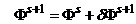 , где s – номер
итерации. Полученные линеаризованные уравнения для , где s – номер
итерации. Полученные линеаризованные уравнения для  решаются методом
матричной прогонки. решаются методом
матричной прогонки.
В
случае квазиравновесной эволюции плазмы со свободной границей итерационный
процесс на каждом временном шаге модифицируется следующим образом:
1. Уравнение равновесия со свободной
границей (2.1) решается совместно с уравнениями цепей (2.2). Потоковые функции 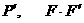 , которые определяют тороидальную плотность тока и величину
полного тороидального тока в плазме, являются входными параметрами для задачи
равновесия. На выходе определяются новая граница плазмы и величина
полоидального потока , которые определяют тороидальную плотность тока и величину
полного тороидального тока в плазме, являются входными параметрами для задачи
равновесия. На выходе определяются новая граница плазмы и величина
полоидального потока 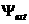 на границе плазмы на границе плазмы
2. Задача квазиравновесной диффузии
магнитного поля (2.3)-(2.8) решается на сетке адаптированной к магнитным
поверхностям при заданной границе плазмы с предыдущего шага. На выходе
определяются потоковая функция 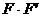 и полный ток в плазме и полный ток в плазме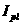 . .
3.
Проверяется сходимость итерационного процесса: при достижении заданной
точности происходит переход к следующему шагу по времени, иначе повторяются
шаги 1.-2.
4. Примеры расчетов
4.1 Квазиравновесная
эволюция плазмы токамака в модели с фиксированной границей плазмы. Ввод неиндукционного
тока.
В качестве исходной равновесной плазменной
конфигурации 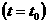 с фиксированной
заданной границей и вложенными
магнитными поверхностями в коде SPIDER
рассчитывается бессиловое с фиксированной
заданной границей и вложенными
магнитными поверхностями в коде SPIDER
рассчитывается бессиловое 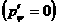 равновесие
токамака-реактора ИТЕР, характеризуемое следующими значениями основных параметров: равновесие
токамака-реактора ИТЕР, характеризуемое следующими значениями основных параметров:
а)
границы плазмы: 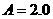 , , 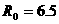 , ,  , , 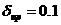 , , 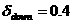 , ,
где
 - аспектное отношение, - аспектное отношение,
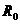 - большой радиус, - большой радиус, 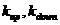 и и 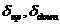 - соответственно, верхняя
и нижняя вытянутости и треугольности границы плазмы, параметризуемой посредством
переменной - соответственно, верхняя
и нижняя вытянутости и треугольности границы плазмы, параметризуемой посредством
переменной 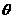 согласно следующей
формуле: согласно следующей
формуле:
 , ,
где
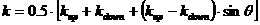 , , 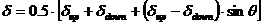 . .
б) заданными профилями потоковых функций: 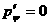 (бессиловое
равновесие), (бессиловое
равновесие), 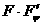 - линейная функция
потоковой переменной - линейная функция
потоковой переменной 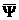 ; ;
в) тороидальный ток плазмы 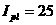 MA, тороидальное
вакуумное магнитное поле MA, тороидальное
вакуумное магнитное поле  T на радиусе T на радиусе 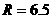 м. м.
В ходе последующей квазиравновесной
эволюции плазмы полагаются заданными и фиксированными во времени следующие
профили следующих потоковых функций:
а) 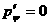 ; ;
б) 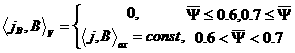 - как функция
нормированного полоидального потока - как функция
нормированного полоидального потока 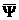 ; ;
в) температура плазмы 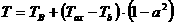 , где в качестве потоковой переменной , где в качестве потоковой переменной 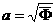 берётся корень квадратный из нормированного тороидального
потока плазмы, берётся корень квадратный из нормированного тороидального
потока плазмы, 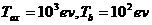 - предписанные
значения температуры на магнитной оси и границе плазмы, соответственно; проводимость
плазмы – спитцеровская: - предписанные
значения температуры на магнитной оси и границе плазмы, соответственно; проводимость
плазмы – спитцеровская:  ~ ~  . .
На Рис.1 приводится соответствующая
исходному равновесию адаптированная к искомым магнитным поверхностям расчетная
потоковая сетка внутри заданной фиксированной границы плазмы – исходная
равновесная конфигурация ИТЕР.

Рис.1 Исходное
равновесие
На
Рис.2 приводятся соответствующие исходному равновесию профили основных параметров
плазмы:
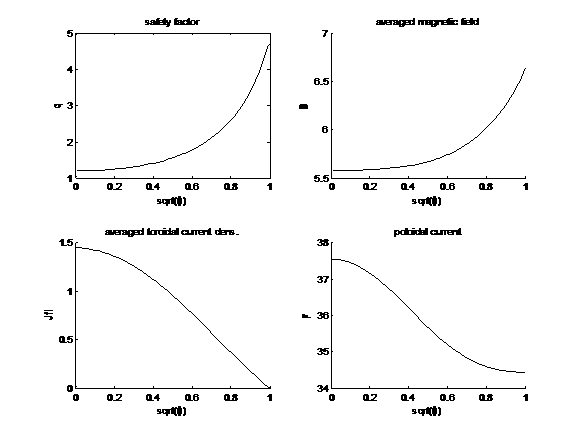
Рис.2 Фактор
запаса устойчивости, осредненное магнитное поле, осредненная плотность
тороидального тока, полоидальный ток
Ввод тока в плазму в процессе
квазиравновесной эволюции происходит следующим образом. Мгновенно введённый -
за один шаг по времени – неиндукционный ток мгновенно компенсируется таким же
наведенным в плазме индукционным током обратного знака. По постановке задачи,
неиндукционный ток не подвергается диффузии, тогда как профиль плотности компенсирующего
его индукционного тока расплывается в процессе эволюции за счет диффузии. Сумма
этих двух токов определяет профиль тороидальной плотности 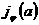 тока плазмы, которые
для трёх различных последовательных моментов времени -1,2,3 – приводятся на Рис.3, как функции корня квадратного из нормированного
тороидального потока тока плазмы, которые
для трёх различных последовательных моментов времени -1,2,3 – приводятся на Рис.3, как функции корня квадратного из нормированного
тороидального потока 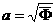 . На этом рисунке же
для тех же моментов времени приводятся профили фактора запаса устойчивости . На этом рисунке же
для тех же моментов времени приводятся профили фактора запаса устойчивости 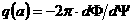 , осредненный по магнитным поверхностям модуль магнитного
поля , осредненный по магнитным поверхностям модуль магнитного
поля 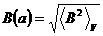 , , 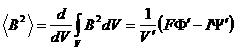 и полоидальный ток
плазмы и полоидальный ток
плазмы 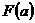 , ,
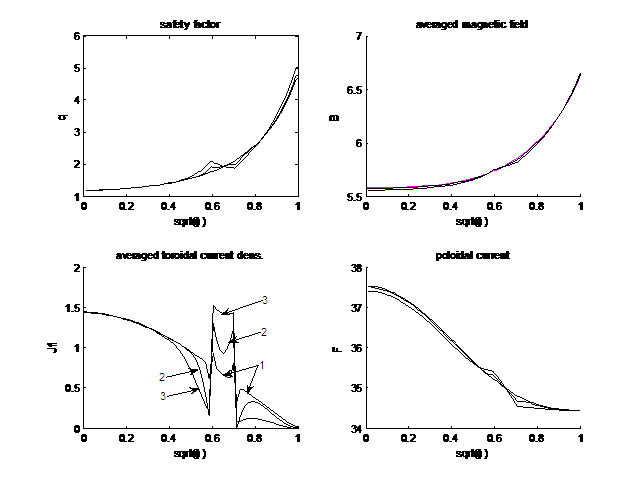
Рис.3 Фактор
запаса устойчивости, осредненное магнитное поле, осредненная плотность
тороидального тока, полоидальный ток
4.2 Квазиравновесная
эволюция плазмы токамака в модели со свободной границей плазмы. Вариант VDE (vertical displacement event) с учётом
диффузии магнитного поля, посадкой и обрезанием плазмы по лимитеру.
В качестве исходной равновесной плазменной
конфигурации  с неизвестной
свободной границей плазмы и вложенными магнитными поверхностями в коде SPIDER рассчитывается бессиловое с неизвестной
свободной границей плазмы и вложенными магнитными поверхностями в коде SPIDER рассчитывается бессиловое  равновесие
токамака-реактора ИТЕР, характеризуемое следующими значениями основных
параметров: равновесие
токамака-реактора ИТЕР, характеризуемое следующими значениями основных
параметров:
а) заданными профилями потоковых функций: 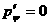 (бессиловое
равновесие), (бессиловое
равновесие), 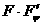 - линейная функция
потоковой переменной - линейная функция
потоковой переменной 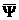 ; ;
б) тороидальный ток плазмы 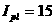 MA, тороидальное
вакуумное магнитное поле MA, тороидальное
вакуумное магнитное поле  T на радиусе T на радиусе 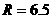 м. м.
в) «геометрией» катушек полоидального
токамака-реактора ИТЕР с предписанными значениями протекающих в них токов:
В ходе последующей квазиравновесной эволюции плазмы со
свободной границей полагаются заданными и фиксированными во времени профили
следующих потоковых функций:
а) 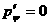 ; ;
в) температура плазмы 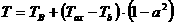 , где в качестве потоковой переменной , где в качестве потоковой переменной 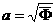 берётся корень квадратный из нормированного тороидального
потока плазмы, берётся корень квадратный из нормированного тороидального
потока плазмы, 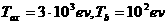 - предписанные
значения температуры на магнитной оси и границе плазмы, соответственно;
проводимость плазмы – спитцеровская: - предписанные
значения температуры на магнитной оси и границе плазмы, соответственно;
проводимость плазмы – спитцеровская:  ~ ~ 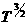 . .
На Рис.4а приводится соответствующая
исходному равновесию со свободной границей адаптированная в области, занятой
плазмой, по  к искомым магнитным
поверхностям расчетная потоковая сетка внутри заданной расчетной
области и, соответственно, исходная равновесная конфигурация ИТЕР. На рисунке
отмечены аппроксимации положения и формы катушек полоидального поля (PFC coils),
окружающих плазму пассивных проводящих структур (first wall, vacuum vessel) и
границы плазмы (plasma boundary). к искомым магнитным
поверхностям расчетная потоковая сетка внутри заданной расчетной
области и, соответственно, исходная равновесная конфигурация ИТЕР. На рисунке
отмечены аппроксимации положения и формы катушек полоидального поля (PFC coils),
окружающих плазму пассивных проводящих структур (first wall, vacuum vessel) и
границы плазмы (plasma boundary).

Рис.4а Исходное
равновесие. Расчетная сетка, адаптивная к магнитным поверхностям в плазме
На Рис.4б приводится исходная
равновесная конфигурация ИТЕР со свободной границей с адаптированной к искомым
магнитным поверхностям расчетной
потоковой сеткой (равномерной по  ) внутри области, занимаемой плазмой. На рисунке отмечено положение лимитерных точек (limiter points), ограничивающих
положение плазмы. ) внутри области, занимаемой плазмой. На рисунке отмечено положение лимитерных точек (limiter points), ограничивающих
положение плазмы.
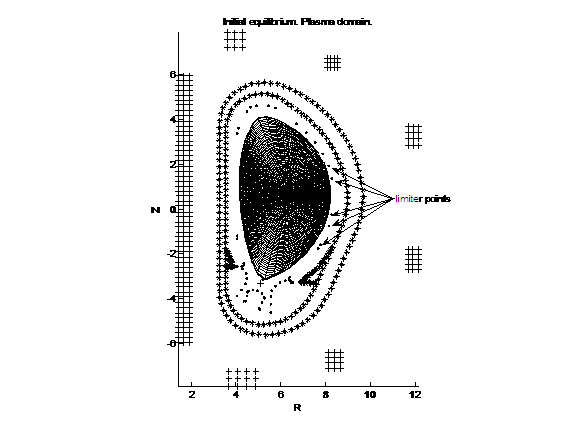
Рис.4б Исходное
равновесие.
На Рис.4в приводятся соответствующие исходному
равновесию профили основных потоковых функций:

Рис.4в   - для исходного
равновесия - для исходного
равновесия
На Рис.4г
приводится соответствующая исходному равновесию картинка плотности тороидального
тока плазмы 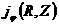 , как функция цилиндрических координат R,Z: , как функция цилиндрических координат R,Z:

Рис.4г
Плотность тороидального тока
На каждом временном шаге
квазиравновесной эволюции самосогласованно решается задача, описываемая
следующей нелинейной системой уравнений:
-
уравнение равновесия аксиально-симметричной плазмы со свободной границей (2.1),
- система
уравнений для расчета токов Фуко (2.2), наведенных в окружающих плазму
проводящих структурах,
- уравнение диффузии магнитного поля (2.3),
с
соответствующими начальными и краевыми условиями.
В ходе VDE-эволюции неустойчивая при отсутствии стабилизации
обратными связями плазма движется по преимуществу в вертикальном направлении по
экспоненциальной временной траектории. На Рис.5 приводятся соответствующие
графики для координат магнитной 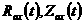 и полного
тороидального тока плазмы и полного
тороидального тока плазмы 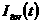 . .
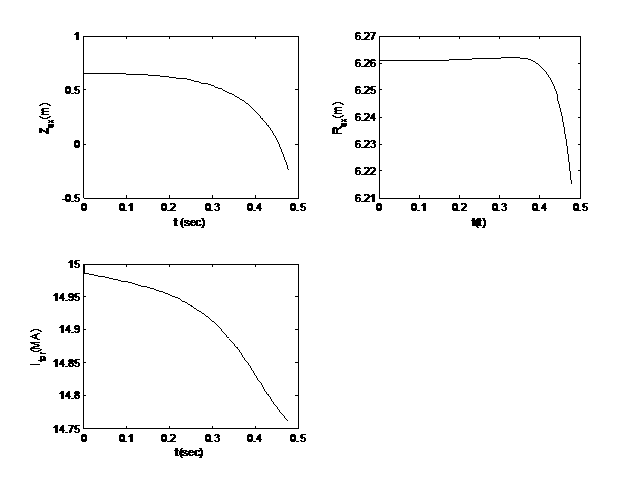
Рис.5 Эволюция
координат магнитной оси и тока плазмы.
В результате
этого движения в некоторый момент времени граница плазмы касается одного из
лимитеров. При этом предполагается, что в ходе дальнейшего движения начинает
срезаться приграничный слой плазмы снаружи от магнитной поверхности, касающейся
данного лимитера, с соответствующей частью полоидального тока F. Срезание части полоидального тока влечет за собой уменьшение
в плазме тороидального магнитного поля и, как следствие, тороидального потока
Ф. На рассматриваемых временах плазма реагирует на такого рода возмущения, как
идеальный проводник, следствием чего является возникновение в приграничном слое
равновесного тока, компенсирующего эти возмущения для сохранения тороидального
потока внутри каждой магнитной поверхности, движущейся вместе с плазмой. В
случае идеально-проводящей плазмы возникающий приграничный ток был бы чисто
поверхностным током, что соответствовало бы разрыву полоидального поля  на границе плазмы. В
случае конечной проводимости распределение поверхностного тока по тонкому
приграничному слою обеспечивает выполнение граничного условия (2.10) - на границе плазмы. В
случае конечной проводимости распределение поверхностного тока по тонкому
приграничному слою обеспечивает выполнение граничного условия (2.10) - 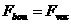 . .
Рисунки 6а,б,в,г для финального
равновесия - последней точке временных траекторий на Рис.5 - соответствуют
рисункам 4а,б,в,г для равновесия исходного.

Рис.6а
Расчетная сетка, адаптивная к магнитным поверхностям в плазме,
на момент времени t=0.478 сек.

Рис.6б
Равновесие плазмы на момент времени t=0.478 сек.
Рис.6в  - для исходного
равновесия - для исходного
равновесия

Рис.6г Плотность тороидального тока
5. Литература
1. V.D.Shafranov, Reviews of Plasma Physics (Consultants Bureau, New York,
1966), Vol.2, p.103.
2. H.Grad and J.Hogan, Phys. Rev. Lett. 24, 1337 (1070).
3. Degtyarev L.M. and Drozdov V.V. Comp. Phys. Reports 2 (1985) 343
4. Ivanov A.A., Khayrutdinov
R.R., Medvedev S.Yu., Poshekhonov Yu.Yu. The SPIDER code – axisymmetric fixed
boundary plasma equilibrium solver. – Preprint KIAM, №7, M., 2006
5. S.Yu.Medvedev, L.Villard,
L.M.Degtyarev, A.A.Martynov, R.Gruber and F.Troyon, 20-th EPS Conf. on Controlled Fusion and Plasma Phys., Lisbon,
Proc. Contrib. Papers, Vol.17C, Part IV,
1279 (1993)
6. Pereversev G.V., Yushmanov H.N.,
Dnestrovskii A.Yu., Polevoi A.R.,
Tarasjan K.N., Zakharov L.E. ASTRA an Automatic System for Transport Analysis
in a tokamak. – IPP 5/42, August 1991, Garching,
Germany
7.. Bateman G. Simulation of
Transport in Tokamaks. – Computer Applications in Plasma Science and
Engeneering. A.T.Drobot, editor, Springer-Verlag, No. 4 (1991) 381
8. R.R.Khayrutdinov and V.E.Lukash. Studies of
Plasma Equilibrium and Transport in a Tokamak Fusion Device with the
Inverse-Variable Technique. – J. Comput. Physics, 109 (1993) 193-201
9. Galkin S.A., Ivanov A.A.,
Medvedev S.Yu., and Poshekhonov Yu.Yu. Nucl. Fusion 37 (1997) 1455
10. Croatinger J.A. et al 1997 CORSICA: a comprehensive simulation of toroidal magnetic
fusion devices. Report UCRL-ID-126284, Lawrence
Livermore
National Laboratory, CA
11. Jardin
S.C., Pomphrey N., and DeLucia J. Dynamic Modeling of Transport and Positional
Control of Tokamaks. - J. Comput. Physics 66 (1986)
481
12. Ivanov A.A.,
Khayrutdinov R.R., Medvedev S.Yu., Poshekhonov Yu.Yu., 32-th EPS Conf. on Controlled Fusion and Plasma Phys., Tarragona,
ECA Vol.29C, P – 5.063 (2005)
13. Захаров Л.Е., Шафранов В.Д. Равновесие плазмы с
током в тороидальных системах. Вопросы
теории плазмы. Вып.11, стр.118, М., Энергоиздат, 1982.
|