Содержание

Введение  

1. Принципы МКСЭ.. 4

2. Обозначения и определения. 8

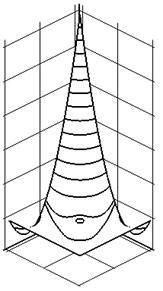
3. Локальная гладкость приближенного решения МКСЭ.. 14

4. Оценки решения по шкале H^M(Ω) 23

Заключение. 28

Список литературы.. 28

Введение

Основанием для разработки и развития метода конечных суперэлементов Федоренко (МКСЭ) является проблема численного решения сложных вычислительных задач, содержащих резкие особенности, или “сингулярности”, решения. В этих случаях размеры расчетной области составляют значительную величину в сравнении с областью проявления особенностей.

Данная работа является продолжением исследований [3 – 12] по выявлению качественных характеристик МКСЭ. В ней определены регулярность приближенного решения МКСЭ, установлена его асимптотика в окрестностях угловых точек разбиения области на подобласти-суперэлементы (СЭ). Работа выполнена на примере задачи Дирихле для уравнения Лапласа. Для достижения поставленной цели использованы теория весовых пространств Соболева и Кондратьева, теория эллиптических задач в областях с угловыми точками, свойства регулярности решений вариационных задач в негладких областях. Работа направлена на поиск оптимальных аппроксимаций метода и способов его применения.

МКСЭ позволяет решать задачи, содержащие мелкие “сингулярности” в расчётной области в пространстве слабых решений, обладая при этом погрешностями, оцениваемыми через ограничения этого решения на гладкие части суперэлементных границ. Это не требует использования сеток, сгущающихся в окрестностях “сингулярностей”, и связано с выбором особых аппроксимирующих пространств. Однако поведение приближений МКСЭ в пространствах сильных и гладких решений также представляет интерес.

При решении задачи рассматриваемая проблема возникает естественным образом. Как правило, искомое решение при достаточно гладкой границе области и подходящих граничных условиях обладает производными (например, суммируемыми с квадратом) до порядка . Вторым распространенным вариантом является гладкое, обладающее производными высокого порядка, решение в окрестностях границ разбиения области на подобласти-суперэлементы.

Производные представляют важные (а часто и определяющие) физические характеристики поставленной задачи. Например, такими характеристиками могут быть скорости и ускорения в механике, гидродинамике; напряжения, деформации и скорость их роста в теории упругости; напряженности и силы в теории поля; мощность тепловых источников и потоки газа в теории переноса теплоты и др. Полученные в работе результаты позволяют определить поведение погрешностей приближения производных решения первого и более высокого порядков.

Связующим звеном такого исследования является определение гладкости приближений МКСЭ, их асимптотического поведения в окрестностях углов декомпозиции. Помимо того, определение возможной гладкости приближенного решения в пределах СЭ и во всей области и нахождение его асимптотики представляют самостоятельный интерес.

1. Принципы МКСЭ

Метод конечных суперэлементов (МКСЭ) предложен в работах Федоренко и его коллег [1–2] и входит в класс численных методов, основанных на декомпозиции области в сочетании с выбором особой аппроксимации решения. Функции, с помощью разложения по которым разыскивается приближенное решение МКСЭ, являются решениями исходной системы уравнений в части области со специальными условиями на ее границе и, следовательно, заведомо содержат в себе ряд характеристик решения рассматриваемой задачи. Для авторов метода и данной работы главный интерес представляют задачи, характеризующиеся наличием ряда резких особенностей, проявляющихся на малых по сравнению с основной областью пространственных подобластях. Такие особенности могут представлять собой “сингулярности” решения, порожденные резкими неоднородностями геометрии области либо физической или математической модели. В работах [1–12] эффективность МКСЭ подтверждена примерами решения задач разнообразного физического происхождения.

Все дальнейшие рассмотрения мы проведем на примере задачи Дирихле для уравнения Лапласа в двумерной области . Область  представляет собой квадрат с исключенными из него кругами, радиус которых мал по сравнению с размерами Ω (рис. 1). Полагаем, что в окрестностях таких мелких отверстий сосредоточены все резкие “сингулярности” решения.

 в ,                                                                                   

 на ,                                                                                   

где  – искомая функция,  – граница расчетной области,  – некоторая известная функция на .

Как и в обычном методе конечных элементов (МКЭ) для численного решения задачи разобьем расчетную область на некоторое число подобластей, называемых суперэлементами. Каждое предполагаемое место сосредоточения особенности (отверстие, неоднородность и т.п.) при этом должно быть заключено строго внутри одного СЭ. На рис. 2 показан пример равномерного разбиения области  на квадратные СЭ  с границей , , где  – общее число подобластей-суперэлементов. Функции, разложением по которым разыскивается приближенное решение, для краткости будем называть базисными. Они являются финитными, их носители связаны с СЭ. При этом задание аппроксимаций в МКСЭ связано не со всей двумерной подобластью , а только с её одномерной границей.

Рассмотрим аппроксимации МКСЭ в одном СЭ , где  - некоторое фиксированное число. На его одномерной границе  зададим набор функций , , которые назовем граничными базисными функциями. В узлах СЭ  и на границе его отверстия  они равны

, , ,                                                    

где  – символ Кронекера. Узлы СЭ  расположены только на его ребрах и в углах (рис. 3). Символ , имеющий нулевой индекс, обозначает не один узел, а всю границу отверстия. В том случае, если СЭ  не содержит отверстия, полагаем, что  на всей .

Ранее в [6; 9] предложены и исследованы различные варианты продолжения этих функций с узлов  на ребра СЭ. Варианты заключаются в представлении базисных граничных функций на каждом из ребер границы некоторым “стандартным” интерполянтом [19]: полиномиальным, кусочно-линейным, сплайном и т.д. Одна из таких функций  при кусочно-линейной зависимости представлена на рис. 4, а при полиномиальной зависимости второго порядка на ребрах границы СЭ – на рис. 5.

Граничные базисные функции заданы для всех узлов и СЭ в области . Предполагается, что функции , , определенные на одном и том же ребре соседних СЭ  и , на нем совпадают, т.е.

, ,

для всех  и всех соседних СЭ ,  . Кроме того, на внешней границе  необходимо удовлетворить главное граничное условие :

, , .

Каждая построенная граничная базисная функция  однозначно определяет функцию  в СЭ . Она является решением задачи Дирихле следующего вида:

 в ,                                                                                

 на .                                                                                  

Функции , , задают базисные функции МКСЭ в СЭ . Базисные функции единообразно задаются в каждом из СЭ , , области расчета . Пример базисной функции  показан на рис. 6. Он соответствует граничной базисной функции , заданной полиномом второго порядка (рис. 5). Представляет интерес дальнейшее рассмотрение вариантов МКСЭ при полиномиальной или сплайновой интерполяции.

Заметим, что сингулярности решения задачи в окрестностях отверстий учтены посредством базисной функции с нулевым индексом  в каждом из СЭ. Остальные функции , , при наличии отверстия в СЭ  обращаются в ноль на его границе согласно . Если в СЭ отверстия нет, то .

При помощи построенного базиса решение исходной задачи внутри каждого отдельного СЭ разыскивается в следующем виде:

, .                                                                

Таким образом определяется приближенное решение МКСЭ  во всей расчетной области . При этом неизвестные значения  находятся с помощью обычного метода Бубнова-Галеркина при выборе функций  в качестве базисных и пробных [3–12].

В классическом случае эллиптических уравнений второго порядка при должных оговорках относительно гладкости границы, коэффициентов и граничных функций слабые решения принадлежат пространству Соболева . Следы этих решений на границе  суперэлементного разбиения области принадлежат пространству Соболева  с полуцелым показателем гладкости [16; 18]. Выбор функции, аппроксимирующей след решения на границе разбиения в норме пространства , и применение МКСЭ приведут к приближенному решению, аппроксимирующему в  точное решение.

В предыдущих работах исследовано влияние выбора метода аппроксимации на границе разбиения на результирующую точность расчетов метода. Получены теоретические (априорные) оценки погрешностей метода в зависимости от способа приближения [10–12]. Неясным остался вопрос о сходимости или расходимости ошибок производных сильного решения разного порядка. Такое исследование изначально затруднено особым “нестандартным” видом получаемого приближенного решения МКСЭ и его ограничениями по гладкости.

Данная работа посвящена теоретическому анализу МКСЭ Федоренко. В ней рассмотрена регулярность приближенного решения, получена его асимптотика в углах суперэлементного разбиения. Она представляет как отдельный интерес, так и служит для получения оценок погрешности производных различного порядка. Результаты получены на примере задачи – .

2. Обозначения и определения

Будем предполагать наличие такой гладкости функции  в (2) и границы области , которые достаточны для того, чтобы искомое решение принадлежало  [16; 23]. Сохраним далее введенные обозначения:  – расчетная область (рис. 2),  – граница СЭ ,  – совокупность всех суперэлементных границ,  – общее число СЭ в области,  – искомое и  – приближенное решение МКСЭ.

Как правило, СЭ  является многоугольником, так что необходимо учитывать тот факт, что  принадлежит классу  непрерывности. Будем рассматривать лишь случай, когда  – граница многоугольника либо граница, состоящая из конечного числа гладких кривых. В таком случае , , где L – число сторон  (или гладких частей границы) СЭ . Полагаем, что все вершины углов границы СЭ направлены во внешность области, то есть раствор углов не превышает π. Рассмотрим варианты МКСЭ, использующие полиномиальной либо сплайн-интерполяцию на границах СЭ. В случае сплайн-интерполяции  обозначают те отрезки разбиения суперэлементных границ, на каждом из которых интерполянт представляет собой полином (L – их число).

Определим объекты нашего рассмотрения.

Пространство всех полиномов порядка не выше  на отрезке  обозначим через . Введем  – пространство заданных на границе S полиномов порядка не выше  на каждой из частей  границы. Обозначим символом  пространство всех сплайнов порядка не выше , построенных на разбиении  на  отрезок длины . При этом . Полиномиальная интерполяция служит частным случаем интерполяции сплайнами, в которой  – число отрезков  на S, поэтому при её рассмотрении вариант полиномиальной граничной интерполяции МКСЭ отдельным образом не выделяется.

Аппроксимирующее пространство  МКСЭ – линейная оболочка, образованная всеми базисными функциями МКСЭ с граничной интерполяцией посредством сплайнов , т.е.

.  

Здесь след функции на S определен равенством . Оператор взятия следа , заданный на  соотношением

,   ,                                                           

непрерывно действует из пространства  в  для всех . При этом существует непрерывный оператор, обратный к  и действующий из  в . Такой общий случай действия оператора  справедлив как для гладкой, так и для многоугольной или просто липшицевой границы  [16; 31]. Отметим, что определение  содержит условие

  почти всюду на ,                                               

для всех  и всех соседних СЭ ,  . Это соотношение, очевидно, не всегда выполнено для пространства слабых решений задачи  (см., например, [36]). Аппроксимирующее пространство МКСЭ содержит его как “главное условие”, накладываемое на все базисные функции. Соотношение не включено в для сохранения более компактной записи. Иногда, если это не вызовет недоразумений, мы будем использовать также символ  без обозначения множества, на котором определена область значений оператора взятия следа.

Аналогичным образом определено и аппроксимирующее пространство  МКСЭ, представляющее собой линейную оболочку, образованную базисными функциями МКСЭ с граничной интерполяцией посредством полиномов  порядка не выше ν.

В определение аппроксимирующего пространства не входят условия совместности функций в узлах  СЭ вида:

, ,                                                

на соседних отрезках  границы S , . Условие , как правило, в МКСЭ выполнено, поскольку введено в определение граничных базисных функций  (см. ). Оно связано с расчетом базисных функций МКСЭ, являющихся решениями задач – , и заданием интерполянта  для них, непрерывного на всей границе . Линейная оболочка таких базисных функций МКСЭ согласно определению и составляет аппроксимирующее пространство. Тем не менее, условие можно ввести без ограничения общности метода, если непрерывность искомой функции в окрестностях узлов СЭ заведомо известна, а все особенности задач заключены строго внутри СЭ. В частности, всегда для сильного решения , .

Отметим, что в определении использован оператор Лапласа, определяющий гармоническую функцию в СЭ. Под гармоничностью некоторого слабого решения  в произвольной области Ω мы понимаем его удовлетворение уравнению Лапласа в следующей обобщенной постановке:

  .                   

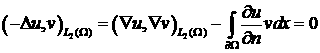
Далее как для слабого, так и для сильного решения продолжаем формально пользоваться кратким обозначением .

Характерным свойством аппроксимации слабых решений МКСЭ является возможность рассмотрения задачи – не просто в энергетическом пространстве , а в некотором его подпространстве, обозначаемом здесь . Это пространство  снабжено дополнительным свойством гармоничности входящих в него функций в каждом из СЭ  по отдельности:

.

Аппроксимирующее пространство МКСЭ является подпространством данного пространства. Определение  включает в себя условие :

 почти всюду на ,                                       

для всех  и всех соседних СЭ ,  . Перепишем его эквивалентно также в виде:

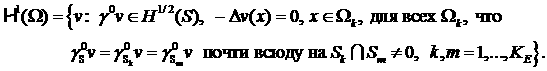
Здесь и далее везде мы будем использовать оператор следа , поэтому сделаем несколько замечаний о смысле данного определения.

Глобальное задание следа на границе  мы связываем с его стандартным определением. На пространстве  оператор следа  задан формулой . Если бы граница  обладала бесконечной гладкостью, то было бы выполнено соотношение  при любом значении . Для произвольной замкнутой липшицевой области  оператор следа  действует из пространства  в , однозначно определен, ограничен и имеет ограниченный обратный только при выполнении условия . При этом, если , то область значений шире, чем , см. [31; 30; 34; 15; 27]. В случае  для шкалы пространств Соболева в липшицевой области известно немного (то же и для более общего случая про­странств Бесова), но, если , то  действует из  в  [28; 14]. Кроме того, гармонические функции обладают дополнительной гладкостью, и имеет смысл рассмотрение случая пространств Бесова [29; 31].

Учитывая тот факт, что  – многоугольная область с границей, гладкой вне стратифицированных особенностей, далее возможно “улучшить” этот результат, вводя определение следа локально. Оператор следа  определен только на каждой из L гладких частей (ребер)  границы , . Локальное определение следа  [26; 20] мы связываем именно с таким заданием, а именно: . Тогда локальный оператор  при  непрерывен и действует из  в 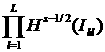. Для следа на всей S: . Обозначение  в зависимости от случая мы далее не меняем. Локальный след, очевидно, совпадает с глобальным, если последний корректно определен. При действии оператора  на функцию из пространства Соболева с произвольным показателем гладкости  считаем оператор следа локальным. Это необходимо учитывать, например, при использовании граничных интегральных уравнений и работе с ними. Локальные следы более высокого порядка также обладают общими свойствами на многоугольной границе, см., напр., [26]. В дальнейшем мы используем запись вида , которая является условным обозначением, и .

Нам понадобятся следующие пространства, обозначаемые через :

  , 

для любых , . При  имеем определение пространства . В определение  включено и условие . Рост показателя R характеризует увеличение гладкости функций  из этого пространства на всех гладких частях суперэлементных границ. Поскольку для следа любой функции  из пространства  справедливо включение , то выполнено включение:

.                                                                              

Обратное вложение при  на границе класса  не имеет места. Кроме того, любая функция  однозначно определена своим следом  на S (см. напр., [32]).

3. Локальная гладкость приближенного решения МКСЭ

Если при аппроксимации решения в пространстве  для ошибки решения, очевидно, справедлива эквивалентность     , то в пространствах более высокой гладкости , , и многоугольной границей разбиения  подобное несправедливо. Более того, показатель гладкости произвольной функции  на , имеющей гладкие следы на частях негладкой границы , ограничен сверху [13]. Это относится к регулярности решения задачи Дирихле в отдельном СЭ  [32; 33; 24]. Ограничение по гладкости может оказаться достаточно жестким и связано с локальным поведением решения в суперэлементных углах. Показатель гладкости зависит как от гладкости правой части граничного условия на отдельных сторонах границы , их совместности в вершинах углов, так и от величины раствора углов, кривизны их сторон и вида исходного уравнения.

3.1. Свойства гладкости приближенного решения МКСЭ

Пусть Λ – один из углов СЭ с границей  раствора α, ; P – его вершина;  – полярная система координат, связанная с Λ. В данном пункте мы рассмотрим преимущественно отдельный угол Λ, полученные таким образом результаты обобщаются на всю расчетную область.

Помимо самого приближенного решения  исследуем также его интерполянт . Отметим, что все полученные здесь результаты для  справедливы и для приближенного решения , а коэффициенты в его разложении, указанные через интерполянт , должны быть заменены аналогичными, заданными через приближенное решение .

Интерполянт  МКСЭ в области СЭ  является решением задачи:

 в ,                                                                           

 на ,                                                                          

где ,  – граничный сплайн-интерполянт решения. Дальнейшие выкладки мы проводим в предположении, что следы совместны для всех углов Λ в СЭ  так, что

,

и аналогично для приближенного решения:

,                                                               

где  и  – отдельные стороны угла Λ, составляющие его границу  и пересекающиеся в точке P.

Утверждение 1 . Пусть граничные базисные функции МКСЭ в некоторой окрестности угла Λ СЭ , на его границах  и , – полиномы порядка не выше ν. Интерполянт приближенного решения  МКСЭ в этой окрестности представим в виде:

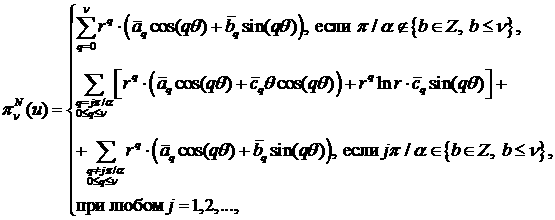
где

,  , ,

,  – коэффициенты решения (граничного полинома ) на границах ,  перед , . Аналогичное утверждение справедливо и для приближенного решения .

Доказательство. Будем искать решение задачи – в угле Λ СЭ как сумму решений  задач следующего вида:

 в ,                                                                                 

  на ,                                                                         

где  – константы, . При этом  на . Согласно [17, с. 47] асимптотика этой задачи в угле Λ такова:

Здесь коэффициенты разложения по переменной r (функции ,  и ) бесконечно дифференцируемы по θ (*).

Получим представление интерполянта приближенного решения:

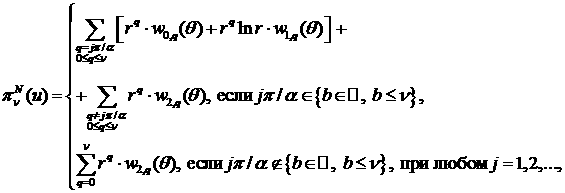
где  .

Уточним результат, рассмотрев константные коэффициенты разложений. Они представляют интерес для дальнейшего рассмотрения. Выбранные полиномиальные граничные значения бесконечно дифференцируемы в окрестности угла. Решение задачи согласно результату [17, с. 50] может быть найдено в виде:

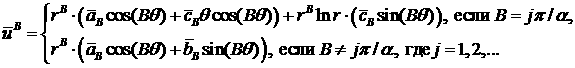
Находим коэффициенты , , , подставляя в задачу . Тогда

, , ,      

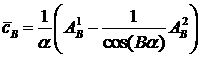где ,  – коэффициенты граничных значений   для различных сторон угла  и  соответственно. Граница  соответствует значениям угла , и  – значению .

Отметим, что в первой сумме выражения . Суммирование по всем B дает разложение приближенного решения  в области Λ (где символ B заменен на q):

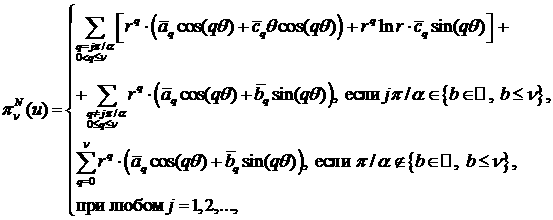
с коэффициентами , , . Выпишем слагаемое при :

в обоих случаях принадлежности . #

Замечание. Из проведенного рассмотрения следует также: ,  при , ; в противном случае решение  и  ограничено.

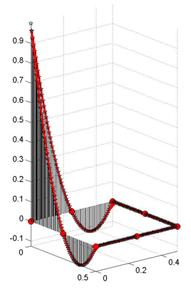
Пример. Для угла квадратного СЭ значение . Приближенное решение МКСЭ , а также его интерполянт в некоторой окрестности углов СЭ представимы в виде следующей конечной суммы:

при линейной интерполяции граничного решения

;

при любой полиномиальной интерполяции порядка выше единицы:

. #

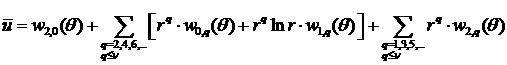Выражение определяет гладкость интерполянта приближенного решения  МКСЭ в соболевских пространствах. Если  и , то  нерегулярна по отношению к граничному условию так, что  для произвольных , , . В противном случае решение в угле Λ обладает бесконечной гладкостью, поэтому приближенное решение в СЭ  имеет максимальную гладкость по отношению к граничному условию на . То же относится к приближенному решению  МКСЭ.

Рассмотрим пространство . Согласно в его определение включено условие . Мы вводим ещё одно важное предположение о совместности следов в узлах  СЭ, а именно:  считаем выполненным условие

 .                                                        

Считаем также, что все углы СЭ направлены во внешность их области: . Пространство , дополненное условием совместности следов , и условием  на раствор углов, обозначим .

Утверждение 2 . Приближенное решение МКСЭ из пространства  принадлежит соболевскому пространству  в пределах каждого СЭ . То же верно для интерполянта .

Доказательство. Предыдущие выкладки показывают, что  в области СЭ , если . Нерегулярный случай  при минимальном значении  из множества  дает . Значит, выполнено . Аналогично для . Заметим, что для дальнейших выкладок это не принципиально, но упрощает некоторые записи. #

3.2. Асимптотическое разложение функции класса H^R(Λ)

Приведем некоторые известные сведения об асимптотическом разложении некоторой функции в многоугольном СЭ. Совместно с пунктом 0 эта информация может быть употреблена для получения ряда оценок. Кроме того, она дает представление и о других возможных вариантах задания граничных базисных функций, не указанных ранее и характеризуемых любой гладкостью по шкале Соболева. Как мы уже отмечали, показатель гладкости такой функции в СЭ всегда ограничен сверху. Это связано с гладкостью  его границы. Получим асимптотическое разложение в окрестностях угловых точек.

Произвольное решение уравнения Лапласа с граничными данными  в угле Λ СЭ  (в некоторой окрестности угловой точки P) разложимо в сумму гладкой и сингулярной частей [24; 25; 35]:

, ,                                                                   

,                                                               

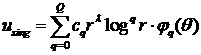где  обладает максимальной гладкостью, порожденной гладкостью функции  граничного условия, а наличие  обусловлено видом области Λ. Здесь  – локальная система координат в угле Λ; набор параметров λ определен некоторыми характеристическими числами, связанными с уравнением, и может быть дополнен конечным числом положительных действительных параметров , ; причем и в том, и в другом случае диапазон λ ограничен сверху гладкостью граничных данных; Q – конечное число;  – константы. Рассматриваемое нами эллиптическое уравнение не содержит членов порядка меньше максимального. Кроме того, границы  СЭ в некоторой окрестности каждого из углов Λ считаем прямыми линиями.

Классическим способом определения регулярности решения линейного эллиптического уравнения с постоянными коэффициентами является метод В.А. Кондратьева(*), использующий преобразование Меллина [21] исходного уравнения в угле Λ в задачу на отрезке , ,  – изображение. Выписанное уравнение на собственные значения  можно получить и определенной заменой переменных, преобразовывающей задачу в угле в задачу на некоторой простой области, например, полосе [17], полупространстве [33] в случае уравнения Лапласа. Несложно определить его решение как решение задачи Штурма-Лиувилля. Оно имеет вид: , , . Обратное преобразование Меллина даст разложение решения: , где  принадлежит конечному промежутку,  

В случае уравнения Лапласа коэффициенты λ разложения включают в себя конечный ряд из полученных характеристических чисел  для  [25; 32].

Наличие неоднородных граничных условий на  приводит к возникновению дополнительных слагаемых в таком разложении, гладкость которых измеряется в пространствах Соболева с весом  [35]. Для определения их полной асимптотики и регулярности в рамках шкалы “обыкновенных” пространств Соболева требуется дополнительное исследование. Например, полиномиальная правая часть в угле раствора  (см. пункт 0) приводит к разложению с порядком . Величина  регулярна при рассмотрении пространства с показателем гладкости , она регулярна также и для некоторых пространств Соболева с весом. При работе в шкале соболевских пространств , , её уже необходимо учитывать как нерегулярную часть. Отметим, что шкала весовых пространств “с однородной нормой”, возникающих при использовании метода Кондратьева, не имеет пересечений со шкалой пространств Соболева  [32]. Мы ее не используем.

Нас интересует множество функций, удовлетворяющих уравнению Лапласа в областях , условиям и со следами класса , . Ранее оно было обозначено через . Вообще говоря, пространство  в угле Λ содержит в себе набор весовых пространств “с неоднородной нормой” , см. [32], характеризующийся индексами ,  определенного диапазона. Уточнение асимптотики выражения – со следами из , , может быть выписано согласно [32, p.p. 284, 300]. А именно, в угле Λ справедливо представление:

         ,                                               

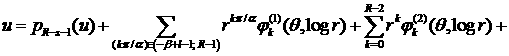
где , ; ; ;  для некоторого . Слагаемое  является полиномом от функции u порядка не выше . Функции , ,  – полиномы от переменной  с коэффициентами (зависящими от ) класса . Функция  обладает максимальной гладкостью по отношению к заданному граничному условию . Функция  действует в пространство  , . Из общих теорем вложения для данных весовых пространств (напр., [26]) следует, что  для . При этом для функции u при  справедливо условие .

Такое разложение достаточно громоздко, но содержит все необходимые нам факты, связанные с асимптотикой  в угле СЭ. Подчеркнем, что вид разложения является общим, его коэффициенты могут зависеть от раствора угла [33], величины R, граничных условий [37] и т.п.

Заметим, что для , асимптотика содержит слагаемое , его гладкость не выше . Для  в общем случае для решения справедливо соотношение . При этом , где  – обозначение целой части числа. Если , то первая сумма содержит слагаемые только в случае угла .

Отсюда для пространства  следует вложение

.                                                                          

Напомним, что из общего определения выполнено вложение вида

, .                                                                    

Отметим, что достаточно хорошо известны результаты и оценки, связанные с сильным решением задачи Дирихле  в многоугольной области  (см. [22; 23]). При этом достаточно легко заметить, что все соотношения в данных работах полностью согласуются с выписанным разложением . Мы не используем данные результаты, поскольку нас интересует весь диапазон возможной гладкости. Используем асимптотику либо её более общий вид . Последующие рассуждения относятся к уточнению таких оценок, что не представляется возможным, оставаясь лишь в рамках шкалы .

Введем ещё одно определение. Оператор следа m-го порядка  в пространстве  задан соотношением

, ,                                                        

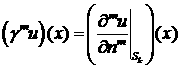где n – внешняя единичная нормаль к границе , . Оператор  действует из  в  для , и допускает “обычное” расширение в слабом смысле, например, :  для .

4. Оценки решения по шкале H^M(Ω)

Пусть задача – обладает гладким решением , . Рассмотрим вопрос об аппроксимации первых производных , как и ранее, в норме пространства . Из того факта, что

,

следует, что нам нужны оценки погрешностей решения u в норме пространства . Обобщая на произвольный порядок производных , , , можно исследовать поведение погрешностей решения u в нормах пространств  и, следовательно, определяя свойства МКСЭ о приближении производных порядка  в норме пространства Соболева .

Рассмотрим пример M = 2. Из гармоничности градиентов искомого и приближенного решений имеем

,                                             

где, вообще говоря, , так как условие совместности для градиентов не выполнено. Пункт 0 показывает, что  в области СЭ , если , поэтому запись ошибки решения в норме  корректна.

Запишем с использованием стандартных преобразований:

       ,  

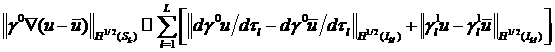где  – производная по направлению касательного вектора  на отрезке ;  – след первого порядка  на , см. .

Если бы выражение для ошибки  допускало принадлежность классу , , , на отдельном отрезке , то стала бы возможной запись неравенства  как следствие непрерывного вложения соответствующих пространств. Тогда слагаемые под знаком нормы в правой части выражения оценивались бы согласно “стандартным” выкладкам [10–12]. Заметим, что здесь нас интересуют не только априорные оценки погрешностей производных, но и сама сходимость производных приближенного решения МКСЭ к точному решению.

Ясно, что . Для следа первого порядка (нормальной производной) приближенного решения  на отрезке  нет точного аналитического выражения, оно известно лишь для следа . Можно определить регулярность  лишь в окрестности узлов , благодаря пункту 0.

Рассмотрим далее угол Λ, поэтому через  будем обозначать произвольную его сторону ; как и ранее, P – вершина угла Λ.

Несложно показать, что на границе угла  справедливо равенство:

.

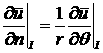Тогда из разложения для интересующего диапазона  получим следующий результат:

       ;

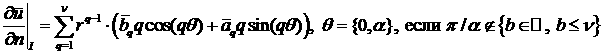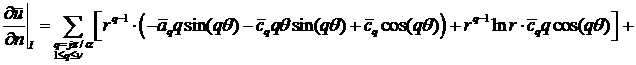
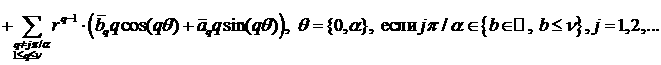
Отметим, что первым слагаемым, характерным для каждого из разложений и имеющим минимальный показатель  (либо ) является величина  при , зависящая от переменной . Здесь также , поскольку .

Перепишем полученные выражения, подставляя  во вторую сумму(*):

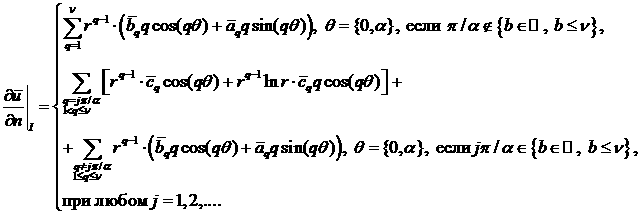
Отсюда ясно, что в окрестности вершины P произвольного угла СЭ Λ раствора α справедливы соотношения:  и  для  или производная  регулярна, если .

Более того, свойства гладкости  можно определить, воспользовавшись следующими результатами.

Утверждение 3 [26]. Элемент  из пространства  является образом некоторой функции  в угле  раствора α с вершиной P в результате действия согласно оператора , тогда и только тогда, когда выполнены соотношения

,                                                                              

,                                 

,                                      

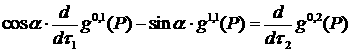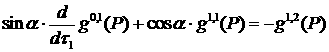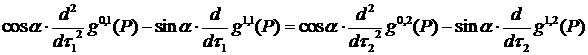
и для , , выполнено некоторое интегральное условие, где  – существующие конечные производные по отношению к касательным векторам  для границы , .

В том случае, когда , условия – принимают вид:

,                                                                              

,                                                                      

,                                                                      

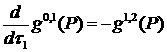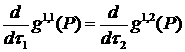
и для , ,

  , при .  

Отметим, что число условий совместности ограничено, несмотря на увеличение показателя s. Это связано с тем, что мы исследуем лишь величины  и ; это число таким образом связано непосредственно с порядком рассматриваемой нормы M.

Вариант  выписан для примера вследствие простоты записи. Не составляет труда перенести результаты на общий случай. Для квадратного СЭ  с узлами  и сторонами , , , справедливо утверждение.

Утверждение 4 [26]. Пусть  и . Элемент , , , из пространства  есть образ при отображении  некоторой функции из пространства Соболева  тогда и только тогда, когда для всех  и для всех , , , выполнено  

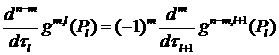,  где ,                

для , , выполнено

,               

и принято обозначение ,  – касательные вектора для границы .

Замечание Пространство , дополненное набором таких условий, не является замкнутым в  в стандартной норме. Оператор  непрерывно действует из  в такое модифицированное пространство и допускает непрерывный обратный при s > 2 в том случае, когда оно снабжено нормой с добавлением слагаемого, совпадающего с левой частью или , см. также [26].#

Таким образом, для исследования свойств нормальной производной  в соответствии с приведенными утверждениями нам нужны только значения  в вершинах  углов СЭ.

Из условий – утверждения 3 в некоторой окрестности угла Λ СЭ раствора  при , , не выполнены условия и для , то есть . Действительно, согласно разложению для  и разложению  для данного случая несложно проверить, что в вершине угла P:

,                                                                 

.                                                                 

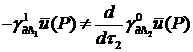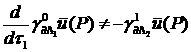Подобный же результат мы получим, исследуя целый СЭ  (см. утверждение 4) для произвольного раствора α. Следовательно, нормальная производная  не является образом локального оператора следа , действующего из  в , а элемент  не обладает гладкостью .

В дальнейшем необходимо дополнительное исследование полученных результатов, а “стандартная” схема не применима для получения верных априорных оценок МКСЭ и определения сходимости производных в энергетической норме пространства . Последующие работы посвящены более точному определению свойств  и погрешностей производных.

Заключение

В работе представлены результаты теоретических исследований МКСЭ Федоренко. Определены регулярность приближенного решения МКСЭ, его асимптотика в окрестностях угловых точек разбиения области на подобласти - суперэлементы. Исследование проведено на примере задачи Дирихле. Определение гладкости приближенного решения в пределах СЭ и во всей области и его асимптотического поведения в окрестностях “неестественного” разбиения исходной области на многоугольные СЭ представляет большой самостоятельный интерес. Помимо этого выполненная работа служит связующим звеном при переходе к определению теоретических оценок погрешностей производных приближенного решения.

Список литературы

[1] Федоренко Р.П. Введение в вычислительную физику. – МФТИ, Москва, 1994. – 528с.

[2] Жуков В.Т, Новикова Н.Д., Страховская Л.Г., Федоренко Р.П., Феодоритова О.Б. Метод конечных суперэлементов в задачах конвекции-диффузии // Препринт ИПМ им. М.В.Келдыша РАН, n. 8, 2001. – 36 с.

[3] Галанин М.П., Савенков Е.Б. К обоснованию метода конечных суперэлементов // Журн. вычисл. мат. и мат. физики, т. 43, n. 5, 2003, c. 711 – 727.

[4] Галанин М.П., Савенков Е.Б. Метод конечных суперэлементов для задачи о скоростном скин-слое // Препринт ИПМ им. М.В. Келдыша РАН, n. 3, 2004.

[5] Galanin M., Savenkov E., Temis J. Finite Superelements Method for Elasticity Problems // Mathematical Modelling and Analysis, v. 10, n. 3, 2005, p. 237 – 246.

[6] Галанин М.П., Лазарева С.А., Савенков Е.Б. Численное исследование метода конечных суперэлементов на примере решения задачи о скважине для уравнения Лапласа // Препринт ИПМ им. М.В. Келдыша РАН, n. 79, 2005.

[7] Галанин М.П., Савенков Е.Б. Совместное использование метода конечных элементов и метода конечных суперэлементов // Журн. вычисл. мат. и мат. физики, т. 46, n. 2, 2006, c. 270 – 283.

[8] Galanin M., Lazareva S., Savenkov E. Numerical investigation of the Finite Superelement Method for the 3D elasticity problems // Mathematical Modelling and Analysis, v. 12, n. 1, 2007, p. 39 – 50.

[9] Galanin M., Lazareva S., Savenkov E. Fedorenko Finite Superelement Method and its Applications // Computational Methods in Applied Mathematics, v. 7, n. 1, 2007, p. 3 – 24.

[10] Галанин М.П., Лазарева С.А., Савенков Е.Б. Качественный анализ и численное исследование метода конечных суперэлементов Федоренко // Тезисы всероссийской конференции по вычислительной математике “КВМ – 2007”, 18 – 20 июня, 2007, Академгородок, Новосибирск, Россия, с. 23.

[11] Лазарева С.А. Априорные оценки погрешностей и гладкость приближенного решения МКСЭ Федоренко // Тезисы конференции “Студенческая научная весна – 2007”, МГТУ им. Н.Э. Баумана, Москва, Россия.

[12] Лазарева С.А. Аппроксимационные свойства метода конечных суперэлементов Федоренко // Вычислительные технологии, 2008, в печати

[13][1] Агранович М.С. Обобщенные функции и соболевские пространства // Лекции Независимого московского университета, 2005. – 60 с.

[14][2] Агранович М.С. Спектральные задачи для сильно эллиптических систем второго порядка в областях с гладкой и негладкой границей // Успехи математических наук, т. 57, вып. 5, 2002, с. 3 – 78.

[15][3] Агранович М.С. Регулярность вариационных решений линейных граничных задач в липшицевых областях // Функциональный анализ и его приложения, т. 40, вып. 4, 2006.

[16] Лионс Ж.-Л., Мадженес Э. Неоднородные граничные задачи и их приложения. Мир, Москва, 1971. – 371 с.

[17] Назаров С.А, Пламеневский Б.А. Эллиптические задачи в областях с кусочно гладкой границей. – Наука, Москва, 1991. – 336 с.

[18] Обэн Ж.-П. Приближенное решение эллиптических краевых задач. Мир, Москва, 1977. – 383 с.

[19] Рябенький В.С. Введение в вычислительную математику. Физматлит, Москва, 1994. – 336 с.

[20] Васильчик М.Ю. Граничные свойства функций из пространства Соболева, определенных в плоской области с угловыми точками // Сибирский математический журнал, т. 36, n. 4, 1995, с. 787 – 804.

[21] Математическая энциклопедия. В 5 т. Т.3: Меллина преобразование /  гл. ред. Виноградов И.М. – Советская Энциклопедия, Москва, 1977.

[22][4] Bacuta C., Bramble J.H., Xu J. Regularity estimates for elliptic boundary value problems with smooth data on polygonal domains // Journal of Numerical Mathematics, v. 11, n. 2, 2003, p. 75 – 94.

[23] Borsuk M., Kondratiev V. Elliptic boundary value problems of second order in piecewise smooth domains. – Elsevier, North-Holland, 2006. – 538 p.

[24][5] Costabel M., Dauge M. Construction of corner singularities for Agmon-Douglis-Nirenberg elliptic systems//Mathematische Nachrichten, v.162,n.1,1993,p.209– 237

[25][6] Costabel M., Dauge M. Stable asymptotics for elliptic systems on plane domains with corners // Communications in Partial Differential Equations, v. 19, n. 9–10, 1994, p. 1677 – 1726.

[26][7] Bernardi Ch., Dauge M., Maday Y. Polynomials in the Sobolev World // Internal Report, Laboratoire Jacques-Louis Lions,Université Pierre et Marie Curie, 2003.–97p.

[27][8] Dahlke St., DeVore R.A. Besov Regularity for Elliptic Boundary Value Problems // Communications in Partial Differential Equations, n. 22, 1997, p. 1 – 16.

[28][9] Ding Z. A proof of the trace theorem of Sobolev spaces on Lipschitz domains // Proceedings of American Mathematical Society, v. 124, n. 2, 1996, p. 591 – 600.

[29] DeVore R.A. Nonlinear approximation // Acta Numerica, n. 7, 1998, p.51 – 150.

[30] Fabes E., Mendez O., Mitrea M. Boundary Layers on Sobolev-Besov Spaces and Poisson’s Equation for the Laplacian in Lipschitz Domains // Journal of Functional Analysis, n. 159, 1998, p. 323 – 368.

[31] Jerison J., Kenig C.E. The inhomogeneous Dirichlet problem in lipschitz domains // Journal of Functional Analysis, n. 130, 1995, p. 161 – 219.

[32][10] Kozlov V.A., Maz’ya V.G., Rossmann J. Elliptic boundary value problems in domains with point singularities. – American Mathematical Society, 1997. – 414 p.

[33] Lehman R.Sh. Developments at an analytic corner of solutions of elliptic partial differential equations // Journal of Mathematics and Mechanics, v. 8, n. 5, 1959, p. 727 – 760.

[34] Mitrea M., Taylor M. Potential Theory on Lipschitz Domains in Riemannian Manifolds: Sobolev-Besov Space Results and the Poisson Problem // Journal of Functional Analysis, n. 176, 2000, p. 1 – 79.

[35][11] Sändig A.-M. Regularity results for linear elliptic boundary value problems in polygons // Lectures at the Charles university Prague, 2005. – 38 p.

[36][12] Showalter R.E. Hilbert space methods for partial differential equations. – Electronic Journal of Differential Equations: Monographs, n. 01, 1994 (Originally of 1977). – 214 p.

[37][13] Sweers G. Hopf’s lemma and two dimensional domains with corners // Rendiconti dell'Istituto di Matematica dell'Università di Trieste, vol. 28, 1997, p. 383 – 419.