Аннотация
Разработан алгоритм расчета уравнений Эйлера для 3-х мерного дозвукового обтекания тел в невязком газе.
Применена схема 2-ого порядка точности, использован оригинальный подход к вычислению газодинамических функций
на поверхности тела. Написана и отлажена программа для расчетов на многопроцессорной машине rsc4.
Проведены контрольные расчеты обтекания кругового цилиндра, подтверждающие полную согласованность с расчетами в двумерном случае,
Проводятся расчеты обтекания крыла. Следующим этапом будет замена характеристических граничных соотношений на
внешней границе на нелокальные граничные условия дальнего поля.
Численный
метод расчета дозвукового обтекания невязким газом
В основе метода лежит
математическая модель дозвукового обтекания, описываемая нестационарными трехмерными уравнениями динамики невязкого газа.
При отыскании стационарного решения используются нестационарные уравнения Эйлера. Задача формулируется как гиперболическая
с соответствующими граничными условиями. Искомое решение находится путем установления. При интегрировании по времени используется
разностная схема типа Лакса-Вендроффа [2]. Решение разностных уравнений осуществляется методом конечных объемов [1], [5].
Дифференциальные
уравнения
Исходные уравнения в декартовых координатах могут быть записаны в следующем виде
 (1) (1)
Будем предполагать, что область  , в которой ищется решение, ограничена некоторой поверхностью Г, на которой заданы дополнительные граничные условия. , в которой ищется решение, ограничена некоторой поверхностью Г, на которой заданы дополнительные граничные условия.
На основе теоремы Гаусса-Остроградского интегральная форма уравнений (1) запишется в виде
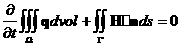 (2) (2)
где
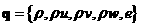

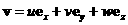
n - единичная внешняя нормаль к поверхности Г , ограничивающей объем  . p, . p,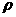 давление и плотность, отнесенные соответственно к p∞ и давление и плотность, отнесенные соответственно к p∞ и 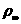 ,
компоненты скорости u,v отнесены к величине (p∞/ ,
компоненты скорости u,v отнесены к величине (p∞/ ) )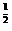 / /
Полная энергия e=p/(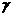 -1)+ -1)+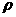 (u (u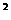 +v +v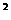 +w +w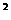 )/2 , где )/2 , где 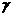 -отношение теплоемкостей. -отношение теплоемкостей.
Квадрат скорости звука a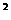 = =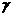 p/ p/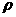 . Геометрические величины отнесены к характерному размеру r . Геометрические величины отнесены к характерному размеру r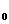 , а время к величине r , а время к величине r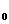 /(p /(p / /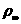 ) )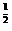 .
Величина H является вектором потока через поверхность .
Величина H является вектором потока через поверхность H=H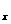 e e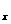 +H +H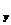 e e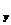 +H +H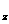 e e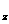 где где H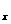 ={ ={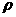 u, u,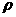 u u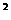 +p, +p,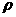 uv, uv,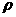 uw,(p+e)u}’ uw,(p+e)u}’ H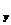 ={ ={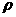 v, v,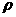 uv, uv,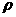 v v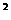 +p, +p,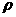 vw,(p+e)v}’ vw,(p+e)v}’ H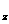 ={ ={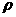 w, w,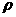 uw, uw,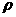 vw, vw,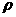 w w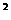 +p,(p+e)w}’ +p,(p+e)w}’ n ds=S - вектор поверхности, равный по модулю площади поверхности и совпадающий по направлению с нормалью к поверхности. dvol-элементарный объем.
Метод
конечных объемов и его дискретизация
Введем в области  некоторую разностную сетку с пространственными индексами ( k,l,m), точки, попавшие на поверхность Г, назовем граничными, а все точки,
лежащие вне Г, назовем внутренними. Таким образом , область некоторую разностную сетку с пространственными индексами ( k,l,m), точки, попавшие на поверхность Г, назовем граничными, а все точки,
лежащие вне Г, назовем внутренними. Таким образом , область  оказалась разбита на некоторое количество шестигранников, не обязательно с ортогональными
сторонами. оказалась разбита на некоторое количество шестигранников, не обязательно с ортогональными
сторонами. Обозначим объем произвольного шестигранника с центром в точке (k,l,m) как 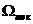 , и ограничивающую его поверхность как , и ограничивающую его поверхность как 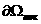 . . Уравнения для элементарного объема запишутся 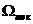 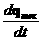 + + [ [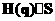 ] ] =0 (3) =0 (3) 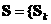 , ,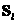 , ,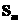 } -векторный элемент поверхности. } -векторный элемент поверхности.
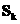 , ,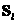 , ,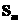 - направлены по внешним нормалям к соответствующим поверхностям. - направлены по внешним нормалям к соответствующим поверхностям.
 -центральный разностный оператор. -центральный разностный оператор. 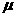 -оператор усреднения. -оператор усреднения. [H S]=[ S]=[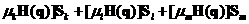 , где , где 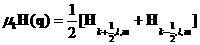  ,аналогично для ,аналогично для 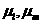 . .
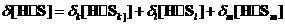 ,где ,где
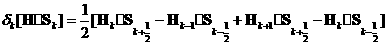
Для реализации численного решения применяется разностная схема, являющаяся модификацией схемы Лакса-Вендроффа, основанная на представлении
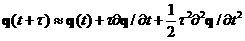 , ,
где вторая производная по времени вычисляется подстановкой 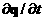 из уравнения (1) в продифференцированное по времени это же уравнение. из уравнения (1) в продифференцированное по времени это же уравнение. 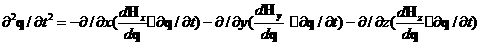

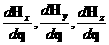 , это матрицы Якоби. , это матрицы Якоби. Область 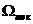 с центром в точке ( k,l,m ) ограничена поверхностями, проходящими через точки ( k с центром в точке ( k,l,m ) ограничена поверхностями, проходящими через точки ( k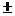 1,l 1,l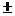 1,m 1,m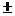 1). Разобьем область 1). Разобьем область 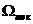 на 8 подобластей
с центрами (k на 8 подобластей
с центрами (k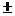 1/2,l 1/2,l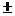 1/2,m 1/2,m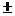 1/2). 1/2). В средних точках областей 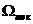 определяются определяются 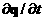 для всех 8 подобластей. для всех 8 подобластей. По средним точкам строится новая подобласть  и в ней окончательно определяется и в ней окончательно определяется 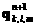 . . Предварительно в подобласти  вычисляются вычисляются 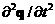 по аналогичной формуле (3). по аналогичной формуле (3). Окончательно имеем 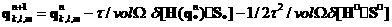
Где 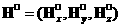 -произведение матриц Якоби на производную -произведение матриц Якоби на производную 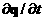 . . Локальный шаг по времени вычислялся на основании спектрального признака.
Уравнения
на границе тела
Для вывода этих уравнений воспользуемся характеристической формой записи уравнений газовой динамики в трехмерном случае [2],[3].
Dp-a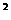 D D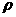 =0 =0 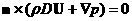 (4) (4)
a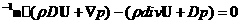 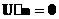
Первые 3 уравнения, это характеристические соотношения, последнее условие непротекания на поверхности тела. D-оператор полного дифференцирования по времени D=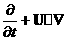 , a – скорость звука. , a – скорость звука. Уравнение 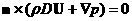 это проекция уравнения движения на касательную плоскость.
Будем предполагать, что известны в касательной плоскости два ортогональных единичных вектора это проекция уравнения движения на касательную плоскость.
Будем предполагать, что известны в касательной плоскости два ортогональных единичных вектора 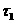 и и 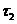 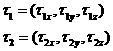 . .
Поскольку 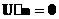 , это значит что вектор скорости лежит в касательной плоскости. , это значит что вектор скорости лежит в касательной плоскости. Обозначим 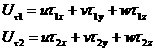

Тогда систему (4) можно привести к дивергентному виду, понизив порядок на единицу, тогда
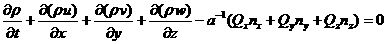
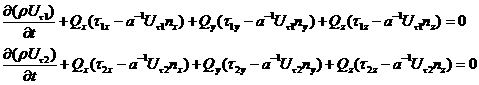
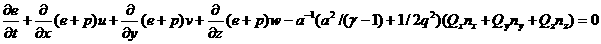
где 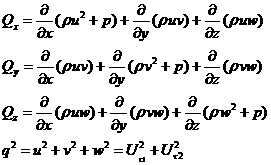
Нас интересует величина поправки  q на n -ом шаге по времени q на n -ом шаге по времени 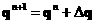 где где 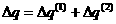
Что соответствует членам 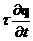 и и 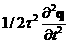 в разложении в разложении 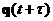 , , введя обозначения   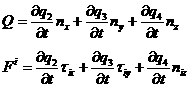
Получим систему 
Обозначим
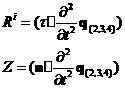
Тогда 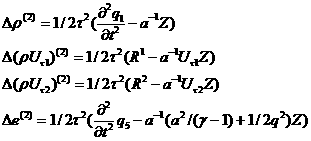
Выражения для 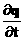 и и 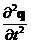 используем из расчета области используем из расчета области  , с учетом, что рассматривается все в касательной плоскости. Вводится дополнительная система
координат и пересчитываются необходимые величины, включая производные, для решения уравнений в касательной плоскости. , с учетом, что рассматривается все в касательной плоскости. Вводится дополнительная система
координат и пересчитываются необходимые величины, включая производные, для решения уравнений в касательной плоскости. После выполнения всех преобразований, получаем 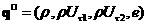 ,окончательно имеем ,окончательно имеем
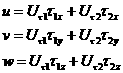
Этим завершается вычисление вектора 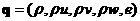 на поверхности тела. на поверхности тела. Аналог подобного алгоритма для двумерного случая был предложен в работе [2], в трехмерном случае эффективность этого подхода подтвердилась.
Уравнения
на внешней границе
При определении значений газодинамических величин на внешней границе используется подход, описанный в [3],[4], основанный на использовании приведенных
уравнений Эйлера к диагональному виду.
Запишем уравнения Эйлера в следующем виде 
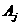 - матрицы Якоби - матрицы Якоби
Повернем систему координат так, чтобы одно из направлений совпало с заданным направлением, например, 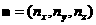 . . Система уравнений Эйлера преобразуется 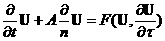
В правой части F собраны члены с производными по направлениям, лежащим в касательной плоскости в точке, в которой задан вектор  . . Нас интересует матрица A . 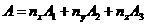 -это пучок матриц. -это пучок матриц.
Существует такое преобразование, что 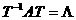 где T неособенная матрица, где T неособенная матрица, 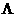 -диагональная матрица из собственных значений матрицы A. -диагональная матрица из собственных значений матрицы A. 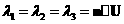
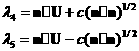
Если  -единичная нормаль, направленная внутрь области, то -единичная нормаль, направленная внутрь области, то 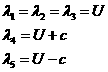
где 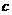 скорость звука скорость звука Матрицы T и 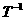 могут иметь следующий вид могут иметь следующий вид 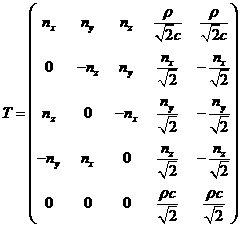 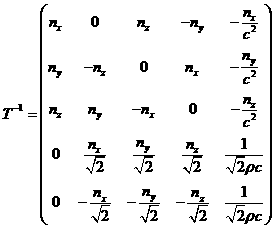
Матрица T состоит из собственных векторов матрицы A . Тогда 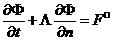 где где 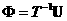
Характеристические переменные  вычисляются по значениям вычисляются по значениям 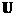 во внутренних узлах сетки для во внутренних узлах сетки для 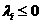 методом экстраполяции по внутренним точкам
области методом экстраполяции по внутренним точкам
области  , а для , а для   вычисляются по параметрам набегающего потока. вычисляются по параметрам набегающего потока. Окончательно получим 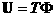
Заключение
Согласно данному алгоритму была написана и отлажена программа на многопроцессорной машине rsc4. В программе предусмотрена возможность расчетов
на любом числе процессов. В качестве тестов использовалось
а) Обтекание кругового цилиндра со сравнением с результатами работы [2]
б) Обтекание крыла сравнивалось с аналогичными расчетами, проведенными по программам Луцкого А.Е. Результаты обтекания цилиндра были тождественны, результаты обтекания крыла дали хорошее совпадение. В продолжении данной работы предполагается, что уравнения на внешней границе, основанные на характеристических соотношениях, в самом ближайшем будущем
будут заменены на граничные условия дальнего поля, разработанные в работе [6] и реализованные для задач трансзвукового обтекания в работах [7], [8].
Литература
[1] Rizzi A.W.,Erikson L.E. Computation of the flow around wings based on the Euler equations. J.Flaid. Mech. v. 148, 1984, 45-71. 2.Софронов И.Л. Быстросходящийся метод решения уравнений Эйлера. ЖВМ. и МФ, том 31, 1991, 575-591. 3.Кенцер Ч. Дискретизация граничных условий на движущихся разрывах. Численные методы в механике жидкостей. М. Мир, 1973, 62-72. 4.Русанов В.В., Нажесткина Э.И. Разностная аппроксимация вблизи границ для гиперболических систем квазилинейных уравнений.
Препринт №32, ИПМ им.М.В.Келдыша АН СССР, 1980. 5.Воскресенский Г.П., Луцкий А.Е., Нажесткина Э.И. Численный метод расчета дозвукового обтекания летательных аппаратов невязким газом.
Препринт №105, ИПМ им. М.В.Келдыша РАН, 1996. 6.Софронов И.Л. Нелокальные искусственные граничные условия для задач трехмерного стационарного обтекания. Матем. Модел. Т.10, №9, 1998,64-86. 7.Нажесткина Э.И., Софронов И.Л. Численная реализация граничных условий дальнего поля для задач трансзвукового аэродинамического обтекания.
Препринт №93 ИПМ им. М.В.Келдыша РАН, 2001. 8.Нажесткина Э.И. Численное исследование нелокальных граничных условий дальнего поля для задач дозвукового обтекания.
Препринт №50 ИПМ им. М.В.Келдыша РАН,2006.
|