Orbital Evolution of the Outer Satellites of Giant Planets. Methods of Analysis and Results
Preprint, Inst. Appl. Math., the Russian Academy of Science
(Эволюция орбит внешних спутников планет-гигантов. Методы анализа и результаты)

1°. Quite a few papers have been dedicated to the analysis of the orbital evolution of actual outer satellites of giant planets. Of the recent studies of this problem we point out the interesting and versatile works (Nesvorny, Alvarellos, Dones, Levison, 2003; Cuk, Burns, 2004; Christou, 2005; Beauge, Nesvorny, 2007; Jewitt, Haghighipour, 2007). These studies were aimed at analyzing various mechanisms of the origin of irregular satellites, identification of families of satellite orbits and various types of resonances. The papers mentioned above also contain extensive bibliography of earlier works. In addition, we also want to index the bibliographical review of the studies of the dynamics of natural planetary satellites (Ural’skaya, 2003). The descriptions of some specific features of the orbital evolution of distant satellites of giant planets can be found in our papers (Vashkov’yak, 2003; Vashkov’yak, Teslenko, 2005, 2007).

Beginning with 1997, ground-based observations allowed the researchers to discover more than one hundred outer satellites of giant planets including 54, 38, 9 and 5 bodies orbiting Jupiter, Saturn, Uranus, and Neptune, respectively. Outer satellites have immediately become popular among celestial mechanists because of their peculiar (irregular) orbits. During their evolution the eccentricities and inclinations of the orbits of these bodies with respect to the plane of the ecliptic may vary over a wide range.

Jupiter has the greatest number of outer satellites discovered so far. The two-component division is especially apparent in the system of outer satellites of this planet. The semi-major axes of prograde orbits range approximately from 7 to 18 million km, whereas those of retrograde orbits span from about 18 to about 34 million km. In the process of their evolution the orbital eccentricities and ecliptic inclinations may reach 0.6 ¸ 0.7 and about 40 ¸ 60 degrees, respectively. In the Saturnian system the intervals of semi-major axes of satellites moving in prograde and retrograde orbits overlap. The Uranian system is currently known to include only 9 outer satellites with only one of them moving in a prograde orbit. The semi-major axis of its orbit lies within the interval of the semi-major axes of retrograde orbits. It is interesting that until 1997 Uranus was the only giant planet with no outer observed satellites. Neptune has the smallest number of discovered outer satellites. However, the evolving orbit of one of the Neptunian satellites has the record high maximum eccentricity 0.9 among the orbits of planetary satellites, and as well as the record average planetocentric distance of one of the satellites 52 mln. km. The decrease of the number of discovered distant satellites from Jupiter to Neptune appears to be due to observations becoming more difficult to perform with increasing distance to the planet. Hence there are strong grounds to believe that further improvement of observational instruments and techniques will allow many more satellites to be discovered in distant neighborhoods of giant planets.

The appreciable orbital evolution of distant satellites (compared to that of inner satellites) made it necessary to develop special analytical as well as numerical-analytical techniques for computing secular and long-period perturbations. The researchers also use extensively more accurate – numerical – methods of integration of equations of perturbed motion over up to one hundred million years long time intervals.

Solar gravity is the main perturbing factor that causes the evolution of orbits of the considered class. It exceeds the effect of the flattening of the central planet and that of other less important perturbations by several orders of magnitude. The above peculiarity of distant satellites allows the well-known model of restricted circular three-body problem to be used (the Sun – Planet – Satellite) to identify the main features of the orbital evolution of these bodies.

2°. In the first (main) approximation the orbital evolution of the satellite is determined by the problem's perturbing function averaged independently over the fastest variables – the mean longitudes of the satellite l and of the perturbing body l₁ (the Sun). In this approximation we neglect the resonances between the orbital periods of the satellite and the planet. An investigation of such double averaged restricted circular three-body problem led N.D.Moiseev to establish the existence of its three independent first integrals (Moiseev, 1945)

                  a = c₀ ,   (1 – e²)cos²i = с₁,    W(a, e, i, w) = c₂                        (1)

Hereafter we use standard designations for the Keplerian elements of the elliptical orbit: a is the semi-major axis; е - the eccentricity; i - the inclination; w - the argument of the pericenter, and W -  the longitude of the ascending node. The angular variables are referred to the plane of the perturbing body and W is the double averaged perturbing function of the problem. However, although this problem is integrable, the analytical formula for function W is too complicated preventing the inversion of the corresponding quadratures. In the case where the satellite orbit lies completely inside the sphere of radius equal to the radius of the orbit of perturbing point a₁ this formula has the form of a power series in a = a/a₁

In  1961  M.L. Lidov  analyzed  the  satellite  variant  of  the  problem  at

a << 1, which is also known as the double averaged Hill problem (Lidov, 1961). He used a simplified formula for function W dropping a³ and higher-order infinitesimal terms. Lidov combined this formula with integral с₁ to derive a new explicit formula for independent integral

                              e²(2/5 – sin²isin²w) = c₂.                                         (2)

This integral, together with с₀ and с₁ allows the problem to be reduced to analysis of the behavior of phase trajectories in the (w, е) plane as a function of с₂ at fixed с₁. The variation of the longitude of the ascending node can be found via a quadrature.

At the same time, the famous Japanese researcher Y.Kozai studied a somewhat more general (asteroid) variant of the problem under weaker condition a < 1. In this case, integral с₂ can be written as a partial sum of a power series in a (Kozai, 1962)

                        W_n (e, i, w)a ²ⁿ = c₂                                                      (3)

The symmetry of the problem allows to analyze the families of phase trajectories to be restricted to the first quarter of the variation domain of the argument of the pericenter, because the double averaged perturbing function depends on w only via cos2w. A qualitative analysis of these families led the researches to interesting celestial-mechanical results.

Firstly, in the case of sufficiently large and physically possible values of с₁ > 0.6, w  varies monotonically with time.

Secondly, at с₁ £ 0.6, the double averaged problem has satellite-orbit solutions with fixed eccentricity and fixed argument of the pericenter. There are the domain of circulation (с₂ > 0) and domain of libration w (с₂<0) separated by the separatrix, i.e. by the limit solution (с₂ = 0).

Thirdly, at small

                        с₁ ,

where a₀ is the radius of the planet, the orbital evolution starting with whatever initial w and е results in such an increase of the eccentricity that the pericenter distance q = c₀ (1 - e) inevitably becomes equal to a₀ and the satellite naturally falls onto the planet. In the particular case of с₁ = 0, when the satellite orbit is perpendicular to the orbital plane of the perturbing point, the orbit evolves into a straight-line segment within a finite time interval and the satellite collides with the attracting center whatever its initial eccentricity and argument of the pericenter. This is author’s formulation of Lidov's theorem and their corollary.

The calculation of the evolution of the lunar orbit hypothetically turned orthogonal to the ecliptic plane performed by Lidov is a dramatic illustration of the “falling effect”. His computations showed that such an “orthogonal Moon” perturbed by the Sun would fall to the Earth within only four and a half years! Professor I.V.Novozhilov of Moscow State University was so impressed by this result that he portrayed Lidov in a friendly caricature (Fig. 1). This illustration is taken from the book of Professor V.V.Beletsky (Beletsky, 2001).

                              Fig. 1. Lidov Drops the Moon on the Earth.

                   Friendly Caricature of Professor I.V.Novozhilov (MSU)        

3°. Note that the property of almost orthogonal satellite orbits, established by Lidov, was inconsistent with quiet existence of the close Uranian satellites known at that time. Their almost circular and almost equatorial orbits are inclined by about 98° to the plane of the ecliptic (or the plane of the Uranocentric orbit of the Sun). However, Lidov’s analysis showed that solar perturbations play no crucial part in the orbital evolution of close Uranian satellites. The double averaged Hill problem with the allowance for the flattening of the central planet as considered by Lidov is nonintegrable (integral c₁ does not exist in the general case with no axial symmetry). However, one of its integrable cases describes the evolution of equatorial satellite orbits when the equatorial plane of the planet is orthogonal to the plane of motion of the perturbing body. This case approximately takes place in the system of inner Uranian satellites. It allows the existence of almost circular orbits whose evolution is determined mostly by flattening of the planet (Lidov, 1963a). Hence the flattening of Uranus prevents its close satellites from falling onto the planet, and allows the conflict to be resolved in terms of a real physical model.

Returning to the double averaged Hill problem (without the allowance for flattening of the planet) let us point out that the stationary singular point and librational variation of the pericenter are usually referred to as the “Kozai-resonance” in special celestial-mechanics publications after the Japanese researcher Y.Kozai, who studied the asteroid variant of the problem one year after Lidov had made his analysis. The work that Lidov published in 1961, became known abroad only after 1962, when it was presented at the international meeting in Paris and was published in English in two leading journals on space research (Lidov, 1962, 1963b). Given that the asteroid case of the problem maintains all the qualitative features found by Lidov, it would be fair to use the term “Lidov-Kozai-resonance” as suggested by Professor A.I.Neishtadt. For the same reason, it would be fair for the possible substantial variation of the eccentricity and the inclination angle of the satellite orbit is referred to as the “Lidov-Kozai-mechanism”. These terms have been used in recent years by some of the authors who analyzed the orbital evolution of a number of outer satellites of giant planets.

They were the discoveries of outer satellites that made it necessary not only to perform a qualitative analysis of the double averaged Hill problem, but also to derive the time dependences of the real orbital elements of such satellites for arbitrary initial conditions. The general solution of the evolutionary problem was constructed in papers (Kinoshita, H.Nakai, 1999, 2007) and in (Vashkov’yak, 1999).

J. Kovalevsky and especially A. A. Orlov further analyzed the satellite variant of the averaged problem. The equations, that describe the satellite orbital evolution in the restricted three-body problem, were derived using the Zeipel method up to third order infinitesimal in the small parameter m - the ratio of the mean motions of the perturbing body and the satellite. Thus the above authors (Kovalevsky, 1964, 1966; Orlov, 1965a, 1965b) constructed an m³ order solution, which is more accurate, than the solution of the double-averaged Hill problem (order m²). The results of Orlov were essentially used by us in developing the numerical- analytical method for the analysis of the orbital evolution of distant satellites.

4°. Not only the model of double averaged restricted circular three-body problem, but also the corresponding singly averaged model may prove to be of use for the analysis of the orbital evolution of some distant Jovian satellites. N. D. Moiseev introduced such an averaged problem (or scheme) in 1945, and it later came to be named after him. In this problem (Moiseev, 1945) only the fastest variable - the mean longitude of the satellite - has been excluded from the perturbing function. At the same time, the evolutionary equations contain the periodic functions of time that are due to the motion of the perturbing body during one satellite revolution. The double-averaged model described above does not contain these functions. However, the effect of perturbations with the intermediate period equal to half the orbital period of the planet may be great.

A combined numerical-analytical method found its application in many problems of celestial mechanics along with analytical and numerical methods. The version of this method that M. L. Lidov proposed in 1978 for Hamiltonian systems includes the following three main components (Lidov, 1978):

The first component is an analytical construction of a sequence of canonical changes of variables to eliminate rapidly oscillating functions of time from the Hamiltonian. These transformations establish a relation between the osculating and average orbital elements. The second component is a derivation of a new Hamiltonian written in terms of average elements (this procedure is also performed analytically). The third component is an effective numerical integration of differential equations written in terms of average elements with a long time step of the order of several orbital periods of the satellite.

Our proposed numerical-analytical method for the computation of the orbital evolution of distant satellites is also based on the main constructive idea of Lidov, the Zeipel method, and the series of Orlov’s papers (Vashkov’yak, 2005).

5°. The first new outer satellites among the large family of such objects discovered were the Uranian satellites U16 (Caliban) and U17 (Sycorax) found in 1997. The ephemerides of these and of other outer satellites of giant-planets, discovered later, are calculated in the papers (Emelyanov, 2005; Emelyanov, Kanter, 2005). These ephemerides are updating constantly in accordance with new observations and are available on the servers (http://lnfm1.sai.msu.su/neb/nss/index.htm) and http://www.imcce.fr/sat.

Our following presentation of the computed orbital evolution of these and other satellites is based on the data from the special Internet server set up by N.V.Emel'yanov (SAI MSU). One can download from this server, in particular the orbital elements refined with using all the observations available for the times of their discovery. We use these elements as the initial values in computations employing various methods. These initial orbital elements usually differ from the preliminary elements posted on the Minor Planet Electronic Circular Internet site (http://cfa-www.harvard.edu/mpec/RecentMPECs.html). We computed the time dependencies of the orbital elements of the outer satellites and, in particular, those of Caliban and Sycorax, using the three methods described above over the time intervals ranging from one to several periods of precession of nodes. In the Fig. 2, 3 and in the other figures the solid lines show the results obtained by numerically integrating the exact equations of motion; the dots - correspond to the results obtained using the numerical- analytical method, and the dashed lines correspond to the analytical solution of the double averaged Hill problem.

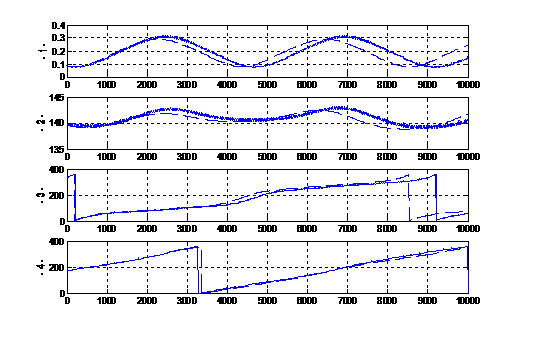
                      Fig. 2 U16 (Caliban); Abscissa axis – time t (years),

                ordinate axis: 1 – e(t), 2 – i_eclip (t),3 - w(t), deg, 4 - W(t), deg,

            strict numerical calculation; ··········  numerical-analytical method;

            analytical method (double averaged Hill problem).

                                          Fig. 3. U17 (Sycorax)

The orbit of satellite U23 (Margaret) (Fig. 4) differs from those of Caliban and Sycorax by the librational variation of the argument of the pericenter and by its prograde motion.

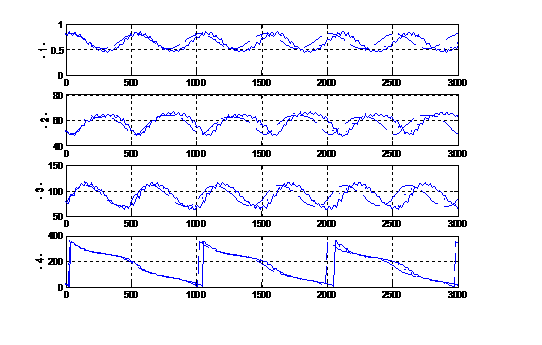
                                     Fig. 4. U23 (Margaret)

The data for the outer Uranian satellites lead us to conclude that the results obtained using numerical method agree well with those obtained using numerical-analytical method. The time dependencies of the orbital elements computed using analytical method differ from the corresponding time dependencies computed using numerical methods. The differences are due mostly to inaccurately computed periods of the variation of the pericenter arguments and of the ascending-node longitudes. However, in the cases where their results agree qualitatively, the two methods yield sufficiently similar extreme parameters of evolution.

The orbital evolution of two Neptunian satellites with circulatory N9 (Halimede) and librational N11 (Sao) variations of the pericenter arguments is characterized by the substantial amplitudes of oscillation of the eccentricities and inclinations in accordance with the Lidov-Kozai-mechanism. The orbital elements of two Jovian satellites – J18 and J46 and two Saturnian satellites – S9 and S24 show similar temporal variations.

The orbits of a number of outer satellites proved to exhibit librational variation of the arguments of the pericenter. This is a rather rarely encountered feature even among the ensemble of several thousand asteroid orbits. Y.Kozai was the first to discover an actual  w - librational orbit of the asteroid Cincinnati. The first w-librators discovered among the planetary satellites by solving the double-averaged Hill problem were the outer Saturnian satellites S22 (Ijiraq) and S24 (Kiviuq). A number of similar orbits were later found in the satellite systems of Jupiter - Carpo, Uranus - Margaret, and Neptune Sao and Neso. All these satellites are demonstrative examples of natural realization of the Lidov-Kozai-resonance in the satellite systems of giant planets. The phenomenon of this resonance was also confirmed via numerical integration of strict equations of motion of the satellites mentioned above.

6°. Note that in some cases the simple evolutionary model initially yielded paradoxical results. The analysis of the orbits of the outer Saturnian satellites S20 (Paaliaq) and S29 (Siarnaq) performed in framework of the double averaged Hill problem implied the librational behavior of the variation of the pericenter arguments w (c₂ < 0). However, the computations made by more accurate numerical and numerical-analytical methods showed that the actual variations of w for these orbits are circulatory. This qualitative discrepancy is due to the fact that the phase point in the (w, e) plane is close to the separatrix of the integrable double averaged Hill problem, where constant c₂ is very close to zero. The allowance for minor perturbations revealed the actually circulatory behavior of the evolution of w for the orbits mentioned above. As a result, the simple evolutionary model was found to be in need of refinement for the domains of orbital parameters e, i and w, lying within the close neighborhood of the separatrix. The same is also true for the orbit of the Saturnian satellite S/2007 S1 and Neptunian satellite N10 (Psamathe). By contrast, the analysis of the orbital evolution of the Neptunian satellite N13 (Neso) made in framework of the double averaged Hill problem yields circulatory behavior of w, whereas more accurate methods show librational variation of this parameter.

The evolutionary model had also to be refined in another case where orbital parameters e, i and w are such that not only c₂ » 0, but c₁ is close to its bifurcation value of 0.6. Under such conditions, the (w, e) plane develops a pair of singular points. Integral surfaces с₂ (w, е) deform along с₁ = 0.95; 0.6; 0.05; 0 (Fig. 5, from above down). First, a sufficiently smooth surface develops singularities (с₁ = 0.6) and then does depressions and “discharges” (с₁ = 0) along which the phase flow «discharges» onto the boundary of the domain (е = 1). When с₁ » 0.6 and с₂ »0 the evolutionary equations become extremely sensitive to any perturbations of the double averaged Hill problem and, hence, their solution may undergo qualitative changes.

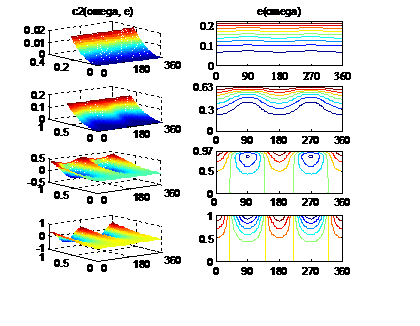 с₁ = 0.95

 с₁ = 0.6

 с₁ = 0.05

 с₁ = 0

          Fig. 5. Integral surfaces с₂ (w, е) (left column) and curves c₂ = const

               (right column) for different values с₁ = 0.95; 0.6; 0.05; 0.

The Fig. 6 shows the separatrices с₂ = 0 in the plane of the initial parameters (i₀, w₀). The circles and triangles, respectively indicate the w-librators and orbits that actually proved to be circulatory. The asterisks indicate the peculiar orbits of three Jovian satellites J49 (Kore), S/2003 J3, and J34 (Euporie).

Fig. 6. Real and supposed w - librators in the plane (i₀, w₀);

sign D -  w  circulates for 4 satellite orbits.

If computed in framework of the simple model, the evolution of w for the orbits of these satellites would have circulatory behavior (c₂ > 0). However, the computations made by the method of numerical integration showed (Fig. 7) that the pericenter arguments w of these orbits vary within limited intervals about the equilibrium value of 90°.

Fig. 7. Time dependences of the elements of the evolving orbit for the Jovian satellite J34 (Euporie) as the result of the numerical integration of the rigorous equations of motion.

This paradox is due to strong periodic solar perturbations that are neglected in the double averaged problem. The Fig. 8 shows the curves с₁ = 0.6 and the above orbits in the plane of initial parameter values (i₀, e₀).

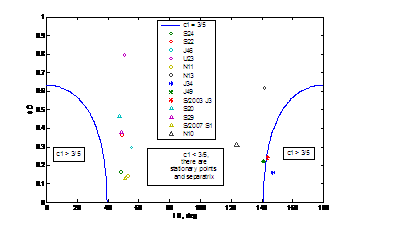
Fig. 8. Real and supposed w -  librators in the plane (i₀, e₀); sign D - w  circulates for 4 satellite orbits.

When с₁ » 0.6, it is the unaccounted about six-year periodic perturbations (with half of the Jovian orbital period) that introduce qualitative changes in the behavior of the evolution of w for the above orbits. Taking into account such perturbations in the singly averaged model allowed qualitatively to explain the librational behavior of the corresponding arguments of the pericenters. It is possible to construct analytically special surface

                        f [e, h = W(t)-l₁(t), w = ± 90°] = Cdw/dt.                                  (4)

The image of this surface is indicative of the reversal of the sign of derivative of w  with respect to t when w = ± 90°. Furthermore, for satellite J34 (Euporie) we also quantitatively confirmed the domain of variation of w  to span from 64° to 116°. For this satellite Fig. 9 shows the phase points on the (w, e) plane, whose positions were computed by numerically integrating the singly averaged Hill problem over a 10000-year long time interval.

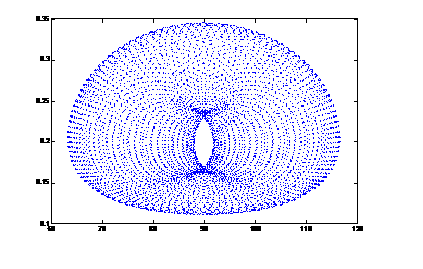
The phase pattern of «classical» w - librators, which are in the state of the Lidov-Kozai resonance, resembles a rather narrow ring-shaped domain. By contrast, the phase points of the orbit of J34 (Euporie) fill virtually the entire domain of libration. The orbits of the Jovian satellites Kore and S/2003 J3 exhibit similar patterns. Note that the ranges of eccentricity variations are wider than those obtained from the strict numerical solution. Therefore the averaged evolutionary model for the orbits of these three Jovian satellites is in need of further refinement.

Acknowledgements.

In conclusion, we consider it necessary to emphasize that this work on the analysis of the orbital evolution of distant satellites is based on the achievements of many celestial mechanists from different countries. I would like to mark with gratitude the special role in my work on this subject of my teachers - the Russian researchers Professors N.D.Moiseev, A.A.Orlov, and M.L. Lidov.

This work is supported by the Russian Foundation for Basic Research (RFBR) within the framework of two international grants № 07-02-92169-NTsNI_a and 07-02-91229-YaF as well as the grant of scientific school № NSh-1123.2008.1.

References.

C.Beaugé, D.Nesvorny, Astron. J. 133, 2537 (2007).

V.V.Beletsky, Essays on the Motion of Celestial Bodies. Translated from

     the Russian by Andrey Iakob. Birkhäuser Verlag. Basel. Boston. Berlin.

     372 p. (2001).

A.A.Christou, Icarus, 174, 215 (2005).

M.Cuk, J. A.Burns, Astron. J. 128, 2518 (2004).

N.V.Emelyanov, Astron. & Astrophys., 435, 1173-1179 (2005).

N.V.Emelyanov, A.A.Kanter, Solar System Research, 39, 2, 112-123 (2005).

D.Jewitt, N.Haghighipour, Annu. Rev. Astron. Astrophys, 45, 261-295 (2007).

H.Kinoshita, H.Nakai, Cel. Mech. & Dyn. Astron., 75, 125-147 (1999).

H.Kinoshita, H.Nakai, Cel. Mech. & Dyn. Astron., 98, 67-74 (2007).

Y. Kozai, Astron. J. 67, pp. 591-598 (1962).

M.L. Lidov, Iskusstvennye Sputniki Zemli, 8, pp. 5-45, (1961, in Russian).

M.L. Lidov, In Dynamics of Satellites (M. Roy Ed.), pp. 168-179,

        Springer-Verlag, Berlin. Göttingen. Heldelberg (1963a),

        Symposium Paris, May 28-30, 1962.

M.L. Lidov, Planet. Space Sci.,  9, pp. 719-759 (1962).

        Translated by H.F. Cleaves from Iskusstvennye Sputniki Zemli,

        No. 8, p.5, 1961.

M.L. Lidov, AIAA Journal, 1, 8, pp. 1985-2002 (1963b).

        Translated from Iskusstvennye Sputniki Zemli,

        (Artificial Earth Satellites) (Academy of Sciences Press,

        Moscow, 1961), No. 8, pp.5-45, 1961.

        Translated by Jean Findlay, Green Bank, West Va.

        Reviewed by Yoshide Kozai, Smithsonian Astrophysical Observatory,

        Cambridge, Mass.

M.L.Lidov, Trudy Inst. Teor. Astron., XVII, 54-61, 1978 (in Russian).

N.D.Moiseev, Trudy Gos. Astron. Inst. im. P.K.Sternberga, XV,

        pp. 100 – 117, 1945 (in Russian).

D.Nesvorny, Jose L.A.Alvarellos, Luke Dones, Harold F.Levison,

       Astron. J. 126, 398 (2003). 

J. Kovalevsky, Acad. Sci. 258, 18  (1964).

J. Kovalevsky, IAU Symp. No.25 (Ed. G.I. Contopoulos), London,

       Academ. Press, p. 326 (1966).

A.A.Orlov, Bull. Inst. Teor. Astron., X, 5(118), p. 360 (1965a, in Russian).

A.A.Orlov, Proc. of XV Intern. Congress on Astronautics

       Paris, Gautier-Villars, Warshawa, PWN-Polish Sci. Publ., 1 (1965b).

V.S.Ural’skaya, Solar Syst. Res. 37, 337 (2003).

M.A.Vashkov’yak, Astronomy Letters, 25, 476-481 (1999).

M.A.Vashkov’yak, Astronomy Letters, 29, 695-703 (2003).

M.A.Vashkov’yak, Astronomy Letters, 31, 64-72 (2005).

M.A.Vashkov’yak, N.M.Teslenko, Astronomy Letters, 31, 140-146 (2005).

M.A.Vashkov’yak, N.M.Teslenko, Astronomy Letters, 33, 780-787 (2007).
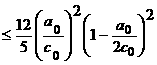