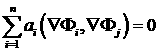Применение метода конечных суперэлементов для расчета распределений электрического потенциала и плотности тока
в проводящих объектах
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
рис. 1 Линейная интерполяция на
8 треугольниках на грани суперэлемента |
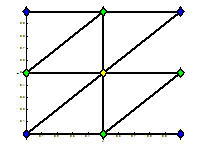
рис. 2 Квадратичная интерполяция на 8 треугольниках на грани суперэлемента |
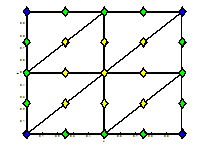
рис. 3 Кубическая интерполяция
на 8 треугольниках на грани суперэлемента |
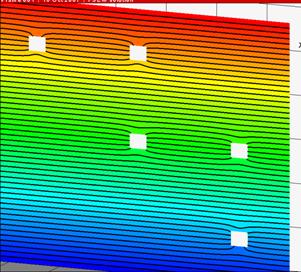
3 Тестовый расчет плотности тока
Результаты
тестового расчета плотности ![]() и потенциала
и потенциала ![]() МКСЭ в сечениях
области для материала с несколькими кубическими порами показаны на рис. 4 и рис. 5. Потенциал
МКСЭ в сечениях
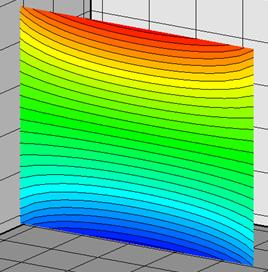
области для материала с несколькими кубическими порами показаны на рис. 4 и рис. 5. Потенциал ![]() внутри одной поры
иллюстрирует рис. 5.
внутри одной поры
иллюстрирует рис. 5.
4 Расчет усредненной проводимости пористого материала
Пусть однородный материал,
заключенный в куб ![]() , имеет искомый усредненный коэффициент проводимости
, имеет искомый усредненный коэффициент проводимости ![]() . Потенциал поля
. Потенциал поля ![]() в таком материале описывается
следующей задачей, аналогичной (7 – 10),
в таком материале описывается
следующей задачей, аналогичной (7 – 10),
![]() в
в ![]() ,
,
с граничными условиями
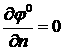 на
на ![]() ,
,
![]() на
на ![]() ,
,
![]() на
на ![]() .
.
Решение такой задачи – линейная
по ![]() функция. Тогда
напряженность электрического поля
функция. Тогда
напряженность электрического поля ![]() постоянна и составляет
постоянна и составляет
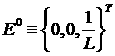 в
в ![]() ,
,
|
|
|
|
рис. 4 Потенциал |
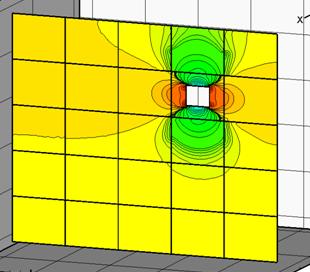
рис.
5 Плотность электрического тока |
|
|
|
|
рис. 6 Потенциал |
|
|
|
|
где ![]() – длина ребра
кубической области
– длина ребра
кубической области ![]() . Плотность электрического тока
. Плотность электрического тока ![]() соответственно равна
соответственно равна
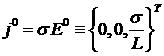 в
в ![]() .
.
Здесь ![]() ,
, ![]() – компоненты напряженности
и плотности тока, соответствующие направлениям координатных осей
– компоненты напряженности
и плотности тока, соответствующие направлениям координатных осей ![]() ,
, ![]() ,
, ![]() .
.
4.1 Способ I. Расчет работы электрического поля
Совершаемая электрическим полем в
объеме ![]() материала работа
переходит в тепловую энергию. Количество тепла, выделяющегося в объеме
материала работа
переходит в тепловую энергию. Количество тепла, выделяющегося в объеме ![]() однородного проводника,
согласно закону Джоуля - Ленца составляет
однородного проводника,
согласно закону Джоуля - Ленца составляет
![]() .
.
В свою очередь для однородного
материала с искомым коэффициентом проводимости ![]() , полем
, полем ![]() и плотностью
и плотностью ![]()
![]() .
.
Приравнивая полученные выражения,
найдем следующее выражение для расчета усредненной проводимости ![]() :
:
![]() .
.
4.2 Способ II. Расчет полного тока через сечение области
Поток плотности электрического
тока через сечение площади ![]() области Ω может быть выражен поверхностным интегралом
вида:
области Ω может быть выражен поверхностным интегралом
вида:
![]() .
.
В качестве сечения ![]() выберем границу
выберем границу ![]() , расположенную перпендикулярно оси
, расположенную перпендикулярно оси ![]() . Выбранное нами сечение есть граница расчетной области и в
данном случае не проходит через поры. Тогда полный ток через сечение пористого
материала равен
. Выбранное нами сечение есть граница расчетной области и в
данном случае не проходит через поры. Тогда полный ток через сечение пористого
материала равен
![]() .
.
Полный ток через то же сечение для материала с усредненными характеристиками даст величину
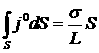 .
.
Равенство потоков приводит к соотношению
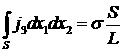 ,
,
откуда может быть найдена искомая
проводимость ![]() .
.
4.3 Способ III. Расчет полного тока по множественным параллельным сечениям
Вычислим сумму полных токов по
различным сечениям ![]() области
области ![]() ,
, ![]() , перпендикулярным оси
, перпендикулярным оси ![]() . Расстояние между ними мало и равно шагу сетки
. Расстояние между ними мало и равно шагу сетки ![]() , введенному ранее (разд. 0). Здесь
, введенному ранее (разд. 0). Здесь ![]() равно числу ребер
расчетной сетки, приходящихся на ребро области - куба
равно числу ребер
расчетной сетки, приходящихся на ребро области - куба ![]() . Полученное значение уточнит результат расчета, определенный
предыдущим способом, где единственное сечение выбрано достаточно произвольно.
Тогда для пористого материала получим
. Полученное значение уточнит результат расчета, определенный
предыдущим способом, где единственное сечение выбрано достаточно произвольно.
Тогда для пористого материала получим
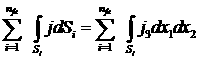 .
.
Для материала с усредненным коэффициентом ![]() в области
в области ![]() с сечениями
с сечениями ![]() ,
, ![]() , соответственно имеем
, соответственно имеем
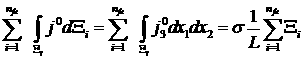 .
.
Отсюда рассчитываем искомое значение
![]() :
:
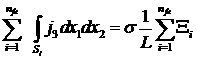 ,
,
Считаем ![]() постоянным по всей
области. Тогда, т.к.
постоянным по всей
области. Тогда, т.к. ![]() – постоянная величина
в пределах каждого сеточного тетраэдра, выражение (24) можно умножить на
– постоянная величина
в пределах каждого сеточного тетраэдра, выражение (24) можно умножить на ![]() и получить
и получить
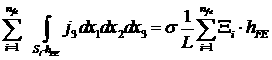 ,
,
что приводит к формуле
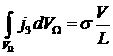 ,
,
где 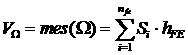 .
.
4.4 Способ IV. Сведение к поверхностному интегралу
Пользуясь теоремой Остроградского – Гаусса, перепишем полученное соотношение следующим образом:
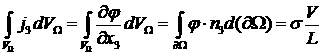 .
.
Далее значение коэффициента
проводимости ![]() рассчитываем из равенства:
рассчитываем из равенства:
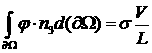 ,
,
где интегрирование по ![]() проходит как по части
внешней границы области, так и по границам пор
проходит как по части
внешней границы области, так и по границам пор ![]() в ней.
в ней.
5 Результаты расчетов
Ниже представлены результаты
расчетов, выполненных для различных распределений и размеров пор в области. При
этом использованы различные разбиения области на суперэлементы, шаги ![]() расчетной сетки, типы
граничной интерполяции МКСЭ, разные значения проводимости σ0
материала.
расчетной сетки, типы
граничной интерполяции МКСЭ, разные значения проводимости σ0
материала.
5.1 Зависимость средних проводимости σ и удельного сопротивления ρ от объемной пористости материала
В расчете использовано значение ![]() исходного материала,
отношение объема одной поры к единице объема области
исходного материала,
отношение объема одной поры к единице объема области ![]() составляет 0.125.
составляет 0.125.
В проведенных
расчетах количество суперэлементов изменялось в пределах от ![]() до
до ![]() , шаг расчетной сетки – от
, шаг расчетной сетки – от ![]() до
до ![]() , использован простейший линейный метод интерполяции МКСЭ на
двух или восьми граничных треугольниках на грани суперэлемента.
, использован простейший линейный метод интерполяции МКСЭ на
двух или восьми граничных треугольниках на грани суперэлемента.
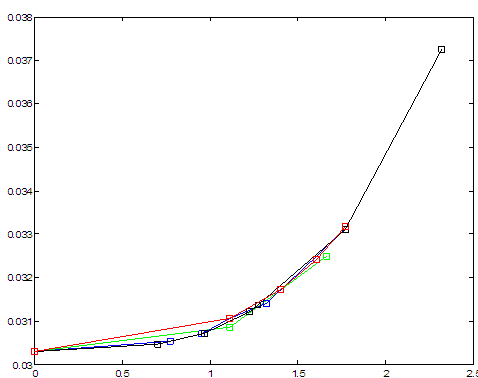
На рис. 7 показана зависимость средней проводимости ![]() от объемной пористости
от объемной пористости
![]() . Различные графики представляют результаты различных
способов расчета, описанных в разд. 4. Маркеры показывают рассчитанные значения для
. Различные графики представляют результаты различных
способов расчета, описанных в разд. 4. Маркеры показывают рассчитанные значения для ![]() . Пунктирная линия дает прямую, проходящую через точки с координатами
. Пунктирная линия дает прямую, проходящую через точки с координатами
![]() и
и ![]() .
.
|
|
|
рис. 7 Зависимость |
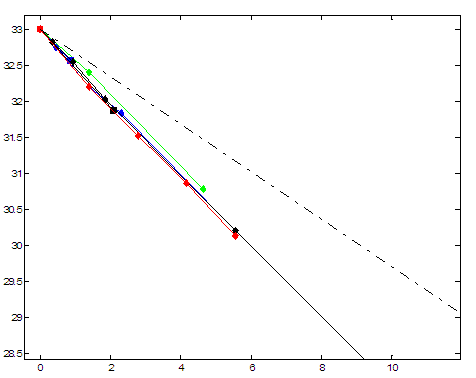
На рис. 8 показана зависимость удельного сопротивления ![]() от характерного
размера
от характерного
размера ![]() для пор в виде кубов
малого размера.
для пор в виде кубов
малого размера.
Все полученные графики качественно сходятся в одну прямую, а различие значений, рассчитанных разными способами, невелико.
Приведем график зависимости
проводимости ![]() от объемной пористости
от объемной пористости
![]() при бóльшем
разбросе параметров. В частности, введем разброс в размерах пор в материале.
Отношение объема поры к единице объема области
при бóльшем
разбросе параметров. В частности, введем разброс в размерах пор в материале.
Отношение объема поры к единице объема области ![]() может изменяться в
промежутке от 0.0046 до 0.4219. Кроме этого, зависимость продолжена: показаны
рассчитанные значения для промежутка
может изменяться в
промежутке от 0.0046 до 0.4219. Кроме этого, зависимость продолжена: показаны
рассчитанные значения для промежутка ![]() . Число суперэлементов
. Число суперэлементов ![]() изменяется в расчетной
области от 8 до 216, шаг расчетной сетки – от
изменяется в расчетной
области от 8 до 216, шаг расчетной сетки – от ![]() до
до ![]() . Аппроксимация проведена для разных граничных интерполянтов
(см. разд. 0) на числе треугольников от 2 до 18 по грани
суперэлемента.
. Аппроксимация проведена для разных граничных интерполянтов
(см. разд. 0) на числе треугольников от 2 до 18 по грани
суперэлемента.
|
|
|
рис. 8
Зависимость |
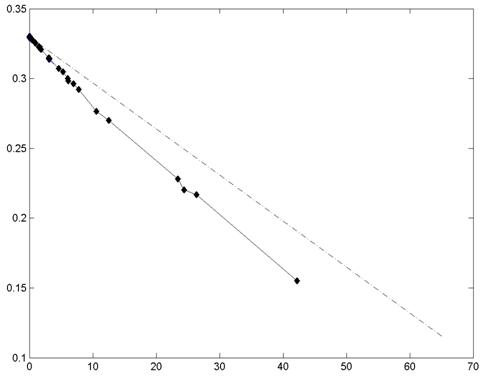
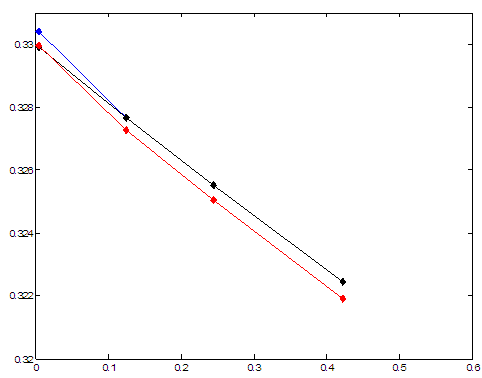
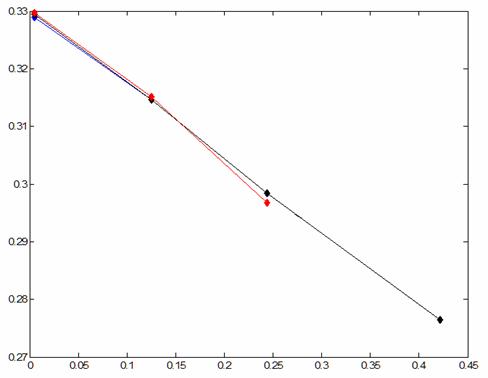
Разброс рассчитанных значений показан на рис. 9 и рис. 10. Результаты расчетов, полученных способами I и IV, приведены на рис. 9. Они практически совпадают и хорошо ложатся на одну линию.
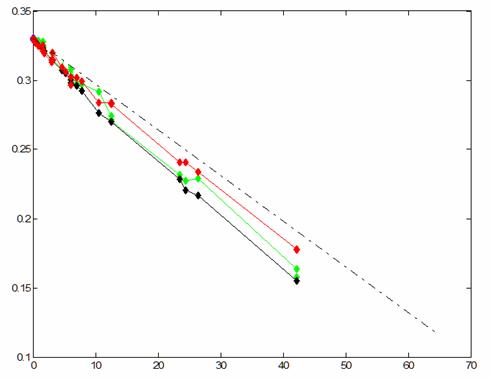
На рис. 10 приведены результаты всех описанных в разд. 4 способов расчета. Способы II и III дают отклонение от результатов других вариантов. При этом способ II дает максимальное локальное отклонение, равное 0.02.
|
|
|
рис. 9 Зависимость |
5.2 Зависимость σ от размера полости
Приведем зависимость средней проводимости от размера
пор в материале. Значение проводимости материала ![]() . Поры одинаковы. При этом отношение объема одной поры к
единице объема области
. Поры одинаковы. При этом отношение объема одной поры к
единице объема области ![]() варьируется в
промежутке от 0.0046 до 0.4219.
варьируется в
промежутке от 0.0046 до 0.4219.
Число суперэлементов ![]() , шаг расчетной сетки изменяется от
, шаг расчетной сетки изменяется от ![]() до
до ![]() , использован линейный способ граничной интерполяции по двум
треугольникам на грани суперэлемента. Зависимость для случая наличия в
материале одной поры показана на рис.
11 – рис.
12. Расчеты проведены I, II, IV способами. Совпадение рассчитанных
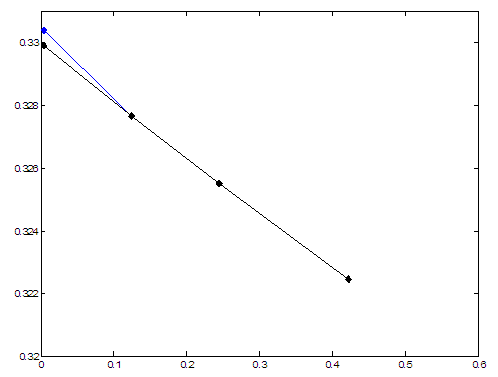
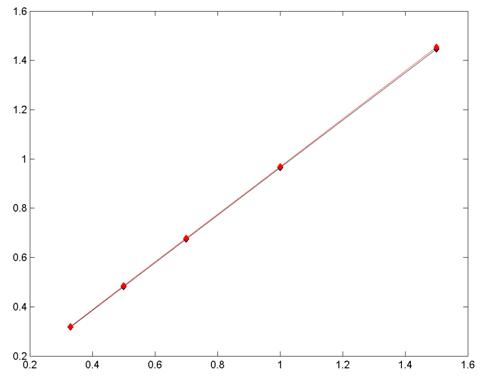
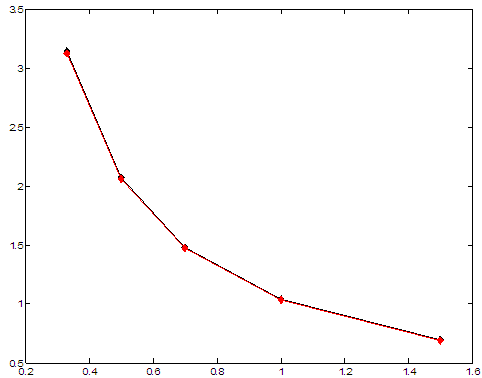
способами I, IV значений показано на рис. 11. Максимальное отклонение расчетных значений наблюдается
на рис.
12 и составляет
, использован линейный способ граничной интерполяции по двум
треугольникам на грани суперэлемента. Зависимость для случая наличия в
материале одной поры показана на рис.
11 – рис.
12. Расчеты проведены I, II, IV способами. Совпадение рассчитанных
способами I, IV значений показано на рис. 11. Максимальное отклонение расчетных значений наблюдается
на рис.
12 и составляет ![]() .
.
На рис. 13 показаны аналогичные зависимости для двух пор в
области в расчетах с количеством суперэлементов ![]() .
.
|
|
|
рис. 10 Зависимость |
5.3 Зависимость от проводимости материала σ0
На рис. 14 представлены зависимости искомой средней проводимости
от величины проводимости материала ![]() . Последняя величина изменяется в пределах
. Последняя величина изменяется в пределах ![]() . Использованы I, II и IV способы расчета. Видно,
что графически их результаты практически совпадают.
. Использованы I, II и IV способы расчета. Видно,
что графически их результаты практически совпадают.
Параметры
данных расчетов являются следующими: число суперэлементов – ![]() , характерный размер шага сетки –
, характерный размер шага сетки – ![]() , метод интерполяции на границе – сокращенный кубический по
двум треугольникам на грани, число пор – 5, их объем – 0.125 по отношению к
объему области
, метод интерполяции на границе – сокращенный кубический по
двум треугольникам на грани, число пор – 5, их объем – 0.125 по отношению к
объему области ![]() .
.
На рис. 15 показана зависимость среднего удельного сопротивления
![]() от
от ![]() при тех же параметрах
МКСЭ и данных о порах в материале.
при тех же параметрах
МКСЭ и данных о порах в материале.
|
|
|
рис. 11 Зависимость |
|
|
|
рис. 12 Зависимость |
|
|
|
рис. 13 Зависимость |
|
|
|
рис.
14 Зависимость |
|
|
|
рис. 15 Зависимость |
5.4 Зависимость от числа суперэлементов
|
|
|
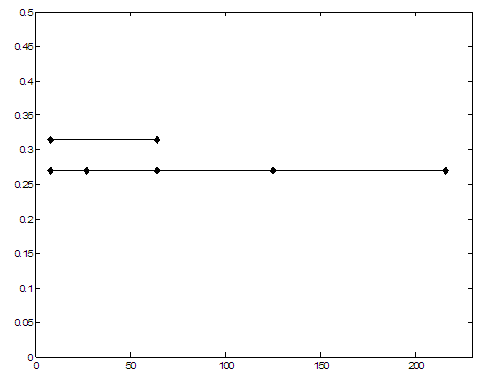
рис. 16 Зависимость |
Покажем, что при изменении числа
суперэлементов в расчетной области искомое среднее значение ![]() практически неизменно.
В данной группе расчетов
практически неизменно.
В данной группе расчетов ![]() , отношение объема одной поры к единице объема области
, отношение объема одной поры к единице объема области ![]() составляет 0.125, шаг
сетки –
составляет 0.125, шаг
сетки – ![]() , вид граничной интерполяции – линейный по двум треугольникам
на грани.
, вид граничной интерполяции – линейный по двум треугольникам
на грани.
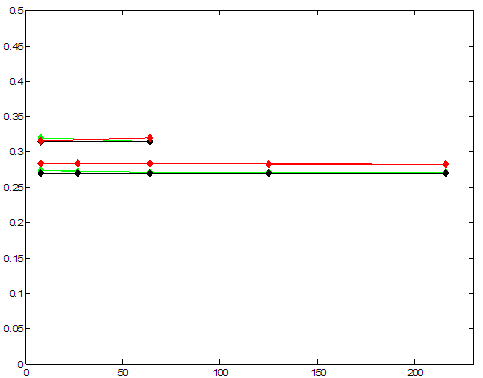
На рис. 16 и рис. 17 показаны расчетные зависимости, из которых верхняя
прямая соответствует количеству пор ![]() , а нижняя – суммарному числу
, а нижняя – суммарному числу ![]() пор в материале. Максимальный
разброс полученной проводимости при изменении числа суперэлементов в области
составляет
пор в материале. Максимальный
разброс полученной проводимости при изменении числа суперэлементов в области
составляет ![]() для I, IV способов расчетов и
для I, IV способов расчетов и ![]() – для II и III вариантов.
– для II и III вариантов.
|
рис. 17 Зависимость |
5.5 Зависимость от способа граничной интерполяции МКСЭ
Результаты расчетов показывают,
что при изменении метода граничной интерполяции МКСЭ, а также числа треугольников,
на которых она проведена, величина ![]() также практически не
меняется. Это связано с достаточной гладкостью тестового решения в окрестностях
границ суперэлементного разбиения.
также практически не
меняется. Это связано с достаточной гладкостью тестового решения в окрестностях
границ суперэлементного разбиения.
Различные
способы граничной интерполяции МКСЭ, показанные в разд. 0, требуют различного числа суперэлементных узлов ![]() в области
в области ![]() . Их число совпадает с числом искомых параметров разложения
решения
. Их число совпадает с числом искомых параметров разложения
решения ![]() .
.
|
|
|
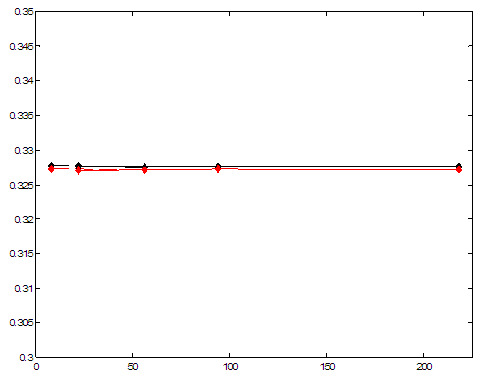
рис. 18 Зависимость |
Зависимость проводимости ![]() от числа узлов
от числа узлов ![]() в одном суперэлементе
приведена на рис. 18. Здесь
в одном суперэлементе
приведена на рис. 18. Здесь ![]() ,
, ![]() ,
, ![]() , число пор – 1, отношение объема одной поры к единице объема
области
, число пор – 1, отношение объема одной поры к единице объема
области ![]() составляет 0.125.
Число треугольников на грани суперэлемента составляет от 2-х до 18-ти.
составляет 0.125.
Число треугольников на грани суперэлемента составляет от 2-х до 18-ти.
5.6 Зависимость проводимости от расположения пор в области
Расчеты проведены для значений ![]() ,
, ![]() ,
, ![]() , число пор – 26, отношение объема одной поры к единице
объема области
, число пор – 26, отношение объема одной поры к единице
объема области ![]() составляет 0.125,
метод граничной интерполяции - сокращенный кубический на 2-х треугольниках.
Поры разбросаны по области случайным образом.
составляет 0.125,
метод граничной интерполяции - сокращенный кубический на 2-х треугольниках.
Поры разбросаны по области случайным образом.
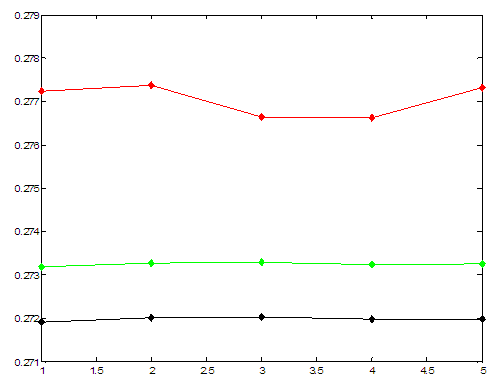
Графики, показывающие значения
рассчитанных ![]() для каждого из вариантов
расположения пор, показаны на рис. 19. Расчеты
для каждого из вариантов
расположения пор, показаны на рис. 19. Расчеты ![]() проведены I – IV способами. Максимальный разброс в
пределах одного из них составляет
проведены I – IV способами. Максимальный разброс в
пределах одного из них составляет ![]() для II варианта расчета и
для II варианта расчета и ![]() – для остальных.
– для остальных.
|
|
|
рис. 19 Зависимость |
5.7 Данные о числовых значениях
Набор данных о полученных числовых значениях можно
представить в виде таблицы в зависимости от объемной пористости ![]() .
.
|
|
σ, сп.I |
σ,сп.II |
σ,сп.III |
σ,спVI |
% поры на ед.об. |
|
Кол. пор |
Тэтр. на СЭ |
Инт.
Тип |
Кол. треуг |
|
|
0.002143 |
0.329360 |
0.330315 |
0.329992 |
0.330013 |
0.004630 |
216 |
1 |
279936 |
1 |
12 |
0.33 |
|
0.017147 |
0.329337 |
0.330206 |
0.329916 |
0.329925 |
0.004630 |
27 |
1 |
279936 |
1 |
12 |
0.33 |
|
0.017147 |
0.329333 |
0.330395 |
0.329916 |
0.329959 |
0.004630 |
27 |
1 |
279936 |
1 |
48 |
0.33 |
|
0.057870 |
0.329342 |
0.329178 |
0.329708 |
0.329802 |
0.004630 |
8 |
1 |
279936 |
1 |
12 |
0.33 |
|
0.115741 |
0.329094 |
0.328975 |
0.329412 |
0.329656 |
0.004630 |
8 |
2 |
279936 |
1 |
12 |
0.33 |
|
0.171468 |
0.328573 |
0.329081 |
0.329129 |
0.329227 |
0.004630 |
27 |
10 |
279936 |
1 |
12 |
0.33 |
|
0.214335 |
0.328405 |
0.328891 |
0.328910 |
0.329447 |
0.004630 |
216 |
100 |
279936 |
1 |
12 |
0.33 |
|
0.222908 |
0.328434 |
0.328684 |
0.328867 |
0.329022 |
0.004630 |
27 |
13 |
279936 |
3 |
12 |
0.33 |
|
0.289352 |
0.328348 |
0.328223 |
0.328529 |
0.328708 |
0.004630 |
8 |
5 |
279936 |
1 |
12 |
0.33 |
|
0.428669 |
0.327523 |
0.327632 |
0.327820 |
0.328356 |
0.004630 |
27 |
25 |
279936 |
1 |
12 |
0.33 |
|
0.462963 |
0.327769 |
0.327589 |
0.327646 |
0.328292 |
0.004630 |
8 |
8 |
279936 |
1 |
12 |
0.33 |
|
0.462963 |
0.329232 |
0.327709 |
0.327711 |
0.327247 |
0.125000 |
27 |
1 |
24576 |
1 |
12 |
0.33 |
|
0.462963 |
0.329189 |
0.327666 |
0.327666 |
0.327272 |
0.125000 |
27 |
1 |
24576 |
1 |
48 |
0.33 |
|
0.462963 |
0.329101 |
0.327566 |
0.327571 |
0.327085 |
0.125000 |
27 |
1 |
24576 |
2 |
12 |
0.33 |
|
0.462963 |
0.329136 |
0.327612 |
0.327613 |
0.327311 |
0.125000 |
27 |
1 |
24576 |
2 |
48 |
0.33 |
|
0.462963 |
0.329134 |
0.327610 |
0.327613 |
0.327209 |
0.125000 |
27 |
1 |
24576 |
2 |
108 |
0.33 |
|
0.462963 |
0.329079 |
0.327540 |
0.327548 |
0.327224 |
0.125000 |
27 |
1 |
24576 |
1 |
108 |
0.33 |
|
0.904225 |
0.328477 |
0.325512 |
0.325512 |
0.325055 |
0.244141 |
27 |
1 |
24576 |
1 |
48 |
0.33 |
|
0.925926 |
0.326802 |
0.325293 |
0.325290 |
0.324963 |
0.125000 |
27 |
2 |
24576 |
1 |
48 |
0.33 |
|
1.562500 |
0.322189 |
0.322191 |
0.325262 |
0.125000 |
8 |
1 |
24576 |
1 |
12 |
0.33 |
|
|
1.562500 |
0.327846 |
0.322853 |
0.322818 |
0.321072 |
0.421875 |
27 |
1 |
196608 |
1 |
12 |
0.33 |
|
1.562500 |
0.327567 |
0.322453 |
0.322450 |
0.321903 |
0.421875 |
27 |
1 |
24576 |
1 |
48 |
0.33 |
|
1.808449 |
0.323699 |
0.320772 |
0.320772 |
0.319660 |
0.244141 |
27 |
2 |
24576 |
1 |
48 |
0.33 |
|
2.314815 |
0.318152 |
0.318156 |
0.319625 |
0.125000 |
27 |
5 |
24576 |
3 |
12 |
0.33 |
|
|
2.314815 |
0.484292 |
0.482048 |
0.482050 |
0.484600 |
0.125000 |
27 |
5 |
24576 |
3 |
12 |
0.50 |
|
2.314815 |
0.678012 |
0.674868 |
0.674875 |
0.677988 |
0.125000 |
27 |
5 |
24576 |
3 |
12 |
0.70 |
|
2.314815 |
0.968584 |
0.964096 |
0.964099 |
0.969199 |
0.125000 |
27 |
5 |
24576 |
3 |
12 |
1.00 |
|
2.314815 |
1.452871 |
1.446145 |
1.446145 |
1.454328 |
0.125000 |
27 |
5 |
24576 |
3 |
12 |
1.50 |
|
3.051758 |
0.324548 |
0.314646 |
0.314645 |
0.313111 |
0.244141 |
8 |
1 |
24576 |
1 |
48 |
0.33 |
|
3.125000 |
0.319666 |
0.314670 |
0.314671 |
0.315102 |
0.125000 |
8 |
2 |
24576 |
1 |
12 |
0.33 |
|
3.125000 |
0.319371 |
0.314389 |
0.314383 |
0.313838 |
0.421875 |
27 |
2 |
24576 |
1 |
48 |
0.33 |
|
3.125000 |
0.314467 |
0.313846 |
0.313853 |
0.320116 |
0.125000 |
64 |
16 |
24576 |
1 |
48 |
0.33 |
|
4.629630 |
0.308560 |
0.307136 |
0.307133 |
0.309077 |
0.125000 |
27 |
10 |
24576 |
1 |
12 |
0.33 |
|
5.273438 |
0.321950 |
0.304944 |
0.304965 |
0.305987 |
0.421875 |
8 |
1 |
196608 |
1 |
12 |
0.33 |
|
6.018519 |
0.301579 |
0.300184 |
0.300183 |
0.302483 |
0.125000 |
27 |
13 |
24576 |
3 |
12 |
0.33 |
|
6.103516 |
0.307741 |
0.298355 |
0.298350 |
0.296738 |
0.244141 |
8 |
2 |
24576 |
1 |
48 |
0.33 |
|
6.944444 |
0.297600 |
0.296223 |
0.296222 |
0.301623 |
0.125000 |
27 |
15 |
24576 |
1 |
12 |
0.33 |
|
7.812500 |
0.296900 |
0.292260 |
0.292261 |
0.299259 |
0.125000 |
8 |
5 |
24576 |
1 |
12 |
0.33 |
|
10.546875 |
0.291877 |
0.276452 |
0.276480 |
0.283691 |
0.421875 |
8 |
2 |
196608 |
1 |
12 |
0.33 |
|
12.037037 |
0.273182 |
0.271917 |
0.271918 |
0.277239 |
0.125000 |
27 |
26 |
24576 |
3 |
12 |
0.33 |
|
12.037037 |
0.273275 |
0.272009 |
0.272011 |
0.277371 |
0.125000 |
27 |
26 |
24576 |
3 |
12 |
0.33 |
|
12.037037 |
0.273296 |
0.272033 |
0.272032 |
0.276637 |
0.125000 |
27 |
26 |
24576 |
3 |
12 |
0.33 |
|
12.037037 |
0.273244 |
0.271981 |
0.271981 |
0.276632 |
0.125000 |
27 |
26 |
24576 |
3 |
12 |
0.33 |
|
12.037037 |
0.273247 |
0.271981 |
0.271983 |
0.277327 |
0.125000 |
27 |
26 |
24576 |
3 |
12 |
0.33 |
|
12.500000 |
0.274460 |
0.270171 |
0.270171 |
0.283849 |
0.125000 |
8 |
8 |
24576 |
1 |
12 |
0.33 |
|
12.500000 |
0.271428 |
0.270170 |
0.270171 |
0.283719 |
0.125000 |
27 |
27 |
24576 |
1 |
12 |
0.33 |
|
12.500000 |
0.271414 |
0.270158 |
0.270159 |
0.283307 |
0.125000 |
27 |
27 |
24576 |
1 |
48 |
0.33 |
|
12.500000 |
0.274440 |
0.270152 |
0.270153 |
0.283278 |
0.125000 |
8 |
8 |
24576 |
1 |
48 |
0.33 |
|
12.500000 |
0.270689 |
0.270161 |
0.270162 |
0.283179 |
0.125000 |
64 |
64 |
24576 |
1 |
48 |
0.33 |
|
12.500000 |
0.270320 |
0.270165 |
0.270165 |
0.282635 |
0.125000 |
216 |
216 |
24576 |
1 |
48 |
0.33 |
|
12.500000 |
0.270432 |
0.270163 |
0.270163 |
0.282949 |
0.125000 |
125 |
125 |
24576 |
1 |
48 |
0.33 |
|
23.437500 |
0.231854 |
0.228214 |
0.228217 |
0.240718 |
0.421875 |
27 |
15 |
196608 |
1 |
12 |
0.33 |
|
24.414063 |
0.227197 |
0.220263 |
0.220264 |
0.240471 |
0.244141 |
8 |
8 |
24576 |
1 |
48 |
0.33 |
|
26.367188 |
0.228941 |
0.216862 |
0.216874 |
0.233868 |
0.421875 |
8 |
5 |
196608 |
1 |
12 |
0.33 |
|
42.187500 |
0.163642 |
0.155012 |
0.155008 |
0.177661 |
0.421875 |
8 |
8 |
196608 |
1 |
12 |
0.33 |
|
42.187500 |
0.157474 |
0.155013 |
0.155009 |
0.177285 |
0.421875 |
27 |
27 |
196608 |
1 |
12 |
0.33 |
Заключение
Работа посвящена применению метода конечных суперэлементов Федоренко для расчета распределений электрического потенциала и плотности тока в проводящих объектах. Материал таких объектов содержит малые диэлектрические поры. Область, занятая проводником, составляет значительную величину по сравнению с областью, занятой порами. На примере модельной задачи реализованы различные варианты МКСЭ. Исследованы зависимости искомого решения от величин объемной пористости, проводимости среды, размеров полостей в материале. Показаны зависимости, имеющие непосредственное отношение к исследуемому методу: удельной проводимости от изменения числа суперэлементов в области, от способа граничной интерполяции и различного взаимного расположения пор. Получены необходимые данные о численных значениях. МКСЭ показывает свою эффективность при правильном выборе способа построения и реализации аппроксимаций.
Список литературы
1. Страховская Л.Г., Федоренко Р.П. Об одном варианте метода
конечных элементов // ЖВМ и МФ. 1979. Т. 19, № 4. С. 950-960.
2. Страховская Л.Г., Федоренко Р.П. Расчет диффузии в
многосвязной области методом конечных суперэлементов // Препр. ИПМ им. М.В.
Келдыша АН СССР. 1987. 171. 26 с.
3. Страховская Л.Г., Федоренко Р.П. Расчет напряжений
в композитном теле методом конечных суперэлементов // Препр. ИПМ им. М.В.
Келдыша АН СССР. 1994. 97. 26 с.
4. Федоренко Р.П. Введение в вычислительную физику.
М.: Изд - во МФТИ. 1994. 528 с.
5. Галанин М.П., Савенков Е.Б. К обоснованию
метода конечных суперэлементов Федоренко // ЖВМ и МФ. 2003. Т. 43, № 5.
С. 713-729.
6. Галанин М.П., Савенков Е.Б. Метод конечных
суперэлементов в задачах математической физики в неоднородных областях //
Информационные технологии и вычислительные системы. 2005. № 3. С. 34 - 49.
7. Галанин М.П., Савенков Е.Б. Совместное использование
метода конечных элементов и метода конечных суперэлементов // ЖВМ и МФ. 2006.
Т. 46, № 2. С. 270 – 283.
8. Галанин М.П., Лазарева С.А., Савенков Е.Б.
Численное исследование метода конечных суперэлементов на примере решения задачи
о скважине для уравнения Лапласа // Препр. ИПМ им. М.В. Келдыша РАН. 2005. №
79. 30 с.
9. Галанин М.П., Савенков Е.Б. Метод
конечных суперэлементов для задачи о скоростном скин – слое // Препр. ИПМ им.
М.В. Келдыша РАН. 2004. № 3. 32 с.
11. Галанин
М.П., Лазарева С.А., Савенков Е.Б. Качественный
анализ и численное исследование метода конечных суперэлементов Федоренко //
Тезисы всероссийской конференции по вычислительной математике “КВМ – 2007”, 18
– 20 июня, 2007, Академгородок, Новосибирск, Россия, с. 23.
12. Galanin M., Savenkov E., Temis J.
Finite Superelements Method for Elasticity Problems. // Mathematical Modelling
and Analysis. 2005. V. 10. N 3. P. 237 – 246.
13.
Galanin M., Lazareva S., Savenkov E. Fedorenko Finite Superelement
Method and its Applications // Computational
Methods in Applied Mathematics. 2007. V. 7, N 1. P. 3 – 24.
14. Galanin M.,
Lazareva S., Savenkov E. Numerical investigation of the
Finite Superelement Method for the 3D elasticity problems // Mathematical
Modelling and Analysis. 2007. V. 12, N 1. P. 39 – 50.
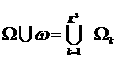 ,
, 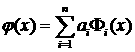 ,
,