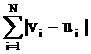О некоторых свойствах оценки метода распознавания символов, основанного на полиномиальной регрессии
|
|
символ |
v_true_min |
v_true_max |
v_true_max/ v_true_min |
v_false_min |
v_false_max |
Рfalse |
|
0 |
35,41 |
113,59
|
3,21 |
56,34 |
101,09 |
106,61 |
|
1 |
42,58 |
173,80 |
4,08 |
52,22 |
131,38 |
128,17 |
|
2 |
38,33 |
105,57 |
2,75 |
61,62 |
109,43 |
120,19 |
|
3 |
39,92 |
103,10 |
2,58 |
55,63 |
95,53 |
118,84 |
|
4 |
50,76 |
106,34 |
2,09 |
56,02 |
123,47 |
131,78 |
|
5 |
36,28 |
130,66 |
3,60 |
52,68 |
98,26 |
126,65 |
|
6 |
44,60 |
115,07 |
2,58 |
55,17 |
103,11 |
105,26 |
|
7 |
40,56 |
101,70 |
2,51 |
53,45 |
93,89 |
114,43 |
|
8 |
50,15 |
119,80 |
2,39 |
57,23 |
115,19 |
121,27 |
|
9 |
47,36 |
120,58 |
2,55 |
54,28 |
117,37 |
127,45 |
На рис.2в-11в представлены
диаграммы зависимости средней оценки распознавания рукопечатного символа (0, 1,
2, 3, 4, 5, 6, 7, 8, 9) от величины
отклонения между полиномиальным вектором х,
построенным по его растру, и
«среднестатистическим» полиномиальным вектором этого символа по базе, которая
используется как для обучения, так и для распознавания.
«Среднестатистический»
полиномиальный вектор конкретного символа получаем следующим образом. Значение
в каждой компоненте вектора, имеющей номер i, равно среднему арифметическому значений i-х
компонент по всем имеющимся в базе растрам рассматриваемого символа. Расстояние
между двумя векторами v=(v1,…,vL) и u=(u1,…,uL) определяем так: вычисляем
модуль разности значений в i-х компонентах, затем суммируем
по всем L компонентам:
||v-u|| =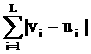 (17)
(17)
Диапазон
отклонений между полиномиальным вектором распознанного верно изображения
символа и «среднестатистическим» вектором этого символа по рассматриваемой базе
лежит от минимального х_true_min до максимального х_true_max. В
таблице 2 приведены значения этих величин для каждого из символов 0, 1, 2, 3,
4, 5, 6, 7, 8, 9.
Делим отрезок [х_true_min, х_true_max] (оси абсцисс на
рис.2в-11в) на 20 равных по длине частей – отрезок и 19 полуинтервалов: [х_true_min, х_true_min + хdv], (х_true_min + хdv, х_true_min + 2хdv], … ,
(х_true_min + 19хdv, х_true_min + 20хdv], где
хdv = (х_true_max – х_true_min)/20.
Затем для совокупности изображений, имеющих полиномиальные векторы, попадающие
в каждый такой участок, вычисляем среднюю оценку распознавания (оси ординат на
рис. 2в-11в). На этих рисунках видно, что средняя оценка
распознавания для каждого из рассматриваемых символов на
соответствующем этому символу отрезке [х_true_min, х_true_max] убывает монотонно (с
некоторыми шумовыми погрешностями) по мере «удаления» от «среднестатистического»
вектора, а для «1» сначала монотонно убывает,
а затем монотонно увеличивается и принимает максимальное значение 255 на
предпоследнем интервале удаления от «среднестатистического» вектора (также с
некоторыми погрешностями). Уровень шумов
в этих зависимостях существенно ниже, а, следовательно, степень монотонности
выше, чем в аналогичных зависимостях для средней оценки распознавания при
отклонении от «среднестатистического» растра.
На рис.2г-11г приведены диаграммы
- «дискретный» аналог функции распределения для распознанных верно изображений
каждого из символов 0, 1, … , 9. А именно, ось абсцисс такая же, как указано в
предыдущем абзаце для рис.2в-11в, а по оси ординат отложено количество
правильно распознанных изображений,
попавших в каждую вышеописанную двадцатую часть отрезка [х_true_min, х_true_max].
Диапазон отклонений между
полиномиальным вектором неправильно распознанного изображения символа и «среднестатистическим»
вектором этого символа по рассматриваемой базе находится от минимального х_false_min до
максимального х_false_max. В таблице 2 приведены значения
этих величин для каждого из символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Средние
оценки неправильного распознавания не приводятся, поскольку они, как нетрудно
догадаться, совпадают с указанными в таблице 1. Отметим, что для каждого из
рассматриваемых символов х_true_min < х_false_min. Тем
не менее, диапазон [х_true_min, х_true_max] отличается от [х_false_min, х_false_max] не очень существенно.
Следовательно, поскольку доля неправильно распознанных символов весьма незначительна,
«дискретный» аналог функции распределения для всех растров (распознанных как
верно, так и неверно) каждого из символов 0, 1, …, 9 мало отличается от приведенных
на рис.2г-11г.
Выше описаны результаты двух
типов: в терминах растров и полиномиальных
векторов. Возникает вопрос, как их сравнивать? Для каждого символа одни и те же
правильно распознанные изображения находятся в первом случае на отрезке [v_true_min, v_true_max], а
во втором на [х_true_min, х_true_max]. Предлагается идеология, основанная на
преобразовании соответствующей оси абсцисс координаты посредством выравнивания
по длине диапазонов отклонения растров / векторов правильно распознанных
изображений каждого из символов от «среднестатистических» растра / вектора данного
символа, а именно [v_true_min, v_true_max] и [х_true_min, х_true_max] . В
этих целях вводятся «отнормированные» (по величине соответствующего диапазона)
координаты.
Таблица 2
|
символ |
х_true_min |
х_true_max |
х_true_max/ х_true_min |
х_false_min |
х_false_max |
|
0 |
2004 |
5290
|
3,21
|
3002 |
5119 |
|
1 |
2416 |
7917 |
4,08 |
3046 |
6437 |
|
2 |
2237 |
5265 |
2,75 |
3491 |
5523 |
|
3 |
2276 |
4954 |
2,58 |
3026 |
4936 |
|
4 |
2798 |
5158 |
2,09 |
3135 |
5619 |
|
5 |
2104 |
6300 |
3,60 |
3142 |
4909 |
|
6 |
2416 |
5161 |
2,58 |
3375 |
4966 |
|
7 |
2324 |
5276 |
2,51 |
2913 |
5621 |
|
8 |
2679 |
5505 |
2,39 |
3335 |
5188 |
|
9 |
2559 |
5482 |
2,55 |
3076 |
5313 |
В таблице 1 приводятся
значения величины v_true_max/v_true_min, а в таблице 2 –
соответственно х_true_max/х_true_min. Сравнение показывает, что
для каждого из символов v_true_max/v_true_min > х_true_max/х_true_min. Следовательно,
как нетрудно показать, v_true_max/(v_true_max-v_true_min) < х_true_max/(х_true_max-х_true_min), а
также v_true_min/(v_true_max-v_true_min) <
х_true_min/(х_true_max-х_true_min). Эти два неравенства означают,
что если на одном луче отложить «отнормированные» координаты v_true/(v_true_max-v_true_min) и
х_true/(х_true_max-х_true_min), то v_true_max/(v_true_max-v_true_min)
будет находиться левее (ближе к началу луча), чем х_true_max/(х_true_max-х_true_min); аналогично, v_true_min/(v_true_max-v_true_min) будет левее (ближе к началу луча), чем х_true_min/(х_true_max-х_true_min). Точка 0 (начало луча)
соответствует «среднестатистическому»
растру / вектору. Следовательно, в
описанных «отнормированных» координатах для каждого из символов имеет место следующее:
величина удаления отрезка, на котором находятся растры правильно распознанных изображений, от «среднестатистического» растра меньше, чем
максимальное удаление отрезка векторов правильно распознанных изображений от «среднестатистического» вектора.
Сравним поведение оценки
распознавания при отклонении от «среднестатистического» растра (рис.2а-11а) и
вектора (рис.2в-11в). Как уже отмечалось, уровень шумов в
диаграммах с вектором существенно ниже, а, следовательно, степень
монотонности выше, чем в диаграммах с растром.
Для более детального
сопоставления совместим отрезки между минимальным и максимальным отклонениями
от «среднестатистических» растра [v_true_min, v_true_max] и полиномиального вектора [х_true_min, х_true_max]. Математически это можно представить так, что
точке с координатой v_true на
первом отрезке соответствует точка с координатой х_true=х_true_min+(v_true-v_true_min)·(х_true_max-х_true_min)/(v_true_max
- v_true_min). На рис.2д-11д точка 0 соответствует минимальному отклонению
от «среднестатистического» растра / вектора; здесь приведены графики,
построенные по соответствующим диаграммам (рис.2а-11а, рис.2в-11в). Вблизи точки 0 и до половины или до третьей
части (в зависимости от символа) величины максимального отклонения от 0 средняя оценка распознавания для вектора
выше, чем для растра. Для более отдаленных участков ситуация меняется на
противоположную (в некоторых случаях для максимально удаленных участках
указанная закономерность не выполнялось, но это неважно, т.к. количество
находящихся там символов ничтожно, как видно на рис.2б-11б, рис.2г-11г). Описанное поведение оценки распознавания
наблюдалось для всех символов, кроме «1».
Для «1» при увеличении
отклонения от 0 сначала наблюдалось уменьшениеоценки, а затем ее рост до
максимальной оценки 255 на наиболее удаленных участках. Возникла гипотеза о
том, что база единиц составлена из двух подбаз.
Дальнейшие действия были проделаны для
«среднестатистических» векторов, поскольку в использующих их зависимостях
уровень шумов существенно ниже, чем для «среднестатистических» растров. Найдя
первоначальное «среднестатистическое» значение полиномиального вектора х0, мы отделили ту часть изображений,
полиномиальные векторы которых удалены от соответствующего х_true_min
более чем на 2/3 величины х_true_max-х_true_min и построили для них «среднестатистическй»
вектор х1. Оказалось, что для изображений,
векторы которых к х1 ближе, чем к х0, при удалении от х1 оценка монотонно падает (рис.3з).
Всего оказалось 714 таких изображений. Для оставшихся 32388 изображений
построили новый среднестатистический вектор
х2, при отклонении от которого имела место аналогичная закономерность
(рис.3е). Для каждой из выделенных подбаз построили функции распределения
(соответственно рис.3и, рис.3ж), которые оказались схожи с функциями распределения
других символов. Дополнительные итерации, несомненно, улучшили бы степень
разделения подбаз.
Несмотря на то, что база
изображений «1», как удалось показать в результате численного эксперимента,
состоит из двух подбаз, каждая из которых имеет свой «среднестатистический»
вектор (также и растр, как нетрудно догадаться), тем не менее, исследуемый
метод распознавания, обученный на совокупности всех изображений «1», выставляет
оценки распознавания, поведение которых при удалении от каждого из этих двух
«среднестатистических» векторов не отличается от имеющего место для баз цифр 2,
3, 4, 5, 6, 7, 8, 9, обладающих одним
«среднестатистическим» вектором (и растром).
4. Выводы
Изучение метода распознавания,
основанного на полиномиальной регрессии, при распознавании рукопечатных цифр по
базе, совпадающей с базой обучения, для каждого из рассматриваемых символов
показало следующее.
Средняя оценка распознавания
для каждого из рассматриваемых символов убывает монотонно (с некоторыми
шумовыми погрешностями) по мере «удаления» от «среднестатистического» вектора,
а для «1» сначала монотонно убывает, а
затем монотонно увеличивается и принимает максимальное значение 255 на
предпоследнем интервале удаления от «среднестатистического» вектора (также с
некоторыми погрешностями). Уровень шумов
в этих зависимостях существенно ниже, а, следовательно, степень
монотонности выше, чем в зависимостях при отклонении от «среднестатистического»
растра.
Численный эксперимент
показал, что база единичных символов состоит из двух подбаз, каждая из которых
имеет свой «среднестатистический» вектор (и растр). Исследуемый метод
распознавания, обученный на совокупности всех изображений «1», выставляет
оценки распознавания, поведение которых при удалении от каждого из этих двух
«среднестатистических» векторов не отличается от имеющего место для баз остальных
цифр, обладающих одним «среднестатистическим»
вектором (и растром).
Для каждого из
рассматриваемых символов средние оценки неправильного распознавания намного
меньше (приблизительно в два раза), чем оценки правильного распознавания. Кроме
того, минимальная по рассматриваемой базе величина отклонения между
изображением символа и «среднестатистическим» растром (вектором) этого символа
для правильно распознанных растров меньше, чем для неправильно распознанных.
Литература
[1] Гавриков М.Б., Пестрякова Н. В.
"Метод полиномиальной регрессии в задачах распознавания печатных и
рукопечатных символов", //Препринт ИПМатем. АН СССР, М., 2004, №22, 12
стр.
[2] Гавриков М.Б., Пестрякова Н. В., Славин О.А,
Фарсобина В.В.. "Развитие метода полиномиальной регрессии и
практическое применение в задаче распознавания", //Препринт ИПМатем. АН
СССР, М., 2006, №25, 21 стр.
[3] Гавриков М.Б., Мисюрев А.В., Пестрякова
Н.В., Славин О.А. Развитие метода полиномиальной регрессии и практическое
применение в задаче распознавания символов. Автоматика и Телемеханика. 2006,
№3, С. 119-134.
[4] Гавриков М.Б., Пестрякова Н. В., Усков А.В.,
Фарсобина В.В. "О некоторых свойствах метода распознавания символов,
основанного на полиномиальной регрессии", //Препринт ИПМатем. АН СССР, М., 2004,
№22, 20 стр.
[5] Sebestyen
G.S. Decision Making Processes in
Pattern Recognition, MacMillan, New York, 1962.
[6] Nilson N. J. Learning
Machines, McGraw-Hill, New York, 1965.
[7] Schürmann J. Polynomklassifikatoren, Oldenbourg, München, 1977.
[8] Schürmann J. Pattern Сlassification,
John Wiley&Sons, Inc., 1996.
[9] Albert
A.E. and Gardner L.A. Stochastic
Approximation and Nonlinear Regression // Research Monograph 42. MIT Press,
Cambridge, MA, 1966.
[10] Becker
D. and Schürmann J. Zur
verstärkten Berucksichtigung schlecht erkennbarer Zeichen in der
Lernstichprobe // Wissenschaftliche Berichte AEG-Telefunken 45, 1972, pp. 97 – 105.
[11] Pao
Y.-H. The Functional Link Net:
Basis for an Integrated Neural-Net Computing Environment // in Yoh-Han Pao
(ed.) Adaptive Pattern Recognition and Neural Networks, Addisson-Wesley,
Reading, MA, 1989, pp. 197-222.
[12] Franke
J. On the Functional Classifier, in
Association Francaise pour la Cybernetique Economique et Technique (AFCET),
Paris // Proceedings of the First International Conference on Document Analysis
and Recognition, St. Malo, 1991, pp.481-489.
[13]
Дж.Себер. Линейный регрессионный анализ. М.:”Мир”, 1980.
[14]
Ю.В.Линник. Метод наименьших квадратов и основы математико - статистической
теории обработки наблюдений. М.:”Физматлит”, 1958.
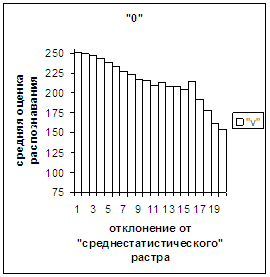
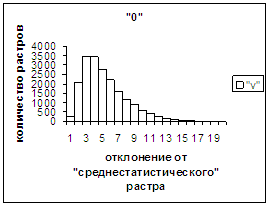
Рис. 2а
Рис. 2б
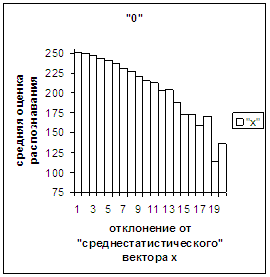
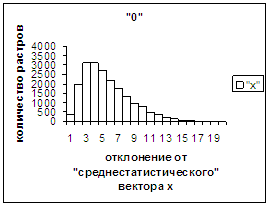
Рис. 2в
Рис. 2г
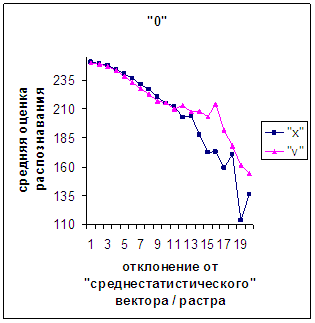
Рис. 2д
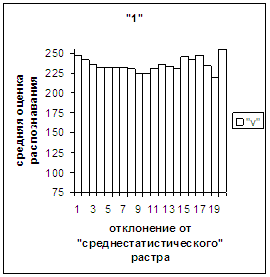
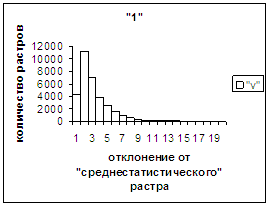
Рис. 3а
Рис. 3б
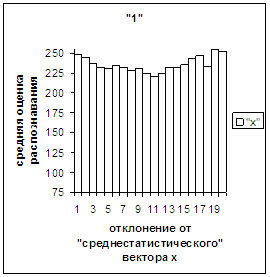
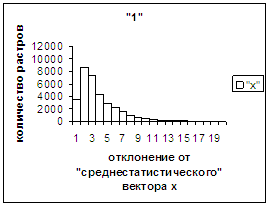
Рис. 3в
Рис. 3г
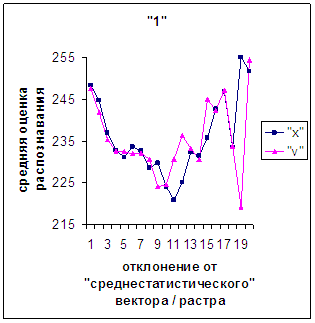
Рис. 3д
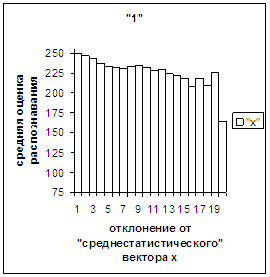
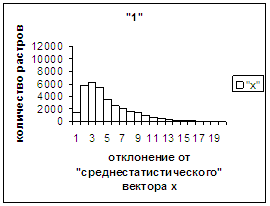
Рис. 3е
Рис. 3ж
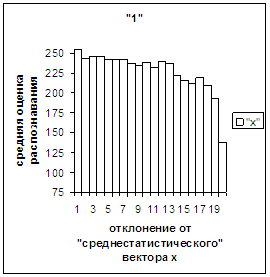
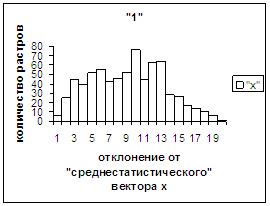
Рис. 3з
Рис. 3и
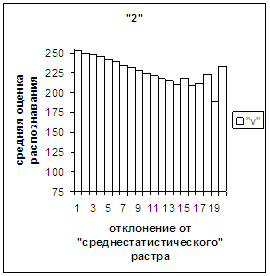
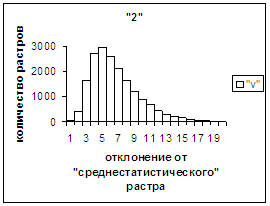
Рис. 4а
Рис. 4б
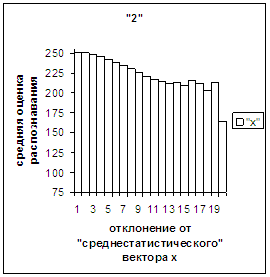
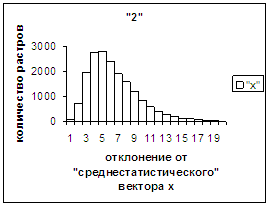
Рис. 4в
Рис. 4г
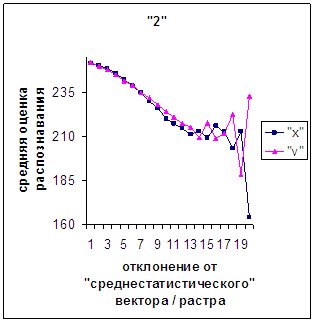
Рис. 4д
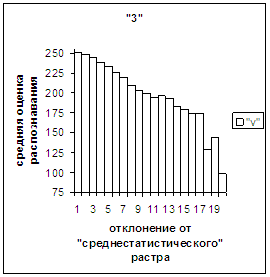
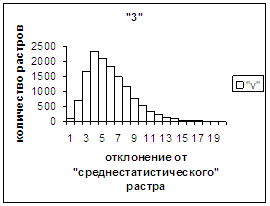
Рис. 5а
Рис. 5б
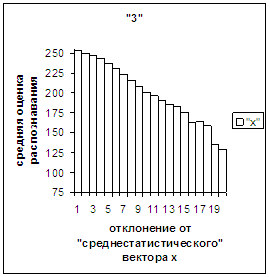
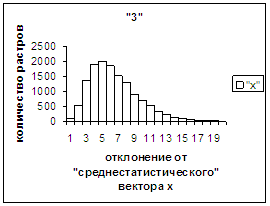
Рис. 5в
Рис. 5г
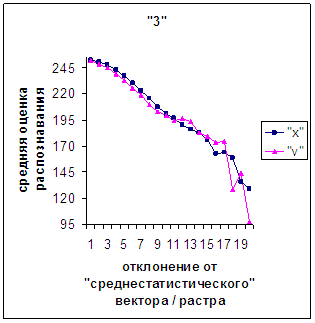
Рис. 5д
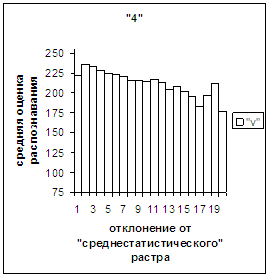
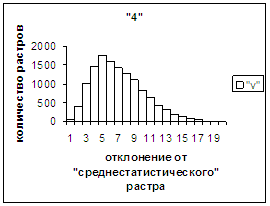
Рис. 6а
Рис. 6б
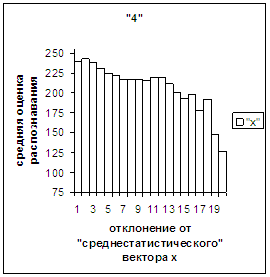
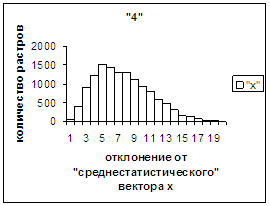
Рис. 6в
Рис. 6г
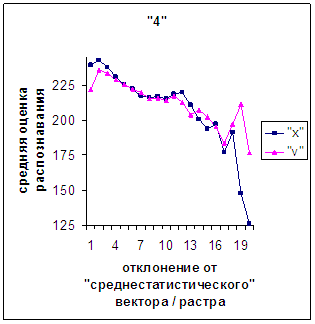
Рис. 6д
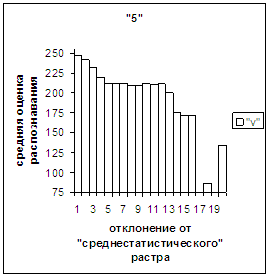
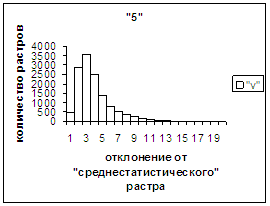
Рис. 7а
Рис. 7б
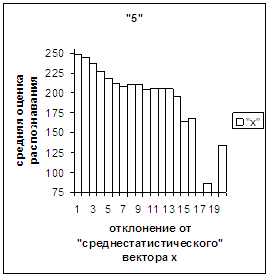
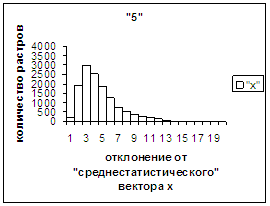
Рис. 7в
Рис. 7г
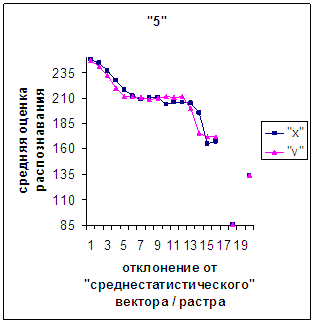
Рис. 7д
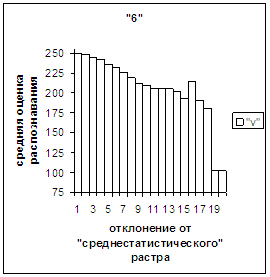
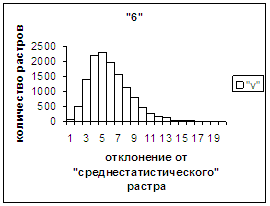
Рис. 8а
Рис. 8б
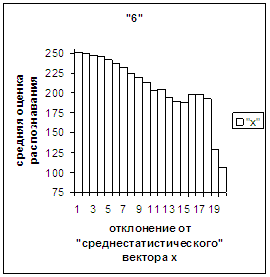
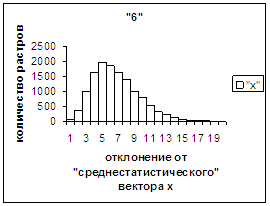
Рис. 8в
Рис. 8г
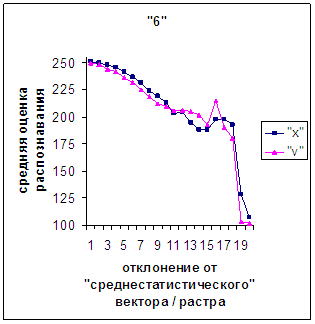
Рис. 8д
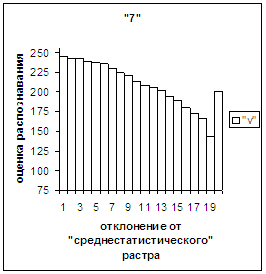
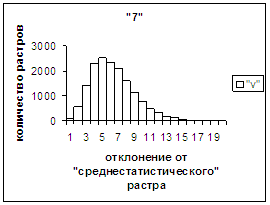
Рис. 9а
Рис. 9б
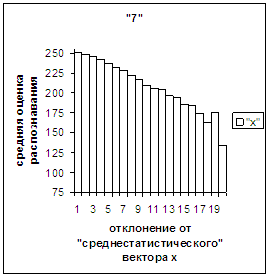
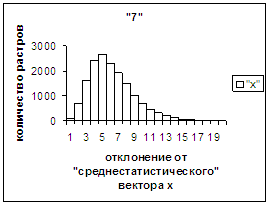
Рис. 9в
Рис. 9г
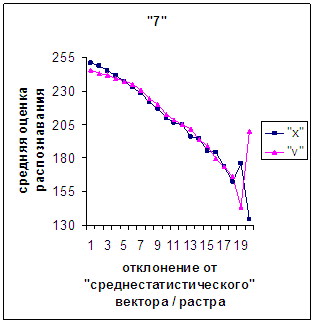
Рис. 9д
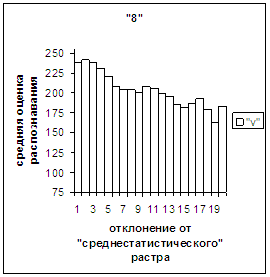
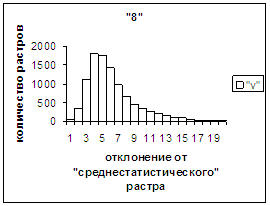
Рис. 10а
Рис. 10б
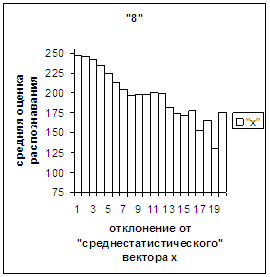
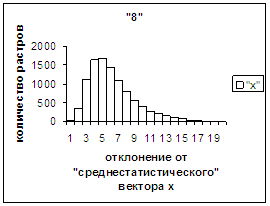
Рис. 10в
Рис. 10г
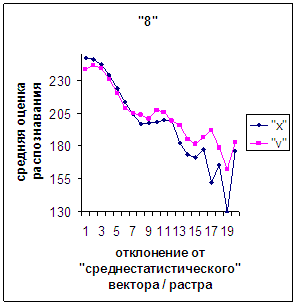
Рис. 10д
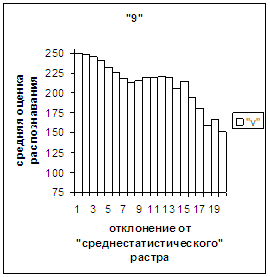
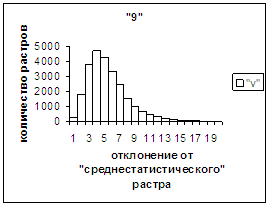
Рис. 11а
Рис. 11б
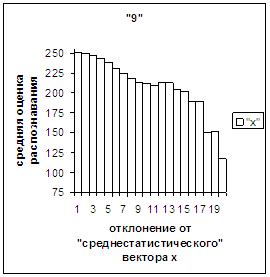
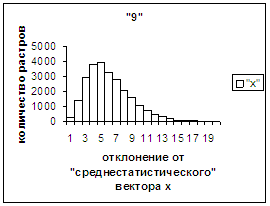
Рис. 11в
Рис. 11г
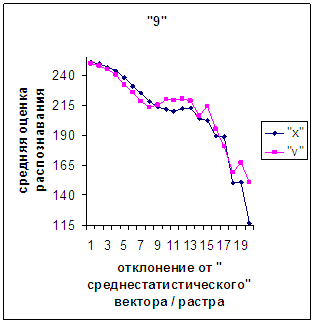
Рис. 11д
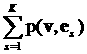
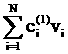 +
+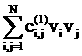 +…
+…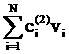 +
+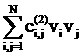 +…
+… +
+ +…
+…
 ]1
]1 ]1
]1