Аннотация
Для системы уравнений многокомпонентной, многофазной фильтрации рассмотрена вычислительная методология, основывающаяся
на понятии «стримлайн» (англ. streamline). Это понятие, как и методология, опирается на существование в реальных
течениях эффекта выделенных направлений, когда основное течение смеси в пласте происходит вдоль некоторых линий,
подобных линиям тока в обычной гидродинамике. Такие линии тока и называются «стримлайнами». Показано, что обычно
используемые операции с этим понятием, как правило, содержат неявные предположения, что затрудняет оценку точности
метода. Приведена новая геометрическая формулировка для понятия «стримлайн», которая является в некотором смысле
«строгой». Продемонстрировано, как с помощью этой геометрической формулировки можно подойти к проблеме оценки точности
методологии «стримлайн».
Abstract
For the system of equations of multi-component, multi-phase filtration the calculation procedure, which is based
on the notion of ‘streamline’, is considered. This notion as well as the methodology has in mind the presence in
real flows of the effect of specific directions when the main flow of the mixture in the reservoir takes place along
some curves that are similar to streamlines in ordinary hydrodynamics. It is shown that conventional application of
this notion, as a rule, contains implicit assumptions. These assumptions make difficult the assessment of the accuracy
of the method. New geometric interpretation of ‘streamline’ concept is shown. Such interpretation can be considered
as in a sense rigorous. It is also demonstrated how one can approach the accuracy assessment problem for ‘streamline’
methodology with the help of geometric formulation.
Введение
В последнее время в области моделирования процессов
добычи углеводородов на месторождениях значительно усилился интерес к так называемой
методологии «стримлайн». Эта методология представляет собой приближенный способ
решения трехмерной системы уравнений, вообще говоря, многокомпонентной,
многофазной, фильтрации с учетом фазовых переходов. Как хорошо известно, эта
система уравнений основывается на соответствующих системах уравнений
гидродинамического типа, выписываемых для каждой компоненты смеси. При этом,
часто, лишь уравнения неразрывности выписываются в полном объеме. Уравнения
сохранения импульса заменяются экспериментальным законом фильтрации Дарси, а
уравнения для энергии игнорируются, т.к. в первом приближении можно считать,
что температура пласта остается постоянной. В более общей постановке уравнения
закона сохранения энергии выписываются, а также учитывается гравитация и другие
физические процессы, например, действие капиллярных сил, учет трещиноватости
(модель двойной пористости), дисперсионных эффектов (куда включается и
диффузия), взаимодействия смеси с породой (геомеханика) и т.п. Описание общих
принципов моделирования процессов фильтрации можно найти, например, в книгах
[1], [7].
«Стримлайн» методология, краткое описание основ
которой мы приведем ниже, замечательна тем, что сводит решение трехмерной
задачи к решению набора одномерных задач и таким образом значительно уменьшает
время, требуемое для расчетов. При этом необходимо делать некоторые допущения,
которые, вообще говоря, приводят к уменьшению точности, т.к. при этом мы
несколько изменяем исходную систему уравнений. Однако опыт численного
моделирования показывает, что эти изменения слабо влияют на результаты
расчетов. Многочисленные сравнения с традиционными коммерческими
конечно-разностными симуляторами продемонстрировали достаточную точность
методологии «стримлайн» и значительное сокращение времени расчета, которое ей
достигается, см., например, для разных реализаций этой методологии работы [5],
[6], [11]. В данной работе мы не освещаем историю вопроса и не претендуем на
полноту цитирования и ниже дополнительно приводим несколько ссылок на работы в
этой области только лишь для того, чтобы можно было составить некоторое
представление о существе вопроса. Литература по методологии «стримлайн»
чрезвычайно обширна, заинтересованный читатель может познакомиться, например, с
публикациями Society of Petroleum Engineers (SPE), ссылка на их сайт www.spe.org.
Экономия расчетного времени, о которой мы упомянули
выше, позволяет приступить к задачам моделирования процессов нефтедобычи на
больших месторождениях и с достаточной степенью подробности. При этом, чтобы
получить реалистичные результаты, необходимо учитывать и сжимаемость смеси, и
сложность ее состава. В то же время встает вопрос об оценке реальной точности
расчетов. Дело осложняется тем, что, насколько известно автору, «строгого» описания
методологии «стримлайн» в сжимаемом случае все-таки не существует (ниже
мы процитируем и опишем некоторые работы в этом направлении). Под термином
«строгое» мы понимаем ситуацию, когда мы можем точно сказать, чем именно мы
пренебрегаем и какую ошибку привносим. Настоящая работа является попыткой
заполнить этот пробел и предоставить строгое описание методологии «стримлайн»
на основе геометрического подхода в случае сжимаемых, многокомпонентных
смесей с фазовыми переходами. При этом, для более ясного изложения идей, мы
будем использовать в некотором смысле «простейшую нетривиальную» модель
фильтрации в случае могокомпонентных смесей, т.е. не будем учитывать влияния
гравитации, капиллярных сил, дисперсионных эффектов, трещиноватости,
геомеханики и т.п. Также мы не будем рассматривать изменений энергии и считать
температуру резервуара постоянной величиной. Как представляется автору на
настоящий момент, включение в постороения всех указанных выше обобщений не
несет принципиальных затруднений. Мы намерены осуществить это в последующих
публикациях.
Далее в §1 приводится общая формулировка рассматриваемой
системы уравнений многофазной многокомпонентной фильтрации в пористой среде и
делаются замечания о ее связи с наиболее часто рассматриваемой системой
многофазной фильтрации, т.е. без учета компонентного состава (заметим, что в
последней системе число уравнений равно числу фаз, тогда как в рассматриваемой
нами – числу компонент). В §2 рассматривается понятие «стримлайн» в том виде,
как оно присутствует в современной литературе, а в §3 это понятие трактуется на
основе геометрического подхода. Как оказывается, традиционный подход
основывается все же на некоторых дополнительных предположениях, которые, как
правило, остаются как бы «за кадром». Наконец, в §4 описывается вычислительный
аспект излагаемого геометрического подхода. Показано, что при его
последовательном применении можно проследить и количественно оценить все
возникающие приближения и невязки. Также приводятся примеры возможных
вычислительных стратегий при применении методологии «стримлайн».
§1.
Общая формулировка системы уравнений многофазной многокомпонентной фильтрации в
пористой среде в простейшем случае
Рассмотрим некоторую смесь веществ, которая содержит 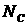 компонент, (например, как
в случае нефтегазовых месторождений, смесь углеводородов, воды и разнообразных
примесей, включая азот, углекислый газ и сероводород) и которая может иметь,
вообще говоря, компонент, (например, как
в случае нефтегазовых месторождений, смесь углеводородов, воды и разнообразных
примесей, включая азот, углекислый газ и сероводород) и которая может иметь,
вообще говоря, 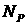 фаз. Записывая
уравнения сохранения массы для каждого компонента, получим следующую систему
уравнений фильтрации (для более подробного вывода всех определяющих уравнений
см., например, книгу [7]) фаз. Записывая
уравнения сохранения массы для каждого компонента, получим следующую систему
уравнений фильтрации (для более подробного вывода всех определяющих уравнений
см., например, книгу [7])
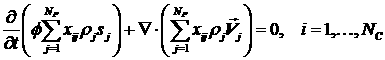 . (1.1) . (1.1)
Здесь
индексы 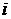 и и 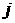 относятся к номеру
компоненты и фазы соответственно; относятся к номеру
компоненты и фазы соответственно; 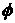 представляет собой
пористость; представляет собой
пористость; 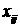 являются равновесными
молярными концентрациями компонента с номером являются равновесными
молярными концентрациями компонента с номером 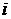 в фазе с номером в фазе с номером 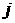 и и
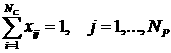 ; (1.2) ; (1.2)
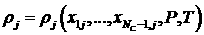 есть молярная
плотность есть молярная
плотность 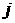 -ой фазы, -ой фазы, 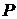 – давление, – давление, 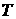 – температура; – температура; 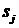 представляет собой насыщенность представляет собой насыщенность 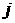 -ой фазы, причем -ой фазы, причем
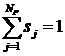 , (1.3) , (1.3)
и,
наконец, 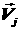 – скорость фильтрации – скорость фильтрации 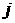 -ой фазы. Плотности фаз -ой фазы. Плотности фаз 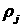 вычисляются на основе термодинамических уравнений состояния.
Равновесные концентрации вычисляются на основе термодинамических уравнений состояния.
Равновесные концентрации 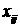 дополнительно связаны
между собой через термодинамические условия равновесия (равенство химических
потенциалов компонент, которые также определяются через соответствующее
уравнение состояния). Термодинамическое описание, скажем, смесей, с которыми
имеют дело в процессах нефтедобычи, см., например, в книге [3]. дополнительно связаны
между собой через термодинамические условия равновесия (равенство химических
потенциалов компонент, которые также определяются через соответствующее
уравнение состояния). Термодинамическое описание, скажем, смесей, с которыми
имеют дело в процессах нефтедобычи, см., например, в книге [3].
Система уравнений (1.1) дополняется
законом фильтрации Дарси (как заменой уравнений сохранения импульса)
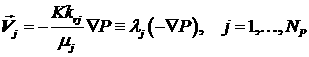 , (1.4) , (1.4)
где 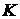 представляет собой так
называемую абсолютную проницаемость; представляет собой так
называемую абсолютную проницаемость; 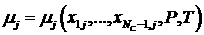 является коэффициентом
вязкости является коэффициентом
вязкости 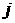 -ой фазы (также вычисляется на основе уравнения состояния); -ой фазы (также вычисляется на основе уравнения состояния); 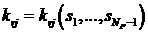 есть относительная
проницаемость есть относительная
проницаемость  -ой фазы (как правило, определяется на основе
экспериментальных корреляций); -ой фазы (как правило, определяется на основе
экспериментальных корреляций);  и и 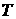 – соответственно
давление и температура. Также отметим, что – соответственно
давление и температура. Также отметим, что 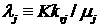 называется
подвижностью фазы называется
подвижностью фазы 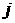 . Напомним, что в настоящем препринте температура . Напомним, что в настоящем препринте температура 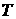 считается постоянной и
фактически является параметром. Поэтому в дальнейшем мы не будем рассматривать
зависимость от температуры. считается постоянной и
фактически является параметром. Поэтому в дальнейшем мы не будем рассматривать
зависимость от температуры.
Заметим, что если в системе (1.1), (1.4) формально
положить 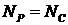 и и 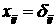 , где , где 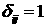 при при 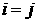 и и 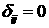 при при 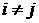 (символ Кронекера), то
мы получим обычную систему многофазной фильтрации без учета компонентного
состава смеси (символ Кронекера), то
мы получим обычную систему многофазной фильтрации без учета компонентного
состава смеси
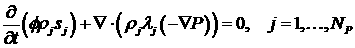 . (1.5) . (1.5)
Объединим теперь уравнения (1.1) и (1.4), так что наша
система уравнений приобретет следующую форму
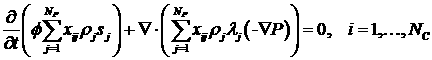 . (1.6) . (1.6)
Просуммировав в (1.6) по индексу 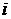 и учитывая (1.2),
получим следующее уравнение и учитывая (1.2),
получим следующее уравнение
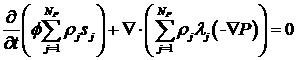 , (1.7) , (1.7)
которое
интересно тем, что не содержит в явной форме равновесных концентраций 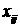 . Ввиду этого свойства уравнение (1.7), или его аппроксимации
и обобщения играют важную роль в методологии «стримлайн», к изложению основ
которой мы сейчас перейдем. . Ввиду этого свойства уравнение (1.7), или его аппроксимации
и обобщения играют важную роль в методологии «стримлайн», к изложению основ
которой мы сейчас перейдем.
Итак, исходную систему уравнений (1.1), (1.4) можно
заменить системой, состоящей из уравнений (1.6), где 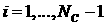 (выкинуть можно любое
из уравнений (1.6)), и уравнения (1.7). (выкинуть можно любое
из уравнений (1.6)), и уравнения (1.7).
§2. Происхождение понятия
«стримлайн» (streamline), его связь с математической
формой основной системы уравнений
Исторически изучение систем уравнений типа (1.5) или
(1.6), (1.7) начиналось с упрощающего предположения о несжимаемости фаз
(например, так называемая модель Баклея-Леверетта). Если дополнительно
предположить, что плотности всех фаз равны, то уравнение (1.7), с учетом (1.3),
преобразуется следующим образом
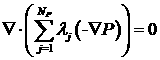 . (2.1) . (2.1)
С учетом уравнения (2.1) система (1.6) превращается
в следующую
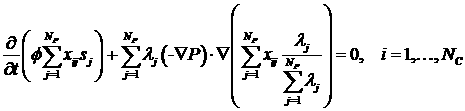 . (2.2) . (2.2)
То есть в терминах вектора скорости  уравнения (2.1), (2.2)
выглядят так уравнения (2.1), (2.2)
выглядят так
 . (2.3) . (2.3)
Второе уравнение в (2.3), кроме дифференцирования по
времени содержит дифференцирование лишь по одному пространственному
направлению 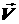 , которое определяется первым уравнением в (2.3). В этом
смысле наша исходная трехмерная система уравнений расщепилась на серию
одномерных задач вдоль поля направлений, задаваемого вектором , которое определяется первым уравнением в (2.3). В этом
смысле наша исходная трехмерная система уравнений расщепилась на серию
одномерных задач вдоль поля направлений, задаваемого вектором 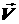 . Этот вектор задает направление потока жидкости (англ. streamline).
На уровне численного алгоритма мы можем действовать методом расщепления и
определить сначала направления потока – стримлайны, – исходя из первого
уравнения в (2.3) (оно будет, вообще говоря, эллиптическим по отношению к
давлению), а затем решить серию одномерных задач вдоль стримлайнов. Заметим
также, что в данном случае, вообще говоря, нельзя считать, что стримлайны не
зависят от времени, т.к. в уравнения (2.2) для эволюции насыщенностей . Этот вектор задает направление потока жидкости (англ. streamline).
На уровне численного алгоритма мы можем действовать методом расщепления и
определить сначала направления потока – стримлайны, – исходя из первого
уравнения в (2.3) (оно будет, вообще говоря, эллиптическим по отношению к
давлению), а затем решить серию одномерных задач вдоль стримлайнов. Заметим
также, что в данном случае, вообще говоря, нельзя считать, что стримлайны не
зависят от времени, т.к. в уравнения (2.2) для эволюции насыщенностей 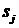 входит их производная по времени, а уравнение (2.1) для
определения стримлайнов содержит величины насыщенностей. входит их производная по времени, а уравнение (2.1) для
определения стримлайнов содержит величины насыщенностей.
Следуя
[2], можно придать системе (2.3) немного другую форму. Правда, строго говоря,
эта форма справедлива только при условии стационарности стримлайнов
(что, вообще говоря, неверно). Однако, сначала просто приведем эту форму
системы (2.3) без комментариев ввиду ее популярности. Пользуясь свойством
бездивергентности поля 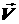 , можно ввести две функции тока (англ. bi-streamfunctions) , можно ввести две функции тока (англ. bi-streamfunctions)  и и 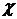 так, что так, что 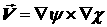 . При этом сам стримлайн будет получаться как пересечение
двух поверхностей . При этом сам стримлайн будет получаться как пересечение
двух поверхностей 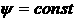 и и 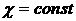 . Если вдоль каждого стримлайна ввести еще координату . Если вдоль каждого стримлайна ввести еще координату 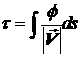 (интегрирование
ведется вдоль самого стримлайна), то уравнения (2.3) приводятся к виду
(отметим, что пористость (интегрирование
ведется вдоль самого стримлайна), то уравнения (2.3) приводятся к виду
(отметим, что пористость 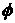 является, как правило,
функцией только от пространственных переменных) является, как правило,
функцией только от пространственных переменных)
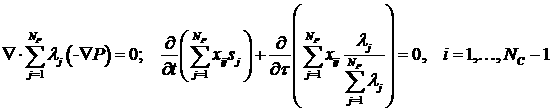 . (2.4) . (2.4)
Координату  часто называют
«координатой времени полета» (англ. time of flight), т.к. фактически величина часто называют
«координатой времени полета» (англ. time of flight), т.к. фактически величина 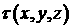 представляет собой
время, затрачиваемое некоторой частицей смеси, для того, чтобы достичь заданной
точки представляет собой
время, затрачиваемое некоторой частицей смеси, для того, чтобы достичь заданной
точки  пространства, двигаясь
вдоль подходящего стримлайна. Часто считается, что функции пространства, двигаясь
вдоль подходящего стримлайна. Часто считается, что функции 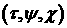 представляют собой
замену координат, в которых система (1.6) записывается в форме (2.4). представляют собой
замену координат, в которых система (1.6) записывается в форме (2.4).
Теперь же обратим внимание
на тот факт, что описанный способ получения системы (2.4) на самом деле
опирается на предположение о неподвижности стримлайна. Однако, поле 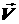 зависит от времени
(хотя в явной форме время не входит в уравнения (2.3)), т.е. сам стримлайн (как
кривая в пространстве) будет изменяться со временем. Тогда и система координат зависит от времени
(хотя в явной форме время не входит в уравнения (2.3)), т.е. сам стримлайн (как
кривая в пространстве) будет изменяться со временем. Тогда и система координат 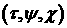 , вообще говоря, зависит от времени. То есть системы
уравнений (2.3) и (2.4) не эквивалентны и переход от (2.3) к (2.4) уже содержит
некоторую ошибку, связанную с нестационарностью (заметим, что оценить вносимую
ошибку довольно сложно – для этого надо, не решая задачи численно, априорно
оценить, насколько стримлайны действительно стационарны). Кроме того, вообще
говоря, другим эффектом нестационарности является то, что , вообще говоря, зависит от времени. То есть системы
уравнений (2.3) и (2.4) не эквивалентны и переход от (2.3) к (2.4) уже содержит
некоторую ошибку, связанную с нестационарностью (заметим, что оценить вносимую
ошибку довольно сложно – для этого надо, не решая задачи численно, априорно
оценить, насколько стримлайны действительно стационарны). Кроме того, вообще
говоря, другим эффектом нестационарности является то, что  не обязан быть
параллельным не обязан быть
параллельным 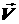 , то есть система координат , то есть система координат 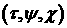 не обязана быть
ортогональной, а значит преобразования векторов в этой системе координат могут
выглядеть более сложно, и это преобразование координат не обязательно приведет
к виду (2.4). В следующем параграфе мы разовьем подробнее тему замены координат
и продемонстрируем, к какому виду системы уравнений может приводить такая
замена. не обязана быть
ортогональной, а значит преобразования векторов в этой системе координат могут
выглядеть более сложно, и это преобразование координат не обязательно приведет
к виду (2.4). В следующем параграфе мы разовьем подробнее тему замены координат
и продемонстрируем, к какому виду системы уравнений может приводить такая
замена.
Изложенный подход авторы работ [4], [9] обобщали и на
случай сжимаемых смесей (правда, без учета многокомпонентности). В этом случае
уравнения (1.5) можно также переписать в форме (2.4) (предположение о
неподвижности стримлайна сохраняется), однако при этом уравнение 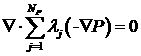 перейдет в некоторое
параболическое уравнение относительно перейдет в некоторое
параболическое уравнение относительно 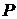 , и во всей системе (2.4) возникнут источниковые члены.
Далее, скорость фильтрации уже не является бездивергентным вектором и, чтобы
контролировать изменение объема при движении вдоль стримлайна, приходится
вводить некоторую искусственную эффективную плотность , и во всей системе (2.4) возникнут источниковые члены.
Далее, скорость фильтрации уже не является бездивергентным вектором и, чтобы
контролировать изменение объема при движении вдоль стримлайна, приходится
вводить некоторую искусственную эффективную плотность 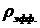 так, чтобы так, чтобы  . Здесь мы не будем останавливаться на дальнейших
предположениях, которые фактически делаются для того, чтобы получить обобщение
системы (2.4) на случай сжимаемых смесей. Отметим лишь, что в целом работы [4],
[9] придерживаются «идеологии несжимаемого случая». . Здесь мы не будем останавливаться на дальнейших
предположениях, которые фактически делаются для того, чтобы получить обобщение
системы (2.4) на случай сжимаемых смесей. Отметим лишь, что в целом работы [4],
[9] придерживаются «идеологии несжимаемого случая».
Ниже мы предлагаем несколько иной подход к проблеме
сжимаемости, который целиком основывается на геометрической интерпретации и
позволяет строго получить уравнения типа (2.4). Далее можно пытаться
отбрасывать какие-то части этих уравнений, чтобы получить более удобную
систему, но теперь мы всегда будем знать, какие члены мы отбрасываем и как
можно пытаться оценить величину вносимой ошибки.
§3. Геометрическая природа
понятия «стримлайн». Преобразование исходной системы уравнений на основе замены
координат
Для того, чтобы более выпукло представить
математическую структуру исходной системы уравнений в форме (1.6), мы
последовательно будем использовать возникшее ранее соображение о замене
координат. А именно, давайте формально введем новую ортогональную
систему координат 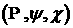 в трехмерном
пространстве в трехмерном
пространстве 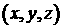 (время (время 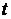 будет играть роль
параметра) по формулам будет играть роль
параметра) по формулам
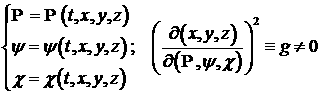 . (3.1) . (3.1)
Легко проверить, что
справедливы следующие соотношения
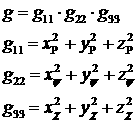 . .
Для
преобразования векторов будем рассматривать физические координаты. Тогда
являются хорошо известными выражения для вида градиента произвольного скаляра  и дивергенции
произвольного вектора и дивергенции
произвольного вектора 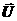 в системе координат
(3.1) в системе координат
(3.1)
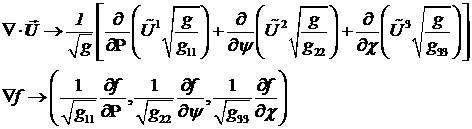 . (3.2) . (3.2)
Используя формулы (3.2), слагаемые, входящие в
систему (1.6), можно переписать в новой системе координат (3.1)
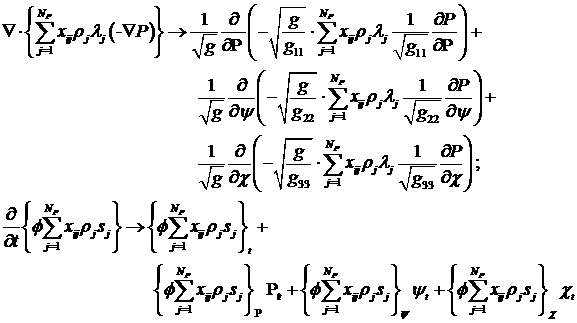 .(3.3) .(3.3)
Смысл произведенной замены
координат состоит в следующем. Пусть мы каким-либо образом угадали координатную
функцию  так, что так, что  . Это означает, что функция . Это означает, что функция 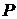 зависит только от зависит только от 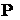 и в (3.3) и в (3.3) 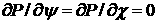 . То есть система (1.6) тогда будет выглядеть так . То есть система (1.6) тогда будет выглядеть так
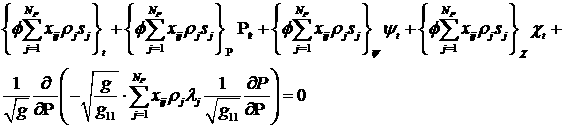 . (3.4) . (3.4)
В случае несжимаемой среды
(все 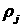 постоянны и совпадают между собой, см. §2), суммируя в (3.4) по индексу постоянны и совпадают между собой, см. §2), суммируя в (3.4) по индексу 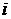 , находим , находим
 . (3.5) . (3.5)
Подставляя (3.5) в (3.4) окончательно получаем
 . (3.6) . (3.6)
Система (3.5), (3.6) является точной записью формы
(2.4), если выбрать замену координат (3.1) так, что 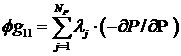 , то , то 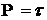 и мы получим (2.4), но
с добавкой дополнительных членов, выражающих собой нестационарность
стримлайнов. и мы получим (2.4), но
с добавкой дополнительных членов, выражающих собой нестационарность
стримлайнов.
Как
легко видеть, точная форма (3.6), которая сейчас, заметим, выписана только для
несжимаемого случая, не очень удобна для практического применения, ввиду
присутствия «нестационарных» членов. Поэтому давайте возьмем замену координат
(3.1) не зависящей от времени (все равно, как мы видели, и в классическом
стримлайн-подходе имеет место предположение о неподвижности стримлайнов). Тогда
мы уже не можем, вообще говоря, предполагать, что 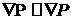 , но зато мы избавимся от «нестационарных» членов, т.е. будем
иметь вместо (3.4) , но зато мы избавимся от «нестационарных» членов, т.е. будем
иметь вместо (3.4)
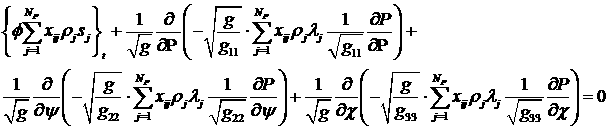 . .
(3.7)
Заметим, что, получая (3.7), мы пока не сделали
никаких дополнительных предположений, и система (3.7) является строгим
следствием системы (1.6) и замены координат (3.1). Если далее следовать
методологии «стримлайн», то мы должны еще получить уравнение для давления, это
можно сделать стандартными методами, суммируя уравнения в (3.7) по индексу 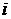 , или используя уравнение (1.7) в декартовых координатах.
Таким путем это уравнение получают и в [4], [9]. , или используя уравнение (1.7) в декартовых координатах.
Таким путем это уравнение получают и в [4], [9].
Итак,
до настоящего момента мы не сделали никаких дополнительных предположений
относительно исходной системы (1.6) и привели эту систему к форме (3.7) с
помощью некоторой замены координат. В следующем параграфе мы уже будем иметь
ввиду, что, вообще говоря, с точки зрения приложений, мы рассматриваем систему
(3.7) на некотором малом временном интервале 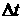 , который является шагом некоторой вычислительной
методологии, используемой для решения системы (1.6) в форме (3.7). Принимая это
во внимание, мы будем преобразовывать и изменять систему (3.7), чтобы привести
ее к более удобному для вычислений виду. При этом, мы всегда будем знать, какие
члены мы отбрасываем и какие выражения нужно оценивать для получения вносимых
ошибок. , который является шагом некоторой вычислительной
методологии, используемой для решения системы (1.6) в форме (3.7). Принимая это
во внимание, мы будем преобразовывать и изменять систему (3.7), чтобы привести
ее к более удобному для вычислений виду. При этом, мы всегда будем знать, какие
члены мы отбрасываем и какие выражения нужно оценивать для получения вносимых
ошибок.
§4. Об использовании
численной методологии «стримлайн» для решения преобразованной системы уравнений
Итак,
следуя обычной для стримлайн-методологии процедуре, получим уравнение для давления из (3.7) путем
суммирования по индексу 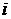
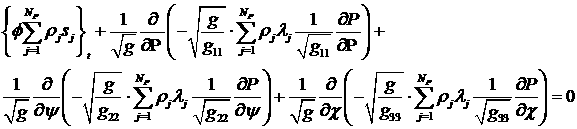 . (4.1) . (4.1)
Однако, уравнение (4.1) не является удобной формой
уравнения для давления, поскольку содержит величины 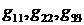 , которые представляется затруднительным оценить априорно.
Поэтому мы будем использовать уравнение для давления в обычной форме (1.7) в
декартовых координатах. Для более ясного представления о структуре уравнения
для давления (1.7) перейдем в системе (1.6), , которые представляется затруднительным оценить априорно.
Поэтому мы будем использовать уравнение для давления в обычной форме (1.7) в
декартовых координатах. Для более ясного представления о структуре уравнения
для давления (1.7) перейдем в системе (1.6),  , (1.7), как это обычно делается, к новым зависимым
переменным. А именно, введем новые переменные , (1.7), как это обычно делается, к новым зависимым
переменным. А именно, введем новые переменные 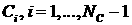 по формуле по формуле
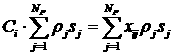 . (4.2) . (4.2)
Тогда функции 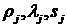 зависят от переменных зависят от переменных 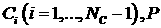 и уравнение (1.7)
можно записать в форме и уравнение (1.7)
можно записать в форме
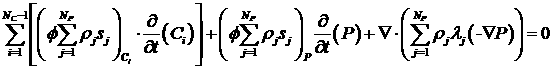 . (4.3) . (4.3)
При этом в переменных (4.2) уравнения (1.6) будут
выглядеть так
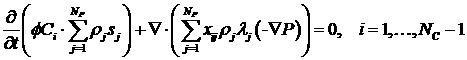 , (4.4) , (4.4)
где функции 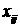 также зависят от также зависят от 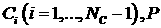 . Из системы уравнений (4.4), вообще говоря, можно выразить
производные . Из системы уравнений (4.4), вообще говоря, можно выразить
производные 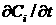 и подставить в (4.3). Тогда (4.3) превращается в уравнение
параболического типа для давления и подставить в (4.3). Тогда (4.3) превращается в уравнение
параболического типа для давления 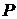 . .
Здесь мы не будем обсуждать
способа решения уравнения (4.3), а также возможности его упрощения с помощью
отбрасывания «не важных» членов. Будем считать, что мы умеем решать уравнение
(4.3) или его аппроксимации. Пусть 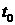 – это некоторый
произвольный момент времени, в который поле
давления уже известно. Выбирая в качестве – это некоторый
произвольный момент времени, в который поле
давления уже известно. Выбирая в качестве 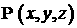 такую функцию, чтобы такую функцию, чтобы 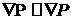 в момент времени в момент времени 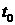 (при определенных
условиях можно выбрать и саму функцию давления), определим замену координат (3.1) (ниже мы более подробно остановимся
на этой процедуре). Теперь из (4.3), зная все интересующие нас функции в
некоторый момент времени (при определенных
условиях можно выбрать и саму функцию давления), определим замену координат (3.1) (ниже мы более подробно остановимся
на этой процедуре). Теперь из (4.3), зная все интересующие нас функции в
некоторый момент времени 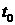 , мы получаем значения давления , мы получаем значения давления 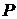 в последующий момент
времени в последующий момент
времени 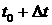 . Далее, мы можем оценить величины последних двух членов в
(3.7), содержащих производные . Далее, мы можем оценить величины последних двух членов в
(3.7), содержащих производные  и и 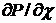
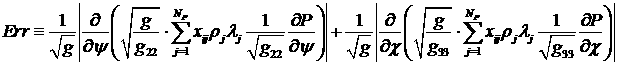 . (4.5) . (4.5)
При этом нам
представляется достаточным характеризовать ошибку (4.5) поведением функций
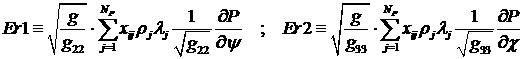 . (4.6) . (4.6)
Опишем
сначала, что получится, если допустить, что ошибка (4.5) мала, т.е. функции 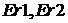 из (4.6) близки к
постоянным. Фактически, это будет означать, что сами стримлайны действительно
можно рассматривать как неизменяющиеся по сравнению с другими величинами в
течение малого шага по времени от из (4.6) близки к
постоянным. Фактически, это будет означать, что сами стримлайны действительно
можно рассматривать как неизменяющиеся по сравнению с другими величинами в
течение малого шага по времени от 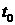 до до 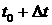 . Тогда система
уравнений (3.7) преобразуется к виду . Тогда система
уравнений (3.7) преобразуется к виду
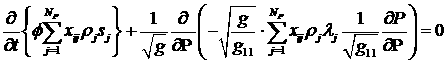 . (4.7) . (4.7)
Дадим некоторые общие геометрические интерпретации
выражений, входящих в (4.7). Для этого перепишем (4.7) несколько более подробно
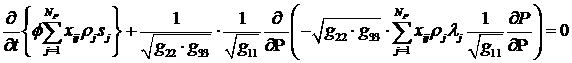 (4.8) (4.8)
и заметим, что 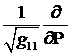 представляет собой
дифференцирование вдоль стримлайна в натуральной параметризации (параметризация
кривой длиной ее дуги), а представляет собой
дифференцирование вдоль стримлайна в натуральной параметризации (параметризация
кривой длиной ее дуги), а 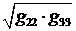 представляет собой
площадь бесконечно малого поперечного сечения стримлайна (фактически – это
представляет собой бесконечно малую трубку тока, англ. streamtube). Т.е. уравнение (4.8)
является уравнением, моделирующем некоторое движение среды в искривленном
канале переменного сечения. представляет собой
площадь бесконечно малого поперечного сечения стримлайна (фактически – это
представляет собой бесконечно малую трубку тока, англ. streamtube). Т.е. уравнение (4.8)
является уравнением, моделирующем некоторое движение среды в искривленном
канале переменного сечения.
Заметим,
что мы расщепили систему (3.7) на уравнение для давления (4.3) и уравнения
вдоль стримлайнов (4.8). При этом два последних члена в (3.7), т.е. выражение
(4.5), представляют собой вносимую нами ошибку. Если величина ошибки (4.5) не
мала, то можно далее решать систему (3.7) стандартными конечно-разностными
методами. При этом подходе сохранится точность решения исходной системы
уравнений (1.6). Подобную цель преследовали и авторы работ [8], [10], но
осуществляли ее несколько другим, по нашему мнению более абстрактным способом,
используя схему предиктор-корректор, и на каждом шаге дополнительно корректируя
решения, полученные вдоль стримлайнов.
Теперь,
как мы и обещали, займемся более детально заменой координат (3.1). Мы
предположили ортогональность нашей системы координат, т.е. должны выполняться
следующие соотношения
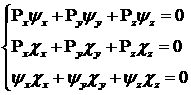 . (4.9) . (4.9)
Кроме того, напомним, что величины 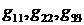 могут быть вычислены
по формулам (см. §3) могут быть вычислены
по формулам (см. §3)
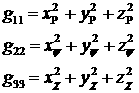 , (4.10) , (4.10)
где соответствующие производные могут быть получены
следующим образом
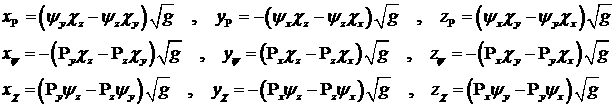 , ,
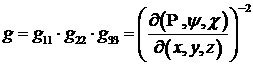 . .
Итак,
мы считаем, что функция 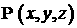 нам известна –
например, это просто давление на предыдущем временном слое. Вначале опишем общий способ построения двух
других координатных функций нам известна –
например, это просто давление на предыдущем временном слое. Вначале опишем общий способ построения двух
других координатных функций 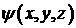 и и 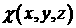 (в настоящей работе мы
не будем принимать во внимание глобальных свойств системы координат (3.1), а
будем работать только локально). Если нарисовать интегральные кривые поля (в настоящей работе мы
не будем принимать во внимание глобальных свойств системы координат (3.1), а
будем работать только локально). Если нарисовать интегральные кривые поля 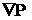 , то это семейство можно локально параметризовать двумя
параметрами , то это семейство можно локально параметризовать двумя
параметрами  и и 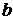 , например, точками пересечения кривых с плоскостью , например, точками пересечения кривых с плоскостью 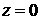 . Запишем это семейство так . Запишем это семейство так
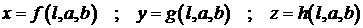 , (4.11) , (4.11)
где  представляет собой
некоторый параметр вдоль кривых. Заметим, что, если представляет собой
некоторый параметр вдоль кривых. Заметим, что, если 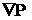 является достаточно
гладкой вектор-функцией, то величины является достаточно
гладкой вектор-функцией, то величины 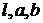 могут быть записаны
как функции могут быть записаны
как функции 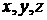 из соотношений (4.11).
Из первых двух уравнений (4.9) следует, что функции из соотношений (4.11).
Из первых двух уравнений (4.9) следует, что функции 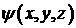 и и 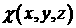 будут постоянными на
кривых (4.11), т.е. имеют форму будут постоянными на
кривых (4.11), т.е. имеют форму
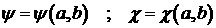 . (4.12) . (4.12)
В силу сделанного
замечания, после обращения (4.11) и подстановки функций  и и 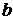 в (4.12), получим
некоторую форму записи для в (4.12), получим
некоторую форму записи для 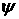 и и 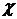 , при которой первые два соотношения (4.9) выполнены.
Подставляя полученные выражения в третье уравнение (4.9), получим уравнение на
сами функции (4.12), откуда можно их получить, и далеко не единственным
образом. , при которой первые два соотношения (4.9) выполнены.
Подставляя полученные выражения в третье уравнение (4.9), получим уравнение на
сами функции (4.12), откуда можно их получить, и далеко не единственным
образом.
Как видно из приведенных соображений, выписать
какие-либо общие формулы довольно трудно. Поэтому, учитывая то, что на практике
мы работаем с конечно-разностными аппроксимациями систем уравнений, попытаемся
получить локальные формулы замены координат, предполагая, что локально функция 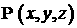 задается с помощью
некоторой гиперплоскости. А именно, будем искать локальную замену
координат в виде задается с помощью
некоторой гиперплоскости. А именно, будем искать локальную замену
координат в виде
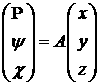 , (4.13) , (4.13)
где  представляет собой
квадратную матрицу представляет собой
квадратную матрицу 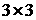 . Поскольку мы интересуемся ортогональной заменой координат,
то . Поскольку мы интересуемся ортогональной заменой координат,
то
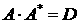 , (4.14) , (4.14)
где 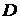 – диагональная (но необязательно единичная) матрица.
Используя векторную алгебру, легко показать, что величины – диагональная (но необязательно единичная) матрица.
Используя векторную алгебру, легко показать, что величины 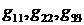 представляют собой
обратные величины к скалярным квадратам строк матрицы представляют собой
обратные величины к скалярным квадратам строк матрицы  . Также нам было бы удобно получить (4.13) так, что . Также нам было бы удобно получить (4.13) так, что
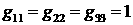 . (4.15) . (4.15)
Поскольку для задания функции 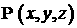 достаточно лишь
соблюдение соотношения достаточно лишь
соблюдение соотношения 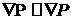 , то можно считать, что , то можно считать, что 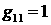 . Функции, входящие в (4.15), легко вычислить по формулам
(4.10). Поскольку функция . Функции, входящие в (4.15), легко вычислить по формулам
(4.10). Поскольку функция 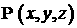 нам известна, то
первая строка матрицы нам известна, то
первая строка матрицы  тоже известна. Но, как
мы только что заметили, соотношения (4.15) фактически представляют собой
утверждение, что скалярные квадраты строк матрицы тоже известна. Но, как
мы только что заметили, соотношения (4.15) фактически представляют собой
утверждение, что скалярные квадраты строк матрицы  равны единице. Таким
образом, принимая во внимание (4.14), задача отыскания локальной системы
координат (3.1) сводится просто к построению некоторого ортонормированного
базиса в равны единице. Таким
образом, принимая во внимание (4.14), задача отыскания локальной системы
координат (3.1) сводится просто к построению некоторого ортонормированного
базиса в 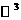 . Заметим, что, если из каких-нибудь априорных соображений известно,
что ошибка (4.5) мала (например производные . Заметим, что, если из каких-нибудь априорных соображений известно,
что ошибка (4.5) мала (например производные  и и 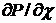 малы, исходя из
физических условий течения), то нам нет необходимости дополнительно
строить функции малы, исходя из
физических условий течения), то нам нет необходимости дополнительно
строить функции 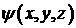 и и 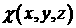 . В этом случае, используя условие (4.15), можно
просто решать систему дифференциальных уравнений (4.8), которая приобретает
дивергентную форму. . В этом случае, используя условие (4.15), можно
просто решать систему дифференциальных уравнений (4.8), которая приобретает
дивергентную форму.
Наконец,
сделаем еще одно важное ЗАМЕЧАНИЕ. Если (3.7) в некотором смысле сводится к
(4.8) с условием (4.15), то эффекты сжимаемости вдоль поверхностей  пренебрежимо малы, т.е. в решаемой задаче в действительности
малы пренебрежимо малы, т.е. в решаемой задаче в действительности
малы  и и 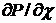 , функции , функции 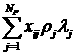 медленно меняются, в итоге медленно меняются, в итоге 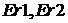 близки к малым
постоянным. Тогда система (4.8) приобретает дивергентный вид и может
быть быстро решена одним из консервативных численных методов для одномерных
задач. Однако, реальные течения, где понятие стримлайн имеет смысл, могут и не
обладать свойством малости производных близки к малым
постоянным. Тогда система (4.8) приобретает дивергентный вид и может
быть быстро решена одним из консервативных численных методов для одномерных
задач. Однако, реальные течения, где понятие стримлайн имеет смысл, могут и не
обладать свойством малости производных  и и 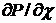 . Однако, предложенная формулировка позволяет оправдать
сведение (3.7) к (4.8) и в этом случае. Для этого всего лишь заметим, что можно
локально выбирать замену координат (4.13), исходя не из условия (4.15), а
исходя из условия, что . Однако, предложенная формулировка позволяет оправдать
сведение (3.7) к (4.8) и в этом случае. Для этого всего лишь заметим, что можно
локально выбирать замену координат (4.13), исходя не из условия (4.15), а
исходя из условия, что 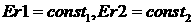 (см. (4.6)). Причем (см. (4.6)). Причем 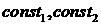 не зависят от номера
ячейки расчетной сетки. Это всегда возможно сделать, поскольку на этом этапе
алгоритма мы считаем известной функцию давления не зависят от номера
ячейки расчетной сетки. Это всегда возможно сделать, поскольку на этом этапе
алгоритма мы считаем известной функцию давления 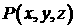 в декартовых
координатах. Тогда (3.7) приобретает вид (4.8), но уже в недивергентной
форме, т.е. величина в декартовых
координатах. Тогда (3.7) приобретает вид (4.8), но уже в недивергентной
форме, т.е. величина  в некотором смысле
заменяет «координату времени
полета» (англ. time of flight),
а величины в некотором смысле
заменяет «координату времени
полета» (англ. time of flight),
а величины 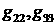 моделируют эффекты
сжимаемости в направлениях, перпендикулярных направлению стримлайнов, т.е.
вдоль поверхностей моделируют эффекты
сжимаемости в направлениях, перпендикулярных направлению стримлайнов, т.е.
вдоль поверхностей  . .
Заметим
также, что функции (4.6) предоставляют нам средства для выбора стратегии
сведения исходной трехмерной задачи к набору одномерных задач, а также средства
для количественной оценки точности этого сведения.
Список Литературы
|
[1]
|
Г.И.Баренблатт,
В.М.Ентов, В.М.Рыжик, Движение
жидкостей и газов в природных пластах. Москва, «Недра» (1984).
|
|
[2]
|
J.Bear, Dynamics of fluid in porous media. Dover Publications, New York
(1973).
|
|
[3]
|
А.И.Брусиловский,
Фазовые превращения при разработке
месторождений нефти и газа. Изд. дом «Грааль», Москва (2002).
|
|
[4]
|
H.Cheng, I.Osako,
A.Datta-Gupta, M.J.King, A rigorous compressible streamline formulation for
two- and three-phase black-oil simulation. SPE Journal, December 2006, pp. 407 – 417 (2006). (See also
earlier SPE 96866, 2005).
|
|
[5]
|
M.Crane, F.Bratvedt,
K.Bradtvedt, P.Childs, R.Olufsen, A fully compositional streamline simulator.
SPE 63156 (2000).
|
|
[6]
|
K.Jessen, F.M.Orr,
Compositional streamline simulation. SPE 77379 (2002).
|
|
[7]
|
F.M. Orr, Theory of Gas Injection Processes,
Stanford University, Stanford, California (2005).
|
|
[8]
|
I.Osako, A.Datta-Gupta,
M.J.King, Timestep selection during streamline simulation via transverse flux
correction. SPE 79688 (2003).
|
|
[9]
|
I.Osako, A.Datta-Gupta, A
compositional streamline formulation with compressibility effects. SPE 106148
(2007).
|
|
[10]
|
M.J.King, I.Osako,
A.Datta-Gupta, A predictor corrector – formulation for rigorous streamline
simulation. 8-th Oxford Institute of Computational Fluid Dynamics Conference
Oxford University, Oxford, England, March 29 – April 1, 2004 (2004).
|
|
[11]
|
M.R.Thiele, R.P.Batycky,
M.J.Blunt, A streamline-based 3D field-scale compositional reservoir
simulator. SPE 38889 (1997).
|
|
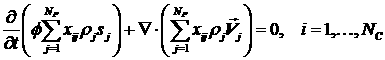 .
.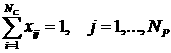 ;
;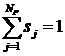 ,
,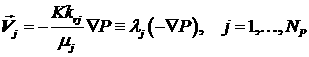 ,
,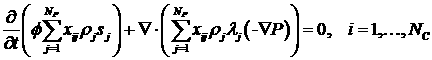 .
.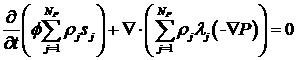 ,
,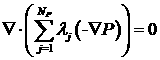 .
.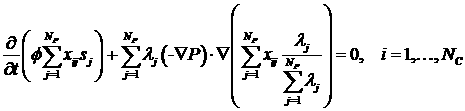 .
.
 .
.
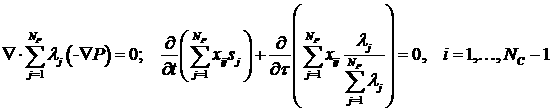
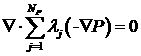
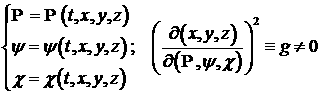 .
.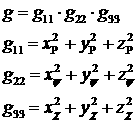 .
.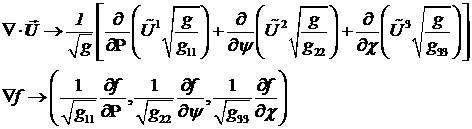 .
.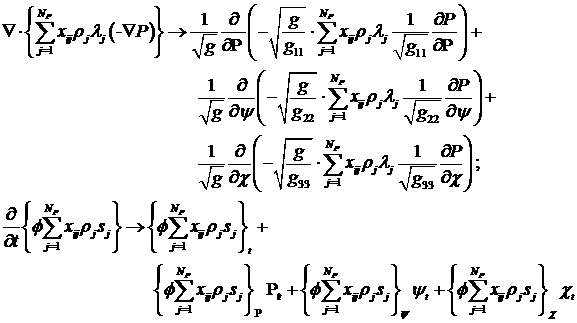 .(3.3)
.(3.3)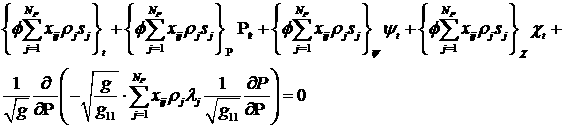
 .
. .
.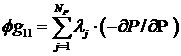 , то
, то 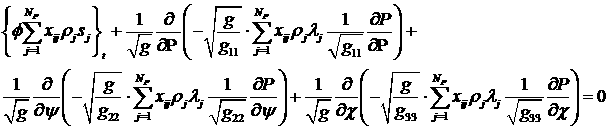
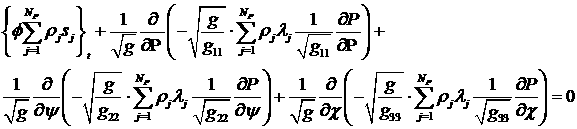 .
.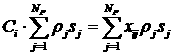 .
.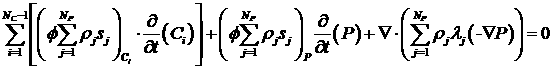 .
.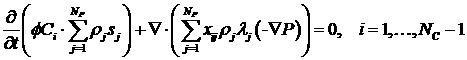 ,
,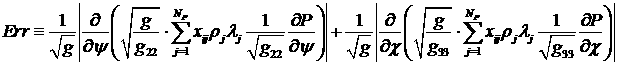 .
.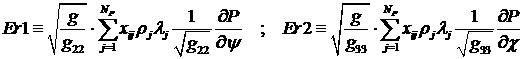 .
.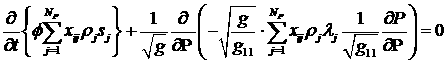 .
. 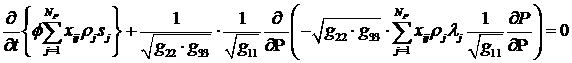
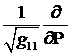
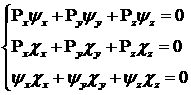 .
. 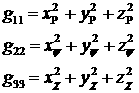 ,
,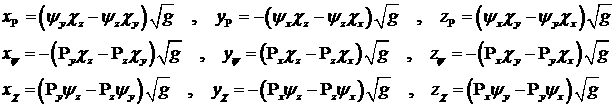 ,
,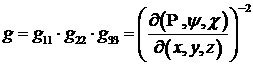 .
.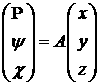 ,
, 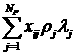 медленно меняются, в итоге
медленно меняются, в итоге