Построение областей достижимости неупругих анизотропных биллиардов

(The investigation of range regions of the non-elastik anisotropos billiards
Preprint, Inst. Appl. Math., the Russian Academy of Science)

         Оглавление

Введение ..........................................................................................  3

1.                Индикатрисное описание рикошетов..........................    3

2.                Неоднородность..............................................................   5

3.                "Задача о камешке".........................................................   6

4.                Задача о спуске КА в атмосфере....................................  8

5.                Способы оценивания анизотропных областей............  13

6.                Построение и классификация индикатрис...................  19

Заключение ...................................................................................... 22

Литература ....................................................................................... 24

          Введение

          Исследование предельных динамических возможностей механических систем является приоритетным направлением  развития современной механики. С одной стороны, решение задач указанного класса позволяет более широко и эффективно использовать существующие механические объекты и более экономично управлять ими. С другой стороны, оптимальное управление находится гораздо ближе к широкому классу неуправляемых механических систем, чем  это может показаться на первый взгляд. В частности, классическое вариационное исчисление можно рассматривать как подраздел теории оптимального управления [1], и значительный ряд соответствующих теорем (например- уравнение Эйлера) может быть выведен из принципа максимума Л.С.Понтрягина.  Более того, хочется вслед за [1] процитировать высказывание Эйлера о том, что "в мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума". В частности,  для ряда механических задач с недостающей или “сложно достающейся” информацией можно использовался метод замены недостающего параметра виртуальным управлением и последующим получением оценки фазового состояния механической системы путем построения ее  "области определения" методами оптимизации [2-5].

          Настоящая работа посвящена обобщению этого подхода для динамического оценивания фазовых состояний и выявления общих структурных свойств квазисингулярных механических систем, где исследование обычными методами классической механики (например - с помощью теории удара) может быть весьма затруднено нелинейностью рассматриваемой квазисингулярности и наличием диссипации.

          Индикатрисное описание рикошетов.

          Представление траектории механической системы как экстремали вариационного принципа в ее расширенном фазовом пространстве было известно со времен Гамильтона. Соответственно становится возможным проводить аналогию между движением объекта ньтоновой механики и распространением светового луча в геометрической оптике в оптической среде с "подходящим образом" построенным показателем преломления [7,9]. В последнем случае роль вариационного принципа играет принцип наименьшего оптического пути (принцип Ферма). При этом можно опираться на хорошо изученные задачи геометрической оптики (а, так же -  геометрической акустики и геометрической электродинамики ).

          Принцип Ферма верен в изотропной, но необязательно однородной среде [см., например, книгу «Современная геометрия» Б.А.Дубровина, С.П.Новикова и А.Т.Фоменко, М., Наука, 1979]. При этом в изотропной среде с переменной скоростью света c(x) свет движется по геодезическим метрики

          gij =   dij / c²(x)               

причем время движения вдоль пути минимально и равно

     t =  óïdxï/c(x)

            õ

          В общем случае учет анизотропии приводит к тому, что тензор метрики gij  , определяющий геодезические, не будет иметь конформно евклидовой формы.

          Учет  диссипативности воздействия на рикошете можно проводить различными способами. Если анализу движения динамических биллиардов без трения посвящено большое количество работ [10,11], то введение учета трения приводит к невозможности непосредственно использовать методы гамильтоновой механики. Исследования посвящены, в основном, построению предельных моделей движения [12],  и не содержат описания областей достижимости.

Имея ввиду тот факт, что рикошеты в ряде задач могут описываться достаточно сложным образом (например-  поверхность шарика квазисферична и имеет сложную форму, площадка соприкосновения тела с отражающей поверхностью на рикошете отлична от точки и, вообще говоря, не обязательно является компактом) зададимся целью описать динамику рикошета как преобразование входного вектора скорости (скорости падения) в вектор выходной скорости (скорость отражения) с помощью некоторого функционала отражения J:³®Â³:

                 V¹º = J( Vº )

          В рамках квазисингулярного подхода считаем участок рикошета пренебрежимо малым по сравнению с участком свободного движения.

          Пусть в декартовых координатах OXYZ таких, что плоскость XOZ совпадает с отражающей плоскостью, входной вектор скорости падения Vº записывается как

          Vº(V0X,V0Y,V0Z)

          Тогда при идеальном рикошете вектор отраженной скорости V¹º будет симметричен Vº относительно плоскости рикошета и запишется как

          V¹º(V0X,V0Y,-V0Z)

          Поэтому целесообразно ввести также функционал преломления I:³®Â³ как:

                 V¹ = I( V¹º )

          В случае идеального отражения функционал I, очевидно, описывается с помощью единичной матрицы 3х3 :

                               æ   1 0 0  ö

                  I =        ê    0 1 0  ï

                               è   0 0 1  ø

          Смысл функционала преломления I таков, что он дает множество концов векторов всех возможных выходных скоростей механического объекта после рикошета, построенных для фиксированного вектора V¹(Vº). Будем считать это множество компактным и имеющим границу - поверхность в ³. По аналогии этого функционала с индикатрисой в  геометрической оптике [6] -  поверхности всевозможных скоростей света, построенных для точки оптической среды (вообще говоря - преломляющей, неоднородной и анизотропной), естественно назвать  I  индикатрисой отражения.

          Неоднородность.

          Для модельной неоднородной изотропной  диссипации на рикошетах              

                   Vº¹ =  l Vºº

 индикатриса отражения запишется как

                                 æ   l 0 0  ö

                  I* =        ê   0 l 0   ï

                                 è   0 0 l  ø

          "Задача о камешке".

          Рассмотрим   камень,   рикошетирующий   с   затуханием   по поверхности воды, и поставим модельную задачу  определения  всех точек на этой  поверхности,  в  которые  он  может  попасть  при фиксированном векторе начальной скорости Vº .

Поверхность  будем для простоты  считать горизонтальной плоскостью.  Очевидно,  вид  искомой области будет  определяться  характером  отражения  камешка  при каждом его соприкосновении  с  водой,  которое, в  свою  очередь, зависит от текущих скорости камешка, его вращения и ориентации в пространстве. Громоздкая задача оптимизации  в  сложной  среде -  построение области   достижимости    указанного    движения,   становится разрешимой,  если использовать следующие модельные допущения.

   1. Приращения функционалов продольной дальности  D  и  бокового отклонения B на участках  непосредственного  отражения  от  воды малы по сравнению с участками свободного полета.

  2. Сопротивлением воздуха на участках свободного  полета  можно пренебречь.

          Фазовое управление вектором скорости после рикошета вводится как способ описать всевозможные "маневры" камешка произвольной формы при взаимодействии с водой на участке отражения. Отличие от описанных выше модельных задач состоит в том, что рикошет описывается более громоздким, но - и более полным образом и, кроме того, возможно не отражение камешка от воды, а погружение на любом "неудачном" рикошете.

          В этом случае форма ОД параметрически определится как

                  n

    D= 1/g  S  Vi²(V,qi-1 ,qi,yi) sin 2qi cos (y 0+...+yi)            (1)

                 i=1                                                                              

                  n

    B= 1/g  S   Vi²(V,qi-1 ,qi,yi) sin 2qi sin (yº  +...+yi)

                 i=1

где n -  число  отражений,  Vi(V,qº,q¹,y¹) - скорость  камня после i-го отражения, зависящая  как  от  траекторного  угла  на выходе q¹ и курсового  угла  y¹ ,  так  и  от  значения  qº  до отражения, g- ускорение свободного  падения.            Динамические свойства  затухания   скорости   при   неупругом   отражении   и дополнительные  потери  скорости  при   развороте   от   текущей траекторной плоскости формально запишутся как

          Vn < Vi   <...< Vº                                

          V¹(V,qº ,q¹,y¹)£V¹(V,qº ,q¹,0)

          Таким образом,  указанная  задача  сводится  к  определению зависимости

          V¹=V¹(Vº,qº ,q¹,y¹) , 

которая может находиться несколькими способами: из расчетов по модели взаимодействия тела со средой; в виде эмпирической таблицы;  по оптимальности  выбора  пар  (qi ,yi), рассматриваемых как дискретные управления на участках отражения.

          Точную верхнюю грань множества всех динамически  допустимых V(Vº,qº ,q¹,y¹) (“индикатрису одного погружения”) будем называть в  дальнейшем  оптимальным маневром (ОМ) и будем обозначать как I(Vº,qº ,q¹,y¹):

          I((V,qº ,q¹,y¹) = sup V (V,qº ,q¹,y¹)

          Очевидно, что динамические возможности ОМ покрывают возможности внутренних точек индикатрисы.

          Для  предельного   случая   изотропности   ОМ-   отсутствии затухания скорости при развороте, можно записать:

     V(Vº,qº ,q¹,y¹) =V((Vº,qº ,q¹,0)

и формулы (1.1) будут описывать, очевидно,  круговую  область достижимости одинаково скачущего во все стороны на поверхности воды камешка - сечение пространственного мультипараболоида безопасности  поверхностью отражения (этот случай разобран выше).

          Рассмотрим оптимальный  маневр

     V¹= l Vº

где l,  введенный выше  коэффициент  затухания     0£l<1 .

          Можно  показать,  что  максимальное  число  отражений (которое имеет место для продольной траектории)  не  превосходит некоторого числа N, такого, что

    N = 1+[log (Vº/Vc )]  ,

                     l

где квадратные скобки означают операцию взятия целого числа, V0- начальное, а Vc- "критическое" (минимальное) значение  скорости, при которой еще происходит отражение камешка от поверхности и он не тонет.

          Выпишем в ряд величины дальности после i-го рикошета:

   l1= pl²,  l2= pl² (1+l²),  ....,

             li+1=pl²(1+l²+...+ l ² )= pl²(1-l²   )/(1-l²),   p= Vº²  /g

          Итоговая дальность:

    l¥ = pl²/(1-l²)

          Нетрудно видеть, что приращения дальности на каждом новом рикошете всегда меньше предыдущих:

           dli+1>dli

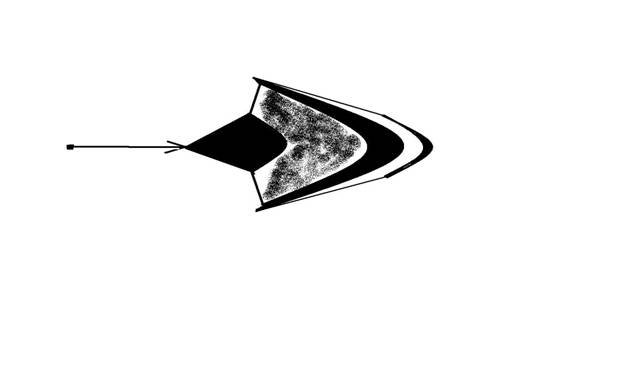
                    Рисунок 1. К построению области достижимости в задаче о рикошетирующем камешке.

          Задача о спуске КА в атмосфере.

          Задача о камешке может служить достаточно хорошим приближением задачи об оптимизации области достижимости при спуске космического аппарата в атмосфере [2-6], где оптимальные траектории также оказываются рикошетирующими на коротких погружениях в плотные слои атмосферы.  

          Полученные в [2,6] при построении  ОД  численными  методами оптимальные законы движения КА можно представить как  структурно отличающиеся от  законов,  найденных  в  предположении  гипотезы квазистационарного  планирования  (либо  малого  отклонения   от такого  движения)  и  малости  гравитационных   воздействий   по сравнению с аэродинамическими.  Опорные  траектории  [2] оказываются состоящими из участков  "изломов"  трасс  в  плотных слоях  атмосферы,  где  происходит  основное  торможение  КА   и аэродинамические воздействия доминируют, и чередующихся с  ними, существенно более  протяженных  участков  полета  в  разреженных слоях  атмосферы,  где  главными   являются гравитационные силы.

          Отражение на участках погружения происходит за счет резкого роста подъемной  силы  в  Зонах  Маневра  (ЗОМ)-  плотных  слоях атмосферы,    которая    "выкидывает"    КА    на    последующие балллистические участки.

          Вышеуказанное  представление  класса  опорных   оптимальных траекторий,  названное  квазисингулярным   представлением   [3-5], спользуется для полуаналитического конструирования ОД с помощью Метода Виртуального Управления (МВУ). Основа метода-  сведение  задачи поиска  оптимума  на  всем  интервале  движения  КА   к   выбору управления  только  на  участках  погружения  в   плотные   слои атмосферы - с использованием заранее известного на этих участках функционального множества оптимальных маневров, с  аналитическим восполнением оптимальных траекторий на баллистических  участках. Протяженность  i-го  баллистического  участка  l i  зависит   от параметров Vi ,qi скорости  КА  и  угла  наклона  траектории  на выходе с i-й ЗОМ. Она находится,  например,  с  помощью  формулы [13]:

          l i(Vi,qi )= 2(Rz +Hº)arctg[Vi² cos q sin q /(m/(Rz +Hº)-Vi²cos²qi )]

где Rz - радиус Земли, m-гравитационная постоянная, Hº -  условная высота точки входа в плотные слои атмосферы.

          Приращения области достижимости на ЗОМах считаются малыми и рассчитываются согласно таблицам соответствующего  оптимального  маневра.

          Таким образом параметры области достижимости представимы в  виде суммы аналитических членов и малых табличных добавок  при  любой     сконструированной последовательности ориентаций скоростей выхода КА из зон оптимального маневра на  баллистические  участки.  При этом   исчезает   необходимость   использования   для   процесса оптимизации  протяженных  траекторий  большого   числа узловых точек [2], а также проводить  идентичные  и  трудоемкие расчеты оптимизации на участках погружения для  получения  новой точки ОД.

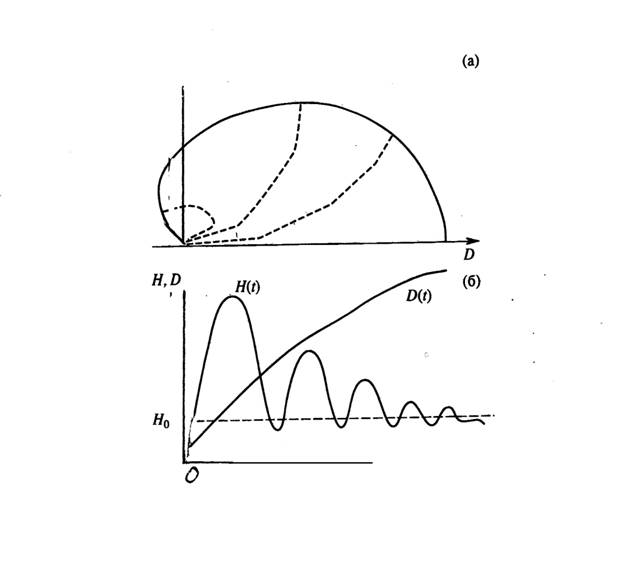
          Рисунок 2. Квазисингулярное представление формирования  области достижимости при спуске КА в атмосфере: а – следы траекторий на одном из симметричных сегментов поверхности роста; б – структура траекторий, приходящих на границу зоны роста.

          Основой Метода Виртуальных Управлений (МВУ) является решение серии оптимальных задач для КА с конкретными аэродинамическими характеристиками строится банк его оптимальных  маневров .  Для  этого  для табличных значений параметров  скорости  входа  в  рикошет  Vºk    и входного траекторного угла - qº   и  значений  на  вылете  из  рикошета траекторного и курсового углов q¹i , y¹j необходимо  решить  серию следующих оптимальных задач на конечном отрезке времени 0<t<T:

          Требуется найти вектор-функцию  управления  u(t), стесненную условиями ¦u¦£1, и соответствующее решение  уравнений движения  центра  масс  КА   [3-5]-   вектор-функцию   фазовых координат  x(t),  обеспечивающие  максимум  фукционала  выходной скорости  КА  при  соблюдении  перечисленных  ниже терминальных и начальных  условий:

          V(T)  ® max - максимизируемый функционал,

          q (T)= qi , y(T)= yj ,  qi=1,...,kq,  y j=1,...,ky             

          H(T)=H

(набор терминальных функционалов)

          V(0)=Vk  , q (0)= ql,   k=1,...,kv, l=1,...,kq

          H(0)=Hº

(начальные  условия, соответствующие   очередной  точке входа в плотные слои атмосферы).

          Здесь Vºk ,q¹ - дискретный набор значений параметров- равномерно  распределенная  по  области  определения   параметров сетка [3,4],

          Vºk³Vc,    qlÎ[0,p/2] .

Конечный момент времени выхода  КА  из  очередного  участка погружения T не  фиксирован  и  подлежит  определению  наряду  с управляющими функциями u(t).

          Согласно результатам, полученным в  [2-5],  по  характерным величинам аэродинамических воздействий точкой входа H  считается точка прохождения КА высоты H=Hº=30  км, критическим  значением скорости Vc - значение 1 км/с.

          Банк множества оптимальных маневров, найденный  в  процессе выполнения процедуры МВУ можно представить  как  сечения гиперповерхности в Â5   V(Vº ,qº ,q¹,y¹)  "табличными"  поверхностями уровня {Vº=Vºi  ; qº=qºj }.  Тогда каждое сечение будет представлять собой некоторую поверхность в  Â³ локальной выходной скорости  КА  I  =V (q¹,y¹),  зависящую  только   от   направления   вылета   и определяемую сферическими координатами q и y.  Такую  поверхность, по аналогии с введенным  в  геометрической  оптике  обозначением множества локальных скоростей света в  неизотропной  среде  [9], было бы естественно назвать ндикатрисой. Вид такой индикатрисы, однако, как уже указывалось выше, может меняться  в  зависимости от входных параметров V  и q. На рис.     представлены в виде срезов найденные  индикатрисы  задачи  о  движении  КА  для некоторых характерных значений входных параметров. Данная сводка дает  представление  о  деформации  индикатрисы  при   изменении параметров.    

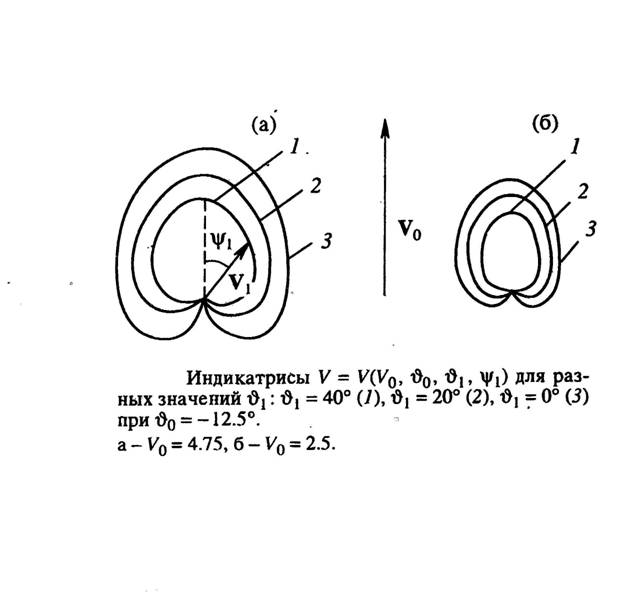
          Отметим    найденные    характерные    особенности индикатрис:

- гладкое, близкое к  косинусоидальному  затухание  скорости  на головном участке поверхности индикатрисы;

- максимальное продольное значение  выходной скорости,  как  и следовало ожидать, меньше ее входного значения, а их  отношение- "коэффициент затухания"- не превышает величину 0.8;

- "крутизна"  индикатрисы  по  бокам  и  с  обратной  стороны  - “почти инвариантность” по углу q°;

-  наличие  "сердцевидного"  невыпуклого  участка   с   обратной стороны, соответствующего динамической  невозможности  разворота движения КА на 180°  на одном погружении;

- относительную гладкость и монотонность деформации  поверхности индикатрисы при переходе к соседним поверхностям уровня (сравним с [1, с.104]).

          Отметим,   что   именно   невыпуклость   заднего    участка индикатрисы порождает в результате аналогичную  “зону молчания” и всей области достижимости.

          Формально задачу определения ОД можно записать как задачу определения проекции на плоскость ОД следующего множества M:

                   M{x(t ,x ,u,t): " u: ¦u¦°1, "tÎ[0,1]}                    

          Здесь   u -    вектор-элемент    функционального пространства со стандартным оператором нормы

              ¦u¦= max    max   ¦u (t)¦                                             

              i=1,2   tÎ[0,1]

          Область достижимости, найденная с помощью МВУ и  описанного выше банка индикатрис [3-5], изображена на рис.2.

          Характерные детали ОД, полученной с  помощью  МВУ, повторяют  особенности  ОД,  найденной  с  помощью   стандартных процедур  оптимизации  [2].

          Способы оценивания анизотропных областей достижимости с  помощью изотропных областей. Обыкновенный и необыкновенный лучи.

          Как известно, Гамильтон ввел в рассмотрение вместо одной траектории, выходящей из заданной точки фазового пространства, целый пучок "соседних" фазовых траекторий, что дает дополнительные возможности исследовать изначальную задачу  [1,9] . В сложных механических задачах динамического оценивания, где в первоначальной постановке не фигурируют управляющие воздействия, они могут возникнуть как вспомогательные элементы построения областей достижимости в форме виртуального управления с помощью изменения фазовых координат [2-5]. Если таким управлением выбирается скорость, то и возникает пучок фазовых траекторий. Для различных значений механической энергии Еi системы на на наборе этих непересекающихся пучков строятся фронты волны как проекции фазовой лагранжевой поверхности, соответствующей Еi на x-пространство [9]. При наличии мгновенной диссипации на рикошете система переходит на лагранжеву поверхность с более низким уровнем Еi и соответствующий волновой фронт Фi на участке свободного полета до следующего отражения (склейка непересекающихся фазовых пучков). Исходя из скрытого, но фундаментального принципа выпуклости в задачах вариационного исчисления и оптимального управления рассматриваемого типа, связанного с выпуклостью образа множества с непрерывной мерой при интегральных отображениях [1], можно утверждать, что совокупность всех промежуточных режимов на достаточно малом промежутке времени можно оценивать указанной дискретной выборкой. При этом экстремальная точка регулярным образом эволюционирует, образуя “поле экстремалей” при изменении параметров возмущения [1]. 

          Таким образом, финальную область достижимости системы можно рассматривать как сглаженную границу дискретного  набора волновых фронтов, построенных на рикошетах с постепенно понижающимся уровнем энергии. В этом смысле такой подход близок к методам описания областей достижимости дискретных объектов фрактальной геометрии [14].

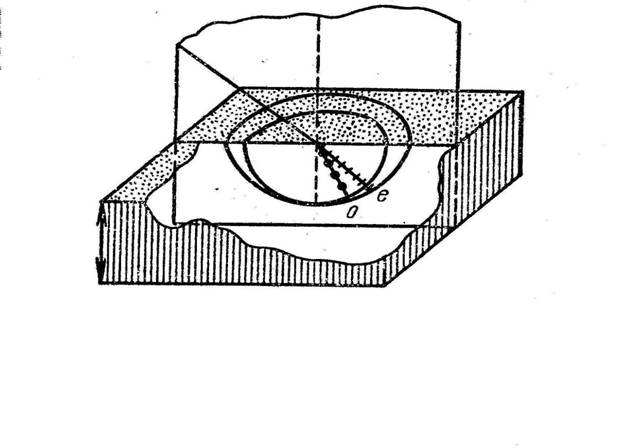
          Рисунок 4. Индикатриса двойного лучепреломления в двуосном кристалле. После преломления образуются два волновых фронта – обыкновенный и необыкновенный (взят из монографии Г.С.Ландсберга «Оптика»).

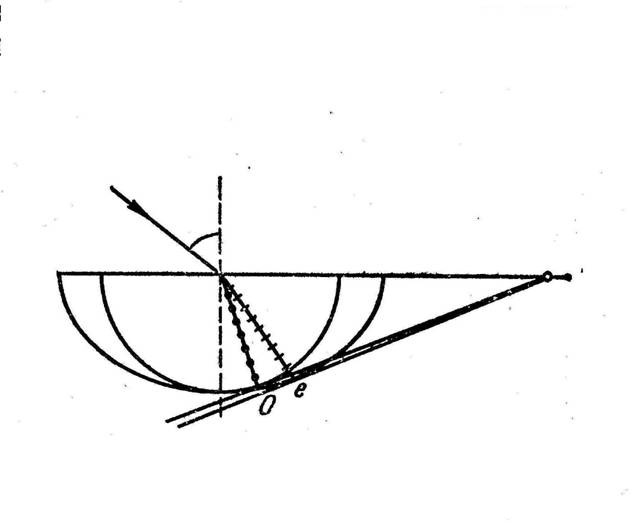
          Рисунок 5. “Построение Гюйгенса“ для вычисления анизотропного распространения лучей, соответствующее случаю рис. 4 (взят там же).

          Рассмотрим индикатрису рикошета, полученную эмпирическими, аналитическими, полуаналитическими, либо численными методами оптимизации (например - [3-5] ):

           I = V(Vº, qº, qk , yk ).

          Без ограничения общности положим, что для вектора скорости падения курсовой угол будет нулевым:

          Vº  Î[0,Vmax], q Î [0, p /2],  yº  = 0,

          Рассмотрим сечение индикатрисы I  соответствующей гиперповерхностью (1.5.1). Оно будет являться некоторым множеством в ³  V(q , y ). Из соображений гладкости и выпуклости [1] будем считать это множество компактным. Тогда по любому из заданных в ³ направлений это множество будет достигать максимума расстояния от точки (0,0,0) (то есть максимума величины вектора выходной скорости V¹ ). (по некотрым “вырожденнным” направлениям может быть    V¹  = 0). Выберем соответствующие максимальные значения по продольному и боковым направлениям рикошета Vd и Vb. Тогда всевозможные движения системы после рикошета будут, очевидным образом, заключены между двумя сферическими фронтами Фd и Фb изотропных движений с Vd и Vb. Причем действительное движение системы после рикошета будет ограничено поверхностью, касающейся каждого из этих фронтов и непрерывно расширяющейся от внутреннего к внешнему. С помощью указанного построения можно получать оценки движения в анизотропной среде через более простые изотропные.

          Необходимо отметить,что значение Vb может быть нулевым и определяется видом индикатрисы для каждого конкретного типа рикошетирующего взаимодействия. Классификация рикошетов будет приведена ниже.

          Вообще говоря, оценки анизотропии двумя изотропными процессами, которые необходимо проводить для пространственных индикатрис дальности, могут отличаться от “оптимально скоростных” аппроксимаций в проекциях на поверхность отражения. Но они практически совпадают, учитывая тот факт, что заведомо неоптимальны  виртуальные  управления,  соответствующие  большим потерям выходной скорости и баллистической дальности на  больших выходных  траекторных  углах q >45°  и ,   в  силу исчезающей малости величины баллистической дальности  для  малых    q : 0<q<5°  .

          Аналогом указанного построения в геометрической оптике может служить построение Гюйгенса для преломленных лучей в двуосных кристаллах, где возникает обыкновенный и необыкновенный преломленные лучи  [монография Г.С.Ландсберга «Оптика», - М., Наука, 1976]. В результате преломленный волновой фронт занимает аналогичное описанному выше промежуточное положение между фронтами обыкновенного и необыкновенного лучей.

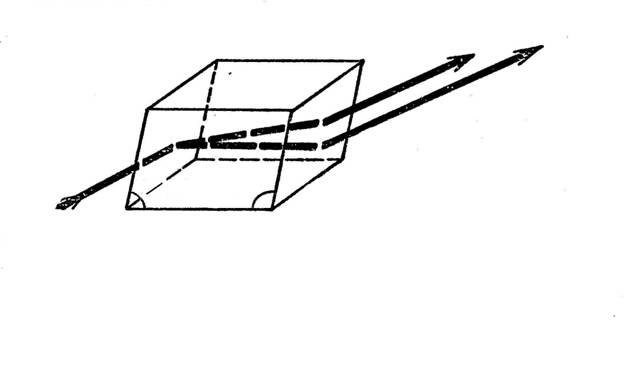
          Рисунок 6. Синтез разнонаправленных траекторий, как анизотропное преломление лучей в кристалле.

          Можно говорить о том, что диссипативная анизотропия соответствует не двуосному преломлению, а бесконечноосному, но ее структура достаточно гладко “укладывается” между двумя изотропными движениями (обыкновенным и необыкновенным лучами в двуосном преломлении либо соответственно между двумя  решениями задачам максимизации на дальность и на боковое отклонение в теории оптимального управления).

          Указанный метод построения модели рикошета может быть применен и в редукции классической теории удара [7] на случай “мягкого” удара. Для этого вместо формул для коэффициентов восстановления Ньютона    æ  и мгновенного трения c  можно использовать эмпирические или модельные индикатрисы двуосного преломления либо рассеяния.

          Структурно схожие типы индикатрис вводятся в оптике – в  теории рассеяния Релея-Бугера [см. вышеуказанную монографию Г.С.Ландсберга], при этом фронтальная часть индикатрисы аналогично вычисленной методами оптимизации индикатрисе оптимального маневра спускаемого КА [4] близка к косинусоидальной по углу между “входным” и “выходным” лучами (рисунок 8). Разница становится существенной на тыльном участке отражения, где для индикатрисы маневра КА возникает  динамически не достижимая “зона молчания”. В этой асимметрии передней и задней части индикатрис динамическая ситуация сопоставима с возникновением зон молчания в геометрической акустике  при распространении ударной волны в воздухе при наличии ветра (см. рисунок 7).

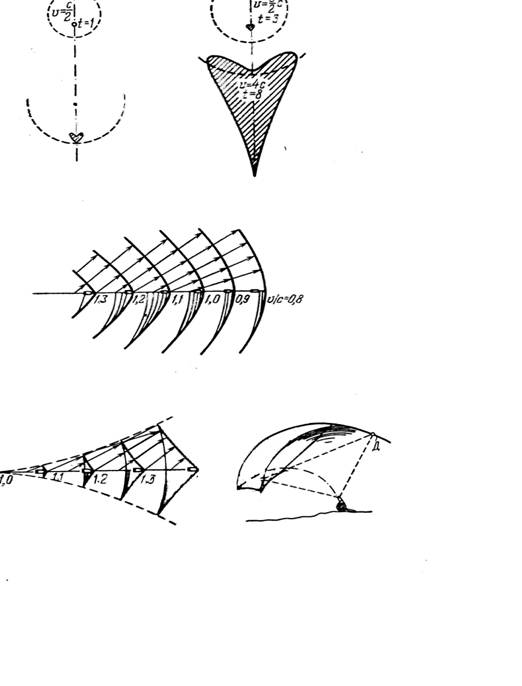
          Рисунок 7. Развитие фронта ударной баллистической волны артснаряда. Взят из книги Д.И.Блохинцева «Акустика   неоднородной движущейся среды».

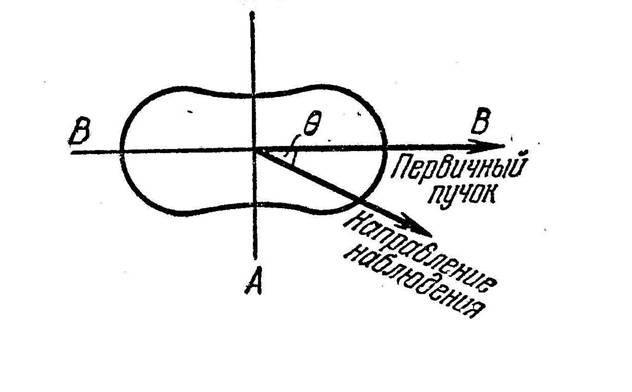
          Рисунок 8 . Индикатриса рассеяния света, соответствующая закону рассеяния Релея-Бугера.

          Вышесказанное приводит к мысли о том, что отражение, неупругий удар или рикошет в расширенном "не абсолютно упругом" понимании следует скорее рассматривать как анизотропное преломление либо как анизотропное рассеяние траектории.

          Построение и классификация индикатрис

          Рассмотрим "квазипотенциальный"  биллиард  -  материальную точку с анизотропными упругими свойствами движущуюся в поле потенциальных сил  на участках между   квазисингулярными   отражениями   от некоторой   поверхности.   Отражения   предполагают некоторую диссипацию энергии движения. Будем описывать  характер отражения путем сопоставления каждому вектору скорости  тела  Vº до отражения некоторой области  M в ³, состоящей  из  всевозможных  векторов скорости тела V¹ после отражения . Внешнюю границу такой области,  в случае   ее   существования,   по   аналогии   с   введенным   в геометрической оптике обозначением множества локальных скоростей света в неизотропной среде  [9], естественно  назвать индикатрисой  I  .

          Классификация.

          Синтез областей достижимости может сильно меняться и приводить к структурно иным результатам в  зависимости от расположения  проекций скорости отражения  на поверхности рикошета относительно "точки  нулевой  скорости" O* .

          В зависимости от этого составим следующую таблицу индикатрис рикошетирования.

        Т а б л и ц а   1

__________________________________________________________

упругость                 -                     -                 -               -                  -

__________________________________________________________

изотропия                -                     -                 +               +                -

__________________________________________________________

O*Î I                        0                    +                 -               +                 -

__________________________________________________________

          Можно выделить следующие классы индикатрис, описывающих характер взаимодействия тела со средой.

          (A). ”Слои” ("Мячик"). Точка O не лежит в I. Характеризует близкий  к упругому и близкий к плоскому характер отражения ("мячик" все время отскакивает в постоянной продольной плоскости).

           (B).”Лист” ("Камешек на воде").  Точка  O  лежит  на  границе  I   и характеризует наличие эффекта поглощения:  существуют  движения, при которых "камешек" тонет и отражения не происходит. Описывает наличие рикошетов в виде отскоков вбок.

          (C)."Эхо". Точка O лежит внутри I . "Выходные" скорости тела имеют  больший  модуль  в  направлении   вектора   скорости   до отражения. Характеризует наличие отражения "назад".

          (D)."Маяк". Точка O лежит в центре  области.  Характеризует изотропное  распространение  волнового   фронта   от   точечного источника света.

    Численно посчитанная модельная ОД для класса  индикатрис (B) (“лист”, "камешек на воде") получена выше.  На рис. 9-10     приведены модельные ОД для наиболее характерных классов  индикатрис.

Отметим,   что   "классическому"   случаю   гравитационного биллиарда [10] соответствует  I  в  виде  одной  точки,  определяющая вектор скорости после  отражения,  равный  исходному  вектору  и характеризующая процесс бесконечного рикошетирования, а редукции этого случая на наличие анизотропного трения - продольный отрезок, не содержащий точку отражения O.

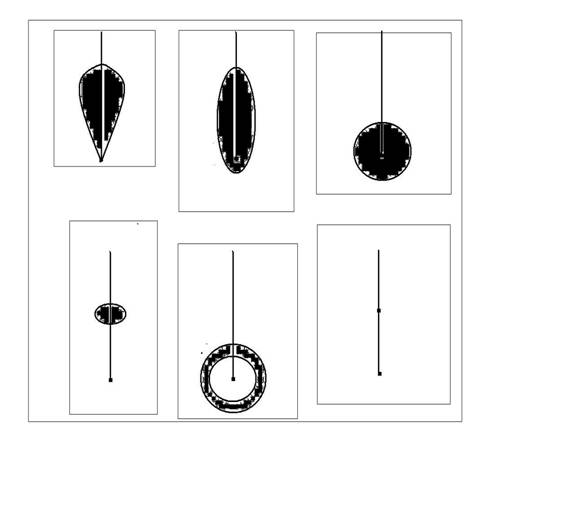
          Рисунок 9. Классификация индикатрис по расположению концов возможных векторов отраженной скорости относительно скорости до отражения. Верхний ряд: В (“лист”), С (“эхо”), D (“маяк”).   Нижний ряд: А (“слои”), Е (“фронт”), F (“плоский неупругий рикошет”)

          Заключение.   

          Поставлены и изучены модельные задачи о камешке, рикошетирующе  скользящем  по  поверхности воды и о неупругом мячике, скачущим либо катящимся по неидеальной          поверхности. наличии эффекта отскока вбок. Даны способы оценки “анизотропных” рикошетирующих процессов  с помощью изотропных.

          Введено “индикатрисное” описание рикошета, проведена классификация основных типов индикатрис отражения на плоскости.

              Рисунок 9.  Область достижимости для случая слабонеупругих рикошетов класса А.

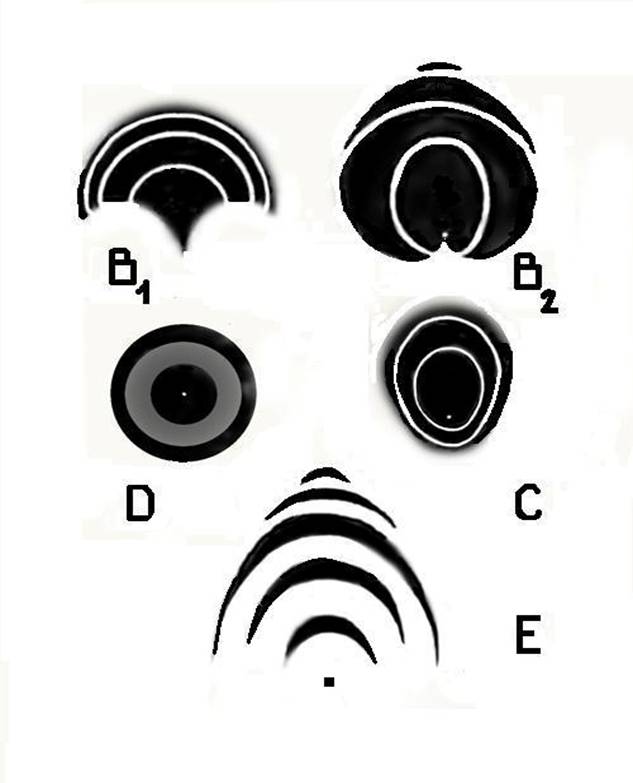
          Рисунок 10. Модельные области достижимости для основных классов индикатрис.

           Литература

1. В.В.Александров, В.Г.Болтянский,  С.С.Лемак, Н.А.Парусников, В.М.Тихомиров. Оптимизация динамики управляемых систем.- М.: МГУ,      2000.

2.  Голубев  Ю.Ф., Хайруллин Р.З. Метод последовательной линеаризации в задачах оптимального управления при входе в атмосферу.- Препринт ИПМ им.М.В.Келдыша АН СССР, 1985, N157.

3. Ю.Ф.Голубев, А.В.Грушевский, Р.З.Хайруллин. Законы управления, обеспечивающие максимальную дальность  при спуске космического аппарата  в атмосфере.- Препринт  ИПМ им.М.В.Келдыша АН СССР, 1988, N3.

4.   Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З. О  структуре области достижимости при спуске  КА.- Препринт ИПМ им.М.В.Келдыша РАН, 993,N 78.

5. Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З. О структуре области достижимости при спуске КА Космические исследования, 1996, N2, с. 180-189.

6. Л.М.Шкадов, Р.С.Буханова, А.Ф.Илларионов, В.П.Плохих. Механика оптимального пространственного движения летательных аппаратов.- : Машиностр., 1972.

7.   Ю.Ф.Голубев. Основы теоретической механики. - М.: МГУ, 2000.

8. А.П.Маркеев. Теоретическая механика. - Москва-Ижевск: Регулярная и хаотическая динамика, 2001.

9. Арнольд В.И. Математические методы классической механики.- М.: Наука, 1974.

10. Белецкий В.В. Регулярные и хаотические движения твердых тел. М.: РХД, 2007.

11. Козлов В.В., Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами.- М.:МГУ, 1991.

12. Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики.- М.: Эдиториал   УРСС, 2002.

13. Охоцимский Д.Е. Динамика космических полетов- М.: МГУ, 1968.

14. Бенуа Б. Мандельброт. Фрактальная геометрия природы. -М., 2002.