Математическая модель процесса электрохимической заточки иглы туннельного микроскопа
|
|
Аннотация |
2 |
|
Введение |
3 |
|
§1. Получение игл методом электрохимического
травления |
4 |
|
§2. Математические модели процесса электрохимического травления иглы |
5 |
|
§3. Стационарные решения |
7 |
|
Выводы |
11 |
Литература |
12 |
Введение
Иглы для туннельного микроскопа в
настоящее время изготавливаются вручную методом электрохимического травления.
Недостатками ручного производства являются невозможность получать стабильные характеристики
игл, иглы с заранее заданными свойствами и экстремальными геометрическими параметрами.
Попытки автоматизировать процесс производства игл пока оказывались
безуспешными. Сложность задачи состоит в том, что о ходе процесса травления
можно судить только по величине тока, протекающего через иглу. Эта зависимость
оказывается нелинейной и неоднозначной, и поэтому не позволяет обойтись
линейными регуляторами. Таким образом, построение автоматического управления
процессом требует математического моделирования процесса и его аналитическое
исследование. Целью такого исследования должно быть нахождение таких способов
управления, которые либо учитывают неоднозначность зависимости тока от
параметров процесса, либо не зависят от нее.
Одним из решений представляется выход на стационарный процесс, в котором
геометрические параметры иглы постоянны, и поэтому предсказуемы заранее.
В настоящей работе исследуется
стационарный процесс для случая, когда на начальный диаметр иглы не наложено
никаких ограничений. Показано, что этот процесс описывается обыкновенным
дифференциальным уравнением, которое допускает аналитическое исследование. В
результате исследования получена оценка зависимости радиуса закругления иглы от
параметров заготовки.
§1. Получение игл
методом электрохимического травления
 В туннельной
микроскопии используются иглы со сверхмалым радиусом закругления конца (до 1
нанометра и менее). Такие иглы можно получить в процессе электрохимического
травления тонкой проволоки (диаметром 0,2 – 0,3 мм) из медленно окисляющихся
металлов (например, вольфрама). Наибольшее распространение получил процесс
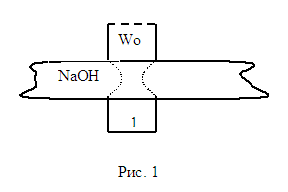
травления в пленке едкого натра (рис.1) [1].
В туннельной
микроскопии используются иглы со сверхмалым радиусом закругления конца (до 1
нанометра и менее). Такие иглы можно получить в процессе электрохимического
травления тонкой проволоки (диаметром 0,2 – 0,3 мм) из медленно окисляющихся
металлов (например, вольфрама). Наибольшее распространение получил процесс
травления в пленке едкого натра (рис.1) [1].
Во время нахождения проволоки в
пленке, часть вещества металла стравливается и к некоторому моменту времени нижняя
часть проволоки (1 на рис. 1) под действием собственной тяжести падает, при
этом на месте разрыва образуется игла, так как слой металла уменьшается в
процессе деформации постепенно.
Оценки показывают, что технология
травления игл в пленке позволяет получать достаточно острые иглы.
Действительно, деформация проволоки ε под действием веса P
ее нижнего конца дается формулой [2] : ![]() , где E – модуль упругости
(примерно 1.10-6 кг/см2), d
– диаметр поперечного сечения проволоки в месте отрыва. Из теории пластичности
известно, что металлическая проволока разрывается при деформациях, лежащих в
диапазоне 0,03 - 0,1. Расчеты с использованием формулы для величины деформации
показывают, что при диаметре иглы d = 0,3 мм и длине
свешивающегося конца 3 мм, диаметр в месте разрыва получается равным всего 30
нм.
, где E – модуль упругости
(примерно 1.10-6 кг/см2), d
– диаметр поперечного сечения проволоки в месте отрыва. Из теории пластичности
известно, что металлическая проволока разрывается при деформациях, лежащих в
диапазоне 0,03 - 0,1. Расчеты с использованием формулы для величины деформации
показывают, что при диаметре иглы d = 0,3 мм и длине
свешивающегося конца 3 мм, диаметр в месте разрыва получается равным всего 30
нм.
Эта величина сама по себе достаточно
мала. Выбирая подходящие материалы, можно получать еще более тонкие иглы.
Например, предполагается, что у вольфрама в месте разрыва образуются волоски,
диаметр которых имеет порядок нанометров.
 Вторым
способом получения сверхострых игл является процесс электрохимической заточки
проволоки в растворе. Он происходит следующим образом.
Вторым
способом получения сверхострых игл является процесс электрохимической заточки
проволоки в растворе. Он происходит следующим образом.
Тонкая проволока помещается в раствор едкого натра и подается напряжение между электродом и проволокой. Постепенно проволока истончается и на своем конце приобретает форму иглы (рис. 2). Этот процесс обычно используется для подтравливания проволоки с целью уменьшения ее диаметра и получения более тонкой иглы в первом процессе.
Вместе с тем, представляется возможным получение иглы со сверхмалым закруглением только во втором процессе. Это предположение основано на том, что уже в первом процессе возможно уменьшение диаметра проволоки до сколь угодно малой величины, и получение сколь угодно малого радиуса закругления. Кроме того, возможно использование технологий растяжения и отрыва конца иглы под действием силы тяжести. Момент отрыва гипотетически можно установить по скачку тока электрохимической реакции.
В связи со сказанным представляет интерес исследование формы, которую принимает игла в процессе электрохимического травления. В настоящей работе делается попытка выяснить, существует ли такой профиль, который не изменяется при травлении. Существование такого профиля позволило бы построить управление процессом получения иглы.
При этом сам факт существования такого профиля не является очевидным. Отличие рассматриваемой математической модели процесса травления состоит в том, что на ширину иглы не накладывается ограничений. В реальных условиях игла получается из проволоки конечного диаметра, поэтому ширина получаемой иглы не может его превосходить. Если же в задачу добавить ограничение на диаметр, то форма иглы соответствующим образом изменится. В модели учтем, что коэффициент скорости растворения не является постоянным и может зависит от различных факторов, например, локальной кривизны проволоки.
§2.
Математические модели процесса электрохимического травления иглы
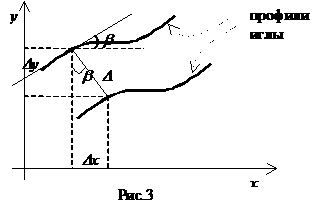
На рис. 3 изображены профили иглы в различные моменты времени. Из рисунка имеем:
![]() ,
, ![]() .
.
Координаты каждой точки кривой преобразуются по следующему закону:
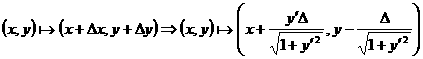 .
.
 Для описания процесса
электрохимического травления можно пользоваться различными моделями. Рассмотрим
некоторые из них.
Для описания процесса
электрохимического травления можно пользоваться различными моделями. Рассмотрим
некоторые из них.
Система уравнений в частных производных от
двух переменных.
Зависимость смещения точки пропорционально времени протекания реакции
выразим равенством Δ = k Δt. На
скорость реакции, которая задается коэффициентом k пока не накладывается никаких ограничений.
Тогда получим систему
уравнений, описывающую процесс травления для любого коэффициента скорости
растворимости:
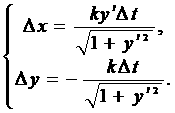
В дифференциальной форме
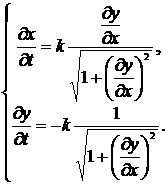
1.
Система уравнений в частных производных от одной переменной.
Предположим, что в любой момент
времени игла является симметричной относительно своей оси.
Обозначим ее профиль в виде функции y
= f(x,t) (переменная x
направлена вдоль оси). Принимая во внимание, что ![]() , получим
, получим
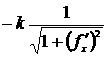
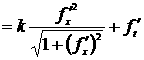 .
.
После преобразований ![]() ,
,![]() , где φ(x)
– начальная форма иглы.
, где φ(x)
– начальная форма иглы.
2.
Учет зависимости скорости травления от кривизны профиля.
Известно, что скорость реакции отличается от средней тем больше, чем большую кривизну имеет поверхность, причем на выпуклых участках она больше, на вогнутых - меньше.
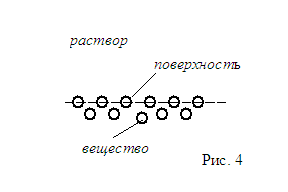
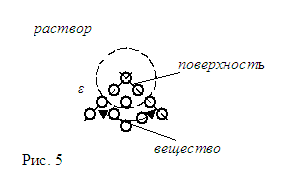
В случае ровной поверхности (на рис. 4 кривизна
равна нулю) атомы, расположенные на ней испытывают примерно одинаковое влияние
(притяжение) как атомов самого вещества, так и вещества растворителя. Однако
соотношение между ними резко меняется на неровных участках (на рис. 5 кривизна
отрицательна), так как степень влияния пропорциональна отношению площадей частей
сферы, заключенной внутри телесных углов вещества и растворителя.
Характер
изменения этого соотношения можно представить себе следующим образом. Если
обозначить через ε отношение угла при
вершине неровности к развернутому полному углу (π), то принимая во
внимание, что площадь поверхности внутри телесного угла пропорциональна
квадрату его раствора, получим, что отношение площадей можно представить
отношением 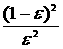 . График этой зависимости приведен на рис. 6.
. График этой зависимости приведен на рис. 6.
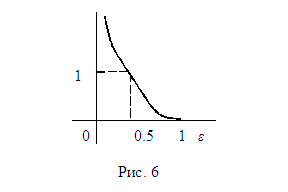 Непосредственно
из рисунка следует, что скорость растворения быстро увеличивается при
уменьшении угла ε (острая выпуклость) и уменьшается до 0 при его
увеличении (глубокая впадина).
Непосредственно
из рисунка следует, что скорость растворения быстро увеличивается при
уменьшении угла ε (острая выпуклость) и уменьшается до 0 при его
увеличении (глубокая впадина).
Зависимость
скорости растворения от кривизны можно учесть с помощью формулы k(x) = w(K(x)), в которой K(x) – кривизна
поверхности в точке. Функция w учитывает знак кривизны с учетом того, что выпуклые
части поверхности травятся быстрее, вогнутые – медленнее. Если поверхность иглы задается в виде функции f(x,t), то
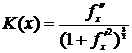 .
.
В итоге уравнение для изменения поверхности
иглы в процессе травления принимает вид:
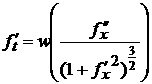
![]() ,
,
с начальным условием в виде контура проволоки φ(x): ![]() .
.
§3.
Стационарные решения
Рассмотрим случай, когда в процессе
травления иглы ее форма (f(x,t)) не меняется. Для
этого достаточно, например, чтобы решение удовлетворяло равенству f(x,t) = g(x
- сt). Геометрически оно означает, что конец иглы
движется (растворяясь) вдоль оси с постоянной скоростью a.
Проволока, из которой получается игла, предполагается бесконечной.
Если скорость растворимости k
постоянна для всех точек поверхности, то стационарное решение должно
удовлетворять уравнению
![]() ,
,
решение которого дает конус.
дает конус.
Недостаток рассмотренной модели
состоит в том, что острие конуса имеет нулевой радиус закругления и, по этой
причине не может быть взято в качестве приближения к результату процесса
травления. Более существенно, что при этом не получается оценки на радиус
закругления иглы ни снизу ни сверху.
Для того, чтобы учесть то
обстоятельство, что участки с большой кривизной травятся быстрее, выберем
коэффициент k пропорциональным кривизне. Будем также считать,
что в любой момент времени игла является выпуклой. В этом случае функция w
должна быть отрицательной. Примем ее равной константе. Рассмотрим плюсы и
минусы такого подхода.
1. При нулевой кривизне
скорость травления становится бесконечной. Поэтому
трудно ожидать, что в качестве решения получатся фигуры со сверхмалым радиусом
закругления. Полученная оценка радиуса закругления будет оценкой сверху.
2. При малой кривизне, т.е. для плоских участков, скорость
травления приближается к нулевой, что не соответствует действительности.
Противоречие с реальностью можно уменьшить, если предположить, что в процессе
травления игла вдвигается в раствор.
Можно также принять во внимание, что в процессе
реакции образуются пузырьки газа, которые, поднимаясь вверх, препятствует
поступлению щелочи к игле. Этот процесс приводит к существенному замедлению реакции
в верхних слоях.
Уравнение образующего контура поверхности иглы примет вид:
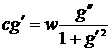 .
.
После преобразований приходим к уравнению
![]() .
.
Делая замену ![]() , понижаем порядок уравнения
, понижаем порядок уравнения
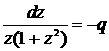
и приходим к решению ![]() . Откуда следует, что
. Откуда следует, что 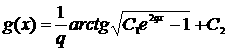 .
.
С учетом рассматриваемого случая, в котором принимается, что при нулевом
радиусе закругления скорость травления иглы бесконечна, получаем условие ![]() . Откуда C1 = 1. Кроме того, не ограничивая общности рассмотрения,
можно принять g(0) = 0. В этом случае, C2 = 0.
График функции
. Откуда C1 = 1. Кроме того, не ограничивая общности рассмотрения,
можно принять g(0) = 0. В этом случае, C2 = 0.
График функции 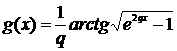 изображен на рис. 7. Он показывает форму иглы в стационарном
случае.
изображен на рис. 7. Он показывает форму иглы в стационарном
случае.
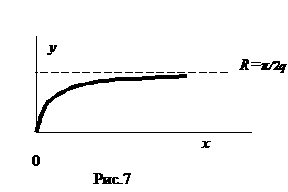
Факт
существования стационарного решения говорит о наличии таких условий, при
которых форма иглы не меняется в процессе растворения. Вопрос о том, будет ли
процесс формирования иглы из проволоки (имеющей форму цилиндра) сходиться к
стационарной форме, требует отдельного рассмотрения.
На конце иглы
(при ![]() )
) 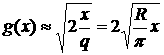 . Чем меньше коэффициент
при
. Чем меньше коэффициент
при ![]() , тем острее игла. В соответствии с полученной формулой в
стационарном решении радиус закругления конца зависит только от диаметра проволоки.
Записав это равенство в виде
, тем острее игла. В соответствии с полученной формулой в
стационарном решении радиус закругления конца зависит только от диаметра проволоки.
Записав это равенство в виде ![]() , находим, что радиус
закругления равен
, находим, что радиус
закругления равен ![]() , что означает, что малый радиус закругления может быть
получен при малом диаметре проволоки. Это объясняется сделанным предположением
о том, что при нулевом радиусе закругления скорость травления бесконечна. Покажем это.
, что означает, что малый радиус закругления может быть
получен при малом диаметре проволоки. Это объясняется сделанным предположением
о том, что при нулевом радиусе закругления скорость травления бесконечна. Покажем это.
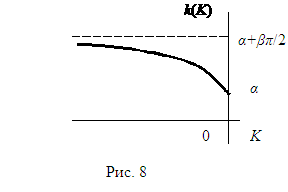
Для того, чтобы учесть особенности растворения при малых и больших
значениях кривизны предположим, что скорость растворения дается формулой: ![]() . Коэффициенты α и β положительны,
кривизна K(x) отрицательна (так как функция g(x) предполагается
выпуклой). График зависимости приведен на рис. 8. Выбирая подходящими
коэффициенты, можно получить любое соотношение между скоростями растворимости
при малых и больших величинах кривизны. В итоге приходим к уравнению
. Коэффициенты α и β положительны,
кривизна K(x) отрицательна (так как функция g(x) предполагается
выпуклой). График зависимости приведен на рис. 8. Выбирая подходящими
коэффициенты, можно получить любое соотношение между скоростями растворимости
при малых и больших величинах кривизны. В итоге приходим к уравнению
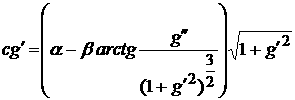 .
.
Оно запрещает решение в виде стержня,
так как не существует решения для α ≠ 0 с асимптотическими условиями ![]() ,
, ![]() при
при ![]() .
.
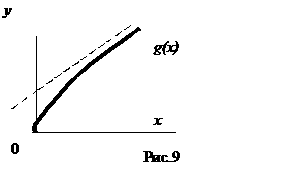
Вместе с тем, возможно решение типа конуса (рис. 9): ![]() ,
, ![]() при
при ![]() .
.
Приняв раствор конуса за γ (![]() ), получим для него уравнение:
), получим для него уравнение: ![]() , которое имеет решение для всех значений α. При этом оказывается, что скорость
растворения иглы в стационарном процессе зависит от только угла раствора конуса:
, которое имеет решение для всех значений α. При этом оказывается, что скорость
растворения иглы в стационарном процессе зависит от только угла раствора конуса:
 .
.
Для того, чтобы
найти радиус закругления иглы рассмотрим решение, в котором ![]() велико. В этом случае уравнение упрощается:
велико. В этом случае уравнение упрощается:
 .
.
Решая
его, получим:
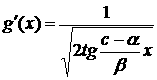 и
и 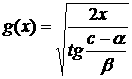 =
=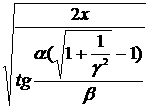 .
.
Непосредственно из
формулы решения следует, что величина радиуса закругления иглы явно зависит от
раствора конуса. Случаю, малого радиуса
закругления соответствуют большие значения знаменателя. Для того, чтобы
удовлетворить этому условию достаточно взять γ << 1. Тогда формула решения упрощается: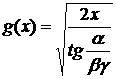 . Эта формула
позволяет сделать вывод о том, что за счет выбора заготовки в виде
конуса с малым раствором можно обеспечить получение иглы со сколь угодно малым
радиусом закругления.
. Эта формула
позволяет сделать вывод о том, что за счет выбора заготовки в виде
конуса с малым раствором можно обеспечить получение иглы со сколь угодно малым
радиусом закругления.
![]()
![]() Результаты и выводы
Результаты и выводы
В работе построена математическая
модель процесса электрохимического травления иглы в растворе. Предложены
способы ее упрощения. Рассмотрены стационарные решения. Получены следующие результаты.
1.
Установлено существование стационарных решений в случаях, если для
всех точек поверхности скорость реакции постоянна либо пропорциональна кривизне
поверхности. Последний случай приблизительно описывает технологию получения
иглы, когда она в процессе травления вдвигается в раствор.
2.
Получены оценки на форму поверхности иглы в случае, когда зависимость
скорости травления от кривизны имеет характеристику, близкую к реальной.
3.
Показано, что с
целью получения игл с минимальными радиусами закругления можно использовать
конические иглы с предельно малыми углами раствора конуса.
Литература
1. В. Миронов. Основы
сканирующей зондовой микроскопии. М.: Техносфера, 2004.
2. С.П.Тимошенко. Сопротивление
материалов. М.: Наука. 1965.