Численный метод решения системы Гельмгольца

( The Numerical Method of the System Helmholtz Solution
Preprint, Inst. Appl. Math., the Russian Academy of Science)

    Настоящая работа посвящена описанию некоторых существенных сторон численных алгоритмов, которые  использовались нами при решении  задачи о микроволновом стримерном  разряде в газе. В общем случае задача трехмерна и состоит в решении системы квазилинейных уравнений эллиптического, гиперболического и параболического типов. Уравнения учитывают процессы электродинамики, гидродинамики, диффузии, теплопроводности, ионизации, химической кинетики и т.п. В названии  данной работы отражено основное содержание ее.

    Полное описание рассматриваемых моделей, точные постановки задач и результаты расчетов содержатся в [1]-[8].

    1˚ Одним из существенных элементов моделей является взаимодействие электромагнитного излучения высокой частоты с проводящим объектом  в виде  плазменного волокна - стримером. Не касаясь здесь вопросов обоснования отметим, что описание этого взаимодействия с помощью  уравнений Максвелла сводится (в соответствующих единицах)  к  системе Гельмгольца эллиптического типа  для  комп­лекс­ных  амплитуд  возмущения  электромагнитного поля  E, H  

                    (2)

где E0 - амплитуда падающей волны, σ - проводимость - заданные функции. Задача ставится во всем пространстве с условиями Зоммерфельда   на бесконечности

E, H ~ exp(i|x|)/|x|   при  |x| ® ¥.    (3)

    Исключая H или E можно свести систему (1), (2) к системе Гельмгольца для E

или для H

    Дискретизация задачи состоит в указании множества расчетных точек и способа замены производных конечными разностями. Избранный нами способ проще всего описать словами. Пространство разбивается на элементарные расчетные ячейки - прямоугольные параллелепипеды с ребрами размера Δx, Δy, Δz, параллельными осям координат. В середине каждого ребра считается компонента электрического поля, параллельная этому ребру. В середине каждой грани считается нормальная к ней компонента магнитного поля. Все производные заменяются симметричными, центральными, разностями. Нетрудно убедиться, что построенное таким образом множество точек порождает систему линейных уравнений, для замыкания которой достаточно задания на внешней границе касательных к ней компонент электрического поля.

    Хотя задача ставится во всем пространстве, интерес представляет решение лишь в окрестности стримера. Сделать область расчета ограниченной можно с помощью следующего приема.

    Вне стримера  s=0,  и каждое из уравнений (4), (5) превращается в уравнение Гельмгольца   (D+1)u=0   для каждой из компонент поля. Как известно,  решение этого уравнения  может быть представлено в виде потенциала слоя, сосредоточенного на границе Г₀  какой-либо области, полностью содержащей проводящий стример,

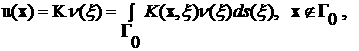                           (6)

где  

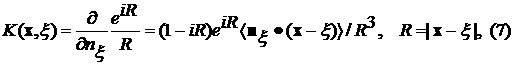
а n  определяется из интегрального уравнения на поверхности Г₀

                                                           (8)

    Таким образом, зная решение на Γ₀  (вне стримера) можем из (8) найти ν, а затем, пользуясь (6), и решение в любой точке пространства вне Γ_0..

    Дискретная реализация этих соотношений (на множестве расчетных точек) и исключение из полученной системы линейных уравнений значений n  дает матрицу – оператор О, отображающий решение с Г₀ на любую внешнюю по отношению к ней поверхность Г₁

                                       u₁=Оu₀                                                     (9)

Это соотношение (эквивалентное условию Зоммерфельда) и используется в качестве граничного условия при решении системы только внутри Г₁. Его выполнение может достигаться итерационным путем. Система решается внутри Г₁  при заданных значениях на границе. Полученные значения на Г₀  дают с помощью (9) новые данные на Г₁ , процесс решения повторяется, и т.д.

    В трехмерном случае объем информации слишком велик, и прямые методы решения линейных систем (1), (2) или (3), (4) нереализуемы. Приходится использовать итерационный процесс и на уровне решения системы уравнений, вводя фиктивное время (номер итерации). Возможны  разные способы. Опишем один из них.

    Дискретный аналог системы (1), (2), построенный  указанным  выше способом,  запишем коротко в виде  Du=f , где

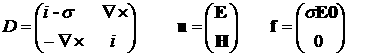                   (10)

Рассмотрим итерационный процесс

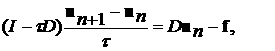                                                       (11)

где I – единичный оператор, n – номер итерации, t - итерационный параметр.

    Проверка сходимости на собственных функциях оператора D, при посто­ян­ных s,  дает положительный результат. Показатель сходимости l=1/(1-td),

где d =i-s/2±( s²/4-k²)^1/2 ,  k~1/Δ,  Δ  – шаг расчетной сетки. Так как Red≤0, то |l|<1. Однако, обращение оператора  I-tD  ничуть не проще прямого решения  системы. Но, если t мало, можно  воспользоваться разложением                      (I-tD)^-1 = I+tD+t²D² + …,  справедливым при  |td|<1,  и,  ограничившись несколькими членами, сделать метод расчета почти прямым.

   Требование малости t  можно ослабить, если выделить из D  легко обращаемую (диагональную) часть D₀ . Полагая D=D₀ + D₁, умножим (11) на  (I-tD₀)^-1.

Получим 

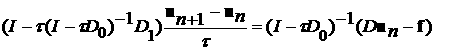(12)

Оператор  D  в разложении заменяется на  (I-tD₀)^-1D₁  и  условие малости t оказывается довольно слабым, t  должно быть порядка шага расчетной сетки. 

    Можно также использовать  различные методы переменных направлений и даже явные схемы, но все они не безупречны. Первые обладают неприятной особенностью - зависимостью результата от порядка перебора направлений прогонки. Вторые  - слишком объемны.

    Описанный алгоритм вычисления поля  (10)-(12)  реализуется путем естественной, указанной выше, аппроксимации оператора градиента. При этом касатель­ные компоненты электрического поля на внешней границе -  прямоугольном параллелепипеде ПП₁  считаются заданными. Они зависят от  значений, полученных в предыдущем расчете на некотором внутреннем параллелепипеде ПП₀, полностью содержащим область, где s>0, . Эта связь, определяемая формулами (6)-(9), реализуется следующим образом.

    Поверхности ПП₀ и ПП₁ разбиваются на прямоугольные элементы  и  интегралы по этим поверхностям заменяются суммами. В результате значения в точках внешней границы ПП₁  выражаются формулой  u₁=K₁₀n , где  K₁₀ – матрица, а n -  значения, которые должны определяться из системы уравнений на ПП₀  вида (2pI+K₀₀)n=u₀. Исключая из этих выражений n, получаем

u₁=K₁₀(2pI+K₀₀) ^-1u₀,

т.е. матрицу О (9), связывающую значения касательных компонент на внешней границе и ПП₀. Соотношение (9) замыкает систему уравнений, являясь ее частью, и может так же быть включенным в итерационный процесс, например, в виде

с некоторым  θ, вообще говоря, комплексным.

    Таким образом, процесс оказывается итерационно-трехступенчатым. Он определяется количеством внешних итераций с параметром  θ, количеством внутренних с параметром  τ  и количеством членов в разложении оператора. Значения параметров и количество итераций подбираются, в основном, эмпирически.

    Полученные  распределения полей (полных, вместе с фоновыми значениями)   передаются в обработку другой, основной, части алгоритма, где используются для вычисления величин  Джоулева нагрева и  магнитного давления. В свою очередь она возвращает новое распределение  проводимости σ(x) на следующем шаге по времени. Поскольку от предыдущего оно отличается незначительно, итерации можно начинать с последних полученных на предыдущем цикле значений поля.

    Двумерные, аксиально-симметричные, варианты этой же задачи значительно проще. Алгоритм (10)-(12) здесь не нужен. От системы  остается одно уравнение вида (5) для угловой компоненты магнитного поля, которое решается стандартным методом матричной прогонки. Значения двух компонент электрического поля выражаются через неё. Итерации сохраняются только для граничных условий, которые строятся тем же приемом (6)-(8), разумеется, с другой функцией K(x,ξ).  Интересная информация по  этой тематике содержится в работах [9]-[11].

    2˚ Для иллюстрации приведем пример одного конкретного расчета.   Проводящая область – эллипсоид, вытянутый вдоль оси z c полуосями X=Y=0.1,  Z=0.5. Проводимость в центре  s=100  и  гладко  спадает к краям  до нуля 

σ=100(1-(x/X)²-(y/Y)²-(z/Z)²)²

    На рисунке 1 изображена примерная конфигурация расчетной области в сечении y=0.

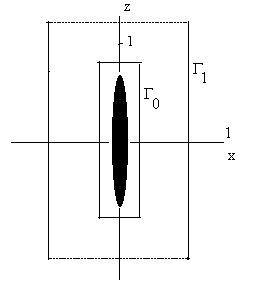
Рис.1 Конфигурация области расчета.

    Размеры параллелепипедов - областей : внешняя ПП₁= Г₁ - 1.4´1.4´2.4, внутренняя  - ПП₀ = Г₀ - 0.4´0.4´1.5. При этом, для подсчета интегралов К они разбиваются, соответственно, на 28´28´60  и  4´4´30 интервалов.

    Падающая электромагнитная волна направлена вдоль оси x,  линейно поляризована - отличны от нуля лишь компоненты  E0_z=-H0_y=exp(ix).

    Расчетные параметры Δx= Δy=0.025, Δz=0.01. Параметр внешней итерации θ=0.1, внутренней τ=0.004. На каждую внешнюю итерацию производятся десять внутренних, а в разложении обратного оператора удерживаются четыре члена. Все эти значения типичны  и  в то же время случайны.

    Представление о характере итерационного процесса дает рис.2, на котором изображено поведение некоторых интегральных величин,  физически бессмысленных, но показательных :  суммы модулей решения и суммы модулей невязок.

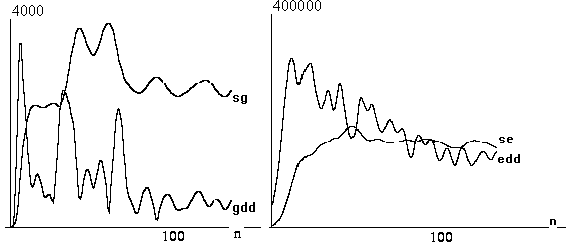
Рис.2 Поведение контрольных сумм модулей решения и невязок.

    Слева даны: сумма модулей граничных значений возмущения электрического поля sg и сумма модулей невязок, т.е. разностей левой и правой частей (9) - gdd. Справа - аналогичные величины, получаемые внутри расчетной области, т.е.  se= Σ|E| и  edd, равная сумме модулей левой части (1).

Начальные значения - нулевые  Е = Н = 0.

    Как видно, уже несколько десятков итераций достаточно для получения приемлемых результатов. Эффективность последующих итераций можно оценивать по-разному.

    К тому же в реальном процессе итерации начинаются с хорошего приближения, лишь уточняя его, и, во вторых, трудоемкость следует учитывать относительную, сравнивая с другими частями расчета. 

    Полученное решение демонстрирует рис.3, на котором даны профили модуля электрического поля |E+E0| и проводимости вдоль оси  z. Поскольку задача симметрична по z, мы даем результаты только для z>0 . Как видно, острый максимум поля (с четырехкратным превышением фонового значения) приходится на полюс эллипсоида. О том же свидетельствует рис.4, на котором изображены линии уровня модуля электрического поля с характерным максимумом на полюсе эллипсоида.

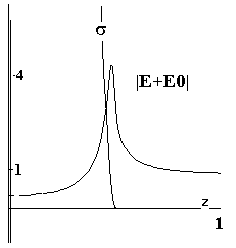
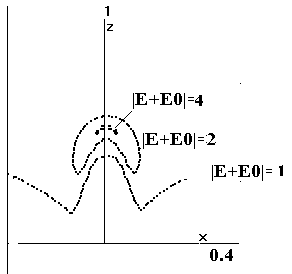
        Рис.3 Поле на оси z.              Рис.4 Распределение поля на y=0.

    На рис.5 показано распределение х - компоненты вектора Пойнтинга (вектора потока электромагнитной энергии)  F=Re[(E+E0)´(H+H0)*]  вдоль х при  у=0 и двух различных, указанных на рисунке, значениях  z.

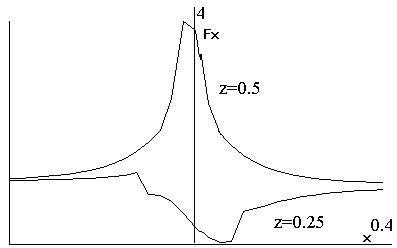
Рис.5 Распределение потока энергии F_x.

    Описать полностью все результаты даже одного конкретного расчета затруднительно, но уже приведенные позволяют утверждать, что при соответствующем выборе параметров можно всегда  добиться удовлетворительных результатов. А при несоответствующем, наоборот, получить расходимость. Что и демонстрирует рис.6, на котором изображено поведение контрольных сумм, тех же, что и на рис.2, но для варианта расчета, отличающегося от вышеописанного лишь одним параметром. А именно, величина проводимости уменьшена в сто раз.

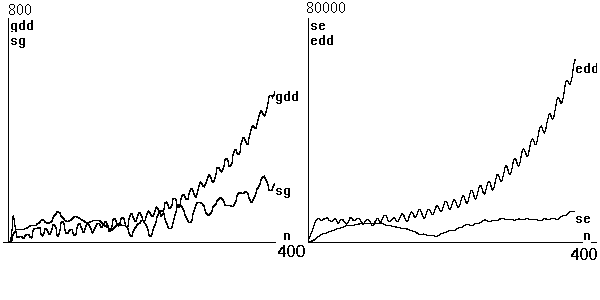
                   Рис.6 Контрольные суммы в варианте  σ ≤ 1.

  3˚ Основная часть модели представляет собой сложный плазмодинамический комплекс, учитывающий ионизацию, диффузию, теплопроводность, физико - химическую кинетику, гидродинамику и т.п. С математической  точки зрения  - это трехмерная квазилинейная система уравнений в частных производных гиперболическо  - параболического типа. Конкретный вид ее, приведенный в любой из работ [1]-[8], нам здесь не понадобится.

    Дело в том, что описывать использованные нами алгоритмы - это значит описывать хорошо известную вычислительную науку. Конкретные же реализации ее сопровождаются приемами вычислительного искусства, цель которых - отнюдь не получение точного решения, а всего лишь получение удовлетворительной информации за реальное время.

    Чтобы получить представление о предмете разговора ограничимся парой примеров. Для расчета гидродинамической части системы применяется давно и хорошо известная схема Лакса - Вендрофа. Ее недостатком является "шахматность" множества расчетных точек. Это мешает ей просто вписываться в множества расчетных точек другой природы, например, описанной выше электродинамической, да и неоправданно увеличивает их число. Выход простой - заменить значения в "лишних" точках средними по ближайшим нормальным точкам. Либо наоборот, интерполировать значения в нормальных точках на "лишние".

    Другой пример. Уравнение ионизации - диффузии  электронов имеет вид (в одномерном случае) U_t=aU_xx+bU. Используя простейшую обычную явную  разностную схему и исследуя ее устойчивость с помощью спектрального признака, получим, что коэффициент роста ошибки (на максимальной частоте) равен 1+∆t(b-4a/∆x²). Поэтому нужно либо уменьшать шаг сетки ∆x, либо увеличить а, введя искусственную диффузию, либо не обращать внимания на колебания  в  решении. А коэффициенты a и b отнюдь не константы и задача трехмерна.

    Кстати, уравнение U_t=aU_xx+bU имеет набор решений U=exp(λt+ikx), c

λ=b-ak² , т.е. имеет место неустойчивость на длинных волнах, именно ей  стримерный разряд обязан своим возникновением из небольшого локального возмущения.

    Результатов расчетов, даже примерных, мы здесь не приводим. Ими заполнена вся указанная далее литература.

                                                   Литература

[1] О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Инициация микроволнового стримерного разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2001, № 13.

[2] О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Численное исследование подкритического микроволнового разряда в газе высокого давления. // ЖТФ, 2002, Т. 72, Вып. 8.

[3] О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик,    К.В. Ходатаев. Расчеты микроволнового стримерного разряда в газе.

 // Препринт ИПМ им. М.В. Келдыша РАН,  2002, № 35.

[4] О.И. Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик. Расчеты микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2003, № 30.

[5] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев  Модель микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2004, № 16.

[6] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев 2-D модель микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2005, № 1.

[7] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик, К.В. Ходатаев 3-D модель микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2005, № 58.

[8] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик. Численное исследование микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2006, № 29.

[9] В.Ф. Дьяченко, Е.В.Шаханова, Взаимодействие волны с проводящим волокном. // Препринт ИПМ им. М.В. Келдыша РАН, 1993, № 29.

[10] О.И. Воскобойникова, Итерационный метод решения задачи о рассеянии волны. // Препринт ИПМ им. М.В. Келдыша РАН, 1997, № 38.

[11] О.И. Воскобойникова. Несколько расчетов микроволнового стримерного разряда. // Препринт ИПМ им. М.В. Келдыша РАН, 2001, № 57.