Аннотация
Получена одножидкостная гидродинамическая модель двухкомпонентной полностью ионизованной
квазинейтральной плазмы, не предполагающей равенства нулю массы электрона и позволяющей
исследовать двухжидкостые эффекты динамики плазмы в любом диапазоне погонных чисел. Учтены
основные диссипативные эффекты. Рассмотрены предельные переходы к классической и
холловской МГД.
Abstract
The system of one–fluid hydrodynamic equations for two–component quasineutral stripped
plasma taking into account dissipative effects is obtained. Electron's mass in view of
system presented do not equal to zero. The two–component's effects may be investigated
on a basis of system obtained. At last, MHD–limit and Hall MHP–limit are considered.
Введение. Гидродинамические модели широко используются для
исследования динамики плазмы. Особенно часто применяются одножидкостные модели
(например, МГД – уравнения), в которых считается равной нулю масса электрона.
Представляет значительный интерес построение одножидкостной гидродинамической
теории плазмодинамики без этого допущения. В этой работе указан конкретный
способ такого построения, составляющий содержание так называемой двухжидкостной
ЭМГД – теории (ЭлектроМагнитной ГидроДинамики).
Как известно,
МГД пригодна для исследования преимущественно крупномасштабных процессов в
плотной плазме. Формально требуется, чтобы погонное число частиц плазмы было
достаточно большим. Для изучения мелкомасштабных процессов и процессов в разреженной плазме обязателен
учет инерции электронов, что с необходимостью приводит к рассмотрению
двухжидкостной гидродинамики плазмы. Оказывается, однако, что двухжидкостную
гидродинамику нерелятивистской плазмы удается свести к одножидкостной
[1]. Это простое, но неочевидное наблюдение приводит в итоге к формально
одножидкостным уравнениям двухжидкостной электромагнитной гидродинамики – ЭМГД – уравнениям , применимость которых уже
не зависит от величины погонного числа частиц. Формальная одножидкостность
позволяет успешно решать многие задачи плазмодинамики, а получаемые при этом
результаты приводят к интересным и нетривиальным двухжидкостным эффектам коллективного течения электронов и ионов.
Основные
идеи развиваемого подхода были изложены
почти 20 лет назад [1]. С тех пор в
условиях целенаправленного уничтожения отечественной фундаментальной науки
удалось продвинуться по ряду важных направлений [2,3,4,5,6]. В данной работе на
новом уровне понимания изложены ключевые положения двухжидкостной ЭМГД –
теории: уравнения динамики плазмы, закон сохранения энергии, дисперсионные соотношения, условия на разрыве, предельные переходы и
пр..
§1. Основные уравнения (бездиссипативный случай).
Набросаем схему учёта инерции электронов в
контексте одножидкостного формализма, возвращаясь впоследствии к более
детальному рассмотрению отдельных её этапов.
Исходной
точкой является двухжидкостная гидродинамическая модель плазмы (для простоты
ниже рассматривается только бездиссипативный случай и предполагается отсутствие
гравитационных и прочих внешних сил):
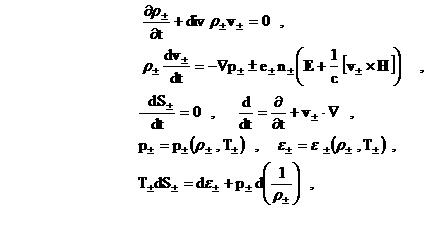 (1) (1)
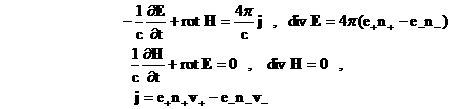 (2) (2)
Выше для
электронного и ионного газов написан стандартный гидродинамический формализм
(1), который замыкается уравнениями электродинамики Максвелла (2). Предполагая
плазму нерелятивистской 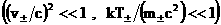 , зачеркнем в системе (1,2) все члены релятивистского порядка
малости. Таких членов всего два, и они содержатся в уравнениях Максвелла –
это , зачеркнем в системе (1,2) все члены релятивистского порядка
малости. Таких членов всего два, и они содержатся в уравнениях Максвелла –
это 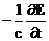 (ток смещения) и (ток смещения) и 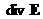 (Ниже эта процедура будет
выполнена математически корректно, поэтому здесь ограничимся сказанным.). В
итоге приходим к системе (1,3), где (Ниже эта процедура будет
выполнена математически корректно, поэтому здесь ограничимся сказанным.). В
итоге приходим к системе (1,3), где
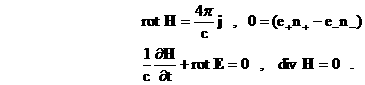 (3) (3)
Система
(1,3) получалась как промежуточный этап в ряде
работ, но всегда браковалась по следующей причине: считалось что в ней
из–за отбрасывания тока смещения в уравнениях Максвелла, отсутствует уравнение
для электрического поля 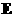 . Это, как мы увидим, ошибочное заключение приводило к
ошибочным действиям: чтобы получить уравнение на . Это, как мы увидим, ошибочное заключение приводило к
ошибочным действиям: чтобы получить уравнение на 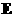 , в уравнении импульсов для электронов выбрасывался
инерционный член , в уравнении импульсов для электронов выбрасывался
инерционный член 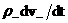 , что мотивировалось малостью отношения , что мотивировалось малостью отношения 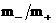 <<1. Не останавливаясь на критическом разборе указанных
тезисов, констатируем, что, в действительности, система (1,3) является
замкнутой и определенной ( количество
неизвестных совпадает с количеством уравнений). Плазма, согласно этой системе,
будет квазинейтральной <<1. Не останавливаясь на критическом разборе указанных
тезисов, констатируем, что, в действительности, система (1,3) является
замкнутой и определенной ( количество
неизвестных совпадает с количеством уравнений). Плазма, согласно этой системе,
будет квазинейтральной 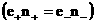 , а электромагнитное поле – квазистационарным. Что касается
уравнения для , а электромагнитное поле – квазистационарным. Что касается
уравнения для 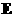 , оно получается заменой неизвестных в системе (1,3): , оно получается заменой неизвестных в системе (1,3):
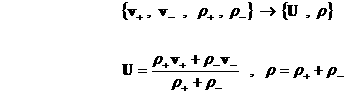 (4) (4)
Вектор 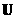 обычно называется коллективной, или массовой
гидродинамической скоростью плазмы
и равен скорости движения центра масс единичного объема плазмы. Обратное
преобразование имеет вид: обычно называется коллективной, или массовой
гидродинамической скоростью плазмы
и равен скорости движения центра масс единичного объема плазмы. Обратное
преобразование имеет вид:
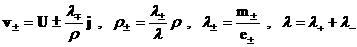 (5) (5)
Замена неизвестных (4) имеет смысл , поскольку из
двух неизвестных плотностей 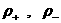 независимой является
(ввиду условия квазинейтральности независимой является
(ввиду условия квазинейтральности 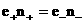 и соотношений и соотношений 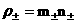 ) только одна, и то же верно для неизвестных скоростей ) только одна, и то же верно для неизвестных скоростей 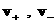 , ввиду закона Ампера: , ввиду закона Ампера:
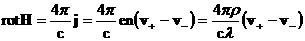
Подставляя в (1,3) выражения (5), после несложных
преобразований получим следующую систему:
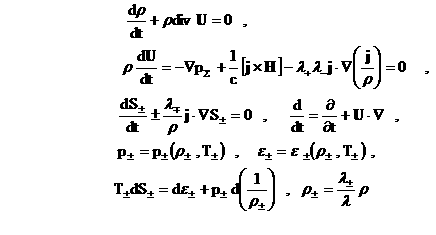 (6) (6)
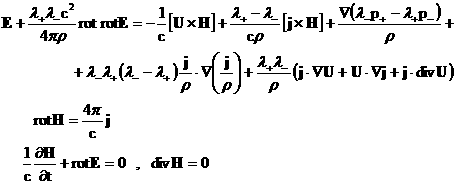   (7) (7)
Система (6,7) называется уравнениями двухжидкостной
электромагнитной гидродинамики плазмы, или ЭМГД – уравнениями.
Уравнения
неразрывности и импульсов (6) получаются сложением, соответственно, уравнений неразрывности и импульсов системы
(1), а уравнение для электрического поля
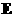 системы (7) (обобщенный
закон Ома) получается вычитанием из "+" – уравнения импульсов
системы (1) , умноженного на системы (7) (обобщенный
закон Ома) получается вычитанием из "+" – уравнения импульсов
системы (1) , умноженного на 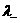 , " –" – уравнения импульсов, умноженного на , " –" – уравнения импульсов, умноженного на 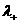 . Системы (6,7) и
(1,3) математически эквивалентны,
поскольку в силу условий квазинейтральности и закона Ампера "±" . Системы (6,7) и
(1,3) математически эквивалентны,
поскольку в силу условий квазинейтральности и закона Ампера "±"  – уравнения неразрывности системы (1) равносильны. – уравнения неразрывности системы (1) равносильны.
Решив
систему (6,7) и найдя, в частности 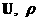 , по формулам (5) восстановим гидродинамические параметры
плазменных компонент. Принципиально важно, что электроны и ионы с получаемыми
таким образом параметрами удовлетворяют точным законам сохранения массы,
энергии, импульса (1). В то же время, как следует из (6,7), ЭМГД – уравнения
дают одножидкостную , но двухтемпературную гидродинамическую модель плазмы. , по формулам (5) восстановим гидродинамические параметры
плазменных компонент. Принципиально важно, что электроны и ионы с получаемыми
таким образом параметрами удовлетворяют точным законам сохранения массы,
энергии, импульса (1). В то же время, как следует из (6,7), ЭМГД – уравнения
дают одножидкостную , но двухтемпературную гидродинамическую модель плазмы.
Следует
подчеркнуть, что изначально вовсе не очевидно, что двухжидкостную систему (1,3)
математически корректно удасться свернуть в одножидкостную. Именно этот
простой, но важный факт лежит в основе
успешного аналитического и численного исследования двухжидкостной
системы (1,3), поскольку сводит такое исследование к изучению решений
одножидкостных уравнений (6,7), что значительно проще. Например, при численном
моделировании рассчитать эволюцию 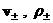 непосредственно из
уравнений системы (1,3) неудобно поскольку эти неизвестные функции не являются
независимыми и значит их дискретизация в каждый момент времени должна
удовлетворять дискретизациям уравнений связи ( условию квазинейтральности и
закону Ампера), что связано с дополнительными непростыми проблемами. непосредственно из
уравнений системы (1,3) неудобно поскольку эти неизвестные функции не являются
независимыми и значит их дискретизация в каждый момент времени должна
удовлетворять дискретизациям уравнений связи ( условию квазинейтральности и
закону Ампера), что связано с дополнительными непростыми проблемами.
Преимущество системы (6,7) по сравнению с системой (1,3) фактически
объясняется удачной заменой переменных (4). Хотя сама замена (4) была известна
давно, но её применение к системе (1,3), вероятно, впервые было проанализировано
в [1].
Сравним
ЭМГД – уравнения с уравнениями холловской МГД [7] – типичной одножидкостной гидродинамической моделью
плазмы, предполагающей массу электронов равной нулю. Рассмотрим наиболее
употребительный случай, когда электроны и ионы суть идеальные политропные газы
с общим показателем адиабаты 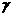 : :
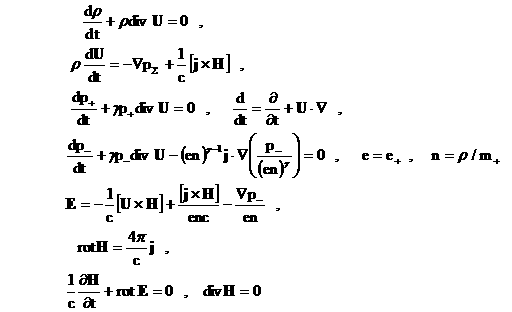 (8) (8)
Уравнения (8) образуют замкнутую систему
относительно неизвестных функций 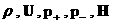 . Поле . Поле 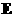 исключается из числа неизвестных с помощью равенства,
называемого обобщенным законом Ома. Система (8) получается из ЭМГД –
уравнений (6,7), если там формально положить всюду исключается из числа неизвестных с помощью равенства,
называемого обобщенным законом Ома. Система (8) получается из ЭМГД –
уравнений (6,7), если там формально положить всюду 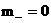 . Тогда . Тогда 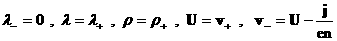 . При этом вместо энтропийных уравнений следует записать
уравнения для давлений . При этом вместо энтропийных уравнений следует записать
уравнения для давлений 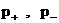 . Это вынужденная мера, поскольку при . Это вынужденная мера, поскольку при 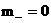 имеем имеем 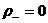 , а , а 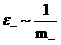 , , 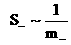 становятся
бесконечными, и возникают проблемы с уравнениями состояния и термодинамикой
электронов. Ниже будет показано, как получить холловскую МГД без этих неприятностей (количество которых увеличится. если считать
электроны неидеальным газом ). Сравнивая (6,7) с (8), заключаем, что ЭМГД – уравнения отличаются
от традиционных МГД – уравнений,
во–первых, дополнительной силой становятся
бесконечными, и возникают проблемы с уравнениями состояния и термодинамикой
электронов. Ниже будет показано, как получить холловскую МГД без этих неприятностей (количество которых увеличится. если считать
электроны неидеальным газом ). Сравнивая (6,7) с (8), заключаем, что ЭМГД – уравнения отличаются
от традиционных МГД – уравнений,
во–первых, дополнительной силой
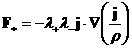 ,
(9) ,
(9)
действующей на единичный объем плазмы, и,
во–вторых, существенным усложнением обобщенного закона Ома. Теперь поле 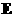 не вычисляется по
явной формуле через остальные параметры плазмы, а ищется как решение
(вырожденной) эллиптической системы уравнений относительно компонент не вычисляется по
явной формуле через остальные параметры плазмы, а ищется как решение
(вырожденной) эллиптической системы уравнений относительно компонент 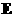 . С другой стороны, в
правой части уравнения для . С другой стороны, в
правой части уравнения для 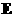 появилось несколько
новых ''холловских'' членов помимо
классического холловского
слагаемого появилось несколько
новых ''холловских'' членов помимо
классического холловского
слагаемого 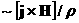 – это комбинации – это комбинации 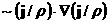 , , 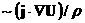 , , 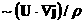 , , 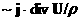 . Они ответственны за дополнительную генерацию поля . Они ответственны за дополнительную генерацию поля 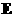 ,
особенно существенную в разреженной плазме, а вторая производная ,
особенно существенную в разреженной плазме, а вторая производная  может привести к появлению больших градиентов компонент
поля может привести к появлению больших градиентов компонент
поля 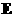
(пограничные и внутренние слои) даже в плотной
плазме.
Физический смысл силы 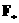 и дивергентный вид
ЭМГД – уравнений. Несложно проверить,
учитывая (5) и (9), что: и дивергентный вид
ЭМГД – уравнений. Несложно проверить,
учитывая (5) и (9), что:
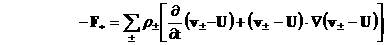 (10) (10)
Квадратная скобка в (10) равна ускорению частицы,
двигающейся в поле скоростей 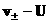 . Поэтому по второму
закону Ньютона правая часть (10) равна суммарной силе, действующей на электроны
и ионы в единичном объеме со стороны движущейся со скоростью . Поэтому по второму
закону Ньютона правая часть (10) равна суммарной силе, действующей на электроны
и ионы в единичном объеме со стороны движущейся со скоростью 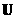 плазмы и вызывающей их относительные движения со
скоростями плазмы и вызывающей их относительные движения со
скоростями 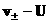 .
Тогда по третьему закону Ньютона на движущуюся со скоростью .
Тогда по третьему закону Ньютона на движущуюся со скоростью 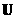 плазму со стороны электронов и ионов действует суммарная
сила, равная, согласно (10), плазму со стороны электронов и ионов действует суммарная
сила, равная, согласно (10), 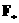 . Тем самым плазма выступает как новая,
"эффективная" сплошная среда с плотностью . Тем самым плазма выступает как новая,
"эффективная" сплошная среда с плотностью 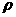 , гидродинамической скоростью , гидродинамической скоростью 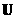 , тензором внутренних напряжений , тензором внутренних напряжений 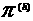 + +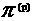 + +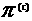 (см.
ниже), законом сохранения полной энергии и т.д., (см.
ниже), законом сохранения полной энергии и т.д.,  обладающая "коллективными" свойствами, не
сводящимися к простому сложению свойств слагающих её электронов, ионов и
электромагнитного поля. обладающая "коллективными" свойствами, не
сводящимися к простому сложению свойств слагающих её электронов, ионов и
электромагнитного поля.
Рассмотрим тензоры:
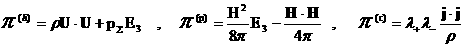 .
(11) .
(11)
Учитывая равенства
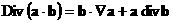 , , 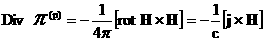 , ,
получим дивергентные выражения для силы 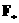 и правых частей
уравнения импульса и обобщенного закона Ома: и правых частей
уравнения импульса и обобщенного закона Ома:
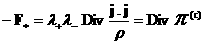
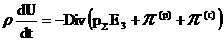
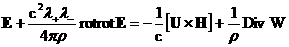 , ,
где тензор 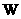 имеет вид: имеет вид:
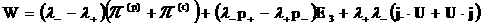 . (12) . (12)
В итоге
приходим к следующей дивергентной форме ЭМГД – уравнений:

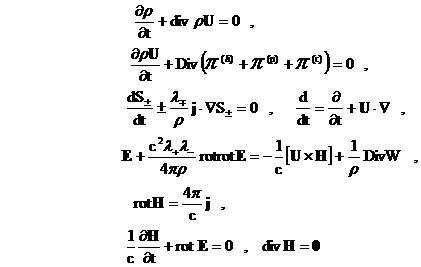 (13)
(13)
где тензоры 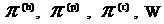 вычисляются по (11) и (12). вычисляются по (11) и (12).
Закон
сохранения энергии в ЭМГД. Из
термодинамических тождеств легко вытекают соотношения (индексы ''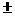 '' у всех величин
опущены): '' у всех величин
опущены):
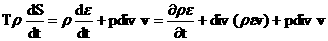 , ,
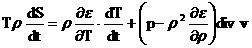 ,
(14) ,
(14)
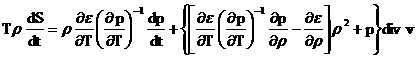 . .
Два последних тождества в (14) сильно упрощаются для
идеального политропного газа (см. ниже):
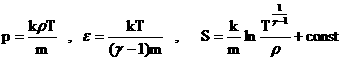 . .
Соотношения (14) позволяют вместо пары энтропийных уравнений написать
пару уравнений относительно любой другой термодинамической характеристики среды
(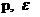 или или  ). Для плотности внутренней энергии это легко сделать в общем
случае: ). Для плотности внутренней энергии это легко сделать в общем
случае:
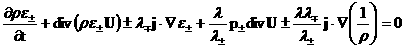 (15) (15)
Для температуры и давления простые явные выражения
получаются в случае идеальных политропных газов:
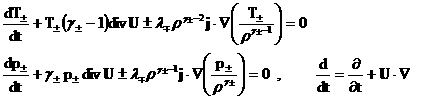 (16) (16)
Заметим,
что в последние два равенства масса 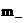 входит несингулярным
образом (что выше уже обыгрывалось при формальном переходе к холловской МГД). входит несингулярным
образом (что выше уже обыгрывалось при формальном переходе к холловской МГД).
Стандартным способом из уравнений (1) получается закон сохранения полной
энергии для компонент:
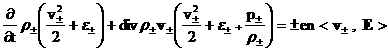 . .
Складывая эти равенства между собой и с законом
сохранения электромагнитной энергии для квазистационарного электромагнитного
поля:
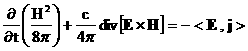 , ,
получим закон сохранения полной энергии в ЭМГД:
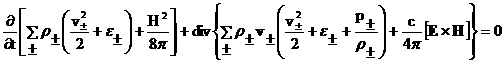 . .
Подставляя сюда соотношения (5), получим
окончательное выражение:
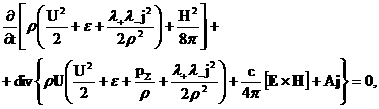 (17) (17)
где:
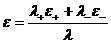 – объёмная плотность
внутренней энергии плазмы, – объёмная плотность
внутренней энергии плазмы,
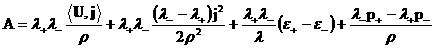 . .
Таким образом, у ЭМГД – плазмы имеется
дополнительная внутренняя энергия с объёмной плотностью
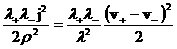 , ,
а полная энергия переносится не только вдоль вектора
гидродинамической скорости 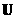 и вектора
Умова-Пойнтинга и вектора
Умова-Пойнтинга 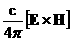 , но и вдоль вектора плотности тока , но и вдоль вектора плотности тока 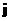 . .
Вырожденная эллиптичность обобщенного закона
Ома.
Обобщенный
закон Ома в ЭМГД, согласно (13), имеет вид:
 ,
(18) ,
(18)
где:
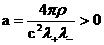 , , 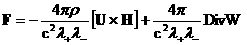 . .
Уравнение (18) является системой уравнений в частных
производных
относительно компонент вектора 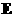 , причем вырожденной, поскольку, как нетрудно проверить,
характеристическая форма [8] этой системы тождественно равна нулю. Тем не менее
решение системы (18), как сейчас будет показано, сводится к решению некоторой
эллиптической системы уравнений. Это дает основание рассматривать обобщенный
закон Ома (18) как, хотя и вырожденную, но все же эллиптическую систему
уравнений. , причем вырожденной, поскольку, как нетрудно проверить,
характеристическая форма [8] этой системы тождественно равна нулю. Тем не менее
решение системы (18), как сейчас будет показано, сводится к решению некоторой
эллиптической системы уравнений. Это дает основание рассматривать обобщенный
закон Ома (18) как, хотя и вырожденную, но все же эллиптическую систему
уравнений.
Введем
новую неизвестную
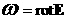 .
(19) .
(19)
Тогда из (18) выразим 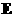 через через 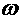 : :
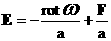 .
(20) .
(20)
Подставляя (20) в (19), получим уравнение на 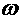 : :
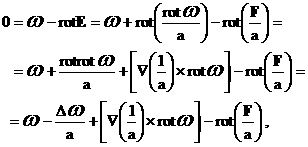
где использованы очевидные равенства:
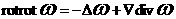 , , 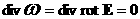
Итак, если 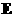 удовлетворяет (18), то
векторная функция удовлетворяет (18), то
векторная функция 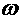 , вычисляемая
по (19), удовлетворяет, очевидно,
системе уравнений: , вычисляемая
по (19), удовлетворяет, очевидно,
системе уравнений:
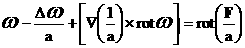 (21) (21)
и условию
 . (22) . (22)
Обратно, пусть решение (21) удовлетворяет условию
(22). Тогда поле 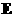 , вычисляемое по (20), удовлетворяет уравнению(18). В самом
деле, повторяя предыдущую выкладку, получим: , вычисляемое по (20), удовлетворяет уравнению(18). В самом
деле, повторяя предыдущую выкладку, получим:
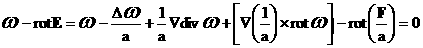
в силу (21) и  (22). Но тогда (18) следует из (20). (22). Но тогда (18) следует из (20).
Итак, для
решения системы (18) необходимо и достаточно решить эллиптическую
систему (21) с дополнительным ограничением (22), при этом решения
систем (18) и (21) связаны формулой (19). Теперь
убедимся, что условие (22) есть
ограничение только на граничные
значения 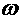 (подразумевается, что
система (21) решается в области (подразумевается, что
система (21) решается в области 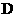 с границей с границей 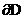 ). Для этого перепишем систему (21) в виде: ). Для этого перепишем систему (21) в виде:
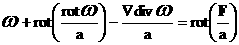 .. ..
Применяя оператор 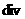 к обеим частям
последнего равенства, получим: к обеим частям
последнего равенства, получим:
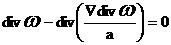 . .
Отсюда для функции
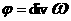  получаем эллиптическое
уравнение: получаем эллиптическое
уравнение:
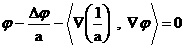
Поскольку 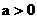 всюду в всюду в 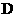 , то из принципа максимума для эллиптических уравнений [9]
следует, что , то из принципа максимума для эллиптических уравнений [9]
следует, что 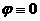 в в 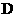 тогда и только тогда,
когда тогда и только тогда,
когда 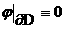 . .
Итак, 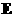 является решением
системы (18) в области является решением
системы (18) в области 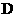 тогда и только тогда, когда функция тогда и только тогда, когда функция 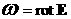 является решением в является решением в 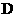 эллиптической системы уравнений (21) с дополнительным
граничным условием эллиптической системы уравнений (21) с дополнительным
граничным условием 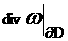 =0. Таким образом,
граничные условия для системы (21) должны удовлетворять дополнительному
соотношению =0. Таким образом,
граничные условия для системы (21) должны удовлетворять дополнительному
соотношению 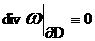 .
В появлении
дополнительного граничного условия и состоит вырождение эллиптической системы
(18). Этот вывод относится
преимущественно к трёхмерным задачам (и для них наличие дополнительного
граничного условия, скорей всего, благо). Для одномерных и двумерных задач
система (18) сводится к паре эллиптических уравнений без всяких дополнительных
граничных условий. Рассмотрим характерный пример двумерной осесимметричной
задачи. .
В появлении
дополнительного граничного условия и состоит вырождение эллиптической системы
(18). Этот вывод относится
преимущественно к трёхмерным задачам (и для них наличие дополнительного
граничного условия, скорей всего, благо). Для одномерных и двумерных задач
система (18) сводится к паре эллиптических уравнений без всяких дополнительных
граничных условий. Рассмотрим характерный пример двумерной осесимметричной
задачи.
Тогда
система (18) даёт:
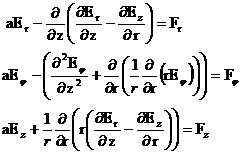 (18`) (18`)
Второе уравнение системы (18`) является
эллиптическим относительно 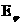 (а (а 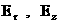 в него не входят) и
дополненное краевыми условиями позволяет найти в него не входят) и
дополненное краевыми условиями позволяет найти 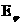 .
Для нахождения .
Для нахождения 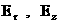 из первого и третьего уравнений системы (18`),
введем новую неизвестную из первого и третьего уравнений системы (18`),
введем новую неизвестную
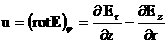 (19`) (19`)
Тогда из (18`):
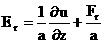 , , 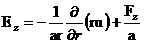 (20`) (20`)
Подставляя (20`) в (19`), получим эллиптическое
уравнение для нахождения 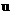 : :
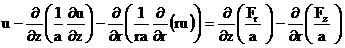 (21`) (21`)
Дополненное граничными условиями, оно позволяет
найти 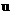 , после чего по (20`) вычисляются , после чего по (20`) вычисляются 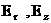 , которые, очевидно,
дают решение (18`). Итак, решение
системы (18) в осесимметричном случае сводится к решению пары эллиптических
уравнений без всяких дополнительных граничных условий. Аналогично в случае
цилиндрической симметрии из (18`) следует, что , которые, очевидно,
дают решение (18`). Итак, решение
системы (18) в осесимметричном случае сводится к решению пары эллиптических
уравнений без всяких дополнительных граничных условий. Аналогично в случае
цилиндрической симметрии из (18`) следует, что 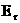 ищется в конечном
виде, а для нахождения ищется в конечном
виде, а для нахождения 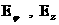 получаем тоже пару
эллиптических уравнений без дополнительных граничных условий. получаем тоже пару
эллиптических уравнений без дополнительных граничных условий.
§2 Уравнения ЭМГД – теории с учетом диссипаций.
Учтем теперь
влияние на динамику плазмы вязкости и теплопроводности электронов и ионов,
омического сопротивления и других диссипативных факторов. Тогда исходная
система (1) перепишется в виде:
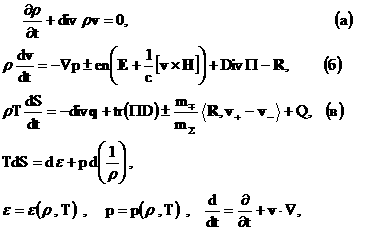 (1`) (1`)
где 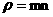 , причем каждое уравнение системы (1`) являет набор двух
уравнений для газов заряженных частиц с массами , причем каждое уравнение системы (1`) являет набор двух
уравнений для газов заряженных частиц с массами 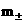 и зарядами и зарядами 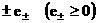 , а все величины в (1`), за исключением , а все величины в (1`), за исключением 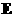 и и 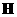 , имеют индексы , имеют индексы 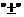 . .
Положим:
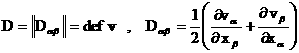 – тензор деформаций, – тензор деформаций,
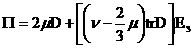 – тензор вязких
напряжений, – тензор вязких
напряжений,
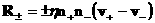  – объемная сила
трения между компонентами, – объемная сила
трения между компонентами,
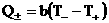 – тепло, передаваемое компонентами плазмы друг
другу – тепло, передаваемое компонентами плазмы друг
другу
при
упругих столкновениях,
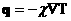 – закон Фурье для
потока тепла в каждой компоненте плазмы. – закон Фурье для
потока тепла в каждой компоненте плазмы.
Переходя к нерелятивистскому пределу в системе (1`, 2), являющейся
исходным
пунктом построения, получим систему (1`, 3). Делая в ней замену переменных (4),
переходим к следующей системе ЭМГД –
уравнений с учетом диссипаций, которую сразу выпишем в дивергентном виде:
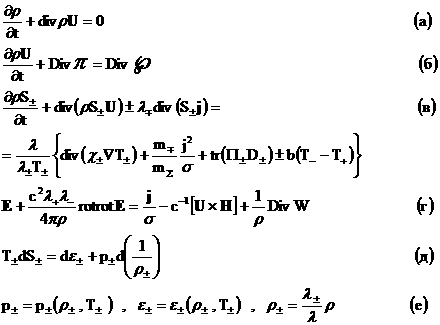 (13´) (13´)
Уравнение
(13`а) получается сложением уравнений (1`,а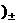 , а уравнение (13`,б )
– сложением уравнений (1`,б) , а уравнение (13`,б )
– сложением уравнений (1`,б)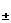 , уравнение (13`,г
) получается вычитанием из уравнения
(1`,б) , уравнение (13`,г
) получается вычитанием из уравнения
(1`,б)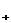 , умноженного на , умноженного на 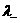 , уравнения (1`,б) , уравнения (1`,б) , умноженного на , умноженного на 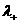 . Тензоры . Тензоры 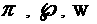 имеют вид: имеют вид:
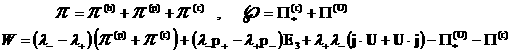 (23) (23)
Здесь и ниже  – единичный тензор, тензоры – единичный тензор, тензоры
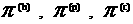 вычисляются по (11), а
тензоры вычисляются по (11), а
тензоры 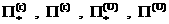 имеют вид: имеют вид:
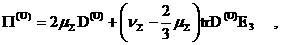 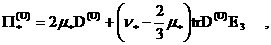
(24)
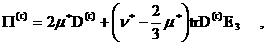 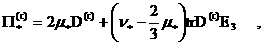
где  – тензоры деформаций. Наконец, – тензоры деформаций. Наконец,
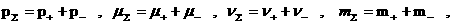
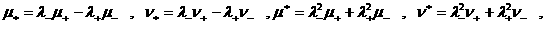 (25) (25)
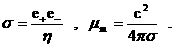 , ,
где  – электропроводность плазмы, – электропроводность плазмы, 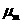 – магнитная вязкость. – магнитная вязкость.
В системе (13׳) след 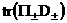 легко выражается через легко выражается через 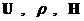 , если воспользоваться
выражениями: , если воспользоваться
выражениями:
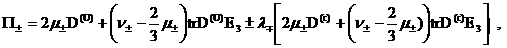
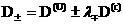 . .
Итак, полная система ЭМГД – уравнений с учетом диссипаций образована
уравнениями систем (13׳, 3). Заметим, коэффициент у дифференциального
оператора  в(13',г) равен в(13',г) равен 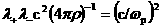 где где 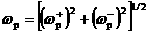 – локальная плазменная частота, – локальная плазменная частота, 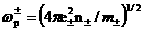 . Энтропийные уравнения (13׳, в) можно заменить на уравнения: . Энтропийные уравнения (13׳, в) можно заменить на уравнения:
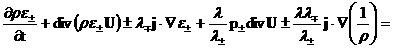
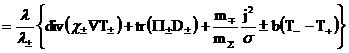
А если компоненты плазмы – идеальные газы, то на
одну из следующих пар уравнений:
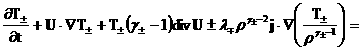
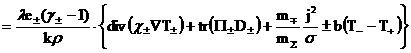 (26) (26)
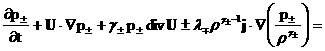
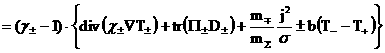
Установим закон сохранения полной энергии для ЭМГД –
уравнений с учетом диссипаций. Воспользуемся уравнением для плотности
внутренней энергии каждой компоненты плазмы:
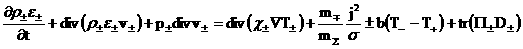 . .
Складывая это уравнение с уравнением (1', б) , скалярно умноженным на , скалярно умноженным на 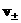 , получим закон
сохранения энергии для каждой плазменной компоненты: , получим закон
сохранения энергии для каждой плазменной компоненты:
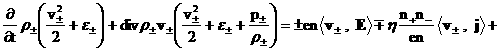
 . .
Складывая последние уравнения между собой и с
законом сохранения электромагнитной энергии (см. §1), получим искомый закон
сохранения полной энергии для ЭМГД – уравнений с учетом диссипаций:
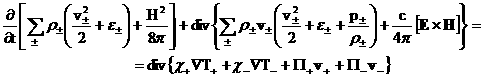 (27) (27)
В случае, когда вязкостью и теплопроводностью
электронов и ионов можно пренебречь, закон сохранения (27) после подстановки
соотношений (5) редуцируется к уже полученной ранее форме (17).
Отметим,
что существуют более сложные способы вычисления тензоров 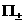 , векторов , векторов 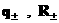 и величин и величин 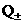 [10], учитывающие, в
частности, анизотропию замагниченной плазмы. Их анализ в контексте ЭМГД –
модели не порождает серьёзных проблем и может оказаться исключительно важным
для исследования тонких эффектов динамики плазмы. [10], учитывающие, в
частности, анизотропию замагниченной плазмы. Их анализ в контексте ЭМГД –
модели не порождает серьёзных проблем и может оказаться исключительно важным
для исследования тонких эффектов динамики плазмы.
§3. Предельные переходы.
Дадим теперь
математически корректный рецепт получения основных гидродинамических моделей
плазмы типа ЭМГД, холловской и классической МГД. Предварительно сделаем несколько общих
замечаний.
Запись физических
законов в виде математических уравнений, как правило, зависит от выбора единиц
измерения физических величин. Чтобы избавиться от этой зависимости, необходимо,
обезразмерить все величины, участвующие в уравнениях. При этом возникает
зависимость уравнений от безразмерных параметров – чисел подобия,
количество которых определяется имеющимися соотношениями между характерными
масштабами. Сами числа подобия тоже определяются неоднозначно: любое взаимно – однозначное гладкое
преобразование чисел подобия снова даёт числа подобия. Формально,  чисел подобия
заполняют множество чисел подобия
заполняют множество 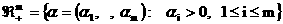 , а физический предельный переход сводится к следующей
математической конструкции. Фиксируется гладкая поверхность , а физический предельный переход сводится к следующей
математической конструкции. Фиксируется гладкая поверхность 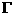 в в 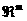 и её предельная
точка и её предельная
точка 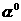 (быть может
бесконечно удаленная). Предполагая решение обезразмеренной системы уравнений аналитически зависящим от
точки на (быть может
бесконечно удаленная). Предполагая решение обезразмеренной системы уравнений аналитически зависящим от
точки на 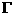 , разложим его в степенной ряд по , разложим его в степенной ряд по 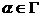 в окрестности в окрестности 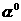 , предварительно выбрав локальные координаты на , предварительно выбрав локальные координаты на 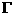 . Тогда уравнения на нулевые коэффициенты разложений дадут
физический предел исходной системы уравнений при . Тогда уравнения на нулевые коэффициенты разложений дадут
физический предел исходной системы уравнений при 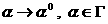 . Физическое содержание предельного перехода определяется
выбором поверхности . Физическое содержание предельного перехода определяется
выбором поверхности 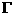 , локальных координат и , локальных координат и
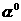 . Есть и математическое требование: цепочка уравнений на
коэффициенты уравнений должна расцепляться, в частности, все коэффициенты
разложений в принципе могут быть найдены. Как правило, за счет удачного выбора
координат в пространстве чисел подобия
удаётся добиться, чтобы . Есть и математическое требование: цепочка уравнений на
коэффициенты уравнений должна расцепляться, в частности, все коэффициенты
разложений в принципе могут быть найдены. Как правило, за счет удачного выбора
координат в пространстве чисел подобия
удаётся добиться, чтобы 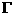 было пересечением
гиперплоскости вида было пересечением
гиперплоскости вида 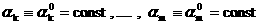 с с 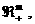 а а 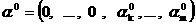 для некоторого для некоторого 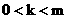 . .
Рассмотрим
теперь безразмерный вид ЭМГД – уравнений. Для простоты из диссипативных
эффектов учитываем только омическое сопротивление и предполагаем электроны и
ионы идеальными политропными газами с общим показателем адиабаты.
 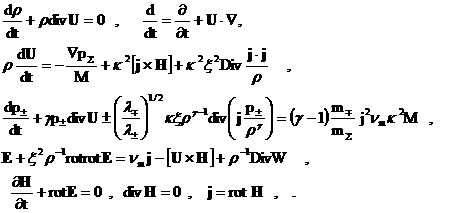 (29) (29)
где тензор 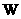 имеет вид: имеет вид:
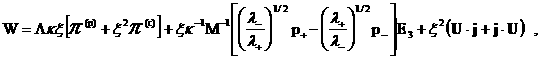
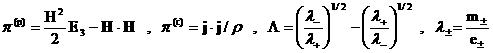 . .
Числа подобия 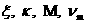 вычисляются по
формулам: вычисляются по
формулам:
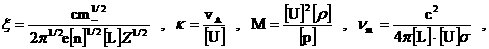
где квадратные скобки означают характерный масштаб
соответствующей величины, 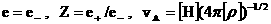 – характерная альфвеновская скорость. При
этом приняты следующие соотношения: – характерная альфвеновская скорость. При
этом приняты следующие соотношения:
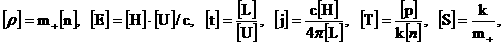 (29) (29)
где 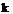 – постоянная Больцмана. Если отказаться от каких–то
соотношений (29), то в системе (28) появятся новые числа подобия. Однако часто,
наоборот, вводят ещё одно соотношение между характерными масштабами: – постоянная Больцмана. Если отказаться от каких–то
соотношений (29), то в системе (28) появятся новые числа подобия. Однако часто,
наоборот, вводят ещё одно соотношение между характерными масштабами:  . Тогда . Тогда 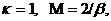 где где 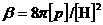 – параметр удержания.
В частности, решения идеальной – параметр удержания.
В частности, решения идеальной 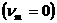 ЭМГД зависят только от
двух безразмерных параметров ЭМГД зависят только от
двух безразмерных параметров 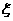 и и 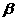 . .
МГД –
предел. Ищем решение системы (28) в виде рядов по
степеням 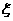 : :
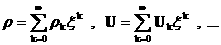 (30) (30)
 (Формально, (Формально, 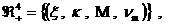
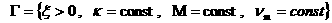 , , 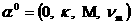 – предельная точка – предельная точка 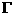 ). Коэффициенты разложений (30) зависят от времени, ). Коэффициенты разложений (30) зависят от времени,
пространственных координат и, как от параметров,
чисел подобия 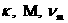 . Подставляя
разложения (30) в систему (28) и приравнивая коэффициенты при одинаковых
степенях . Подставляя
разложения (30) в систему (28) и приравнивая коэффициенты при одинаковых
степенях 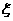 в каждом уравнении
системы, получим бесконечное семейство уравнений. Несложно устанавливается
следующий результат. в каждом уравнении
системы, получим бесконечное семейство уравнений. Несложно устанавливается
следующий результат.
Теорема 1. Семейство уравнений на коэффициенты разложений
можно разбить в последовательность групп уравнений, занумерованных целыми
числами 0, 1, 2, …, так что:
1)
Уравнения 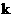 – ой группы, – ой группы, 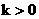 , образуют замкнутую определенную линейную систему
дифференциальных уравнений в частных производных относительно , образуют замкнутую определенную линейную систему
дифференциальных уравнений в частных производных относительно 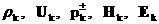 , коэффициенты и
правые части которой зависят только от коэффициентов разложений с индексами , коэффициенты и
правые части которой зависят только от коэффициентов разложений с индексами 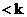 ; причем коэффициенты линейной системы зависят только от
коэффициентов разложений с нулевыми индексами, а дифференциальный оператор
уравнений ; причем коэффициенты линейной системы зависят только от
коэффициентов разложений с нулевыми индексами, а дифференциальный оператор
уравнений 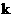 – группы, – группы, 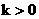 , не зависит от , не зависит от 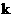 . .
2) Уравнения 0 – ой группы образуют замкнутую определенную нелинейную
систему дифференциальных уравнений в частных производных относительно 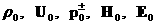 , в размерном виде совпадающую с уравнениями классической
двухтемпературной МГД , в размерном виде совпадающую с уравнениями классической
двухтемпературной МГД
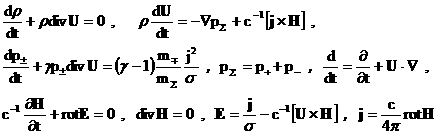 (31) (31)
В частности, сложением ± – уравнений для давлений из неё получается
система уравнений классической (однотемпературной) МГД .
Итак,
уравнения классической МГД получаются из ЭМГД – уравнений предельным переходом 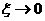 и никак не связаны,
вопреки существующему мифу, с малостью отношения масс и никак не связаны,
вопреки существующему мифу, с малостью отношения масс 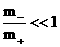 (для электрон – ионной
плазмы). Из выражения для (для электрон – ионной
плазмы). Из выражения для 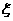 следует, что
предельный переход следует, что
предельный переход 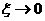 физически
соответствует неограниченному увеличению погонного числа частиц (в
данном случае электронов), физически
соответствует неограниченному увеличению погонного числа частиц (в
данном случае электронов), 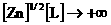 и, следовательно, МГД
– теория описывает крупномасштабные процессы в плотной плазме. Из безразмерных выражений и, следовательно, МГД
– теория описывает крупномасштабные процессы в плотной плазме. Из безразмерных выражений
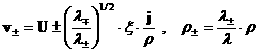
вытекает, что в пределе 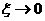 для нулевых
коэффициентов разложений для нулевых
коэффициентов разложений
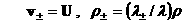 . Поэтому в МГД – пределе электроны и ионы, сцепившись,
двигаются как единое целое с общей гидродинамической скоростью . Поэтому в МГД – пределе электроны и ионы, сцепившись,
двигаются как единое целое с общей гидродинамической скоростью 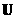 . Этот вывод вступает в противоречие с исходной идеей,
согласно которой в плазме электроны оторваны от ионов и могут свободно
перемещаться, сдерживаемые лишь силами электрического и магнитного
взаимодействия (не считая внешних сил). Указанное противоречие свидетельствует
о переупрощенном характере МГД – теории.
Наконец, из Теоремы 1 следует, что цепочка уравнений на
коэффициенты разложений (30) расцепляется, и все коэффициенты в принципе могут
быть найдены. . Этот вывод вступает в противоречие с исходной идеей,
согласно которой в плазме электроны оторваны от ионов и могут свободно
перемещаться, сдерживаемые лишь силами электрического и магнитного
взаимодействия (не считая внешних сил). Указанное противоречие свидетельствует
о переупрощенном характере МГД – теории.
Наконец, из Теоремы 1 следует, что цепочка уравнений на
коэффициенты разложений (30) расцепляется, и все коэффициенты в принципе могут
быть найдены.
Предел
холловской МГД. Рассмотрим отрезки разложений (30), состоящие
из первых двух членов:
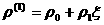 , , 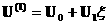 , … , …
Несложно проверить, что с точностью до
слагаемых ~ 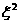 функции функции 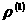 , ,
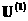 , … удовлетворяют
следующей размерной системе уравнений: , … удовлетворяют
следующей размерной системе уравнений:
 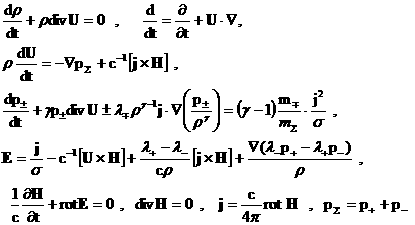 (32) (32)
При этом:
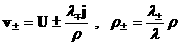 .
(32`) .
(32`)
Получили почти холловскую МГД. Если положить в (32)
и (32`) 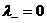 , то приходим к традиционной холловской МГД (см. систему (8) из §1). , то приходим к традиционной холловской МГД (см. систему (8) из §1).
Развивая
предыдущую идею, можно получить систему уравнений, выполненных с точностью до
слагаемых ~ 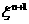 для отрезков
разложений (30), состоящих из для отрезков
разложений (30), состоящих из 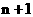 слагаемых: слагаемых:
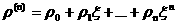 , , 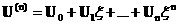 , … . , … .
Однако, возникающие таким образом системы
"суперхолловских" МГД – (назовем их
холловскими МГД порядка 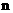 ) необходимо забраковать. Причина этого поучительна, в том
числе и для понимания места самой классической холловской МГД в плазмодинамике,
поэтому остановимся на этом подробнее. ) необходимо забраковать. Причина этого поучительна, в том
числе и для понимания места самой классической холловской МГД в плазмодинамике,
поэтому остановимся на этом подробнее.
При выводе уравнений для 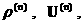 … необходимо использовать выражения для предыдущих
приближений. Например, для … необходимо использовать выражения для предыдущих
приближений. Например, для 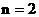 функции функции 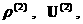 … удовлетворяют с точностью до членов ~ … удовлетворяют с точностью до членов ~ 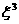 следующей размерной системе уравнений: следующей размерной системе уравнений:
 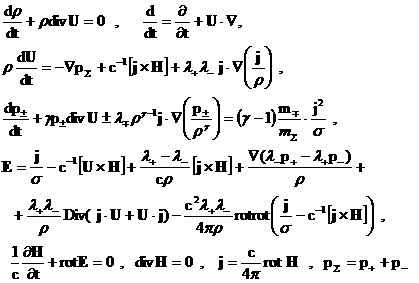 (33) (33)
Система
(33) отличается от ЭМГД – уравнений только
упрощенным обобщенным законом Ома: для вычисления 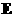 теперь не надо решать
систему дифференциальных уравнений, а можно воспользоваться явной формулой. То
же будет и для теперь не надо решать
систему дифференциальных уравнений, а можно воспользоваться явной формулой. То
же будет и для 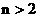 : система уравнений на : система уравнений на
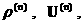 … отличается от ЭМГД – уравнений только обобщенным законом Ома, который сводится к явной, хотя и весьма
громоздкой формуле для … отличается от ЭМГД – уравнений только обобщенным законом Ома, который сводится к явной, хотя и весьма
громоздкой формуле для 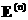 . При . При 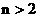 рекуррентная формула
для рекуррентная формула
для 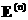 имеет вид: имеет вид:
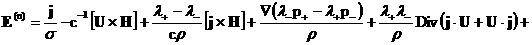
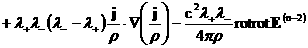 , ,
где 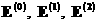 вычисляются по
формулам систем (31), (32), (33) соответственно. вычисляются по
формулам систем (31), (32), (33) соответственно.
Чтобы
оценить полученные системы уравнений, рассмотрим акустику однородной
неподвижной идеальной плазмы в силу системы уравнений холловской МГД порядка 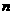 для для 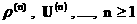 . Дисперсионное уравнение для волн ~ . Дисперсионное уравнение для волн ~ 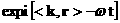 имеет вид: имеет вид: 
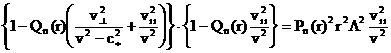 ,
(34) ,
(34)
где
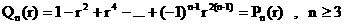
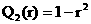 , , 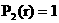 , , 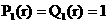
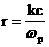 , , 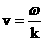 , , 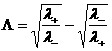 . .
В частности, для классической холловской МГД (32)
имеем дисперсионное уравнение:
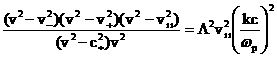 ,
(35) ,
(35)
где
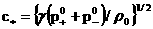 –
коллективная скорость звука, –
коллективная скорость звука,
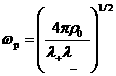 – плазменная частота, – плазменная частота,
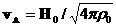 –
альфвеновская скорость, –
альфвеновская скорость,
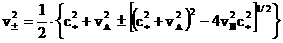 –квадраты быстрой (+)
и медленной –квадраты быстрой (+)
и медленной 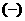 магнитозвуковых
скоростей. магнитозвуковых
скоростей.
Напомним, 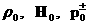 – параметры невозмущенной плазмы, а
символы – параметры невозмущенной плазмы, а
символы 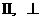 означают проекции вектора вдоль и поперек волнового
вектора означают проекции вектора вдоль и поперек волнового
вектора 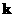 , определяющего
направление распространения волны. , определяющего
направление распространения волны.
Дисперсионное уравнение (35) позволяет выявить узкое место классической
холловской МГД, а уравнение (34) заставляет забраковать холловские МГД
порядка n при n>1.
Согласно (35), уравнения акустики однородной неподвижной плазмы в силу
классической холловской МГД имеет три ветви колебаний. Ветвь, имеющая
асимптотику в нуле 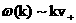 (называемая БМ3 –
ветвью), на бесконечности имеет асимптотику (называемая БМ3 –
ветвью), на бесконечности имеет асимптотику 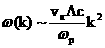 , а значит её
групповая скорость , а значит её
групповая скорость 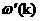 стремится к стремится к  при при 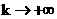 . Но групповая скорость . Но групповая скорость 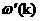 равна
скорости пространственного перемещения волнового пакета колебаний с длиной волн равна
скорости пространственного перемещения волнового пакета колебаний с длиной волн
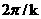 . Поскольку решение уравнений акустики распадается в сумму
волновых пакетов по всем . Поскольку решение уравнений акустики распадается в сумму
волновых пакетов по всем 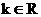 и всем веткам
дисперсионной кривой, то из неограниченности групповой скорости и всем веткам
дисперсионной кривой, то из неограниченности групповой скорости 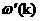 для БМ3 – ветви следует, что начальное возмущение
однородной плазмы мгновенно, с бесконечной скоростью распространится на все
пространство, что физически абсурдно. Это не так лишь в случае для БМ3 – ветви следует, что начальное возмущение
однородной плазмы мгновенно, с бесконечной скоростью распространится на все
пространство, что физически абсурдно. Это не так лишь в случае 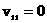 , т.е. для поперечного распространения волн. , т.е. для поперечного распространения волн.
Неудивительно поэтому, что успешные приложения холловской МГД относятся
именно к случаям течения плазмы поперек силовых линий магнитного поля (Z–пинчи,
плазменные ускорители, плазменные двигатели и пр.). К сожалению, подавить
бесконечный рост групповой скорости с
помощью системы уравнений холловской МГД порядка n
при n>1 на функции
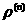 , , 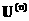 ,… не удается. Более
того, неприятности начинаются и при поперечном ,… не удается. Более
того, неприятности начинаются и при поперечном
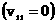 распространении волн.
Действительно, как следует из (34), при распространении волн.
Действительно, как следует из (34), при 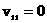 для БМ3–ветви: для БМ3–ветви:
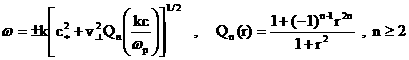
Но при
n четном, очевидно,
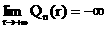
и значит для
всех достаточно больших k
последнее подкоренное выражение отрицательно, поэтому для всех достаточно
больших k колебания с длиной волны 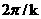 заведомо
неустойчивы. заведомо
неустойчивы.
При n
нечетном имеем
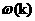 ~ ~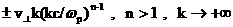 , ,
что приводит к физически
абсурдному бесконечному росту групповой скорости 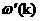 уже и для БМ3–ветви.
Но это значит, что, на первый взгляд разумные, холловские МГД порядка n на самом деле непригодны при n>1 даже для описания (и тем более, численного
исследования) течений плазмы поперек магнитного поля. В то же время, хотя
традиционная холловская МГД применима для моделирования поперечных течений квазинейтральной
нерелятивистской плазмы, но она в принципе непригодна для исследования течений
под произвольным углом к магнитному полю. уже и для БМ3–ветви.
Но это значит, что, на первый взгляд разумные, холловские МГД порядка n на самом деле непригодны при n>1 даже для описания (и тем более, численного
исследования) течений плазмы поперек магнитного поля. В то же время, хотя
традиционная холловская МГД применима для моделирования поперечных течений квазинейтральной
нерелятивистской плазмы, но она в принципе непригодна для исследования течений
под произвольным углом к магнитному полю.
Принято
считать [7], что параметр 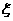 учитывает различие
электронной и ионной скоростей. В полном объеме это различие содержится в ЭМГД
– уравнениях, в 1–м приближении – в уравнениях холловской МГД (32), во 2–м приближении – в
системе (33) и т.д. Но, как только что было показано, такой способ
приближенного учета различия электронной и ионной скоростей неудачен. Поэтому
укажем ещё один путь теоретически сколь угодно точного учета этого различия.
Имеем систему уравнений, выполненных с точностью до слагаемых ~ учитывает различие
электронной и ионной скоростей. В полном объеме это различие содержится в ЭМГД
– уравнениях, в 1–м приближении – в уравнениях холловской МГД (32), во 2–м приближении – в
системе (33) и т.д. Но, как только что было показано, такой способ
приближенного учета различия электронной и ионной скоростей неудачен. Поэтому
укажем ещё один путь теоретически сколь угодно точного учета этого различия.
Имеем систему уравнений, выполненных с точностью до слагаемых ~ 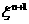 : :
  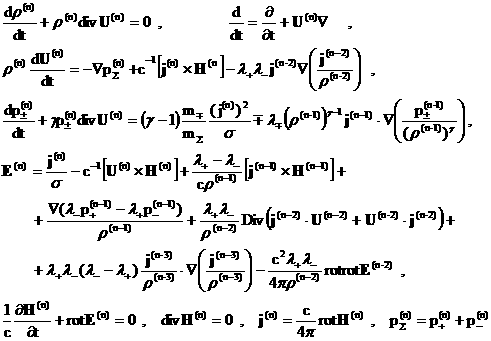 (36) (36)
Если для какого–то n верхний индекс
<0, то соответствующее
слагаемое выпадает. В частности, верхний индекс
<0, то соответствующее
слагаемое выпадает. В частности, 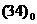 – это классическая
(двухтемпературная) МГД. Система – это классическая
(двухтемпературная) МГД. Система 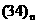 позволяет на каждом временном
шаге за n итераций вычислить позволяет на каждом временном
шаге за n итераций вычислить 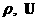 с точностью с точностью 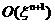 , обращая на
каждой итерации один и тот же дифференциальный оператор классической МГД с
правой частью , вычисляемой по предыдущим приближениям. Возможны различные
стратегии счета на каждом шаге: либо делать заданное (быть может, зависящее от шага) число итераций, либо
итерировать до установления и т.д. , обращая на
каждой итерации один и тот же дифференциальный оператор классической МГД с
правой частью , вычисляемой по предыдущим приближениям. Возможны различные
стратегии счета на каждом шаге: либо делать заданное (быть может, зависящее от шага) число итераций, либо
итерировать до установления и т.д.
ЭМГД–предел. Рассмотрим математически корректный способ
вывода ЭМГД– уравнений. За отправной пункт возьмем уравнения общей теории
относительности (ОТО) Эйнштейна [11] и
для простоты ограничимся случаем идеальной плазмы. Из уравнений ОТО для смеси
электронного, ионного газов и электромагнитного поля легко выводятся [12]
уравнения релятивистской электромагнитной газодинамики (РЭМГД–уравнения):
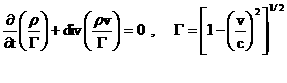
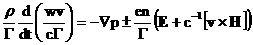 (37) (37)
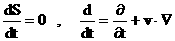
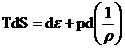 , ,
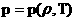 , , 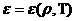
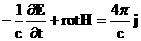 , , 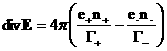
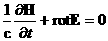 , , 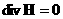
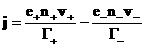 , , 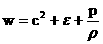 , ,
где гидро – и термодинамические  уравнения суть пары
уравнений для уравнения суть пары
уравнений для
электронов и ионов, а все величины, за
исключением 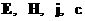 , имеют индексы “±” .
Здесь , имеют индексы “±” .
Здесь 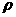 – плотность массы
покоя, – плотность массы
покоя, 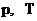 – давление и
температура в собственной системе координат, – давление и
температура в собственной системе координат, 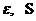 – плотность внутренней
энергии и энтропии на единицу массы покоя. В системе (37) помимо диссипативных
эффектов не учитывается производство энергии за счет ядерных, химических
реакций и гравитации. Если электроны и ионы – идеальные политропные газы с общим показателем адиабаты – плотность внутренней
энергии и энтропии на единицу массы покоя. В системе (37) помимо диссипативных
эффектов не учитывается производство энергии за счет ядерных, химических
реакций и гравитации. Если электроны и ионы – идеальные политропные газы с общим показателем адиабаты 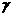 , то энтропийные уравнения заменяются на следующие: , то энтропийные уравнения заменяются на следующие:
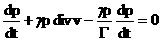 . .
В безразмерном
виде РЭМГД – система (для идеальной плазмы с политропными электронами и ионами)
сводится к уравнениям:
 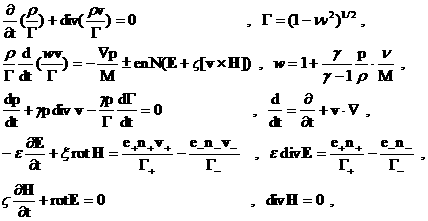 (38) (38)
где 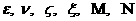 – числа подобия: – числа подобия:
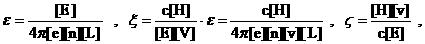
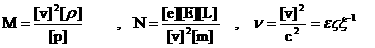
и приняты соглашения о характерных масштабах:
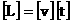 , , 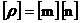 . .
Здесь квадратные скобки означают характерный масштаб
величины;  – характерный заряд, – характерный заряд, 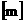 – характерная масса, – характерная масса, 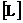 – характерная длина и
т.д. – характерная длина и
т.д.
Если ввести, как это часто делается, дополнительные
соотношения между характерными масштабами:
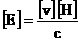 , , 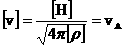 , ,
то остается только три независимых числа
подобия 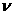 , , 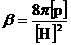 – параметр удержания, – параметр удержания, 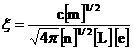 , а остальные
равны , а остальные
равны 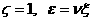 , , 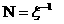 , , 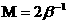 . Ищем решение безразмерной системы РЭМГД – уравнений (38) в
виде рядов по степеням . Ищем решение безразмерной системы РЭМГД – уравнений (38) в
виде рядов по степеням 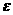 : :
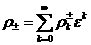 , , 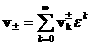 ,
…
(39) ,
…
(39)
где коэффициенты разложений зависят от времени,
пространственных координат и, как от параметров, чисел подобия 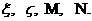 Подставляя разложения
(39) в уравнения системы (38) и приравнивая в каждом уравнении коэффициенты при
одинаковых степенях Подставляя разложения
(39) в уравнения системы (38) и приравнивая в каждом уравнении коэффициенты при
одинаковых степенях 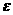 , получим семейство
уравнений на коэффициенты разложений. , получим семейство
уравнений на коэффициенты разложений.
Теорема 2. Семейство уравнений на
коэффициенты разложений (39) распадается в последовательность групп уравнений,
занумерованных целыми числами 0, 1, 2, …, так
что:
1)Уравнения к – ой группы, к>0 образуют замкнутую определенную линейную
систему дифференциальных уравнений в частных производных относительно 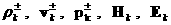 , коэффициенты и
правые части которых зависят только от коэффициентов разложений с индексами <к
, причем коэффициенты системы зависят
только от нулевых коэффициентов разложений, а дифференциальный оператор
уравнений к – ой группы,
к>0 не зависит от к. , коэффициенты и
правые части которых зависят только от коэффициентов разложений с индексами <к
, причем коэффициенты системы зависят
только от нулевых коэффициентов разложений, а дифференциальный оператор
уравнений к – ой группы,
к>0 не зависит от к.
2) Уравнения 0 – ой группы образуют нелинейную замкнутую
определенную систему дифференциальных уравнений в частных производных
относительно 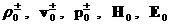 , в размерном виде совпадающую с ЭМГД – уравнением
для идеальной плазмы с политропными электронами и ионами: , в размерном виде совпадающую с ЭМГД – уравнением
для идеальной плазмы с политропными электронами и ионами:
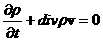
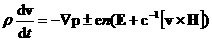
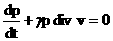 , , 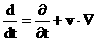
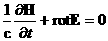 , , 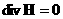
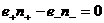 , , 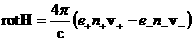
Заметим, что сами доказательства Теорем 1,2 и им подобных сводятся к несложной проверке.
Ключевым и неочевидным моментом является выбор параметров разложения,
обеспечивающих, с одной стороны, нахождение всех коэффициентов разложения
(цепочка уравнений на коэффициенты разложений должна расцепляться), а, с
другой, – получение нужной предельной системы.
§4. Благодарности.
Автор
выражает благодарность К.В.Брушлинскому,
А.Н.Козлову, В.В.Савельеву и другим коллегам по работе за участие в
обсуждении различных вопросов,
относящихся к двухжидкостной плазмодинамике.
Автор
признателен также Российскому Фонду Фундаментальных Исследований за финансовую
поддержку этой работы.
Автор
выражает благодарность М.С. Михайловой за качественный набор текста.
Литература.
1. М.Б.Гавриков. Линейные волны в нерелятивистской магнитной
гидродинамике. Препринт ИПМ им.М.В.Келдыша АНСССР,1988,N199.
2. М.Б.Гавриков. Апериодические колебания холодной плазмы.
Препринт ИПМ им.М.В.Келдыша АНСССР. 1991, N33.
3. М.Б.Гавриков,
М.С.Михайлова. Двухкомпонентная
квазинейтральная плазма в плоском канале (установившееся течение) Сб. Динамика
неоднородных систем под ред. Ю.С.Попкова ИСА РАН, N8, 2004, стр.186-211.
4. М.Б.Гавриков, М.С.Михайлова.
Установившееся течение двухкомпонентной вязкой плазмы в цилиндрической трубе и
цилиндрическом слое. Препринт ИПМ им.М.И.Келдыша РАН, 2004, N7.
5. М.Б.Гавриков, Р.В.Сорокин. О
вынужденных колебаниях плазмы в круглой цилиндрической трубе. Часть I.
Препринт ИПМ им.М.В.Келдыша РАН, 2005, N76.
6. М.Б.Гавриков, М.С.Михайлова.
Уравнение равновесий плазмы в двухжидкостной плазмостатике. Препринт ИПМ
им.М.В.Келдыша РАН, 2005, N74.
7. А.И.Морозов, Л.С.Соловьев,
Стационарное течение плазмы в магнитном поле. Вопросы теории плазмы. Сб. статей
под ред. М.А.Леонтовича. Вып.8, М., Атомиздат, 1974, стр. 3-87.
8. А.В.Бицадзе. Уравнения
математической функции. М., "Наука", 1976, стр.9-15.
9. И.А.Шишмарев. Введение в
теорию эллиптических уравнений. Изд-во МГУ, 1979, стр.6-12.
10.
С.И.Брагинский. Вопросы теории плазмы. Сб. статей под
ред.М.А.Леонтовича. Вып.1, М. Госатомиздат, 1963, стр.183-272.
11.
Einstein A. // Ann. D.
Phys., 1916, Vol.49, p.769.
12.
Л.С.Соловьев. К релятивистской гидродинамике. Препринт ИАЭ, N3362/1, М., 1980.
(Л.С.Соловьев. Собрание трудов в двух томах, т.II. М., "Наука",
2001, стр7-34).
|