Аннотация
В работе рассмотрена проблема распространения мощного лазерного фемтосекундного импульса в
воздухе. Исследован вопрос о выборе математических моделей и адекватных алгоритмов для
математического моделирования процессов филаментации. Для моделирования распространения
реальных лазерных импульсов был создан параллельный программный комплекс, особенности
реализации которого также обсуждаются в работе.
Abstract
In the thesis the problem of intensive laser beam propagation in the medium with a cubic
nonlinearity is considered. The mathematical models and adequate algorithms choice is
investigated, partially, the choice of optimal grids and difference schemes for the
mathematical modeling of filamentation processes. The multiprocessor program was realized
for modeling the propagation of real laser impulses. Features of it are discussed in the paper.
Введение
Задача моделирования распространения
фемтосекундного импульса в воздухе на дальние дистанции может быть использована
в области дистанционного зондирования. Основу явления составляет процесс
филаментации – образования тонких нитевидных структур высокой интенсивности.
Для импульсов большой мощности нити могут наблюдаться на протяжении нескольких
десятков метров.
Существует значительное количество работ различных
авторов, посвященных математическому моделированию процесса филаментации
[1-4;7;8]. Рассматриваемая для данного явления система уравнений для медленно
меняющейся амплитуды светового поля является нестационарной 3-х мерной задачей.
Для того чтобы иметь возможность сравнить экспериментальные данные с расчетами
при условии учета мелкомасштабных возмущений, требуется порядка ~1016
счетных ячеек. Такое большое количество делает счет уравнений при больших
расстояниях слишком долгим. Для качественного исследования образования филамент
и их упорядочивания в кластеры применяется упрощенная физическая модель,
которая в совокупности с использованием технологий параллельных вычислений
позволяет в обозримое время провести счет задачи.
В настоящее время четырьмя институтами Франции и
Германии выполняется проект «Teramobile» по экспериментальному и численному исследованию
распространения мощных фемтосекундных импульсов [8]. В результате этих
экспериментов по распространению терраватных импульсов наблюдалось несколько
десятков филаментов, которые упорядочивались в группы (кластеры) протяженностью
более десяти метров.
1.
Физическая модель
задачи.
На сегодняшний день
модель распространения лазерного импульса можно считать устоявшийс. У авторов
различаются лишь подходы к ее математическому моделированию. Для
описания процесса распространения коротких импульсов в среде с кубической
нелинейностью обычно используется следующая система уравнений [8]: нелинейное
уравнение Шредингера (НУШ) для огибающей электрического поля  , движущейся с
групповой скоростью , движущейся с
групповой скоростью 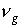 (здесь (здесь 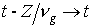 , , 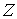 – переменная, вдоль
которой распространяется импульс, – переменная, вдоль
которой распространяется импульс,  – поперечная
направлению распространения импульса плоскость): – поперечная
направлению распространения импульса плоскость):
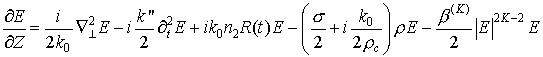 , (1.a) , (1.a)
где 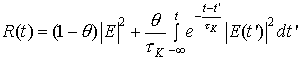 (1.б) (1.б)
и модель Друда [19] для
локальной плотности плазмы 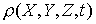 : :
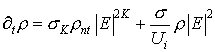 , (1.в) , (1.в)
где
λ0=800нм
– длина волны;
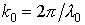 – центральное волновое число;
n2=
3.1·10-19
см2/Ватт
– индекс преломления эффекта Керра;
k″=0.2фс2/см
– коэффициент дисперсии групповой скорости;
τK=70фс
– время релаксации;
ρc=1.8·1021см-3
– критическая плазменная плотность;
β(K)=4.25·10-98см13/Ватт7
– коэффициент многофотонного поглощения; – центральное волновое число;
n2=
3.1·10-19
см2/Ватт
– индекс преломления эффекта Керра;
k″=0.2фс2/см
– коэффициент дисперсии групповой скорости;
τK=70фс
– время релаксации;
ρc=1.8·1021см-3
– критическая плазменная плотность;
β(K)=4.25·10-98см13/Ватт7
– коэффициент многофотонного поглощения;
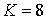 – число фотонов,
которое требуется для ионизации;
σ=5.44·10-20см2
– коэффициент каскадной ионизации и
плазменного поглощения в поперечном сечении для обратного тормозного излучения;
σK=2.88·10-99см16/с·Ватт8
– коэффициент многофотонной ионизации;
Ui=12.1e Вольт
– промежуточный потенциал ионизации молекул
кислорода;
ρnt=5.4·1018см-3
– эффективная плотность нейтральных молекул,
равная 20% от стандартной
ρat=2.7·1019см-3
. Рекомбинация
электронов в кинетическом уравнении (1.в) не учитывается из-за малой длины
рассматриваемых импульсов. – число фотонов,
которое требуется для ионизации;
σ=5.44·10-20см2
– коэффициент каскадной ионизации и
плазменного поглощения в поперечном сечении для обратного тормозного излучения;
σK=2.88·10-99см16/с·Ватт8
– коэффициент многофотонной ионизации;
Ui=12.1e Вольт
– промежуточный потенциал ионизации молекул
кислорода;
ρnt=5.4·1018см-3
– эффективная плотность нейтральных молекул,
равная 20% от стандартной
ρat=2.7·1019см-3
. Рекомбинация
электронов в кинетическом уравнении (1.в) не учитывается из-за малой длины
рассматриваемых импульсов.
В целях сокращения времени счета для качественного исследования задачи
можно применить следующий алгоритм упрощения данной модели. Во-первых,
пренебрежимо мало действие обратного тормозного излучения при
продолжительностях импульса менее пикосекунды, поэтому положим 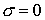 . Также не будем
учитывать изменение второй производной по времени . Также не будем
учитывать изменение второй производной по времени 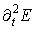 , т.к. комплексная
амплитуда световой волны медленно меняется со временем. Во-вторых, в
предположении, что в области высокой интенсивности излучения световые поля
имеют Гауссов профиль по временной координате и могут быть представлены в виде
произведения, , т.к. комплексная
амплитуда световой волны медленно меняется со временем. Во-вторых, в
предположении, что в области высокой интенсивности излучения световые поля
имеют Гауссов профиль по временной координате и могут быть представлены в виде
произведения,
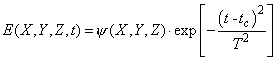 , ,
где 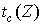 - временной слой, где формируется максимальный
по интенсивности пик с полушириной - временной слой, где формируется максимальный
по интенсивности пик с полушириной 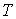 , сохраняющейся все
время распространения [8]. , сохраняющейся все
время распространения [8].
Применяя сделанные выше предположения, сначала
найдем 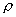 из уравнения (1.в): из уравнения (1.в):
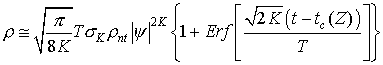 , ,
где 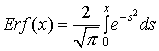 . Далее в уравнение
1(a) подставим
найденное . Далее в уравнение
1(a) подставим
найденное 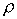 и уравнение (1.б), затем умножим получившееся
уравнение на и уравнение (1.б), затем умножим получившееся
уравнение на 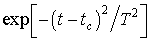 и проинтегрируем по всему временному домену,
т.е. (-∞;+∞). Распишем все подробно: и проинтегрируем по всему временному домену,
т.е. (-∞;+∞). Распишем все подробно:
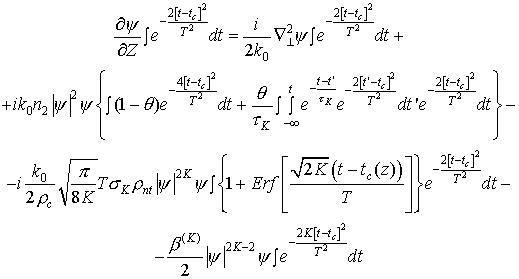
Далее, учитывая значение
интеграла 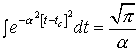 , упростим
получившееся выражение: , упростим
получившееся выражение:
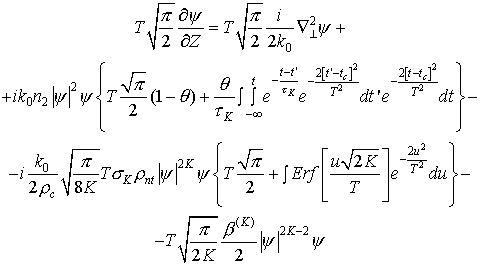 (2) (2)
Рассмотрим первый из двух
оставшихся интегралов уравнения (2):
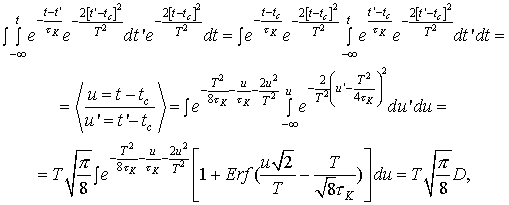
где 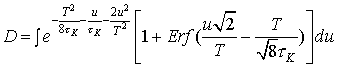 . .
Второй интеграл 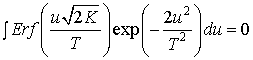 , т.к.
подынтегральное выражение – нечетная функция. Введя в уравнении (2) обозначения , т.к.
подынтегральное выражение – нечетная функция. Введя в уравнении (2) обозначения
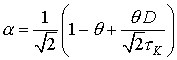 и и 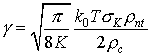 , ,
окончательно получим:
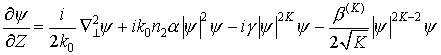 . (3) . (3)
Влияние
комбинационного рассеяния на нелинейный отклик в воздухе наблюдается при 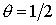 . Также положим
значение . Также положим
значение 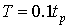 ( ( – длительность
импульса) для изучения процесса филаментации при наличии многофотонной ионизации,
которая укорачивает длительность импульса. Чтобы обезразмерить уравнение (3),
вводим переменные: – длительность
импульса) для изучения процесса филаментации при наличии многофотонной ионизации,
которая укорачивает длительность импульса. Чтобы обезразмерить уравнение (3),
вводим переменные:
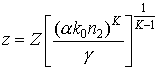 , ,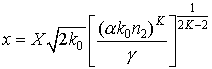 , , 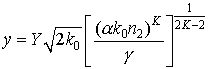 , ,
поле: 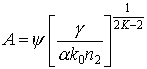 и параметр: и параметр: 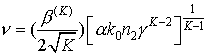 . После подстановки
и упрощения получим: . После подстановки
и упрощения получим:
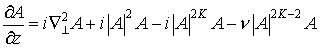 , (4) , (4)
где параметр 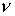 примет значение примет значение 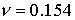 при выбранных выше параметрах при выбранных выше параметрах  и и  . .
3.
Численая схема.
Оценка размерности моделируемой задачи
Решаемая задача представляет собой нелинейное
уравнение параболического типа. Уравнение можно считать двумерным (относительно
переменных x, y) и нестационарным
относительно переменной z, которая в данном
случае принимает роль времени. Для решения задачи составим для квадратной
области в координатах 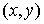 равномерную (в общем случае) сетку с шагом равномерную (в общем случае) сетку с шагом 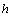 с общим количеством ячеек с общим количеством ячеек 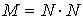 . Составим неявную
разностную схему (значение функции . Составим неявную
разностную схему (значение функции 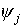 будем брать в середине j-ой ячейки составленной сетки): будем брать в середине j-ой ячейки составленной сетки):
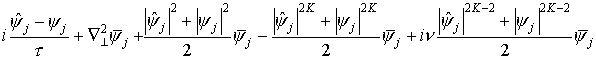 =0, =0, 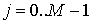 , (5) , (5)
где приняты стандартные обозначения: 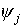 - значение на нижнем слое, - значение на нижнем слое, 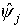 - значение на верхнем слое, - значение на верхнем слое, 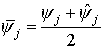 - среднее арифметическое. Для предложенной
разностной схемы, имеющей порядок аппроксимации - среднее арифметическое. Для предложенной
разностной схемы, имеющей порядок аппроксимации 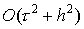 , в случае отсутствия многофотонного поглощения ( , в случае отсутствия многофотонного поглощения ( ) выполняются
разностные аналоги интегральных законов сохранения мощности ) выполняются
разностные аналоги интегральных законов сохранения мощности
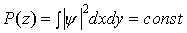
и гамильтониана
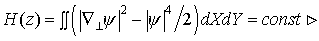 . .
Нелинейная задача решается методом Ньютона. Условие
окончания итерационного процесса в методе Ньютона выбираются следующие:
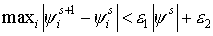 , ,
где 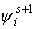 - i-ая компонента
вектора решения на текущей (s+1)-ой итерации по
нелинейности,
ε1 и ε2
- числа, определяющие необходимую точность
сходимости метода. - i-ая компонента
вектора решения на текущей (s+1)-ой итерации по
нелинейности,
ε1 и ε2
- числа, определяющие необходимую точность
сходимости метода.
При решении задачи выбирается область, превышающая
ширину моделируемого импульса в 5-6 раз, на границе ставятся условия второго
рода 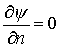 . В качестве
начальных условий выбирается профиль: . В качестве
начальных условий выбирается профиль:
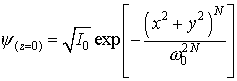 , (7) , (7)
где  – начальная ширина импульса; – начальная ширина импульса;  - начальная
амплитуда. Степень N обычно берут равной 1 (гауссов импульс) или 2
(супергаусс). - начальная
амплитуда. Степень N обычно берут равной 1 (гауссов импульс) или 2
(супергаусс).
Для предложенной разностной схемы был проверен порядок аппроксимации и
монотонность. Для оценки качества численного алгоритма проводилось сравнение с
солитонным решением двумерного (x,z) уравнения без ионизационных членов
 . .
Задавая начальные условия в виде
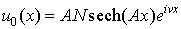 , ,
при 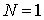 , , 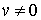 будем иметь один
солитон с амплитудой будем иметь один
солитон с амплитудой 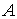 , движущийся со скоростью , движущийся со скоростью 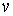 : :
 . .
При 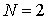 , , 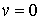 задача имеет
двухсолитонное решение: задача имеет
двухсолитонное решение:
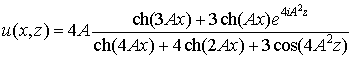 . .
Кроме того, на
нелинейной стадии для достаточно больших значений величины R, характеризующей отношение амплитуды сигнала к начальной амплитуде,
критерием корректности численного метода может служить правильная передача
скорости приближения к асимптотике автомодельного решения вблизи точки
коллапса.
Чтобы оценить необходимые размеры расчетной сетки,
воспользуемся следующими условиями и результатами экспериментов [Teramobile]:
·
для изучения
процесса филаментации используется мощный (от 100GW до 3TW) лазерный импульс, начальная ширина которого
может достигать 2 см;
·
ширина
образующейся филаменты, как мелкомасштабного эффекта, постоянна и достигает
100-150 мкм, а интенсивность в фокусе
филаменты может превышать интенсивность фона в десятки раз;
·
наблюдаемая
длина распространения импульса составляет от десятков до сотен метров.
Таким образом, длина ребра квадрата расчетной сетки может достигать 10 см, чтобы избежать влияния границ. Длина
же ребра одной ячейки должна быть не более 10-15 мкм для удовлетворительной передачи характера мелкомасштабных
эффектов. Таким образом, количество ячеек в расчетной области 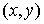 может достигать может достигать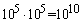 . Шаг по z выбирается ~ . Шаг по z выбирается ~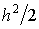 , и уменьшается
обратно пропорционально максимальной интенсивности , и уменьшается
обратно пропорционально максимальной интенсивности 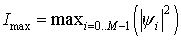 . Тем самым
обеспечена не только устойчивость, но и точность. Оценка размерности задачи
показывает, что для моделирования реального эксперимента по распространению
мощного фемтосекундного лазерного импульса на длинные дистанции в атмосфере
необходимо использовать методы параллельного программирования. . Тем самым
обеспечена не только устойчивость, но и точность. Оценка размерности задачи
показывает, что для моделирования реального эксперимента по распространению
мощного фемтосекундного лазерного импульса на длинные дистанции в атмосфере
необходимо использовать методы параллельного программирования.
4.
Параллельный
вычислительный комплекс
Создание параллельного программного комплекса –
трудоемкий технический процесс, упрощение и систематизация которого приводит к
значительному выигрышу затраченного исследователем времени. Процесс создания
параллельного программного комплекса можно разделить на несколько блоков:
1.
Блок подготовки данных.
2.
Блок расчета
3.
Блок интерпретации результатов
В зависимости от объема входных данных решаемой
задачи и объема визуализируемых расчетов блоки подготовки данных и
интерпретации результатов могут выполняться как на персональном компьютере, так
и на параллельном комплексе. В созданном программном комплексе блок подготовки
данных находился в теле основной программы расчетов, т.к. не требовал задания
каких либо сложных пользовательских данных с помощью удобного интерфейса. Программа
для интерпретации результатов написана как интерфейсное приложение (среда
разработки: MFC) для персонального компьютера.
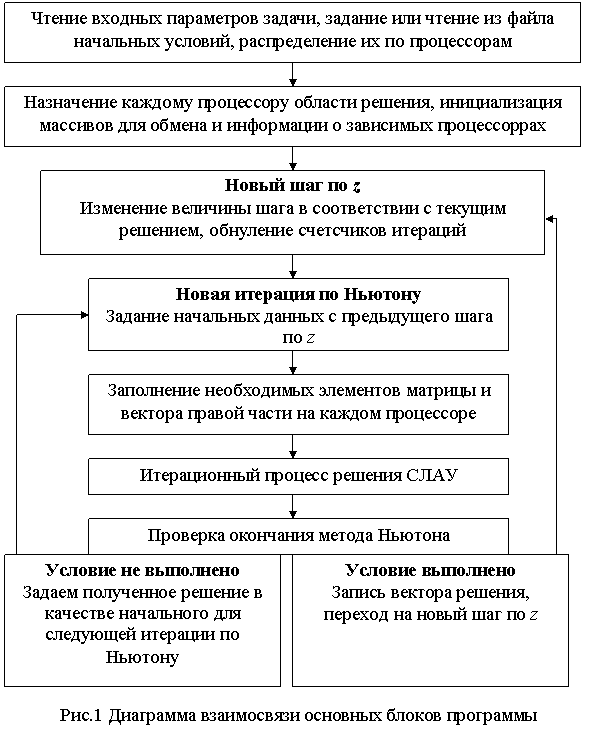
На рис. 1 представлена диаграмма взаимосвязи
основных блоков программы.
Основное
внимание требуется уделить написанию блока расчета. Параллельная программа
должна быть компактна и обладать прозрачной логической структурой. В
сформулированной выше постановке задачи основным ресурсоемким процессом
является решение систем линейных уравнений. Из-за процесса линеаризации за один
шаг по координате z требуется несколько
раз выполнять решение системы. При реализации программного кода было принято
решение использовать пакет Aztec [10], разработанный в исследовательской
лаборатории параллельных вычислений Сандии (США), как достаточно эффективный и
удобный в использовании пакет для решения итерационными методами системы
уравнений. Предоставляемые средства трансформации данных позволяют легко
создавать разреженные неструктурированные матрицы для решения как на однопроцессорных,
так и на многопроцессорных системах [11]. Aztec включает в себя процедуры, реализующие ряд
итерационных методов:
·
метод сопряженных градиентов (CG),
·
обобщенный
метод минимальных невязок (GMRES),
·
квадратичный
метод сопряженных градиентов (CGS),
·
метод квазиминимальных невязок
(TFQMR),
·
метод
бисопряженного градиента со
стабилизацией (BiCGStab).
Все методы используются совместно с различными
предобуславливателями (полиномиальный метод и метод декомпозиции областей,
использующий как прямой метод LU, так и неполное LU разложение в подобластях).
В процессе моделирования подбиралась наиболее
эффективная по производительности пара итерационного метода и
предобуславливателя. В таблице представлены значения времени, затраченные на
счет одного шага по 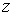 при выборе соответствующего итерационного
метода (столбцы таблицы) и предобуславливателя (строки таблицы). при выборе соответствующего итерационного
метода (столбцы таблицы) и предобуславливателя (строки таблицы).
|
|
CGS
|
TFQMR
|
BiCGStab
|
|
Нет
|
0.77
(2)
|
0.76
(2)
|
1.37
(6)
|
|
LS
|
0.68 (2)
|
0.71
(2)
|
1.35
(6)
|
|
LU
|
0.82
(2)
|
0.81
(2)
|
1.41
(6)
|
|
ILU
|
0.68 (2)
|
0.78
(2)
|
0.78
(2)
|
|
Sym_GS
|
0.77
(2)
|
0.75
(2)
|
1.52
(6)
|
Таблица 1.
Таблица сравнения результатов счета для разных сочетаний итерационных методов и
предобуславливателей.
В итоге был выбран квадратичный метод сопряженных
градиентов (CGS) и предобуславливатель ILU (Incomplete LU).
Хотя матрица может быть общего вида, пакет
ориентирован на матрицы, возникающие при конечно-разностной аппроксимации
дифференциальных уравнений в частных производных (Partial Differential Equations - PDE). Пакет Aztec может использовать представления разреженных
матриц в виде:
·
поэлементный
формат модифицированной разреженной строки (MSR),
·
блочный
формат переменной блочной строки (VBR).
 Для анализа эффективности параллельных алгоритмов
обычно используются такие понятия, как эффективность и ускорение. Ускорением
параллельного алгоритма ( Для анализа эффективности параллельных алгоритмов
обычно используются такие понятия, как эффективность и ускорение. Ускорением
параллельного алгоритма (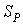 ) называют
отношение времени выполнения алгоритма на одном процессоре ( ) называют
отношение времени выполнения алгоритма на одном процессоре (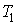 ) ко времени
выполнения на системе из ) ко времени
выполнения на системе из 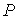 процессоров ( процессоров (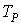 ). Эффективностью
параллельного алгоритма ( ). Эффективностью
параллельного алгоритма (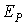 ) называют
отношение его ускорения к числу процессоров, на котором это ускорение получено. ) называют
отношение его ускорения к числу процессоров, на котором это ускорение получено.
 , , 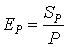 . .
Максимальное значение эффективности 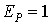 , но на практике
это значение меньше из-за затрат на обмен данными между процессорами. На рис.2
приведены значения , но на практике
это значение меньше из-за затрат на обмен данными между процессорами. На рис.2
приведены значения 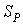 для одной итерации по Ньютону и всего шага по
времени, включающего в себя 2 итерации по Ньютону по 2 и 6 итераций решения
линейной системы в каждой. для одной итерации по Ньютону и всего шага по
времени, включающего в себя 2 итерации по Ньютону по 2 и 6 итераций решения
линейной системы в каждой.
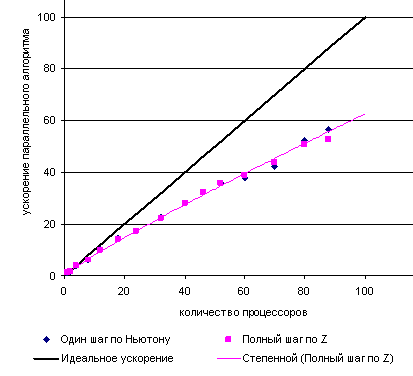
Рис.2 Ускорение параллельного алгоритма
5.
Особенности
реализации параллельных процедур
При решении уравнений с помощью неявных разностных схем возникает
необходимость в процедуре решения системы линейных уравнений. При параллельной
реализации такой процедуры неизменно встает вопрос о разделении элементов
матрицы получившейся системы между
процессорами и обеспечении обмена необходимыми элементами между процессорами.
Необходимо таким образом распределить вычислительную и иную нагрузку между
процессорами системы, чтобы по возможности исключить простои отдельных
процессоров и наиболее эффективно использовать доступные ресурсы.
При разделении расчетной области между процессорами в параллельный алгоритм
вводятся следующие множества индексов:
|
Internal
|
– внутренние, модифицируется без коммуникации
|
|
Border
|
– граничные, модифицируется с коммуникацией
|
|
External
|
– внешние, не
модифицируются, но используются для модификации элементов Border
|
Update =
{ (Internal) U (Border) } – изменяемые
элементы для данного процессора
Рисунок поясняет, как определить упомянутые множества при распределении
вершин сетки.
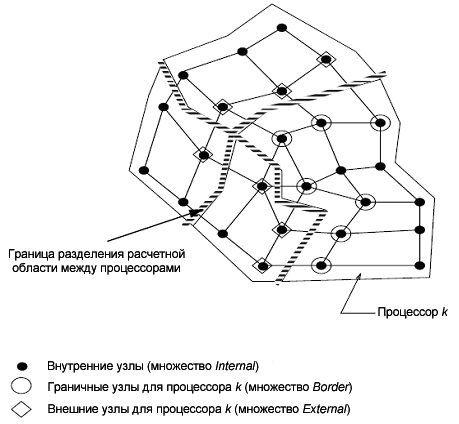
Рис. 3 Распределение расчетной сетки между
процессорами
Таким образом, учитывая тот
факт, что время на передачи информации от процессора к процессору является
основным фактором эффективности параллельного алгоритма и зависит от
технических характеристик вычислительного комплекса, при распределении расчетной
области между процессорами следует уделить внимание его минимизации. Этого можно добиться,
задавая границу между расчетными блоками по возможности минимальной и
одинаковой для каждого процессора, т.е. чтобы длина множества External была бы как можно короче и почти одинаковой для различных процессоров.
Также следует отметить, что
при реализации как явных, так и неявных схем в параллельных алгоритмах большую
роль играет двойная нумерация расчетных элементов: глобальная (global, для всей расчетной
области в целом) и локальная (local, отдельно для каждого процессора). От реализации
взаимодействия этих двух нумераций зависит сложность написания и эффективность
параллельной программы.
Используемый в данной работе
пакет Aztec
содержит встроенные функции для удобного распределения расчетной области между
процессорами:
·
линейная
·
задаваемая
пользователем
При этом согласование
глобальной и локальной нумерации происходит автоматически за счет встроенных
процедур, т.е. необходимые для взаимосвязи процессоров массивы создаются во
внутренней структуре пакета и обновление необходимых элементов происходит
автоматически. Также в пакете реализовано множество часто используемых
параллельных процедур над распределенными между процессорами массивами данных,
упрощающих реализацию алгоритма. Это, например, алгоритмы сортировки, поиска
минимальных и максимальных значений, матрично-векторного вычисления, временные
процедуры.
Стандартные функции пакета,
тем не менее, не позволяют максимально эффективно решать нелинейные системы,
требующие многократного решения матриц одинаковой структуры, но с изменяющимися
коэффициентами. Для этой цели был написан программный модуль, сохраняющий
массивы преобразования глобальной индексации матрицы в локальную для каждого
процессора, что существенно ускорило выполнение процедуры решения системы.
В качестве наиболее
оптимального сочетания для решения данной задачи выбран итерационный метод
квадратичных сопряженных градиентов (CGS) и неполное LU (Incomplete LU) разложение в качестве прекондиционера.
6.
Результаты
вычислений
В качестве примера
расчета приводим расчет для среднего по мощности ( ) импульса с полушириной
˜ω0=
3мм. Расчетная область представляет собой квадрат с длиной стороны
2см. На начальном профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке ) импульса с полушириной
˜ω0=
3мм. Расчетная область представляет собой квадрат с длиной стороны
2см. На начальном профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке  ячеек. ячеек.
|

|

|
|
Рис.4–а.
Распределение интенсивности при z=1м
|
Рис.4–б.
Распределение интенсивности при z=3м
|
|

|

|
|
Рис.4–в.
Распределение интенсивности при z=4м
|
Рис.4–г.
Распределение интенсивности при
z=6м
|

Рис.5 Линии уровня 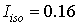 распространения импульса распространения импульса
с мощностью  на расстояние около
9м. на расстояние около
9м.
|
|
|
|
Рис.6-а
Мощность
|
Рис.6-б
Максимальная интенсивность
|
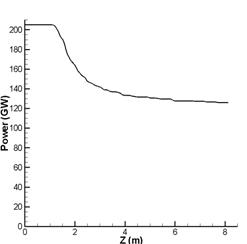
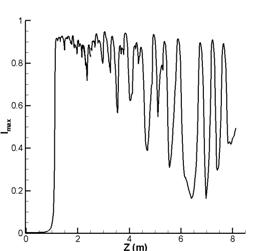
Результаты развития мощности (рис.6-а) и
интенсивности (рис. 4,5,6-б) импульса совпадают с полученными результатами
проекта Teramobile [8]. Как правило, для
большей кучности филамент, на практике применяется эллиптическое распределение
начального профиля.
Целью настоящей работы была разработка эффективных
алгоритмов для расчета явлений филаментации, позволяющих произвести
математическое моделирование процесса филаментации в различных лазерных
системах. Были использованы симметричные разностные схемы, обладающие свойством
консервативности, создан параллеленный программный комплекс для расчета таких
задач и представления результатов расчета. В работе также показана
эффективность параллельного алгоритма и проведено сравнение коминаций
стандартных параллельных итерационных методов и предобуславливателей для
решения такого рода задач.
1. J.Kasparian, M.Rodrigues, G.Mejean, J.Yu, E.Salmon, H.Wille,
R.Bourayou, S.Frey,
Y.-B.Andre,
A.Mysyrowicz, R.Souerbrey, J.-P.Wolf,
L.Woste, Science, 301, 61 (2003)
2. A. Braun et al., Opt. Lett. 20,
73 (1995); E.T.J. Nibber-ing et al., Opt. Lett. 21, 62 (1996)
3. A. Brodeur et al., Opt. Lett. 22,
304 (1997).
4. B.LaFontaine et al., Phys.
Plasmas, №6, p.1615, (1999)
5. R.Y.Chiao, Phys.Rev.Lett, V13,
N5, (1964)
6. В.И.Беспалов,
В.И.Таланов. О нитевидной структуре пучков света в нелинейных жидкостях //
Письма в ЖЭТФ, Т.3, с.471, (1966)
7. G.Fibich, B.Ilan. Vectorial and
random effects in self-focusing and in multiple filamentation // Phisica D,
157: 113-147, (2001)
8. S.Skupin, L.Berge et al., Phys.
Rev. E, 70, 046602, (2004)
9. А.Д.Балашов,
А.Х.Пергамент. Математическое моделирование процессов филаментации в средах с
кубической нелинейностью. – М.: ИПМ им. М.В.Келдыша РАН, препринт №40, (2004)
10. Aztec. A Massively Parallel Iterative Solver Library for Solving Sparse
Linear Systems. - http://www.cs.sandia.gov/CRF/aztec1.html
11. В.Н. Дацюк, А.А. Букатов, А.И. Жегуло. Многопроцессорные
системы и параллельное программирование. – Ростов: Ростовский государственный
университет, http://rsusu1.rnd.runnet.ru/koi8/index.html
12. Ю.Н.Карамзин, А.П.Сухоруков, В.А.Трофимов.
Математическое моделирование в нелинейной оптике – М.: Издательство Московского
университета, (1989)
13. Л.И. Миркин, М.А. Рабинович, Л.П. Ярославский.
Метод генерирования коррелированных гауссовских псевдослучайных чисел на ЭВМ //
ЖВМ и МФ, V. № 5. С. 1353-1357, (1972)
14. В.М.Волков. Консервативные разностные схемы с
улучшенными дисперсионными свойствами для нелинейных уравнений шредингерского
типа // Дифференциальные уравнения, Т.29, №7, (1993)
|
![]() Для анализа эффективности параллельных алгоритмов
обычно используются такие понятия, как эффективность и ускорение. Ускорением
параллельного алгоритма (
Для анализа эффективности параллельных алгоритмов
обычно используются такие понятия, как эффективность и ускорение. Ускорением
параллельного алгоритма (![]() ) называют
отношение времени выполнения алгоритма на одном процессоре (
) называют
отношение времени выполнения алгоритма на одном процессоре (![]() ) ко времени
выполнения на системе из
) ко времени
выполнения на системе из ![]() процессоров (
процессоров (![]() ). Эффективностью
параллельного алгоритма (
). Эффективностью
параллельного алгоритма (![]() ) называют
отношение его ускорения к числу процессоров, на котором это ускорение получено.
) называют
отношение его ускорения к числу процессоров, на котором это ускорение получено. ,
, ![]() .
.![]() , но на практике
это значение меньше из-за затрат на обмен данными между процессорами. На рис.2
приведены значения
, но на практике
это значение меньше из-за затрат на обмен данными между процессорами. На рис.2
приведены значения ![]() для одной итерации по Ньютону и всего шага по
времени, включающего в себя 2 итерации по Ньютону по 2 и 6 итераций решения
линейной системы в каждой.
для одной итерации по Ньютону и всего шага по
времени, включающего в себя 2 итерации по Ньютону по 2 и 6 итераций решения
линейной системы в каждой.

![]() ) импульса с полушириной
˜ω0=
3мм. Расчетная область представляет собой квадрат с длиной стороны
2см. На начальном профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке
) импульса с полушириной
˜ω0=
3мм. Расчетная область представляет собой квадрат с длиной стороны
2см. На начальном профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке ![]() ячеек.
ячеек.
![]() распространения импульса
распространения импульса ![]() на расстояние около
9м.
на расстояние около
9м.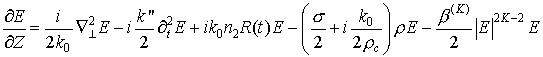
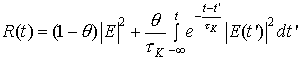
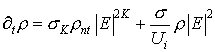
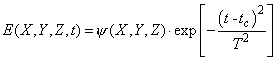
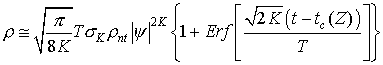
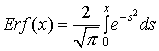
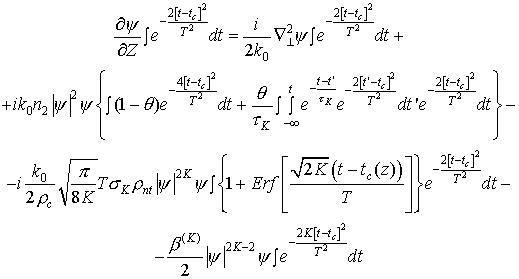
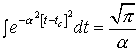
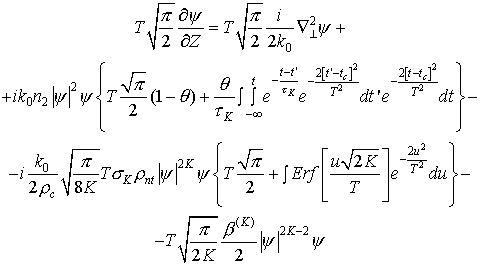
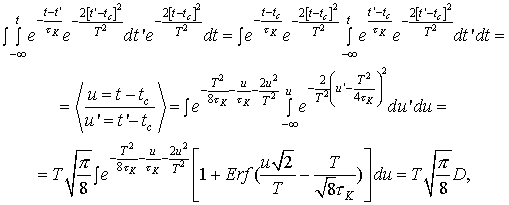
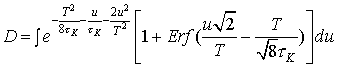
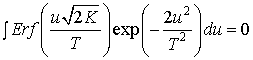
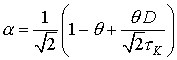
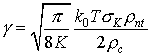
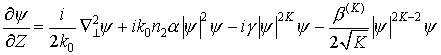
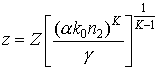
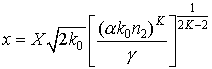
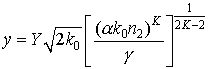
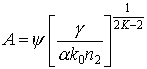
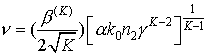
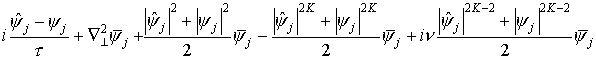
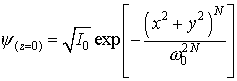
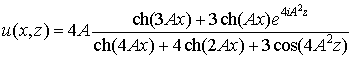 .
.





