1. Описание метода Карунена-Лоэва  5

1.1  Дискретное преобразование Карунена-Лоэва  7

1.2  Непрерывное преобразование Карунена-Лоэва  8

2. Оператор нахождения контуров на растровых изображениях  (оператор Хюккеля) 9

2.1........ Описание оператора  10

2.2........ Минимизация ошибок окружения на периферии окна  10

2.3........ Помехоустойчивость оператора  11

2.4........ Определение оператора  12

3.  Ступенчатая модель границы разделения зон контрастности  14

3.1.... Формирование вектора признаков  15

4.  Исследование базиса Карунена-Лоэва для ступенчатой границы скачка яркости. 17

4.1.... Описание рассматриваемых случаев  17

4.1.1....... Фиксированный угол  18

4.1.2....... Фиксированное смещение  19

4.1.3....... Общий случай  19

4.2.... Аналитический анализ базисных функций  21

4.2.1....... Фиксированный угол  22

4.2.2....... Фиксированное смещение  23

4.2.3....... Общий случай (модель границы Хюккеля) 24

Заключение  27

Использованная литература  28

Введение

Естественные сцены обычно состоят из множества трехмерных объектов. Телевизионные растровые или фотографические изображения являются двумерной проекцией таких сцен и представляют собой области с различными характеристиками яркости отдельных элементов изображения ("пикселов" – от англ. "picture element"). Главным источником информации, извлекаемой из изображения, является положение, величина и взаимозависимость яркостей соседних пикселов. Хотя растровые изображения и удобны для зрительного восприятия полученного изображения человеком, однако для автоматического распознавания содержания сцены более удобны векторные описания изображений. Последние позволяют более ёмко описать сцену, более просто выделить геометрические границы её объектов и, в ряде случаев, описать сцену на более высоком понятийном уровне.  

Для получения векторного описания исходного растрового изображения трёхмерных сцен хорошо применим предложенный М.Хюккелем оператор, позволяющий преобразовать растровое изображения во множество линейных отрезков фиксированной длины [1]. В своей работе Хюккель решал более частную задачу отображения растровой картины яркости в круглом окне фиксированного радиуса в уравнение прямой, аппроксимирующей позицию и направление линии максимумов градиентов яркости в точках окна. С этой целью он предложил совокупность гладких базисных функций и их дискретное представление для двумерного разложения изображения внутри окна. Подробное исследование этих функций, выполненное в [2], показало, что они удовлетворяют критерию минимума ошибки между элементами исходного изображения и наиболее вероятным положением линии градиентов яркости.

Заметим, что замена растрового изображения меньшей по объёму совокупностью отрезков, отображающих лишь локальные направления изменения яркостей, по-прежнему остаётся удобной лишь для зрительного восприятия изображения сцены, но не для программного распознавания её содержания. Для этого требуется либо семантически управлять движением окна в процессе анализа изображения, либо построить процедуру анализа семантики полученного множества отрезков на изображении.  Однако в работе Хюккеля содержится важная идея постановки задач работы с изображением: для этого следует найти удобный базис некого интегрального преобразования, адекватного решаемой задаче. Этот подход явился предтечей более позднего метода вейвлет-преобразований, заметно потеснившего в настоящее время двумерные преобразования Фурье.

Действительно, для получения лаконичного описания содержания сцены следует выделить из её изображения только "нужные" (зависящие от искомого содержания) элементы пространственных взаимосвязей пиксельных яркостей, исключив "ненужную" (избыточную) и восполнив утерянную (в результате наличия шумов фотоприемника) информацию. Здесь возникает задача построения такого способа описания изображения, в котором элементы описания слабо зависимы.

Одним из наиболее перспективных методов решения этой, очень непростой проблемы является поиск двумерного ортогонального базиса для интегрального преобразования растрового изображения, адекватного задаче распознавания сцены,  и такого (что важно), который обеспечивает сосредоточение искомой информации в минимальном числе коэффициентов разложения. Эти - "старшие гармоники" спектра разложения несут, как правило, искомую информацию об интегральных перепадах яркости, в то время как высокочастотные составляющие спектра отражают лишь избыточную информацию, - например, в задаче поиска контуров областей изображения.

Заметим, что Хюккель не описал, как именно он получил свой набор ортогональных двумерных функций с ограниченным носителем в виде единичного круга (см. ниже). Выполненная в работе [2] проверка подтвердила адекватность базиса Хюккеля поставленной им задаче. Однако, представляется крайне желательным иметь формальный метод для построения базиса, адекватного решаемой задаче обработки изображения. Такой метод удалось построить, используя другое, хорошо известное в теории распознавания образов, преобразование Карунена-Лоэва ("КЛ-преобразование").

В литературе КЛ-преобразование описывается в рамках вероятностной модели сигнала, при этом известно, что для стационарных, в широком смысле, случайных полей изображений оптимальной аппроксимацией КЛ-преобразования асимптотически (при увеличении размеров исходного изображения)  являются преобразование Фурье и (в дискретном случае) косинусное преобразование. Но, безусловно, метод Карунена-Лоэва носит более общий характер, - он применим для совокупности не обязательно случайных элементов изображения, для которых существует знание аналога корреляционной функции их яркости.

КЛ-преобразование обладает рядом свойств, позволяющих его выделить среди остальных линейных преобразований. Оно дает лучший результат в некотором смысле, определенном ниже. Главным недостатком преобразования Карунена-Лоэва является отсутствие быстрых алгоритмов вычисления (известно, что если N – число отсчетов изображения, то число операций, необходимых для выполнения КЛ-преобразования пропорционально ).  Поэтому на практике КЛ-преобразование применяется редко.

Ниже метод Карунена-Лоэва в его дискретном и непрерывном вариантах используется в методе формального вывода ортогонального базиса, наиболее подходящего для интегрального преобразования выбранной модели оконного элемента изображения. Полученный метод описывается на примерах построения операторов преобразования изображений, схожих с оператором Хюккеля.  В частности, приводится формальный вывод базиса для оператора Хюккеля и анализ значимости его гармоник.

1. Общее описание метода Карунена-Лоэва

Преобразование Карунена-Лоэва было предложено независимо финским математиком Каруненом  (Kari Karhunen) в 1946 и французским математиком Лоэвом  (Michel Loève) в 1955. Метод известен под различными названиями, такими как "разложение Карунена-Лоэва", "преобразование Хотеллинга" (дискретный вариант преобразования Карунена-Лоэва),  "квазигармонические моды", "собственное ортогональное разложение", "эмпирическое разложение на собственные функции". С формально-математической точки зрения преобразование Карунена-Лоэва представляет собой разложение сигнала X(t) по базису ортогональных функций, каждая из которых является собственной функцией интегрального "характеристического" уравнения с симметричным непрерывным ядром:

и , 0£t£T,  E{a_n a_n}=í

Основная идея заключается именно в существовании и использовании некого ядра, связанного со свойствами сигнала X(t). При заданном виде ядра приведенное интегральное уравнение определяет ортогональный базис разложения по его собственным функциям, что упрощает разложение и минимизирует (см. [4]) квадрат ошибки.

Чаще всего K(t,s) трактуется в виде корреляционной функции R(t,s)=E{x(t) x(s)} в общем случае непериодического и нестационарного случайного процесса с нулевым математическим ожиданием E(X(t)) и существующим вторым моментом  E(X(t))² . В задачах распознавания случайных образов ядро определяется как

K(t,s)=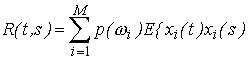

т.е. – в виде корреляционной функции между классами сигналов, с некоторой вероятностью p(w_I) принадлежащих одному из M искомых образов (см. [3], с.291-303).

В дискретном случае оно диагонализирует матрицу некоторой заданной квадратичной формы K, т.е. приводит её к виду , где -искомая диагональная матрица, а  - матрица собственных векторов искомого преобразования y=Fx. Метод во многом носит геометрический характер, но в большинстве источников он описывается с точки зрения теории вероятности. В таком описании матрица K является дискретным представлением корреляционной функции R(t,s) в общем случае непериодического случайного процесса наблюдения сигнальных векторов x(t).

                                                                                                                                             Мы рассматриваем КЛ-преобразование применительно к растровым изображениям. Такое изображение всегда содержит избыточную информацию, как следствие содержательного и шумового взаимовлияния его соседних элементов. В связи с этим рассматриваются:

·        ковариационная матрица K, которая описывает аппроксимацию отсчетов в координатной плоскости изображения (х,у) многомерной гауссовой функцией распределения и

·        соответствующая ей  корреляционная матрица R.

Важным методом многомерного статистического анализа служит исследование массива данных не только в их естественных координатах, но и в системах координат с более удобными свойствами. В частности, весьма полезными оказались системы координат, основанные на собственных значениях и собственных векторах ковариационной матрицы K. Преобразование координат, определяемое матрицей  собственных векторов  матрицы квадратичной формы, рассматриваемой в качестве линейного оператора исходного пространства, обладает тем свойством, что оно производит преобразование заданного массива чисел в другой с некоррелированными элементами, причем получающиеся компоненты имеют убывающие дисперсии.

Пусть собственные значения матрицы K расставлены в убывающем порядке и пронумерованы. Пусть собственные векторы, связанные с ними, расставлены в том же порядке. Тогда матрица собственных векторов  обладает тем свойством, что умножение ее на вектор-изображение g дает вектор  , имеющий некоррелированные компоненты, причем компоненты вектора G  оказываются расставленными в порядке убывания их дисперсий, что является свойством дискретного варианта разложения Карунена – Лоэва.

Полезность КЛ-преобразования  для сокращения избыточности изображений очевидна. Массив отсчетов изображения заменяется набором переменных, имеющих различные статистические веса. Отбрасывая переменные с малым статистическим весом, и сохраняя остальные, можно достигнуть многократного сжатия изображения. В процессе отбрасывания переменных возникает среднеквадратичное отклонение от оригинала. Особенность КЛ-преобразования состоит в том, что из всех линейных преобразований именно оно обеспечивает минимальную величину такого отклонения.

В литературе приводится информация, которая проверена экспериментально в рамках данной работы, что очень многие элементы этой матрицы близки к нулю, т.е. коэффициент корреляции между отсчетами быстро стремится к нулю с увеличением расстояния между соответствующими точками изображений. Расстояние, при котором коэффициент корреляции между яркостями элементов изображения становится настолько малым, что его можно приравнять нулю (например, 5 или 10 % максимального значения), называется радиусом  корреляции отсчетов; его можно выразить через целое число  отсчетов. Зная это расстояние, все изображение можно разбить на блоки, размер которых больше радиуса корреляции, но сравним с ним. Это даёт возможность выбрать компромисс между размером ковариационной матрицы и скоростью, с которой коэффициент корреляции отсчетов приближается к нулю  (для большинства изображений берут ).

В работе не заостряется внимание на факте близости нулю коэффициентов корреляции между далекими точками, поскольку для нашей задачи это не представляет интереса. Но убедиться в этом, в рамках данного текста, возможно на примере ковариационных функций в непрерывном варианте преобразования для рассматриваемых случаев.

Еще раз выпишем основные достоинства КЛ-преобразования:

-         концентрация мощности (дисперсии) в минимально возможном числе признаков,

-         минимальная среднеквадратичная погрешность восстановления исходного изображения при заданном числе признаков,

-         некоррелированность, а в случае нормального распределения яркости исходного изображения и независимость, рассчитываемых признаков.

Для всего вышесказанного приведем теоретические основы КЛ-преобразования для произвольного случайного вектора  в объеме, необходимом для данной работы. В дальнейших главах мы определим, что является вероятностным пространством в случае модели Хюккеля и на растровом изображении.

1.1  Дискретное преобразование Карунена-Лоэва

Рассмотрим вектор признаков размерности

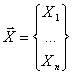              (1.1)

Компоненты вектора принимают случайные значения  и описываются коэффициентами разложения по некоторому ортонормированному базису размерности . Обозначим этот базис через . В общем случае компоненты в этом базисе коррелируют между собой.

Решается задача поиска такого базиса, в котором вектор  может быть аппроксимирован  компонентами с минимальным среднеквадратичным отклонением.

Итак, если ,    где  - коэффициенты разложения

Аппроксимация   ,             (1.2)

Ошибка                  (1.3)

Среднеквадратичное отклонение 

             (1.4)

Значение  меняется в зависимости от выбора базисных векторов и констант .

Минимизация  по этим параметрам приводит к следующим результатам:

1.  , тогда

,                    (1.5)

где  ковариационная матрица .

2.  Уравнению на минимум ошибки относительно базисных функций удовлетворяет матрица из собственных векторов матрицы . Отсюда компоненты вектора  в новом базисе не коррелируют между собой, поскольку ковариационная матрица в новом базисе диагональна.

Преобразование

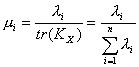, где              (1.6)

позволяет оценить значение ошибки , а также оценить статистический вклад каждого нового базисного вектора, поскольку

           (1.7)

в силу ортогональности собственных векторов.

1.2  Непрерывное преобразование Карунена-Лоэва

Пусть  - случайный процесс, описывается ансамблем реализаций.

Требуется найти базис , в котором  некоррелированы (рассматриваются  и ). Представление  в таком базисе является результатом применения непрерывного преобразования Карунена-Лоэва. Итак, требуется:

,              (2.1)

где  - корреляционная функция .

Далее 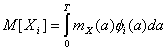 , то условие (2.1) принимает вид

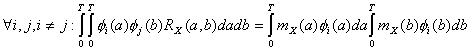         (2.2)

 или

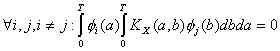,         (2.3)

где  - ковариационная функция . В случае  мы получим значение для дисперсии. Тогда общий вид условия

      (2.4)

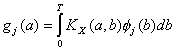           (2.5)

Одно из решений достигается в случае предположения, что . Таким образом

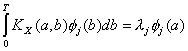.     (2.6)

Ядро  удовлетворяет условиям теоремы Мерсера  [4], поэтому справедливо разложение

.            (2.7)

В [2] приведены формулы для вычисления коэффициентов разложения:

         (2.8)

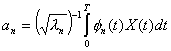   (2.9)

Аналогично дискретному случаю набор  может рассматриваться как средние энергии потока спроецированного на базис . Упорядочим собственные значения . В [3] приводится оценка, что в первых  P коэффициентах разложения по базису  сосредоточена большая энергия, чем в любом другом базисе :

.       (2.10)

2. Оператор нахождения контуров на растровых изображениях (оператор Хюккеля)

Информация об изображении в пиксельном представлении требует не только большого объема памяти для хранения, но и неудобна для анализа запечатленной сцены. Описание картинки множеством отрезков несет уже информацию не только о яркостной характеристике, но и об особенностях её вариации. Такое описание можно свести к выделению контуров на исходном изображении, которые являются его первичными признаками.

В работах Хюккеля и Хаммела был предложен метод автоматического выделения отрезков на растровом изображении, который, является результатом формализации требований и вывода соответствующих формул.

2.1           Описание оператора

Имеется пиксельное изображение размера . Пусть D – множество клеток сетки, наилучшим образом аппроксимирующиее круглое окно, принадлежащее изображению.

На Рис. 1, a показан пример входного окна D, состоящего из 52 элементов. Через  обозначим значение яркости изображения в точке p.

На Рис. 1, б показан идеальный элемент контура, наилучшим образом аппроксимирующий эмпирический элемент контура, изображенный на Рис. 1, а. Входом оператора является любая функция . На первом этапе вычисляются восемь промежуточных чисел по формуле:

.     (2.1.1)

На втором этапе осуществляется нелинейное преобразование этих чисел в шесть конечных контурных данных, которые будут определены ниже. Совокупность чисел  образует матрицу из констант, которые получаются из аналогичных непрерывных функций .

2.2           Минимизация ошибок окружения на периферии окна

Оператор выводится с непрерывной граничной линией, как показано на Рис. 1, б.

Определим границу идеального окна

.

Формула (2.1.1) выписана для дискретного случая. Для непрерывного случая:

    (2.2.1)

При наложении идеального и дискретного окна друг на друга

 - углы некоторых клеток дискретного окна выходят за границы идеального окна

 - углы некоторых клеток дискретного окна, внешних по отношению к идеальному окну, попадают внутрь идеального окна.

Таким образом, при переходе от непрерывного к дискретному случаю возникает ошибка. Введем критерии по которым мы будем минимизировать эту ошибку.

Во-первых, размер “неправильных” углов минимизировался посредством выбора конкретных размеров окон.

Во-вторых переход от формулы (2.2.1) к формуле (2.1.1) осуществлялся преобразованием

Ошибка, которая возникает из-за того, что углы некоторых клеток из D выходят за пределы идеального круга компенсируется условием .

Отсюда же возникает желание, чтобы на границе функции , а приближении к границе окна точки учитывались с меньшим весом. В качестве такой весовой функции выбрана функция .

2.3           Помехоустойчивость оператора

Множество всех непрерывных на окне  функций образует гильбертово пространство. Полная ортонормированная последовательность функций , заданных на определяет декартов базис в этом гильбертовом пространстве. Вектор  в этом базисе имеет координаты , где

    (2.3.1)

Этот вектор является спектром Фурье, если  являются пространственно-периодическими функциями и если они строго упорядочены по возрастанию частот.

В соответствии со сформулированными выше требованиями диаграммы первых восьми функций имеют вид указанный на Рис. 2. Сплошными линиями показаны нулевые значения.

Определим функции  как функции низких или высоких пространственных частот в зависимости от  или  Для вычисления оператора существенны функции низких частот. Потому сократим гильбертово представление до первых восьми компонент . Тем самым первый шаг действия оператора может рассматриваться как низкочастотный фильтр. Учет высоких частот не нужен вследствие наличия размытости и(или) шумов на изображениях.

2.4           Определение оператора

Пусть  и  - функции такого типа, как показано соответственно на Рис. 2.1.1, а и 2.1.1, б.  непрерывна и постоянна в пределах каждой клетки растра и произвольна во всех остальных точках.  - непрерывна и постоянна всюду, кроме линии контура . Для нормализации этого уравнения положим . Пусть A – меньшая, а A+B – большая из двух яркостей, соответствующих ступенчатой функции . Тогда имеем:

Между идеальными краевыми элементами  и пятерками чисел  существует взаимно-однозначное соответствие. В действительности независимых параметра только четыре, т.к. . Определять функции  и  вне окна нет необходимости.

В качестве критерия оптимальности оператора был выбран минимум квадрата гильбертова расстояния между  и :

.

Пусть набор функций  является полным и ортонормальным базисом в гильбертовом пространстве функций, заданных на круге . Определим

.

Тогда выражение принимает вид:

.    (2.4.1)

Из-за вычислительной сложности данный критерий заменяют критерием:

.    (2.4.2)

Приведем вид базисных функций , полученный Хюккелем. Пусть:  , , .

Тогда:

,

,

,

,

,

,

,

.

Определение: Набор  будем называть функциями Хюккеля.

 Примечание: В статье Хюккеля высказано предположение, что исключение весовой функции не влияет на вид функций .

В [4] с доказательством приводится теорема о решении, в соответствии с которой минимизируется (2.4.2). Также приводятся выражения для функций  и . Теорема позволяет в более простой форме реализовать работу оператора на ЭВМ. Её смысл заключается в сведении минимизации исходного критерия к поиску экстремумов другого критерия. Для выяснения, являются ли полученные контурные данные достаточно свободными от шума, сравнивают первоначальные данные с полученным идеальным элементом контура путем вычисления корреляционной зависимости между ними. В работе [5] приведены результаты работы оператора.

3.  Ступенчатая модель границы

разделения зон контрастности

В данном пункте приводится математическое описание границы разделение зон контрастности, использованной Хюккелем.

Пусть имеется функция в ортонормированной системе координат (0,x,y):

,  где                     (3.1.1)

    ,  .

Эта функция представляет собой модель границы, разделяющей две контрастные области, см. Рис. 3  Модель ступенчатой границы скачка яркости для круглого окнаи описывает идеальный элемент контура в статье Хюккеля. При переходе через эту границу происходит скачок с одного постоянного значения яркости на другое. Пусть A – значение для меньшей интенсивности, а  A+B для большей. В двумерном случае граница скачка яркостей проходит вдоль прямой, определяемой параметрами угла наклона  и смещения . Значение для интенсивности в точке (x,y) равно .

Задача аппроксимации исходного круглого окна на исходном изображении идеальным элементом контура сводится к подбору значений параметров  и , удовлетворяющих критерию минимума квадрата отклонения (2.4.1). Промежуточная задача состоит в определении значений A, B.  Если не обращать внимания на корреляцию значений параметров в близких окнах, можно говорить что их значения носят случайный характер. Экспериментальная проверка показала, что такое допущение возможно. При аналитическом исследовании мы определим вероятностное пространство параметров. Здесь же будем считать, что они носят случайный характер с неизвестным распределением.

Растровое изображение состоит из дискретных элементов-пикселей. Потому введём функцию дискретизации идеальной границы скачка яркости в круглом окне:

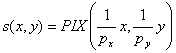     (3.1.2)

где и  - расстояния между двумя дискретными элементами.

Дадим следующие определения:

Определение:  Функцию описания яркостной характеристики идеального круглого окна

назовём моделью Хюккеля разделения зон контрастности.

Определение:  Функцию описания яркостной характеристики дискретизированного идеального круглого окна

назовём дискретной моделью Хюккеля разделения зон контрастности.

3.1        Формирование вектора признаков

Обратимся к дискретному варианту преобразования Карунена-Лоэва. Формирование ковариационной матрицы осуществляется на основе реализаций вектора признаков.

В нашем случае этот вектор характеризует яркостную характеристику изображения. Эмпирический элемент контура, упоминаемый при описании оператора Хюккеля (Рис. 1), представляет собой выборку яркостей точек участка изображения ограниченного круглым окном. Реализацию вектора признаков получаем построчным сканированием значений яркостей пикселов эмпирического элемента контура Рис. 4.

Значения яркостей точек окна, фрагмент которого указан на рисунке, построчно выбираются и выстраиваются в столбец значений. Полученная совокупность векторов используется для составления ковариационной матрицы.

Набор эмпирических элементов контуров получается из реализаций дискретной модели Хюккеля разделения зон контрастности с выбранными законами изменения параметров. В работе рассматривалось два варианта получения параметров:

1.  Покрытие плоскости изображений сцен дискретными круглыми окнами и дальнейшей их аппроксимацией эмпирическими элементами контуров.

2.  Выборка значений параметров с определенным шагом, а также случайная выборка значений при помощи стандартных генераторов случайных чисел.

Экспериментальная проверка показала, что во всех случаях базисные вектора преобразования Хотеллинга совпадают с точностью до порядка следования, что скорее объясняется объемами выборок.

На Рис. 5 приводится график статистических вкладов собственных векторов в порядке убывания их собственных значений.

Из графиков хорошо видно преимущество преобразования Карунена-Лоэва - основная часть информации сосредоточена в коэффициентах разложения по первым базисным векторам.

В работе [1] приводятся примеры применения оператора Хюккеля.

4.  Исследование базиса Карунена-Лоэва для ступенчатой границы скачка яркости

В данной главе будет рассмотрен базис Карунена-Лоэва в форме Хотеллинга (дискретный вариант преобразования) для круглого окна со ступенчатой границей скачка яркости для случаев с фиксированными параметрами и общий случай. Будет произведено аналитическое расссмотрение полученных результатов при помощи непрерывного преобразования Карунена-Лоэва. Частные случаи представляют как самостоятельный интерес, как примеры оптимальных базисов, и как проверка совпадения практических и теоретических результатов во введенном вероятностном пространстве.

Исследуется связь между базисом Хюккеля и базисом Карунена-Лоэва для введенной модели изменения яркости.

Примечание:  Все изображения базисных функций преобразования Хотеллинга будут приводиться в порядке убывания соответствующих им собственных значений (слева направо).

4.1           Описание рассматриваемых случаев

Вспомним ступенчатую модель границы скачка яркости, использованную при выводе оператора Хюккеля (см. 3.1.6).

,   (4.1.1)

где A и A+B значения яркости по разные стороны границы

, 

Рассмотрим результаты применения преобразования Хотеллинга при свободных и фиксированных значениях параметров  и . А именно:

Случай 1:  ,  - изменяется.

Случай 2:   - изменяется, .

Случай 3:   - изменяется,  - изменяется   -  модель Хюккеля границы разделения зон контрастности.

Далее для тех же случаев рассмотрим непрерывный вариант преобразования Карунена-Лоэва.

В Таблица 1 приведены параметры, использованные при вычислении преобразования Хотеллинга

Таблица 1   Таблица параметров реализаций рассмотренных ниже случаев

4.1.1   Фиксированный угол

Граница скачка яркости задаётся как

, где ,    (4.1.1.1)

где R-радиус окна. В этом случае можно повернуть систему координат так, чтобы в новых координатах . Тогда для любого выбранного зафиксированного y значения  равны для всех x. Без ограничения общности будем считать . На Рис. 7 представлен фрагмент выборки для получения ковариационной матрицы.

На Рис. 8 представлены первые десять базисных векторов.

На основе изображений можно предположить, что в рассматриваемой системе координат базисные функции имеют вид:

,    (4.1.1.2)

В пользу этого говорят коэффициенты Фурье преобразования, которое дает четкие пики для соответствующих кратностей синусоиды.       

4.1.2   Фиксированное смещение

Граница задаётся как

, где .    (4.1.2.1)

Пример выборки на Рис. 9

Первые двадцать базисных векторов на Рис. 10

Общий вид функций из рисунков в полярных координатах :

,     (4.1.2.2)

В отличие от первого случая здесь нет функций четных синусов вида .

4.1.3   Общий случай

Граница задаётся как

, где ,    (4.1.3.1)

что соответствует модели Хюккеля. Фрагмент выборки:

Первые базисные векторы:

На Рис. 13  приведен график статистических (информационных) вкладов базисных векторов в порядке убывания соответствующих собственных значений.

Поскольку набор базисных векторов одинаков и для произвольного изображения, и для упорядоченной выборки, то возможно сократить объем самой выборки и ограничиться синтезом искусственной, меньшей по объему выборки, которая охватывает все положения границы (с заданной мелкостью шага).

4.2           Аналитический анализ базисных функций

Рассмотрим функцию, заданную в круге D=

      (4.2.1)

,  ,

Параметры  и  определяют прямую

    (4.2.2)

По одну сторону от этой прямой функция принимает значение 1, по другую 0, что соответствует Хюккелевской модели идеальной границы разделения зон контрастности для  значений  и . Эти значения мы будем использовать при аналитическом исследовании.

Пусть значения  и  случайны с функциями плотности  и  соответственно, т.е. распределены равномерно. Такое распределение выбрано из оценки экспериментальных результатов.

Тогда значения функции  носят случайный характер в зависимости от случайного положения границы разделения.

Запись вида  будет говорить об усреднении по случайным параметрам.

Далее будем говорить не о значении функции в точке, а о вероятности значения

    (4.2.3)

Такая модель описывает случайную границу разделения зон контрастностей, соответствующую модели Хюккеля

Дискретное приближение этой функции описывает случайные вектора в модели ступенчатой границы скачка яркости при выполнении преобразования Хотеллинга. Проведем анализ описанных выше случаев с введенным вероятностным пространством. Для этого еще раз приведем рассматриваемые случаи:

Случай 1:  ,  - случайно.

Случай 2:   - случайно, .

Случай 3:   - случайно,  - случайно   -  модель Хюккеля границы скачка яркости.

Будем считать, что функция  удовлетворяет свойству марковости. Рассмотрение частных случаев, помимо самостоятельного интереса построения оптимального базиса в этих случаях, даёт возможность проверки соответствия теоретических результатов во введенном вероятностном пространстве с практическими.

Далее проводится аналитическое исследование собственных функций преобразования Карунена-Лоэва при помощи его непрерывного варианта и сравнение с дискретным вариантом (преобразование Хотеллинга) и результатами Хюккеля.

Рассматривается уравнение на собственные функции (в соответствии с формулой 1.4.6):

, где   (4.2.4)

 - ковариационная функция случайной функции .

4.2.1   Фиксированный угол

Рассмотрим , где значение  фиксировано, а . Без ограничения общности положим .

Для удобства сдвинем координаты и запишем , где . В этом случае зависимость присутствует только по одной координате, поэтому будем искать базисные функции, как функции одной переменной . Значение функции:

    (4.2.1.1)

Откуда получаем ковариационную функцию:

.     (4.2.1.2)

Функции  ищем с точностью до масштабирующей константы.

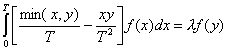   (4.2.1.3)

откуда получаем решения вида:

,  ,       (4.2.1.4)

Этот результат совпадает с предположением о виде базисных функций  из пункта 4.1.1 (см.  4.1.1.2).

4.2.2   Фиксированное смещение

Этот случай рассмотрим в полярных координатах . Тогда граница разделения значений запишется как

Константой является радиус-вектор , а не только его модуль. Без ограничения общности возьмем .

Тогда функция .

Фиксируем две произвольные точки в круге

 и .

Ковариационная функция имеет вид:

        (4.2.2.1)

Уравнение на собственные функции:

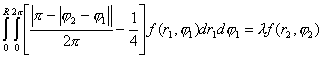    (4.2.2.2)

Зависимости по нет, поэтому нас интересуют решения по .  Для данного уравнения они имtют вид:

,     .    (4.2.2.3)

Таким образом, видно, что действительно для модели пункта 4.1.2 базисные функции представляют собой нечетные синусоиды. (см. 4.1.1.2)

Стоит заметить, что случаям 2.1 и 2.2 удовлетворяют и sin() и cos(), этим объясняются внешне одинаковые изображения пар базисных функций, смещенных относительно друг друга по фазе на , в чем можно убедиться простой подстановкой.

4.2.3  Общий случай (модель границы Хюккеля)

Будем искать базис в полярных координатах. Уравнение границы

.

 и  - принимают случайные значения в соответствии с законом описанным выше.

Фиксируем две произвольные точки в круге

 и .

Ковариационная функция, как этого следовала ожидать, симметрична относительно переменных:

   (4.2.3.1)

Уравнение на собственные функции:

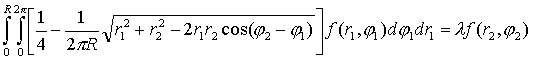    (4.2.3.2)

Заметим что, как и двух предыдущих случаях, в ядре уравнения присутствует функция расстояния. Преобразуем уравнение к более удобному для анализа виду.

В данном уравнении можно выделить производящую функцию для полиномов Лежандра [6]. Это позволяет привести уравнение к виду:

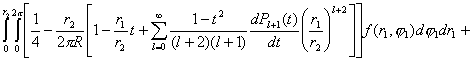
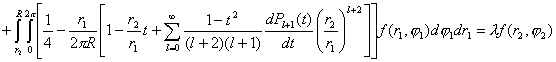. (4.2.3.3)

где  - система полиномов Лежандра.

Предполагая, что искомые функции Хюккеля есть простейшие куполообразные, выделим низкочастотную составляющую ядра. Рассмотрим  подынтегральные ряды с точностью до членов второго порядка включительно.

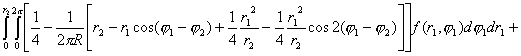
(4.2.3.4)

На основе изображений базисных функций дискретного варианта преобразования ищем решения в виде

, где .  (4.2.3.5)

Рассмотрим решения для  n=0,1,2.

1.     n=0

Решение, полученное в среде Matlab, является функцией набора гипергеометрических функций и степеней r:

,  ;   (4.2.3.6)

2.     n=1

Уравнение даёт аналитическое решение:

 и ,  k=1,2…;  (4.2.3.7)

3.     n=2

Условия на решение  .

Решение, полученное в среде Matlab, является функцией набора тригонометрических функций и степеней r:

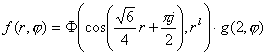, j=0,1, l=0,1,2…;  (4.2.3.8)

Для n=0,1,2  численные решения уравнения по  имеют вид:  

В случае n=2 наблюдается затухание амплитуды при возрастании r.

Заключение

В работе получены следующие результаты:

1. Проведено исследование свойств базисных векторов преобразования Хотеллинга.

2. Реализована программа аппроксимации изображения круглыми окнами с Хюккелевской моделью границы скачка яркости. Реализована программа расчета собственных чисел и векторов преобразования Хотеллинга для выбранных окон и их визуализация.

3. Экспериментально проведена возможность выделения элементов контура на изображении при помощи собственных функций преобразования Хотеллинга.

4.  Рассмотрены частные и общий случаи модели ступенчатой границы скачка яркости. Проведён аналитический анализ собственных функций для всех случаев при помощи непрерывного преобразования Карунена-Лоэва.

5. Произведен сравнительный анализ полученных решений с результатами Хюккеля.

В результате можно сделать следующие выводы (обозначение П. Х. М. здесь приняты применительно к Хюккелевской модели границы зон контрастности):

1.  В коэффициентах разложения по первым восьми базисным функциям преобразования Карунена-Лоэва сосредоточено ~99% информации об изображении. П. Х. М. 

2.  Собственные функции преобразования Карунена-Лоэва П. Х. М. с фиксированием части параметров положения границы описываются тригонометрическими функциями.

3.   В модели границы (П. Х. М.) со свободными параметрами, функции Хюккеля описываются выборкой низкочастотных решений уравнения на собственные функции преобразования Карунена-Лоэва на отрезке [0;1]. 

4.  В функциях Хюккеля сосредоточено порядка 90% информации о низкочастотной составляющей изображения для рассматриваемой модели.

Использованная литература

1.     Hueckel М., An Operator which Locates Edges in Digitized Pictures, Stanford University, CM, 18, №1, 113-125, 1971

2.     Болденков А.В., Исследование характеристик оператора Хюккеля, Магистерская диссертация  (рук. А.К.Платонов), МФТИ, 2004

3.     Ту Дж., Гонсалес. Р. Принципы распознавания образов. М.:Мир, 1978

4.     Петровский И.Г. Лекции по теории интегральных уравнений. М., 1965

5.     Andrew J. Newman, Model Reduction via the Karhunen-Loeve Expansion. Part I: An Exposition, University of Maryland, 1996

6.     Позднухов А.Н., Применение статистической теории обучения к анализу и моделированию данных по окружающей среде.

7.     Julio Enrique Castrillon-Candas, Kevin Amaratunga, Fast Estimation of Continuous Karhunen-Loeve Eigenfunctions Using Wavelets, 2002

8.     Пальцев Б.В., Сферические функции, Учебное пособие УДК 517.586.