Аннотация
В работе выведены уравнения равновесия плазмы, обобщающие в аксиально симметричном случае
известное уравнение Грэда-Шафранова. Последнее уравнение является предельным и вырожденным
случаем полученных. Особо рассмотрены случаи цилиндрической симметрии, Θ–пинча, Z–пинча.
Abstract
Plasma equilibrium equations for two – fluid and quasineutral plasma are derived
in this work. Well known Grad – Shafranov equation in MHD is limiting and degenerating
case ot equations obtained. The cases of cylindrical symmetry, Θ–pinch, Z–pinch are
considered.
Введение.
Задачи плазмостатики исторически возникли как составная часть программы УТС
[1]. В центре внимания плазмостатики находится расчет равновесных конфигураций
плазмы и удерживающего её магнитного поля. Технические конструкции, реализующие
равновесные конфигурации, называются магнитными ловушками.
Теоретической основой расчета магнитных ловушек на сегодняшний день является
МГД – теория.
Практически
наиболее интересны равновесные конфигурации, обладающие определенной
симметрией: цилиндрической, плоской, осевой, винтовой. В случае осевой
симметрии равновесная МГД – конфигурация ищется как решение уравнения Грэда
– Шафранова [1,2]:
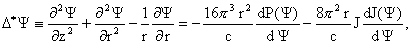
где 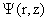 – функция магнитного потока, – функция магнитного потока,
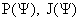 – произвольные заданные функции, имеющие смысл давления
плазмы и функции полного тока. – произвольные заданные функции, имеющие смысл давления
плазмы и функции полного тока.
В работе
выведены уравнения плазмостатики (общие и в случаях цилиндрической и осевой
симметрии), базирующиеся на существенно более точных ЭМГД (ЭлектроМагнитных ГидроДинамических) –
уравнениях плазмы, предельным случаем
которых – при стремлении погонного числа частиц к
бесконечности – являются МГД – уравнения.
ЭМГД –
теория [3], предполагая квазинейтральность и нерелятивистский характер
плазменных процессов, в полном объеме, в отличие от МГД, учитывает инерцию электронной компоненты.
В случае
осевой симметрии уравнения ЭМГД – равновесия сводятся к паре дифференциальных
уравнений 2-го порядка относительно функций магнитного потока  и полного тока и полного тока 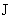 (уравнения (25-27) из
§5). В практически важных предельных случаях (уравнения (25-27) из
§5). В практически важных предельных случаях 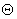 – пинча и – пинча и 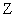 – пинча полученная
система редуцируется к одному уравнению 2-го порядка относительно – пинча полученная
система редуцируется к одному уравнению 2-го порядка относительно  (уравнение (14) из §4)
и (уравнение (14) из §4)
и 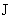 (уравнение (37) из
§7), соответственно. (уравнение (37) из
§7), соответственно.
Выведенные уравнения ЭМГД – равновесия принципиально отличаются от уравнения Грэда –
Шафранова.
Во-первых,
для ЭМГД семейства поверхностей уровня 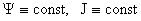 , , 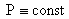 не
совпадают между собой, как это было в МГД, а, напротив, функции не
совпадают между собой, как это было в МГД, а, напротив, функции 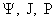 функционально независимы. функционально независимы.
Во-вторых,
ЭМГД – равновесные конфигурации зависят от распределения плотности плазмы,
которая, в отличие от МГД – теории, не может выбираться произвольно, но
подлежит нахождению.
В-третьих,
в ЭМГД – плазмостатике разреженная и плотная плазма подчиняется разным законам
равновесия. Математически это выражается в том, что полученные уравнения ЭМГД –
равновесия являются смешанного типа системой дифференциальных уравнений
относительно  и и 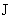 , гиперболической для разреженной плазмы и эллиптической для
плотной (см. § 7). , гиперболической для разреженной плазмы и эллиптической для
плотной (см. § 7).
В-четвертых,
ЭМГД – равновесия существенно определяются уравнениями состояния плазменных
компонент (см.§5).
Уравнения ЭМГД – плазмостатики в МГД –
пределе переходят в уравнение Грэда – Шафранова. Количественной мерой различия
двух теорий является параметр
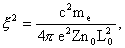
где 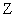 – кратность заряда ионов, – кратность заряда ионов, 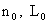 – характерные
плотности числа частиц и длины. Теоретически, ЭМГД – плазмостатика переходит в
МГД – плазмостатику при – характерные
плотности числа частиц и длины. Теоретически, ЭМГД – плазмостатика переходит в
МГД – плазмостатику при  . Однако, для параметров реальной плазмы . Однако, для параметров реальной плазмы 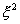 конечно, и различие
двух теорий может быть существенным, причем не только количественно , но и
качественно, поскольку дифференциальный оператор уравнений ЭМГД – равновесия
является сингулярным по конечно, и различие
двух теорий может быть существенным, причем не только количественно , но и
качественно, поскольку дифференциальный оператор уравнений ЭМГД – равновесия
является сингулярным по 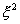 и значит в МГД –
пределе, и значит в МГД –
пределе,  , вырождается. Поэтому уравнение Грэда – Шафранова является
не просто предельным, но вырожденным случаем ЭМГД – плазмостатики. , вырождается. Поэтому уравнение Грэда – Шафранова является
не просто предельным, но вырожденным случаем ЭМГД – плазмостатики.
§
1. ЭМГД
– модель плазмы.
Течение
бездиссипативной квазинейтральной нерелятивистской плазмы с учетом инерции
электронов подчиняется следующей системе уравнений (ЭМГД–уравнения) [3] :
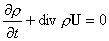 ,
(а) ,
(а)
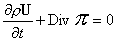 , (б) , (б)
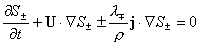 , (в) (1) , (в) (1)
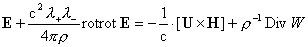 , (г) , (г)
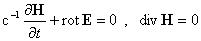 , (д) , (д)
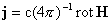 ,
(е) ,
(е)
Тензор напряжений
 и тензор и тензор 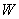 вычисляются по
формулам: вычисляются по
формулам:
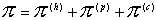
(2)
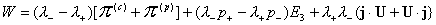
А гидродинамическая 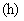 , пондеромоторная , пондеромоторная 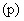 и токовая и токовая  части тензора
напряжения определяются соотношениями: части тензора
напряжения определяются соотношениями:
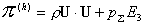 , ,
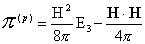 ,
(3) ,
(3)
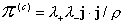 . .
Выше считалось  , , 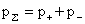 , , 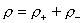 , , 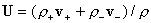 , где , где 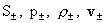 –
энтропии, давления, плотности и гидродинамические скорости электронов и
ионов полностью ионизованной плазмы с массами частиц –
энтропии, давления, плотности и гидродинамические скорости электронов и
ионов полностью ионизованной плазмы с массами частиц 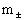 и зарядами и зарядами 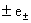 . Система (1-3)
замыкается уравнениями состояния для электронов и ионов . Система (1-3)
замыкается уравнениями состояния для электронов и ионов 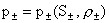 , при этом для каждой
компоненты выполнено термодинамическое тождество , при этом для каждой
компоненты выполнено термодинамическое тождество 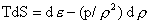 . Решив систему
(1-3), по элементарным формулам: . Решив систему
(1-3), по элементарным формулам:
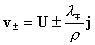 , , 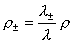 , , 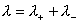 , ,
находим гидродинамические скорости и плотности
плазменных компонент. Нетривиальность этих соотношений в том, что в силу
системы (1-3) так вычисляемые скорости и плотности компонент плазмы
удовлетворяют точным законам сохранения
массы, энергии, импульса.
В случае,
когда компоненты плазмы суть идеальные политропные газы с общим показателем
адиабаты 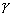 , идеальная МГД получается предельным переходом из системы
(1-3) при стремлении к бесконечности погонного числа частиц плазмы: , идеальная МГД получается предельным переходом из системы
(1-3) при стремлении к бесконечности погонного числа частиц плазмы:
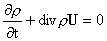 , , 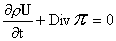 , , 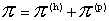 , ,
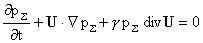 , , 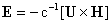 , ,
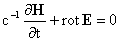 , , 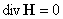 , , 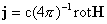 . .
§2. Уравнения ЭМГД –
плазмостатики.
Рассмотрим решения системы (1-3), предполагая 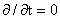 , , 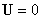 . .
Теорема
1. Система (1-3) с 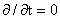 , , 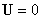 равносильна
соотношениям: равносильна
соотношениям:
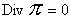 , ,
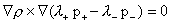 , ,
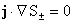 ,
(4) ,
(4)
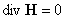 . .
При этом ток 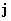 , электрическое поле , электрическое поле 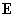 и тензор и тензор  вычисляются по
формулам: вычисляются по
формулам:
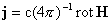 , , 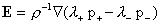 , ,
(5)
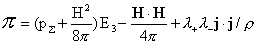 . .
Доказательство.
Равенства 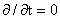 , , 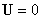 , подставленные в систему (1-3), приводят к соотношениям: , подставленные в систему (1-3), приводят к соотношениям:
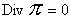 , , 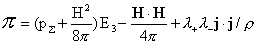 (а) (а)
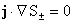 ,
(б) ,
(б)
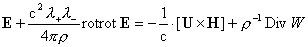 , (в) , (в)
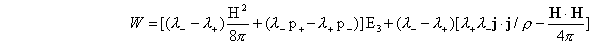
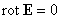 ,
(г) ,
(г)
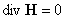 .
(д) .
(д)
С
учетом (г) получаем для 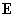 : :
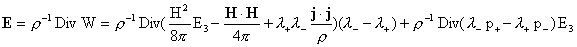
Но
из уравнения (а):
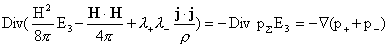 . .
Откуда:
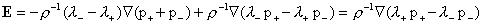
Но
тогда условие (г) приводит к соотношению:
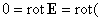 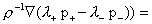
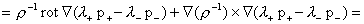
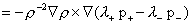 , ,
откуда получается равенство 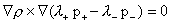 . Тем
самым получили все соотношения (4), (5). Очевидно, что и обратно: при
выполнении (4) и (5) выполняются уравнения (а – д), а значит и уравнения системы (1 – 5)
с . Тем
самым получили все соотношения (4), (5). Очевидно, что и обратно: при
выполнении (4) и (5) выполняются уравнения (а – д), а значит и уравнения системы (1 – 5)
с 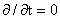 , , 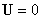 , ч. т. д. , ч. т. д.
Итак,
стационарная (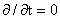 ) в среднем неподвижная ( ) в среднем неподвижная (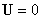 ) плазменная конфигурация является решением системы (4 – 5).
Эта система включает 6 неизвестных скалярных функций ) плазменная конфигурация является решением системы (4 – 5).
Эта система включает 6 неизвестных скалярных функций 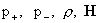 и состоит из 9 скалярных уравнений. Чтобы получить из неё
уравнения ЭМГД – плазмостатики, воспользуемся следующей математической
теоремой, являющейся несложным следствием теорем о неявной и обратной функциях. и состоит из 9 скалярных уравнений. Чтобы получить из неё
уравнения ЭМГД – плазмостатики, воспользуемся следующей математической
теоремой, являющейся несложным следствием теорем о неявной и обратной функциях.
Теорема
2. Пусть 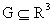 – открытое, – открытое, 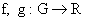 – функции класса – функции класса
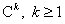 , причем (а) , причем (а) 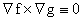 в в 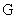 , (б) в любой точке из , (б) в любой точке из 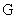 векторы векторы 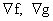 одновременно не
равны 0. Тогда образ одновременно не
равны 0. Тогда образ 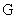 при отображении при отображении 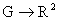 , , 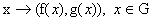 есть одномерное
подмногообразие. есть одномерное
подмногообразие.
Условия (а)
и (б) из формулировки Теоремы 2 равносильны требованию чтобы ранг
отображения 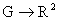 , из Теоремы 2
всюду в , из Теоремы 2
всюду в 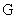 тождественно равнялся
бы 1. Утверждение Теоремы 2 означает функциональную зависимость тождественно равнялся
бы 1. Утверждение Теоремы 2 означает функциональную зависимость 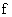 и и 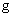 . Поясним точный смысл этого утверждения. Пусть . Поясним точный смысл этого утверждения. Пусть 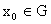 – произвольная, тогда
найдется открытое – произвольная, тогда
найдется открытое 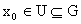 , для которого
либо , для которого
либо  , либо , либо 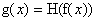 , для всех , для всех 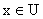 , где , где 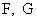 – функции класса – функции класса 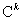 , заданные на некоторых
интервалах. Это локальная версия функциональной зависимости. Глобальная
может и не иметь место. Тем не менее Теорема 2 в дальнейшем будет
основанием для заключения о функциональной зависимости либо вида , заданные на некоторых
интервалах. Это локальная версия функциональной зависимости. Глобальная
может и не иметь место. Тем не менее Теорема 2 в дальнейшем будет
основанием для заключения о функциональной зависимости либо вида 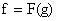 , либо – , либо – 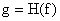 . .
Важно, что справедливость указанных функциональных
зависимостей достаточна для выполнения равенства 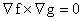 . Поэтому решения получаемых ниже посредством Теоремы 2 уравнений равновесия заведомо будут являться
и решениями системы (4–5). А Теорема
2 гарантирует при этом
отсутствие, вообще говоря, других
равновесий. . Поэтому решения получаемых ниже посредством Теоремы 2 уравнений равновесия заведомо будут являться
и решениями системы (4–5). А Теорема
2 гарантирует при этом
отсутствие, вообще говоря, других
равновесий.
Из Теоремы
2 и второго равенства системы (4)
следует:
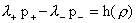 , ,
где
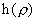 – произвольная гладкая
функция. Поэтому, учитывая равенства – произвольная гладкая
функция. Поэтому, учитывая равенства
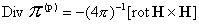 , , 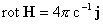 , ,
для нахождения 6 скалярных величин 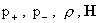 получим из (4-5) семь
скалярных уравнений: получим из (4-5) семь
скалярных уравнений:
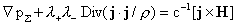
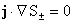
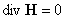 (6) (6)
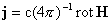
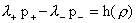
с произвольной гладкой функцией  . Дополненные уравнениями состояния плазменных компонент . Дополненные уравнениями состояния плазменных компонент 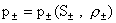 , ,  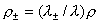 , они дают систему
уравнений ЭМГД – плазмостатики. , они дают систему
уравнений ЭМГД – плазмостатики.
Учтем
теперь присутствие внешних токов 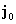 . Тогда в системе ЭМГД – уравнений (1-3) изменятся только уравнения (1.б, г, е): . Тогда в системе ЭМГД – уравнений (1-3) изменятся только уравнения (1.б, г, е):
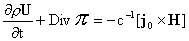 , ,
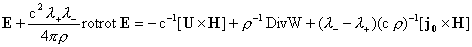
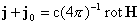 . .
Полученную систему уравнений обозначим (1′).
Подчеркнем, что в (1′) тензо-ры 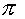 и и 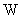 вычисляются по старым формулам (2–3). Полагая в системе
(1′, 2, 3) вычисляются по старым формулам (2–3). Полагая в системе
(1′, 2, 3) 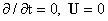 и дословно повторяя
приведенные выше рассуждения, приходим к следующей системе уравнений ЭМГД –
плазмостатики с учетом внешних
токов: и дословно повторяя
приведенные выше рассуждения, приходим к следующей системе уравнений ЭМГД –
плазмостатики с учетом внешних
токов:
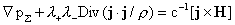
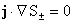
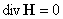 (6′) (6′)
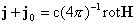
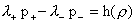
где  – произвольная гладкая
функция и фиксированы уравнения состояния – произвольная гладкая
функция и фиксированы уравнения состояния
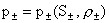 , , 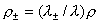 . При этом электрическое поле . При этом электрическое поле 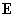 в равновесной конфигурации вычисляется по старой формуле (5). в равновесной конфигурации вычисляется по старой формуле (5).
§3. Равновесия в цилиндрически симметричном
случае.
В отсутствие внешних токов, 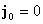 , система (6) в случае , система (6) в случае
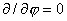 , , 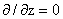 приводит к
соотношениям: приводит к
соотношениям:
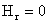 , , 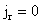 , , 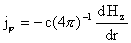 , , 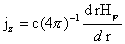 . .
С учетом этого второе и третье уравнения в (6)
выполнены тождественно, а пятое позволяет по известным 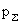 и и 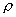 найти найти 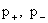 из линейной системы с ненулевым
определителем: из линейной системы с ненулевым
определителем:
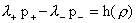
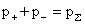 . .
Оставшееся первое векторное уравнение в (6) сводится
к одному скалярному равенству:
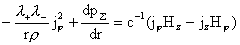 , ,
которое, учитывая выражения для 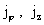 , дает следующее уравнение
равновесия: , дает следующее уравнение
равновесия:
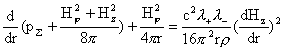 .
(7) .
(7)
Итак, в
случае цилиндрической симметрии система уравнений ЭМГД – плазмостатики (6)
сводится к одному уравнению (7). В МГД – пределе 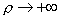 , уравнение (7) переходит в известное уравнение равновесия в
МГД для цилиндрически симметричной конфигурации [4]: , уравнение (7) переходит в известное уравнение равновесия в
МГД для цилиндрически симметричной конфигурации [4]:
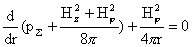 . .
В случае 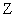 – пинча ( – пинча (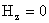 ) уравнения равновесия в МГД – и ЭМГД – теориях совпадают. В
случае ) уравнения равновесия в МГД – и ЭМГД – теориях совпадают. В
случае 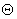 – пинча – пинча  из (7) следует: из (7) следует:
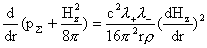 . (8) . (8)
Значит в 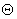 – пинче полное давление плазмы – пинче полное давление плазмы 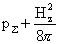 не постоянно, как в
МГД – теории, но монотонно растет с удалением от оси не постоянно, как в
МГД – теории, но монотонно растет с удалением от оси 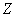 , причем тем быстрее, чем меньше плотность плазмы , причем тем быстрее, чем меньше плотность плазмы 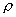 и больше азимутальный
ток и больше азимутальный
ток 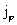 . В частности, диамагнетизм цилиндрического . В частности, диамагнетизм цилиндрического 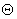 – пинча сильнее, чем предсказывает МГД – теория. В МГД для – пинча сильнее, чем предсказывает МГД – теория. В МГД для 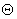 – пинча имеем – пинча имеем 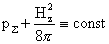 . В
ЭМГД ситуация сложнее. . В
ЭМГД ситуация сложнее.
Рассмотрим (8) как дифференциальное уравнение
относительно 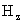 : :
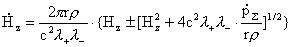 (9) (9)
где точка над буквой – дифференцирование по 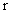 . Тогда в МГД – пределе решения одного из дифференциальных
уравнений (9) переходят в МГД – равновесия, а решения другого не сходятся ни к
какому МГД – равновесию и, значит, дают принципиально новые равновесные конфигурации,
не укладывающиеся в МГД – теорию. Продемонстрируем это на частном примере. Если . Тогда в МГД – пределе решения одного из дифференциальных
уравнений (9) переходят в МГД – равновесия, а решения другого не сходятся ни к
какому МГД – равновесию и, значит, дают принципиально новые равновесные конфигурации,
не укладывающиеся в МГД – теорию. Продемонстрируем это на частном примере. Если
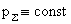 , то из (9) получаем два решения: , то из (9) получаем два решения:
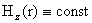 , , 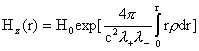 , ,
где 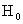 – значение – значение 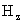 на оси на оси 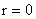 . Первое решение – то же, что и в МГД, а второе в МГД –
пределе вовсе не стремится к константе, т.е. к МГД – равновесию. Выбирая
различные . Первое решение – то же, что и в МГД, а второе в МГД –
пределе вовсе не стремится к константе, т.е. к МГД – равновесию. Выбирая
различные 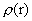 , получим из второго решения различные равновесные
конфигурации, не имеющие аналогов в МГД. Например, пусть в равновесном
плазменном шнуре радиуса , получим из второго решения различные равновесные
конфигурации, не имеющие аналогов в МГД. Например, пусть в равновесном
плазменном шнуре радиуса 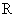 плотность равна плотность равна 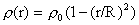 , тогда для , тогда для 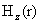 получим: получим:
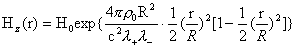 . .
Важную роль играет безразмерная комбинация 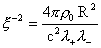 . МГД – предел отвечает переходу . МГД – предел отвечает переходу  . Но тогда . Но тогда 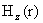 поточечно на поточечно на 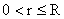 сходится к сходится к 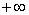 и никакого МГД –
равновесия в пределе не возникает. Математически указанный эффект объясняется
наличием малого параметра при старшей степени в уравнении (8). Другой
интегрируемый случай, когда и никакого МГД –
равновесия в пределе не возникает. Математически указанный эффект объясняется
наличием малого параметра при старшей степени в уравнении (8). Другой
интегрируемый случай, когда 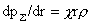 , , 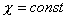 . Тогда интеграция (9) дает: . Тогда интеграция (9) дает:
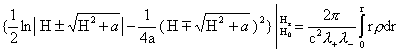 , , 
где 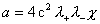 , , 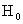 – значение – значение 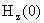 . .
В общем случае, выбирая распределение плотности по
закону:
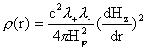 , ,
получим равновесие с постоянным по радиусу полным
давлением,
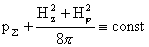 , ,
Основное
уравнение (7) можно рассматривать как формулу для вычисления распределения
плотности 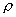 в равновесной цилиндрически симметричной
конфигурации по произвольным полям в равновесной цилиндрически симметричной
конфигурации по произвольным полям 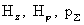 : :
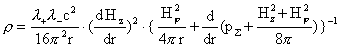 (10) (10)
Единственное физическое ограничение 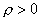 приводит к
неравенству: приводит к
неравенству:
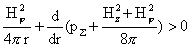
Таким образом, ЭМГД – плазмостатика в цилиндрически
симметричном случае сводится к неравенству:
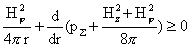 , ,
которое в зонах, где
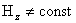 , должно быть строгим и тогда по (10) в этих зонах,
однозначно находится распределение плотности , должно быть строгим и тогда по (10) в этих зонах,
однозначно находится распределение плотности 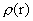 . А в зонах, где . А в зонах, где 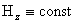 , указанное неравенство переходит в точное равенство,
совпадающее с уравнением МГД – плазмостатики в цилиндрически симметричном
случае ( а плотность , указанное неравенство переходит в точное равенство,
совпадающее с уравнением МГД – плазмостатики в цилиндрически симметричном
случае ( а плотность 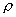 в этих зонах
произвольная). в этих зонах
произвольная).
§ 4.
Равновесия в аксиально симметричном случае: 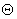 – пинч. – пинч.
В случае 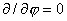 , переходя к цилиндрическим координатам в системе (6′) , переходя к цилиндрическим координатам в системе (6′)
и считая 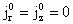 , получим: , получим:
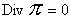 :
(а) :
(а)
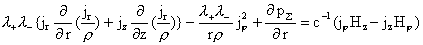
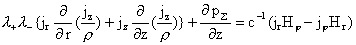
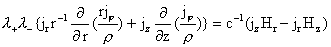
 : : 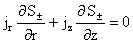 (б) (б)
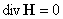 : : 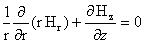 (в) (в)
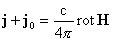 : (г) : (г)
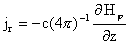 , , 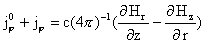 , , 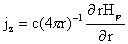
Введем функции
магнитного потока  и полного тока и полного тока 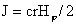 : :
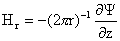 , , 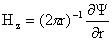 , , 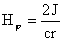
Тогда соотношения (г) перепишутся в виде:
 , ,  (г′) (г′)
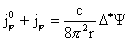 , , 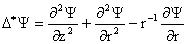 . .
Теорема 3. Пусть 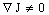 тождественно, тождественно, 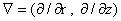 , тогда: , тогда:
1) 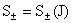 – произвольные
гладкие функции, – произвольные
гладкие функции,
2)  , где , где 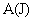 – произвольная
гладкая функция. – произвольная
гладкая функция.
При
соблюдении этих условий второе равенство в (6′) и соотношение 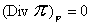 выполнены тождественно. выполнены тождественно.
Доказательство.
Рассмотрим 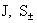 как функции от трёх
переменных как функции от трёх
переменных 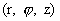 , тогда условие , тогда условие 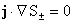 с учетом выражений
(г′) равносильно векторному равенству: с учетом выражений
(г′) равносильно векторному равенству:
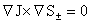 , , 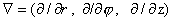
Поскольку 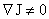 , то выполнены все условия Теоремы 2 и значит , то выполнены все условия Теоремы 2 и значит 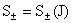 , что доказывает 1). , что доказывает 1).
Третье соотношение (а) с учетом (г′) и
выражений для 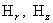 перепишется так: перепишется так:

Группируя подобные члены,
получим:
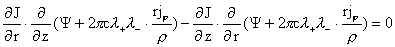
Последнее равенство равносильно
соотношению (см. начало доказательства):

Поскольку 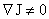 , то на основании Теоремы
2 заключаем, что , то на основании Теоремы
2 заключаем, что
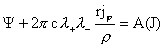 , ,
где 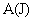 – произвольная гладкая
функция. Ч.Т.Д. – произвольная гладкая
функция. Ч.Т.Д.
Проанализируем уравнения равновесия
(6′) сначала в вырожденном случае, когда 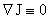 , т.е. когда , т.е. когда 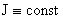 . Физически это соответствует . Физически это соответствует 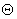 – пинчу. – пинчу.
Итак,
пусть 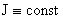 , тогда из (г′) получим , тогда из (г′) получим 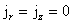  . Значит равенство (б) и третье равенство (а) выполнены
тождественно. Равенство (в) выполнено всегда, а первые два уравнения (а) с
учетом выражений для . Значит равенство (б) и третье равенство (а) выполнены
тождественно. Равенство (в) выполнено всегда, а первые два уравнения (а) с
учетом выражений для 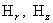 дают: дают:
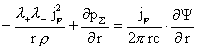
(11)
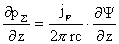
К этим равенствам надо добавить
выражение для 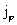 через через 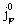 и и  : :
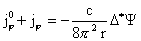 (12)
(12)
Если из системы (11 – 12) найдены функции
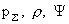 , то пятое уравнение (6′) позволяет найти функции , то пятое уравнение (6′) позволяет найти функции 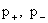 из системы линейных
уравнений с ненулевым определителем: из системы линейных
уравнений с ненулевым определителем:
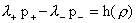
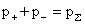
Проинтегрируем систему (11-12).
Теорема 4. Пусть 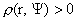 – произвольная гладкая функция, – произвольная гладкая функция, 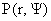 – произвольное решение уравнения в частных производных 1-го
порядка: – произвольное решение уравнения в частных производных 1-го
порядка:
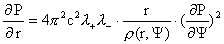 ,
(13) ,
(13)
а  – решение
эллиптического уравнения – решение
эллиптического уравнения
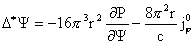 . (14) . (14)
Тогда функции 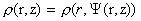 , , 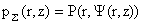 , , 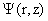 являются решением
системы (11–12) и любое решение этой системы, для которого являются решением
системы (11–12) и любое решение этой системы, для которого 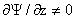 тождественно, получается указанным способом. тождественно, получается указанным способом.
Доказательство. Найдем решения системы
(11–12), для которых 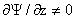 тождественно. Тогда
можно сделать замену переменных, перейдя от переменных тождественно. Тогда
можно сделать замену переменных, перейдя от переменных 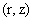 к переменным к переменным 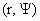 . Пусть в новых переменных . Пусть в новых переменных
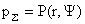 – одна из искомых
функций. Из второго уравнения (11) выводим: – одна из искомых
функций. Из второго уравнения (11) выводим:
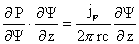 . .
А т.к. 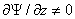 , то отсюда следует , то отсюда следует
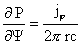
и значит
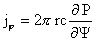
Подставляя полученные выражения для 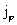 в первое уравнение
(11): в первое уравнение
(11):
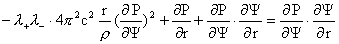 , ,
получим уравнение на функцию 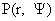 : :
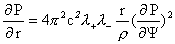 , ,
которое совпадает с (13). Наконец, подставляя
полученные выше выражения для 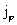 в равенство (12),
получаем уравнение (14). Ч.Т.Д. в равенство (12),
получаем уравнение (14). Ч.Т.Д.
В МГД –
пределе, 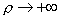 , (13) дает, , (13) дает, 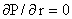 , т.е. , т.е. 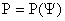 , но тогда (14)
совпадает с уравнением Грэда – Шафранова. (см. Введение) в случае , но тогда (14)
совпадает с уравнением Грэда – Шафранова. (см. Введение) в случае 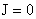 . Итак, отличие от МГД – теории проявляется в функциональной
зависимости давления не только от магнитного потока . Итак, отличие от МГД – теории проявляется в функциональной
зависимости давления не только от магнитного потока  , но и от радиуса , но и от радиуса 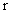 . Этому есть простое физическое объяснение. Поскольку в ЭМГД
– теории, в отличие от МГД, ток есть движение заряженных частиц, то при наличии
азимутального тока . Этому есть простое физическое объяснение. Поскольку в ЭМГД
– теории, в отличие от МГД, ток есть движение заряженных частиц, то при наличии
азимутального тока 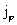 заряженные частицы
плазмы вращаются вокруг оси заряженные частицы
плазмы вращаются вокруг оси 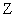 (в среднем покоясь при
этом) и значит на них действует центробежная сила, равная, как легко
подсчитать, (в среднем покоясь при
этом) и значит на них действует центробежная сила, равная, как легко
подсчитать, 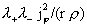 . Поэтому градиент давления должен уравновесить не только
пондеромоторную силу (как это было в МГД), но и центробежную. В итоге градиент
давления распадается в сумму двух
слагаемых. Первое, равное . Поэтому градиент давления должен уравновесить не только
пондеромоторную силу (как это было в МГД), но и центробежную. В итоге градиент
давления распадается в сумму двух
слагаемых. Первое, равное 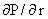 , уравновешивает
центробежную силу – соответствующий баланс сил выражен уравнением (13), второе
слагаемое, равное , уравновешивает
центробежную силу – соответствующий баланс сил выражен уравнением (13), второе
слагаемое, равное  , уравновешивает пондеромоторную силу – этот баланс сил
записан в уравнении (14). Таким образом, приходим к системе (13 – 14).
Уравнение (13) показывает, что давление непостоянно на магнитных поверхностях , уравновешивает пондеромоторную силу – этот баланс сил
записан в уравнении (14). Таким образом, приходим к системе (13 – 14).
Уравнение (13) показывает, что давление непостоянно на магнитных поверхностях 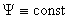 . Более того, на каждой магнитной поверхности оно возрастает
по мере удаления точки поверхности от оси . Более того, на каждой магнитной поверхности оно возрастает
по мере удаления точки поверхности от оси 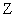 . Именно за счет этого роста градиент давления уравновешивает
центробежную силу. . Именно за счет этого роста градиент давления уравновешивает
центробежную силу.
В отличие
от МГД – теории, ЭМГД – равновесия определяются распределением плотности 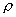 . Это приводит к недоопределенности системы (13 – 14),
поэтому в буквальном смысле её решение тривиально. Выберем любую функцию . Это приводит к недоопределенности системы (13 – 14),
поэтому в буквальном смысле её решение тривиально. Выберем любую функцию 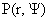 , лишь бы , лишь бы 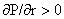 . Для этой функции, с одной стороны, решим эллиптическое
уравнение (14) и найдем . Для этой функции, с одной стороны, решим эллиптическое
уравнение (14) и найдем  , а с другой – вычислим из (13) функцию , а с другой – вычислим из (13) функцию 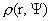 . После этого, подставив в . После этого, подставив в 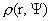 и и 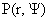 найденную функцию найденную функцию  , получим пространственные распределения , получим пространственные распределения 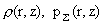 . Таким образом, содержательная постановка задачи для системы
(13 – 14) должна опираться на некоторые физические гипотезы относительно
искомой равновесной конфигурации, позволяющие установить функциональную связь
между . Таким образом, содержательная постановка задачи для системы
(13 – 14) должна опираться на некоторые физические гипотезы относительно
искомой равновесной конфигурации, позволяющие установить функциональную связь
между 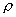 и и 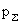 . Например, будем
искать равновесные . Например, будем
искать равновесные
конфигурации, для которых
энтропии электронов и ионов однородны по пространству. Для таких
конфигураций:
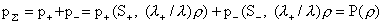
суть известная функция от 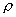 , поскольку , поскольку
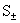 – константы. Условие изоэнтропичности можно
заменить на изотермичность, либо условие – константы. Условие изоэнтропичности можно
заменить на изотермичность, либо условие
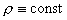 и т.д. В общем виде
эту идею можно сформулировать так. Пусть задана функция и т.д. В общем виде
эту идею можно сформулировать так. Пусть задана функция 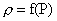 (гладкая,
положительная в области (гладкая,
положительная в области 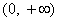 и монотонно
возрастающая). Ищем решение уравнения и монотонно
возрастающая). Ищем решение уравнения
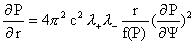 (15) (15)
и для найденной функции 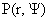 решаем уравнение
(14). Если решаем уравнение
(14). Если  его решение, то его решение, то 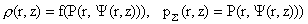 , ,  задают параметры
искомой равновесной конфигурации. Уравнение (15) может быть решено в явном
виде. задают параметры
искомой равновесной конфигурации. Уравнение (15) может быть решено в явном
виде.
Теорема
5. Пусть 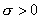 , тогда уравнение в частных производных 1-го порядка , тогда уравнение в частных производных 1-го порядка
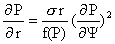 (15′) (15′)
имеет следующий полный интеграл
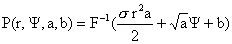
где 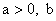 – произвольные, а – произвольные, а
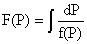 . .
Доказательство. Можно прямой подстановкой убедиться, что для любых фиксированных
вещественных 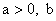 функция функция 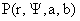 является точным решением уравнения
(15′). С другой стороны, делая замену является точным решением уравнения
(15′). С другой стороны, делая замену 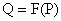 в уравнении
(15′), приведем его к виду: в уравнении
(15′), приведем его к виду:
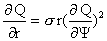
Но это уравнение относится к типу уравнений с
разделяющимися переменными [5, стр.388] и его решение [5, там же] по
стандартной схеме приводит к искомому результату. Ч.Т.Д.
Уравнение
(15′) имеет решение двух сортов. Во-первых, это функции, возникающие из
полного интеграла, т.е. вида 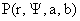 для любых
фиксированных для любых
фиксированных 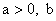 . Во-вторых, это функции вида . Во-вторых, это функции вида 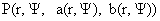 , где , где 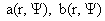 вычисляются по произвольной гладкой функции вычисляются по произвольной гладкой функции 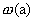 по следующему правилу: по следующему правилу:
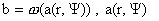 – решение уравнения – решение уравнения 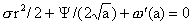 относительно относительно 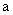 . Других решений уравнение (15′) не имеет. Подробности
смотри в [5]. . Других решений уравнение (15′) не имеет. Подробности
смотри в [5].
Наконец,
приведем количественную оценку различия ЭМГД – и МГД – равновесий 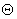 – пинча водородной плазмы. Выберем характерные масштабы – пинча водородной плазмы. Выберем характерные масштабы 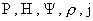 так, чтобы : так, чтобы :
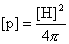 , , 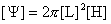 , , 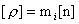 , ,  , ,
где 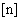 – характерная
плотность числа частиц, – характерная
плотность числа частиц, 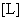 – характерная длина и
т.д. Обезразмерим уравнения (13), (14): – характерная длина и
т.д. Обезразмерим уравнения (13), (14):
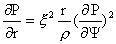 ,
(13′) ,
(13′)
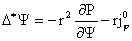 ,
(14′) ,
(14′)
где в гауссовской системе единиц:
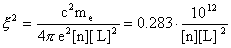
безразмерный параметр (см.§3). МГД предел
соответствует переходу  . Очевидно, если
погонное число частиц . Очевидно, если
погонное число частиц 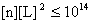 , то ЭМГД – и МГД – равновесия будут существенно
различаться. Но даже при , то ЭМГД – и МГД – равновесия будут существенно
различаться. Но даже при 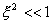 и малом различии
функций и малом различии
функций 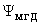 и и 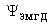 соответствующие им магнитные поверхности
могут иметь принципиально разную топологию. соответствующие им магнитные поверхности
могут иметь принципиально разную топологию.
§
5. Аксиально симметричные равновесия:
общий случай.
Разберем
теперь основной случай, 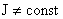 тождественно, считая тождественно, считая  . Тогда, согласно Теореме
3, имеют место первые интегралы: . Тогда, согласно Теореме
3, имеют место первые интегралы:
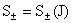 (16) (16)
 ,
(17) ,
(17)
где  – произвольные гладкие функции. Отсюда – произвольные гладкие функции. Отсюда
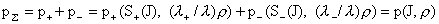 (18) (18)
известная функция от
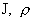 . Пятое уравнение системы (6') накладывает на эту функцию
определенное ограничение, которое будет рассмотрено ниже, но вывод уравнений
равновесия от этого ограничения не зависит. Первый интеграл (17) вместе с двумя
первыми уравнениями (а) из §4 и с учетом (18) образует систему из трех
уравнений для нахождения трех неизвестных функций . Пятое уравнение системы (6') накладывает на эту функцию
определенное ограничение, которое будет рассмотрено ниже, но вывод уравнений
равновесия от этого ограничения не зависит. Первый интеграл (17) вместе с двумя
первыми уравнениями (а) из §4 и с учетом (18) образует систему из трех
уравнений для нахождения трех неизвестных функций 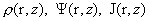 . Получим эту систему в явном виде. Выразим . Получим эту систему в явном виде. Выразим 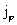 из (17) из (17)
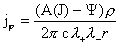 (19) (19)
и подставим полученное выражение в первые два
уравнения (а) из §4, учтя при этом выражения (г′) для 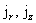 и формулы для и формулы для 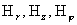 . Принципиально важно, что результат подстановки можно
записать в следующем симметризованном виде: . Принципиально важно, что результат подстановки можно
записать в следующем симметризованном виде:
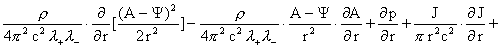
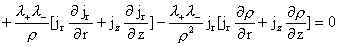
(20)
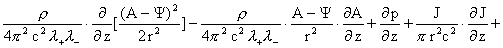
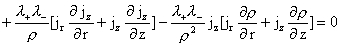
Умножим первое уравнение (20) на 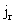 ,
а второе на ,
а второе на 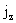 и сложим: и сложим:
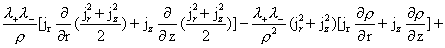
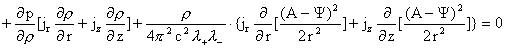 . .
Группируя члены, получим:
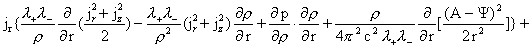
(21)
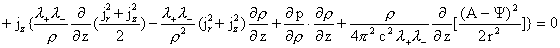
Теперь заметим, что разделив равенство (21) на 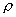 в фигурных скобках
получим выражения вида: в фигурных скобках
получим выражения вида:
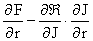 , , 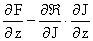  , ,
где
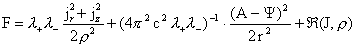
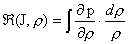 (22) (22)
Поэтому равенство (21) примет вид:
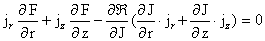
Учитывая выражение для 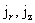 , получим в итоге: , получим в итоге:
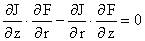
Последнее соотношение эквивалентно векторному
тождеству:
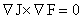
и т.к. 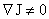 , то на основании Теоремы 2 заключаем, что , то на основании Теоремы 2 заключаем, что 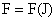 – произвольная гладкая
функция. Итак, получили еще один первый интеграл – произвольная гладкая
функция. Итак, получили еще один первый интеграл
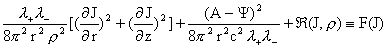 (23) (23)
Используя выражение (19) для 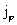 , этот интеграл можно переписать в виде: , этот интеграл можно переписать в виде:
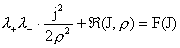 , , 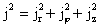
Наконец, преобразуем выражение для 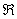 , интегрируя (22) по частям: , интегрируя (22) по частям:
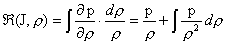
Теперь немного термодинамики. Если рассматривать все
термодинамические параметры как функции энтропии и плотности, то из 2-го закона
термодинамики 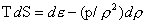 следует, что следует, что 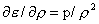 . Поэтому: . Поэтому:
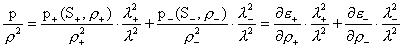 , ,
где 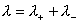 . .
Откуда
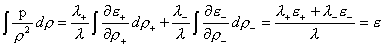 , ,
где 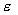 – плотность внутренней
энергии плазмы. Поэтому окончательно имеем: – плотность внутренней
энергии плазмы. Поэтому окончательно имеем:
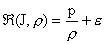 . .
Итак, интеграл (23) может быть переписан в виде:
 .
(24) .
(24)
Продолжим вывод уравнений равновесия. Выразим из
интеграла (23) комбинацию 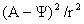 и подставим её под
знак дифференцирования в любое из двух уравнений (20): и подставим её под
знак дифференцирования в любое из двух уравнений (20):
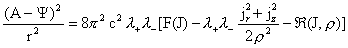
Тогда приходим к одному и тому же дифференциальному
уравнению относительно функции 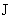 : :
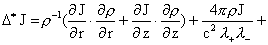
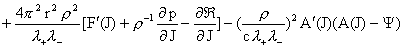
Наконец, подставляя выражение (19) для 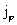 в равенство в равенство
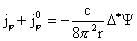
получаем дифференциальное уравнение относительно  . В итоге получим следующую систему уравнений для нахождения
функций . В итоге получим следующую систему уравнений для нахождения
функций 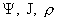 : :
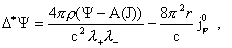
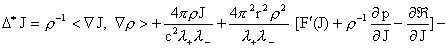
 (25) (25)
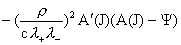 , ,
 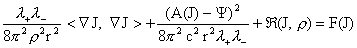 , ,
где
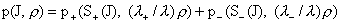 , ,
(26)
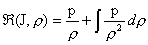 , ,
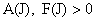 – произвольные гладкие
функции, – произвольные гладкие
функции, 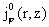 – произвольная
функция, – произвольная
функция, 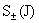 – произвольные гладкие функции, подчиненные ограничению
((равносильному пятому уравнению системы
( – произвольные гладкие функции, подчиненные ограничению
((равносильному пятому уравнению системы
(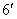 )): )):
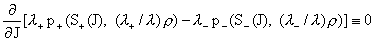 (27) (27)
тождественно по всем
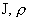 . Система (25–27) и является искомой системой уравнений
ЭМГД – плазмостатики в присутствии внешних токов и для произвольных уравнений
состояния электронов и ионов. . Система (25–27) и является искомой системой уравнений
ЭМГД – плазмостатики в присутствии внешних токов и для произвольных уравнений
состояния электронов и ионов.
Особо отметим роль уравнений состояния в
ЭМГД – плазмостатике. Условие (27) заведомо всегда выполнено для
изоэнтропических равновесий, когда 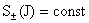 . Тогда уравнения равновесия (25) упрощаются, т.к. . Тогда уравнения равновесия (25) упрощаются, т.к. 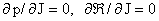 . Существует ли неизоэнтропические равновесные конфигурации,
зависит от уравнений состояния плазменных компонент. Вот простой пример. . Существует ли неизоэнтропические равновесные конфигурации,
зависит от уравнений состояния плазменных компонент. Вот простой пример.
Пусть электроны и ионы – идеальные
политропные газы с показателями адиабаты 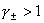 . Тогда: . Тогда:
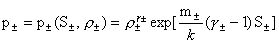 , ,
где 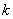 – постоянная Больцмана. Условие (27) дает – постоянная Больцмана. Условие (27) дает
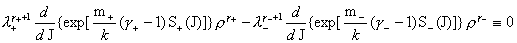
Если показатели адиабаты
различные, 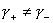 , то функции , то функции 
линейно независимы и последнее условие может быть
выполнено для всех 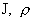 только в случае только в случае 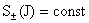 , т.е. только для изоэнтропических равновесий. Но если
показатели адиабаты , т.е. только для изоэнтропических равновесий. Но если
показатели адиабаты  равны, равны, 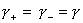 , то , то 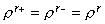 и условие (27)
равносильно равенству: и условие (27)
равносильно равенству:
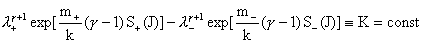 , ,
что позволяет константу 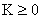 и гладкую функцию и гладкую функцию  выбрать произвольно
(тогда выбрать произвольно
(тогда 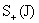 однозначно
вычисляются). При этом: однозначно
вычисляются). При этом:
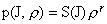 , , 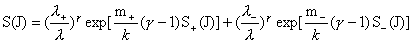
(27′)
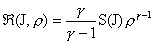 , ,
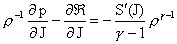
Можно предположить, что для сложных уравнений состояния,
когда зависимости 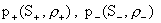 как функции от
плотности принципиально различны, возможны только изоэнтропические равновесия. как функции от
плотности принципиально различны, возможны только изоэнтропические равновесия.
Укажем на
физический смысл интеграла (24). Это закон сохранения энергии для равновесной
конфигурации. Можно установить следующий закон сохранения полной энергии в ЭМГД
– теории: на решении системы (1-3) выполнено тождество:
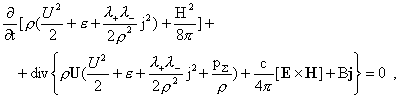
где 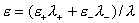 и и
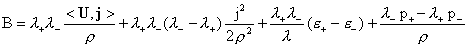 . .
Полагая в законе сохранения  , , 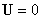 , получим: , получим:
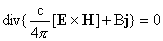 .
(28) .
(28)
Учитывая соотношение  нетрудно проверить,
что в аксиально симметричном случае соотношение (28) и (24) эквивалентны. нетрудно проверить,
что в аксиально симметричном случае соотношение (28) и (24) эквивалентны.
§6. МГД – предел.
Рассмотрим
МГД – предел уравнений ЭМГД – плазмостатики (25).
Принципиально важно убедится, что в МГД – пределе
получаются уравнения Грэда – Шафранова МГД – плазмостатики. Приведем систему
(25) к безразмерному виду, выбрав характерные масштабы соответствующих величин,
обозначаемых скобками, так что:
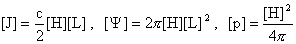 , ,
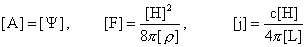 . .
Пусть
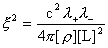
безразмерный параметр. Тогда в безразмерном виде
система (25) дает:
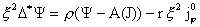
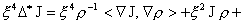
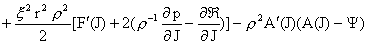 (25′) (25′)
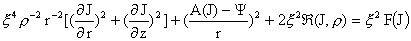
МГД –
предел соответствует переходу  . Разложим функции . Разложим функции 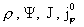 по степеням по степеням 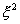 : :
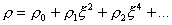 , ,
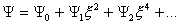 ,
(29) ,
(29)
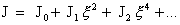 , ,
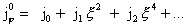 , ,
где 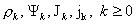 – функции от – функции от 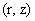 . Тогда: . Тогда:
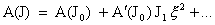
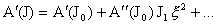
Оказывается, нулевые коэффициенты разложений 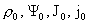 связаны определенными соотношениями. Чтобы
получить их, подставим разложение связаны определенными соотношениями. Чтобы
получить их, подставим разложение
(29) в уравнения (25′) и ограничимся первыми двумя членами
разложения по параметру 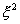 : :

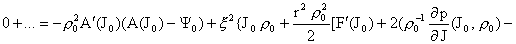
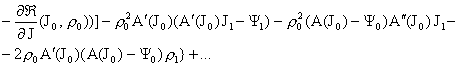
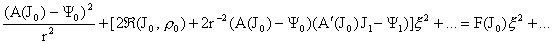
Приравнивая коэффициенты при одинаковых степенях 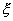 получим из 1-го
уравнения получим из 1-го
уравнения 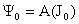 (здесь учтено (здесь учтено 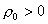 ). С учетом этого дальнейшее приведение подобных членов дает: ). С учетом этого дальнейшее приведение подобных членов дает:
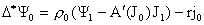 ,
,
 (30) (30)
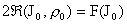
из последнего уравнения следует, что 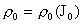 (т.к. (т.к. 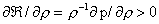 и значит полученные
нелинейное уравнение всегда разрешимо относительно и значит полученные
нелинейное уравнение всегда разрешимо относительно 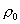 ), в частности, все три функции ), в частности, все три функции 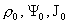 (а значит и (а значит и 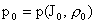 ) функционально зависимы. Далее, ) функционально зависимы. Далее,
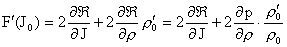 . .
Подставляя это соотношение и выражение 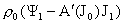 из первого уравнения
системы (30) во второе уравнение, получим, сокращая на из первого уравнения
системы (30) во второе уравнение, получим, сокращая на 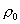 : :
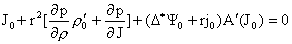 . .
Но для 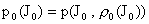 имеем: имеем:
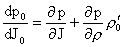
Учитывая 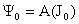 ,
получим: ,
получим:
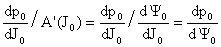 , , 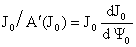 . .
Окончательно, приходим к соотношению:
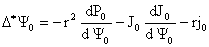 , ,
которое в размерном виде совпадает в точности с
уравнением Грэда - Шафранова:
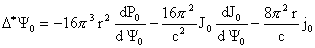 , ,
где 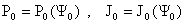 . .
Процесс
разложения можно продолжить и получить уравнения, связывающие 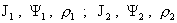 и т.д. Таким образом,
цепочка уравнений на коэффициенты разложений (29) расцепляется: в принципе,
последовательно можно найти все коэффициенты разложений. и т.д. Таким образом,
цепочка уравнений на коэффициенты разложений (29) расцепляется: в принципе,
последовательно можно найти все коэффициенты разложений.
§7.
Неэллиптичность уравнений равновесия.
Рассмотрим
более подробно систему уравнений ЭМГД – плазмостатики (25). Третье уравнение
этой системы – нелинейное недифференциальное уравнение
относительно плотности 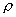 . Исключая из него . Исключая из него 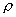 и подставляя полученное
выражение в первые два уравнения системы (25), получим систему из двух
дифференциальных уравнений 2-го порядка относительно функций и подставляя полученное
выражение в первые два уравнения системы (25), получим систему из двух
дифференциальных уравнений 2-го порядка относительно функций 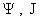 . Нас интересует тип дифференциального оператора старших
производных полученной системы. Реализация намеченного плана зависит от вида
нелинейной функции . Нас интересует тип дифференциального оператора старших
производных полученной системы. Реализация намеченного плана зависит от вида
нелинейной функции 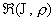 , т.е. от уравнений состояния плазменных компонент. Проанализируем случай, когда
электроны и ионы являются идеальными политропными газами с общим показателем
адиабаты , т.е. от уравнений состояния плазменных компонент. Проанализируем случай, когда
электроны и ионы являются идеальными политропными газами с общим показателем
адиабаты 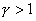 . Тогда система (25) конкретизируется формулами (27′),
и третье уравнение системы (25) имеет вид: . Тогда система (25) конкретизируется формулами (27′),
и третье уравнение системы (25) имеет вид:
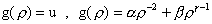 ,
(31) ,
(31)
где
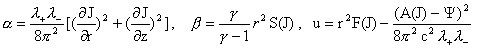 . .
Для реальных (рациональных) показателей 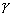 нахождение нахождение 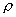 сводится к поиску
корней некоторого алгебраического многочлена. сводится к поиску
корней некоторого алгебраического многочлена.
Поскольку 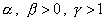 , то уравнение (31)
имеет два решения при , то уравнение (31)
имеет два решения при 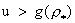 , одно при , одно при 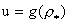 и не имеет решений
при и не имеет решений
при  , где , где 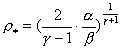 – точка абсолютного
минимума функции – точка абсолютного
минимума функции 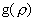 в области в области 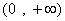 . График функции . График функции 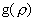 состоит из двух
ветвей, исходящих из точки минимума и уходящих на состоит из двух
ветвей, исходящих из точки минимума и уходящих на 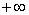 при при 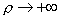 (″плотная″
ветвь) и (″плотная″
ветвь) и
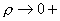 (″разреженная″ ветвь). Поэтому в области (″разреженная″ ветвь). Поэтому в области 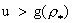 уравнение (31) имеет
два гладких решения уравнение (31) имеет
два гладких решения 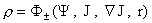 , где знак , где знак  ″–″
отвечает значениям ″–″
отвечает значениям 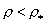 (″разреженная″ ветвь решений). а знак ″+″ – значениям (″разреженная″ ветвь решений). а знак ″+″ – значениям  (″плотная″ ветвь решений).
При (″плотная″ ветвь решений).
При 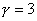 функции функции 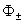 имеют явные выражения: имеют явные выражения:
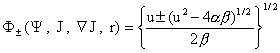 (32) (32)
с учетом формул (31) для 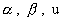 . Условие . Условие 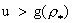 равносильно условию равносильно условию 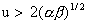 . (Можно бы везде ограничиться случаем . (Можно бы везде ограничиться случаем 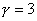 , поскольку
качественная картина решений, вероятно, не будет зависеть от , поскольку
качественная картина решений, вероятно, не будет зависеть от 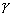 .) .)
Теорема
6. После подставки функций 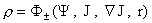 , в первые два уравнения
системы ЭМГД- плазмостатики (25)
операторы старших производных 1-го и 2-го уравнений имеют
соответственно вид: , в первые два уравнения
системы ЭМГД- плазмостатики (25)
операторы старших производных 1-го и 2-го уравнений имеют
соответственно вид:
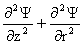 , (33) , (33)
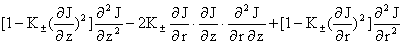 , (34) , (34)
где 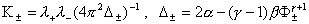 . .
Доказательство теоремы дадим ниже. Ясно, что оператор (33) всегда эллиптический.
Тип дифференциального оператора (34) определяется типом квадратурной формулы с
матрицей коэффициентов:
 . .
Имеем с учетом определений 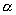 и и 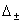 : :
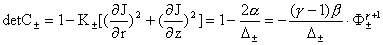 . .
Очевидно
 . .
Значит 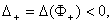 т.к. т.к. 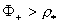 , а , а 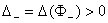 , т.к. , т.к. 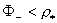 . .
Поэтому 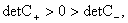 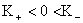 . Отсюда следует, что
квадратичная форма с матрицей коэффициентов . Отсюда следует, что
квадратичная форма с матрицей коэффициентов
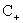 положительно
определена, и значит дифференциальный оператор (34) для знака ″+″ эллиптический, а квадратичная форма с матрицей
коэффициентов положительно
определена, и значит дифференциальный оператор (34) для знака ″+″ эллиптический, а квадратичная форма с матрицей
коэффициентов 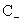 знакопеременная и
значит дифференциальный оператор (34) для знака знакопеременная и
значит дифференциальный оператор (34) для знака  ″–″ гиперболический. Итак, если для исключения ″–″ гиперболический. Итак, если для исключения 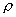 используется
ветвь используется
ветвь 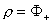 , то возникающая
система дифференциальных уравнений второго порядка относительно функций , то возникающая
система дифференциальных уравнений второго порядка относительно функций 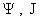 имеет эллиптический
тип, а если — ветвь имеет эллиптический
тип, а если — ветвь 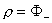 , то —
гиберболический. Решение этой системы должно удовлетворять условию , то —
гиберболический. Решение этой системы должно удовлетворять условию 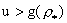 , которое эквивалентно
неравенству: , которое эквивалентно
неравенству:
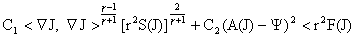 , ,
где
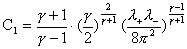 , , 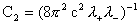 . .
Таким образом, уравнения ЭМГД – плазмостатики (25)
являются смешанного типа системой уравнений,
эллиптической в области плотных равновесий,  и гиперболической в
области разреженных равновесий, и гиперболической в
области разреженных равновесий, 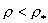 . Условие . Условие  , учитывая выражения
для , учитывая выражения
для 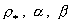 , легко преобразуется к виду: , легко преобразуется к виду:
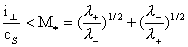 (35) (35)
где 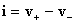 – токовая скорость, – токовая скорость, 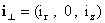 – её поперечная
проекция, – её поперечная
проекция, 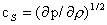 – адиабатическая
скорость звука. Итак, число Маха поперечной токовой скорости в
области плотного равновесия всюду меньше критического значения – адиабатическая
скорость звука. Итак, число Маха поперечной токовой скорости в
области плотного равновесия всюду меньше критического значения 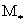 , вычисляемого по (35), а в области разреженного равновесия
всюду больше , вычисляемого по (35), а в области разреженного равновесия
всюду больше 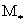 . Разреженная и плотная плазма подчиняются разным законам
равновесия, что принципиально важно для постановки краевых задач в ЭМГД
– плазмостатитике. . Разреженная и плотная плазма подчиняются разным законам
равновесия, что принципиально важно для постановки краевых задач в ЭМГД
– плазмостатитике.
В
концентрированном виде указанное различие проявляется для равновесия 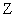 – пинча – пинча 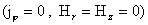 , реализуемых частными
решениями системы (25) для , реализуемых частными
решениями системы (25) для 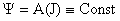 : :
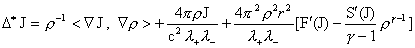
(36)
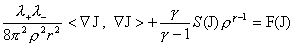
Рассмотрим для простоты изоэнтропические
равновесия 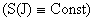 , считая , считая 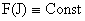 и и 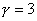 . Исключая . Исключая 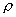 из второго уравнения
системы (36) по формуле (32) и подставляя в первое, сведем задачу о равновесии из второго уравнения
системы (36) по формуле (32) и подставляя в первое, сведем задачу о равновесии 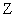 – пинча к одному уравнению: – пинча к одному уравнению:
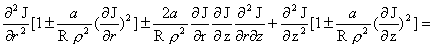
(37)
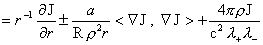 , ,
где  , , 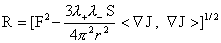 , , 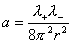 , и мы ищем решения
(37), удовлетворяющие неравенству , и мы ищем решения
(37), удовлетворяющие неравенству
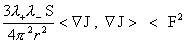 . .
Очевидно, уравнение (37) эллиптично при выборе
знака ''+'' и гиперболично при выборе знака ''–''
.
Доказательство
теоремы 6. Уравнение (31) задает ветви 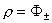 как неявные функции
от как неявные функции
от 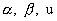 : :
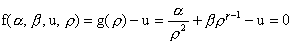 . .
Существование неявной функции гарантируется условием:
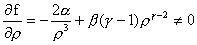 . .
Тип дифференциального уравнения относительно  определится
результатом подстановки определится
результатом подстановки 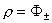 в производные в производные
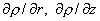 во второе уравнение
системы (25). (Первое уравнение (25) не зависит от производных во второе уравнение
системы (25). (Первое уравнение (25) не зависит от производных 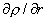 , ,
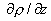 , поэтому
дифференциальный оператор старших производных этого уравнения не изменится при
подстановке , поэтому
дифференциальный оператор старших производных этого уравнения не изменится при
подстановке 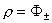 и значит, совпадает с
(33).) имеем: и значит, совпадает с
(33).) имеем:
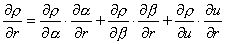
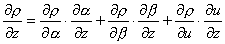 . .
Производные 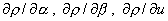 неявной функции
получаются из уравнения неявной функции
получаются из уравнения 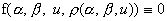 : :
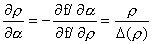 , , 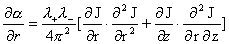
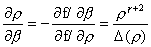 , , 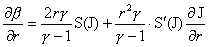
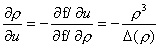 , , 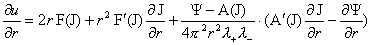
и аналогичные вычисления
для 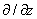 : :
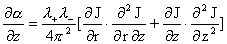 , ,
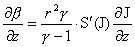 , ,
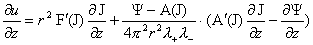 , ,
где 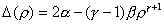 . Вторые производные в уравнении для . Вторые производные в уравнении для 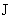 в (25) содержатся в
операторе в (25) содержатся в
операторе  и в слагаемом и в слагаемом 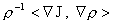 , причем в его части, которая образована суммой , причем в его части, которая образована суммой 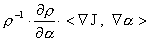 . Собирая вместе все
вторые производные . Собирая вместе все
вторые производные 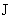 приходим к оператору
(34), ч.т.д . приходим к оператору
(34), ч.т.д .
Литература.
1. К.В.Брушлинский,
В.В.Савельев. Магнитные ловушки для удержания
плазмы. Мат. Моделирование, т.11 N 5,
1999, стр.3-36.
2. В.Д.Шафранов. В сб.: Вопросы теории плазмы.
Вып.2. Под ред.
М.А.Леонтовича. М., Атомиздат,
1963, стр.92.
3. М.Б.Гавриков. Линейные волны в
нерелятивисткой магнитной
гидродинамике. Препринт ИПМ им.
М.В.Келдыша АНСССР, 1988, N199.
4. В.С.Имшенник,
Н.А.Боброва, Динамика столкновительной
плазмы.
М., Энергоатомиздат. 1997,
стр.49.
|