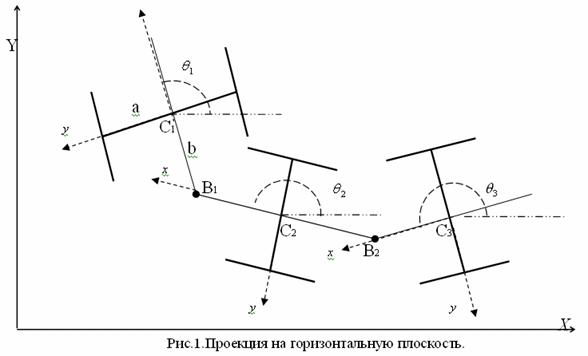
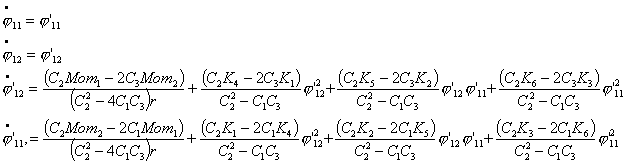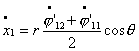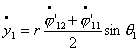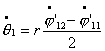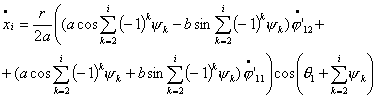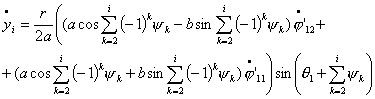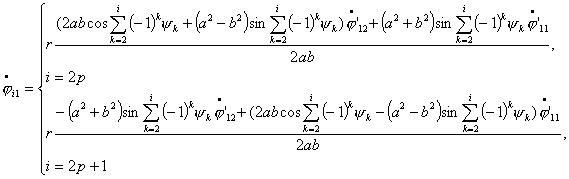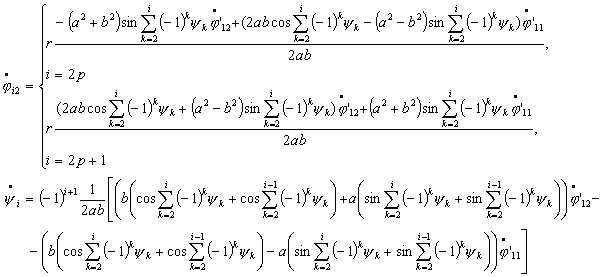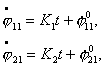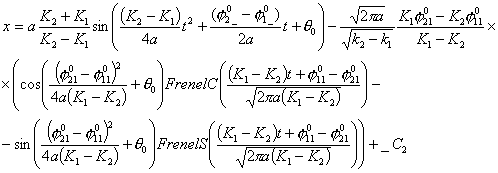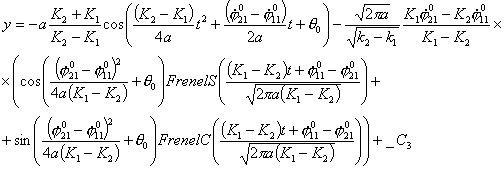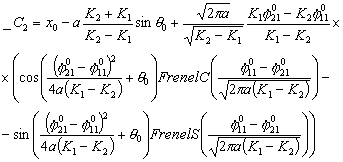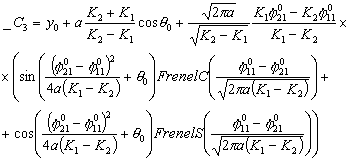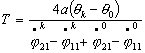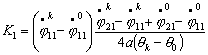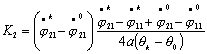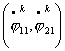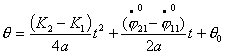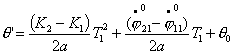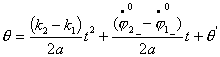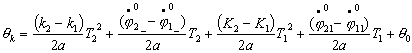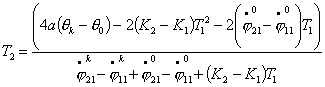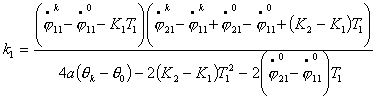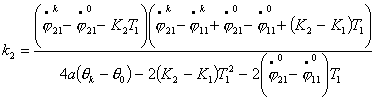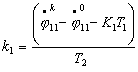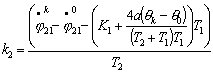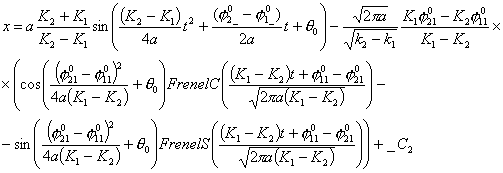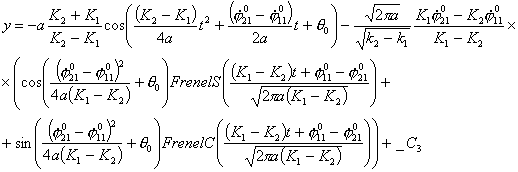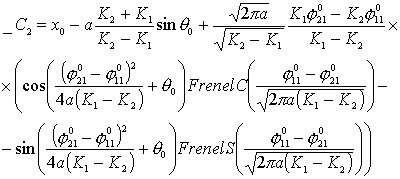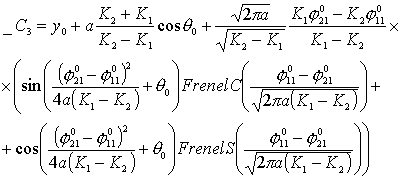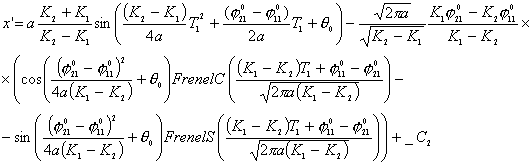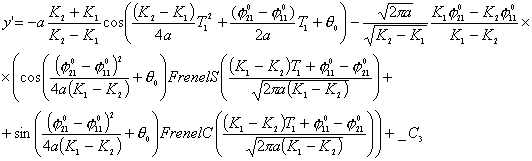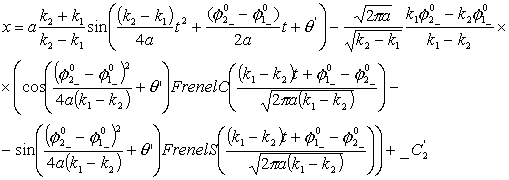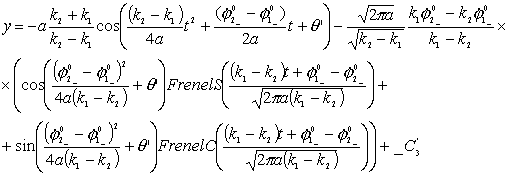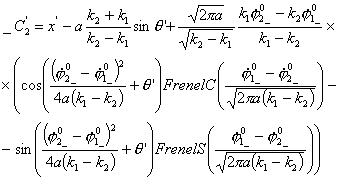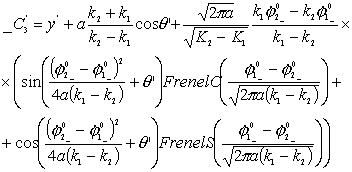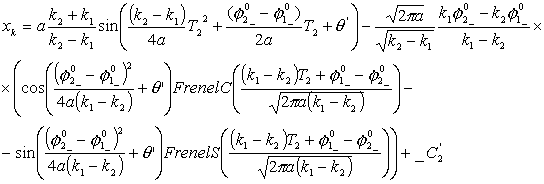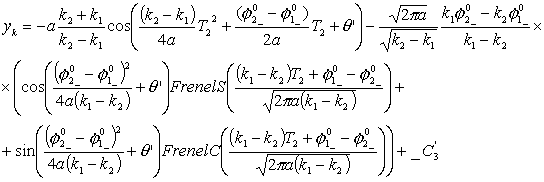Исследование динамики движения цепочки "Робопоезд". Методы планирования движения

( Research of dynamics of movement of a chain of "Robotrain". Methods of planning of movement
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Содержание

Введение…………………………………………………………………..…………………....3

1. Краткое описание механической системы …………………..…………………………....3

2. Переход из заданной точки декартового, конфигурационного, фазового пространства

в другую заданную точку ………………………………………………………………….…5

3. Алгоритм планирования движения между двумя точками………………………..……..8

4. Численно-аналитическое исследование движения по двум спиралям.

Выбор оптимальных параметров …………………………………………………………...14

5. Принцип  «коридоров» планирования траектории…………………………….…….…..18

6. Принцип реперных точек планирования траектории……………………………..……..22

7. Реализация алгоритмов планирования движения……………………………………..…24

Заключение…………………………………………………………………………………....30

Список литературы……………………………………………………………………….….31

Введение

Данная работа является продолжением работ [1],[2] в которых приведено полное описание системы, рассмотрено свободное и управляемое движение цепочки подвижных колесных объектов, построены уравнения движения и их частные решения. Построен класс программных движений (прямая, окружность, спираль).

Целью данной работы является синтез и исследование алгоритмов планирования движения такой системы.

1.     Краткое описание механической системы.  

Рассматривается система, состоящая из объектов, которые мы будем называть «тележками». Каждая тележка представляет собой невесомую ось L длины 2b  и перпендикулярную ей невесомую ось длины 2a, на которую насажены два одинаковых колеса. Каждое колесо является плоским однородным диском массы m, радиуса r, перпендикулярным оси тележки. Кузов тележки имеет массу  и может перемещаться только параллельно плоскости движения. Вообще говоря, массы кузова у разных тележек могут быть различными. Будем считать, что центр масс тележки совпадает с центром оси колес. Тележки соединены друг с другом при помощи шарнира. Активной назовем тележку, вращением колес которой можно управлять при помощи электродвигателей. Пассивной назовем тележку без управления. Тележки движутся по абсолютно шероховатой горизонтальной плоскости в однородном поле силы тяжести.

На рис.1 изображена проекция системы на горизонтальную плоскость.

Пусть OXYZ - неподвижная система координат, плоскость OXY совпадает с горизонтальной плоскостью; C_{1 …} С_n - соответственно центры осей тележек; C₁xyz … C_nxyz - системы координат, жестко связанные с тележками (осями тележек), , ,..., - углы поворота осей L соответствующих тележек вокруг вертикали, в дальнейшем кроме углов ,..., будем рассматривать углы поворота оси L i-й тележки () относительно оси  L предыдущей тележки , где , x₁, y₁ ,…,x_n, y_n - координаты точек C_1,…,С_n  соответственно, , , … , , - углы поворота колес соответствующих тележек относительно их осей, отсчитываемые от проекции положительного направления оси Cz на плоскость колеса против часовой стрелки (если смотреть в сторону вектора ).

На i-ю тележку в точках ,  действуют неизвестные силы  реакции соответственно - и . Условие качения без проскальзывания обуславливает наличие неинтегрируемых связей.

Обобщенные координаты q = (x₁, y₁,…, x_n, y_n; ,_; , ,…, , ) определяют положение механической системы в каждый момент времени.

Движение системы из n тележек описывается системой уравнений [1]:

…

                                       (1.1)

Где -  известные функции ,…,.

2. Переход из заданной точки декартового, конфигурационного, фазового пространства в другую заданную точку.

В работе [2] были рассмотрены  базовые программные движения  нашей системы при условии линейного изменения угловых скоростей вращения колес ведущей тележки. Траекториями получившихся движений стали: прямая, окружность и спираль Корню. Тогда, при планировании движения будем использовать отрезки прямых, дуги окружностей и спиралей Корню. Следует отметить, что при планировании движения задним ходом можно использовать такой же способ , что и при движении вперед с учетом того, что траектория движения составляется для центра последней тележки в цепи, а не ведущей.

Рассмотрим движение вперед. Допустим, в начальный момент времени координаты ведущей тележки (поскольку движение всей системы определяется движением ведущей тележки, то для планирования движения важны координаты именно ведущей тележки) удовлетворяют следующим начальным условиям: центр тележки находится в точке с координатами , угол поворота оси ведущей тележки относительно оси ОХ - , угловые скорости вращения колес ведущей тележки - ; именно эти параметры являются основными при планировании движения системы.

В качестве первой задачи рассмотрим задачу перехода системы из одной заданной точки декартового пространства в другую заданную точку, будем при этом считать, что так должна переместиться точка С₁ – центр оси и корпуса передней тележки. Очевидно, что для заданных для такого перехода начальных условий  всегда найдется траектория (либо прямая, либо окружность, либо спираль), которая проходит через две заданные точки, начальную и конечную, и при этом не единственная [1-2]. При этом для осуществления такого перемещения достаточно одного отрезка одной из перечисленных выше траекторий. Следовательно ([1-2]), перемещение из одной заданной точки в другую заданную точку декартова пространства всегда возможно, причем, не единственным способом. При этом, однако, конечная ориентация ведущей тележки (угол между ее осью и осью Ох), вообще говоря, может быть произвольной, так же как и угловые скорости вращения колес ведущей тележки. Эта ситуация не позволяет продолжить планирование движение в последующие точки.

Далее рассмотрим задачу перехода с выполнением условия, когда ориентация ведущей тележки и углы поворота ее колес заданы в начальной и конечной точках. Фактически, это задача перехода между точками конфигурационного пространства.

Для анализа воспользуемся уравнениями движения для случая линейного изменения угловых скоростей ведущей тележки (переход по отрезку спирали Корню):

Тогда угол между тележками меняется следующим образом:

а координаты центра ведущей тележки по закону:

где

Из полученных соотношений следует, что угол ориентации меняется по квадратичному закону и соотношения эти разрешимы. Следовательно, и задача перехода из одной точки конфигурационного пространства в другую разрешима. Аналогичный вывод можно сделать в отношении угловых скоростей. Система всегда может попасть из точки с одними угловыми скоростями в точку с заданными другими угловыми скоростями, т.к. эти скорости меняются по линейному закону, и всегда можно найти необходимые коэффициенты этого закона.

Теперь перейдем к случаю, когда заданы все начальные параметры , ,  и конечные параметры движения , . Эта задача является задачей построения траектории перехода в фазовом пространстве системы. Выясним, всегда ли существует движение, соответствующее этим условиям. Используем для этого приведенные выше уравнения. Допустим, время движения от начальной точки до конечной равно Т. Тогда справедливы следующие выражения:

Откуда, решая полученную систему, имеем

Следовательно, для заданных таким образом начальных и конечных условий, получаем единственное выражение параметров Т, , . Тогда, координаты  определяются однозначно и не могут назначаться произвольно.

Рассмотрим еще случай, когда начальные и конечные параметры заданы следующим образом: начальные параметры -, ,  и конечные параметры движения - , . Снова имеем три уравнения и три  неизвестных. Уравнения для координат содержат интегралы Френеля, найти их решения можно, например, численно. И здесь получается вариант, когда уже  определяются однозначно и не могут назначаться произвольно. И, следовательно, можно сделать вывод, что одного отрезка спирали недостаточно для решения задачи перемещения из одной точки в другую с выполнением условий на начальные и конечные угловые скорости и ориентацию. Проведенный анализ показывает, что необходимо использовать комбинацию различных траекторий.

3. Алгоритм планирования движения между двумя точками.

Из предыдущего параграфа ясно, что перемещение системы из одной точки в другую с выполнением конечных и начальных условий по ориентации и скоростям вращения колес не всегда возможно  при помощи траектории (движения) одного вида. Тогда рассмотрим комбинацию различных видов траекторий. Для планирования движения будем использовать отрезки прямых и дуги спиралей. Заметим, что, вообще говоря, возможны и другие комбинации.

Движение по прямой задается  следующими уравнениями на угловые скорости вращения колес:  т.е. при k=0 происходит равномерное движение по прямой со скоростью , при k>0 равномерный разгон по прямой, при k<0 равномерное торможение. Следовательно,  первое: такое движение  возможно, если в начальный момент времени угловые скорости колес ведущей тележки равны; второе: движение будет осуществляться по прямой в направлении начальной ориентации ведущей тележки; третье: скорости вращения колес ведущей тележки будут пропорциональны, либо равны скоростям вращения колес ведущей тележки в начальный момент и равны друг другу. Из этого можно сделать следующий вывод: по прямой система может перейти из одной  заданной точки в другую, если начальные скорости вращения колес равны друг другу, и обе точки лежат на прямой, угол наклона которой совпадает с углом начальной ориентацией ведущей тележки.

Если это условие не выполнено, необходима склейка движения из начальной точки и движения в конечную точку. Для склейки  прямых с заданными начальными и конечными скоростями и ориентациями, необходимо построение переходного процесса, задаваемого уравнениями:

Результатом такого переходного процесса с одинаковыми начальными скоростями в любом случае будут получаться различные скорости вращения колес в конечный момент. И, следовательно, полученные в ходе такого движения конечные условия не могут служить начальными условиями  для движения по прямой. Чтобы обеспечить это условие рассмотрим еще один переходный процесс, который задается уравнениями:

где ,Т₁– время движения по первой спирали.

Исследуем результаты движения по двум спиралям Корню. Под начальными и конечными условиями в данном случае будем понимать начальные условия для первой спирали и конечные после движения по второй спирали. Пусть

  -  координаты начальной точки;

  - координаты конечной точки;

   – начальные скорости вращения колес ведущей тележки

   – конечные скорости вращения колес ведущей тележки

,     -  начальный и конечный угол ориентации

      - время движения по первой и второй спирали соответственно.

Законы изменения скоростей на первой  и второй спирали заданы выше.

Тогда, условие склейки по скоростям будет следующим:

                           (3.1)

Закон изменения угла ориентации для первой спирали:

                                         (3.2)

Тогда в конечный момент движения по первой спирали имеем:

Закон изменения угла ориентации для второй спирали:

Тогда, в конечный момент имеем:

          (3.3)

- условие склейки по углам ориентации.

Их этих условий можно выразить переменные T₂, k₁, k₂ через переменные T₁, К₁, К₂:

Или - переменные К₂, k₁, k₂ через переменные T₁, К₁, Т₂:

                                           (3.4)

_{Закон изменения координат центра ведущей тележки  при движении по первой спирали таков:}

где

Итогом такого движения станет точка с координатами:

Тогда, уравнения для изменения координат при движении по второй спирали будут следующими:

где

Следовательно, итогом движения по двум спиралям будут следующие значения основных характеристик движения:

(3.5)

- координаты конечной точки;

 - значения угловых скоростей вращения колес ведущей тележки в конечный момент;

-  угол поворота ведущей тележки относительно оси ОХ в конечный момент.

При этом параметры T₁, К₁, К₂,T₂, k₁, k₂ изначально не определены, но их можно выразить из полученных уравнений. Как уже было показано выше, три параметра из шести являются независимыми. Допустим, К₂, k₁, k₂ выражаются через параметры T₁, К₁, Т₂. Тогда, подставив все уравнения в последние 2 уравнения для координат конечной точки, получим  два уравнения и три неизвестных параметра T₁, К₁, Т₂. Такая задача полностью разрешима (причем, не единственным образом). Таким образом, при помощи построения движения по двум спиралям, можно перевести систему из одной точки декатрового, конфигурационного, фазового пространства в другую  заданную точку.

Таким образом, полное планирование движения можно осуществлять следующим образом: вся траектория разбивается на прямолинейные участки и участки склейки (две спирали), после такого разбиения получаем контрольные точки с заданными координатами, начальными скоростями и начальной ориентацией в каждой такой точке. После этого рассчитываются параметры для движения по прямолинейным отрезкам (коэффициент и время линейного разгона-торможения) и участкам склейки (коэффициенты спиралей и время движения по их отрезкам) для выполнения заданных условий.

4. Численно-аналитическое исследование движения по двум спиралям. Выбор оптимальных параметров.

В предыдущем параграфе были получены уравнения, позволяющие решить задачу планирования движения на переходном отрезке при помощи двух спиралей. Так как эта задача разрешима неединственным способом, проведем численное исследование полученных уравнений для выбора оптимальных параметров движения, вычисления будем проводить в пакете MAPLE.

Рассмотрим задачу исследования поведения конечных координат от таких параметров движения, как: Т₁, Т₂, К₁. Сразу, однако, вместо параметров Т₁ и Т₂ будем рассматривать их  отношение . Тогда при фиксированном К₁=1 и изменении 0<К<1 получим  множество конечных точек, изображенное на следующих графиках:

Рис.2. Множество конечных точек при изменении соотношения К=Т₁/Т₂

Для первого графика начальные условия таковы: , ,  и конечные параметры движения , . Для второго графика начальные параметры те же, а конечные отличаются только ориентацией: .

На рис.3 приведены графики четырех множеств конечных точек для тех же начальных условий, что и выше, при этом конечные ориентации таковы: , а коэффициент К>1и постоянен.

Рис.3.Множество конечных точек при изменении угла конечной ориентации. К>1.

Рассмотрим геометрическое место финальных точек при К=1 (Т₁=Т₂) и различных К₁. На следующих графиках приведено множество конечных точек при тех же начальных условиях, что и выше при 0<К₁<10, Т₁=Т₂=1.

Рис.4.Множество конечных точек при изменении угла конечной ориентации. К=1

Из полученных графиков видно, что при одинаковом времени движения по первой и второй спирали результирующая точка будет лежать на одной прямой для любого значения параметра K₁, при этом угол наклона этой прямой  к оси ОХ зависит от разности углов начальной и конечной ориентации. Приведем таблицу результатов, полученных при численном исследовании.  В ней приведены координаты финальных точек в зависимости от суммы углов конечной  и начальной ориентации.

Таблица 1.  

Таким образом, из численного эксперимента можно сделать предположение, что при равных интервалах движения по одной и второй спирали (Т₁=Т₂) геометрическим местом финальных точек будет прямая.

Докажем это аналитически.

Рассмотрим уравнения движения по двум спиралям в предположении, что Т₁=Т₂=Т, , тогда, преобразуя уравнения (3.5), получим:

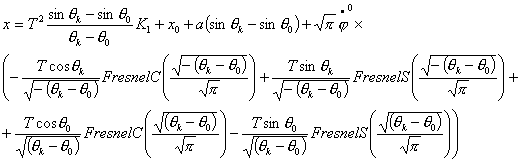
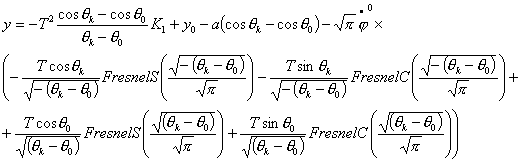
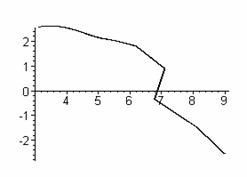
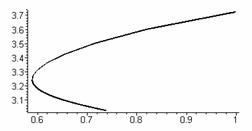
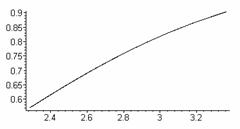
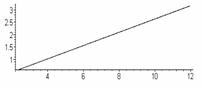
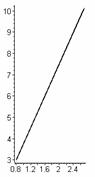
Из полученных уравнений следует, что координаты результирующей точки линейно зависят от параметра К₁ и параметрически задают прямую. На рис.5 изображены графики зависимостей координат х и у от параметра К₁ при , ,  , , Т=1.

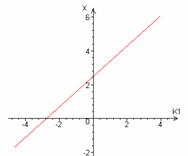
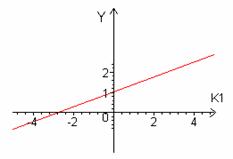
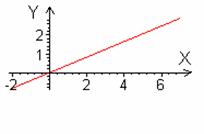
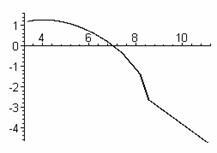
Рис.5 Зависимость координат х и у от параметра К₁ и результирующая прямая.

Геометрическое место конечных точек показано на подграфике 3 рис.5. Оно представляет собой прямую, уравнение которой имеет вид:

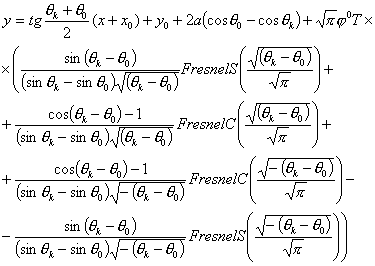
Проанализируем полученные параметрические уравнения 

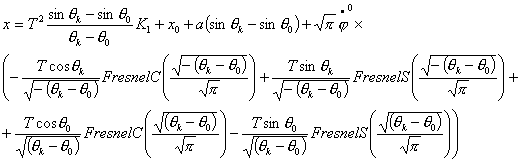
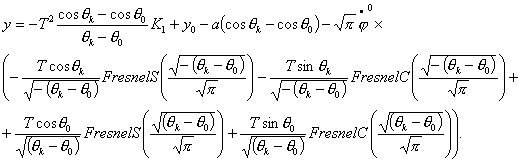
Из этих уравнений видно, что положение финальной точки на найденной прямой зависит не только от коэффициента К₁, но и от таких параметров системы как начальные скорости вращения колес ведущей тележки , интервала времени Т движения по дугам первой и второй  спиралей, геометрических параметров тележки. Чем больше начальная скорость и временной интервал, тем дальше будет находиться на этой прямой конечная точка от начальной.

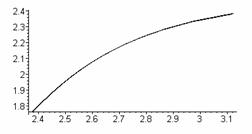
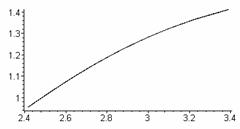
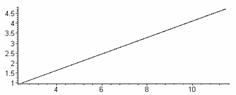
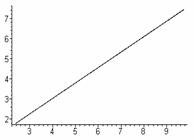
На рис.6 показана закономерность изменения координат финальной точки от параметра Т при фиксированном К₁. Из первого графика видно, что эта зависимость квадратичная, второй график подтверждает, что конечные точки лежат на одной прямой.

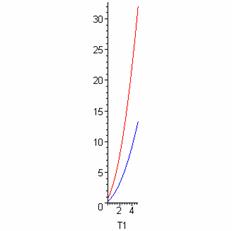
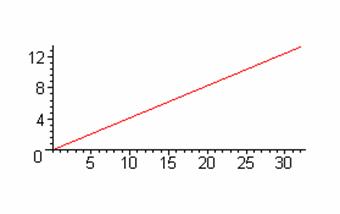
Рис.6. Закономерность изменения координат финальной точки от параметра Т.

Таким образом, известен аналитический вид уравнения характеристической прямой, которой будут принадлежать финальные точки и, используя это параметрическое описание, можно задавать параметр К₁ таким образом, чтобы за интервал времени 2Т из начальной точки система переходила в заданную конечную точку на этой характеристической прямой. Именно это свойство будем использовать для планирования движения.

5. Принцип  «коридоров» планирования траектории.

Трассу движения можно задавать различными способами. Рассмотрим два принципа задания трассы. В этом параграфе будем исследовать возможность планирования траектории по принципу «коридоров». Трасса в этом случае задается следующим образом: заданы отрезки некоторых прямых и окрестность около них. Необходимо спланировать движение системы в окрестности заданных отрезков. Вид подобной траектории показан  на следующем рисунке 7:

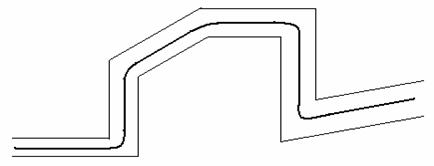
Рис.7. Задание трассы методом «коридоров»

Зададим траекторию движения следующим образом. Пусть траектория состоит из четырех отрезков, каждый из которых задается уравнениями прямой:

При этом начало и конец отрезков определяются точками пересечения прямых, строго в указанном порядке. Начало и конец трассы заданы точками  и , расположенными на первой и последней прямой.

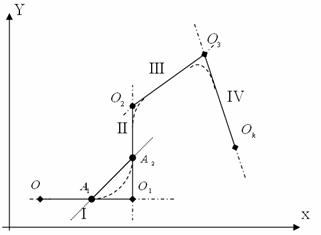
                                          Рис.8. Этапы планирования движения.

Предположим, что в начальной точке трассы угловые скорости вращения колес равны, угол ориентации ведущей тележки совпадает с углом наклона прямой, задающей первый отрезок. Условия движения по прямой при таких начальных условиях известны. Переход с одной прямой на другую будем осуществлять при помощи движения по двум спиралям, используя результаты предыдущего параграфа. Движение по коридору, заданному двумя отрезками, разбивается на три участка:

- движение по прямой, задающей первый отрезок, от начальной точки до точки  (выбирается самостоятельно на первой прямой):

-движение по двум дугам спиралей от точки  до точки  (принадлежит прямой, задающей второй отрезок движения, точные координаты определяются ниже):

-движение по прямой, задающей второй отрезок, до нужной точки.

При движении по прямой, задающей первый отрезок, от начальной точки до точки  угол ориентации не меняется и совпадает с углом наклона прямой, задающей первый отрезок. Угловая скорость вращения колес может равномерно меняться до необходимой (при этом, в точке угловые скорости обоих колес  ведущей тележки будут одинаковыми). Определим параметры для осуществления такого движения. Пусть угловые скорости вращения колес ведущей тележки меняются по следующему закону:

Тогда, координаты центра ведущей тележки будут меняться по следующему закону:

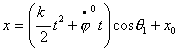
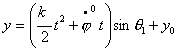
Из этих уравнений можно определить интервал времени, за который центр ведущей тележки переместится из начальной точки с координатами  в точку .

Для того чтобы система могла перейти на второй отрезок из точки , которая принадлежит первому отрезку, двигаясь по двум спиралям с заданной ориентацией, необходимо подобрать параметры движения по этим спиралям. Для этого рассмотрим следующую последовательность действий.

Первый шаг. Найдем углы ориентации ведущей тележки в начальный и конечный момент для движения по заданным отрезкам. В точке  угол ориентации совпадает с углом наклона прямой, задающей первый отрезок. В конечной точке угол ориентации должен совпадать с углом наклона прямой, задающей второй отрезок.

Таким образом, имеем

, ,

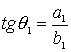откуда находим начальный и конечный углы ориентации.

Второй шаг. Найдем точку пересечения прямых, задающих первый и второй отрезки движения. Эта точка будет иметь следующие координаты:

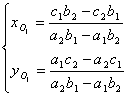
Третий шаг. Находим координаты точки  . Принадлежность этой точки первой прямой выражается условием: .

Допустим, система должна начать поворот на расстоянии   от точки пересечения первой и второй прямой, т.е. , это условие выражается следующей формулой:

.

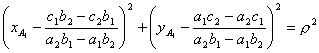Используя первое и второе условие, получим следующие координаты точки:

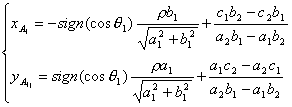
Так получаем начальные координаты для движения по двум спиралям.

Четвертый шаг. Из предыдущего параграфа следует, что геометрическим местом финальных точек, конечный угол ориентации в которых совпадает с заданным, является прямая вида:

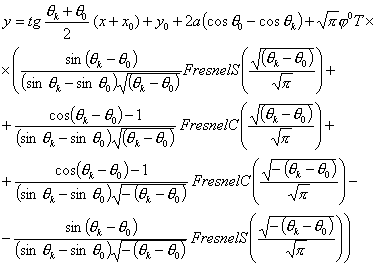
где , .

Запишем  уравнение этой прямой в следующем виде: .

Найдем точку пересечения этой прямой и прямой, задающей второй отрезок. Это будет точка  с координатами .

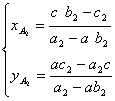
где                                

Пятый шаг. Так как точка  принадлежит прямой , то ее координаты удовлетворяют параметрическим уравнениям этой прямой, а, следовательно, верно следующее уравнение

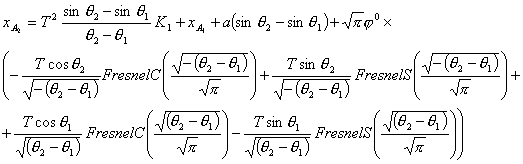
Откуда находим параметр К₁

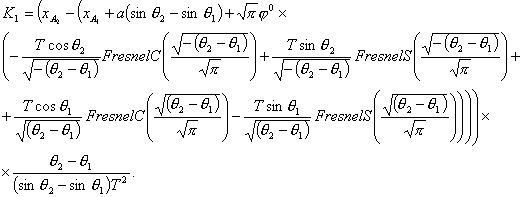
Теперь, зная параметр К₁, и,  используя выводы предыдущего параграфа, можно определить значения  основных характеристик для движения по двум спиралям, для того чтобы из одной точки система могла перейти в другую с заданной ориентацией.

Движение по второму отрезку из точки  до нужной точки осуществляется  так же, как и по первому отрезку прямой, но для него ищется свой интервал времени.

Далее проведем ту же процедуру для второго и третьего отрезков движения и так далее до конечной точки.

Следует заметить, что ширина «коридора» зависит от точности прохождения трассы системой тележек. Этот вопрос рассматривался в [2].

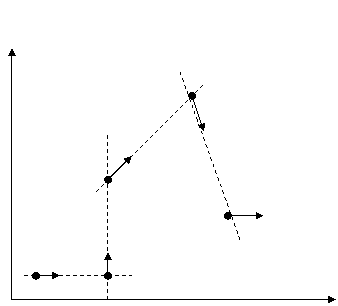
6. Принцип реперных точек планирования траектории.

В этом параграфе рассмотрим другой принцип задания трассы. Предположим, на исходном этапе планирования трасса задана следующим образом. Пусть на плоскости задано нумерованное множество точек своими координатами. Так же в каждой точке заданы скорости вращения колес ведущей тележки (в данном случае будем считать, что они в каждой точке равны), и углы ориентации. Нужно пройти все точки заданного множества в нужном порядке и с заданными в каждой точке условиями на угол ориентации и скорость.

Y

X

Рис. 9. Задание трассы методом реперных точек.

В реализации такого движения возникают следующие трудности.  В предыдущих параграфах данной главы было показано, что существуют ограничения в возможностях перемещения из одной точки декартового, конфигурационного и фазового пространства в другую заданную точку. А именно, если мы хотим попасть из одной точки с заданными начальными условиями в другую точку, угол ориентации в которой будет точно задан, то при движении по двум спиралям эта точка должна будет лежать на заданной определенным образом прямой и никак иначе. Таким образом, далеко не всегда можно попасть из одной точки в другую с заданными таким образом условиями. Для преодоления указанного ограничения нужно планировать движение при помощи отрезков прямых и дуг спиралей. Для этого построим траекторию движения следующим образом.

Рассмотрим две соседние точки  и . Каждая из них задает прямую, проходящую через эту точку, и угол наклона которой совпадает с углом ориентации в этой точке  и . Тогда уравнения этих прямых будут иметь следующий вид:

Тогда на первой прямой рассмотрим точку , находящуюся на расстоянии  от заданной точки в направлении движения, а на второй прямой рассмотрим точку , находящуюся на расстоянии  от второй заданной точки, но в направлении, обратном направлению движения. Координаты этих точек выражаются следующим образом:

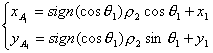
и

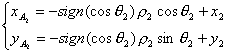
Теперь построим прямую, соединяющую эти две точки. Её уравнение будет иметь следующий вид:

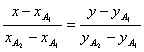
Y     

                                                                X

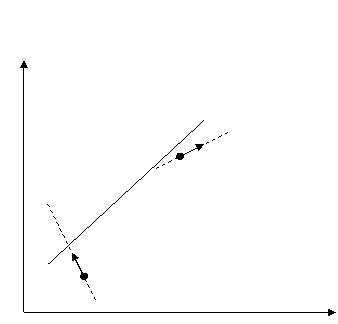
Рис.10. Построение дополнительной прямой при переходе из одной точки в другую.

Таким образом, мы построили траекторию, состоящую из отрезков прямых (Уравнение каждой прямой задано). Планировать движение по такой траектории мы можем при помощи принципа «коридоров». Следовательно, задача планирования траектории по реперным точкам сводится  к задаче планирования движения по принципу «коридоров».

7. Реализация алгоритмов движения в пакете Matlab.

Сначала рассмотрим реализацию принципа «коридоров». Пусть траектория движения задана отрезками следующих прямых:

1.

2.

3.

4.

5.

Тогда точками пересечения этих прямых будут:

, , ,

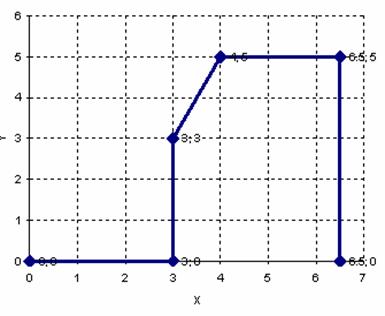
Рис.11.Траектория планируемого движения.

Начальная точка  имеет координаты (0,0), конечная  имеет координаты (6.5, 0). Положим, что ориентация системы в начальный момент совпадает с направлением прямой, задающей первый отрезок движения. Скорости вращения колес ведущей тележки в начальной и конечной точке равны нулю. Определим параметры для осуществления движения по такой траектории.

Вначале зададим координаты точек, в которых нужно начинать переход с одного отрезка заданной траектории на другой. Положим, что расстояния от точки пересечения прямых, задающих рассматриваемые отрезки до точки начала перехода с одной прямой на другую, для каждого отрезка равны единице. Тогда координаты начальных точек  переходного процесса для каждого отрезка будут следующими: ,,,.

Далее найдем уравнения вспомогательных прямых, проходящих через полученные точки и имеющих вид ().

Для точки  это будет прямая  . Она пересекает второй отрезок в точке . Для точки  это будет прямая . Она пересекает третий отрезок в точке . Для точки  это будет прямая . Она пересекает четвертый отрезок в точке . Для точки  это будет прямая . Она пересекает пятый отрезок в точке .

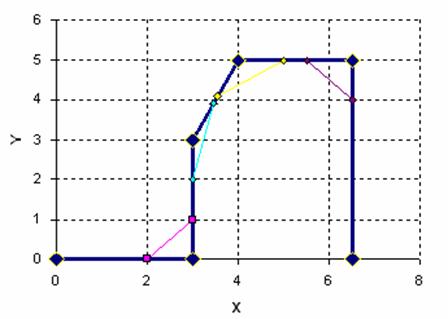
Рис.12. Траектория планируемого движения и отрезки вспомогательных прямых.

Тогда движения по заданной траектории можно разбить на следующие этапы:

- разгон по прямой из начальной точки  до точки , (при этом, значения угловых скоростей вращения колес ведущей тележки линейно меняются от 0 до 1). Параметры движения следующие: Т=1, К₁=К₂=1.

- равномерное движение по прямой   из точки  до точки . Параметры движения следующие: Т=1, К₁=К₂=0.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки  первого отрезка в точку второго отрезка. Параметры движения определяются, используя результаты предыдущего параграфа. Т=1, К₁=-1,87, К₂=1.27, k₁=1,87, k₂=-1,27.

- равномерное движение по прямой   из точки  до точки . Параметры движения следующие: Т=1, К₁=К₂=0.

- переход со второго отрезка траектории (заданного прямой ) на третий отрезок (заданный прямой ). Движение по дугам двух спиралей из точки  второго отрезка в точку третьего отрезка. Параметры движения определяются, с использованием результатов предыдущего параграфа. Т=1, К₁=0,45, К₂=-0,47, k₁=-0,45, k₂=0,45.

- равномерное движение по прямой   из точки  до точки . Параметры движения следующие: Т=0,23, К₁=К₂=0.

- переход с третьего отрезка траектории (заданного прямой ) на четвертый отрезок (заданный прямой ). Движение по дугам двух спиралей из точки  третьего отрезка в точку  четвертого отрезка. Параметры движения определяются, используя результаты предыдущего параграфа. Т=1, К₁=0,97, К₂=-1,24, k₁=-0,97, k₂=1,24.

- равномерное движение по прямой   из точки  до точки . Параметры движения следующие: Т=0,5, К₁=К₂=0.

- переход с четвертого отрезка траектории (заданного прямой ) на пятый отрезок (заданный прямой ). Движение по дугам двух спиралей из точки  четвертого отрезка в точку  пятого отрезка. Параметры движения определяются с использованием результатов предыдущего параграфа. Т=1, К₁=1,27, К₂=-1,87, k₁=-1,27, k₂=1,87.

- торможение по прямой  из точки  до точки , (при этом, значения угловых скоростей вращения колес ведущей тележки линейно меняются от 1 до 0). Параметры движения следующие: Т=8, К1=К2=-0,125.

На рисунке 13 приведены графики  изменения основных характеристик движения при выполнении описанной выше траектории. При этом геометрические параметры системы таковы: a=b=r=1. Из последнего графика видно, как отличается траектория движения второй тележки от траектории движения первой. Максимальное отклонение равно 0,5.

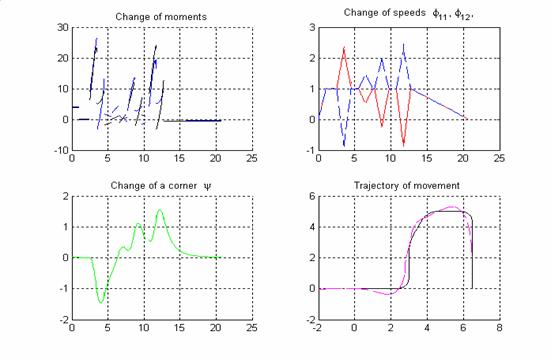
Рис.13 Траектория движения и его основные параметры при реализации принципа        «коридоров» планирования движения

Теперь рассмотрим реализацию принципа реперных точек. Пусть траектория движения задана реперными точками: , , , , ,  и углами ориентации ведущей тележки в данных точках: , , , , , . Тогда, следуя выводам предыдущего параграфа, для осуществления заданного движения необходимо построить вспомогательную траекторию.

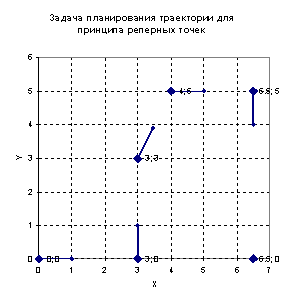
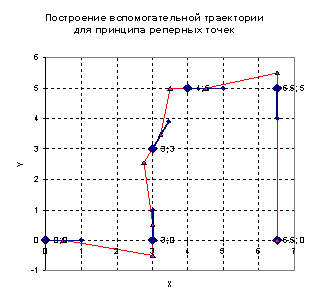
Рис.14. Траектория планируемого движения методом реперных точек.

Вспомогательная траектория строится согласно предыдущему параграфу следующим образом. Сначала необходимо построить вспомогательные точки, которые для каждой заданной реперной точки лежат на прямой, заданной углом ориентации в этой точке на заданном расстоянии от неё. Положим, что для всех реперных точек это расстояние задано и равно 0.5. Тогда в рассматриваемом примере координаты вспомогательных точек будут следующими:

Теперь,  соединим эти точки и реперные точки отрезками прямых, уравнения которых в данном случае будут иметь вид:

1.

2.

3.

4.

5.

6.

7.

8.

9.

Теперь можно использовать метод «коридоров» для построения алгоритма управления. Тогда движения по заданной траектории можно разбить на следующие этапы:

- разгон по прямой из начальной точки  до точки (0.1,0), (при этом, значения угловых скоростей вращения колес ведущей тележки линейно меняются от 0 до 1). Параметры движения следующие: Т=0.2, К₁=К₂=5.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (0.1, 0) в точку (0.89, -0,08). Параметры движения таковы: Т=1, К₁=-0.9, К₂=-1.1, k₁=0.9, k₂=1.1.

- равномерное движение по прямой   из точки (0.89, -0,08) до точки (2.51,-0.42). Параметры движения следующие: Т=1.75, К₁=К₂=0.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (2.51,-0.42) в точку (3,0). Параметры движения таковы: Т=1, К₁=-2.87, К₂=-1.1, k₁=2.87, k₂=1.1.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (3,0) в точку (2.95, 0,99). Параметры движения таковы: Т=1, К₁=-1.07, К₂=-0.96, k₁=1.07, k₂=0.96.

- равномерное движение по прямой   из точки (2.95,0,99) до точки (2.83, 2.06). Параметры движения следующие: Т=1.05, К₁=К₂=0.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (2.83, 2.06) в точку (3, 3). Параметры движения таковы: Т=1, К₁=-0.43, К₂=-1, k₁=0.43, k₂=1.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (3,3) в точку (3.31, 3.95). Параметры движения таковы: Т=1, К₁=-1.28, К₂=-0.99, k₁=1.28, k₂=0.99.

- равномерное движение по прямой   из точки (3.31,3.95)  до точки (3.41, 4.5). Параметры движения следующие: Т=0,54, К₁=К₂=0.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (3.41, 4.5)в точку (4, 5). Параметры движения таковы: Т=1, К₁=0.33, К₂=-1.06, k₁=-0.33, k₂=1.06.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (4,5) в точку (4,99, 5,12). Параметры движения таковы: Т=1, К₁=-1.25, К₂=-1, k₁=1.25, k₂=1.

- равномерное движение по прямой   из точки (4,99, 5,12)  до точки (6.02, 5.38). Параметры движения следующие: Т=1.06, К₁=К₂=0.

- переход с одного отрезка траектории на другой. Движение по дугам двух спиралей из точки (6.02, 5.38) в точку (6.5, 5). Параметры движения таковы: Т=1, К₁=0.7, К₂=-1.11, k₁=-0.7, k₂=1.11.

- равномерное движение по прямой   из точки (6.5, 5)  до точки (6.5, 4). Параметры движения следующие: Т=1, К₁=К₂=0.

- торможение по прямой  из точки  до точки , (при этом, значения угловых скоростей вращения колес ведущей тележки линейно меняются от 1 до 0). Параметры движения следующие: Т=8, К₁=К₂=-0,125.

На рис.15 изображены графики изменения основных характеристик движения при исполнении данной траектории и сама траектория движения ведущей тележки и хвостовой части цепи.

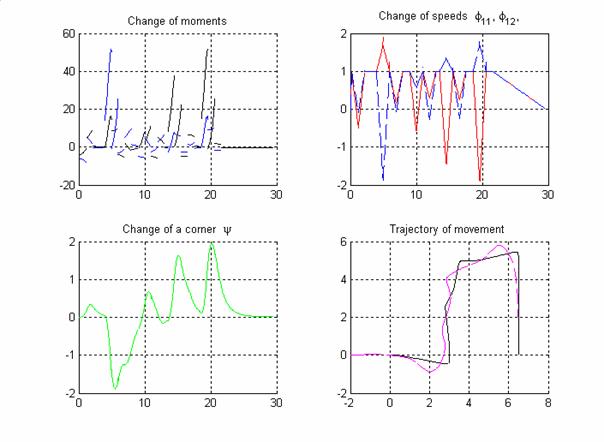
Рис.15. Траектория движения и его основные параметры при реализации принципа        реперных точек планирования движения.

В данном случае отклонение реальной траектории от спланированной не превышает 0.7. Достигнутую точность можно считать достаточной, при необходимости точность можно улучшить  соответствующей коррекцией промежуточных точек.

ЗАКЛЮЧЕНИЕ

Предложены методы управления цепочкой «робопоезд» при переходе между точками различных пространств – декартова, конфигурационного и фазового. Фактически, это задачи следующих классов: переход системы в заданную конечную точку, переход системы в заданную конечную точку с заданной ориентацией в ней, переход системы в заданную конечную точку с заданными в ней ориентацией и скоростями. Показана разрешимость перечисленных задач.

На основе предложенных методов разработаны два принципа планирования движения описанной системы принцип «коридоров» и принцип реперных (опорных) точек. Дана оценка размеров коридора, необходимого для прохождения  всей системой заданной трассы. Численные расчеты показали эффективность предложенных методов построения движения цепочки «робопоезд» и достаточные точности исполнения движения.

Данная работа завершает цикл, начатый в [1-2] и позволяет перейти к фазе экспериментальных исследований.

Список литературы

1.     В.Е.Павловский, Н.В.Петровская. Исследование динамики движения цепочки «робопоезд». Уравнения движения, частные решения. Препринт ИПМ им.М.В.Келдыша РАН, 2005.

2.     В.Е.Павловский, Н.В.Петровская, В.В.Евграфов. Исследование динамики движения цепочки «робопоезд».. Управляемое движение. Препринт ИПМ им.М.В.Келдыша РАН, 2005.

3.     Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. − М.: Наука, 1967.−520 с.

4.     Голубев Ю.Ф.  Основы теоретической механики: Учебник.  М.: Изд-во Моск. Ун-та., 2000.-719c.

5.     Маркеев А.П.  Теоретическая механика: Учебное пособие.  М.: Наука, 1990.-416c.