О выводе и решении уравнений Максвелла в задачах с заданным волновым фронтом

А.В. Березин, А.С.Воронцов, М.Б. Марков, Б.Д. Плющенков

Институт прикладной математики им. М.В.Келдыша РАН

Представлен вывод уравнений Максвелла в четырехмерном виде для системы координат, включающей собственное время фронта электромагнитной волны. Определен вид уравнений, показана корректность замены переменных в уравнениях для 3-векторов напряженности электрического и магнитного поля. Показана положительная определенность плотности энергии электромагнитного поля, доказана единственность решения задачи Гурса для уравнений Максвелла в собственном времени. Представлена локально-одномерная разностная схема для трехмерных уравнений Максвелла. Схема построена для задач с начальными данными на характеристической поверхности и имеет второй порядок суммарной аппроксимации в сеточной норме на равномерной сетке. Разностный аналог теоремы о скорости изменения энергии электромагнитного поля построен как алгебраическое следствие уравнений схемы. Теорема гарантирует сходимость разностного решения к точному со вторым порядком в энергетической норме. Скорость сходимости проверена путем сравнения с аналитическими решениями.

 

ON THE CONCLUSION AND DECISION OF MAXWELL’S EQUATIONS FOR

THE PROBLEMS WITH GIVEN WAVEFRONT

A.V. Berezin, A.S.Vorontsov, M.B.Markov, B.D. Plyushchenkov

Keldysh Institute of Applied Mathematics, Russian Academy of Science.

The conclusion of the 4-D Maxwell's equations in coordinate system including self-time of an electromagnetic wave front is represented. The equations are determined; the correctness of variables replacement in the 3-equations is shown. The positive definiteness of electromagnetic field’s energy density is shown, the uniqueness of the decision of Gursa problem for the Maxwell's equations is proved. The locally one-dimensional finite-difference scheme for three-dimensional Maxwell’s equations is represented. The scheme destines for numerical solving of problems with initial data on the characteristic surface and has the second order of summary approximation in  grid norm on uniform grids. Energy change theorem for presented scheme is constructed as a algebraic corollary of its equations. This theorem guarantees convergence of difference solution to exact solution with the second order in the energy norm. The convergence speed is checked by the comparison with analytical solutions.

ВВЕДЕНИЕ

Математические модели электромагнитных полей, генерируемых при ионизации больших объемов газа импульсными потоками фотонов, могут основываться на трехмерных уравнениях Максвелла с начальными условиями на фронте ионизации. Примером такого процесса является образование электромагнитного поля тормозным гамма-излучением, образующимся при воздействии электронов ускорителя на мишень. Если длительность импульса фотонов мала по сравнению с характерным линейным размером заполненного газом объема, то плотность стороннего тока комптоновских электронов и вторичная ионизация образуются в узком слое за фронтом гамма-излучения. Этот факт и обуславливает необходимость выделения переднего фронта. Мишень является, по сути, изотропным источником фотонов. Поскольку длины пробегов квантов существенно превышают размер мишени, существенные участки фронта их потока имеют форму, близкую к сферической. Электромагнитное поле также имеет сферический фронт. Выделение переднего фронта целесообразно также при моделировании распространения коротких электромагнитных импульсов в средах с заданным распределением электрофизических параметров. Это позволяет, с одной стороны, исключить из рассмотрения те точки пространства-времени, до которых импульс еще не распространился, а с другой – достаточно подробно описать его временную зависимость, сохраняя крупную пространственную сетку.

Выделение переднего фронта и формулировка соответствующих начальных условий превращают задачу Коши для уравнений Максвелла в задачу с существенно отличающимися свойствами. В частности, возникают проблемы, связанные с единственностью решения. Эти проблемы проявляются и при построении алгоритмов численного решения таких задач. Например, ни одна явная разностная схема для этого класса задач не может быть устойчива.

Решение задач для уравнений Максвелла с начальными данными на фронте электромагнитной волны в простейшем случае вакуумоподобной среды подразумевает переход от лабораторного времени к так называемому собственному [1]. Фронт электромагнитной волны имеет сферическую форму, поэтому уравнения Максвелла записываются в переменных, где  – лабораторное время, – скорость света в вакууме ­– пространственные координаты, а. Уравнения Максвелла не обязаны быть инвариантны относительно такой замены переменных, поскольку она не входит в группу Лоренца.

Построение численных алгоритмов для уравнений Максвелла сталкивается с проблемой обоснования свойств разностных схем, которые должны отражать свойства дифференциальной задачи. Основным здесь является закон изменения энергии электромагнитного поля, позволяющий в лабораторной системе координат обосновывать единственность решения задачи Коши и доказывать сходимость разностных схем в энергетической норме. В собственном времени структура плотности энергии электромагнитного поля существенно изменяется, что затрудняет исследование разностных схем.

Данная работа ставит своей целью вывод уравнений Максвелла в собственном времени и установление соответствий некоторых величин, характеризующих электромагнитное поле в лабораторном и собственном времени. Вывод основан на исследовании преобразований тензоров электромагнитного поля и энергии-импульса. С помощью такого вывода можно однозначно определить вид энергии электромагнитного поля в произвольной системе координат и попытаться выявить дополнительные свойства уравнений Максвелла и их решений. Излагается один численный алгоритм решения задач Гурса для уравнений Максвелла, исходной посылкой для создания которого послужила необходимость численного решения ряда трехмерных задач на доступной вычислительной технике.

1. Замена координат.

Уравнения Максвелла для зарядов в вакууме, получаемые путем вариации функционала действия, представляют собой соотношения, связывающие компоненты тензора электромагнитного поля и 4-вектора плотности электрического тока. Тензор электромагнитного поля является кососимметричным тензором второго ранга типа. В лабораторной системе координат, он имеет следующий вид [2]:

                                                                                                (1)

Наборы компонент и   тензора   составляют 3-векторы электрического   и магнитного  полей соответственно.

Лабораторные координаты в дальнейшем будем обозначать,. Введем координаты , соответствующие собственному времени:

, , ,.                                                                                     (2)

Рассмотрим – тензор электромагнитного поля в координатах:

 

                                                                                                (3)

Установим соответствие между компонентами тензоров  и. Для этого построим матрицы Якоби замены координат  на:

,     ,                                               (4)

и вычислим явно, как преобразуется тензор электромагнитного поля [3]:

,

откуда

.

Первая пара уравнений Максвелла в тензорном виде имеет следующий вид [2]:

                                                                                                                                       (5)

Здесь операция  – внешнее дифференцирование кососимметрического тензора

. 

Эта операция является тензорной [4], то есть ее координатная запись не зависит от выбора системы координат. Поэтому

. 

В силу этого первая пара трехмерных уравнений Максвелла в собственном времени:

,

где, ,    и  обозначают дивергенцию и ротор в координатах, а.

Рассмотрим преобразование 4-вектора плотности электрического тока  при переходе (2) из координат  в координаты . Пусть в координатах , где  – плотность заряда,  – 3-плотность электрического тока. Тогда в координатах

.                                                                                  (6)

Вторая пара уравнений Максвелла с помощью тензора электромагнитного поля и 4-вектора плотности тока записывается в следующем виде:

,                                                                                                                              (7)

где  обозначает ковариантное дифференцирование, а

,

где– метрический тензор в координатах,

 .

В координатах

.

Ковариантное дифференцирование является тензорной операцией. Уравнение (7) в произвольных координатах имеет следующий вид:

,                                                                                         (8)

где – символы Кристоффеля.

Рассмотрим второе слагаемое в уравнении (8). Вычислим символы Кристоффеля в координатах  [4]:

.

Среди всех комбинаций, возможных в правой части, только , , отличны от нуля. Во второе слагаемое (8) входят только те символы Кристоффеля вида , которые равны нулю. Третье слагаемое представляет собой свертку символов Кристоффеля, симметричных по нижним индексам  с тензором, кососимметрическим по тем же индексам, поэтому оно равно нулю. Значит, в координатах  уравнение (8) имеет вид:

Отсюда следует вторая пара трехмерных уравнений Максвелла:

,

где .

Таким образом, полная система уравнений Максвелла в собственном времени, то есть в координатах  имеет следующий вид:

,

.                                                (9)

Обратимся к энергетическим соотношениям. Выпишем с точностью до постоянного коэффициента тензор энергии-импульса электромагнитного поля [2]:

.

В координатах  для тензора  имеет место соотношение [2,4]:

.                                                                                                                      (10)

В координатах   данное соотношение приобретает следующий вид:

                                                                                                     (11)

Символы Кристоффеля  могут быть отличны от нуля только при . Поэтому в соотношении (11) . При этом , вообще говоря, отличны от нуля. Рассмотрим соотношение (11) при . Все  в этом соотношении равны нулю, а само соотношение можно записать так:

.                                                                                                                                   (12)

Соотношение (12) есть закон сохранения энергии электромагнитного поля в координатах. Соотношение (10) при  представляет этот закон в координатах, причем  – плотность энергии, а  () – вектор Пойнтинга.

Рассмотрим, как преобразуются плотность энергии и вектор Пойнтинга при переходе в координаты :

,

.

Таким образом, закон сохранения электромагнитной энергии, имеющий в координатах  вид:

,                                                                                              (13)

в координатах  записывается так:

.                                                                       (14)

Заметим, что все результаты остаются верными для произвольной замены координат, где  – произвольная дифференцируемая функция. При этом  везде поменяется на .

Уравнения Максвелла (9) и закон сохранения энергии электромагнитного поля (14) могут быть получены, минуя тензорное рассмотрение. Достаточно выполнить замену переменных  в уравнениях Максвелла в лабораторном времени, используя инвариантность полного дифференциала скалярной функции. Однако при этом теряется однозначность понятия электромагнитной энергии и вектора Пойнтинга. Тензорное рассмотрение позволяет однозначно определить эти величины. Заметим, что компоненты электромагнитного поля преобразуются по-разному для различных пар уравнений Максвелла. Простая замена переменных выявить этот факт не позволяет.

2. О единственности решения задачи Гурса

Энергия электромагнитного поля в лабораторной системе координат является положительно определенной величиной, то есть она положительна, если отлична от нуля хотя бы одна из компонент электромагнитного поля и обращается в ноль только в том случае, когда все компоненты электромагнитного поля равны нулю. Этот факт используется при доказательстве единственности решения различных задач для уравнений Максвелла. Рассмотрим пример.

Пусть уравнения Максвелла в лабораторном времени

,                                                                                    (15)

решаются в области  с границей, причем задано произвольное начальное условие при  и одно из двух граничных условий:

                                                         (16)

где  – единичный вектор в направлении нормали к поверхности .

Соотношение (13) может быть получено из уравнений (15) с однородной правой частью. Интегрируя (13) по области , пользуясь положительной определенностью плотности энергии легко показать, что однородная задача имеет только тривиальное решение, что и доказывает единственность решения задачи (15-16) с произвольными начальными данными.

Ситуация изменяется, если необходимо исследовать единственность решения задачи Гурса. Пусть начальное условие задано при . Выполним замену координат, в результате чего уравнения (15) превратятся в уравнения (9). Вектор Пойнтинга и формулировка граничных условий не изменятся. Энергия преобразуется к виду

Положительная определенность такой конструкции не очевидна.

Рассмотрим ее более подробно. Эта величина неотрицательна. Действительно:

.

Определим условия на  и, при которых  равно нулю. Поскольку

,

искомые условия имеют вид:

.                                                                                                 (17)

Заметим, что из (17) следует, что

.                                                                                                 (18)

Подставим  и, удовлетворяющие условиям (17) и (18), в уравнения Максвелла:

,       .                                                                                                     (19)

Заметим, что уравнения, содержащие дивергенции, обратятся в тождества типа.

Если  , то  представимо в виде градиента скалярной функции, причем  в силу. Из того, что  следует. Значит, в шаре любого радиуса  с центром в точке  скаляр  является гармонической функцией и доставляет решение однородной задаче  Неймана:

.                                                                                   (20)

Задача (20) имеет своим решением произвольную функцию переменной, не зависящую от переменных  [5]. В силу этого ее градиент, представляющий собой магнитное поле, равен нулю. Равенство нулю электрического поля  следует из (17).

Таким образом, плотность энергии электромагнитного поля  в координатах  является величиной, положительно определенной на решениях уравнений Максвелла.

Если замена переменных имеет вид , необходимо дополнительно потребовать, чтобы поверхности уровня  были компактными. В частности, при замене ,  может быть любой гармонической функцией переменных  и .

3. Уравнения Максвелла в среде

Рассмотрим уравнения Максвелла в среде с диэлектрической проницаемостью  и магнитной проницаемостью . Область за фронтом электромагнитного поля будет определяться неравенством , где  – функция координат. Собственное время фронта будет иметь вид . Правую часть зададим в виде плотности тока , где – проводимость среды, а  – плотность стороннего тока.

Напомним, как выводятся макроскопические уравнения Максвелла [6]. Рассмотрим микроскопические уравнения:

                                                (21)

Здесь  и означают компоненты микроскопического электромагнитного поля, а  и – микроскопические плотности заряда и тока, в том числе, ответственные за поляризацию и намагниченность среды.

Рассмотрим ту пару уравнений Максвелла, которая не содержит  и. Усредним их по пространственным переменным, обозначая , . Значок  означает усреднение.

Пусть , где  – плотность внешнего заряда, а  – плотность заряда, создающего поляризацию. На масштабах усреднения интеграл  по любому объему равен нулю. Поэтому  можно представить в виде , где  – векторное поле, которое называют поляризацией среды. Рассмотрим третье уравнение системы (21). Применяя к нему процедуру усреднения, получим уравнение

                                                                                                                                          (22)

где  – индукция электромагнитного поля.

Величина  определена с точностью до любого соленоидального векторного поля. Продифференцируем (22) по времени и воспользуемся непрерывностью заряда:

                                                                                                                        (23)

Величина под знаком дивергенции в (23) может быть представлена в виде ротора некоторого векторного поля . Получим последнее макроскопическое уравнение Максвелла:

                                                                                                                          (24)

Для того, чтобы определить систему макроскопических уравнений Максвелла, постулируем, что , .

Величины  и  получены прямым усреднением компонент электромагнитного поля, которые являются компонентами тензора. Это означает, что

                                                                                                 (25)

является кососимметричным тензором второго ранга типа. Поскольку  и  зависят от  и  линейно, можно ввести тензор

,                                                                                            (26)

который связан с тензором  соотношением , где  – кососимметричный по парам индексов  и  тензор, описывающий свойства среды.

С помощью введенных тензоров уравнения Максвелла в среде могут быть записаны в следующем виде:

,                                                                                                           (27)

Уравнения (27) можно получить вариацией функционала действия, если действие для поля представить в виде . Тогда тензор энергии-импульса можно записать в следующем симметричном виде:

.

Отсюда энергия в координатах  представляется в виде , а вектор Пойнтинга – . В координатах  , .

Уравнения (27) дают основание записывать уравнения Максвелла в среде в собственном времени  так:

,                 ,

где , энергию электромагнитного поля:

,

а закон ее сохранения

.

В системе координат  уравнения Максвелла имеют вид:

, (28) ,(32)

, (29),(32)

, (30),(33)

где .

2.Дифференциально-разностная схема

Пусть– область изменения пространственных переменных, в которой рассматривается решение уравнений Максвелла. Введем разностную сетку по переменной:

;

;

Разностную сетку для переменных  введем аналогично.

Выберем параметры сетки так, чтобы разрывы коэффициентов системы уравнений Максвелла разместились на поверхностях ,  и .  Будем считать, что значения коэффициентов заданы в точках сетки с дробными пространственными индексами.  Эти точки совпадают с центрами прямоугольных параллелепипедов, образованных пересечением плоскостей ;  и  . Внутри этих параллелепипедов все коэффициенты системы, плотности стороннего тока и компоненты электромагнитного поля непрерывны.

Компонента напряженности электрического поля, нормальная к поверхности разрыва, может претерпевать разрыв при переходе через эту поверхность. Касательная к этой поверхности компонента напряженности электрического поля при этом непрерывна. Поэтому сеточные компоненты электрического поля,  и  определим в середине соответствующих ребер указанных выше прямоугольных параллелепипедов.

Сохраним обозначения для сеточных функций. Соответствие  между сеточными и дифференциальными компонентами электрического поля следующее:

; ;

.

Сеточные компоненты напряженности магнитного поля  разместим в центрах граней параллелепипедов.

Нормальная к поверхности разрыва  компонента напряженности магнитного поля терпит разрыв, а нормальная к этой поверхности компонента индукции магнитного поля непрерывна. Определим усредненные на разрыве значения сеточных компонент напряженности магнитного поля:

где:

 для , если  считать, что .

Там, где это не вызывает недоразумений, название пространственной переменной в обозначениях для шагов сетки и значения пространственных индексов у значений сеточных функций будем опускать. Соотношения для сеточных значений напряженности и индукции магнитного поля  удобно записать в виде:

Легко проверить, что справедливо тождество

.

Аналогично определим остальные сеточные компоненты магнитного поля:

;

.

Заметим, что для них справедливы аналогичные тождества.

Дифференциально-разностные аналоги построим интегрированием уравнений Максвелла по площадкам, определенным в Таблице 1:

 

Таблица 1

Уравнение	Площадка интегрирования	Набор индексов
(28)		i = 0, … , Nx – 1; j = 0, … , Ny ; k = 0, … , Nz .
(29)		i = 0, … , Nx j = 0, … , Ny–1 k = 0, … , Nz
(30)		i = 0, … , Nx ;  j = 0, … , Ny ; k = 0, … , Nz-1 .
(31)		i = 0, … , Nx ; j = 0, … , Ny-1 ;  k = 0, … , Nz-1
(32)		i = 0, … , Nx-1 ;  j = 0, … , Ny ;   k = 0, … , Nz-1 .
(33)		i = 0, … , Nx-1;  j = 0, … , Ny-1 ;  k = 0, … , Nz .

 

Дифференциально-разностный аналог уравнения (28):

где: ,

.

Здесь и далее используются следующие символы.

Символ  обозначает следующее средневзвешенное значение сеточной функции, заданной в узлах сетки с дробными индексами  в точке сетки с индексами 

.

Символ  обозначает следующее средневзвешенное значение сеточной функции, заданной в узлах сетки с дробными индексами  в точке сетки с индексами 

Дифференциально-разностный аналог уравнения (29):

где:

 .

Дифференциально-разностный аналог уравнения (30):

где:;

Дифференциально-разностный аналог уравнения(31):

,

где:,

Дифференциально-разностный аналог уравнения (32):

,

где;

.

 

Дифференциально-разностный аналог уравнения (33):

,

где ;

.

 

Для обеспечения положительной определенности разностного аналога энергии в дифференциально-разностных уравнениях, вместо  следует написать

,

,

.

4. Дифференциально-разностная теорема об изменении энергии

Помножим и просуммируем дифференциально-разностные уравнения в соответствии с таблицей 2.

Таблица 2

Сложим соответствующие компоненты и получим дифференциально-разностный аналог уравнения скорости изменения «энергии» электромагнитного поля:

,

где - разностный аналог мощности тепловых потерь, мощности сторонних токов, а  потока энергии через поверхность расчетной области  .

Выражение для плотности разностной энергии элементарного объема  приводится к виду:

, 

,

где:

является разностным аналогом плотности «энергии» электромагнитного поля , так как  и  аппроксимирует ее со вторым порядком, а  является неотрицательной величиной второго порядка размера элементарного объема, что следует из:

где

,

,

,

,

,

;

,

,

;

,

,

;    

,

,

.

, ,

    ,

,  ,

Величина  обеспечивает положительную определенность конструкции  как квадратичной формы значений сеточных компонент электромагнитного поля.

5.Решение сеточных уравнений

Запишем исходную систему уравнений Максвелла в матричном виде:

                (28)

где u – вектор значений напряженности электрического и магнитного поля

;;;;

;;

Введем неравномерную сетку по переменной . Обозначим ее узлы , . Разобьем интервал  на шесть промежуточных интервалов одинаковой длины. Будем считать матрицы C и F на интервале  постоянными. На каждом из промежуточных интервалов заменим систему дифференциальных уравнений своей системой разностных уравнений. Обозначим.

Введем вспомогательную индексацию временных слоев и обозначим:

u⁰ = u(t₀); u¹ = u(t₁),…, u⁶ = u(t₆),  u⁰¹ = (u⁰+u¹)/2,u¹² = (u¹+u²)/2,…, и т.д.

Рассмотрим разностную аппроксимацию исходных уравнений по переменной. Для сокращения записи в дальнейшем под всеми величинами, входящими в (28) будем понимать их разностные аналоги, введенные в предыдущем разделе. Разностные уравнения на промежуточных интервалах примут следующий вид:

                                                              (28.1)

                                              (28.2)

                                              (28.3)

                                                (28.4)

                                                               (28.5)

                                                (28.6)

Система уравнений (28.1-6) является симметричной разностной схемой. Очевидно, что ни одно из уравнений схемы не аппроксимирует уравнение (28). Сложим уравнения (28.1-6):

Разлагая все функции, входящие в дифференциальную постановку, в ряд Тейлора по времени нетрудно убедиться, что данное уравнение аппроксимирует  дифференциальное уравнение с порядком O(τ²) при постоянном шаге по переменной.

Рассмотрим более подробно уравнение (28.1). Оно представляет собой систему шести разностных уравнений относительно компонент вектора u:

                                                                                          (28.1.1)

                                    (28.1.2)

                                    (28.1.3)

                                                                                          (28.1.4)

                                      (28.1.5)

                                     (28.1.6)

Уравнения (28.1.1) и (28.1.4) являются явными.

Система уравнений (28.1.2), (28.1.6) при каждом j и   k  распадается на подсистемы, зависящие только от значений функций при данных  j и k с неизвестными E_y¹ и H_z¹ на верхнем слое. Эта система решается прогонкой по переменной x.

В уравнения (28.1.3) и (28.1.5) входят неизвестные E_z¹ и H_y¹ с верхнего временного слоя. Она также решается прогонкой по x.

Заключение

Тензорный вывод уравнений Максвелла в собственном времени сферического фронта электромагнитной волны подтвердил вид уравнений и позволил однозначно определить преобразование плотности энергии поля и вектора Пойнтинга. Инвариантность вектора Пойнтинга относительно замены перехода в собственное время подтверждает возможность использования традиционных граничных условий. Исследование плотности энергии электромагнитного поля в собственном времени показало ее положительную определенность на функциях  и, являющихся решениями уравнений Максвелла в собственном времени. Следствием этого является единственность решения.

Представленная разностная схема позволяет использовать сетки с переменным шагом. Это дает возможность достаточно точно описывать поведение компонент электромагнитного поля на поверхностях разрыва электрофизических параметров, не сгущая сетку во всей расчетной области. Абсолютная устойчивость схемы позволяет достаточно сильно увеличивать шаг по времени по сравнению с шагом по пространству. Использование промежуточных слоев по времени исключает из расчета процедуры типа обращения матриц.

ЛИТЕРАТУРА

1. В.И. Турчанинов Численная методика решения трехмерных уравнений Максвелла в сферических переменных в неоднородной диссипативной среде с выделением  переднего фронта. М. Препринт ИПМ им. М.В. Келдыша РАН, 1993 №18

2. Л.Д. Ландау, Е.М. Лифшиц. Теория поля. – М.:Наука, 1976.

3. В.В. Киселев. Классическая электродинамика. – Семинары по курсу «Теория поля». – Изд. ГНЦ РФ «Институт физики высоких энергий», Протвино, 2004.

4. Б.А. Дубровин, С.П. Новиков, А.Т. Фоменко. Современная геометрия. – М.: Наука, 1986.

5. Р. Курант. Уравнения с частными производными. – М.: МИР, 1964. 

6. Л.Д. Ландау, Е.М. Лифшиц. Электродинамика сплошных сред. – М.:ГИФМЛ, 1959.
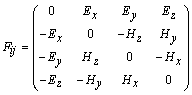
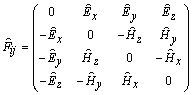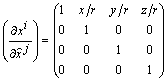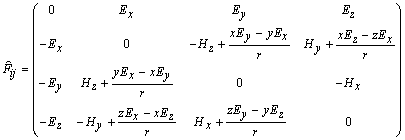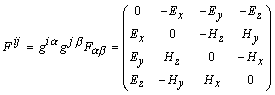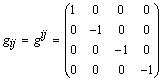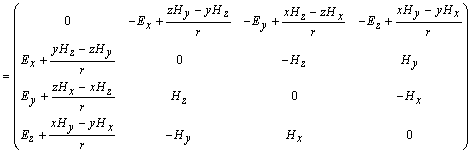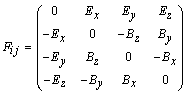
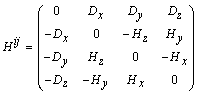
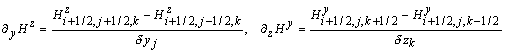
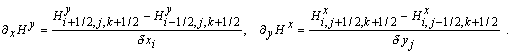
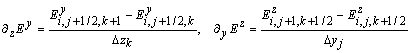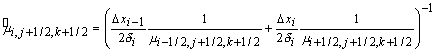
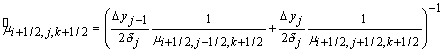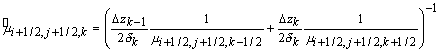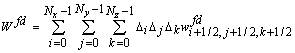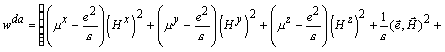
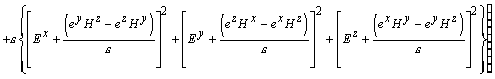
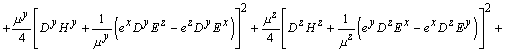
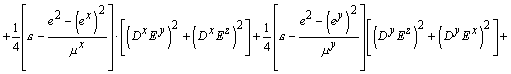
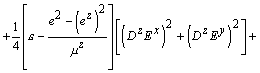
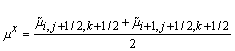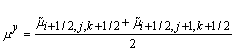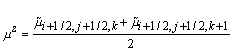
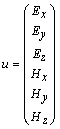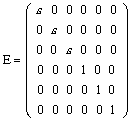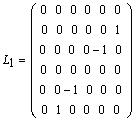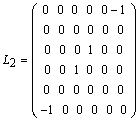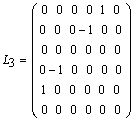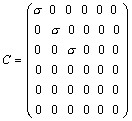