Contents

Introduction                                                                                              3

1. Description of hydraulic control system for exoskeleton                          3

2. Mathematical model of hydraulic control system for exoskeleton              5

2.1. Electrical-hydraulic amplifier                                                                  5

2.2. Hydraulic actuator                                                                                 8

2.3. Pump with pressure control                                                                   8

2.4. Structure of control system                                                                 11

3. Results of modeling                                                                               11

References                                                                                                14

Introduction

Exoskeleton is a device, which is put on a human and is intended for human's augmentation, in particular, to increase the efforts that a person may apply. Application of this system may be useful during execution of heavy works such as cargo handling works, in places where there is no opportunity of application of wheel loaders, and repair works on heavy objects, military tasks, to help soldiers carry heavy weapon for long distance, and for rehabilitation of people received serious damage of backbone.

As the actuators of joints of exoskeleton, it is most logical to use hydraulic drives as they have a number of advantages in comparison with electrical and pneumatic actuators. Important among them are high speed and high specific capacity (power to weight ratio) that allows designing a more compact drive.

As an energy source, an internal combustion engine may be considered.

1.     Description of a hydraulic control system for exoskeleton

Fig.1 shows the structural view of an experimental exoskeleton.  The number of active degrees of mobility on legs and hands is 10. A kinematic model of the exoskeleton has been designed at the Robotics Research Centre (RRC) of Nanyang Technological University (NTU), Singapore.

The basic arrangement of hydraulic actuators for the lower half of exoskeleton is shown in Fig.2. It consists of 10 linear hydraulic actuators, corresponding to 10 active joints. A hydraulic power pack and control elements need to be added in due course.

         For the preliminary design analysis, rotary hydraulic actuators are considered as the drives. Joint torques and power requirements at the joints are calculated and are given in Table №1.

In this paper, for the purpose of hydraulic design analysis, linear hydraulic actuators are considered as drives. They better correspond to the physiological structure of muscles of human. It is also expected that the use of linear actuators will result in creation of more compact design with better mass characteristics. Rotary hydraulic actuators have large dimensions, lesser twisting moments and lower reliability in comparison to linear hydraulic actuators. (A final decision regarding type of actuators may be taken after the mock-up exoskeleton has been built and all aspects of safety and operational efficiency are fully analyzed.)

Kinematic diagrams of a leg and humeral joint with the application of hydraulic cylinders are shown in Fig.2 and Fig.3. Position of leg and hand in its extremity and corresponding actuator positions are shown.

Table №1

Hydraulic Power Pack

Hydraulic power pack includes a pump with pressure regulator. Continuous flow of pressurized fluid at set pressure is supplied by the pump. Energy characteristics of the hydraulic system with pump with pressure control is shown in Fig.5a.

In Fig.4a, the basic diagram of the pump with a pressure-control valve, manufactured by Rexroth A10 VSODR, is presented. For the improvement of dimensional characteristics and configuration of a hydraulic drive, and also with the purpose of improvement of thermal balance, it is better to place the pump in a tank with a working fluid (Fig.6).

As flow control equipment, servo directional valve, which are widely used in robotics and aerospace, are considered. They have relatively small dimensions approximately 80х46х80 mm and mass ~ 0.64kg, with high dynamic characteristics.

Electric-hydraulic amplifiers (servo valves) with the mechanical feedback have wide applications in hydraulic actuators.  A schematic diagram of a servo valve is shown in Fig.7,8. The servo valve represents a combination of electromechanical converter (EMC) (1), the hydraulic amplifier of a jet-flapper type (2) and a spool, which is connected with the flapper by elastic feedback rod. Jet and flapper together represent an adjustable throttle, resistance of which can be changed by changing the distance between jet and flapper.

When an electric signal is applied to EMC, an electromagnetic force is developed and this in turn rotates the armature core. The angle of rotation depends on the level of input voltage. Along with the armature, the flapper and the feedback spring also rotate, thus changing the distance between the flapper and the jet. Due to this, the resistance of adjustable throttles changes resulting in a pressure differential at the end faces of the spool (3). This pressure differential causes the spool to move from its neutral position, thus opening the flow ports of the spool casing, to allow fluid flow. The movement of spool continues till the moment from the feedback rod becomes equal to the electromagnetic moment of the armature. Thus a constant flow of fluid through the valve is maintained as long as the input electric signal is maintained constant. The flow is proportional to the input electric signal. Fig.7,8 shows the Electric Hydraulic Amplifier (EHA) stage.

Since each part of exoskeleton requires independent motion, they need to be controlled individually with dedicated control valves and control strategy. The proposed hydraulic circuit diagram for the exoskeleton (for 3 joints)  is  shown  in Fig.9.  It includes the power pack, hydraulic cylinders, and servo valves.      Estimated weight of elements of various elements of the proposed 10 d.o.f. exoskeleton is given in Table №2.

Table №2

The total weight of the hydraulic drive of exoskeleton, without taking into account the weight of pipelines, is equal ~64.1kg, which is 46kg less than that of rotary hydraulic actuators.

2. Mathematical model of hydraulic control system for exoskeleton

2.1. Electric-hydraulic amplifier (servo valve) (Fig.8)

The equation of voltage in electric circuit of electromagnet:

,                                          (2.1)       

where voltage on the output of electronic amplifier;  active resistance of a control coil of electromagnet;  inductance of a coil of electromagnet;  coefficient of back EMF; electric current in control coil; angle of flapper and an anchor of electromagnet, rigidly connected to it.

Value of   coefficient of back EMF is determined according to the following ratio 

,                                                                      (2.2)

where length of the average line of anchor; ; air backlash between the anchor and the feedback rod.

The equation of motion of the armature with flapper

                                         (2.3)

where moment of inertia of armature; coefficient of a viscous amortization of armature; moment of the hydro-dynamical force , force of electromagnet; rigidity of a spring of flapper,

.

, where force, bending a feedback rod in the time of flapper angle and spool displacement.

, where module of elasticity of the material, of which the feedback rod is made, moment of inertia of the section of  feedback rod  relatively of  the main central axis, perpendicular to the plane of bending force, deflection of  the end of  feedback rod - is equal to the sum of the deflections caused by the turn of the flapper relatively of  the center O  on the angle   and displacement of   of the spool, 

.

Equation of consumption of working liquid in the control cascade:

                   ,                                (2.4)

where  consumption of working fluid, providing control of the main spool; square area of  the end face of spool of the main spool; displacement of the spool of the main spool; coefficient, which is taking into account  the compressibility of a working fluid in the face chambers of the main spool; volume of the face chamber of a spool;  module of volumetric elasticity of a working liquid; pressure of  liquid in the control chambers under the end faces of spool of  the main spool.

Consumption   is defined by known ratios from hydraulics:

,

where conductivity of a throttle of the servo valve; pressure of the pump;  coefficient of  consumption of liquid through the throttle;  square area of the throttle,  specific conductivity of  the jet  at neutral position  of a flapper,

,   function, determining the through passage section between the end face of jet and a flapper,  displacement of a flapper, distance between the jet and the flapper at neutral position.

Equation of the spool motion in hydraulic amplifier (servo valve)

                                 (2.5)

where mass of  the spool;  coefficient which is taking into account  a  viscous friction in a backlash between the spool and a sleeve; rigidity of the spring of the main spool; the hydro-dynamical force acting on the spool of  the main spool from the side of working fluid; force of viscous friction acting  on the spool of the main spool; pressure difference of working liquid at the end faces of the spool of the main spool; the square area of the end face of the spool of the servo valve.

Equation of consumption of fluid through the main spool

where  coefficient of consumption of the spool window(hole);  diameter of spool of the main spool; displacement of the spool; coefficient of overlapping of a spool sleeve; pressure of the pump; pressure in the cavities of hydraulic cylinder.

Equation of pressures in the cavities of   hydraulic actuator

                                                                  (2.6)

Here the square area of the piston of hydraulic actuator,  - elasticity of a working liquid,  - volume of a liquid under the end face of the piston of a hydraulic actuator,  - factor of compressibility of a working fluid.

     2.2. Hydraulic actuator (hydraulic cylinder)

,                        (3.1)

where the mass of the link, attached to a hydraulic cylinder,  displacement of the piston rod of a hydraulic cylinder, coefficient of friction of hydraulic cylinder, pressure in the cavities of a hydraulic cylinder, external force applied to the piston rod of hydraulic cylinder.

   2.3. The pump with regulator of pressure

Diagram of the pump with a regulator of pressure is given on fig 4a, 4c. Volume flow of the pump  is determined by the following ratio:

,                                                     (4.1)

where displacement of the pump;  maximal angle of swashplate turn; angular speed of rotation of a shaft of the pump;  current value of the angle of turn of the pump swashplate.

Dependence between the displacements of the piston of the control hydraulic cylinder and the angle of inclination of the pump swashplate is defined by a expression:

,                                           (4.2)

where coordinate, determining the position of piston of the hydraulic cylinder; maximal value, which  may accept; radius of the basic swashplate of the pump.

We consider the pipelines, which connect the pump with the hydraulic cylinders, short enough, so that we could consider processes in them without taking into account distribution of parameters of a working environment along the length of a hydraulic line. Then, proceeding from the condition of incompressibility of fluid, the equation of consumption in the pressure head hydraulic line can be written as follows:

                                             (4.3)

where  volumetric flow of the pump,  consumption, required for functioning of the hydraulic drives; flow rate of the liquid going for control;  coefficient, which is taking into account a compressibility of a working liquid in the pipelines; pressure of the pump.

Consumption of fluid, necessary for the operation of hydraulic drives:

                                                     (4.4)

where  flow rate of liquid, consumed by  hydraulic drive; number of hydraulic drives connected to the pump.

Equation of motion of the spool of pressure regulator

    (4.5)

where mass of the spool and of the mobile parts of the pressure regulator spool, attached to it; displacement of the pressure compensator spool;  coefficient, which is taking into account the viscous friction in a backlash between the spool and a sleeve;  rigidity of the spring of pressure compensator; force of the preliminary compression of the spring; hydro-dynamical force, acting on the spool from working fluid; square  area of the end face of the pressure compensator  spool.

Equation of motion of the pump swashplate and of the control hydraulic cylinder

                          (4.6)

where mass of piston of the control cylinder and attached to it mobile parts of the mechanism of adjustment of  pump flow;  coefficients  of viscous friction in the  backlashes between the pistons and  the sleeves of the  control cylinders; rigidity of the  spring of  control cylinder; force of the preliminary compression of the spring; square areas of piston of the control hydraulic cylinders; total moment of resistance, applied to the regulating element of the pump, displacement of  the  rod of the control hydraulic cylinder, pressure in the cavity of the control cylinder.

Pressure in cavity of control cylinder

         If y < 0.5 x_{огд. max}

  -   Pressure in control cylinder.

If y > 0.5 x_{огд. max}

 - flow through the spool of pressure regulator.

2.4. Structure of control system (fig.10)

All servo valves and hydraulic cylinders are incorporated into a united control system. On this slide the control system for one hydraulic cylinder is shown.

         The specifying signal from a top level control system and signal from the gauge of a feedback of the hydraulic cylinder enter to summation device. Feedback signal has an opposite sign.

Further the signal enters on input of servo valve amplifier. Resulting signal acts on the coils of servo valve magnet. Displacement of a spool corresponds to a level of a signal which enters on an input of servo valve.

The flow of a working fluid and speed of cylinder accordingly, depends on displacement of a spool of servo valve.

3. Results of modeling

Each leg of exoskeleton has three active degrees of freedom. Accordingly, three executive hydraulic cylinders should drive one leg; also three servo valves are required. Two hydraulic cylinders are required to actuate one hand, and two electric-hydraulic amplifiers (directional servo valve) to control them. Thus, exoskeleton includes 10 hydraulic cylinders. All of them are powered from one pump.

The system of equations, describing the functioning of the hydraulic drives for two legs, two hands and the pump with the pressure regulator, represents the system of the ordinary differential equations (ODE) of the order of 116, written down in normal form of Cauchy. For the decision of the ODE system, a Runge-Kutta method of integration, in the modification of  Merson  was used.

For the definition of adequacy of the composed mathematical models of the elements, which are included in the hydraulic drive, a mathematical modeling of the separate elements was carried out, in particular, - servo valve. Characteristics of servo valves, designed by the Rexroth company are given in Fig.11, which represent the reaction of servo valves to a step input electric signal at various values of pressure.

In Fig.12, a similar characteristic, obtained from modeling of servo valves, is presented. A stepping signal was applied to the input of servo valves. Supply pressure was set at 210bar.

It is visible from the results that the simulated performance of the servo valve is similar to the valve characteristics presented in the manufacturers catalogue.

The program for modeling a hydraulic control system of exoskeleton allows setting an input voltage as step input or a sinusoidal signal.

The torque loads acting on the various joints have been calculated and are presented in Table №1. Proceeding from the geometrical sizes of parts of exoskeleton, the forces, acting on the hydraulic cylinders, were determined. Based on the assumptions that these values of torques are the maximum, joint positions, where maximum torque is acting, were determined. For the legs, it is a position when the angle in the knee joint is equal to 90°.

In Fig.13-23, results of modeling of operation of the hydraulic drive of exoskeleton are given. Two modes of the most typical motion of the human were chosen for modeling.

The first mode corresponds to the getting up of the human from the semi-sitting position and a simultaneous rising of hands. Motion is carried out from the position, where the knee joint is at 90° w.r.t. the sheen bone, and the thigh bone is in a horizontal position. Final position corresponds to the movement when the person is in vertical standing position. Such motion is typical for the human, when he is lifting the loads.

A sinusoidal type voltage was applied to the input of each tracing drive. The period of a sinusoid corresponds to the rising up of exoskeleton from the semi-sitting position for 1.5sec and a knee-bend for the same period. The maximal loadings, acting on the hydraulic cylinders, have been obtained from the values of twisting moments in each of the joints, obtained at the Nanyang Technological University of Singapore. Proceeding from the kinematic diagram of exoskeleton, in which hydraulic cylinders are used as executive hydraulic actuators, loadings at each of the joints have been obtained.

                                                Table №3

          The loading, acting on the hydraulic cylinder, has a constant value. Values of loadings are given in Table №3. While rising up, the hydraulic cylinders belonging to the opposite sides of exoskeleton move in one phase with identical speeds. Motions of the rods of hydraulic cylinders are limited to the maximal values of displacements, obtained from the kinematic diagram of exoskeleton.

From the diagrams of displacements of the hydraulic cylinders of the hip (Fig.15), knee (Fig.14), shins (Fig.13), elbow (Fig.16), and shoulder (Fig.17), it is visible that hydraulic drives trace an input signal. In Fig.18, the power of the pump and the useful power developed by the hydraulic cylinders of all parts of exoskeleton are given. This diagram characterizes the power efficiency of a hydraulic actuator. Apparently from the diagram, the efficiency of a hydraulic drive averages 50% and higher, that for a hydraulic drive with throttle control with pressure control pump is quite satisfactory.

The second mode of motion models the walking of the human. At motion one leg is in a phase of a support, this phase is characterized by the relatively high loadings and small speeds, the second leg is in a phase of carry, which is characterized by the small loadings and high speeds.

As there is no dependence between the values of displacements of hydraulic cylinders and the loadings, applied to them, we have chosen the sine wave law of change of loadings with the amplitude equal to a maximal loading. The loadings acting on hydraulic cylinders, and also their speeds may considerably differ at different modes of operation of exoskeleton.

As there are no data about the loading arising in the joints of exoskeleton during walking, we have chosen, as loading characteristics, a sine wave law of their change. The loading was changed on a sinusoid with frequency 2Hz for hydraulic actuators of legs and frequency 1 Hz for hydraulic actuators of hands. Amplitude of loadings in degrees of freedom:  knee - 1000N, shin - 1200N, hip - 1500N, shoulder - 1000N, elbow - 1000N. Thus both the input signal and the loadings, working on the same hydraulic cylinders and belonging to the opposite sides, change with a 180 degree phase shift. The  results  of simulation  show that the hydraulic drive well traces input signals (Fig. 20-22). Displacements of hydraulic cylinders, belonging to the opposite side, have the same kind of diagrams, only with an opposite phase.

Power characteristics can be estimated under the diagram of power of the pump and useful power (Fig.23). The efficiency is on the average equal 30%. A mathematical modeling of the several modes with various values of frequency and amplitude was carried out. For all modes, the hydraulic drive well traces an input signal and has the efficiency 30-40%,  that is a good value for a hydraulic drive with the volume-throttle regulation. More precise results can be obtained by knowing the loading characteristics for each joint of exoskeleton.

Based on the results obtained from the above analysis, it is possible to draw the following conclusions. The pump, working at constant pressure, supports constant pressure in the system. Therefore such pump may not provide high power characteristics in all range of changes of working pressure of hydraulic drives of exoskeleton. It is visible from the power characteristic given on fig 8. If the pressure in hydraulic cylinders is close to the pressure of adjustment of the pump, then losses in hydraulic system will be minimal as pressure losses in the servo valves will be less. Thus, adjustment and control of the working pressure of the pump in dependence of the mode of motion of exoskeleton, may improve power characteristics of the hydraulic drive.

The regulator of pressure may change working pressure of the pump in a range from 20 up to 210bar. It is provided by the value of preliminary compression of the pressure limiting spool spring. During the operation of exoskeleton, there is no accessibility to adjust the value of spring compression and hence this has to be done through remote control. The basic hydraulic diagram of such pump is given on Fig.4b.

For example, when exoskeleton overcomes significant loadings and the high pressure is required in the hydraulic cylinders, then the regulator of pressure should be adjusted to a high pressure. Results of modeling of the first mode may serve as an example: when exoskeleton rises up from a semi-sitting position with loading. During walking with small loading, high pressure in hydraulic cylinders is not required, the regulator may be adjusted to a smaller pressure and hence reduce losses of pressure in servo valves. Thus, by adjusting the regulator pressure of the pump with reference to the loading and mode of motion, it is possible to optimize power characteristics.

As a signal for changing working pressure of the pump may be used signal from the load detector installed at the any limb of exoskeleton for example at back or at hip. Depending of the value of the signal from detector it’s possible to define the loads which act on the cylinders and depending on it install the pump working pressure.

In the whole the offered hydraulic system provides the functioning of exoskeleton at various modes of operation.

List of literature

1.          Borovin G.K. Computer Simulation of Hydraulic Control System of the Walking Machine. Proceedings 2^nd Tampere Intern. Conference on Machine Automat, ICMA'98, p.p. 179-192.

2.          Borovin G.K. Computer Simulation of Hydraulic Control System of the Walking Machine. Preprint KIAM RAS  №106, М., 1995г. 28p. (in russian)

3.          Borovin G.K., Kostyuk A.V. Computer Simulation of Hydraulic Actuator with LS-control of the Walking Machine. Preprint RIAM RAS  №54, М., 2001г. 28p. (in russian)

4.          Borovin G.K., Kostyuk A.V. Computer Simulation of Hydraulic System of the Walking Machine. // Proceedings 11^nd Conference «Extremal robotics», St-Petrsburg, StPSTU, 2001, p.p. 96-106. (in russian)

5.          Borovin G.K., Kostyuk A.V. Computer Simulation of Hydraulic Control System of the Walking Machine. // Proceedings Conference «Mobile robots and mechatronny systems», Моscow, МSU, december 2001, 15p. (in russian)

6.          Borovin G.K., Kostyuk A.V. Computer Simulation of Hydraulic Control System of the Walking Machine. // Theory and control systems. 2002, №4. (in russian)

7.          Borovin G.K., Kostyuk A.V. Computer Simulation of dynamics of Hydraulic Actuator  of the Walking Machine. №8, М., 2002, 28p. (in russian)

8.          Manessmann Rexroth, Brueninghaus Hydromatik. “Product Catalogue Axial Piston Units”, Horb, Germany, 1997.

Fig  1. The kinematic diagram of exoskeleton

Fig 2. Kinematic diagram of leg of exoskeleton with the use of hydraulic cylinders

Fig. 2a. Kinematical diagram of exoskeleton with the use of hydraulic cylinders (passive degrees of freedom are not shown)

Fig 3. Kinematic diagram of a shoulder and a hand with application of hydraulic cylinders

Fig. 3a. Kinematic diagram of the hands and shoulders with application of hydraulic cylinders (passive degrees of freedom are not shown)

Fig 3b. Legs of exoskeleton with servo valves and hydraulic cylinders

Fig. 4a. The basic hydraulic circuit of the pump with pressure control

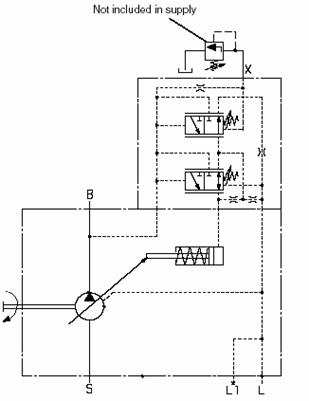
Fig. 4b. The basic hydraulic circuit of the pump with the

pressure regulator with remote control

Fig. 4c. Scheme of the pump with pressure regulator

Fig.5a. The characteristic of the hydraulic drive working with pump with

pressure regulator

Fig. 5b. The characteristic of the pump working on constant pressure

Fig. 6. The circuit of an arrangement of the pump inside a tank

Fig. 7. The electric-hydraulic amplifier of type (servo directional valve)

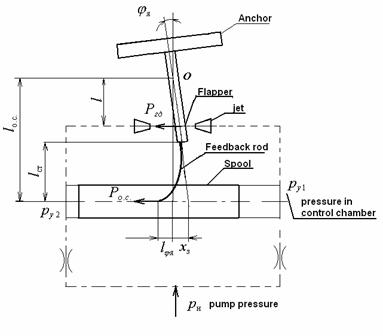
Fig. 8. The diagram for calculation of the electric-hydraulic

amplifier (servo valve) with a force feedback from a spool to a flapper

Fig 9. The basic hydraulic circuit of exoskeleton

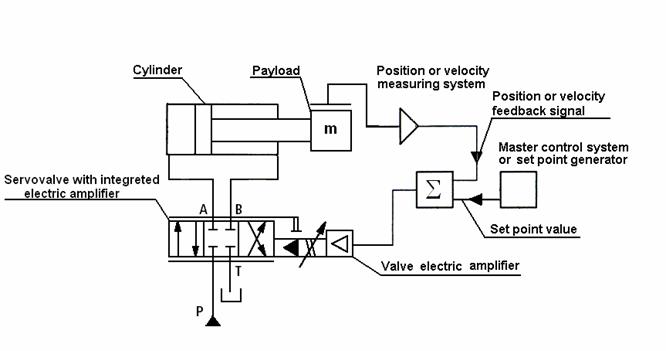
Fig.10. Diagram of hydraulic driver control system

Fig 11. Characteristic of servo valve at step input influence