Аннотация
Предложен численный метод расчета гармонического электромагнитного поля в металлической трубе
при наличии вращательной симметрии. Особенностью задачи является удаленность источника поля
от области интереса и необходимость нахождения решений для разных положений источника вдоль оси.
Метод основан на прямом решении системы разностных уравнений, аппроксимирующих
дифференциальную задачу конечными разностями второго порядка. На торцах цилиндрической
расчетной области применяются точные разностные граничные условия, причем неоднородные,
если источник находится за пределами этой области.
Abstract
A numerical method of calculating harmonic electromagnetic field in the metallic pipe with
rotational symmetry is proposed. The problem can have source located sufficiently far from
the domain of interest, as well as multiple positions of the source along the axis. The method
is based on the direct solution of discrete equations approximating differential problem by
second order finite-differences. Exact non-local difference boundary conditions are used on
faces, which are inhomogeneous if the source is outside the domain of interest.
Аннотация. Предложен численный метод расчета гармонического
электромагнитного поля в металлической трубе при наличии вращательной
симметрии. Особенностью задачи является удаленность источника поля от области
интереса и необходимость нахождения решений для разных положений источника
вдоль оси. Метод основан на прямом решении системы разностных уравнений,
аппроксимирующих дифференциальную задачу конечными разностями второго порядка.
На торцах цилиндрической расчетной области применяются точные разностные
граничные условия, причем неоднородные, если источник находится за пределами
этой области.
Введение
Цель настоящей работы состоит в разработке метода расчета
гармонического электромагнитного поля в цилиндрической (r,z)-геометрии. Основные особенности рассматриваемого класса
задач состоят в следующем:
1. Задача
ставится в неограниченной области (протяженная металлическая труба), хотя
область, где необходимо знать решение, ограничена (окрестность небольшой части
трубы);
2. При
одной и той же геометрии ищутся решения для разных правых частей (положение
источника меняется по z);
3. Источник
может быть достаточно удален от области, где необходимо знать решение;
4. Магнитная
проницаемость и электрическая проводимость могут испытывать разрывы (например,
переход металл-воздух);
5. Численное
решение должно обеспечивать достаточную точность как вдали так и вблизи от
разрывов (например, для вычисления вторых производных от решения), и
аппроксимацию на разрывах;
6. Алгоритм
решения должен быть достаточно быстр и надежен, поскольку он необходим также и
для последующего построения метода решения обратных задач (определение свойств материалов
и геометрии по известному электромагнитному полю).
В
работе предлагается описание метода, который, по мнению авторов, вполне отвечает указанным требованиям.
Приводятся результаты численного тестирования алгоритма, реализующего данный
метод.
Отметим
основные особенности предложенного метода:
1. Задача
сводится к решению скалярного эллиптического уравнения для угловой компоненты
электрического поля;
2. Дискретизация
проводится конечными разностями на неравномерной регулярной сетке;
3. На
торцах цилиндрической расчетной области применяются точные разностные граничные
условия, причем неоднородные, если источник находится за пределами этой
области;
4. Система
разностных уравнений решается прямым методом с машинной точностью с использованием
матричной прогонки;
5. Число
операций, необходимое для решения 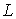 задач на сетке из задач на сетке из 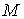 узлов по радиусу и узлов по радиусу и 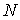 узлов по оси
оценивается как узлов по оси
оценивается как 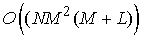 . .
Структура
работы следующая. В первом параграфе формулируется постановка задачи. Во втором
параграфе описывается дискретизация. Третий параграф посвящен построению
нелокальных граничных условий на торцах. В четвертом параграфе описан метод
решения системы разностных уравнений. Пятый параграф содержит результаты
тестирования алгоритма.
Работа выполнена при поддержке РФФИ, грант № 04-01-00567 и при поддержке гранта
RM0-1298, CRDF. Авторы благодарны также А.В.
Мясникову за помощь в разработке алгоритма.
1
Формулировка задачи
Рассмотрим
задачу расчета электромагнитного поля в (r,z)-координатах вблизи стенки трубы. Стенка трубы может
иметь круговые дефекты (канавки), которые – для простоты – являются
прямоугольными в плоскости (r,z). Источники (катушка),
возбуждающие электромагнитное поле, также круговые, причем с осью,
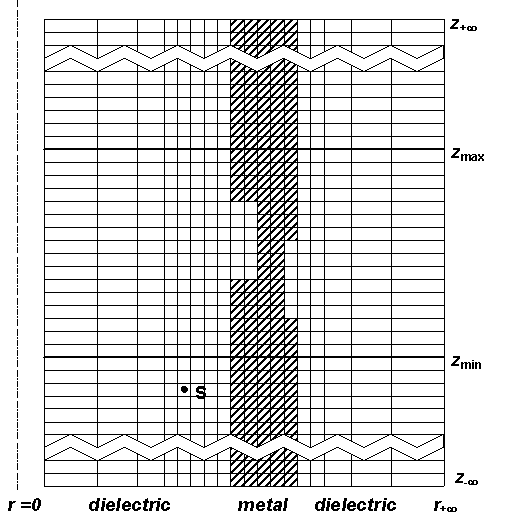
совпадающей с осью трубы. Общий вид (r,z) геометрии задачи представлен на Рис. 1‑1, где ось системы координат схематично показана слева,
штриховкой обозначена стенка трубы с двумя канавками, буквой S обозначен точечный источник (виток). Приведена также
прямоугольная сетка, используемая для дискретизации.
Система
уравнений Максвелла для гармонических по времени решений (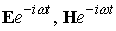 ) с частотой ) с частотой 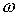 имеет вид: имеет вид:
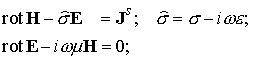
где
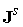 – плотность тока источника, удовлетворяющая
условию – плотность тока источника, удовлетворяющая
условию 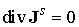 ; ; 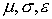 – независящие от времени параметры среды. С учетом вращательной симметрии задачи
уравнения сводятся к одному скалярному уравнению второго порядка для угловой
компоненты электрического поля – независящие от времени параметры среды. С учетом вращательной симметрии задачи
уравнения сводятся к одному скалярному уравнению второго порядка для угловой
компоненты электрического поля 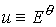 : :
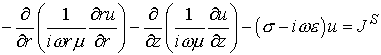
где 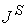 – заданная угловая компонента плотности тока. – заданная угловая компонента плотности тока.
Толщина провода
возбуждающего витка обычно много меньше размера расчетной ячейки. Поэтому мы
будем рассматривать элементарную задачу с точечным
источником тока, т.е. рассматривать правую часть вида 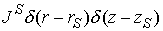 , где , где 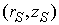 – координаты
точечного источника, – координаты
точечного источника, 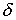 – функция Дирака. Если
же возбуждающая обмотка имеет площадь, покрывающую несколько ячеек некоторой
расчетной сетки, то, очевидно, решение можно найти путем суммирования решений
соответствующих элементарных задач. – функция Дирака. Если
же возбуждающая обмотка имеет площадь, покрывающую несколько ячеек некоторой
расчетной сетки, то, очевидно, решение можно найти путем суммирования решений
соответствующих элементарных задач.
Для невысоких частот обычно используют квазистационарное приближение, см. [[1]], полагая 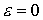 . Тогда основное уравнение принимает вид: . Тогда основное уравнение принимает вид:
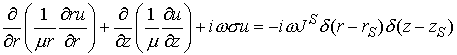 . .
Исходная
задача рассматривается в неограниченной области, причем решение убывает на
бесконечности. Поэтому мы ставим граничное условие 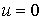 на границах
прямоугольника на границах
прямоугольника 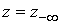 , , 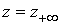 и и 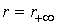 , расположенных достаточно далеко от области, в которой нам
необходимо знать решение. Эта область определяется неравенством , расположенных достаточно далеко от области, в которой нам
необходимо знать решение. Эта область определяется неравенством 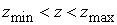 , где , где 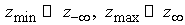 , и находится внутри трубы. Кроме того, естественное условие , и находится внутри трубы. Кроме того, естественное условие 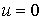 ставится на оси ставится на оси 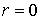 . .
Важной
особенностью постановки задачи является то, что необходимо вычислить решения
группы задач, различающихся положением источника (точнее – коротких отрезков,
составленных из точечных источников), пробегающим вдоль протяженного отрезка с
фиксированной координатой  . Иными словами мы приходим к необходимости решения набора
элементарных задач с разными значениями координаты . Иными словами мы приходим к необходимости решения набора
элементарных задач с разными значениями координаты 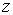 точечного источника S вдоль некоторого отрезка. точечного источника S вдоль некоторого отрезка.
2
Разностная схема
Разобьем
всю большую область 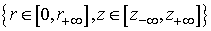 на прямоугольные
ячейки, см. Рис.
1‑1, имеющих
размер на прямоугольные
ячейки, см. Рис.
1‑1, имеющих
размер 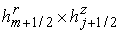 и введем сеточные
координаты: и введем сеточные
координаты:
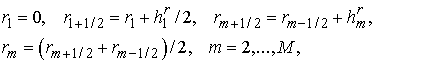
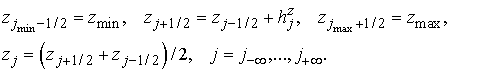
Шаги двойственной
сетки 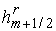 и и 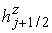 определяются как
расстояния между центрами ячеек, поэтому определяются как
расстояния между центрами ячеек, поэтому
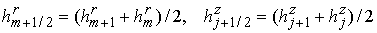 . .
Согласно этим определениям,
границы ячеек соответствуют полуцелым точкам . .
Неизвестная функция 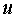 представляется
сеточной функцией представляется
сеточной функцией 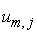 , приписанной к центру
ячейки , приписанной к центру
ячейки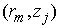 . .
Уравнение
аппроксимируется следующей разностной схемой:
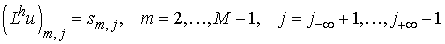
где
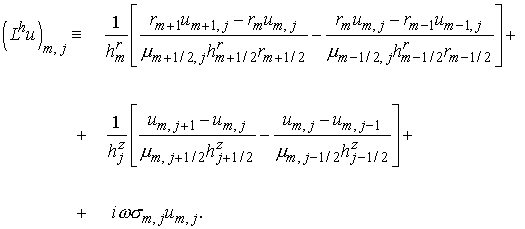
При
выводе этих уравнений мы полагали, что 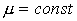 внутри ячейки, и
использовали условия непрерывности функции внутри ячейки, и
использовали условия непрерывности функции 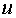 и потоков и потоков
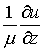 и и 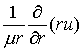 , ,
вытекающие из физики задачи, чтобы найти величины с полуцелыми индексами (на
границах ячейки). Аппроксимация первого потока дает связи
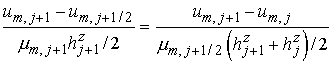
и
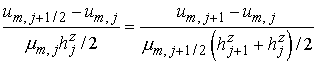 . .
Тогда, исключая 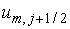 , получаем выражение , получаем выражение
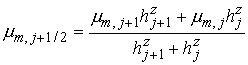 . .
Аналогично из условий,
аппроксимирующих второй поток,
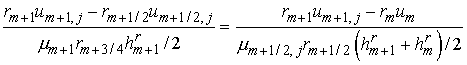
и
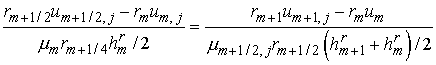 , ,
получаем, что
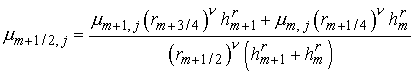
где использованы обозначения
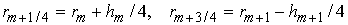 . Заметим, что
последнее уравнение может быть записано в виде . Заметим, что
последнее уравнение может быть записано в виде
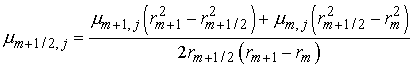 . .
Правая часть
разностного уравнения имеет вид
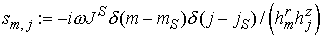 , ,
где индексы 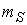 , ,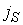 соответствуют координате точечного источника. соответствуют координате точечного источника.
Окончательно
разностная задача замыкается однородными граничными условиями Дирихле:

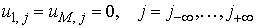 , ,
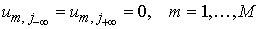
3
Нелокальные граничные условия на торцах
расчетной области
Чтобы резко сократить вычислительные затраты, мы будем использовать
область 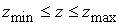 , где действительно необходимо знать решение, в качестве вычислительной области (вместо всей,
«большой», области , где действительно необходимо знать решение, в качестве вычислительной области (вместо всей,
«большой», области 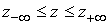 , где ставится задача). Это, очевидно, возможно, если мы
построим на границах , где ставится задача). Это, очевидно, возможно, если мы
построим на границах 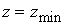 и и 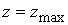 искусственные граничные условия такие, что решение с
ними задачи в вычислительной области совпадает с решением задачи – в большой области. искусственные граничные условия такие, что решение с
ними задачи в вычислительной области совпадает с решением задачи – в большой области.
Для
этого полагаем, что вне вычислительной области
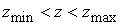 стенка трубы не имеет дефектов, а параметры стенка трубы не имеет дефектов, а параметры 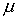 и и  являются постоянными как в металле так и в
диэлектрике. являются постоянными как в металле так и в
диэлектрике.
Вначале построим искомые граничные условия на
границе 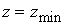 . В соответствии с постановкой задачи, источники
могут находиться как внутри так и вне области . В соответствии с постановкой задачи, источники
могут находиться как внутри так и вне области 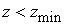 . Поэтому граничные
условия могут быть неоднородными. . Поэтому граничные
условия могут быть неоднородными.
3.1
Однородные граничные условия
Будем
строить однородные граничные условия в виде
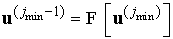 , ,
где 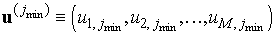 – вектор значений
функции на линии – вектор значений
функции на линии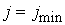 , а оператор (матрица) , а оператор (матрица) 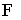 должен быть таким, что справедливо
для любого решения задачи – с нулевой
правой частью в области должен быть таким, что справедливо
для любого решения задачи – с нулевой
правой частью в области 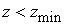 . .
Отметим,
что идея построения такого рода точных нелокальных разностных условий
принадлежит В.С. Рябенькому и использовалась в работах [[2]],
[[3]].
Очевидно,
что если на линии 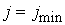 известен след
некоторого решения известен след
некоторого решения 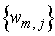 исходной задачи в
«большой» области, то восстановить это
решение на линии исходной задачи в
«большой» области, то восстановить это
решение на линии 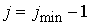 можно путем решения
задачи Дирихле для в области можно путем решения
задачи Дирихле для в области 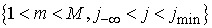 со следующими
граничными условиями: со следующими
граничными условиями:
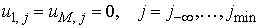 , ,
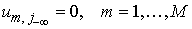 , ,
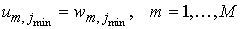 . .
Рассмотрим
базисные вектора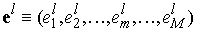 , где , где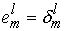 , т.е все компоненты вектора , т.е все компоненты вектора 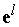 равны нулю кроме компоненты равны нулю кроме компоненты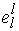 , равной единице. Обозначим вектор , равной единице. Обозначим вектор 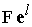 через через 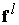 . Тогда . Тогда
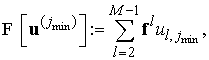
а
искомое условие принимает вид
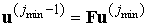 , ,
где
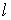 -ый столбец матрицы -ый столбец матрицы 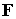 является вектором является вектором 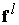 при при 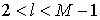 , а первый и , а первый и 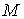 -ый столбцы – нулевые. Очевидно, что для вычисления -ый столбцы – нулевые. Очевидно, что для вычисления 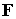 нужно решить серию указанных
задач Дирихле. нужно решить серию указанных
задач Дирихле.
Вычисление
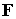 осуществляется
достаточно быстро с помощью метода Фурье – за осуществляется
достаточно быстро с помощью метода Фурье – за 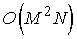 операций, где операций, где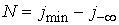 . Для этого мы используем равномерную сетку . Для этого мы используем равномерную сетку  в области в области 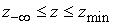 , т.е. для , т.е. для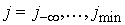 . Вектор . Вектор 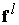 является следом на является следом на 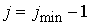 решения задачи решения задачи
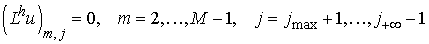 , ,
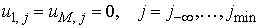 , ,
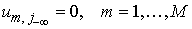 , ,
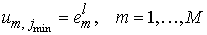 . .
Чтобы применить метод
Фурье, мы полагаем 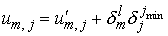 , где , где 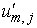 является решением
уравнения является решением
уравнения
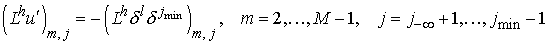
с
однородными граничными условиями
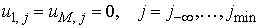 , ,
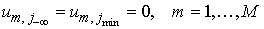 . .
Опишем
алгоритм нахождения решения. Рассмотрим уравнение с дельта-функцией в правой части:
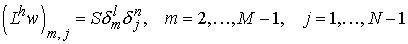
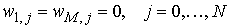 , ,
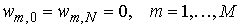 , ,
где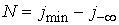 , ,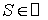 . Мы полагаем, что коэффициенты . Мы полагаем, что коэффициенты 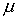 и и  уравнения зависят
только от индекса уравнения зависят
только от индекса 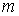 , а шаг , а шаг 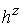 – постоянный. Тогда оператор – постоянный. Тогда оператор
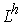 имеет вид имеет вид
Подставляя
дискретное синус-преобразование  по индексу по индексу 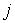
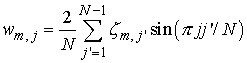 , , 
в
и учитывая,
что
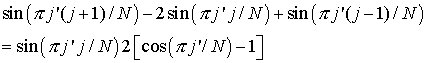 , ,
мы
получаем следующий набор уравнений для коэффициентов Фурье 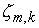 : :
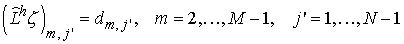
с
однородными граничными условиями
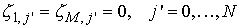 , ,
где
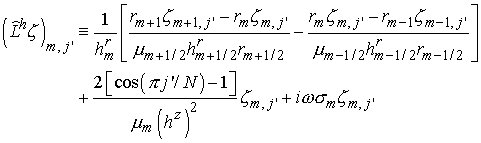 , ,
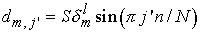 . .
Уравнения можно
переписать для каждой 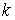 -ой гармоники -ой гармоники 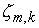 следующим образом: следующим образом:
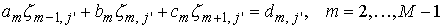 , ,
где
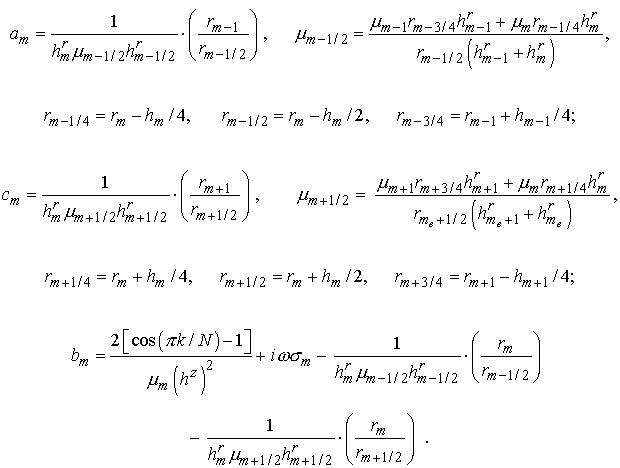
Уравнения
решаем
прогонкой: вначале вычисляем коэффициенты
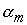 и и 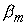 по формулам по формулам

а затем получаем решение рекурсией
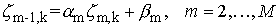
с 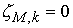 . .
После
решения элементы матрицы 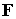 вычисляются как вычисляются как
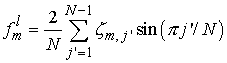 . .
Заметим,
что если сетка в области 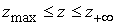 такая же как и
рассмотренной области такая же как и
рассмотренной области 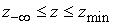 , то из-за инвариантности уравнений относительно замены
переменных , то из-за инвариантности уравнений относительно замены
переменных  искусственные
граничные условия на границе искусственные
граничные условия на границе 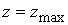 будут определяться той
же матрицей: будут определяться той
же матрицей:
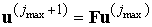 . .
3.2
Неоднородные граничные условия
Очевидно,
что в этом случае условие на границе 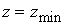 будет иметь вид будет иметь вид
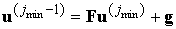
с
той же матрицей 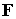 и некоторым вектором и некоторым вектором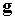 , зависящим от местоположения и значения правой части. , зависящим от местоположения и значения правой части.
Чтобы
определить вектор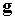 , мы заметим, что если решение , мы заметим, что если решение 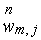 задачи – с некоторой ненулевой правой
частью в области задачи – с некоторой ненулевой правой
частью в области 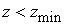 известно на линии известно на линии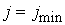 , то его можно восстановить на линии , то его можно восстановить на линии 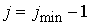 путем решения задачи
Дирихле для в области путем решения задачи
Дирихле для в области 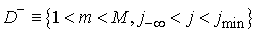 с граничными условиями с граничными условиями
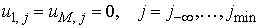 , ,
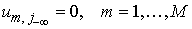 , ,
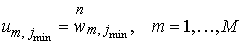 . .
Рассмотрим решение 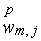 указанной задачи с
условиями указанной задачи с
условиями
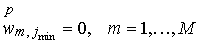
вместо . Очевидно, что функция 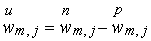 будет являться
решением однородного уравнения будет являться
решением однородного уравнения
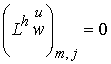
в области 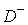 с граничными условиями с граничными условиями
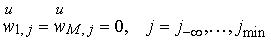 , ,
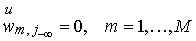 , ,
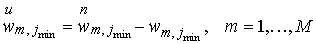 . .
Такая задача была
рассмотрена в предыдущем параграфе. Поэтому мы получаем
связь
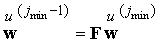
или
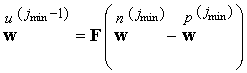 . .
Следовательно
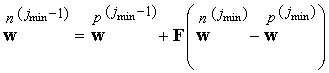 , ,
откуда
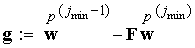
или
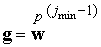
из-за .
Краевая задача для 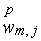 аналогична задаче . Таким образом, вычисление аналогична задаче . Таким образом, вычисление 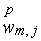 осуществляется по тому
же алгоритму с источником осуществляется по тому
же алгоритму с источником 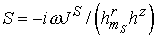 , , 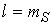 , ,  , поэтому , поэтому
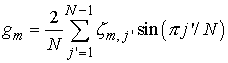 . .
Замечание.
Для серии задач с различным положением источников вдоль оси 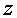 в области в области 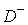 ( (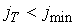 ) можно сократить объем вычислений, беря одно и то же
приближенное решение ) можно сократить объем вычислений, беря одно и то же
приближенное решение 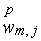 для подготовки всех
необходимых для подготовки всех
необходимых 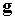 . В самом деле, обозначим через . В самом деле, обозначим через 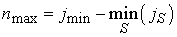 максимальную глубину
проникновения источника в область максимальную глубину
проникновения источника в область 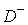 и предположим, что и предположим, что 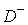 – бесконечная область с – бесконечная область с 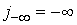 . Тогда, очевидно, из-за сдвиговой инвариантности достаточно
взять решение задачи с параметрами . Тогда, очевидно, из-за сдвиговой инвариантности достаточно
взять решение задачи с параметрами
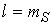 , , 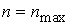 , , 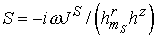 и вычислить и вычислить 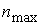 векторов: векторов:
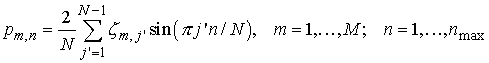 . .
Соответствующие
векторы 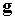 для источника в точке для источника в точке 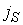 вычисляются затем как вычисляются затем как
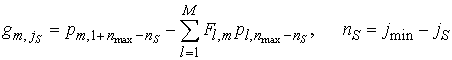 . .
Эти векторы являются
точными. Возвращаясь к случаю конечной области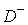 , мы тогда уже получим приближенные значения векторов при
использовании . Однако, погрешность такого приближения можно
сделать как угодно малой, выбрав достаточно длинную область с , мы тогда уже получим приближенные значения векторов при
использовании . Однако, погрешность такого приближения можно
сделать как угодно малой, выбрав достаточно длинную область с 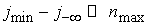 . .
Рассмотренный
выше метод построения точных разностных граничных условий легко
распространяется на трехмерные задачи в цилиндрической геометрии 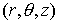 для соответствующего скалярного уравнения,
т.к. в основе получения матрицы для соответствующего скалярного уравнения,
т.к. в основе получения матрицы  лежит метод разделения
переменных. Если сетка по угловой переменной равномерная с
соответствующим шагом лежит метод разделения
переменных. Если сетка по угловой переменной равномерная с
соответствующим шагом  , то, используя Фурье-разложение периодической по индексу , то, используя Фурье-разложение периодической по индексу 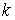 разностной функции разностной функции 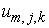
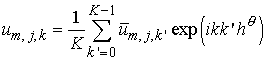 , , 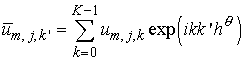 , ,
мы
приходим к серии двумерных задач для функций 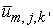 , , 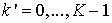 . .
Таких
задач в общем случае должно быть 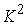 – произведение числа
угловых гармоник на число возможных угловых положений дельта-образных правых
частей. Однако, в силу вращательной симметрии геометрии задачи и равномерности угловой
сетки искомая «трехмерная» матрица – произведение числа
угловых гармоник на число возможных угловых положений дельта-образных правых
частей. Однако, в силу вращательной симметрии геометрии задачи и равномерности угловой
сетки искомая «трехмерная» матрица 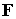 является
блочно-диагональной по углу; причем зависимость от угла выражается как является
блочно-диагональной по углу; причем зависимость от угла выражается как
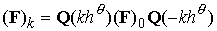 , ,
где 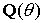 – матрица поворота на
угол – матрица поворота на
угол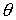 , а , а 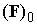 – «частная трехмерная»
матрица для случая правой части только при – «частная трехмерная»
матрица для случая правой части только при 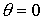 . .
Для
вычисления 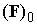 надо решать те же вспомогательные уравнения , но зависящие от индекса надо решать те же вспомогательные уравнения , но зависящие от индекса 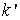 . Эта зависимость состоит в изменении центрального
коэффициента . Эта зависимость состоит в изменении центрального
коэффициента
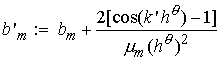
и правой части
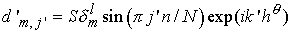 . .
Число таких уравнений ровно в 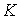 раз больше, чем для
двумерного случая. Поэтому число операций для вычисления «трехмерной» матрицы раз больше, чем для
двумерного случая. Поэтому число операций для вычисления «трехмерной» матрицы 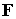 возрастет в возрастет в 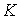 раз и составит раз и составит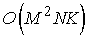 . .
Вычислительная
область D ограничена значениями индексов в интервале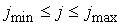 . Разностное уравнение имеет вид . Разностное уравнение имеет вид
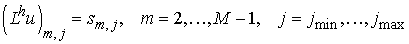 , ,
см.
, с локальными граничными условиями на боковых сторонах
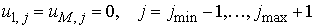
и
нелокальными граничными условиями
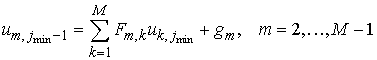
на
нижнем торце и
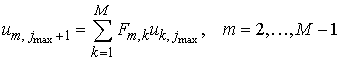
на
верхнем торце.
Если
источник попадает вовнутрь области D, (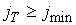 ), то ), то
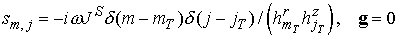 ; ;
иначе
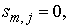 а вектор а вектор 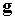 задан в . задан в .
Запишем
эту систему линейных уравнений в алгебраической форме:
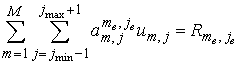 , ,
где
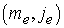 – номер уравнения.
Соответствующие коэффициенты определяются следующим образом: – номер уравнения.
Соответствующие коэффициенты определяются следующим образом:
для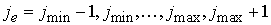 , если , если 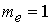 или или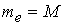 : :
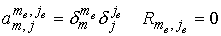 ; ;
для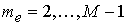 , , 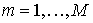 , если , если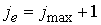 : :
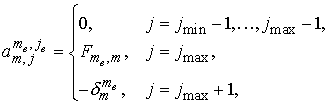 , , 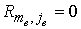 ; ;
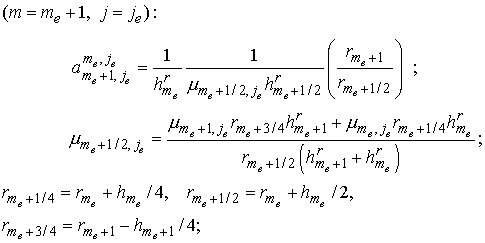
для
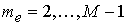 , , 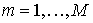 , если , если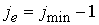 : :
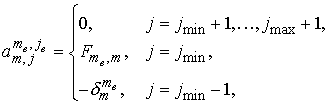 , , 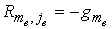 ; ;
для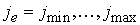 , ,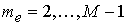 : :
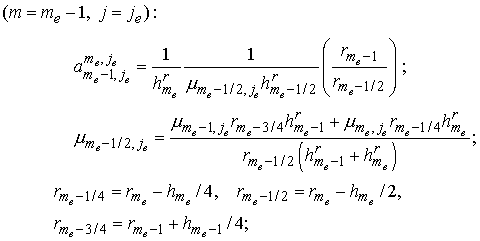
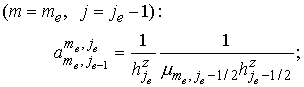
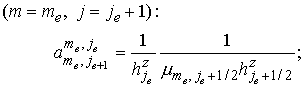
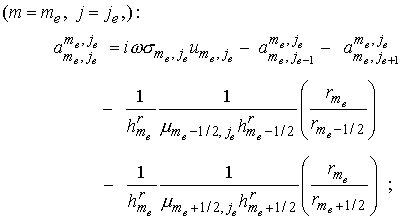
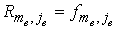 ; ;
для
остальных индексов 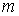 и и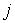
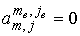 . .
Очевидно,
что коэффициент 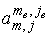 не равен нулю только
если не равен нулю только
если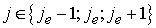 . Таким образом система принимает вид . Таким образом система принимает вид
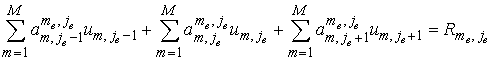 . .
Перепишем
ее в матричной форме:
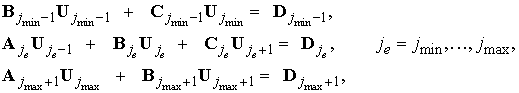
где
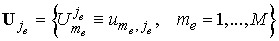 , ,
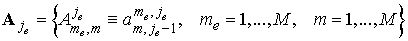 , ,
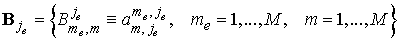 , ,
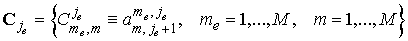 , ,
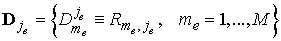 . .
Эту
систему мы решаем матричной прогонкой. Сначала вычисляем матрицы
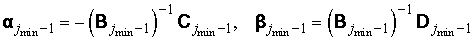
и
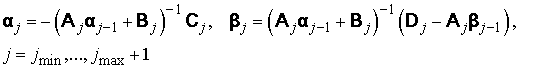 . .
Затем
совершаем обратную рекурсию
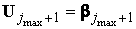
и
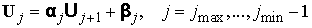 . .
Очевидно,
что для случая серии задач с 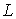 различными правыми
частями различными правыми
частями 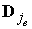 является прямоугольной
матрицей, т.е. является прямоугольной
матрицей, т.е.
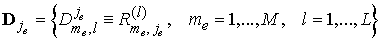 . .
Соответственно
возникают прямоугольные матрицы
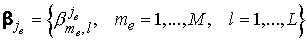 ; ;
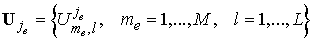 . .
Поэтому
все 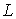 вариантов вычисляются
одновременно (они различаются по параметру вариантов вычисляются
одновременно (они различаются по параметру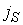 ). ).
Оценим
необходимые вычислительные затраты.
Алгоритм матричной прогонки
требует 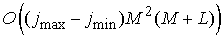 операций и операций и 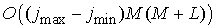 ячеек памяти.
Вычисление матрицы и правой части в операторе граничных условий на торцах требует дополнительно ячеек памяти.
Вычисление матрицы и правой части в операторе граничных условий на торцах требует дополнительно 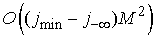 операций и ячеек
памяти. операций и ячеек
памяти.
Обсудим
эти оценки с точки зрения значений типичных параметров. В наших приложениях
типичные параметры таковы: 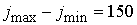 , , 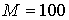 , , 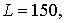 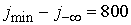 . Очевидно, что затраты на операции для торцевых граничных
условий несущественны по сравнению с решением задачи в основной области. Но эти
нелокальные торцевые условия позволяют в несколько раз сократить размер
вычислительной области вдоль . Очевидно, что затраты на операции для торцевых граничных
условий несущественны по сравнению с решением задачи в основной области. Но эти
нелокальные торцевые условия позволяют в несколько раз сократить размер
вычислительной области вдоль 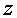 . Если решать данную задачу каким-либо итерационным
алгоритмом, то соответствующие затраты составят по крайней мере . Если решать данную задачу каким-либо итерационным
алгоритмом, то соответствующие затраты составят по крайней мере 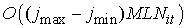 операций, где операций, где 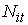 – число итераций.
Сравнивая эту оценку с оценкой для алгоритма матричной прогонки, мы видим, что
разница заключается в множителях – число итераций.
Сравнивая эту оценку с оценкой для алгоритма матричной прогонки, мы видим, что
разница заключается в множителях 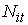 и и 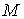 , соответственно. Учитывая, что сетка, как правило, содержит
сильно вытянутые ячейки (она неравномерная вдоль , соответственно. Учитывая, что сетка, как правило, содержит
сильно вытянутые ячейки (она неравномерная вдоль 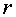 ), коэффициенты системы имеют сильные разрывы ( ), коэффициенты системы имеют сильные разрывы (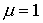 для воздуха и для воздуха и 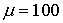 для металла), можно
вполне обосновано предположить, что даже самый продвинутый итерационный метод
будет требовать не менее сотни итераций для рассматриваемых параметров. Т.е. наш
алгоритм удовлетворяет самой оптимистичной оценке для удачного итерационного
алгоритма. Следует также подчеркнуть, что предложенный алгоритм дает решение
задачи с машинной точностью. для металла), можно
вполне обосновано предположить, что даже самый продвинутый итерационный метод
будет требовать не менее сотни итераций для рассматриваемых параметров. Т.е. наш
алгоритм удовлетворяет самой оптимистичной оценке для удачного итерационного
алгоритма. Следует также подчеркнуть, что предложенный алгоритм дает решение
задачи с машинной точностью.
5
Тестовые расчеты
Для тестовой задачи мы
выбрали следующие параметры:
- металлическая труба внутренним радиусом 10
дюймов и толщиной стенки 0.5 дюйма;
- проводимость трубы
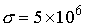 сименс/метр,
относительная магнитная проницаемость сименс/метр,
относительная магнитная проницаемость 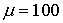 ; ;
- внутри и вне трубы находится воздух с нулевой
проводимостью и
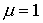 ; ;
- в качестве дефекта трубы рассматривается
внутренняя канавка длиной 1 дюйм и глубиной в половину стенки;
- возбуждающая катушка имеет радиус 2 дюйма и
длину 20 дюймов.
Описанная геометрия отражена
на Рис.
5‑1.
Первая
серия расчетов позволяет получить представление о характере решения. На Рис. 5‑1 показаны изолинии
амплитуды и фазы решения 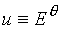 . .
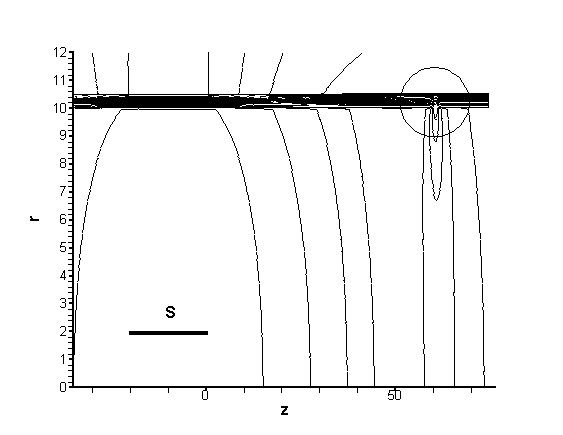
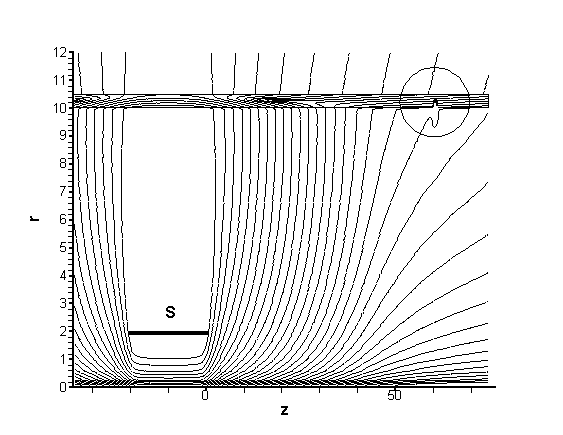
Размеры
указаны в дюймах. Левая и правая границы рисунков являются границами
вычислительной области, т.е. на них поставлены нелокальные граничные
условия. При этом границы области 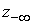 и и 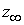 , используемой для вычисления оператора граничных условий
отодвинуты на расстояние 600 дюймов. По
радиусу вычислительная область простирается до значения , используемой для вычисления оператора граничных условий
отодвинуты на расстояние 600 дюймов. По
радиусу вычислительная область простирается до значения 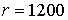 . Показаны положение возбуждающей катушки . Показаны положение возбуждающей катушки 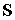 и фрагмент трубы с
кольцевым дефектом при и фрагмент трубы с
кольцевым дефектом при 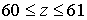 (в кружочке). Параметры сетки следующие: (в кружочке). Параметры сетки следующие: 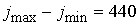 , , 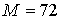 , , 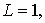 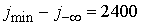 . Частота переменного тока равна . Частота переменного тока равна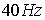 . .
На
Рис.
5‑2 показаны графики амплитуды и фазы вдоль линии с
координатой 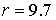 . .
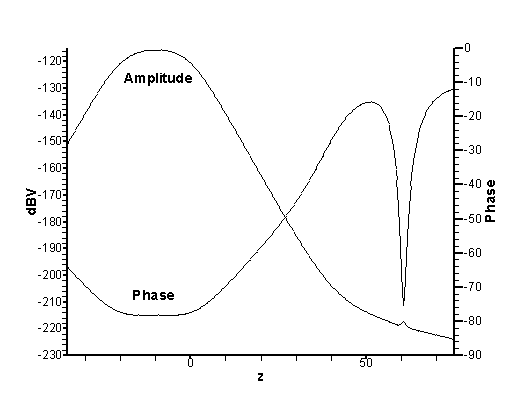
Отметим,
что решение может вести себя нерегулярно с изменением частоты. Например,
на Рис.
5‑3 видно, что при
частоте 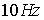 возникает
дополнительный пик амплитуды в районе возникает
дополнительный пик амплитуды в районе 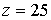 , не связанный с дефектом; фаза оказывается приподнятой. , не связанный с дефектом; фаза оказывается приподнятой.
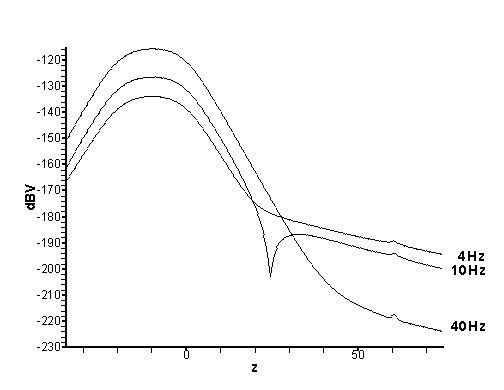
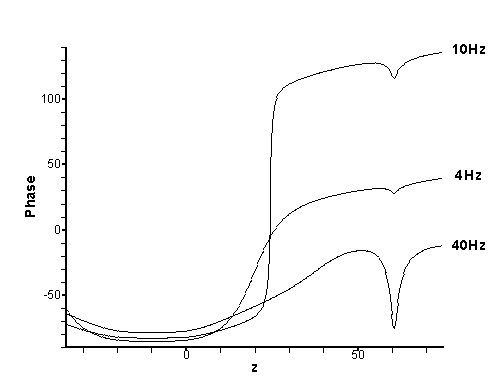
Вторая
серия расчетов является тестом для проверки правильности работы оператора
торцевых граничных условий. Графики решений, полученных для трех различных
вычислительных областей – большой ( ), средней ( ), средней ( ) и маленькой ( ) и маленькой (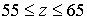 ) – изображены на Рис. 5‑4. Для наглядности области помечены прямоугольниками. Частота ) – изображены на Рис. 5‑4. Для наглядности области помечены прямоугольниками. Частота
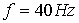 . Все три решения совпадают в маленькой области вплоть до
четвертого знака. Это небольшое различие вызвано применением упрощенного
(«дешевого») подхода к вычислению правой части . Все три решения совпадают в маленькой области вплоть до
четвертого знака. Это небольшое различие вызвано применением упрощенного
(«дешевого») подхода к вычислению правой части 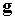 в операторе граничного
условия, см. замечание в конце параграфа 3.3. в операторе граничного
условия, см. замечание в конце параграфа 3.3.

Наконец,
третья серия расчетов демонстрирует ожидаемую точность алгоритма. Здесь мы уже задействуем
режим одновременного расчета решений с различным положением возбуждающей
катушки. Для каждого нового решения катушка сдвигается вправо на один шаг сетки
по 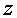 . В качестве грубой сетки выбраны параметры . В качестве грубой сетки выбраны параметры 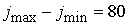 , , 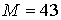 , , 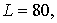 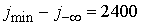 . Частота . Частота 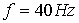 . Вычислительная область расположена в пределах . Вычислительная область расположена в пределах 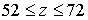 . Начальное положение
возбуждающей катушки . Начальное положение
возбуждающей катушки 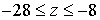 . На графиках мы
рисуем амплитуду и фазу каждого решения, взятого в одной точке с координатой . На графиках мы
рисуем амплитуду и фазу каждого решения, взятого в одной точке с координатой 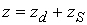 , где , где 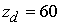 – левый край дефекта, – левый край дефекта, 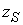 – текущая координата правого края возбуждающей катушки. – текущая координата правого края возбуждающей катушки.
Расчеты
проведены на трех сетках: грубой, средней и мелкой. Средняя сетка имеет
удвоенное значение по каждому числу интервалов, т.е. 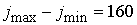 , , 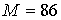 , , 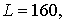 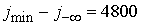 . Для мелкой сетки эти
параметры еще раз удваиваются. . Для мелкой сетки эти
параметры еще раз удваиваются.
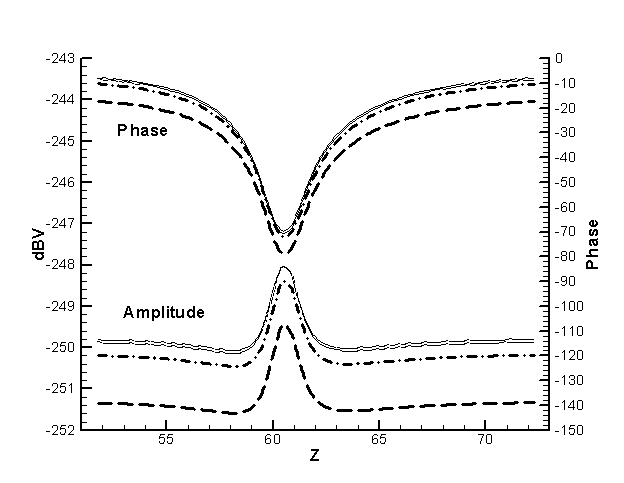
Так
как ожидаемая точность имеет второй порядок по шагу сетки, мы применяем для
проверки экстраполяцию по Ричардсону:
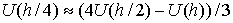 , ,
где через 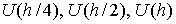 обозначены решения,
полученные с шагами обозначены решения,
полученные с шагами 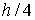 , , 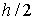 и и 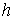 соответственно. На Рис. 5‑5 сплошными линиями изображены решения,
полученные на мелкой сетке и экстраполяцией. Линии практически сливаются, что
подтверждает второй порядок точности. соответственно. На Рис. 5‑5 сплошными линиями изображены решения,
полученные на мелкой сетке и экстраполяцией. Линии практически сливаются, что
подтверждает второй порядок точности.
В заключение
отметим, что время решения описанных примеров не превосходит одной минуты на
персональном компьютере с тактовой частотой два гигагерца.
Список литературы
[1]. Тамм И.Е. Основы теории электричества. – М.: Наука,
1966, 624 с.
[1]. Зуева Н.М., Михайлова М.С.,
Рябенький В.С.
Перенос граничных условий из бесконечности на искусственную границу для
разностного уравнения Лапласа. – М., 1991, – (Препр. / ИПМ им. М.В. Келдыша АН
СССР, №110).
[1].
Брушлинский К.В., Рябенький В.С.,
Тузова Н.Б. Перенос граничного
условия через вакуум в осесимметричных задачах // ЖВМ и МФ. – 1992. – № 12. –
С. 1929–1939.
Список литературы
[1]. Тамм И.Е. Основы теории электричества. – М.: Наука,
1966, 624 с.
[2]. Зуева Н.М., Михайлова М.С.,
Рябенький В.С.
Перенос граничных условий из бесконечности на искусственную границу для
разностного уравнения Лапласа. – М., 1991, – (Препр. / ИПМ им. М.В. Келдыша АН
СССР, №110).
[3].
Брушлинский К.В., Рябенький В.С.,
Тузова Н.Б. Перенос граничного
условия через вакуум в осесимметричных задачах // ЖВМ и МФ. – 1992. – № 12. –
С. 1929–1939.
|