О несжимаемом погранслое на игле
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Глава II |
|
ОБТЕКАНИЕ ИГЛЫ ВЯЗКОЙ НЕСЖИМАЕМОЙ |
|
ЖИДКОСТЬЮ |
|
§ 1. Преобразование системы уравнений Навье-Стокса |
Рассмотрим систему уравнений Навье-Стокса [1], описывающую стационарный
поток вязкой несжимаемой жидкости в пространстве
|
|
| (1.1) |
|
Здесь x, y и z
- прямоугольные координаты; u, v и w - компоненты вектора
скорости потока соответственно по осям x, y и z; p
- давление; r - плотность; n - кинематический коэффициент вязкости; r, n =
const.
После перехода к
цилиндрическим координатам система приобретает вид [1]
|
|
| (1.2) |
|
где ∇2
[( def) || ( = )]
∂
2/
∂
r2+(1/r)
∂
/
∂
r+(1/r2)
∂
2/
∂
e2+
∂
2/
∂
x2; x, r и e - цилиндрические координаты y=rsine, z=rcose; Vx, Vr и Ve - компоненты вектора скорости потока. Для осесимметричного
потока можно исключить из системы угловую компоненту e и соответствующую компоненту вектора скорости потока Ve. Тогда система (1.2) принимает вид
|
| (1.3) |
|
Используя третье уравнение,
введем функцию тока y по
формулам
| (1.4) |
Тогда система (1.3) принимает
вид
|
| (1.5) |
|
|
§ 2. Первые приближения решения в
бесконечности
Рассмотрим теперь обтекание
полубесконечной иглы, занимающей полупрямую {x,y,z: x
≥
0, y=z=0 },
стационарным потоком вязкой несжимаемой жидкости в положительном направлении
оси x. Такое обтекание описывается системой уравнений Навье-Стокса (1.1)
с граничными условиями
| (2.1) |
В цилиндрических координатах
это обтекание описывается системой (1.3) с граничными условиями
| (2.2) |
Согласно (1.4)
осесимметричное обтекание также описывается системой (1.5) с граничными
условиями в бесконечности и на игле
| (2.3) |
| (2.4) |
Заменой координат y = 2n2u∞-1[(y)\tilde], x=2nu∞-1[(x)\tilde],
r=2nu∞-1[(r)\tilde]
эта задача сводится к задаче с u∞ = 2, n =
1, которая рассматривается ниже.
Лемма 1. Граничные условия
|
(2.5) |
имеют место для x
∈
(-
∞
,+∞).
Доказательство. Заметим, что функции y = r2, p=p0
аннулируют каждый из членов в уравнениях (1.5). Следовательно, функции (2.5)
являются решением любой укороченной системы для системы (1.5). Поэтому при x
< 0 и r
→
∞
выражения (2.5) являются граничными условиями, которые продолжают граничные
условия (2.3). Более того, они продолжаются и для x > 0, r
→
∞. Лемма доказана.
Лемма 2. Для системы (1.5) укороченная система,
соответствующая пограничному слою на игле и граничным условиям (2.4),
(2.5), единственна. Она имеет нормальный вектор P=(2,1,2,0) и есть
|
| (2.6) |
| (2.7) |
а автомодельные координаты
x, h(x) и p(x) для задачи
(2.4)-(2.7) суть
|
(2.8) |
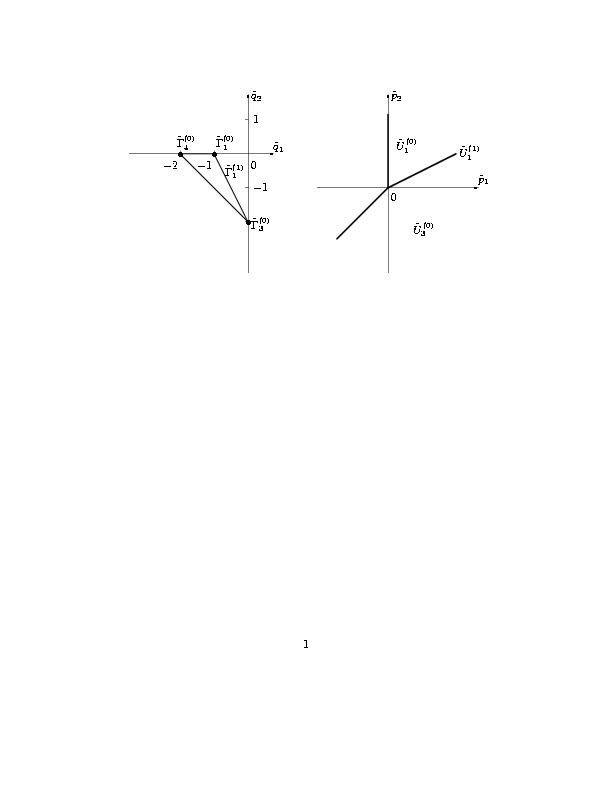
|
Рис. 2. Проекции носителей уравнений системы (1.5) (a) |
|
и нормальные конуса проекций (б). |
Доказательство. Носители уравнений системы (1.5) представлены в
таблице 1. Ее первый столбец содержит номер i уравнения fi=0,
второй столбец содержит номер k точки Qk носителя,
третий столбец содержит сами точки Qk носителей S(fi).
В уравнениях системы (1.5) в квадратные скобки объединены члены с одним и тем
же векторным показателем степени.
|
Здесь Dk[( def) || ( = )] б [(P)\tilde],[(Q)\tilde]k с . |
|
i |
k |
Qk |
1 проекция: [(P)\tilde]=(2,1) |
2 проекция: [(P)\tilde]=(1,1) |
||||
|
|
|
|
[(Q)\tilde]k |
Dk |
T |
[(Q)\tilde]k |
Dk |
T |
|
1 |
1 |
-1, -4, 2, 0 |
-1, 0 |
-2 |
+ |
3, -4 |
-1 |
+ |
|
|
2 |
-1, 0, 0, 1 |
-1, 0 |
-2 |
+ |
-1, 0 |
-1 |
+ |
|
|
3 |
0, -4, 1, 0 |
0, -2 |
-2 |
+ |
2, -4 |
-2 |
|
|
|
4 |
-2, -2, 1, 0 |
-2, 0 |
-4 |
|
0, -2 |
-2 |
|
|
2 |
5 |
-2, -3, 2, 0 |
-2, 1 |
-3 |
|
2, -3 |
-1 |
+ |
|
|
6 |
0, -1, 0, 1 |
0, -1 |
-1 |
+ |
0, -1 |
-1 |
+ |
|
|
7 |
-1, -3, 1, 0 |
-1, -1 |
-3 |
|
1, -3 |
-2 |
|
|
|
8 |
-3, -1, 1, 0 |
-3, 1 |
-5 |
|
-1, -1 |
-2 |
|
Из граничного условия (2.5)
видно, что при r→+∞ имеются граничные условия вида (1.7) главы I
|
|
Каждому из них соответствует
носитель, состоящий из двух точек. А именно: S(f3) состоит из
точек Q9=(0,0,1,0) и Q10=(0,2,0,0); S(f4)
состоит из точек Q11=(0,0,0,1) и Q12=(0,0,0,0).
Согласно теореме 2 главы I вектор P=(p1,p2,p3,p4)
должен удовлетворять условиям
б
Q9,Pс = бQ10,Pс и бQ11,Pс = бQ12,Pс, т.е.
|
(2.9) |
В обозначениях главы I здесь m
′
=l=2 и R′3=(0,2), R′4=(0,0).
По теореме 2 главы I, согласно полученным на вектор P условиям (2.9),
вектора Qk можно спроецировать на плоскость [(Q)\tilde]=([(q)\tilde]1,[(q)\tilde]2)
по формулам [(q)\tilde]1=q1, [(q)\tilde]2=q2+2q3,
а значением q4 мы пренебрегаем. Четвертый столбец таблицы 1
содержит проекции [(Q)\tilde]k = (q1,q2+2q3)
векторов Qk. Проекции [S\tilde] (f1) и
[S\tilde] (f2) носителей уравнений системы (1.5), их выпуклые
оболочки [(G)\tilde]1, [(G)\tilde]2 и их нормальные конуса
представлены на рис. 2.
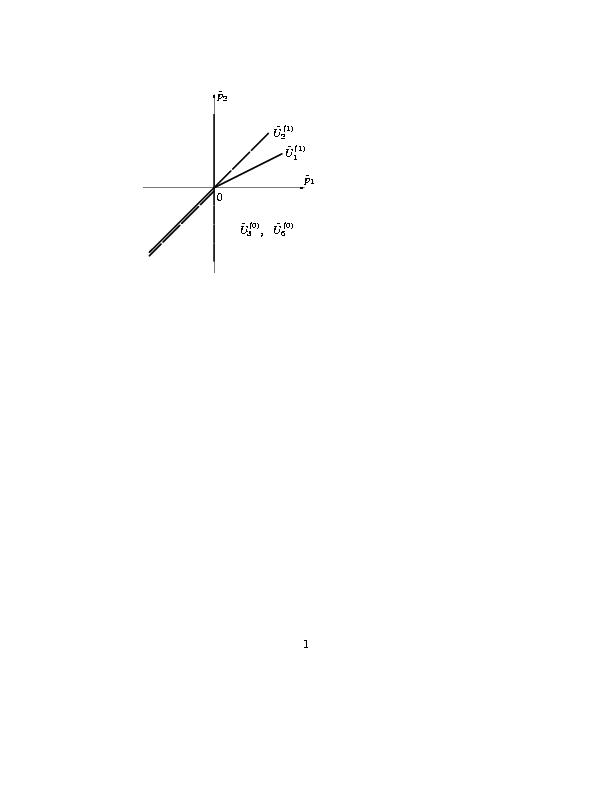
|
Рис. 3. Совмещенные нормальные конуса проекций |
|
носителей уравнений системы (1.5). |
Игла описывается как x
≥
0, r=0. Вблизи
иглы, при x→+∞ и r→ 0, имеем p1 > 0, p2
< 0. Следовательно, игле соответствует IV квадрант плоскости (p1,p2).
Граничные условия (2.5) при x→+∞
и r→+∞ означают, что p1,p2
> 0, т.е. им соответствуют точки из I квадранта плоскости (p1,p2).
Нас интересуют такие грани проекций [(G)\tilde]1 и [(G)\tilde]2, расширенный нормальный конус которых содержит как
IV квадрант, так и точки из I квадранта плоскости (p1,p2).
Совмещение рисунков нормальных конусов проекций показано на рис. 3. Из него
видно, что IV квадрант и точки из I квадранта содержаться только в расширенном
нормальном конусе системы
∨
UJD=
∨
U1(1)
∩
∨
U3(0). Направляющий вектор
нормального конуса [U\tilde]1(1) это вектор [(P)\tilde]=(2,1).
По вектору [(P)\tilde]=(p1,p2)
восстанавливаем вектор P=(p1, p2,p3,p4)
согласно равенствам (2.9) и получаем в исходных координатах (p1,
p2,p3,p4) вектор P=(2,1,2,0).
Полученному вектору P соответствуют грани носителей S(f1)
и S(f2), содержащие точки Q1, Q2,
Q3, Q6. Этим точкам соответствует
укороченная система (2.6), (2.7).
Пятый столбец таблицы 1
содержит значения скалярных произведений Dk=б[(P)\tilde],[(Q)\tilde]kс = бP, Qkс для [(P)\tilde]=(2,1), P=(2,1,2,0). В
шестом столбце (T) знак "+" отмечает
максимальные значения б[(P)\tilde],[(Qk)\tilde]с для данного i, соответствующие им члены суммы fi
включены в укорочение [^(f)]i1(di)
в (2.6), (2.7).
В обозначениях § 1 главы
I имеем l=2 и полученный вектор P=(P′,P"), т.е. P′=(2,1). Кроме того, вектор B1′=(-1,2)
составляет базис в пространстве векторов Q′=(q1,q2),
удовлетворяющих условию бP′,Q
′
с = 0. Тогда согласно теореме 3 главы I, T3′=(1,0), T4′=(0,0) и автомодельные координаты x, h, p имеют вид
|
что соответствует (2.8).
Лемма 2 доказана.
§ 3. Автомодельные решения задачи
(2.4)-(2.7)
В автомодельных координатах
(2.8) система уравнений (2.6), (2.7) принимает вид
|
(3.1) |
|
(3.2) |
где ′=d/dx. Из уравнения (3.2) следует, что
|
следовательно, из уравнения
(3.1) получаем
|
(3.3) |
Для полученной системы (3.1),
(3.2) граничные условия (2.4), (2.5) в автомодельных координатах (2.8) имеют
вид
|
(3.4) |
|
(3.5) |
Из (3.2) и (3.4) следует, что
|
Таким образом, получили
уравнение (3.3) с граничными условиями (3.5) и
|
(3.6) |
Итак, доказана
Лемма 3. В автомодельных координатах (2.8) задача
(2.6), (2.7), (2.4), (2.5) сводится к задаче (3.2)-(3.5), которая,
после исключения p, сводится к задаче (3.3), (3.5), (3.6).
Лемма 4. Уравнение (3.3) не имеет решений,
удовлетворяющих граничному условию (3.5).
Доказательство. Носитель уравнения (3.3) состоит из двух точек Q1=(-2,2) и Q2=(-2,1). Носитель, его выпуклая оболочка и нормальные
конуса ее граней показаны на рис. 4. Граничное условие (3.5) накладывается при x
→
0, т.е. p1
≤
0. Из граничного условия (3.5) видно, что ищутся
решения h→ 0
при x
→
0, т.е. p2
≤ 0. Запишем h и x в виде (1.2) главы I, тогда x = b1tp1, h=b2tp2, т.е. h=b3xp2/p1, где b1,
b2, b3 - постоянные, тогда h′=b4x-1+p2/p1, где b4
- постоянная. По граничному условию (3.5) h
′
→ 0 при x
→
0, т.е. -1+p2/p1 ≤ 0, следовательно, p2 ≤ p1. Таким образом, получен конус
задачи K={p2 ≤ p1 ≤ 0}. Он заштрихован на рис. 4б, из которого видно, что
с конусом задачи пересекается только нормальный конус U2(0),
который соответствует вершине Q2=G2(0).
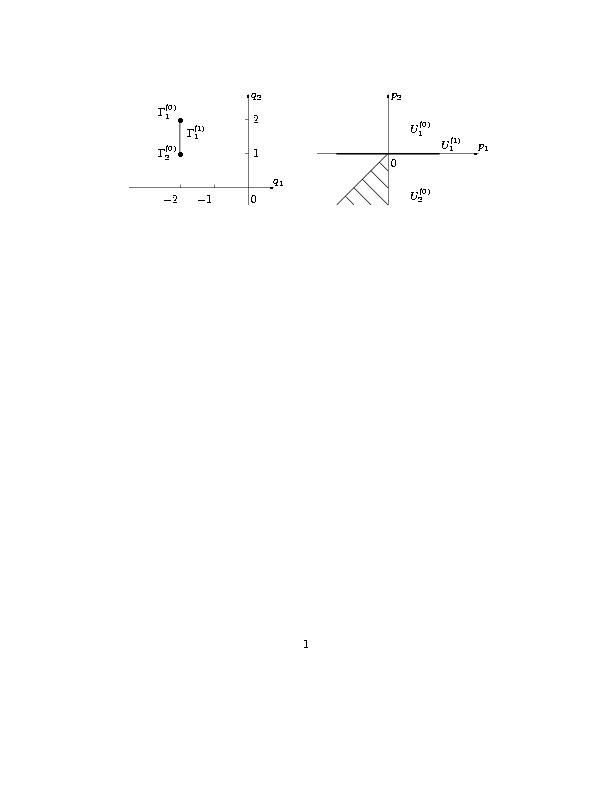
|
Рис. 4. Носитель уравнения (3.3), его выпуклая оболочка (a) |
|
и нормальные конуса ее граней (б). |
Вершине Q2=G2(0) соответствует укороченное уравнение
|
(3.7) |
которое после умножения на x2
становится уравнением Эйлера с характеристическим уравнением
|
его корни l1=0 и l2=1
(кратный корень). Следовательно, все решения уравнения (3.7) имеют вид h=c0+c1x+c2xlnx,
т.е. h′=c1+c2+c2lnx, где c0, c1, c2
- произвольные постоянные. Из условия (3.5) на h′ получаем, что c2=c1=0,
а из условия на h, получаем, что c0=0. Следовательно, h
≡
0. Таким образом,
укороченное уравнение, соответствующее вершине Q2, не имеет
нетривиальных решений, удовлетворяющих граничному условию (3.5). Согласно
теореме 1 главы I, уравнение (3.3) не имеет нетривиальных асимптотик решений
вблизи иглы.
Следовательно, уравнение
(3.3) не имеет нетривиальных решений, удовлетворяющих граничному условию (3.5).
Лемма доказана.
Итак, задача (2.4)-(2.7) не
имеет автомодельного решения. Этот результат имеется в статье Лайтхила и
Глауэрта [13] (см. также [10,§ 35]).
§ 4. Неавтомодельные решения задачи
(2.4)-(2.7)
В уравнениях (2.6), (2.7)
делаем замену переменных
|
(4.1) |
т.е. в качестве независимых
переменных берем x и x.
Тогда
|
| (4.2) |
| (4.3) |
Граничные условия (2.4),
(2.5) принимают вид
|
(4.4) |
|
(4.5) |
Лемма 5. Система уравнений (4.2), (4.3) не имеет
решений, удовлетворяющих граничным условиям (4.4), (4.5).
Доказательство. Из граничного условия (4.5) имеем p=p0,
т.е.
∂
p/
∂
x=0 при x
→∞
. Из уравнения (4.3) следует, что
∂
p/
∂
x = 0, т.е. давление p не зависит от x. Следовательно, свойство
∂
p/
∂
x=0 можно
продолжить на x ∈ (0,∞).
Тогда уравнение (4.2) после сокращения на 4 принимает вид
|
(4.6) |
Носитель уравнения (4.6)
состоит из двух точек Q1=(-1,-2,2) и Q2=(-1,-2,1).
У них совпадает координата q1. Следовательно [5 гл. VI
§ 3] делаем логарифмическое преобразование t=lnx. Тогда
|
и уравнение (4.6) принимает
вид
|
(4.7) |
Носитель этого уравнения
состоит из трех точек Q′1=(-1,-2,2),
Q′2=(0,-2,2),
Q′3=(0,-2,1).
У нас x
→
∞,
поэтому t
→
∞,
т.е. p1
≥
0. Из бP,Q′1с = бP,Q′2
с
-p1 следует, что бP,Q′2с > бP,Q′1с. Согласно § 1 главы I, при t
→
∞ первым приближением уравнения (4.7) является
уравнение
|
(4.8) |
При фиксированном x
≥
0 из уравнения (4.8) и граничного условия (4.4)
следуют уравнение (3.3) с граничным условием (3.5). По лемме 4 уравнение (3.3)
не имеет решений, удовлетворяющих граничному условию прилипания на игле (3.5).
Следовательно, уравнение (4.8) не имеет решений, удовлетворяющих граничное
условие (4.4). Согласно теореме 1 главы I, уравнение (4.7) также не имеет таких
решений. Это же относится к уравнению (4.6) и системе (4.2), (4.3). Лемма
доказана.
Итак, из лемм 4 и 5 следует
Теорема 1. Задача (2.4)-(2.7) не имеет решений.
§ 5. Двухслойные автомодельные решения
Рассмотрим возможность
существования двуслойного решения системы (1.5), удовлетворяющего граничным
условиям (2.4), (2.5). Граничные условия на бесконечности (2.5) дают проекцию
носителей системы (1.5), описанную в доказательстве леммы 2 и показанную на
рис. 2. Но в этом случае для получения укороченной системы,
соответствующей внешнему слою, рассматриваем расширенный конус системы
∨
UJD=
∨
U1(1)∩
∨
U2(1) (рис. 3).
Направляющий вектор нормального конуса [U\tilde]2(1) это
вектор [(P)\tilde]=(1,1). Согласно условиям (2.9), восстанавливаем по
нему вектор P=(1,1,2,0). Полученному вектору P соответствуют
грани носителей S(f1) и S(f2), содержащие
точки: Q1, Q2, Q5, Q6.
Этим точкам соответствует укороченная система
| (5.1) |
|
В обозначениях § 1 главы
I имеем P=(P′,P"),
т.е. P′=(1,1);
B′1=(-2,2).
Согласно теореме 3 главы I, T′3=(2,0), T′4=(0,0) и
автомодельные координаты для задачи (5.1), (2.4), (2.5) имеют вид
|
(5.2) |
В этих автомодельных
координатах система (5.1) является системой обыкновенных дифференциальных
уравнений
| (5.3) |
| (5.4) |
Из (5.3) следует равенство
|
Подставляя его в уравнение
(5.4), получаем уравнение
|
(5.5) |
Граничные условия на
бесконечности (2.5) в автомодельных координатах (5.2) принимают вид
|
(5.6) |
|
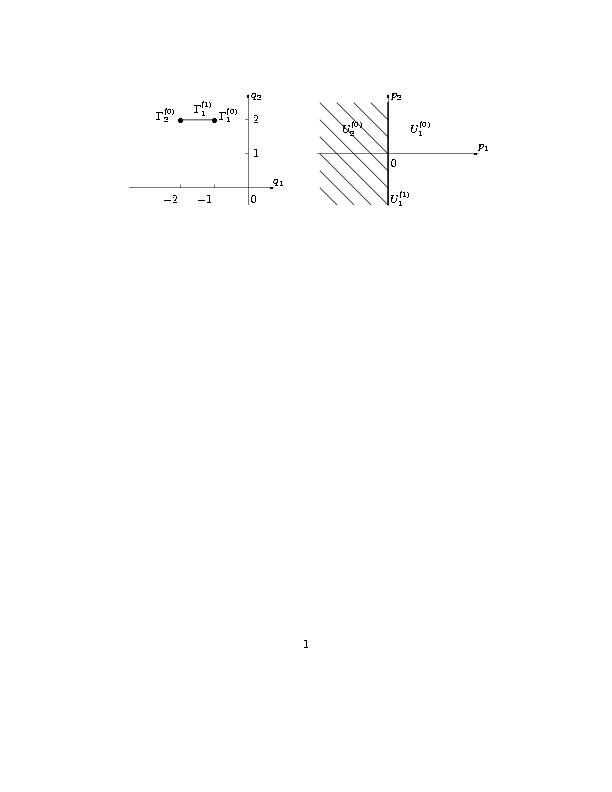
Рис. 5. Носитель уравнения (5.5), его выпуклая оболочка (a) |
|
и нормальные конуса ее граней (б). |
Рассмотрим асимптотики
решений уравнения (5.5) при h
→
0, т.е. при приближении к внутреннему слою. Носитель уравнения (5.5) состоит из
двух точек Q1=(-1,2), Q2=(-2,2), их выпуклая оболочка - это горизонтальный отрезок, их
соединяющий. Носитель, выпуклая оболочка и нормальные конуса ее граней показаны
на рис. 5. Нас интересуют решения при h
→
0, т.е. p1 ≤ 0. В эту полуплоскость попадают нормальные конуса U2(0)
и U1(1). Нормальному конусу U2(0)
соответствует вершина Q2=G2(0), которой соответствует укороченное уравнение [^(j)]2(0)[( def) || ( = )] -2gg"=0. Все его решения имеют вид g=b0+b1h, где b0,b1 -
произвольные постоянные. Это значит, что при h
→
0 уравнение (5.5) имеет асимптотики решений
|
(5.9) |
Согласно (5.2), в исходных
координатах, во внешнем слое, асимптотики функции тока при h = r2/x2→ 0 имеют вид
|
Нормальному конусу U1(1)
соответствует все уравнение (5.5). Методами § 2 легко показать, что
решения этого уравнения не имеют асимптотик при h
→
0.
Следовательно, для
внутреннего слоя получаем два варианта граничных условий на бесконечности
|
(5.10), |
|
(5.11). |
Граничные условия (5.10)
аналогичны условиям (2.5) и им соответствует проекция носителей системы (1.5),
сделанная в доказательстве леммы 2. Более того, для получения укороченной
системы, соответствующей внутреннему слою, применима лемма 2 и все дальнейшие
вычисления для однослойного решения, сделанные в § 3. Согласно лемме 4 в
этом случае на внутреннем слое нет автомодельного решения, удовлетворяющего
граничным условиям на игле.
|
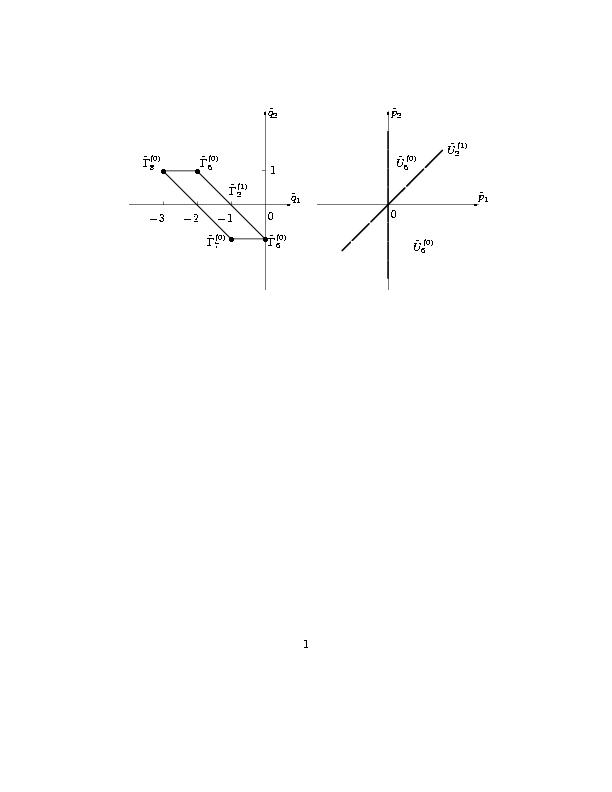
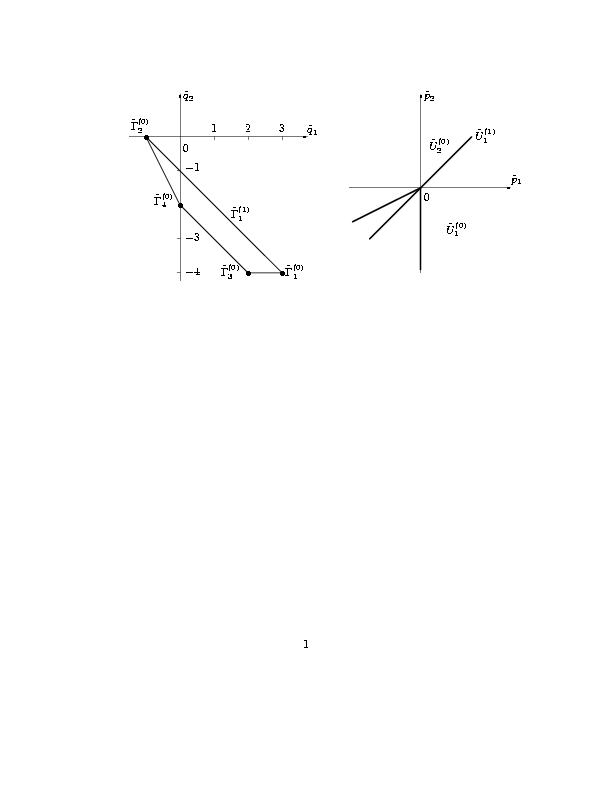
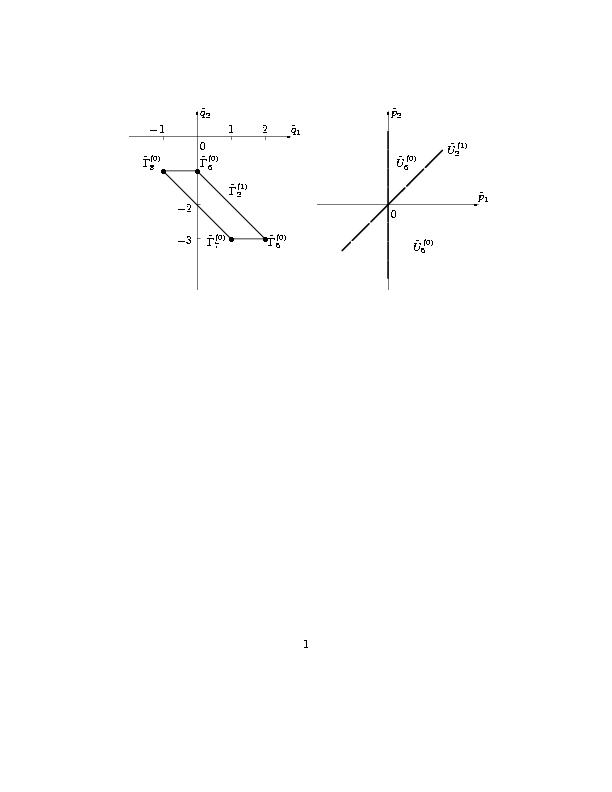
Рис. 6. Проекции носителей уравнений системы (1.5) (a) |
|
и нормальные конуса проекций (б). |
Граничные условия (5.11)
перепишем в виде f3[( def)
|| ( = )] y-c1x2=0, f4[( def) || ( = )] p-p0=0, где p0=const. Этим условиям
соответствуют носители: S(f3) состоит из точек Q13=(0,0,1,0)
и Q14=(2,0,0,0), S(f4) состоит из точек Q11=(0,0,0,1)
и Q12=(0,0,0,0). Согласно теореме 2 главы I вектор P=(p1,p2,p3,p4)
должен удовлетворять условиям бQ13,Pс = бQ14,Pс и бQ11,Pс = бQ12,Pс, т.е.
|
(5.12) |
Согласно этим условиям на
вектор P, вектора Qk можно спроецировать на плоскость
[(Q)\tilde]=([(q)\tilde]1,[(q)\tilde]2)
по формулам [(q)\tilde]1=q1+2q3,
[(q)\tilde]2=q2, а значением q4
мы пренебрегаем. Проекции [(Q)\tilde]k точек Qk
носителей уравнений системы (1.5) содержатся в седьмом столбце таблицы 1.
Проекции носителей, их выпуклые оболочки и нормальные конуса их граней показаны
на рис. 6. Как и в доказательстве леммы 2, игле соответствует IV квадрант плоскости
(p1,p2). Граничному условию (5.11)
соответствуют точки из I квадранта плоскости (p1,p2).
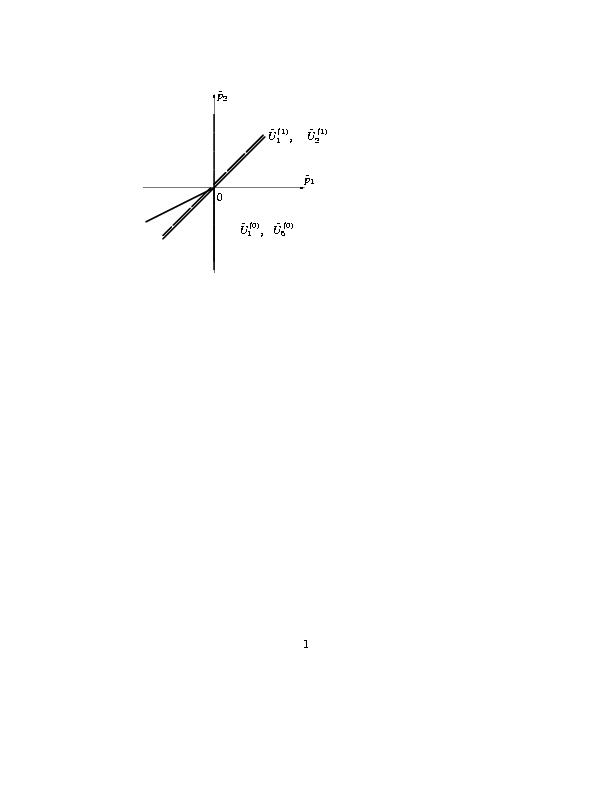
Совмещение рисунков нормальных конусов проекций показано на рис. 7. Из него
видно, что IV квадрант и точки из I квадранта содержаться только в расширенном
нормальном конусе системы
∨
UJD=
∨
U1(1)∩
∨
U2(1). Направляющий вектор
нормального конуса [U\tilde]1(1) это вектор [(P)\tilde]=(1,1).
Согласно условиям (5.12), восстанавливаем по нему вектор P=(1,1,2,0).
Восьмой столбец таблицы 1 содержит значения скалярных произведений Dk=б[(P)\tilde],[(Q)\tilde]kс для [(P)\tilde]=(1,1).
|
Рис. 7. Совмещенные нормальные конуса проекций |
|
носителей уравнений системы (1.5). |
Полученному вектору P
соответствуют грани носителей уравнений системы (1.5) S(f1) и
S(f2), содержащие точки: Q1, Q2,
Q5, Q6. Этим точкам соответствует
укороченная система (5.1) и автомодельные координаты (5.2). В девятом столбце (T) таблицы 1 знак "+" отмечает максимальные
значения б[(P)\tilde],[(Qk)\tilde]с для данного i, соответствующие им члены суммы fi
включены в укорочение [^(f)]i1(di)
в (5.1).
В автомодельных координатах
(5.2) граничное условие (2.4) принимает вид
|
(5.13) |
Для системы (5.1), как уже
известно, решения при h
→
0
имеют асимптотики (5.9). Они удовлетворяют условию (5.13) только при b0=b1=0,
т.е. g ≡ 0.
Следовательно, на внутреннем слое задача (1.5), (2.5), (5.10) не имеет
автомодельных решений удовлетворяющего всем граничным условиям.
Итак, доказана
Лемма 6. Задача (1.5), (2.4), (2.5) не имеет
двуслойных автомодельных решений.
§ 6. Двухслойные неавтомодельные решения
В результате замены
переменных
|
(6.1) |
система (5.1) принимает вид
|
| (6.2) |
|
|
| (6.3) |
Граничные условия (2.4),
(2.5) принимают вид
|
(6.4) |
|
(6.5) |
У слагаемых в уравнениях
(6.2) и (6.3) векторные показатели степени Q=(q1, q2,
q3, q4) имеют q1=-1 и q1=0 соответственно. Делаем
логарифмическое преобразование
|
(6.6) |
тогда
∂
g/
∂
x=x-1
∂
g/
∂
t. Получим
| (6.7) |
|
|
| (6.8) |
Носители уравнений (6.7),
(6.8) состоят из следующих точек
|
|
|
Поскольку t=lnx,
то t
→
∞ при стремлении x
к бесконечности, т.е. p1 > 0. Следовательно, бQ′1,Pс > бQ′2,Pс и бQ′4,Pс > бQ′3,Pс. Во втором уравнении бQ′5,Pс > бQ′6,Pс > бQ′7,Pс. Согласно § 1 главы I, при h
→
0, x
→
∞ первым приближением системы уравнений (6.7), (6.8)
является укороченная система, которая является в точности системой (5.3),
(5.4). При h
→
0 ее решения суть g=b0(t), g=b1(t)h, где b0(t), b1(t)
- многочлены от t, т.е. в исходных координатах асимптотики функции тока
при h = r2/x2→ 0 имеют вид
|
(6.9) |
b0(lnx),
b1(lnx) - многочлены от lnx. Носители
полученных асимптотик в точности совпадают с носителями асимптотик (5.10),
(5.11). Следовательно, при выделении укорочений системы (1.5), соответствующих
двум вариантам граничных условий (6.9) все построения и вычисления совпадают с
построениями и вычислениями, сделанными для граничных условий (5.10), (5.11).
Граничному условию (5.10)
соответствует укороченная система (2.6), (2.7). После замены (4.1), она
становится системой (4.2), (4.3), а граничное условие на игле принимает вид
(4.4). Согласно лемме 5 система (4.2), (4.3) не имеет решений, удовлетворяющих
граничному условию (4.4). Следовательно, в случае граничного условия (5.10), на
внутреннем слое нет неавтомодельных решений, удовлетворяющих граничному условию
на игле.
Граничному условию (5.11)
соответствует укороченная система уравнений (5.1). После замен (6.2), (6.6),
она переходит в систему уравнений (6.7), (6.8). При h
→
0, x
→
∞ первым приближением системы уравнений (6.7), (6.8)
является укороченная система, из которой при фиксированном x
≥
0 следует система (5.3), (5.4). При этом из
граничного условия (6.4) следует условие (5.13). При h
→
0 решения системы (5.3), (5.4) суть (5.9). Они
удовлетворяют условию (5.13) только при b0=b1=0,
т.е. g ≡ 0.
Следовательно, на внутреннем слое задача (1.5), (5.11) не имеет
неавтомодельного решения, удовлетворяющего граничным условиям на игле (2.5).
Итак, доказана
Лемма 7. Задача (1.5), (2.4), (2.5) не имеет
двуслойных неавтомодельных решений.
Из лемм 6 и 7 следует
Теорема 2. Задача (1.5), (2.4), (2.5) не имеет
двуслойных решений.
|
ЛИТЕРАТУРА |
[1] Л.Г.
Лойцянский. Механика жидкости и газа. М.: Наука, 1978.
[2] М.М.
Васильев. Об осесимметричных течениях вязкого теплопроводного газа. Препринт N
11, М.: ИПМ, 2001. 13 с.
[3] M.M.
Vasiliev. Obtaining the Self-Similar Asymptotics of Solutions to the
Navier-Stokes Equations by Power Geometry // Progress in Analysis. Proceedings
of the 3rd International ISAAC Congress (Eds. H. G. Begehr,
R. P. Gilbert, M. W. Wong), Singapore: World Scientific,
2003, vol. 1, p. 93-101.
[4] M.M.
Vasiliev. Asymptotics of some viscose, heat conducting gas flows // Proceedings
of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of
Western Australia, 2002, p. 251-256.
[5] А.Д.
Брюно. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.:
Физматлит, 1998.
[6] А.Д.
Брюно. Автомодельные решения и степенная геометрия // Успехи мат. наук, 2000,
т. 55, вып. 1, с. 3-44.
[7] А.Д.
Брюно. Степенные разложения решений системы алгебраических и дифференциальных
уравнений // ДАН, 2001, т. 380, N 3, с. 298-304.
[8] Т.В.
Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью.
Препринт N 36, М.: ИПМ, 2002. 21 с.
[9] А.Д.
Брюно. Степенные разложения решений одного алгебраического или
дифференциального уравнения // ДАН, 2001, т. 380, N 2, с. 155-159.
[10] Л.Г.
Лойцянский. Ламинарный пограничный слой. М.: Физматлит, 1962.
[11] L.
Prandtl. Über Flüssigkeitsbewegung bei sehr kleiner Reibung //
Verhandlungen des III. Internat Math.-Kongr., Heidelberg, 1904. Leipzig:
Teubner 1905. S. 484-491.
[12] H.
Blasius. Grenzschichten in Flüssigkeiten mit kleiner Reibung // Zeit.
für Math. und Phys. 1908. V. 56. P. 1-37.
[13] M.B.
Glauert, M.J. Lighthill. The axisymmetric boundary layer on a long thin
cylinder // Proc. Roy. Soc., ser. A, 1955, 230, no. 1181, p. 188-203.
[14] А.Д.
Брюно. Асимптотики и разложения решений обыкновенного дифференциального
уравнения. Препринт N 9, М.: ИПМ, 2003. 39 с.
[15] А.Д.
Брюно, Т.В. Шадрина. Об осесимметричном обтекании иглы вязкой несжимаемой
жидкостью // ДАН, 2002, т. 387, N 5, c. 589-595.
[16] T.V.
Shadrina. The Axially Symmetric Boundary Layer around a Needle // Proceedings
of BAIL 2002 (Eds. S. Wang and N. Fowkes), Perth: University of
Western Australia, 2002, p. 213-220.
[17] А.Д.
Брюно. Степенные асимптотики решений обыкновенного дифференциального уравнения
// ДАН, 2003, т. 392, N 3, с. 295-300.
[18] А.Д.
Брюно. Степенно-логарифмические разложения решений обыкновенного
дифференциального уравнения // ДАН, 2003, т. 392, N 4, с. 439-444.
[19] А.Д.
Брюно. Нестепенные асимптотики решений обыкновенного дифференциального
уравнения // ДАН, 2003, т. 392, N 5, с. 586-591.
[20] А.Д.
Брюно. Асимптотики и разложения решений обыкновенного дифференциального
уравнения // УМН, 2004, т. 59, N 3, с. 31-80.
[21] А.Д.
Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле. Препринт N 64,
М.: ИПМ, 2003. 32 с.
[22] А.Д.
Брюно, Т.В. Шадрина. Осесимметричный пограничный слой на игле // ДАН, 2004,
т. 394, N 3, с. 298-304.
[23] S.
Goldstein. On the two-dimensional steady flow of a viscous fluid behind a solid
body // Proceedings Royal Soc. London A 142 (1933), 545-562.
[24] K.
Stewartson. On asymptotic expansions in the theory of boundary layers // J.
Math. and Phys., 36 (1957), 173-191.
[25] A.I.
Van de Vooren, D. Dijkstra. The Navier-Stokes solution for laminar flow past a
semi-infinite flat plate // J. Engineer. Math., vol. 4, no. 1 (1970), 9-27.
[26] R.I.
MacLachlan. The boundary layer on a finite flat plate // Phys Fluids A, v.3,
no.2 (1991), 341-348.
[27] R.A.
Seban, R. Bond. Skin-friction and heat-transfer characteristics of a laminar
boundary layer on a cylinder in axial incompressible flow // J. Aeronaut. Sci.
18 (1951), 671-675.
[28] H.R.
Kelly. A note on the laminar boundary layer on a circular cylinder in axial
incompressible flow // J. Aeronaut. Sci. 21 (1954), 634.
[29] Lord
Rayleigh. On the motion of solid bodies through viscous liquid // Phil. Mag.
(6) 21, (1911), 697-711.
[30] K.
Pohlhausen. Zur näherungsweisen Integration der Differentialgleichung der
laminaren Grenzschicht // Ebenda [Zs. f. angew. Math. u. Mech. 1 (1921)],
252-268.
[31] K.
Stewartson. The asymptotic boundary layer on a circular cylinder in axial
incompressible flow // Quarterly J. Mech and Appl. Math 13 (1955), 113-122.
[32] Шадрина
Т.В. Пограничный слой при осесимметричном обтекании иглы // Дифференциальные
уравнения, 2002, т. 38, N 6, с.853-854.
[33] Шадрина
Т.В. Об осесимметричном обтекании иглы вязкой несжимаемой жидкостью. // XXVIII
Гагаринские чтения. Тезисы докладов. М: МАТИ, 2002, т.2, с. 98-99.
[34] Bruno
A.D., Shadrina T.V. The axially symmetric boundary layer around a needle //
International Conference on Differential and Functional Differential Equations.
Abstracts. M.: MAI, 2002, p.18-19.
[35] Bruno
A.D., Shadrina T.V. The axially symmetric boundary layer around a needle // International
Conference "Navier-Stokes Equations and Related Topics" (NSEC8).
Abstracts. S.Petersburg: Euler Inst., 2002, p.18-19.
[36] Шадрина
Т.В. Осесимметричный пограничный слой на игле // XIV Всероссийская конференция
"Теоретические основы и конструирование численных алгоритмов для решения
задач математической физики". Тезисы докладов. Дюрсо, с.167-168.
File translated from TEX
by TTH, version 3.40.
On 17 May 2005, 16:55.