Аннотация
В работе найдены
установившиеся течения полностью ионизованной
несжимаемой вязкой электропроводной
и квазинейтральной плазмы в цилиндрической трубе и слое между двумя
коаксиальными цилиндрами, Полученные решения обобщают известные из
гидродинамики течения Пуазейля и Куэтта. Показано, что взаимодействие
электронов и ионов ведет к появлению трёх критических значений полного тока,
при переходе через которые происходит перестройка эпюры гидродинамической скорости, что приводит к появлению
пристеночных течений и встречных потоков плазмы в трубе. В частности, параметры установившегося течения
кардинально меняются при изменении
полярности электродов. Вычислены критические значения полного тока, сила
трения электронов и ионов о стенку трубы. Показано, что определяющим параметром
течения является безразмерная комбинация 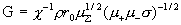 ( (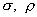 – электропроводность
и плотность плазмы, – электропроводность
и плотность плазмы, 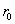 – радиус трубы, – радиус трубы, 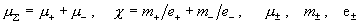 – вязкости, массы и
заряды плазменных компонент). – вязкости, массы и
заряды плазменных компонент).
Abstract
In this work steady – state flows of hydrodynamic plasma in cylindrical channel and in
channel bounded by two coaxial surfaces are obtained. The plasma in channels is taken to be
viscous electrically noncompressible two – component and quasineutral. The flows obtained
are similar to famous Poiseuille’s and Couette’s flows. Modifications of hydrodynamic
velocity’s profile, is shown, are due to ion – electron’s interaction when total current
goes through three critical values. It leads to wall – adjacent flow and countermotion.
As result, stead – state plasma flow’s parameters depend on the sign of total current.
Critical values of total current and ion’s and electron’s wall viscous friction are calculated.
Введение. В работе рассматривается влияние взаимодействия электронов и ионов на
установившееся течение плазмы в бесконечной цилиндрической трубе круглого
сечения и в цилиндрическом слое
(пространстве между двумя бесконечными коаксиальными цилиндрами). Плазма
считается гидродинамической несжимаемой вязкой квазинейтральной и
электропроводной, течения –
цилиндрически симметричными. Найденные решения являются аналогами известных из
гидродинамики вязкой несжимаемой жидкости течений Пуазейля и Куэтта.
Характер установившегося течения
вязкой несжимаемой жидкости по круглой бесконечной трубе в предположении цилиндрической симметрии всех
параметров течения за исключением давления был исследован Пуазейлем (J.L.M.Poiseuille, 1840г.), который получил
формулу для распределения скорости 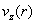 по радиусу по радиусу 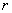 (ось (ось 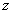 направлена вдоль
трубы, направлена вдоль
трубы, 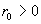 – радиус трубы): – радиус трубы):
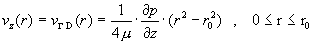 , ,
(1)
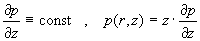 , ,
где 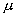 – коэффициент
вязкости жидкости, – коэффициент
вязкости жидкости, 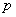 – давление, и
считалось – давление, и
считалось 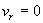 , , 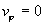 . .
В случае вязкой несжимаемой
электропроводной МГД – плазмы в предположении цилиндрической симметрии всех
параметров течения за исключением давления характер установившегося течения в
бесконечной круглой трубе радиуса 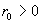 мало чем отличается
от гидродинамического случая, мало чем отличается
от гидродинамического случая,
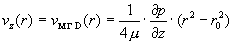 , ,
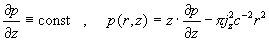 , ,
(2)
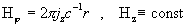 , ,
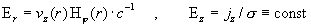 , ,
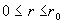 , ,
где 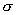 – проводимость плазмы, – проводимость плазмы, 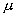 – коэффициент
гидродинамической вязкости, – коэффициент
гидродинамической вязкости, 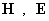 – напряженности
магнитного и электрического полей, – напряженности
магнитного и электрического полей, 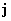 – плотность тока в
плазме. При этом – плотность тока в
плазме. При этом 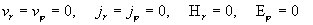 . Как следует из
формулы (2), на гидродинамику плазмы в трубе наличие электромагнитного поля и тока никак не влияет: профиль . Как следует из
формулы (2), на гидродинамику плазмы в трубе наличие электромагнитного поля и тока никак не влияет: профиль 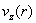 такой же, что и в чисто гидродинамическом случае (1). Этот результат
неправдоподобен и объясняется лишь грубостью МГД – модели плазмы. Естественно предположить, что в присутствии токов
и электромагнитного поля профиль скорости плазмы в трубе начнет
деформироваться. Кроме того, из граничных условий “прилипания” на стенке такой же, что и в чисто гидродинамическом случае (1). Этот результат
неправдоподобен и объясняется лишь грубостью МГД – модели плазмы. Естественно предположить, что в присутствии токов
и электромагнитного поля профиль скорости плазмы в трубе начнет
деформироваться. Кроме того, из граничных условий “прилипания” на стенке
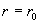 трубы следует равенство трубы следует равенство 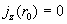 , которое при , которое при 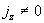 несовместно с решением
(2). Последнее противоречие выражает один из дефектов МГД – теории: в ней
нарушается привычная связь плотности тока с гидродинамическими скоростями
электронов и ионов. Характер ожидаемой деформации профиля несовместно с решением
(2). Последнее противоречие выражает один из дефектов МГД – теории: в ней
нарушается привычная связь плотности тока с гидродинамическими скоростями
электронов и ионов. Характер ожидаемой деформации профиля 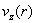 может быть прояснен
учетом взаимодействия электронов и ионов (которое игнорируется МГД – моделью),
что и является одной из целей настоящей работы. может быть прояснен
учетом взаимодействия электронов и ионов (которое игнорируется МГД – моделью),
что и является одной из целей настоящей работы.
Как показано в работе, профиль
скорости 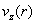 определяется полным
током J,
протекающим через трубу. При этом под определяется полным
током J,
протекающим через трубу. При этом под 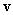 надо понимать
скорость центров масс единичных объемов плазмы надо понимать
скорость центров масс единичных объемов плазмы
 , где , где 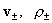 – скорости и плотности
плазменных компонент, – скорости и плотности
плазменных компонент, 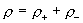 . Пусть движение
электрон – ионной плазмы вызвано постоянным перепадом . Пусть движение
электрон – ионной плазмы вызвано постоянным перепадом 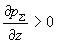 суммарного давления суммарного давления  . Тогда, как показано
ниже (см. § 7), существуют три критические значения полного тока, . Тогда, как показано
ниже (см. § 7), существуют три критические значения полного тока,  , качественно определяющие профиль , качественно определяющие профиль 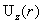 . Если . Если 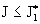 , то профиль , то профиль 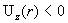 колоколообразный и
расположен выше колоколообразный и
расположен выше 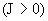 или ниже или ниже 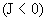 (магнито)
гидродинамической параболы (магнито)
гидродинамической параболы
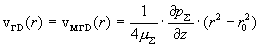 , ,
где 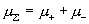 – суммарная вязкость плазмы. Если – суммарная вязкость плазмы. Если 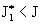 , то возникает
пристеночная область, в которой плазма
течет против перепада давления (а в остальной части трубы она, как и положено,
течет вдоль антиградиента давления , то возникает
пристеночная область, в которой плазма
течет против перепада давления (а в остальной части трубы она, как и положено,
течет вдоль антиградиента давления 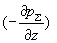 ). С ростом ). С ростом 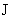 эта область
расширяется и при эта область
расширяется и при 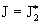 захватывает всю
трубу. Таким образом, при захватывает всю
трубу. Таким образом, при  всюду всюду 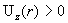 (за исключением,
конечно, стенки трубы, где (за исключением,
конечно, стенки трубы, где 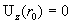 ). Иными словами,
плазма течет не туда, куда толкает ее гидродинамическое давление, а в
противоположную сторону. Однако профиль ). Иными словами,
плазма течет не туда, куда толкает ее гидродинамическое давление, а в
противоположную сторону. Однако профиль 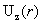 не колоколообразный,
а имеет впадину в окрестности оси
трубы не колоколообразный,
а имеет впадину в окрестности оси
трубы 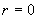 . Эта впадина исчезает с
дальнейшим ростом полного тока . Эта впадина исчезает с
дальнейшим ростом полного тока 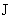 и при и при 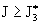 профиль профиль 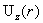 снова становиться колоколообразным, однако теперь колокол
профиля обращен в сторону градиента давления снова становиться колоколообразным, однако теперь колокол
профиля обращен в сторону градиента давления 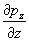 (а не антиградиента,
как было при токах (а не антиградиента,
как было при токах 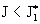 ). В работе получены следующие явные формулы для профиля ). В работе получены следующие явные формулы для профиля 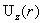
и критических токов 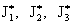 : :
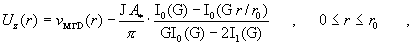
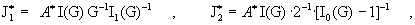
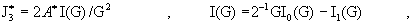
где величины 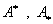 вычисляются по
формулам: вычисляются по
формулам:
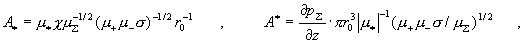
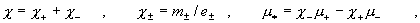
а 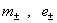 – массы и заряды плазменных компонент, – массы и заряды плазменных компонент, 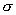 – проводимость
плазмы, – проводимость
плазмы, 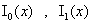 – функции Бесселя мнимого аргумента индексов 0
и 1 соответственно. Наконец, – функции Бесселя мнимого аргумента индексов 0
и 1 соответственно. Наконец, 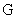 – безразмерный параметр, равный: – безразмерный параметр, равный:
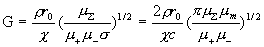 , ,
где 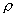 – постоянная плотность плазмы в трубе, – постоянная плотность плазмы в трубе,
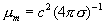 – коэффициент магнитной
вязкости. – коэффициент магнитной
вязкости.
Скорость
центров масс 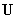 является усредненной
характеристикой течения. Более точную информацию дают скорости компонент
плазмы является усредненной
характеристикой течения. Более точную информацию дают скорости компонент
плазмы 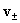 . Профили . Профили 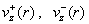 тоже полностью
определяются полным током тоже полностью
определяются полным током  , но деформируются при изменении , но деформируются при изменении 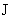 принципиально
различным образом. В зависимости от знака принципиально
различным образом. В зависимости от знака 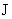 один из профилей для
всех токов выбранного знака остается колоколообразным и располагается ниже
(магнито) гидродинамической параболы один из профилей для
всех токов выбранного знака остается колоколообразным и располагается ниже
(магнито) гидродинамической параболы 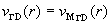 , а другой лежит выше , а другой лежит выше
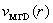 и меняется с
изменением и меняется с
изменением  точно так же как и
профиль точно так же как и
профиль 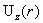 выше. Соответственные
критические значения тока, однако, отличаются от выше. Соответственные
критические значения тока, однако, отличаются от 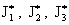 , они найдены в
работе, равно как и выражения для , они найдены в
работе, равно как и выражения для 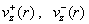 (см.§ 5). При
изменении знака тока (см.§ 5). При
изменении знака тока 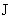 на противоположный
профили на противоположный
профили 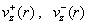 в описанном сценарии
меняются ролями, так что в итоге имеются два набора критических значений
полного тока в описанном сценарии
меняются ролями, так что в итоге имеются два набора критических значений
полного тока 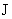 . Это приводит к еще более важному выводу: течение плазмы в трубе реагирует на
изменение полярности электронов, обусловливающее направление тока. . Это приводит к еще более важному выводу: течение плазмы в трубе реагирует на
изменение полярности электронов, обусловливающее направление тока.
Существование установившегося
цилиндрически симметричного течения плазмы по трубе возможно только при
определенных значениях электрического и магнитного полей в вакууме, вне трубы.
Пусть стенка занимает область  ( (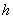 – толщина стенки), а вакуум – область – толщина стенки), а вакуум – область 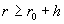 . Как показано в
работе (§ 7), в вакууме поля . Как показано в
работе (§ 7), в вакууме поля 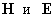 должны удовлетворять
условиям: должны удовлетворять
условиям:
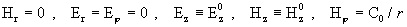 , ,
где 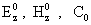 –константы. Константа –константы. Константа
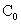 связана с полным
током, протекающим по трубе и стенке формулой: связана с полным
током, протекающим по трубе и стенке формулой:

Таким образом, выбор константы 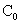 равносилен выбору
полного тока равносилен выбору
полного тока 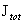 . Константы . Константы  , , 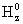 выбираются
произвольно, а выбираются
произвольно, а 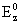 вычисляется по
формуле: вычисляется по
формуле:
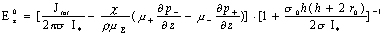 , ,
(3)
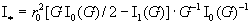 , ,
где стенка
считается проводником с конечной проводимостью
 . При этом полный ток . При этом полный ток
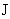 , протекающий только по трубе и определяющий профили , протекающий только по трубе и определяющий профили 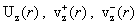 , равен: , равен:
 . .
В частности,
полный ток, протекающий по стенке равен 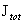 – –  . При . При 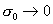 стенка становится
изолятором, и мы имеем стенка становится
изолятором, и мы имеем 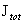 = = 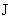 , , 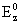 не зависит от толщины
стенки не зависит от толщины
стенки 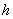 . Взглянем теперь на течение плазмы по цилиндрической трубе с
другой точки зрения. . Взглянем теперь на течение плазмы по цилиндрической трубе с
другой точки зрения.
Взаимодействие
электронов и ионов и закон Ома. Для металлических проводников
известен закон Ома, связывающий плотность тока 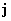 с напряженностью
электрического поля с напряженностью
электрического поля  линейной зависимостью: линейной зависимостью:
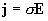 , ,
где 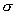 – проводимость металлического проводника.
Если проводник – цилиндр (проволока) круглого сечения с
радиусом – проводимость металлического проводника.
Если проводник – цилиндр (проволока) круглого сечения с
радиусом 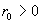 и однородное
поле и однородное
поле 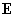 направлено по оси
цилиндра (которую примем за ось OZ), то для полного тока направлено по оси
цилиндра (которую примем за ось OZ), то для полного тока 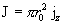 получим: получим:
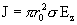 .
(4) .
(4)
Таким образом,
равенство (4) выражает закон Ома в случае цилиндрического металлического
проводника.
Заменим теперь металлический проводник
на плазму: плазма течет по цилиндрической трубе круглого сечения радиуса 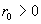 под действием
однородного электрического поля под действием
однородного электрического поля 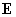 , направленного по оси цилиндра, и постоянного перепада по
оси z гидродинамического давления плазмы. Как теперь связан полный ток , направленного по оси цилиндра, и постоянного перепада по
оси z гидродинамического давления плазмы. Как теперь связан полный ток 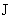 с электрическим полем с электрическим полем
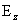 ? Для несжимаемой
вязкой МГД – плазмы с проводимостью ? Для несжимаемой
вязкой МГД – плазмы с проводимостью 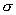 , как следует из формул (2), закон Ома совпадает с законом
(4) для металлических проводников. Если
учесть взаимодействие плазменных компонент (§1), то, как вытекает из формул (3)
для случая , как следует из формул (2), закон Ома совпадает с законом
(4) для металлических проводников. Если
учесть взаимодействие плазменных компонент (§1), то, как вытекает из формул (3)
для случая 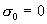 , закон Ома принимает вид: , закон Ома принимает вид:
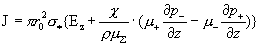 (5) (5)
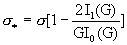 . .
Закон Ома (5)
естественно сопоставить с законом Ома (4) для металлических проводников и МГД –
плазмы в случае 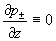 . При . При 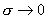 (плохо проводящая
плазма) имеем (плохо проводящая
плазма) имеем 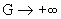 , откуда , откуда  и значит закон Ома
(5) переходит в закон Ома (4). При и значит закон Ома
(5) переходит в закон Ома (4). При 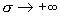 (хорошо проводящая
плазма) имеем (хорошо проводящая
плазма) имеем 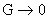 , откуда , откуда
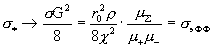
Итак, наличие гидродинамической вязкости у
плазменных компонент приводит к электрическому сопротивлению даже идеальной 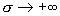 плазмы. Таким образом, при плазмы. Таким образом, при 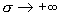 законы Ома (4) и (5)
кардинально различаются: при законы Ома (4) и (5)
кардинально различаются: при 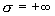 закон Ома (4)
равносилен равенству закон Ома (4)
равносилен равенству 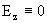 , а закон Ома (5) – равенству , а закон Ома (5) – равенству 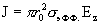 . Наличие конечной эффективной проводимости . Наличие конечной эффективной проводимости 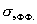 у бесконечно
проводящей плазмы согласуется со здравым смыслом: электроны и ионы идеальной,
но вязкой плазмы “цепляются” за стенки трубы и тем самым тормозят течение плазмы, не давая току у бесконечно
проводящей плазмы согласуется со здравым смыслом: электроны и ионы идеальной,
но вязкой плазмы “цепляются” за стенки трубы и тем самым тормозят течение плазмы, не давая току 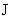 расти до
бесконечности. Из закона Ома (5) вытекает еще один важный вывод: перепад
гидродинамического давления по оси трубы вызывает дополнительный “гидродинамический” электрический ток в трубе расти до
бесконечности. Из закона Ома (5) вытекает еще один важный вывод: перепад
гидродинамического давления по оси трубы вызывает дополнительный “гидродинамический” электрический ток в трубе 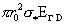 , где добавочное “гидродинамическое” электрическое поле равно : , где добавочное “гидродинамическое” электрическое поле равно :
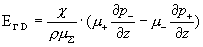 . .
Итак, электрон – ионное взаимодействие ответственно за появление в
законе Ома добавочного электрического поля
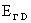 и нелинейный характер
зависимости коэффициента пропорциональности и нелинейный характер
зависимости коэффициента пропорциональности
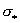 от проводимости
плазмы от проводимости
плазмы 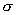 . Причем даже при . Причем даже при 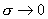 закон Ома (5) не переходит в закон Ома (4) для несжимаемой
МГД – плазмы, поскольку остается добавка закон Ома (5) не переходит в закон Ома (4) для несжимаемой
МГД – плазмы, поскольку остается добавка 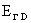 . .
В работе вычислены важные
характеристики установившегося течения: расход плазмы (количество вещества
плазмы, протекающее в единицу времени через сечение трубы) 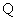 и силы трения
электронов и ионов о стенку трубы и силы трения
электронов и ионов о стенку трубы 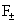 . Показано, что . Показано, что 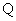 линейно зависит от
полного тока линейно зависит от
полного тока 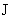 : :
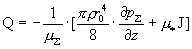 . .
В частности, при
значении полного тока
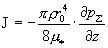 , ,
расход плазмы
равен 0, а при  для расхода получится
то же выражение, что и в гидродинамическом случае. для расхода получится
то же выражение, что и в гидродинамическом случае.
Суммарная сила
трения 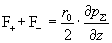 такая же как и в
гидродинамическом случае, но соотношение такая же как и в
гидродинамическом случае, но соотношение 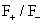 может быть любым,
исключая лишь случай может быть любым,
исключая лишь случай  . Это следует из
явных выражений для . Это следует из
явных выражений для 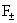 , полученных в работе: , полученных в работе:
 , ,
где выражение для
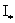 указано выше. указано выше.
Укажем на одно из возможных
практических применений полученных результатов.
Экспериментальное
получение величин 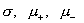 . Изложенная выше теория позволяет выдвинуть следующую идею
экспериментального определения вязкостей плазменных компонент и ее
электропроводности. Рассмотрим цилиндрическую трубу фиксированного круглого
сечения . Изложенная выше теория позволяет выдвинуть следующую идею
экспериментального определения вязкостей плазменных компонент и ее
электропроводности. Рассмотрим цилиндрическую трубу фиксированного круглого
сечения 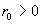 , заполненную плазмой
с плотностью , заполненную плазмой
с плотностью 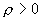 . Создадим фиксированный перепад давления . Создадим фиксированный перепад давления 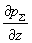 по оси трубы.
Допустим, для каждого полного тока по оси трубы.
Допустим, для каждого полного тока  , проходящего через трубу, возможно экспериментально
построить эпюру средних скоростей , проходящего через трубу, возможно экспериментально
построить эпюру средних скоростей 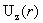 плазмы в трубе. Меняя
ток плазмы в трубе. Меняя
ток 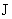 от 0 до достаточно
больших значений, экспериментально зафиксируем критические токи от 0 до достаточно
больших значений, экспериментально зафиксируем критические токи  , когда происходит перестройка профиля , когда происходит перестройка профиля 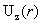 . Тогда из формул для критических токов: . Тогда из формул для критических токов:
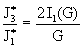 . .
Правая часть
этого равенства – монотонно возрастающая функция, а 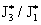 – известная
величина, полученная экспериментально. Поэтому, численно решая полученное выше
уравнение, находим величину – известная
величина, полученная экспериментально. Поэтому, численно решая полученное выше
уравнение, находим величину 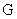 . Снова рассмотрим плазму в трубе, находящуюся в заданном
электрическом поле . Снова рассмотрим плазму в трубе, находящуюся в заданном
электрическом поле 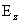 при нулевом перепаде
давления. Измеряя протекающий по плазме полный ток при нулевом перепаде
давления. Измеряя протекающий по плазме полный ток 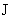 , простым вычислением из закона Ома (5) находим проводимость
плазмы: , простым вычислением из закона Ома (5) находим проводимость
плазмы:
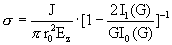 , ,
ибо величины 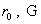 нам известны. Зная нам известны. Зная 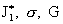 , получим для , получим для 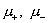 : :
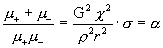
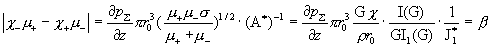 . .
Из этой системы с
двумя неизвестными 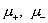 ( (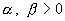 – известные величины) ищутся коэффициенты вязкости: – известные величины) ищутся коэффициенты вязкости:
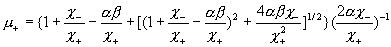
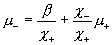 . .
Если
экспериментально легче фиксировать эпюры электронных или ионных скоростей, то
аналогичный способ нахождения 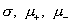 , можно указать, базируясь на критических значениях тока , можно указать, базируясь на критических значениях тока 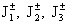 (см. §5). (см. §5).
§1. Уравнения гидродинамики двухкомпонентной
несжимаемой плазмы.
МГД – теория не учитывает
взаимодействия электронов и ионов. В квазинейтральном потоке вязкой
электропроводной несжимаемой плазмы это взаимодействие полностью учитывается
системой [1]:
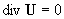 , ,
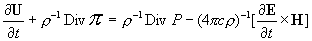 , ,
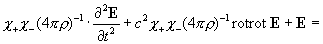
(6)
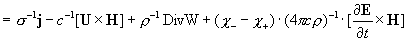 , ,
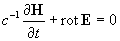 , ,
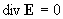 , ,
где 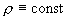 – плотность плазмы, – плотность плазмы,
 , , 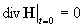 . .
Выражения для тензоров 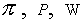 имеют вид: имеют вид:
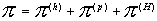 , ,  , ,
(7)
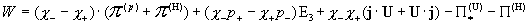 . .
Входящие в эти выражения тензоры 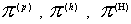 вычисляются по
формулам: вычисляются по
формулам:
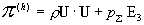 , , 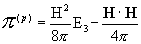 , , 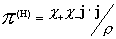 , (8) , (8)
где 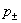 давления плазменных
компонент, давления плазменных
компонент, 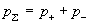 – суммарное давление, – суммарное давление, 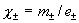 . А тензоры . А тензоры 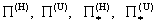 выражаются через тензоры
деформаций выражаются через тензоры
деформаций 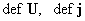 по формулам: по формулам:
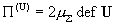 , ,  , , 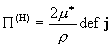 , , 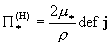 (9) (9)
где 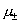 – гидродинамические
вязкости компонент плазмы, – гидродинамические
вязкости компонент плазмы, 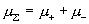 – суммарная вязкость
и – суммарная вязкость
и
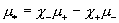 , , 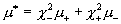 . .
Система (6)÷(9) состоит из 11 скалярных уравнений и
позволяет в принципе найти 11 скалярных неизвестных функций – компоненты полей 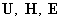 и давления и давления 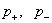 . После этого
гидродинамические скорости электронов и ионов, . После этого
гидродинамические скорости электронов и ионов, 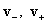 , вычисляются по
формулам: , вычисляются по
формулам:
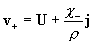 , ,  . (10) . (10)
Уравнения для температур 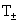 электронов и ионов
см. в [1]. электронов и ионов
см. в [1].
§2. Постановка
задачи о течении плазмы в цилиндрической трубе.
Рассмотрим установившееся 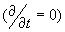 течение вязкой
электропроводной квазинейтральной полностью ионизованной несжимаемой
двухкомпонентной и гидродинамической плазмы по цилиндрической трубе радиуса течение вязкой
электропроводной квазинейтральной полностью ионизованной несжимаемой
двухкомпонентной и гидродинамической плазмы по цилиндрической трубе радиуса 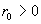 . Это течение, согласно формулам (6), подчиняется системе
уравнений: . Это течение, согласно формулам (6), подчиняется системе
уравнений:
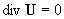 , ,
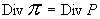 , ,
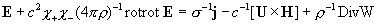 , (11) , (11)
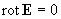 , ,
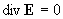 , ,
 , ,
где 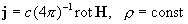 , а выражения для
тензоров , а выражения для
тензоров 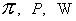 описаны в §1. Пусть
ось симметрии трубы совпадает с осью OZ. Ищем решение системы (11) вида: описаны в §1. Пусть
ось симметрии трубы совпадает с осью OZ. Ищем решение системы (11) вида:
 . .
Поставленную задачу дополним краевыми условиями:
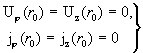 – условия “прилипания”, – условия “прилипания”,
(12)
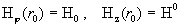 , ,
где  – заданные значения.
Кроме того, считаем что все функции не имеют особенностей по оси трубы – заданные значения.
Кроме того, считаем что все функции не имеют особенностей по оси трубы 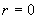 и и
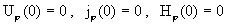 , ,
(13)
 . .
В силу условий (13) уравнения 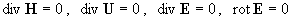
равносильны равенствам 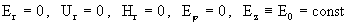 . Как станет ясно ниже, константы . Как станет ясно ниже, константы 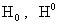 выбираются произвольно, а константа выбираются произвольно, а константа 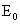 однозначно
вычисляется по однозначно
вычисляется по 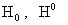 . Таким образом, нахождению подлежат только функции: . Таким образом, нахождению подлежат только функции:
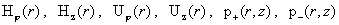 , ,
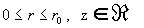 , ,
где 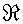 – совокупность всех действительных чисел. – совокупность всех действительных чисел.
Ниже проводимость плазмы 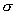 и вязкости компонент и вязкости компонент 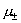 считаются постоянными. считаются постоянными.
§3. Решение
задачи об установившемся течении плазмы в цилиндрической трубе.
Несложно проверить, что 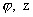 – уравнения основной
системы – уравнения основной
системы
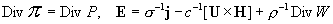 дают: дают:
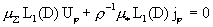 , ,
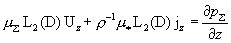 , ,
(14)
 , ,
 , ,
где 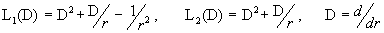 – дифференциальные операторы, – дифференциальные операторы, 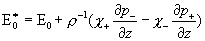 , ,
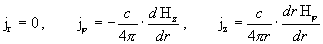 . .
При этом 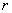 – уравнения основной
системы дают возможность найти давления – уравнения основной
системы дают возможность найти давления 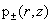 . Из них следует, что . Из них следует, что
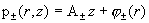 , ,
где константы 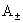 должны задаваться, а
функции должны задаваться, а
функции 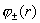 ищутся (см. ниже). В
частности ищутся (см. ниже). В
частности 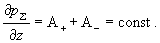 С учетом этого
система (14) позволяет найти функции С учетом этого
система (14) позволяет найти функции 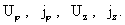 Очевидно, система
(14) распадается на две подсистемы, из одной находятся Очевидно, система
(14) распадается на две подсистемы, из одной находятся 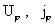 , а из другой – , а из другой – 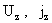 . Ниже, в §4, будет показано, что . Ниже, в §4, будет показано, что 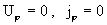 . А для нахождения . А для нахождения 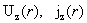 имеем систему: имеем систему:
 , ,
(15)
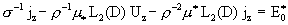 . .
Проще всего ее решить так. Если
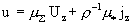 , то из первого уравнения системы (15) следует , то из первого уравнения системы (15) следует 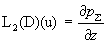 . Общее решение этого
линейного неоднородного уравнения легко находится: . Общее решение этого
линейного неоднородного уравнения легко находится:
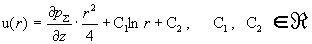 . .
Поэтому
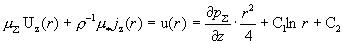 . .
Выражая отсюда 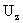 через через 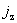 и подставляя
полученное выражение во второе уравнение системы (15), получим следующее
дифференциальное уравнение относительно и подставляя
полученное выражение во второе уравнение системы (15), получим следующее
дифференциальное уравнение относительно 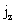 : :
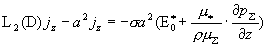 , ,
где 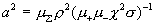 .
Делая в последнем уравнении замену независимой переменной .
Делая в последнем уравнении замену независимой переменной 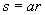 , получаем для нахождения , получаем для нахождения 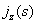 неоднородное
модифицированное уравнение
Бесселя 0-го
индекса: неоднородное
модифицированное уравнение
Бесселя 0-го
индекса:
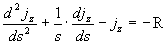 (16), (16),
где константа 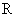 связана с константой связана с константой 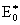 условием: условием:
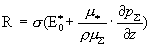 . .
Общее решение уравнения (16) имеет вид:
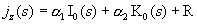 , , 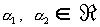 , ,
где 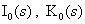 – функция Бесселя мнимого аргумента 0-го индекса ( – функция Бесселя мнимого аргумента 0-го индекса ( – функция
Макдональда) [2], откуда: – функция
Макдональда) [2], откуда:
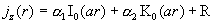 . .
Граничные условия (12), (13) дают 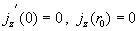 , поэтому , поэтому 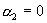 , , 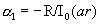 . Отсюда: . Отсюда:
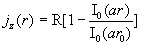 , ,
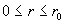 . .
Выясним физический смысл константы  . Полный ток через трубу равен: . Полный ток через трубу равен:
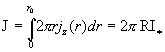 , ,
где
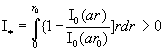 . .
Отсюда 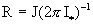 и окончательно имеем: и окончательно имеем:
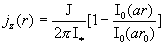 , , 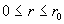 . .
Теперь находим 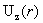 : :
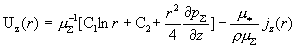 . .
Из граничных условий (12), (13)
получим 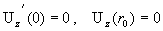 , откуда , откуда 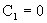 , , 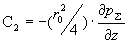 , поэтому окончательно
имеем: , поэтому окончательно
имеем:
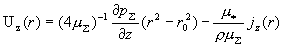 , ,
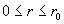 . .
Теперь из соотношений (10) находим 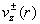 . Итоговые формулы для . Итоговые формулы для
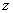 – –  компонент скоростей и плотности тока таковы: компонент скоростей и плотности тока таковы:
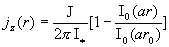
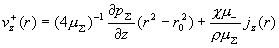
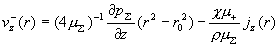 (17) (17)
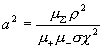 , , 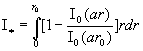 , ,
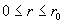 , ,
где 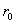 – радиус трубы, – радиус трубы, 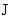 – полный ток через трубу. Константа – полный ток через трубу. Константа 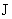 связана с константой связана с константой  формулой: формулой:
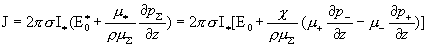 (18) (18)
Обсудим эти формулы позже (см.
§5), а сейчас найдем остальные параметры течения. Как отмечалось, 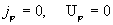 . Но из . Но из  следует следует 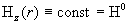 – заданное значение – заданное значение 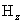 на стенке трубы на стенке трубы 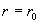 . Для . Для 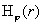 имеем: имеем:
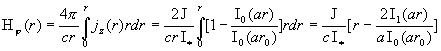 , , 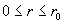 , ,
где 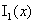 – функция Бесселя
мнимого аргумента индекса 1 и при интегрировании использовано известное [2] тождество – функция Бесселя
мнимого аргумента индекса 1 и при интегрировании использовано известное [2] тождество  . Аналогично устанавливается формула для . Аналогично устанавливается формула для 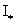 (см.§5): (см.§5):
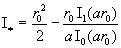 . (19) . (19)
Кроме того, 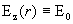 , где , где 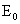 выражается через выражается через  по формуле (18). В
свою очередь константа по формуле (18). В
свою очередь константа 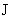 связана очевидным образом
с граничным условием связана очевидным образом
с граничным условием 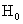 для для 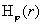 на стенке на стенке 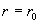 : :
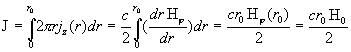 . .
Наконец, функции 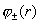 , определяющие давление констант, ищутся из уравнений: , определяющие давление констант, ищутся из уравнений:
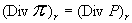
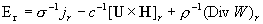 . .
Они дают систему линейных уравнений относительно 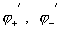 : :
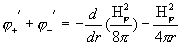
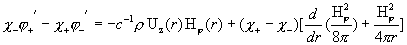 . .
Отсюда получаем:
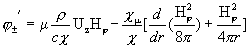 . .
Поэтому функции 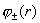 , а значит и давления , а значит и давления 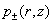 определяются
однозначно с точностью до константы. определяются
однозначно с точностью до константы.
Итак, задача об
установившемся течении плазмы в трубе полностью решена.
§ 4. Выводы соотношения 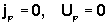 . .
Из системы (14) для 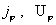 имеем следующие
уравнения: имеем следующие
уравнения:
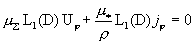
(20)
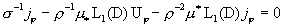
Покажем, что эта система имеет только нулевое решение, удовлетворяющее
поставленным выше граничными условиями (12),
(13). Функция
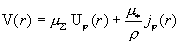
удовлетворяет уравнению 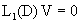 с граничными
условиями с граничными
условиями 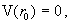  . Но . Но
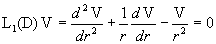
есть уравнение Эйлера. Заменой независимой переменной 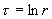 оно приводится к
виду: оно приводится к
виду:
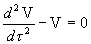 . .
Откуда:
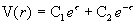 , , 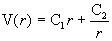 , , 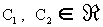 . .
Из граничных условий следует 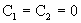 и значит и значит 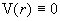 . Поэтому . Поэтому 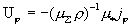 . Подставляя это выражение во второе уравнение
системы (20), получим: . Подставляя это выражение во второе уравнение
системы (20), получим:
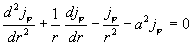 , , 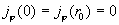 . .
Последнее уравнение заменой 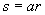 сводится к
модифицированному уравнению Бесселя индекса 1: сводится к
модифицированному уравнению Бесселя индекса 1:
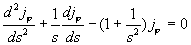 , , 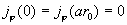 . .
Откуда 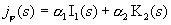 , где , где  – функции Бесселя
мнимого аргумента индекса 1. Из граничных условий немедленно следует – функции Бесселя
мнимого аргумента индекса 1. Из граничных условий немедленно следует 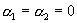 . Значит . Значит 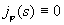 , откуда , откуда 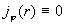 и значит и значит 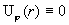 , что и требовалось установить. , что и требовалось установить.
§
5. Анализ картины течения электронов и
ионов в трубе.
Если ток в трубе отсутствует (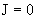 ), то профили электронной и ионной скоростей совпадают между
собой и с параболическим профилем ), то профили электронной и ионной скоростей совпадают между
собой и с параболическим профилем 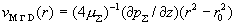 . При появлении тока профили . При появлении тока профили 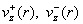 деформируются, причем
неодинаково. Пусть деформируются, причем
неодинаково. Пусть 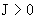 . Тогда профиль электронной скорости . Тогда профиль электронной скорости 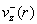 , оставаясь
колоколообразным, лежит ниже параболического профиля , оставаясь
колоколообразным, лежит ниже параболического профиля 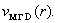 С ростом он все более вытягивается и заостряется. Профиль же
ионной скорости С ростом он все более вытягивается и заостряется. Профиль же
ионной скорости 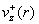 лежит выше
параболы лежит выше
параболы 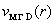 и поначалу с ростом и поначалу с ростом 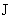 затупляется,
оставаясь колоколообразным при этом. Сплющивание профиля затупляется,
оставаясь колоколообразным при этом. Сплющивание профиля 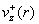 приводит в конце
концов к новому явлению: для достаточно большого тока приводит в конце
концов к новому явлению: для достаточно большого тока  появляется
пристеночная область, в которой ионы двигаются в противоположную по отношению к
электронам сторону, а профиль ионной скорости теряет колоколообразную форму.
Эта область постепенно расширяется, и в итоге
(при появляется
пристеночная область, в которой ионы двигаются в противоположную по отношению к
электронам сторону, а профиль ионной скорости теряет колоколообразную форму.
Эта область постепенно расширяется, и в итоге
(при  ) захватывает всю трубу. С этого момента
электроны и ионы по всей трубе двигаются в разные стороны. Наконец, для еще больших
токов ( ) захватывает всю трубу. С этого момента
электроны и ионы по всей трубе двигаются в разные стороны. Наконец, для еще больших
токов ( 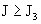 ) профиль ионной
скорости опять становится колоколообразным, однако колоколы профилей
электронной и ионной скоростей обращены теперь в разные стороны. Критические
токи ) профиль ионной
скорости опять становится колоколообразным, однако колоколы профилей
электронной и ионной скоростей обращены теперь в разные стороны. Критические
токи  вычисляются по
формулам: вычисляются по
формулам:
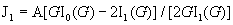 , ,
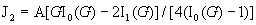 , (21) , (21)
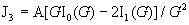 , ,
где
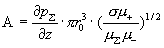
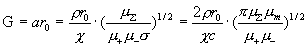 . .
Вторая величина
это, очевидно, безразмерный параметр.
Обоснование формул (21). Описанный выше сценарий целиком
основан на формулах (17). Если 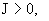 то из (17) следует, что при то из (17) следует, что при
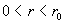 справедливы
неравенства справедливы
неравенства 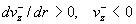 и значит электронная
скорость имеет колоколообразный профиль, лежащий ниже параболы и значит электронная
скорость имеет колоколообразный профиль, лежащий ниже параболы 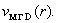 Вершина колокола профиля лежит в точке Вершина колокола профиля лежит в точке
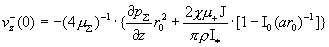 , ,
которая с ростом 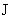 стремится к – ¥. стремится к – ¥.
Поведение ионной скорости 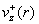 зависит от величины
тока зависит от величины
тока 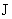 . Из (17), учитывая равенство . Из (17), учитывая равенство 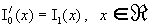 , получим: , получим:
 (22) (22)
Будет ли производная (22) обращаться в 0 на отрезке 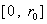 ? ?
Напомним [2], функция 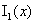 монотонно возрастает
и выпукла вниз на монотонно возрастает
и выпукла вниз на 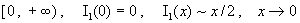 . Но из выпуклости
вниз . Но из выпуклости
вниз 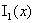 следует, что
график следует, что
график 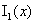 , , 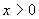 лежит
выше прямой лежит
выше прямой 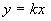 при при 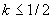 . При . При 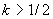 прямая прямая 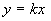 пересекает
график пересекает
график 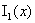 , , 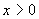 ровно
в одной точке ровно
в одной точке 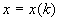 , причем при , причем при 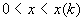 график график 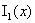 лежит ниже
прямой лежит ниже
прямой 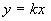 , а при , а при 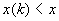 – выше. Из этого анализа и формулы (22) теперь
вытекает неравенство – выше. Из этого анализа и формулы (22) теперь
вытекает неравенство 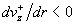 для всех для всех 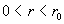 при при
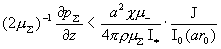 (23) (23)
и неравенство 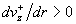 для всех для всех 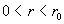 при при
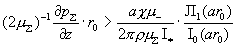 . (24)
Случай, когда неравенства (23) и (24) обращаются в равенства, дают
значения двух критических токов . (24)
Случай, когда неравенства (23) и (24) обращаются в равенства, дают
значения двух критических токов  и и 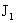 соответственно. При соответственно. При 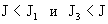 профиль профиль 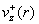 колоколообразный, но
в первом случае колокол профиля повернут вниз ( колоколообразный, но
в первом случае колокол профиля повернут вниз (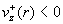 для всех для всех
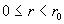 ), а во втором случае
– вверх ( ), а во втором случае
– вверх (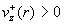 для всех для всех
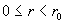 ). ).
При  производная производная 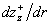 имеет ровно один нуль
на интервале имеет ровно один нуль
на интервале  в некоторой
точке в некоторой
точке 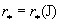 . Поскольку . Поскольку 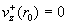 , то , то 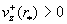 . Поэтому пока . Поэтому пока
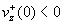 (25) (25)
функция  имеет ровно один нуль
на интервале имеет ровно один нуль
на интервале  в некоторой точке в некоторой точке 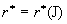 , причем , причем 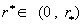 . Случай, когда
неравенство (25) обращается в точное равенство, дает еще одно критическое
значение тока . Случай, когда
неравенство (25) обращается в точное равенство, дает еще одно критическое
значение тока  , а неравенство (25) равносильно неравенствам , а неравенство (25) равносильно неравенствам 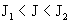 . Для таких . Для таких 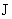 в пристеночной
области в пристеночной
области 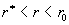 имеем имеем  и значит электроны и
ионы в этой области двигаются в разные стороны; при и значит электроны и
ионы в этой области двигаются в разные стороны; при  наоборот наоборот  и значит здесь
электроны и ионы двигаются в одну сторону. Дальнейший анализ очевиден. и значит здесь
электроны и ионы двигаются в одну сторону. Дальнейший анализ очевиден.
Вычислим значение 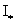 . Снова воспользуемся известным равенством . Снова воспользуемся известным равенством 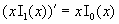 . Тогда: . Тогда:
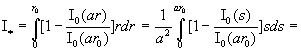
=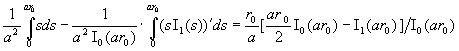 . .
В частности для
комбинации 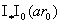 получаем выражение
: получаем выражение
:
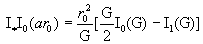 , ,
где 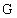 – безразмерный
параметр из формул (21). Поэтому критические значения тока полностью выражаются
через бесселевы функции – безразмерный
параметр из формул (21). Поэтому критические значения тока полностью выражаются
через бесселевы функции  , и мы приходим к выражениям (21). , и мы приходим к выражениям (21).
Соотношения
критических токов и полярность электродов. Легко вычисляются отношения
критических значений полного тока, зависящие только от параметра 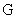 . Из формул (21) выводим: . Из формул (21) выводим:
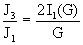 , , 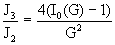 , , 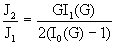 . .
При 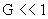 все эти отношения
близки к 1 и значит токи все эти отношения
близки к 1 и значит токи 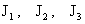 близки друг к другу и
к общему критическому значению тока близки друг к другу и
к общему критическому значению тока  , поскольку , поскольку 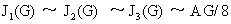 при при 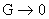 . В этом случае при увеличении полного тока . В этом случае при увеличении полного тока 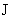 мы практически сразу
попадаем в ситуацию, когда электроны и ионы по всей трубе двигаются в разные
стороны. мы практически сразу
попадаем в ситуацию, когда электроны и ионы по всей трубе двигаются в разные
стороны.
При 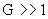 из известной [2] асимптотики из известной [2] асимптотики 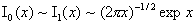 , , 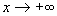 следуют соотношения при следуют соотношения при 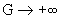 : :
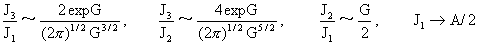 , ,
Где 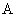 – параметр из формул (21). Поэтому в этом случае – параметр из формул (21). Поэтому в этом случае 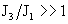 , , 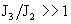 , , 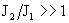 , а , а
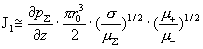 , , 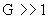 . .
При изменении направления тока 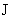 (т.е. (т.е. 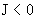 ) профили ) профили  меняются ролями.
Теперь меняются ролями.
Теперь 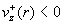 для всех для всех 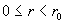 и профиль ионного
тока колоколообразный и всегда лежит ниже параболы и профиль ионного
тока колоколообразный и всегда лежит ниже параболы 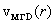 . Профиль же . Профиль же 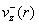 с ростом с ростом 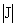 претерпевает
изменения, описанные выше. Абсолютные величины критических значений тока претерпевает
изменения, описанные выше. Абсолютные величины критических значений тока 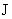 получаются из формул
(21) заменой получаются из формул
(21) заменой  . В частности, . В частности,
 , ,
где верхний индекс “+” отвечает случаю 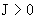 (выше (выше 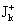 обозначались просто обозначались просто  ), а верхний индекс “–“ – случаю ), а верхний индекс “–“ – случаю 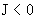 . В частности,
для электрон – ионной плазмы . В частности,
для электрон – ионной плазмы 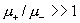 (ибо (ибо 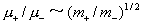 , см. [3]) и значит , см. [3]) и значит 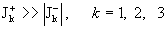 . Отсюда вытекает важный вывод: изменение полярности электронов приводит к изменению картины течения
плазмы. Допустим, например, . Отсюда вытекает важный вывод: изменение полярности электронов приводит к изменению картины течения
плазмы. Допустим, например, 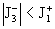 . Это неравенство равносильно такому: . Это неравенство равносильно такому:
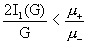 , ,
которое выполнено для всех 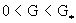 , где , где 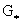 – единственный
положительный корень уравнения – единственный
положительный корень уравнения 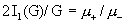 . Если теперь . Если теперь 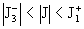 , то при изменении направления тока , то при изменении направления тока 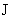 (т.е. изменении
полярности электродов) картина распределения ионного и электронного токов по
сечению трубы совершенно меняется: профили электронного и ионного токов
колоколообразные, но при (т.е. изменении
полярности электродов) картина распределения ионного и электронного токов по
сечению трубы совершенно меняется: профили электронного и ионного токов
колоколообразные, но при  они направлены в одну
сторону, а при они направлены в одну
сторону, а при 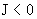 – в разные.
Разумеется, в зависимости от взаимного расположения величин – в разные.
Разумеется, в зависимости от взаимного расположения величин 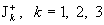 и и 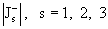 число возможных
ситуаций значительно возрастает. число возможных
ситуаций значительно возрастает.
§
6. Некоторые физические характеристики
течения плазмы в трубе.
Вычислим расход плазмы ( т.е. количество вещества плазмы, проходящее в
единицу времени через сечение трубы) и силы трения электронов и ионов о стенку
трубы.
1). Расход плазмы 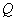 , очевидно равен: , очевидно равен:


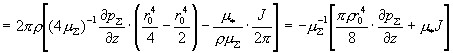 , ,
где была использована формула
для 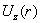 из §3 и определение величины из §3 и определение величины 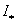 . .
Итак, расход плазмы 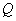 линейно зависит от
полного тока линейно зависит от
полного тока 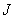 .При .При 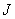 = 0 для = 0 для 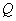 получается известное
из гидродинамики выражение. При значении полного тока получается известное
из гидродинамики выражение. При значении полного тока
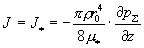
расход плазмы равен 0, т.е. масса электронов, проходящих в единицу
времени через сечение трубы в одну сторону уравновешивается массой ионов,
протекающих в единицу времени через сечение трубы в другую сторону. Заметим,
что 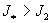 . .
2). Силы трения
электронов и ионов о стенку трубы равны:
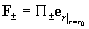
где 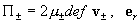 – единичный вектор, имеющий в цилиндрических
координатах компоненты (1,0,0). Из выражений (10) следует, что – единичный вектор, имеющий в цилиндрических
координатах компоненты (1,0,0). Из выражений (10) следует, что
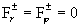 и и
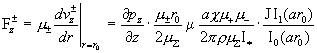 . .
Отсюда получается выражение для силы трения всей плазмы о стенку трубы:
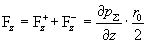 , ,
совпадающее с известным выражением для силы трения в газодинамике.
Соотношение для трения 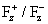 может быть любым в
зависимости от величины полного тока J: исключается лишь случай может быть любым в
зависимости от величины полного тока J: исключается лишь случай 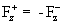 . Например при . Например при 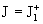 имеем имеем 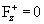 , и о стенку трутся
только электроны, а при , и о стенку трутся
только электроны, а при 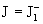 наоборот наоборот 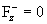 , и о стенку трутся только ионы. При , и о стенку трутся только ионы. При
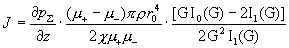
силы трения электронов и ионов равны:
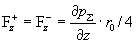 . .
§
7. Профиль средней
скорости 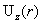 . .
Анализ профиля 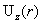 вполне аналогичен рассмотрению профилей вполне аналогичен рассмотрению профилей 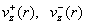 . Имеем, согласно (17): . Имеем, согласно (17):
 , ,
где 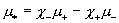 . Для электрон – ионной плазмы . Для электрон – ионной плазмы 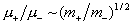 и и  . Для электрон – позитронной плазмы возможны и значения . Для электрон – позитронной плазмы возможны и значения 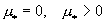 . Для определенности будем полагать . Для определенности будем полагать 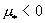 . Из выражения для
производной . Из выражения для
производной
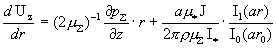
дословно повторяя
рассуждения § 5 при анализе профиля  , заключаем, что есть три критических значения тока , заключаем, что есть три критических значения тока  , определяющих различные типы профилей , определяющих различные типы профилей 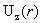 . Явные выражения для критических токов и анализ типов
профилей . Явные выражения для критических токов и анализ типов
профилей 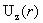 приведен во Введении. приведен во Введении.
§
8. Заключительные замечания.
1. Граничные условия. Существование
установившегося цилиндрически симметричного течения плазмы
по трубе возможно только при определенных значениях электрического и магнитного
полей в вакууме, вне трубы. Пусть стенка занимает область 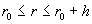 ( (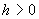 – толщина стенки),
а вакуум – область – толщина стенки),
а вакуум – область 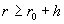 . Тогда проведенное в § 3 исследование надо дополнить
решением уравнений электродинамики в стенке и вакууме и затем “склеить” полученные решения между
собой и с найденными полями в плазме ( . Тогда проведенное в § 3 исследование надо дополнить
решением уравнений электродинамики в стенке и вакууме и затем “склеить” полученные решения между
собой и с найденными полями в плазме ( ) на граничных цилиндрических
поверхностях ) на граничных цилиндрических
поверхностях 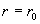 и и 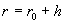 по непрерывности.
При этом предполагается, что стенка незаряженная и отсутствуют поверхностные
токи и заряды. Кроме того, надо ввести в рассмотрение векторы по непрерывности.
При этом предполагается, что стенка незаряженная и отсутствуют поверхностные
токи и заряды. Кроме того, надо ввести в рассмотрение векторы 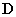 и и  – электрической и
магнитной индукции, для которых в плазме и вакууме постулируются соотношения – электрической и
магнитной индукции, для которых в плазме и вакууме постулируются соотношения 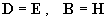 , а в стенке – , а в стенке – 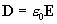 , , 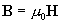 , где , где 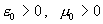 – заданные константы
(электрическая и магнитная проницаемости материала стенки). Стационарные
уравнения Максвелла в вакууме имеют вид: – заданные константы
(электрическая и магнитная проницаемости материала стенки). Стационарные
уравнения Максвелла в вакууме имеют вид:
 , ,
а в проводящей стенке с конечной проводимостью 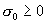 : :
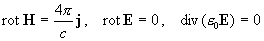 , ,
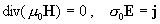 . .
На поверхностях 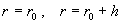 раздела двух сред
(плазма – стенка, стенка – вакуум) условия “склейки” имеют вид [4]: раздела двух сред
(плазма – стенка, стенка – вакуум) условия “склейки” имеют вид [4]:
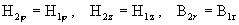
(*)
 , ,
где индексы 1 и 2 относятся к значениям полей 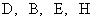 на поверхностях
раздела на поверхностях
раздела 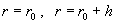 , получаемых предельным переходом соответственно изнутри
(индекс 1) и извне поверхностей. Решая указанные уравнения в вакууме и стенке
(в предположении цилиндрической симметрии всех функций) и склеивая решения по
формулам (*), приходим к результатам, , получаемых предельным переходом соответственно изнутри
(индекс 1) и извне поверхностей. Решая указанные уравнения в вакууме и стенке
(в предположении цилиндрической симметрии всех функций) и склеивая решения по
формулам (*), приходим к результатам,
сформулированным во Введении.
2. Течение между двумя соосными
цилиндрами, Пусть плазма занимает пространство между двумя коаксиальными
цилиндрами радиусов 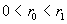 , равномерно вращающихся
против часовой стрелки вокруг общей оси (которую примем за ось , равномерно вращающихся
против часовой стрелки вокруг общей оси (которую примем за ось 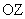 ) с угловыми скоростями ) с угловыми скоростями  . соответственно. Рассмотрим установившееся . соответственно. Рассмотрим установившееся 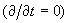 течение плазмы,
считая что все параметры течения, кроме давлений, зависят только от течение плазмы,
считая что все параметры течения, кроме давлений, зависят только от 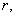 а а  . Такое течение
является решением системы (11) вида: . Такое течение
является решением системы (11) вида:
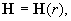 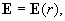 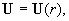 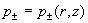 , ,
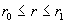 , , 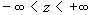 . .
На границах отрезка 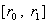 для скоростей для скоростей  ставятся граничные
условия “непротекания” и ”прилипания” , которые для ставятся граничные
условия “непротекания” и ”прилипания” , которые для  дают: дают:
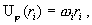 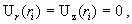  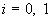 . .
Тогда из (11) следует  и в физически
интересном случае и в физически
интересном случае 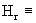 0 для нахождения 0 для нахождения 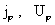 получим краевую
задачу: получим краевую
задачу:
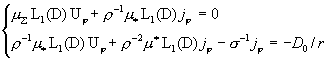
(I)
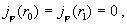 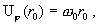 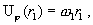
а для нахождения 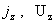  имеем следующую
краевую задачу: имеем следующую
краевую задачу:
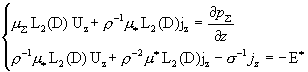
(II)
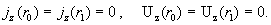
Здесь

Решение краевых задач (I) и (II) ищется по схеме §3. В результате приходим к следующим явным выражениям:
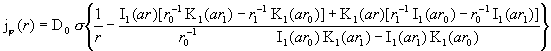 , ,
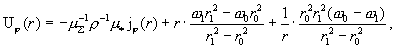
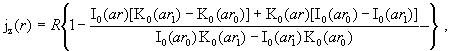
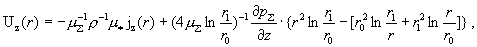
где как и в §3:
 , , 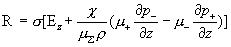 . .
Кроме того, 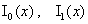 – функции Бесселя
мнимого аргумента индексов 0 и 1 соответственно, – функции Бесселя
мнимого аргумента индексов 0 и 1 соответственно, 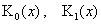 – функции Макдональда
индексов 0 и 1. Отсюда для скоростей плазменных компонент получим: – функции Макдональда
индексов 0 и 1. Отсюда для скоростей плазменных компонент получим:
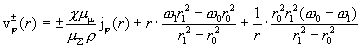 , ,
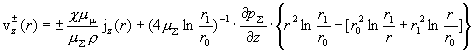 . .
Если азимутальное электрическое поле отсутствует, 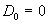 , то азимутальные движения электронов и ионов совпадают с
известным из гидродинамики течением
Куэтта. , то азимутальные движения электронов и ионов совпадают с
известным из гидродинамики течением
Куэтта.
Исходя из полученных формул
нетрудно вычислить силу сопротивления вращению цилиндра, рассмотреть случай
малого зазора между цилиндрами (теория плазменной смазки). Интересен случай,
когда внутренний цилиндр – материальное тело (проводящее или диэлектрик), а
также случай, когда внешний цилиндр имеет бесконечный радиус (задача о движении
снаряда в ионосфере; при этом несложно учесть в полученных выше формулах
допущение о движении внутреннего и внешнего цилиндров с постоянными скоростями
вдоль оси 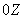 , а именно, если внутренний цилиндр двигается с постоянной
вертикальной скоростью , а именно, если внутренний цилиндр двигается с постоянной
вертикальной скоростью 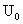 , а внешний – , а внешний – 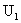 , то в формулах для , то в формулах для 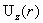 , , 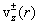 появится добавка появится добавка 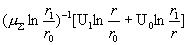 , все остальные формулы остаются без изменения). Что касается
давлений, то как и в §3 они имеют вид , все остальные формулы остаются без изменения). Что касается
давлений, то как и в §3 они имеют вид 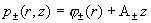 , где константы , где константы 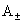 задаются, а функции задаются, а функции  ищутся по той же
схеме, что и выше. Наконец, представляет значительный
интерес анализ зависимости эпюр скоростей ищутся по той же
схеме, что и выше. Наконец, представляет значительный
интерес анализ зависимости эпюр скоростей 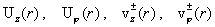 от параметров
течения. от параметров
течения.
3. Некоторые предельные переходы. Рассмотрим два предельных перехода.
А) Гидродинамический предел, J→0. Тогда согласно формулам (17), равномерно на 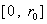 имеют место
сходимости имеют место
сходимости
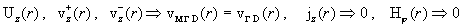 . .
И мы приходим к установившемуся течению вязкой несжимаемой жидкости,
находящейся в постоянном и однородном продольном электрическом и магнитном
поле, не взаимодействующим с веществом.
Б) МГД – предел,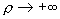 . Тогда . Тогда 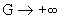 и значит и значит 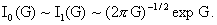 Поэтому из формул
(17) следует Поэтому из формул
(17) следует 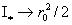 . Поскольку при . Поскольку при 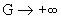 , , 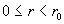 имеет место
эквивалентность имеет место
эквивалентность 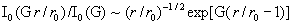 , то из формул (17) вытекает , то из формул (17) вытекает 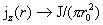 при при 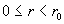 и и 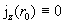 . Итак, при . Итак, при 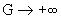 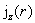 поточечно сходится к
разрывной функции. Из выражения для поточечно сходится к
разрывной функции. Из выражения для 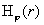 следует, что при следует, что при 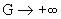 функция функция 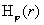 на на 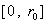 поточечно сходится к поточечно сходится к 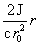 . Наконец, очевидно, . Наконец, очевидно,  , , 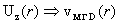 равномерно на равномерно на 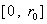 . Итак, предельные значения всех параметров течения при . Итак, предельные значения всех параметров течения при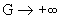 – это в точности МГД
– решение задачи об установившемся течении вязкой несжимаемой МГД – плазмы в
трубе (см. Введение). – это в точности МГД
– решение задачи об установившемся течении вязкой несжимаемой МГД – плазмы в
трубе (см. Введение).
4.Упрощенные формулы. Как уже говорилось, при 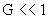 три критические значения тока три критические значения тока 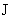 примерно совпадают
между собой. В этом случае из (17) вытекают следующие упрощенные формулы для
профилей скорости: примерно совпадают
между собой. В этом случае из (17) вытекают следующие упрощенные формулы для
профилей скорости:
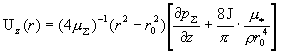 , ,
 . .
В частности, при 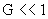 существуют
единственные критические значения полного тока существуют
единственные критические значения полного тока  , при прохождении через которые происходит перестройка
профилей скоростей , при прохождении через которые происходит перестройка
профилей скоростей  : :
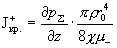 , , 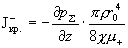 , , 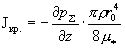 . .
§ 9.
Благодарности.
Авторы
выражают благодарность
К.В.Брушлинскому,
А.Н.Козлову, В.В.Савельеву, В.С.Рябенькому за участие в обсуждении различных вопросов, относящихся к
двухкомпонентной плазмодинамике.
Авторы
также признательны Российскому Фонду Фундаментальных Исследований за финансовую
поддержку этой работы.
Литература.
[1] М.Б.Гавриков, М.С.Михайлова “Установившееся течение
двухкомпонентной квазинейтральной плазмы
в плоском канале”.
Препринт ИПМ N 54 2003г..
[2] Лебедев Н.Н. Специальные
функции и их применения.
М. ГИТТЛ, 1953г. с.148.
[3] Брагинский С.И. В сб. “Вопросы теории плазмы” . Под ред.
М.А.Леонтовича. Вып.1 М.:
Госатомиздат, 1963, с.183.
[4] Тамм И.Е. Основы теории электричества, М. “Наука” , 1966г.
|