Аннотация
Работа посвящена разработке математической модели, ее численной и программной реализации для
расчета погонной индуктивности электромагнитных ускорителей типа рельсотрон со сложной
системой электропитания. Рассмотрение проведено на примере ускорителя с каналом, имеющим
обращенный подвод тока к якорю со стороны дульного среза. Приведены результаты расчетов
погонной индуктивности для нескольких конструкций каналов с варьируемыми геометрическими
размерами электродов.
Abstract
The work is denoted to development of mathematical model, its numerical and software
realization for the calculation of inductance per unit length for electromagnetic launchers
of railgun type with complex electro feeding system. The consideration is conducted on the
example of “muzzle – fed” railgun. There are presented the results of calculations of
inductance per unit length for the set of constructions.
Содержание
1. Введение и постановка
задачи.
2. § 1. Математическая
модель.
3. § 2. Результаты
математического моделирования.
4. Заключение.
5. Литература.
Введение и постановка задачи.
Настоящая работа посвящена расчету погонной индуктивности
электромагнитных ускорителей типа "рельсотрон" [1, 2] со сложной
системой электропитания. Все рассмотрение проведено на примере ускорителя с
обратным токоподводом, хотя алгоритм расчета применим и для других видов электродинамических
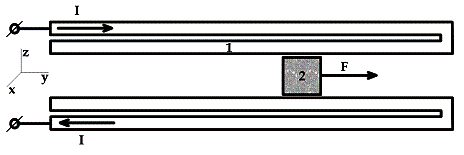
ускорителей. Простейшая схема и типичное сечение канала такого ускорителя
показаны на рис. 0.1.
|
Рис.
0.1. Схема рельсотрона с обратным токоподводом. 1 - обратный токоподвод, 2 -
ускоряемое тело.
|
|
Как видно, рельсотрон с с обратным токоподводом представляет
собой две пары токопроводящих рельсов и замыкающее их ускоряемое тело (в
дальнейшем - якорь). Протекающий по рельсам и якорю ток создает магнитное поле,
которое взаимодействует с током в якоре и ускоряет его вдоль оси y. Впервые
идея подвода тока к якорю со стороны
дульной части была высказана в [3] и аргументирована возможностью подавления
скоростного скинирования тока в зоне контакта.
Канал рельсотрона с обратным токопроводом по сравнению с классической
схемой, где обратный токопровод отсутствует, позволяет расширить зону втекания
в якорь тока, что может привести к
уменьшению токовых и тепловых нагрузок на якорь. В конечном итоге можно
ожидать увеличения выходной
скорости тела без эрозионного разрушения скользящих контактов и
повышения ресурса работы канала. Подробнее физико - технические детали такого
ускорителя описаны в [4-8]. Однако в этих работах отмечалось, что использование
обратного токоподвода одновременно и
неизбежно приводит к относительному уменьшению ускоряющей силы F, которая определяется
конфигурацией магнитного поля в канале. В результате выбор оптимального
решения конструкции канала, который в
данном случае представляет пару вложенных
объемных полосковых линий, может быть проведен только с помощью достаточно
корректных расчетов.
Геометрической особенностью рельсотрона является резкое (на 1 -
2 порядка) различие размеров в поперечном (x, z) и продольном (y) направлении.
С боковых сторон (границы по x, z) канал рельсотрона обычно окружен хорошо проводящим кожухом. В реальной конструкции кожух
играет роль силового бандажа, фиксирующего токоподводы-рельсы. Токи в рельсотроне достигают мегаамперных
величин, а скорости якоря - километров в секунду.
Одной из важнейших характеристик рельсотрона является погонная
индуктивность - продольный градиент индуктивности канала ствола. Погонная
индуктивность используется при расчете ускоряющей силы, действующей на якорь в
процессе разгона. В простейших математических моделях [1, 2, 9] ускоряющая сила
определяется величиной полного протекающего тока I и продольным градиентом
индуктивности канала 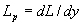 : :
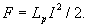 (0.1) (0.1)
Очевидно, что данное выражение не совсем верно отражает реальную
ускоряющую силу, которая равна 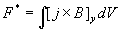 , где интеграл берется по всему объему токовой перемычки.
Здесь и далее используется система координат, приведенная на рис. 0.1. Как ранее показали трехмерные расчеты [10 - 12], сила (0.1) с хорошей точностью
описывает интегральную картину ускорения.
В работе [5] вопрос об адекватности вычисления ускоряющей силы по величине погонной индуктивности
обсуждался отдельно. Было показано, что величина , где интеграл берется по всему объему токовой перемычки.
Здесь и далее используется система координат, приведенная на рис. 0.1. Как ранее показали трехмерные расчеты [10 - 12], сила (0.1) с хорошей точностью
описывает интегральную картину ускорения.
В работе [5] вопрос об адекватности вычисления ускоряющей силы по величине погонной индуктивности
обсуждался отдельно. Было показано, что величина 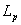 является важнейшей характеристикой ускорителя, по
крайней мере, в длинном канале и при квазастационарных токах. В реальных
ускорителях - рельсотронах оба эти
условия обычно выполнены. является важнейшей характеристикой ускорителя, по
крайней мере, в длинном канале и при квазастационарных токах. В реальных
ускорителях - рельсотронах оба эти
условия обычно выполнены.
Для конкретного ускорителя 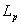 может быть рассчитана
прямым способом через объемный интеграл: может быть рассчитана
прямым способом через объемный интеграл: 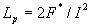 , как это сделано в [10 - 12]. Более распространен расчет , как это сделано в [10 - 12]. Более распространен расчет 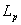 по потоку магнитного
поля через входное (или выходное) сечение ускорителя [9, 13, 14]. В этом случае
для данной системы координат по потоку магнитного
поля через входное (или выходное) сечение ускорителя [9, 13, 14]. В этом случае
для данной системы координат
 , (0.2) , (0.2)
где
интеграл берется по некоторому контуру C в
сечении y = const, x = 0 [9, 13, 14]. В
данной работе мы будем использовать (0.2).
При использовании последнего алгоритма погонная индуктивность
ускорителя с обратным токоподводом равна разности погонной индуктивности,
рассчитанной по входу (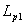 ), и погонной индуктивности, рассчитанной
по выходу из канала ускорителя ( ), и погонной индуктивности, рассчитанной
по выходу из канала ускорителя (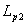 ): ):
 (0.3) (0.3)
Перейдем к более подробной постановке математической задачи.
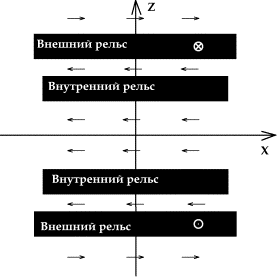
Иллюстрации для рассматриваемой конструкции приведены на рис. 0.2.
Здесь и далее будем использовать следующие обозначения: E - напряженность электрического поля, H - напряженность магнитного поля, B - магнитная индукция, j - плотность тока проводимости, A - векторный потенциал, σ -
удельная электропроводность, Gk – область, занимаемая k - м
проводником, Sk - её площадь, G/G1/G2 -
область вакуума, L - индуктивность, Lp - погонная индуктивность.
Индексы k, равные 1 или 2, у величин G, S, I, σ означают верхний и нижний
рельс ускорителя соответственно.
|
|
|
|
Рис.
0.2.а. Сечение рельсотрона плоскостью y = const. Картина токов на входе
ускорителя (расчет 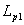 ). ).
|
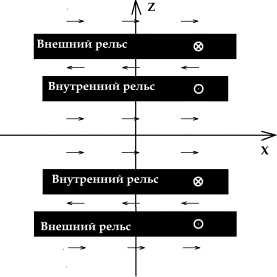
Рис.
0.2.б. Сечение рельсотрона плоскостью y = const. Картина токов на выходе из
ускорителя (расчет 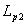 ). ).
|
Соотношения (0.2), (0.3) не накладывают никаких ограничений на
размерность математической модели. Однако в (0.2), (0.3) используется поле
только во входном и выходном сечениях рельсотрона. При этом длина (по y)
ускорителя много больше его поперечных размеров. Учтем также, что единственной
заданной извне электромагнитной величиной можно считать полный ток, протекающий
по рельсам. Поэтому естественно считать, что на торцах рельсотрона
электромагнитное поле соответствует бесконечно длинной (по y) системе проводников,
для каждого из которых задан полный ток. Тогда векторы напряженности
электромагнитного поля имеют вид H = (Hx, 0, Hz), E = (0, Ey, 0). Это поле является
решением соответствующей пространственно двумерной (в переменных (x, z))
задачи, которую необходимо решить для определения погонной индуктивности.
Рассмотрим изображенное на рис. 0.2 сечение рельсотрона
плоскостью y = const.
Стрелками на нем условно показано направление магнитного поля при действующих
токах.
Очевидно, что компонента Hx (Hz) напряженности магнитного поля
симметрична четным (нечетным) образом относительно плоскости z = 0 и имеет аналогичную
симметрию относительно плоскости x = 0.
Электрическое поле (Ey) ведёт
себя аналогично: четная симметричность относительно x = 0 и симметричность с обратным
знаком относительно z = 0.
Ясно, что для определения электромагнитных полей достаточно рассмотреть первую
четверть координатной плоскости, поставив на соответствующих плоскостях
симметрии граничные условия. Поэтому далее будет рассматриваться только первая
четверть плоскости.
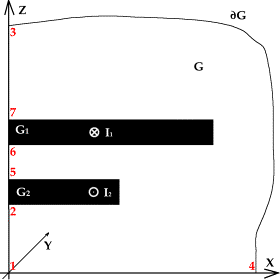
Рассмотрим рис. 0.3. Единственными заданными величинами будем
считать полные токи I1(t), I2(t), геометрические размеры,
форму рельсов и экрана. При этом либо I2(t) = 0 (входное сечение), либо I2(t) = - I1(t) (выходное сечение). Характерное
время изменения токов сравнительно велико, так что можно пользоваться
квазистационарным приближением. Используем систему координат, изображенную на
рис. 0.1 – 0.3.
Получаем следующую пространственно двумерную задачу. В области G
имеется два проводника достаточно произвольной формы G1 и G2,
симметричные относительно Oz, через
которые протекают заданные токи I1(t) и I2(t) соответственно. Проводники
являются бесконечно длинными в направлении оси Oy. Вне
проводников находится диэлектрик (вакуум). На внешней границе области G
(полной) находится идеально проводящий экран.
|
Рис.
0.3. Пространственная область, в которой ищется решение задачи.
|
|
В силу симметричности начальной области (рис. 0.2) на границе 1
- 3 (x = 0) имеем нулевое условие на тангенциальную компоненту H, а на
границе 1 - 4 (z = 0) имеем аналогичное условие на E:
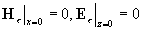 . (0.4) . (0.4)
Начальные условия нулевые.
Роль контура C, интеграл по которому (0.2)
дает погонную индуктивность, в данной задаче играет участок 1 - 2 границы x =
0.
Работа выполнена при
частичной финансовой поддержке Российского фонда фундаментальных исследований
(проект РФФИ № 03 – 01 - 00461).
§ 1. Математическая модель.
Для описания электромагнитного поля будем использовать систему
уравнений Максвелла в квазистационарном приближении [15]. В данной задаче
удобно вести описание полей с помощью векторного потенциала, имеющего одну
ненулевую компоненту A = (0, A, 0). Расчет напряженности
электромагнитного поля и погонной индуктивности по известному векторному
потенциалу является тривиальной задачей.
Для
решения полной пространственно трехмерной задачи в [7, 16] рассмотрена
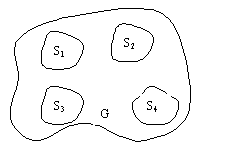
предварительно следующая двумерная задача. Пусть в области G (рис. 2.1) имеется N проводников,
по которым протекают заданные токи 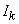 , где , где 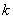 £ N. При этом использована система координат вида рис. 0.1 – 0.3, то
есть точки £ N. При этом использована система координат вида рис. 0.1 – 0.3, то
есть точки 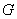 имеют координаты имеют координаты 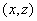 . Проводники считаются бесконечно длинными в направлении оси . Проводники считаются бесконечно длинными в направлении оси 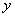 . В этом случае электромагнитное поле имеет . В этом случае электромагнитное поле имеет 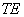 структуру [17, c.
203]. структуру [17, c.
203].
|
Рис. 2.1. Схема
пространственно двумерной области.
|
|
В [7,
16] на основе системы уравнений Максвелла построена модель, обеспечивающая
удовлетворение условий протекания заданных токов в двумерном случае. Всем
необходимым условиям на границе раздела сред можно удовлетворить, если
допустить скачок продольной компоненты Ey при переходе через
границу на величину ck(t), подлежащую определению.
Причина
появления такого скачка состоит в том, что классическое решение задачи с
заданными начальными и граничными условиями, которое имеет непрерывные 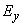 , , 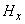 , , 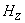 при переходе через
границу и интегрируемо с квадратом в G,
определяется единственным образом в ограниченной области G (см. [14, 15]). Тем самым классическое решение задачи с нулевыми
начальными и граничными условиями (предполагается его существование)
тождественно равно нулю и является единственным. Оно не может обеспечить
протекание заданного тока, поэтому необходимо использование другой модели. при переходе через
границу и интегрируемо с квадратом в G,
определяется единственным образом в ограниченной области G (см. [14, 15]). Тем самым классическое решение задачи с нулевыми
начальными и граничными условиями (предполагается его существование)
тождественно равно нулю и является единственным. Оно не может обеспечить
протекание заданного тока, поэтому необходимо использование другой модели.
Отказ от
классических [14, 15] условий сопряжения на границах проводников позволяет
обеспечить выполнение требования протекания заданного тока. При этом получается
задача, содержащая интегро - дифференциальное уравнение.
Вместо обычной
системы в терминах A [15],
соответствующей рассматриваемой ситуации, имеем:
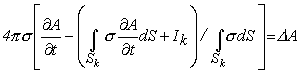 в Gk , k = 1, 2 … N, (1.1) в Gk , k = 1, 2 … N, (1.1)
DA = 0 в G/G1/G2 ,
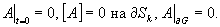
Конечномерная
дискретизация дифференциальных частей этих уравнений не составляет трудностей и
делается так же, как и ранее [7, 15, 16]. Учет же интегрального члена
составляет особенность данной задачи. При численном решении (1.1) хорошие
результаты удается получить за счет расширения числа неизвестных разностной
задачи на N, равное количеству проводников в двумерной области, с последующей
симметризацией разностного оператора. Каждое новое неизвестное есть численная
квадратура, соответствующая (1.1).
При
решении трехмерных задач данная задача является лишь вспомогательной. При этом
ее решение позволяет найти тангенциальные компоненты H на границе, что дает необходимое граничное условие для решения
трехмерной задачи. Она позволяет найти интересующие нас пространственно
трехмерные поля H, E, T и т.д. Отметим, что в случае
рельсотрона необходимо решать вспомогательные двумерные задачи на обоих торцах
рассматриваемой области. В данной работе задача (1.1) является основной.
Для численного решения данной задачи использован метод конечных
элементов первого порядка на треугольной сетке. Конечномерная дискретизация
задачи проведена с помощью модифицированного метода Галеркина в стиле [7, 15].
Для этого в области G введены две системы конечно - элементных базисных функций:
система единичных кусочно - линейных функций и система кусочно - постоянных
единичных на ячейках Дирихле функций. Последние функции используются для
аппроксимации слагаемых с временной производной.
Для программной реализации численного решения разработан
программный комплекс на языке С++, который позволяет быстро и надежно
производить решение системы.
К ключевым особенностям программы можно отнести: легкость
использования и задания входных данных; возможность одновременного расчета
нескольких задач; возможность задания произвольной геометрии проводников;
расширенную визуализацию расчетных данных; оптимизацию под большие системы
линейных алгебраических уравнений (СЛАУ); низкие аппаратные требования;
возможность прерывания расчетов и их возобновления с той же точки в
произвольный момент; постоянный контроль расчетных данных на соответствие
физическим законам и входным данным.
Для решения СЛАУ использован метод Холесского [18, 19] исходя из
устойчивости метода при решении задачи с разреженной матрицей и минимальности
требований к объему оперативной памяти компьютера и продолжительности
вычислений.
Программа решает СЛАУ, содержащую порядка 30 тысяч уравнений, за
0.1 - 0.2 секунды на компьютерах с частотой процессора 1 ГГц.
§ 2. Результаты
математического моделирования.
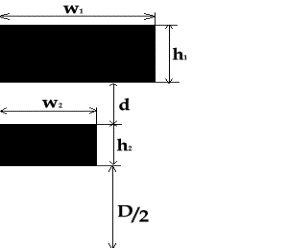
Приведем значения параметров, использованных в качестве базовых
величин в дальнейших расчетах (они пояснены на рис. 2.1):
высота верхнего проводника h1 = 7 10-3
м,
высота нижнего проводника h2 = 5 10-3
м,
ширина верхнего проводника w1 = 1 10-2 м,
ширина нижнего проводника w2 = 1 10-2 м,
калибр ствола D = 2 10-2 м,
расстояние между проводниками d = 5 10-3 м,
σ = 58 106 См/м (Cu),
I = 5 105 а,
длительность процесса равна 10-3 сек,
токи - синусоидальные с периодом, равным 2 миллисекундам,
внешний идеально проводящий экран имеет форму дуги окружности,
находящейся на радиусе R = 3 м
от центра.
|
Рис.
2.1. Типичная форма расчетной области.
|
|
Все рассчитанные значения напряженности электрического,
магнитного полей, векторного потенциала и распределение плотности токов
приводятся на момент времени t = 0.0005 сек.
1. Группа расчетов № 1. Прямоугольные проводники.
В данной группе проводились расчеты проводников прямоугольного
сечения. Типичная форма таких проводников показана на рис. 2.1.
Количество расчетных узлов – 12000 - 16000, элементов – 22000 -
31000.
1.1. Зависимость погонной
индуктивности от ширины верхнего рельса.
Всего произведено 7 расчетов для различных размеров верхнего
рельса. Все параметры расчетов одинаковы, за исключением ширины верхнего
проводника, которая росла с каждым расчетом на величину 0.3 см. Таким образом,
она менялась от 1 см в первом расчете до 2.8 см в седьмом расчете. Полученные
значения погонной индуктивности приведены в табл. 2.1.1.
Табл.
2.1.1.
|
№
|
w1, см
|
Lp1,
Гн/м
|
Lp2,
Гн/м
|
Lp,
Гн/м
|
|
1
|
1.0
|
3.73
10-7
|
1.33
10-7
|
2.40
10-7
|
|
2
|
1.3
|
3.58
10-7
|
1.43
10-7
|
2.15
10-7
|
|
3
|
1.6
|
3.40
10-7
|
1.53
10-7
|
1.87
10-7
|
|
4
|
1.9
|
3.21
10-7
|
1.62
10-7
|
1.59
10-7
|
|
5
|
2.2
|
3.03
10-7
|
1.71
10-7
|
1.32
10-7
|
|
6
|
2.5
|
2.87
10-7
|
1.77
10-7
|
1.10
10-7
|
|
7
|
2.8
|
2.71
10-7
|
1.84
10-7
|
0.87
10-7
|
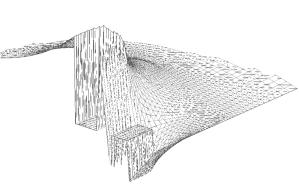
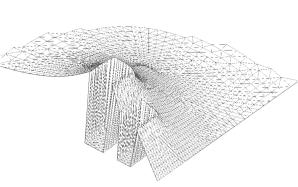
Как несложно заметить, с увеличением ширины рельса происходит
уменьшение значения искомой погонной индуктивности конструкции. На рис. 2.2
показаны рассчитанные картины распределений компонентов полей в рельсотроне в
различных сечениях. Они типичны для данных расчетов.
|
|
|
|
Напряженность
электрического поля.
|
|

|
|
|
Напряженность
магнитного поля.
|
|
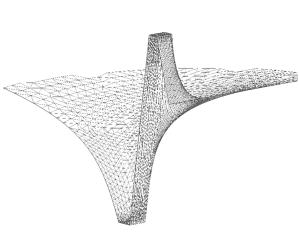
|

|
|
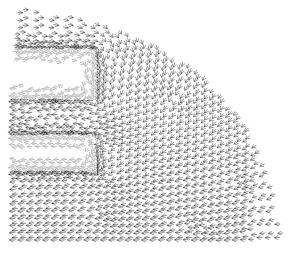
Поле
векторного потенциала.
|
|
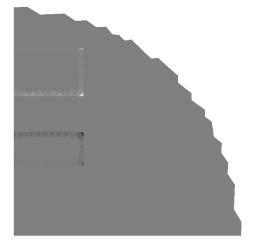
|

|
|
Распределение
токов по проводникам.
|
|
Поля
в выходном сечении ускорителя.
|
Поля
во входном сечении ускорителя.
|
|
Рис.
2.2. Картины полей в сечениях ускорителя.
|
1.2. Зависимость погонной
индуктивности от калибра ствола и расстояния между рельсами.
Данные расчеты посвящены изучению зависимости погонной
индуктивности от калибра ствола и расстояния между верхним и нижним рельсами.
Произведено, как и ранее, семь расчетов. Конфигурации отличались изучаемыми
размерами. Ширина верхнего проводника бралась равной 2.8 см.
Рассчитанные значения погонной индуктивности представлены в
Табл. 2.1.2.
Табл.
2.1.2.
|
№
|
D/2,
см
|
d, см
|
Lp1,
Гн/м
|
Lp2,
Гн/м
|
Lp,
Гн/м
|
|
1
|
1.0
|
0.5
|
2.59
10-7
|
1.82
10-7
|
0.77
10-7
|
|
2
|
0.8
|
0.5
|
2.39
10-7
|
1.96
10-7
|
0.43
10-7
|
|
3
|
0.7
|
0.5
|
2.19
10-7
|
2.13
10-7
|
0.06
10-7
|
|
4
|
0.6
|
0.5
|
1.97
10-7
|
2.32
10-7
|
-0.35
10-7
|
|
5
|
0.5
|
0.5
|
1.93
10-7
|
2.56
10-7
|
-0.83
10-7
|
|
6
|
0.5
|
0.3
|
1.88
10-7
|
1.97
10-7
|
-0.09
10-7
|
|
7
|
0.5
|
0.1
|
2.71
10-7
|
0.98
10-7
|
1.12
10-7
|
Как видно, погонная индуктивность быстро падает с уменьшением
калибра ствола вплоть до отрицательных значений, что приводит к невозможности
разгона якоря в нужном направлении для таких конфигураций.
С уменьшением зазора между проводниками от 0.5 см до 0.1 см
наблюдается увеличение Lp до 1.12 10-7 Гн/м. Аналогичные
результаты были получены в [7].
2. Группа расчетов № 2. Рельс - "скобка".
Рассмотрим конструкцию, схема которой представлена на рис. 2.3.
Теперь верхний рельс имеет форму "скобки" и частично прикрывает
нижний проводник.
В вариантах расчетов изменялись параметры d и Wзаз -
высота и ширина зазора между проводниками соответственно, H - высота
"скобки".
Количество расчетных узлов – 13000 - 17000, элементов – 24000 -
33000.
|
Рис.
2.3. Типичный вид конфигурации с рельсом - "скобкой".
|
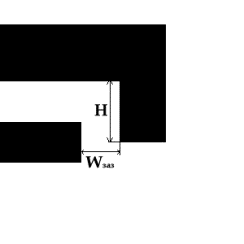
|
Результаты расчетов приведены в табл. 2.2.1.
Табл.
2.2.1.
|
№
|
d, см
|
Wзаз,
см
|
H, см
|
Lp1,
Гн/м
|
Lp2,
Гн/м
|
Lp,
Гн/м
|
|
1
|
0.5
|
0.5
|
0.5
|
2.88
10-7
|
1.74
10-7
|
1.14
10-7
|
|
2
|
0.5
|
0.5
|
1.0
|
2.78
10-7
|
1.84
10-7
|
0.74
10-7
|
|
3
|
0.5
|
0.5
|
1.5
|
1.94
10-7
|
2.03
10-7
|
-0.09
10-7
|
|
4
|
0.5
|
0.8
|
1.5
|
1.75
10-7
|
2.19
10-7
|
-0.44
10-7
|
|
5
|
0.5
|
1.1
|
1.5
|
1.71
10-7
|
2.26
10-7
|
-0.55
10-7
|
|
6
|
0.5
|
0.2
|
1.5
|
1.77
10-7
|
1.50
10-7
|
0.27
10-7
|
|
7
|
0.2
|
0.2
|
1.5
|
1.84
10-7
|
1.15
10-7
|
0.69
10-7
|
Как видно, погонная индуктивность падает при увеличении степени
закрытости нижнего проводника и растет при уменьшении зазора между
проводниками. Видно также, что данные результаты качественно совпадают с
результатами п. 1.1 и п. 1.2.
3. Группа расчетов № 3. Цилиндрические проводники.
|
Рис.
2.4. Цилиндрические направляющие - рельсы.
|
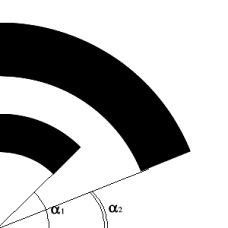
|
Рассмотрим вариант рис. 2.4, в котором оба рельса имеют
цилиндрическую форму.
В проведенных расчетах изменялись параметры α1 и
α2. Количество расчетных узлов – 15000 - 19000, элементов –
29000 - 38000.
Результаты расчетов приведены в табл. 2.3.1.
Табл.
2.3.1.
|
№
|
α1,
град
|
α2,
град
|
Lp1,
Гн/м
|
Lp2,
Гн/м
|
Lp,
Гн/м
|
|
1
|
45
|
45
|
2.96
10-7
|
1.52
10-7
|
1.44
10-7
|
|
2
|
45
|
38
|
2.77
10-7
|
1.65
10-7
|
1.12
10-7
|
|
3
|
45
|
31
|
2.58
10-7
|
1.73
10-7
|
0.85
10-7
|
|
4
|
45
|
24
|
2.28
10-7
|
1.85
10-7
|
0.43
10-7
|
|
5
|
45
|
17
|
2.09
10-7
|
1.99
10-7
|
0.10
10-7
|
|
6
|
45
|
10
|
1.50
10-7
|
2.10
10-7
|
-0.60
10-7
|
|
7
|
55
|
10
|
1.54
10-7
|
2.49
10-7
|
-0.95
10-7
|
Как и в п. 2, погонная индуктивность падает при увеличении
степени закрытости нижнего проводника, а ее значения качественно соответствуют
результатам предыдущих расчетов.
4. Группа расчетов № 4. Положение экрана.
Расчеты данной группы проведены с целью исследования зависимости
погонной индуктивности от радиуса удаления идеально проводящего защитного
контура.
В качестве базовой конфигурации выбрана первая задача (п. 1.1).
Соответствующие результаты, в частности, приведены в расчете № 1 в табл. 2.1.1.
Результаты расчетов для различных R
представлены ниже.
Табл.
2.4.1.
|
№
|
R, м
|
Lp1,
Гн/м
|
Lp2,
Гн/м
|
Lp,
Гн/м
|
|
1
|
0.6
|
3.7277
10-7
|
1.3365
10-7
|
2.3912
10-7
|
|
2
|
1.5
|
3.7327
10-7
|
1.3345
10-7
|
2.3982
10-7
|
|
3
|
3.0
|
3.7334
10-7
|
1.3339
10-7
|
2.3995
10-7
|
|
4
|
4.5
|
3.7335
10-7
|
1.3338
10-7
|
2.3997
10-7
|
Как показали расчеты, для получения погонной индуктивности, с
высокой точностью соответствующей бесконечно удаленному экрану, достаточно
сравнительно небольшого удаления экрана. Отметим, что во всех других группах
расчетов, приведенных ранее, использовалось удаление экрана на 3 метра.
Заключение.
Данная работа
посвящена расчету погонной индуктивности электромагнитных ускорителей типа
рельсотрон со сложной системой токоподводов. Для этого использовано
пространственно двумерное приближение, в котором погонная индуктивность
рассчитывается через поток магнитного поля на торцах области. Магнитное поле в
свою очередь есть результат решения интегро – дифференциального уравнения для
компоненты векторного потенциала. Для такого уравнения разработан и программно
реализован вычислительный алгоритм. Примеры его применения в виде рассчитанных
значений погонной индуктивности для ряда распространенных конструкций
представлены в работе.
Литература.
1.
Материалы I Всесоюзного семинара по динамике сильноточного дугового разряда в
магнитном поле (Новосибирск, 10-13 апреля 1990 г.). // Под ред. М.Ф. Жукова.
Новосибирск. Изд. Инст. Теплофизики СО АН СССР. 1990. 350 с.
2.
Материалы II Всесоюзного семинара по динамике сильноточного дугового разряда в
магнитном поле (Новосибирск, 4-6 декабря 1991г.). // Под ред. В.Е. Накорякова.
Новосибирск. Изд. Инст. Теплофизики СО РАН. 1992. 367 с.
3. M.Cowan. A Momentum Limit for Electromagnetic Rialgun.
IEEE Transaction on Magnetics, v.29,No1,1993, p.391-396.
4.
Крылов М.К., Кузнецов В.В., Лотоцкий А.П., Халимуллин Ю.А., Галанин М.П.,
Савичев В.В. Структура электрической части рельсотрона с распределенным вдоль
канала вводом энергии. Коммутация токов индуктивных накопителей. // Препринт
ГНЦ РФ ТРИНИТИ. 2001. № 0082 – А. 26 с.
5.
Крылов М.К., Кузнецов В.В., Лотоцкий А.П., Халимуллин Ю.А., Галанин М.П.,
Савичев В.В. Магнитная конфигурация канала рельсотрона с обращенным
токоподводом. Перенос тока в зоне якоря. // Препринт ГНЦ РФ ТРИНИТИ. 2001. № 0083 – А. 23 с.
6. A A.P. Lototsky,
Yu.A. Kareev, A.A.Nikolashin, Yu.A. Halimullin, E.P.Polulyah, M.P.Galanin,
S.S.Khramtsovsky. Recent Muzzle - Fed
Railgun Experiment on Metal Armature for Arcless Acceleration. // IEEE Trans. On Magn. 1999. V. 35. № 1. P. 79 - 85.
7. М.П.
Галанин, А.П. Лотоцкий, Ю.П. Попов, С.С. Храмцовский. Численное моделирование
пространственно трехмерных явлений при электромагнитном ускорении проводящих
макротел // Математическое моделирование. 1999. Т. 11. № 8. С. 3 - 22.
8. М.П. Галанин,
А.Д. Лебедев, А.П. Лотоцкий, К.К. Миляев. Тепловые и электромагнитные процессы
на контактах электродинамического ускорителя // Препр. ИПМ им. М.В. Келдыша
РАН. 2000. № 42. 32 с.
9. Г.А. Кнопфель.
Сверхсильные импульсные магнитные поля. М., Мир. 1972. 391 с.
10. М.П. Галанин,
В.П. Игнатко, Ю.П. Попов, С.С. Храмцовский. Пространственно трёхмерные расчеты
электродинамического ускорения проводящих макротел. // ЖТФ. 1995. Т. 65. Вып.
6. С. 9-20.
11. М.П.
Галанин. Компьютерное моделирование в задачах конвертирования электромагнитной
и кинетической энергии. Задачи и модели. // Информационные технологии и
вычислительные системы. 2002. № 4. С. 109 - 123.
12. М.П. Галанин.
Компьютерное моделирование в задачах конвертирования электромагнитной и
кинетической энергии. Решение задач. // Информационные технологии и
вычислительные системы. 2003. № 1 – 2. С. 112 - 127.
13. П.Л. Калантаров, Л.А. Цейтлин. Расчет индуктивностей. Лен - д,
Энергоатомиздат. 1986. 488 с.
14. Тамм И.Е. Основы теории электричества.
М. Наука. 1966. 624 с.
15. М.П. Галанин, Ю.П. Попов.
Квазистационарные электромагнитные поля в неоднородных средах: Математическое
моделирование. М. Наука, Физматлит. 1995. 320 с.
16. М.П. Галанин, С.С.
Храмцовский. Решение пространственно трехмерных задач электромагнитного
ускорения в системе длинных проводников. // Препр. Инст. Прикл. Матем. им. М.В.
Келдыша РАН. 1998. № 29. 20 с.
17. Никольский В.В, Никольская Т.И.
Электродинамика и распространение радиоволн. М. Наука. 1989. 544 с.
18. D.S. Kershaw.
The incomplete Cholessky - Conjugate Gradient Method for the iterative solution
of system of a linear equations. // J. Comput. Phys. 1978. V. 26. P. 43 - 65.
19. А. Джордж, Дж. Лю. Численное решение
больших разреженных систем уравнений. М. Мир. 1984. 333 с.
|