Аннотация
В условиях малости модифицированного числа Маха и числа Струхаля, выведена система, описывающая движение твердого тела в газе с произвольной гладкой выпуклой границей в приближении постоянной массы и геометрии масс. Учитываются зеркально-диффузное взаимодействие молекул газа с поверхностью и сорбция, относительный вклад которых зависит от координаты поверхности. Получено условие финитности системы и показано существование стационарного решения. Найдено условие единственности и глобальной устойчивости стационарного решения. Показано, что при этом условии асимтотикой координатной траектории является цилиндрическая спираль.
Abstract
Under the condition of little Mach number and Strouhal number the dynamical system describing dynamics of solid with smooth convex surface was driven in the approach of steady mass and steady mass geometry. The interaction is considered be nonuniform combination of diffuse, elastical and sorption. The condition of finiteness of system solution was derived. The condition of uniqueness and global stability of steady state solution was found. Under this condition the asymptotic of coordinate trajectory is shown to be a cylindrical helix, that is qualitatively correspond some experimental results.
Введение
Задача описания
движения твердого тела в газе, молекулы которого могут осаждаться на его
поверхности, возникла из приложения. В 90 гг. группой, возглавляемой И. В.
Мелиховым, было открыто явление, названное хемореактивным движением [9]. Оно
заключалось в том, что в газе при неоднородном по поверхности твердой частицы
химическом процессе тело приходило в дополнительное движение. Позже на
основании их идей в ESA (European Space Agency) был поставлен эксперимент [12], в котором в
условиях микрогравитации наблюдалось движение растущих кристаллов уротропина.
Траектории частиц оказались спиралевидными.
В работе [6] была
предложена простейшая модель, позволившая на основании кинетического подхода
получить уравнения, среди приближенных решений которых были спиралевидные
траектории, что позволило качественно объяснить эксперимент.
Эти идеи получили
дальнейшее развитие в [2,3] где на основании кинетического подхода были
выведены уравнения динамики твердого тела произвольной выпуклой формы в
газе при наличии сорбции. В том числе
был предложен способ учесть изменение геометрии поверхности и геометрии масс.
В §1 содержится
описание модели, в §2 получены основные уравнения. В §2 обсуждается необходимое
условие применимости модели – финитность решения, которое обеспечивается
диссипативностью линейной части системы, а также устанавливается существование
стационарного решения. В §3 найдено условие единственности и глобальной
устойчивости стационарного решения. В §4 устанавливается вид асимптотики
координатных траекторий при условии глобальной устойчивости стационара.
§1 Описание модели
Рассмотрим твердое
тело, движущееся в разреженном газе. Пусть 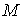 - его масса, - его масса, 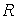 - координаты центра
масс, - координаты центра
масс, 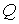 - импульс, - импульс, 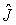 - тензор инерции относительно центра масс, - тензор инерции относительно центра масс, 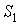 , ,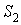 , ,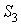 - единичные векторы, направленные вдоль главных осей
инерции, - единичные векторы, направленные вдоль главных осей
инерции, 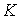 - кинетический
момент. Наряду с импульсом и кинетическим
моментом будут использованы связанные с
ними величины: - кинетический
момент. Наряду с импульсом и кинетическим
моментом будут использованы связанные с
ними величины: 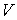 - поступательная скорость центра масс и - поступательная скорость центра масс и 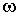 - угловая скорость.
Стандартно: - угловая скорость.
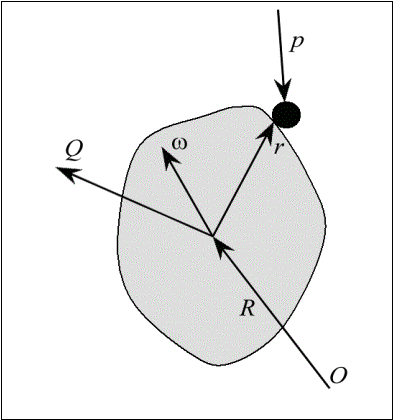
Стандартно: 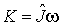 и и 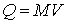 . (Рис. 1) . (Рис. 1)
Обозначим обобщенное
произведение двух векторов как: 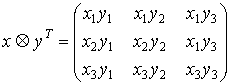 . Тогда если . Тогда если 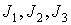 - главные центральные
моменты инерции, то тензор инерции тела можно представить в виде: - главные центральные
моменты инерции, то тензор инерции тела можно представить в виде: 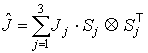 . .
Если 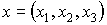 - трехмерный вектор, сопоставим ему в
соответствие объект - трехмерный вектор, сопоставим ему в
соответствие объект 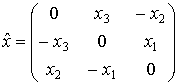 . Тогда обычное векторное произведение . Тогда обычное векторное произведение 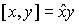 . .
Будем учитывать три
типа взаимодействия молекул газа с поверхностью[6,7]: зеркальное или упругое
отражение, диффузное отражение и сорбция. Будем обозначать слагаемые,
соответствующие каждому типу взаимодействия индексами 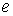 (elastic)- зеркальный тип, (elastic)- зеркальный тип, 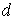 (diffuse)- диффузный тип, (diffuse)- диффузный тип, 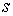 (sorption) - сорбция. (sorption) - сорбция.
Силы и моменты
действующие на твердое тело в газе [2,3]:
(1) 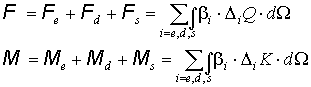
Здесь функции 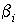 , , 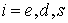 есть веса,
указывающие относительную долю соударений каждого типа. В принципе их
аргументами могут быть координата поверхности есть веса,
указывающие относительную долю соударений каждого типа. В принципе их
аргументами могут быть координата поверхности 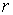 , относительная скорость , относительная скорость 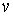 и нормаль и нормаль 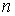 к поверхности в точке
падения молекулы газа: к поверхности в точке
падения молекулы газа: 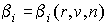 , но мы будем рассматривать упрощенную ситуацию, при которой
функции , но мы будем рассматривать упрощенную ситуацию, при которой
функции 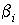 зависят только от
координаты поверхности: зависят только от
координаты поверхности: 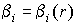 . Координата поверхности задается в собственной (связанной с
телом) системе координат. Весовые функции . Координата поверхности задается в собственной (связанной с
телом) системе координат. Весовые функции 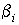 должны удовлетворять
условию неотрицательности должны удовлетворять
условию неотрицательности 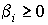 , , 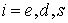 и в сумме давать
тождественную единицу при всех допустимых значениях аргументов: и в сумме давать
тождественную единицу при всех допустимых значениях аргументов: 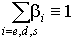 . .
Пусть 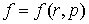 - функция
распределения молекул газа по пространственной координате и импульсу [7,11].
Тогда дифференциальная частота столкновений молекул газа с телом есть число
молекул в элементарном фазовом объеме
падающих за единицу времени на тело извне его границы. Она определяется выражением: - функция
распределения молекул газа по пространственной координате и импульсу [7,11].
Тогда дифференциальная частота столкновений молекул газа с телом есть число
молекул в элементарном фазовом объеме
падающих за единицу времени на тело извне его границы. Она определяется выражением:
(2) 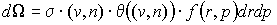 . .
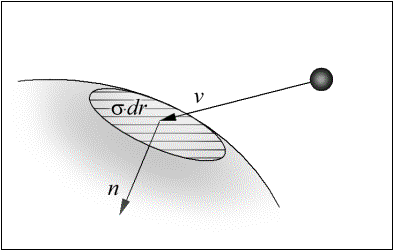
где 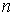 - внутренняя нормаль в точки поверхности тела - внутренняя нормаль в точки поверхности тела 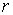 , а , а 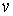 - относительная скорость: - относительная скорость: 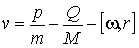 . (Рис. 2) . (Рис. 2)
Геометрическое
сечение столкновений 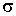 в случае тела с
выпуклой границей, заданной уравнением в случае тела с
выпуклой границей, заданной уравнением 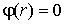 , где , где 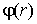 - кусочно-гладкая функция в - кусочно-гладкая функция в 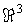 , может быть записано в виде [2,3]: , может быть записано в виде [2,3]:
(3) 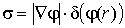 . .
Укажем изменения
динамических величин для различных типов взаимодействий [2, 3]. При упругом
(зеркальном ) отражении:
(4') 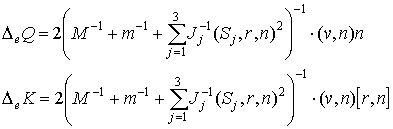
При диффузном отражении:
(4") 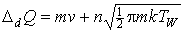 , , 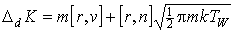 . .
При сорбции:
(4'") 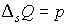 , , 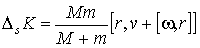 , ,
Сделаем следующие предположения:
I. Функция распределения молекул газа – максвелловская [7,11]:
(5) 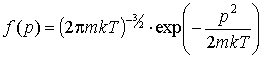 . .
II. Модифицированное число Маха 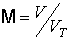 и число Струхаля и число Струхаля 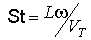 [4] малы по сравнению
с единицей. Здесь [4] малы по сравнению
с единицей. Здесь 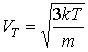 - тепловая скорость
молекул газа, - тепловая скорость
молекул газа, 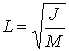 - характерный линейный размер тела, - характерный линейный размер тела, 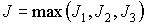 - максимальный главный момент инерции. - максимальный главный момент инерции.
III. Либо 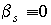 , либо изменение
массы и геометрии масс
пренебрежимо малы по
ходу процесса. Малость
изменения геометрии
масс при сорбции подразумевает,
что тело не обладает динамической симметрией: , либо изменение
массы и геометрии масс
пренебрежимо малы по
ходу процесса. Малость
изменения геометрии
масс при сорбции подразумевает,
что тело не обладает динамической симметрией: 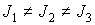 , причем , причем 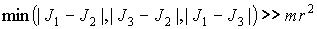 во всех точках во всех точках 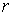 , где , где 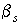 принимает ненулевые
значения. принимает ненулевые
значения.
Условие I, с одной стороны
является физически естественным для движения в разреженном газе. С другой
стороны, вместе с тем допущением, что функции 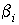 зависят только от
координаты поверхности, это условие
позволяет провести интегрирование по скоростям в выражениях для силы и момента
сил (1). Условие II обеспечивает возможность линеаризовать силу и
момент по динамическим переменным. Условие III позволяет пренебречь
изменением массы и геометрии масс в уравнениях динамики [2,3]. зависят только от
координаты поверхности, это условие
позволяет провести интегрирование по скоростям в выражениях для силы и момента
сил (1). Условие II обеспечивает возможность линеаризовать силу и
момент по динамическим переменным. Условие III позволяет пренебречь
изменением массы и геометрии масс в уравнениях динамики [2,3].
§2 Основные уравнения
Итак, найдем силу и момент
сил в линейном приближении (вывод см. дополнение):
(6) 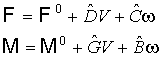
Здесь члены нулевого
порядка:
(7) 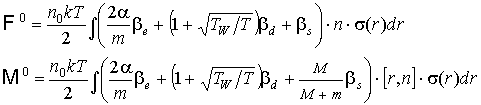
где 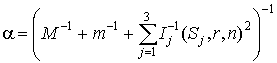 ; ;
матрицы коэффициентов в
членах первого порядка:
(8) 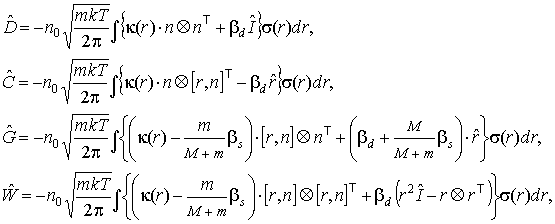
где 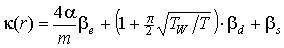 . .
В неподвижной системе
координат динамическая система будет иметь вид:
(9) 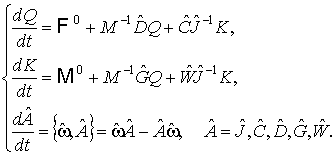
Здесь третья часть системы
отражает зависимость матриц коэффициентов (8) и тензора инерции от времени
из-за вращения собственной системы координат.
Воспользуемся условием III и перейдем в
собственную систему координат, базис которой составляют орты, направленные
вдоль собственных осей. Такой переход есть линейное преобразование 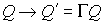 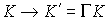 , определяемое матрицей Грамма , определяемое матрицей Грамма 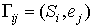 , компоненты которой есть проекции векторов главных осей на
орты неподвижного базиса , компоненты которой есть проекции векторов главных осей на
орты неподвижного базиса 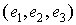 . Опустим штрихи во избежание громоздкости записей, в
следующем и всех дальнейших выражениях полагая (если не оговорено противное)
все величины заданными в собственной системе координат. Итак, получим динамическую систему: . Опустим штрихи во избежание громоздкости записей, в
следующем и всех дальнейших выражениях полагая (если не оговорено противное)
все величины заданными в собственной системе координат. Итак, получим динамическую систему:
(10) 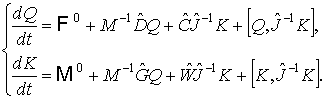
где векторы
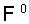 и
и
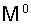 , а также все матрицы коэффициентов постоянны.
, а также все матрицы коэффициентов постоянны.
Замечание. Если в системе (10)
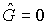 , или наложена связь , или наложена связь 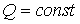 , то уравнение на кинетический момент , то уравнение на кинетический момент 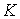 с точностью до
постоянного члена (и обозначений) совпадает с уравнением для динамики твердого
тела в сопротивляющейся среде [5]. с точностью до
постоянного члена (и обозначений) совпадает с уравнением для динамики твердого
тела в сопротивляющейся среде [5].
(10’) 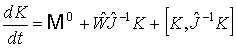
Авторы
книги [5] указали на возможный случай, когда уравнение на кинетический момент
может совпадать с известной системой Лоренца. Однако, следует уточнить, что
указанное ими условие диссипативности линейной части – отрицательность следа
соответствующей матрицы – является
недостаточным, а лишь необходимым. В действительности критерием диссипативности
является отрицательная определенность матрицы 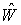 (легко убедиться что
матрица (легко убедиться что
матрица 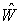 , определенная в (8)
этому критерию удовлетворяет). , определенная в (8)
этому критерию удовлетворяет).
Тем не
менее, система Лоренца
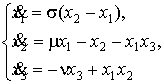 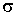 , ,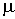 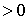
действительно может быть
получена из (10’) преобразованием сдвига 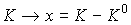 , если: , если:
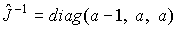 , , 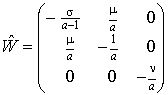 , ,
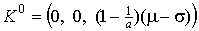 , , 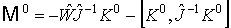
Здесь параметр 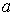 выбирается следующим
образом: если выбирается следующим
образом: если 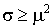 , то , то 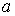 произвольное число
из интервала произвольное число
из интервала 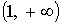 , если , если 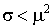 , то , то 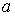 берется из интервала берется из интервала
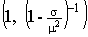 . .
Этот
факт может служить иллюстрацией того, что в общем случае система (10) может
обладать довольно сложным поведением.
§3
Финитность и существование стационара
По определению механическая энергия системы
есть:
(11) 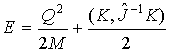
Исследуем вопрос об убывании
энергии в силу линейной части уравнения:
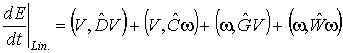
Условием диссипативности линейной части
является существование положительной константы:
(12) 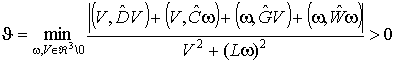
Введем
вектор 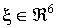 : : 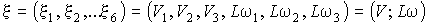 . И определим матрицу: . И определим матрицу: 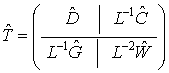 . Тогда . Тогда 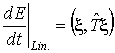 , и условие диссипативности линейной части запишется в виде: , и условие диссипативности линейной части запишется в виде:
(13) 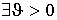 : : 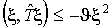 . .
Замечание. Рассмотрим
квадратичную форму:
(3.13') 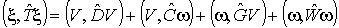 . .
из (3.8) получим:
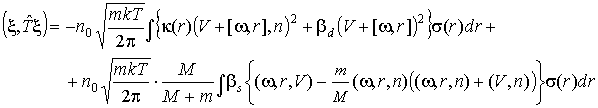 Таким образом, квадратичная форма (3.13') может быть
представлена в виде суммы двух, одна из которых строго отрицательно определенная,
а другая линейно зависит от коэффициента сорбции. Получим, что если Таким образом, квадратичная форма (3.13') может быть
представлена в виде суммы двух, одна из которых строго отрицательно определенная,
а другая линейно зависит от коэффициента сорбции. Получим, что если 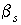 достаточно мало, так
что норма первой больше, чем второй, то линейная часть диссипативна. достаточно мало, так
что норма первой больше, чем второй, то линейная часть диссипативна.
Нетрудно
заметить, что если 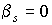 , то , то 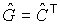 Таким образом,
перекрестные коэффициенты, соответствующие зеркально-диффузному взаимодействию,
удовлетворяют принципу симметрии Онзагера. Коэффициенты, соответствующие
сорбции ему не удовлетворяют, что объясняется тем, что сорбция – процесс принципиально
неравновесный. Таким образом,
перекрестные коэффициенты, соответствующие зеркально-диффузному взаимодействию,
удовлетворяют принципу симметрии Онзагера. Коэффициенты, соответствующие
сорбции ему не удовлетворяют, что объясняется тем, что сорбция – процесс принципиально
неравновесный.
Также
при 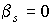 энергия убывает в
силу линейной части для любой геометрии тела. Если энергия убывает в
силу линейной части для любой геометрии тела. Если 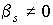 , то это, вообще говоря, не так, и зависит от геометрии
системы. , то это, вообще говоря, не так, и зависит от геометрии
системы.
Заметим,
что в силу эйлеровой части уравнений (квадратичные члены, возникшие за
счет перехода во вращающуюся систему
координат) энергия сохраняется. Поэтому, в тех случаях, когда линейная часть
диссипативна, всякое решение уравнений (10) финитно. Строгое доказательство
этого факта дает следующая теорема.
Теорема 1. Если линейная
часть системы (10) диссипативна, т.е. существует константа 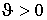 , то любое решение её финитно (заключено в некоторой ограниченной области). , то любое решение её финитно (заключено в некоторой ограниченной области).
Доказательство:
Предположим, что энергия
превышает некоторое пороговое значение: 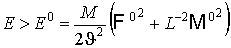 , тогда квадрат модуля , тогда квадрат модуля 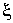 удовлетворяет
неравенству: удовлетворяет
неравенству:
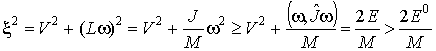
Отсюда легко получить оценку на скорость
изменения энергии по времени:
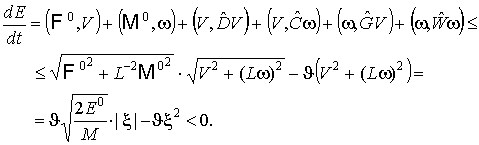
Таким образом, если энергия
системы больше, чем 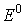 , то она убывает в силу динамической системы. Следовательно,
для любого решения, начиная с некоторого момента времени, решение будет
принадлежать множеству, на котором , то она убывает в силу динамической системы. Следовательно,
для любого решения, начиная с некоторого момента времени, решение будет
принадлежать множеству, на котором 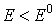 . Поскольку энергия есть положительно определенная
квадратичная форма динамических переменных, решение системы финитно. ▲ . Поскольку энергия есть положительно определенная
квадратичная форма динамических переменных, решение системы финитно. ▲
Следствие 1. Если система
финитна, то у нее, согласно теореме о трансверсальной поверхности векторного
поля [8, гл. 3, §14] существует стационарное
решение. В данном случае трансверсальной поверхностью к векторному полю
скоростей системы (10) является поверхность уровня энергии 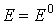 . .
Будем рассматривать только финитные системы, у которых энергия убывает
в силу линейной части, так как в случае неограниченного роста решения выбранное
приближение станет неприменимым.
§4
Условие глобальной устойчивости стационара.
Обозначим 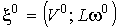 - стационарную точку в пространстве скоростей,
соответствующую стационарным значениям импульса - стационарную точку в пространстве скоростей,
соответствующую стационарным значениям импульса 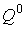 и кинетического
момента и кинетического
момента 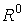 . Из теоремы 1 следует, что для стационарного решения
справедлива оценка: . Из теоремы 1 следует, что для стационарного решения
справедлива оценка:
(15) 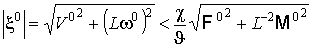 , где , где 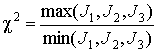
Найдем условие, при котором
стационарное решение будет устойчиво.
Рассмотрим функцию:
(16) 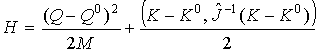
Продифференцируем ее по времени в силу
системы (10).
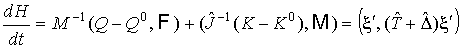
 где где 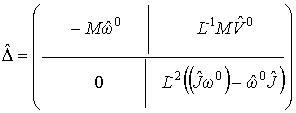 , , 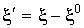 . .
Теорема 2. (Достаточное
условие глобальной устойчивости) Пусть для системы (10) существует 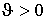 , и верно неравенство: , и верно неравенство:
(17) 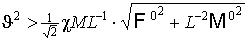
Тогда стационарное решение единственно и
глобально устойчиво.
Доказательство: Выполним оценку, используя
неравенство (16):
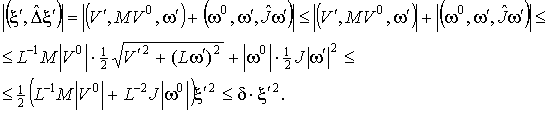
Здесь
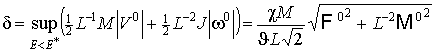 . .
Отсюда и из
неравенства (17) следует,
что 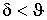 . Следовательно . Следовательно 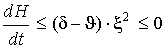 , причем ноль достигается только в стационарной точке.
Поскольку функция , причем ноль достигается только в стационарной точке.
Поскольку функция 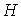 - выпуклая функция своих аргументов, она стремится к своему
единственному минимуму, а решение, соответственно, к стационарной точке, в которой этот минимум достигается. - выпуклая функция своих аргументов, она стремится к своему
единственному минимуму, а решение, соответственно, к стационарной точке, в которой этот минимум достигается.
§5
Вид траекторий в координатном пространстве.
Рассмотрим случай,
когда система финитна, постоянная сила и момент (7) не равны нулю одновременно
и выполнено условие (17). Тогда, в
собственной системе координат все траектории системы (10) сходятся к
единственной точке 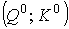 . Найдем асимптотику траекторий в координатном пространстве.
Предельные значения скорости и угловой частоты в собственной системе координат . Найдем асимптотику траекторий в координатном пространстве.
Предельные значения скорости и угловой частоты в собственной системе координат 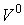 и и 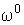 . Тогда в неподвижной системе: . Тогда в неподвижной системе:
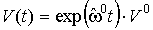
Интегрируя, получим,
что с точностью до аддитивной постоянной:
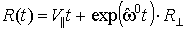 , ,
где 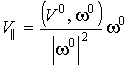 , , 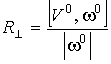 . Такое движение есть движение по цилиндрической спирали с
шагом . Такое движение есть движение по цилиндрической спирали с
шагом 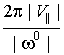 и радиусом и радиусом 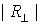 . В частных случаях полученная спираль может вырождаться в
окружность или прямую, если соответственно ее шаг или диаметр соответственно
станет равным нулю. . В частных случаях полученная спираль может вырождаться в
окружность или прямую, если соответственно ее шаг или диаметр соответственно
станет равным нулю.
Заключение
В данной работе были получены и
исследованы уравнения, описывающие динамику твердого тела в газе под действием
сил возникающих при неоднородном по поверхности взаимодействии газа с телом.
Найдено условие типа неравенства,
обеспечивающее сходимость к сравнительно простому движению: вращению с
постоянной угловой скоростью и поступательное движение центра масс вдоль
цилиндрической спирали.
Фактически найденное условие
единственности и глобальной устойчивости стационара есть условие малости
постоянных компонент силы и момента по отношению к диссипативным силам и
моментам, или, что то же самое, это есть ограничение на вклад неоднородности и
неравновесности поверхностных процессов. При невыполнении этого условия следует
ожидать более сложного поведения системы, что представляет большой интерес для
дальнейших исследований.
Автор благодарит В. В. Веденяпина, М.
В. Масленникова и Ю. Н. Орлова, чьи советы и замечания в значительной мере
содействовали этой работе.
Литература
1. Арнольд В. И., Математические методы
классической механики. М.: Эдиториал
УРСС, 2000.
2. Батищева Я. Г. «К выводу уравнений
динамики твердого тела в газе, реагирующем с ним неоднородно по поверхности»//
Комплексный анализ и математическая физика.
Сборник научных трудов посвящ. 100-летию профессора А.А. Темлякова. М.:
Изд. МГОУ, 2003. С.57-64.
3. Батищева Я. Г. «К выводу уравнений
динамики твердого тела в газе, реагирующем с ним неоднородно по поверхности».
Препринт ИПМ РАН №18, 2003.
4. Белецкий В. В., Яншин А. М. Влияние
аэродинамических сил на вращательное движение спутников. Киев, Наукова думка, 1984.
5. Борисов А. В., Мамаев И. С. Динамика
твердого тела. Ижевск: НИЦ «Регулярная
и хаотическая динамика», 2001.
6. Веденяпин В. В., Батищева Я. Г., Мелихов
И. В., Горбачевский А. Я. О движении
твердого тела в газе с неоднородными поверхностными химическими процессами
// Мат.моделирование, 2003г. Т.
15, №6. С. 6-10.
7. Веденяпин В. В., Кинетические
уравнения Больцмана и Власова. – М.: Физматлит, 2001.
8. Дубровин Б.А., Новиков С.П., Фоменко А.Т.
Современная геометрия. Методы и приложения. Геометрия и топология многообразий.
Т. 2. М.: Эдиториал УРСС, 2001.
9. Мелихов И. В., Симонов Е. Ф., Ведерников
А. А. Хемореактивное движение частиц катализатора в газовой среде при
гетерогенном катализе // Ж. Физ. Хим.,
1998. Т 72, №12. С. 2300 - 2306.
10. Пярнпуу
А. А. Взаимодействие газов с поверхностями. М., "Наука", 1974.
11. Черчиньяни К.
Теория и приложение уравнения Больцмана.
М., "Мир", 1978.
12. Willneff
J., Maas H.-G. Design and calibration of four-headed camera system for use
in microgravity research.// IAPRS, Vol. XXXIII, Amsterdam, 2000. P 894-899.
Рисунки

Дополнение
Вычисление сил и моментов, действующих на тело в газе
с максвелловской функцией распределения, в линейном приближении по
поступательной и угловой скоростям.
Итак, требуется в линейном
приближении по поступательной и угловой скоростям вычислить интегралы (1):
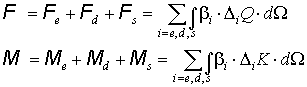
Где дифференциальная частота столкновений:
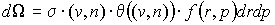
зависит от геометрической
формы поверхности через геометрическое сечение 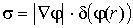 , и функции
распределения молекул газа, которая выбрана максвелловской: , и функции
распределения молекул газа, которая выбрана максвелловской:
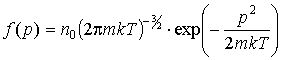 . .
Микроскопические изменения импульса и момента представлены в табл. 2
стр. Линейное приближение по скоростям означает, что искомые выражения могут
быть представлены в виде:
(п1) 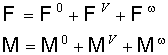 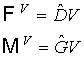 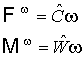
где векторы 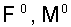 и матрицы и матрицы 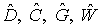 не зависят от
динамических переменных. Для вычисления этих величин выполним разложение
подынтегральных множителей - дифференциальной частоты столкновений: не зависят от
динамических переменных. Для вычисления этих величин выполним разложение
подынтегральных множителей - дифференциальной частоты столкновений:
(п3) 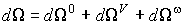 , ,
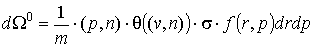 , ,
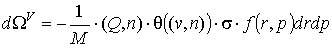 , ,
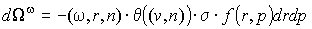 , ,
и микроскопических изменений импульса кинетического момента. При упругом
взаимодействии:
(п4) 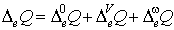 , , 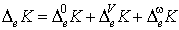 , ,
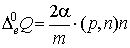 , , 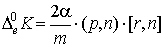 , ,
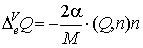 , , 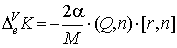 , ,
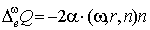 , , 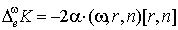 . .
где 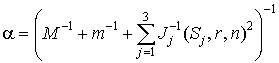 . .
При диффузном отражении:
(п4') 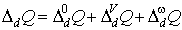 , , 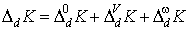 , ,
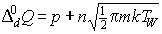 , , 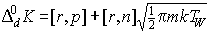 , ,
 , , 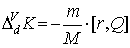 ,
,
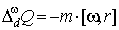 , , 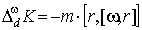 . .
При сорбции:
(п4") 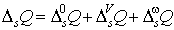 , , 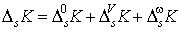 , ,
 , , 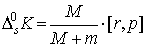 , ,
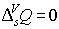 , , 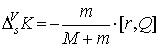 , ,
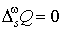 , , 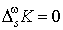 .
.
Для вычисления нулевых и первых членов разложения сил и моментов сил
нам понадобятся значения интегралов вида 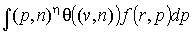 , где , где 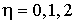 , и , и 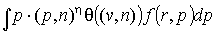 , где , где 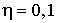 . Во-первых, заметим,
что в силу симметрии функции распределения относительно поворотов: . Во-первых, заметим,
что в силу симметрии функции распределения относительно поворотов:
(п5) 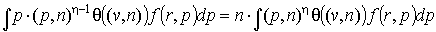 , , 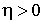 . .
Вычислим интеграл:
(п6) 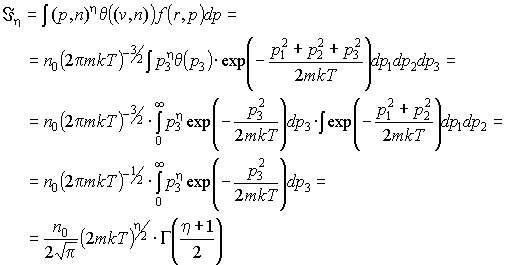
Получим:
(п7) 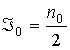 , , 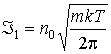 , , 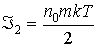
(п8) 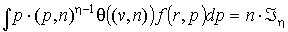 , , 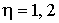 . .
Перейдем к вычислению
нулевых членов разложения сил и
моментов. Для сил:
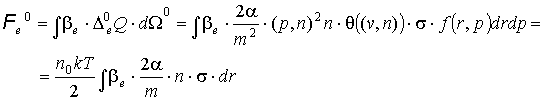
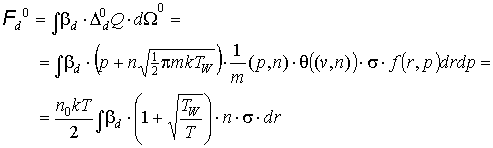
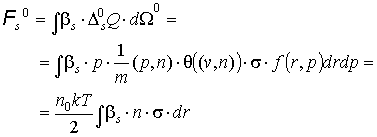
Для моментов:
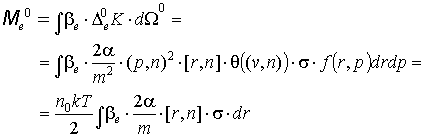
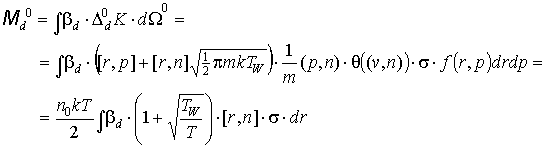
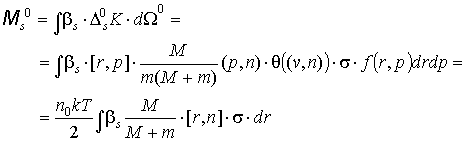
Итак, получим (7):
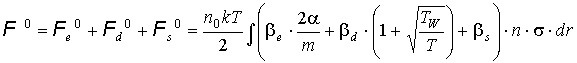
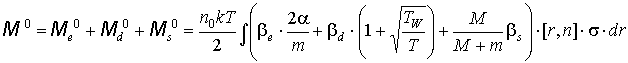
Итак, получим:
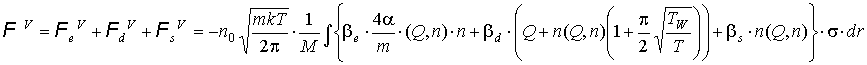
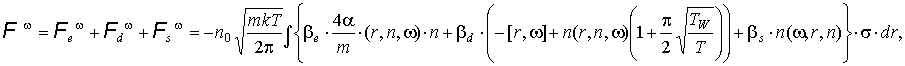 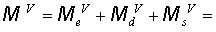
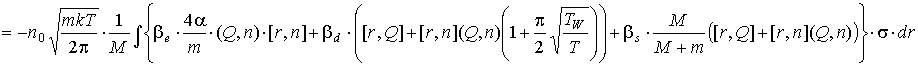
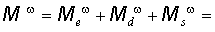
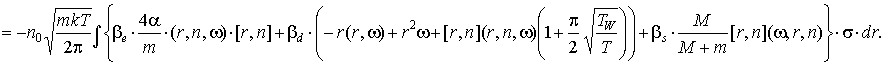
Итак, получим:
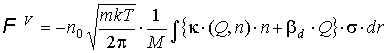 , ,
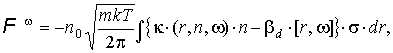
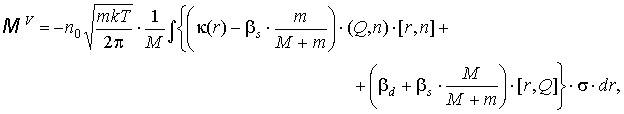 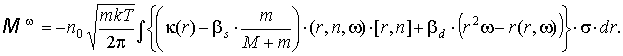 где где 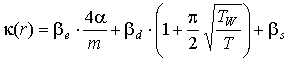 . .
Отсюда с учетом (п1) найдем матрицы
коэффициентов в линейных членах разложения (8):
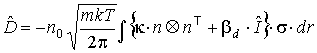 , ,
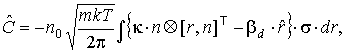
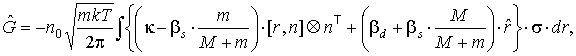
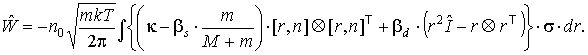
|