Аннотация
Рассмотрены некоторые краевые задачи одномерного стационарного уравнения Вигнера, описывающего частицы во внешнем поле. Для потенциала, являющегося суперпозицией линейного и ступенчатого потенциалов, найдено общее решение Фурье-представления уравнения Вигнера. Разработан алгоритм получения аналитического решения краевой задачи уравнения Вигнера в случае краевых условий, задаваемых на бесконечности.
Abstract
Some boundary problems of the one-dimensional stationary Wigner equation have been discussed for the external field case. General solution of the Fourier representation of the Wigner equation has been constructed for the superposition of the linear and stepwise potentials. The algorithm of the finding of the Wigner equation boundary problem solution has been constructed for the case of the boundary conditions assigned at the infinite points.
§1 Фурье
представление уравнения Вигнера и его решение
для суперпозиции
ступенчатого и линейного потенциалов.
В этой
работе рассматриваются различные краевые задачи для стационарного уравнения
Вигнера (в одномерном как по пространству, так и по импульсу случае) с заданным потенциалом, являющегося
суперпозицией ступенчатых и линейного потенциалов. (Одномерное уравнение
правомерно применять либо в случае нанонити, либо подразумевая, что одномерная
функция распределения есть интеграл по всем остальным измерениям фазового
пространства от исходной функции.) Уравнение Вигнера в рассматриваемом случае
имеет вид [1]:
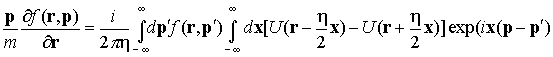 (1) (1)
Здесь f(r,p) - функция Вигнера [1], U – потенциал,
остальные обозначения - стандартные.
Перейдем к безразмерной форме
(1) , вводя следующее обезразмеривание:
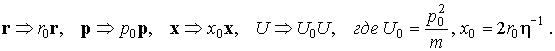
Используя это обезразмеривание и,
отказываясь, ввиду одномерности p и r от векторных обозначений, получим:
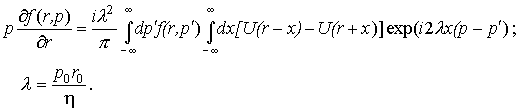 (1a) (1a)
Отметим, что из уравнения
следует 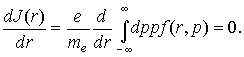
(Ток в системе постоянен по r.)
Перейдем в (1a) к
фурье-представлению f(r,p) : 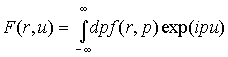 . .
В результате получим каноническую форму
гиперболического уравнения для функции двух переменных:
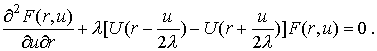 (2) (2)
Будем искать частное
решение (2) в виде 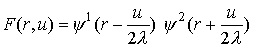 . .
В этом случае переменные разделяются и обе функции 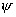 удовлетворяют
обезразмеренному стационарному уравнению Шредингера : удовлетворяют
обезразмеренному стационарному уравнению Шредингера :
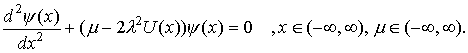 (3) (3)
В (3) m -
произвольный параметр (безразмерная
энергия). Рассмотрим на действительной оси (-¥,¥) потенциал являющейся суперпозицией ступенчатого
потенциала
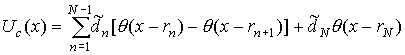
и линейного 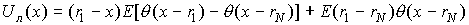
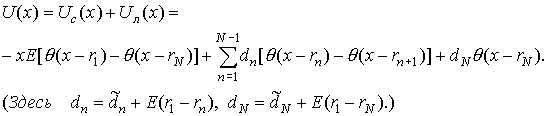 (4) (4)
В формуле (4) q (x) – функция
Хевисайда, E > 0, dn , rn - константы (rn занумерованы в порядке
возрастания, для r < r1 полагаем
потенциал равным нулю). Потенциал (4) разбивает ось x на серию интервалов. Вне
интервала (r1,rN) решение уравнения (3) имеет вид
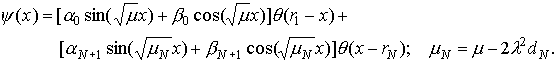 (5) (5)
Для отрицательных 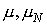 синусы и косинусы
переходят, соответственно в синусы и косинусы
переходят, соответственно в 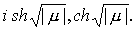 На каждом из интервалов (rn,rn+1) запишем решение уравнения (3) в виде: На каждом из интервалов (rn,rn+1) запишем решение уравнения (3) в виде:
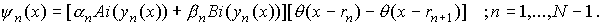 (6)
(6)
Здесь Ai, Bi –
функции Эйри [2 ], 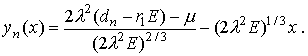 (7) (7)
Обозначим через 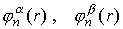 соответствующие функции на интервале (rn, rn+1), стоящие
перед коэффициентами соответствующие функции на интервале (rn, rn+1), стоящие
перед коэффициентами 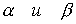 в
формулах (5,6) . Для того, чтобы суперпозиция функций
(5,6) являлась решением (3)
в классе С1 на всей
оси x, необходимо
в каждой точке rn+1 потребовать выполнения условий (являющихся
следствием непрерывности функций ψ и
их первых производных в точках rn+1: в
формулах (5,6) . Для того, чтобы суперпозиция функций
(5,6) являлась решением (3)
в классе С1 на всей
оси x, необходимо
в каждой точке rn+1 потребовать выполнения условий (являющихся
следствием непрерывности функций ψ и
их первых производных в точках rn+1:
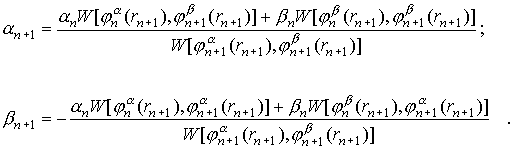 (8) (8)
Систему уравнений (8) можно, также, записать в матричном
виде:
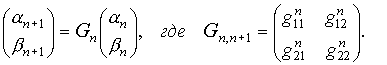 (8*) (8*)
Если условия (8) выполнены, то частным
решением (из класса непрерывно дифференцируемых на плоскости (r,w) функций) уравнения (2) для потенциала (4) будет
функция:

В (9) введено обозначение 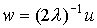 . .
§2 Условия на функцию распределения, и ее моменты.
Вид коэффициентов a и b.
В выражение (9) входят
4(N+1) коэффициентов, которые должны
удовлетворять 4N условиям (8) . Кроме принадлежности F(r,w) к классу непрерывно дифференцируемых функций, каковую
обеспечивают условия (8), на F(r,w) необходимо также наложить дополнительные условия, вытекающие из физических свойств функции
распределения f(r,p) и ее моментов. А именно: потребуем действительности
функции распределения f(r,p), не отрицательности
плотности числа частиц n(r) и
действительности и постоянства тока J(r).
Из определения соответствующих
моментов и обратного Фурье-преобразования f(r,p) следует
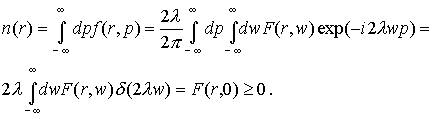
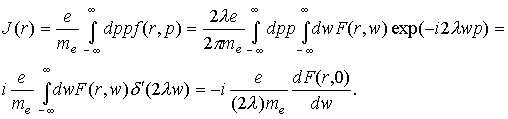 (10) (10)
(Из (10) следует, в частности,
что коэффициенты в (9) суть комплексные числа.)
При w=0 в формуле (9) остается только сумма
произведений диагональных элементов. Общий вид F(r,0) дает формула (11). 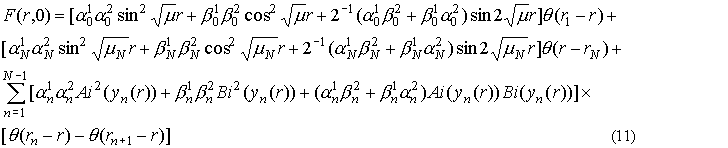 Рассмотрим n - й член суммы. Для
действительности и не отрицательности Fn(r,0) необходимо выполнения следующих
условий: Рассмотрим n - й член суммы. Для
действительности и не отрицательности Fn(r,0) необходимо выполнения следующих
условий:
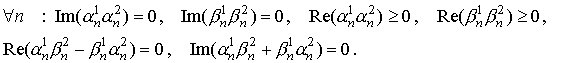 (12) (12)
Значение производной F(r,w) при w=0 получим, дифференцируя (9) и учитывая условия сшивки
функций j. На
интервалах, где поле E не равно нулю
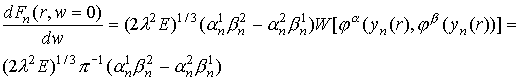 (13)
(13)
В областях, где
поле отсутствует
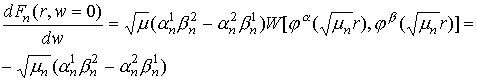 (13*) (13*)
( Производные во
вронскианах берутся по переменной yn в (13) и 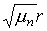 в (13*).) в (13*).)
Для действительности тока
необходимо выполнения условия
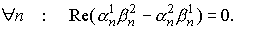 (14)
(14)
Для того чтобы
ток был одинаковым на всех интервалах, необходимо, чтобы
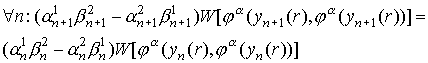 (14*) (14*)
(Здесь во
вронскианах производные берутся по переменной r.)
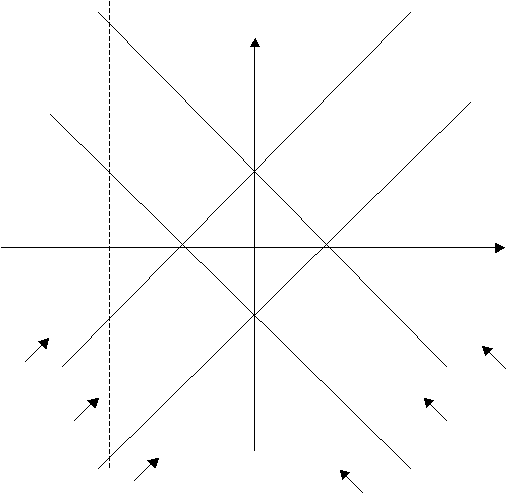
Если
представить функцию распределения f(r,p) в виде обратного Фурье-преобразования от F(r,w), то, как видно из
ниже представленного рисунка 1, обратное Фурье-преобразование можно разбить на
сумму членов, каждый из которых имеет вид
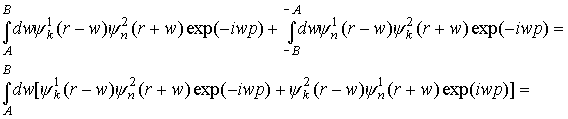
(представляя функции ψ в виде:  ) )
 w w
r*
r
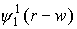 
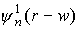 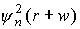
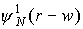 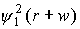
Рис. 1
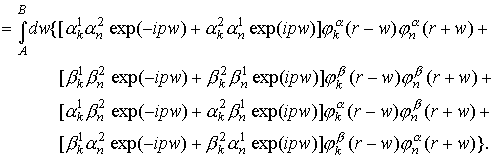 (15) (15)
Из (15) и
действительности функции распределения f(r,p)
следует:
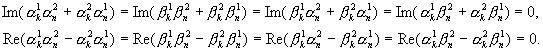 (16) (16)
Найдем, используя условия (12,14,
16) вид коэффициентов αn и βn. Пусть
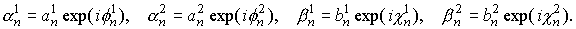
Тогда из условий (12) следует:
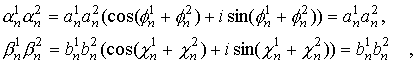 (17) (17)
откуда имеем 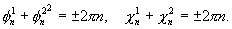
Из условий (12) также следует, что

Используя связь между углами в 17,
получаем: 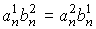 . Из полученных результатов
ясно, что коэффициенты . Из полученных результатов
ясно, что коэффициенты 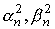 являются комплексно
сопряженными соответствующим коэффициентам являются комплексно
сопряженными соответствующим коэффициентам 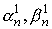 . Непосредственной
проверкой легко установить, что
коэффициенты такого вида удовлетворяют и условиям (16). . Непосредственной
проверкой легко установить, что
коэффициенты такого вида удовлетворяют и условиям (16).
Таким
образом, наиболее общий вид коэффициентов α и β, удовлетворяющих
условиям 12,14,16 имеет вид:
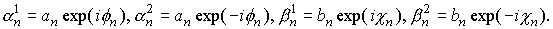 (18) (18)
При этом,
произведения коэффициентов α и β можно записать в виде
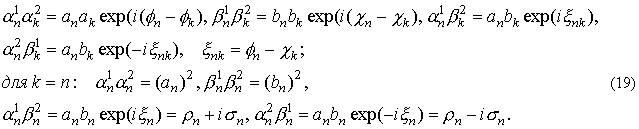 Если на каком-либо интервале (rn rn+1) задать
коэффициенты в виде (18), то преобразования (8,8*) очевидно сохраняют этот вид. Если на каком-либо интервале (rn rn+1) задать
коэффициенты в виде (18), то преобразования (8,8*) очевидно сохраняют этот вид.
Условия 12,14 (что определяет
выбор коэффициентов в виде 18) на самом деле являются достаточными для не
отрицательности плотности числа частиц n(r). Действительно, на любом интервале (rn,rn+1)
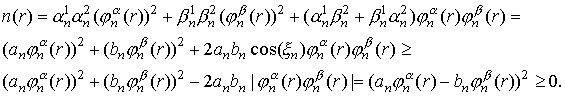
Ток во всей цепи должен быть
постоянной величиной для всех r. Покажем, что для выбранного вида
коэффициентов это утверждение выполняется.
Введем обозначения:
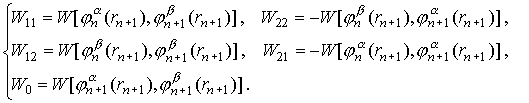 (20) (20)
Из (8) следует:
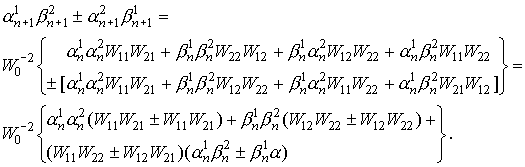 (21) (21)
Из 21 следует, что
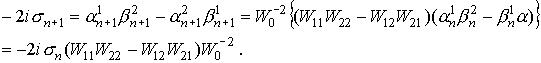
Расписывая вронскианы (см. 20),
получим:
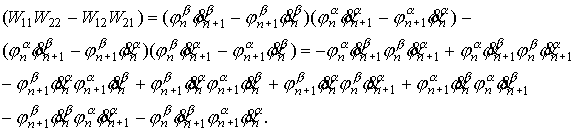 (22) (22)
Первые четыре члена в правой части 22 взаимно сокращаются;
группируя оставшиеся члены, имеем,
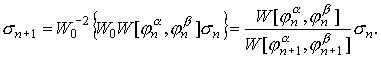 (23) (23)
(Вронскианы в (23) берутся в точке rn+1 .)
Таким образом, получено соотношение 14*, выполнение которого
обеспечивает постоянство тока.
Следовательно, доказана теорема.
Теорема.
Если на одном из
интервалов (rn rn+1) коэффициенты a, b выбраны в
виде (18), переход с интервала на интервал осуществляется согласно формулам (8),
то справедливы следующие утверждения. На всех
интервалах коэффициенты a, b можно
представить в виде (18). Для них
выполняются условия (12,14,14*,16). Плотность числа частиц неотрицательна и
принадлежит классу С1
на всей
действительной оси r. Ток действителен и постоянен на всей действительной оси r. Функция F(r,w) является непрерывно дифференцируемой на плоскости r,w. Функция распределения f(r,p) –
действительна.
Моменты функции
распределения выше первого не накладывают дополнительных условий на
коэффициенты. Действительно, используя уравнение (3), имеем, например, для
второго момента функции распределения.
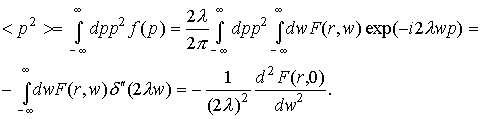 (24) (24)
При этом на n -
м интервале (индексы n опускаем):
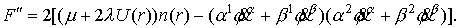 (25) (25)
Очевидно,
что если коэффициенты a, b имеют вид (18), то выражение (25)
действительно (кроме того, второе произведение в нем неотрицательно).
Для
коэффициентов a, b вида (18) формулы (11, 13, 13*) принимают следующий вид.
 (26) (26)
На интервале (rn,rn+1) 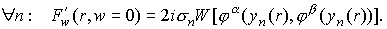 (27) (27)
(В (27)
дифференцирование во вронскианах производится по переменной r.)
Функция, задаваемая формулой (9),
является частным решением уравнения (2) при фиксированном значении параметра m. Однако суперпозиция частных решений с различными
значениями параметра m также
будет решением уравнения (2). Поэтому мы можем искать решение (2) в виде 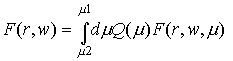 .
(28) .
(28)
§3 Краевые задачи.
Рассмотрим
различные виды краевых задач для уравнения Вигнера. Нашей конечной целью будет
определение коэффициентов функции F(r,w), вид
функции Q(m) и
нахождение связи между током J и полем E .
Для удобства
начнем рассмотрение со случая N=2. В этом случае поле действует лишь на одном интервале и,
рассмотрев на этом интервале соответствующую краевую задачу для моментов
функции распределения (для определения четырех коэффициентов a, b, ρ, σ и параметра μ необходимо,
учитывая связь между коэффициентами, задать 4 условия), казалось бы, можно
получить искомую связь между током и напряжением. Однако коэффициенты σ, определяющие
величину тока, в выражение для плотности не входят. Поэтому задание на границах
интервала любых комбинаций из величин плотности и ее производных (например, на
обеих границах задаются величины плотности и ее градиента) не позволяет
определить σ.
Задавая величину тока J можно, используя 13, найти σ, но не связь
между током и полем. Так как величина 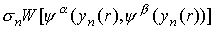 согласно 26 является
инвариантом для всех n, то ситуация не изменится и для N > 2. согласно 26 является
инвариантом для всех n, то ситуация не изменится и для N > 2.
Рассмотрим
решение F(r,w,m) в
некоторой точке r* < r1. Оно представимо
в виде
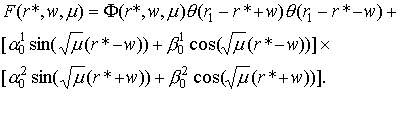
Обозначая :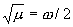 , используя в первом слагаемом формулы для произведения
соответствующих тригонометрических функций и, введенные выше обозначения,
получим. , используя в первом слагаемом формулы для произведения
соответствующих тригонометрических функций и, введенные выше обозначения,
получим.
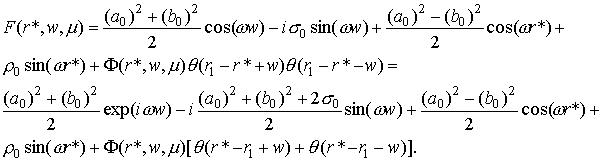 (29) (29)
Обратное
преобразование Фурье от тригонометрических функций порождает дельта функции
вида δ(p), δ(2λp – ω), δ(2λp + ω), что не
соответствует реальным функциям распределения. Поэтому мы не будем
рассматривать краевые задачи для решений вида F(r,w,m) при постоянных
значениях параметра m в силу
«бедности» и «нефизичности» соответствующих им функций распределения, а перейдем
сразу к краевым задачам для решений вида 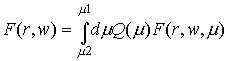 . .
Функция 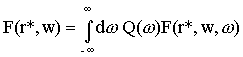 совпадает с
Фурье-образом функции распределения в точке r*, при условии, что
функция Q(2lp)/2p совпадает с функцией распределения f(r*,p) в точке r*→-∞ , выполнены равенства совпадает с
Фурье-образом функции распределения в точке r*, при условии, что
функция Q(2lp)/2p совпадает с функцией распределения f(r*,p) в точке r*→-∞ , выполнены равенства 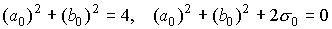 , а остальные члены при интегрировании по w с весом Q(2lw) равны нулю. (Используется лемма
об осцилляции.) Первое условие в этом утверждении следует из цепочки равенств (полагаем,
что F(w,w) = exp(iww)): , а остальные члены при интегрировании по w с весом Q(2lw) равны нулю. (Используется лемма
об осцилляции.) Первое условие в этом утверждении следует из цепочки равенств (полагаем,
что F(w,w) = exp(iww)):
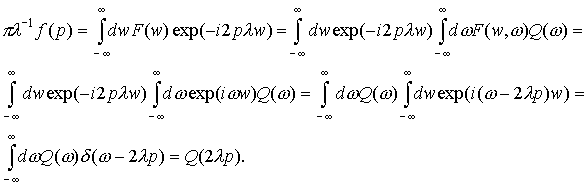
Например, выбрав Q(w) в виде
ступеньки Ферми, с импульсом Ферми pF и
средним импульсом 2p0,
получим 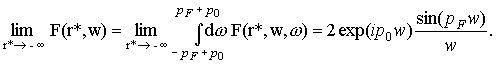
Условий 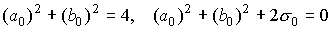 недостаточно для
однозначного определения коэффициентов. Вторую пару условий можно получить для
коэффициентов (aN)2, (bN)2 , sN , ρN задавая
функцию распределения (а значит и F(r,w) ) в
точке r = ¥. недостаточно для
однозначного определения коэффициентов. Вторую пару условий можно получить для
коэффициентов (aN)2, (bN)2 , sN , ρN задавая
функцию распределения (а значит и F(r,w) ) в
точке r = ¥.
Вид функции F(r,w,m) в точке r** > rN имеет вид (29) с заменой индекса 0 на индекс N и
частоты ω на ωN , где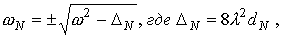
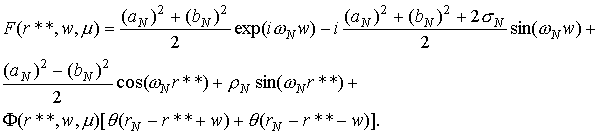 (30) (30)
Устремив r** к +∞ , получим:
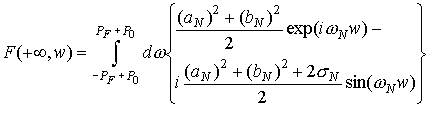 (31) (31)
Коэффициенты в (31) определяются с помощью рекуррентных формул
(8), однако проще воспользоваться рекуррентными формулами (32) для определения величин
(aN)2, (bN)2 , sN , ρN.
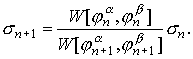
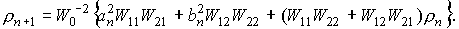 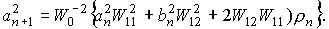 (32)
(32)
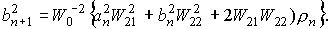
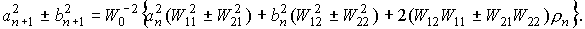
Следует отметить, что кроме
величин 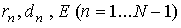 коэффициенты в (30)
зависят также от μ, а
следовательно от ω, но не
зависят от w. Вариация коэффициентов коэффициенты в (30)
зависят также от μ, а
следовательно от ω, но не
зависят от w. Вариация коэффициентов
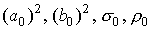 , при условии выполнения равенств , при условии выполнения равенств 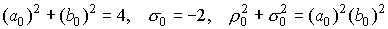 определяет семейство
допустимых граничных условий в точке r = +¥, если в
точке r = -¥ задана ступенька Ферми. определяет семейство
допустимых граничных условий в точке r = +¥, если в
точке r = -¥ задана ступенька Ферми.
Задание
вида функции распределения на одной из границ в реальных физических задачах,
как правило, невозможно. Обычно на границах задается часть функции распределения,
а именно, функция распределения для импульсов, направленных внутрь
рассматриваемой области (открытая система). Зададим функцию Q(ω) в виде:
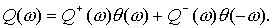
Тогда в точке r = -¥ функцию
распределения f(p,-¥) можно
записать, используя известные формулы для преобразования Фурье синусов и
косинусов
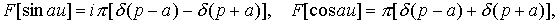 в виде: в виде:
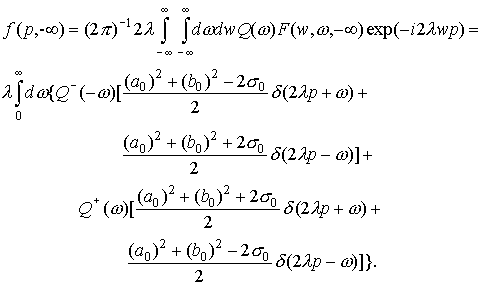 (33) (33)
Вводя обозначения: 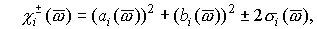 получим. получим.
Для p>0 : 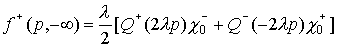 . (34) . (34)
Для p<0 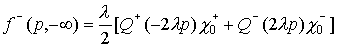 . (35) . (35)
Аналогично, в точке r = +¥.
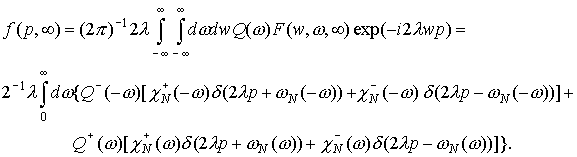 (36) (36)
Аргументы дельта функций имеют
два корня, но один из них можно отбросить, потребовав, чтобы функция 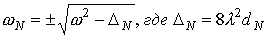 стремилась к ω/2 при ∆N → 0, т.е. положим стремилась к ω/2 при ∆N → 0, т.е. положим 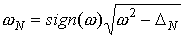 , выбрав, для определенности, случай , выбрав, для определенности, случай 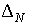 < 0. < 0.
Тогда для p>0
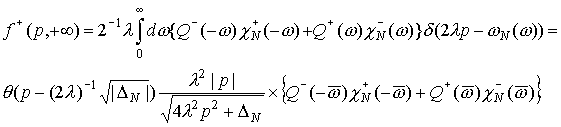 (37) (37)
Для p<0
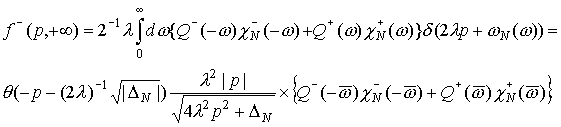 (38) (38)
Здесь 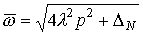
Таким образом, задавая две из
четырех функций 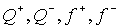 системы уравнений
(34,35,37,38), казалось бы, можно определить остальные две. Однако это
выполнимо либо при задании системы уравнений
(34,35,37,38), казалось бы, можно определить остальные две. Однако это
выполнимо либо при задании 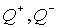 , как в примере, рассмотренном выше, либо при dN = 0. Действительно,
на интервале , как в примере, рассмотренном выше, либо при dN = 0. Действительно,
на интервале 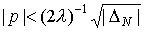 функции функции 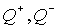 в формулы (37,
38) не входят, а функции распределения
в точке r = +¥ на нем равны нулю.
Для выхода из этой ситуации необходимо
интегрировать не только по положительным μ, но и по отрицательным (что соответствует мнимым значениям ω). При этом формулы (34,35) не изменятся
(из-за отсутствия корней на мнимой оси у аргумента дельта функций в формуле (33)). в формулы (37,
38) не входят, а функции распределения
в точке r = +¥ на нем равны нулю.
Для выхода из этой ситуации необходимо
интегрировать не только по положительным μ, но и по отрицательным (что соответствует мнимым значениям ω). При этом формулы (34,35) не изменятся
(из-за отсутствия корней на мнимой оси у аргумента дельта функций в формуле (33)).
В точке r = +¥ дополнительное интегрирование по мнимой оси даст следующий
результат: формулы (37,38), модифицируясь, распространяются на всю ось -¥ <
p < +¥.
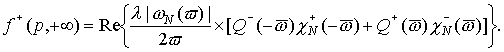 (37*) (37*)
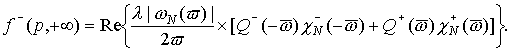 (38*) (38*)
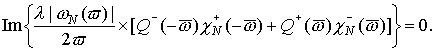 (37**)
(37**)
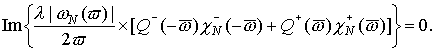 (38**) (38**)
Здесь также, 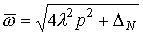 , но при
отрицательном подкоренном выражении (малые модули импульсов), корень становится
мнимым, что следует учитывать при
вычислении коэффициентов , но при
отрицательном подкоренном выражении (малые модули импульсов), корень становится
мнимым, что следует учитывать при
вычислении коэффициентов 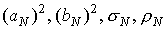 по формулам (32).
Кроме того, связь между знаками p и по формулам (32).
Кроме того, связь между знаками p и 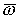 становится
неоднозначной (однако для упрощения в дальнейшем предполагается, что знаки p и становится
неоднозначной (однако для упрощения в дальнейшем предполагается, что знаки p и 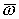 по-прежнему
совпадают). Из (34,35, 37*,38*,37**,38**) можно получить решение открытой
краевой задачи. Например, задавая по-прежнему
совпадают). Из (34,35, 37*,38*,37**,38**) можно получить решение открытой
краевой задачи. Например, задавая 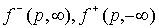 , вводя обозначение: , вводя обозначение: 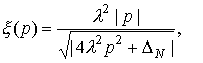 получаем для действительных значений получаем для действительных значений 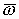
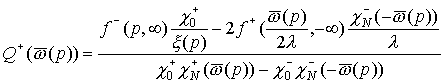 , ,
(39)
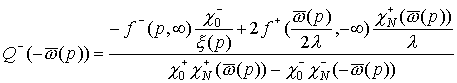 . .
Для мнимых значений 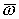
 , ,
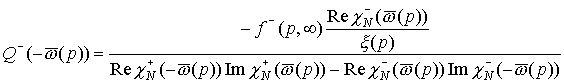 . (39*) . (39*)
Следовательно, для 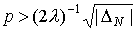 : :
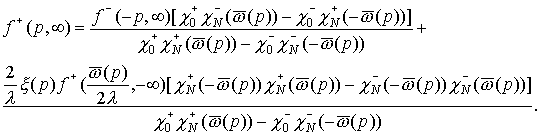
Для 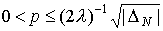 (40) (40)
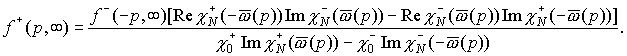
Для
p < 0
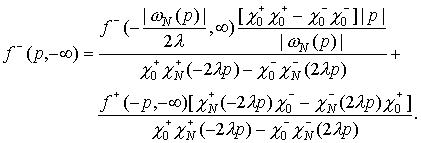
Таким образом,
полностью определена функция распределения на границах, а также функции Q, с помощью которых, используя обратное преобразование Фурье,
можно найти (хотя бы формально) функцию распределения во всем фазовом
пространстве. Полученные выражения зависят от трех параметров 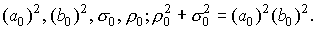
Ток в системе вычисляется путем
интегрирования с весом p суперпозиции найденной и заданной частей функции
распределения на одной из границ.
Рассмотрим два
частных случая. В случае постоянного потенциала формулы приводят к очевидному
результату 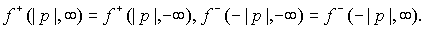
Из (32) следует, что  Положив Положив 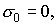 получим получим 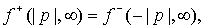
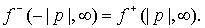 (В этом случае
происходит полное отражение заданных потоков, ток равен нулю.) (В этом случае
происходит полное отражение заданных потоков, ток равен нулю.)
Приложение.
Используя обозначения (20)
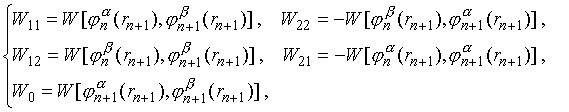
можно представить рекуррентную
систему для коэффициентов в виде:
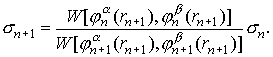
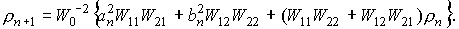
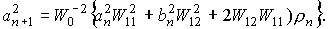 (П1)
(П1)
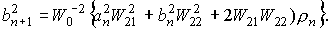
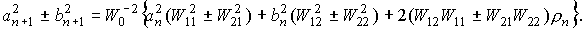
Для функций  , квадратичные и билинейные комбинации вронскианов,
используемые в (П1) можно представить в следующем виде. , квадратичные и билинейные комбинации вронскианов,
используемые в (П1) можно представить в следующем виде. 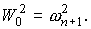
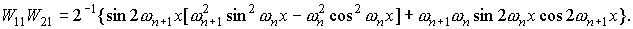
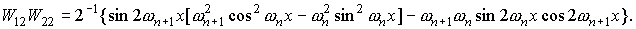
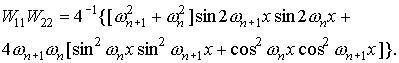
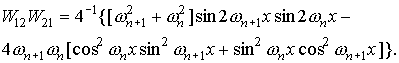
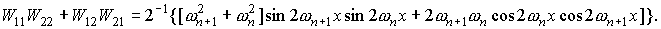 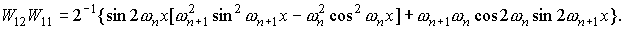
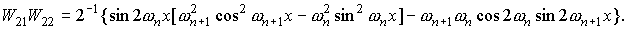
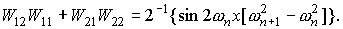
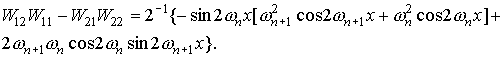
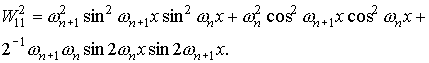
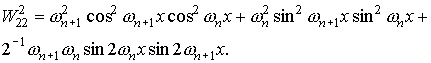
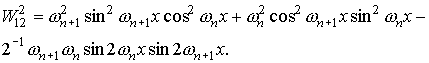
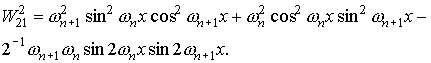
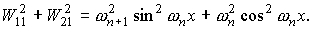
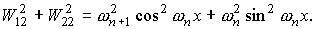
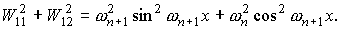
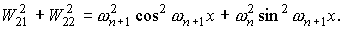
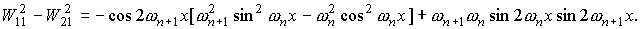
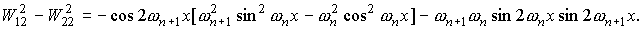
При использовании в системе П1
вышеприведенных формул в следует
положить x = rn+1 .
Литература.
- Климонтович Ю.Л. Статистическая физика. Москва, Наука, 1982.
- Справочник по специальным функциям. Под редакцией
М.Абрамовица и И.Стиган. Москва, Наука, 1979.
- В.Кеч, П.Теодореску. Введение в теорию обобщенных
функций с приложениями в технике. Москва, «Мир», 1978.
|