Аннотация
Исследование генерации электромагнитных полей в ряде практически важных случаев подразумевает моделирование столкновений пучковых электронов с нейтральными молекулами газа. Рассматривается модель потока электронов в самосогласованном электромагнитном поле. Учитываются ионизационные и упругие столкновения электронов с нейтральными молекулами газа. Предложен способ определения плотности тока и концентрации электронов, позволяющий использовать для расчета электромагнитного поля метод частиц.
Abstract
The investigation of the electromagnetic field’s generation implies the simulation of the beam electron’s collisions in the number of practically important cases. The model of the electron flux in the self-consistent electromagnetic field is considered. The ionizing and elastic collisions between electrons and neutral gas molecules is taking into account. The way of the electronic current density’s and concentration’s determination, which can be used for calculation of electromagnetic field by particle’s method, is offered.
ВВЕДЕНИЕ
Моделирование столкновений
электронов высокой энергии является актуальной проблемой в задачах о
самосогласованном электромагнитном поле, образующемся при эмиссии потоков
электронов в газовую среду. Частоты плазменных колебаний, столкновений с
нейтральными молекулами среды и генерации электронного потока в ряде
практически важных задач сравнимы между собой. Пренебречь можно только
столкновениями между электронами.
Рассмотрим поток электронов
с энергиями 10 КэВ – 1 МэВ [9] в исходно нейтральном газе.
Баланс числа электронов в элементе фазового пространства переменных 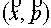 , где , где 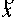 – декартовы
координаты в физическом пространстве, а – декартовы
координаты в физическом пространстве, а 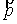 – импульс электрона,
описывается уравнением Больцмана [1] с интегралами упругого и
неупругого рассеяния. Если начальный спектр электронов сосредоточен вблизи
1 МэВ, то для обоих процессов рассеяния можно использовать приближение
Фоккера-Планка [2], причем неупругие процессы превалируют при больших
энергиях, а упругие становятся главными по мере деградации начального спектра. – импульс электрона,
описывается уравнением Больцмана [1] с интегралами упругого и
неупругого рассеяния. Если начальный спектр электронов сосредоточен вблизи
1 МэВ, то для обоих процессов рассеяния можно использовать приближение
Фоккера-Планка [2], причем неупругие процессы превалируют при больших
энергиях, а упругие становятся главными по мере деградации начального спектра.
Пространственно-трехмерное
уравнение Фоккера-Планка представляет собой уравнение второго порядка в частных
производных относительно шести независимых переменных. Решение такого
уравнения, а тем более уравнения переноса, разностными методами на современном
уровне развития вычислительной техники весьма затруднительно.
Ряд практически
важных задач состоит в вычислении значений компонент электромагнитного поля и
не требует детального описания функции распределения. Данная работа, не
претендуя на совершенство математических формулировок, предлагает конструкцию
функции распределения, которая позволяет определять самосогласованное
электромагнитное поле при допустимых приближениях методом частиц [3].
1 Неупругие
столкновения
Основным неупругим
процессом взаимодействия электронов высокой энергии с нейтральными молекулами
является ионизационное рассеяние. В результате такого столкновения в
непрерывном спектре образуется два тождественно неразличимых электрона. Сечение
ионизационного рассеяния обратно пропорционально квадрату переданной энергии [4], поэтому наиболее
вероятно сообщение одному из образовавшихся электронов существенно большей кинетической
энергии, чем второму. В рамках данной работы рассмотрим электроны с высокой
энергией. Электроны с низкой энергией в электродинамических задачах такого типа
можно исследовать отдельно [5].
Интеграл
ионизационных столкновений электронов с высокой энергией в приближении малых
передач энергии можно представить в следующем виде:
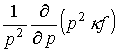 ,
(1) ,
(1)
где [6]:
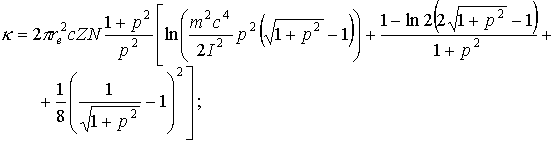
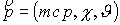 – импульс электрона в
сферической системе координат; – импульс электрона в
сферической системе координат;
Z – атомный номер рассеивающего вещества;
N – концентрация атомов
рассеивающего вещества;
f – функция распределения электронов;
m – масса электрона;
с – скорость света;
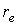 – классический радиус
электрона; – классический радиус
электрона;
I – средний потенциал ионизации нейтральных
молекул газа.
Коэффициенты при
первых производных по угловым компонентам импульса обращаются в ноль вследствие
угловых симметрий сечения. Коэффициент при второй производной по модулю
импульса вычисляется интегрированием произведения дифференциального сечения и
квадрата переданной энергии и не содержит отношения кинетической энергии
электрона к потенциалу ионизации. Изотропизацией электронного потока за счет
ионизационных столкновений можно пренебречь по сравнению с аналогичным
следствием упругих процессов. Кинетическое уравнение для электронов с
интегралом столкновений (1) можно представить в следующем виде:
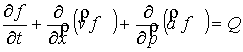 , (2) , (2)
где 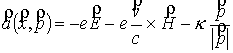 ; ;
 ; ;
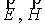 – самосогласованное электрическое и магнитное поле
соответственно; – самосогласованное электрическое и магнитное поле
соответственно;
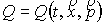 – источник электронов. – источник электронов.
Покажем, что решение
уравнения (2) представимо в виде:
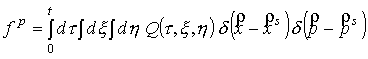 , (3) , (3)
где 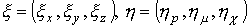 –внутренние векторные переменные интегрирования,
соответствующие по физическому смыслу начальной координате и импульсу частицы,
движение которой описывается функциями –внутренние векторные переменные интегрирования,
соответствующие по физическому смыслу начальной координате и импульсу частицы,
движение которой описывается функциями 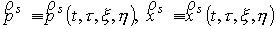 , причем , причем 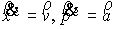 . .
Обозначим 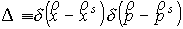 , подставим функцию (3) в уравнение (2), умножим на финитную
гладкую пробную функцию и проинтегрируем по всем переменным. Приведем
промежуточные результаты. , подставим функцию (3) в уравнение (2), умножим на финитную
гладкую пробную функцию и проинтегрируем по всем переменным. Приведем
промежуточные результаты.
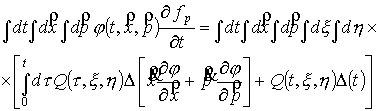 , ,
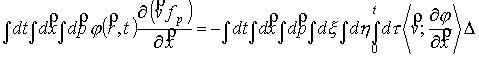 , ,
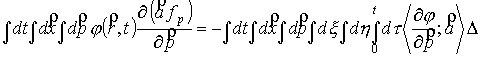 . .
Учтем, что 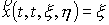 , , 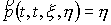 . Тогда, в силу того, что . Тогда, в силу того, что
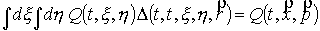 , ,
можно утверждать, что подстановка (3)
обращает уравнение (2) в тождество.
2 Упругие столкновения
Рассмотрим
кинетическое уравнение Больцмана для электронов с интегралом неупругих
столкновений в приближении средних потерь энергии и линейным по функции
распределения интегралом упругих столкновений [7] с неподвижными
нейтральными молекулами воздуха.
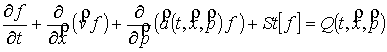 , (4) , (4)
где 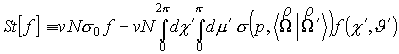 ; ;
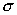 –дифференциальное сечение упругого рассеяния, зависящее от
модуля импульса и косинуса угла между направлениями –дифференциальное сечение упругого рассеяния, зависящее от
модуля импульса и косинуса угла между направлениями 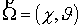 и и 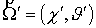 (далее (далее 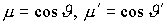 ); );
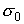 –полное сечение упругого рассеяния, зависящее от модуля импульса. –полное сечение упругого рассеяния, зависящее от модуля импульса.
Разложим функцию 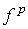 в ряд по сферическим
функциям в ряд по сферическим
функциям 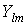 переменных μ и χ. Получим: переменных μ и χ. Получим:
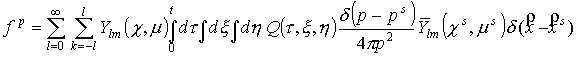 , ,
где верхняя черта означает комплексное
сопряжение.
Введем в правую
часть дополнительный коэффициент. Построим новую функцию распределения:
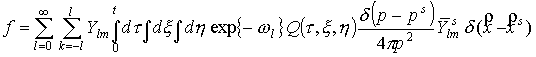 . (5) . (5)
Здесь 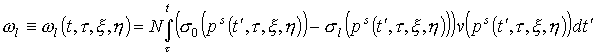 . .
В соответствии с
теоремой сложения для сферических функций правая часть (5) может быть
представлена как разложение в ряд по полиномам Лежандра Р.
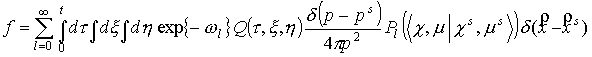 (6) (6)
где 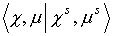 – косинус угла между
векторами – косинус угла между
векторами 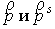 . .
Подставим данную функцию
в уравнение (1), умножим это уравнение на произвольную пробную функцию 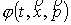 и проинтегрируем по
всем аргументам. Рассмотрим промежуточные выкладки. и проинтегрируем по
всем аргументам. Рассмотрим промежуточные выкладки.
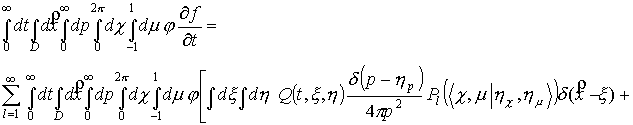
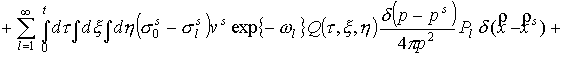
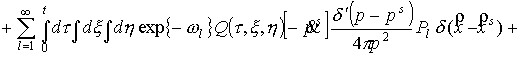
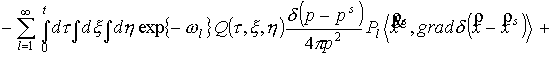
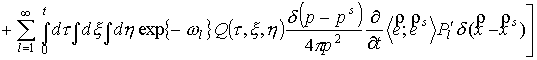 . (7) . (7)
Штрихи у функций
означают дифференцирование по всему аргументу, а
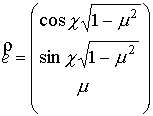 . .
Учтено: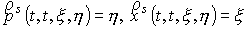 , , 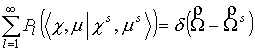 . .
В третьем и
четвертом слагаемых выполним интегрирование по частям:
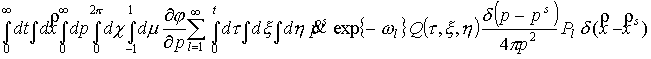
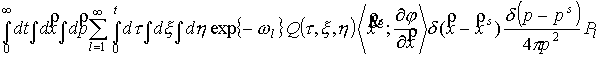
Выполним подстановку
функции (6) во второй член уравнения (4) и первое слагаемое третьего члена.
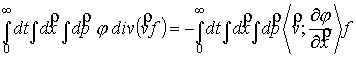 (8) (8)
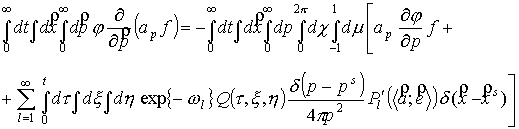 .
(9) .
(9)
Подстановка (6) в
интеграл упругих столкновений уравнения (4) даст:
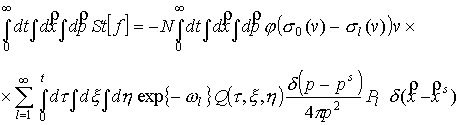 . (10) . (10)
Подставим (7-10) в
исходное уравнение (4). Имея в виду, что 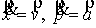 в декартовых
координатах, получим невязку: в декартовых
координатах, получим невязку:
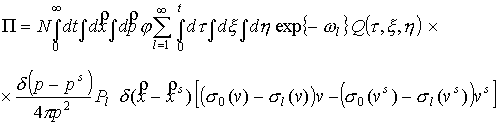 .
(11) .
(11)
Невязка представляет
собой бесконечный ряд. Вычисляя интеграл по модулю импульса, получим, что члены
этого ряда равны нулю. Данное утверждение справедливо для всех 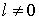 . Распространять данное утверждение на нулевой член ряда
некорректно, поскольку . Распространять данное утверждение на нулевой член ряда
некорректно, поскольку 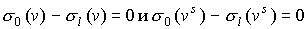 при при 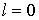 . Проверка справедливости равенства умножением его на ноль не
является корректной процедурой. . Проверка справедливости равенства умножением его на ноль не
является корректной процедурой.
3 Нулевой момент
Рассмотрим случай 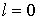 . Введем следующие обозначения: . Введем следующие обозначения:
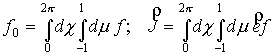 . .
Проинтегрируем
уравнение (4) по импульсным углам. Получим:
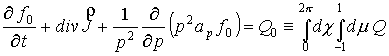 . (12) . (12)
Величина 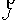 может быть вычислена
с помощью (6), поскольку для случая может быть вычислена
с помощью (6), поскольку для случая 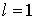 приведенное выше
рассмотрение справедливо. приведенное выше
рассмотрение справедливо.
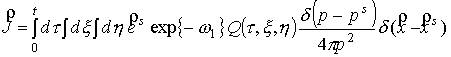 , (13) , (13)
где 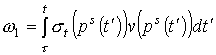 , а , а 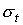 – транспортное
сечение упругого рассеяния. Таким образом, для нулевого члена разложения
решения уравнения (4) получено следующее уравнение – транспортное
сечение упругого рассеяния. Таким образом, для нулевого члена разложения
решения уравнения (4) получено следующее уравнение
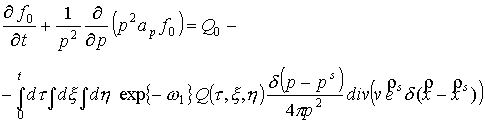 .
(14) .
(14)
Итак, функция 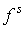 , представляющая собой бесконечный ряд , представляющая собой бесконечный ряд
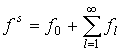 , (15) , (15)
где 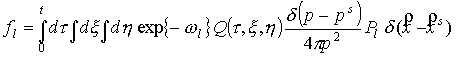 , а , а 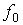 определяется решением
уравнения (14), является решением уравнения (4). определяется решением
уравнения (14), является решением уравнения (4).
Рассмотрим более
подробно уравнение (14). Проинтегрируем его так, чтобы получить уравнение для
концентрации электронов 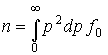 . .
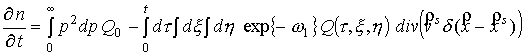 (16)
(16)
Представим решение
уравнения (16) в виде суммы двух функций
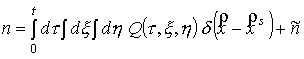 . (17) . (17)
Подставим (17) в
(16) и потребуем выполнения уравнений движения  . Получим: . Получим:
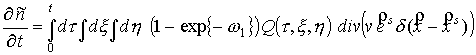 .
(18) .
(18)
Представление
концентрации электронов в виде суммы (17) имеет простой физический смысл.
Концентрация электронов в данной точке пространства определяется как переносом
электронов, который описывается первым слагаемым суммы, так и изотропизацией
исходного потока в результате упругого рассеяния, что описывается вторым слагаемым.
Решение уравнения
(14) также можно представить в виде аналогичной суммы:
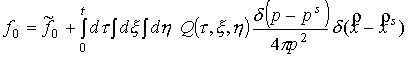 , (19) , (19)
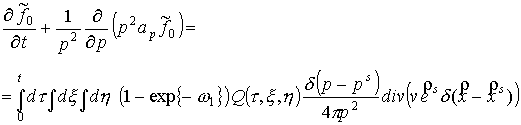 .
(20) .
(20)
Уравнения (18) и
(20) дают возможность корректно рассчитывать источник электронов с низкой
энергией, учитывая, что изотропизовавшиеся электроны, функция распределения
которых описывается уравнением (4), сохраняют высокую энергию и вносят
существенный вклад в процесс ионизации.
4 Обобщенное решение и уравнения движения
Функция,
определенная соотношениями (15), является приближенным решением уравнения (1)
из пространства основных функций, поскольку содержит интегрирование по
переменным  и и 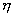 . Заменим формально указанное интегрирование суммированием в
конечных пределах. . Заменим формально указанное интегрирование суммированием в
конечных пределах.
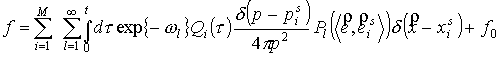 ,
(21) ,
(21)
где 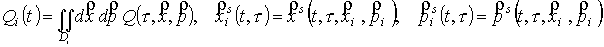 , , 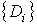 – система непересекающихся подобластей, содержащих точку
фазового пространства – система непересекающихся подобластей, содержащих точку
фазового пространства 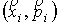 , покрывающая область решения задачи в фазовом пространстве,
а , покрывающая область решения задачи в фазовом пространстве,
а 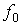 является решением
уравнения является решением
уравнения
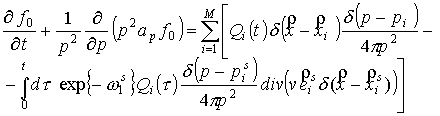 (22) (22)
Подставим (21) в
(4), умножим на произвольную функцию из основного пространства и проинтегрируем
по всем переменным. Под основным пространством понимается множество бесконечно
гладких финитных функций всех рассматриваемых переменных. Проверка практически
аналогична процедуре, представленной в предыдущем параграфе. Действительно,
интегрирование по переменным 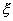 и и 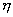 используется только в
первом слагаемом соотношения (7). Остальные действия не затрагивают эти
переменные. Поэтому они справедливы и для случая, когда интегрирование по переменным используется только в
первом слагаемом соотношения (7). Остальные действия не затрагивают эти
переменные. Поэтому они справедливы и для случая, когда интегрирование по переменным
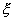 и и 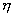 заменяется конечной суммой. Для конечной суммы
достаточно проверить нормировку коэффициентов. Пусть заменяется конечной суммой. Для конечной суммы
достаточно проверить нормировку коэффициентов. Пусть 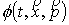 – произвольная
функция из основного пространства. Тогда невязка, возникающая при подстановке
(22) в (1) составит следующую величину: – произвольная
функция из основного пространства. Тогда невязка, возникающая при подстановке
(22) в (1) составит следующую величину:
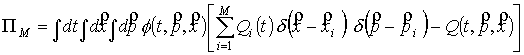 . (23) . (23)
Отсюда
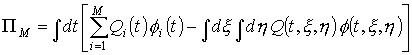 , (24) , (24)
где 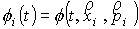 . .
Рассмотрим
концентрацию и плотность потока электронов, соответствующую функции
распределения (21-22). Проинтегрируем (22) по модулю импульса с единичным
весом. Получим:
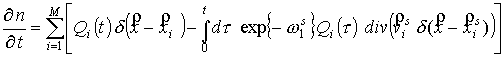 .
(25) .
(25)
Аналогично (17)
представим концентрацию в виде суммы двух слагаемых.
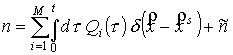 . .
Тогда при выполнении
уравнений движения
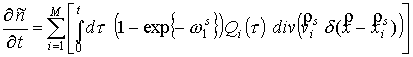 . .
Плотность потока
электронов представляется в следующем виде:
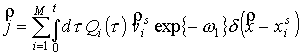 .
(26) .
(26)
Выполнение уравнения
непрерывности (закона сохранения заряда) для
концентрации и плотности потока, заданной уравнением (26) очевидно ввиду
справедливости (21).
Рассмотрим второй
момент уравнения (4), связывающий плотность потока электронов с давлением
электронной системы 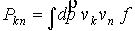 . Выполним интегрирование (4) по импульсам с весом . Выполним интегрирование (4) по импульсам с весом 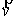 : :
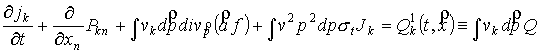 . (27) . (27)
Проверка выполнения
соотношения (27) для обобщенной функции (21) состоит в подстановке (21) и (26)
в (27), умножении (27) на произвольную бесконечно гладкую финитную функцию и
интегрировании по всем переменным. Рассмотрим первое слагаемое (27).
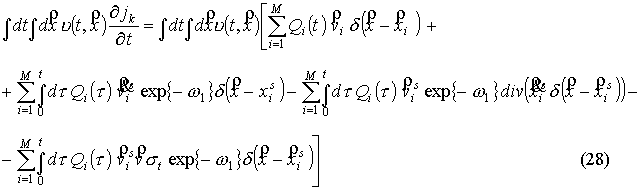
Второе слагаемое
(27) преобразуется следующим образом:
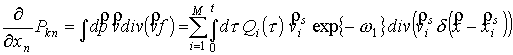 . (29) . (29)
Третий член
уравнения (27) рассмотрим в декартовых координатах для импульса:
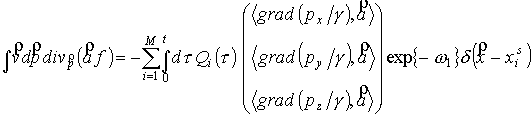 . (30) . (30)
Четвертый член
преобразуется простым интегрированием
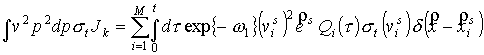 .
(31) .
(31)
Итак, невязка
уравнения (27) при выполнении уравнений движения и с учетом того, что 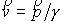 представляет собой
следующую конструкцию: представляет собой
следующую конструкцию:
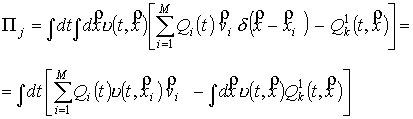 . (32) . (32)
Конструкция невязки,
как следует из (32), определяется как разность точного значения интеграла от
функции и его же представления в виде конечной суммы. Представление решения в
виде (22-23) означает, что полное число членов суммы (М) должно быть достаточным для правильной аппроксимации функции распределения.
Соотношение (32) означает, что интеграл источника должен вычисляться с помощью
того же количества значений подынтегральной функции.
ЗАКЛЮЧЕНИЕ
Функция
распределения электронов, удовлетворяющая уравнению (4), имеет следующий вид:
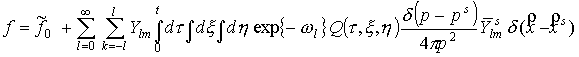 , (33) , (33)
причем для функции 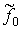 справедливо уравнение справедливо уравнение
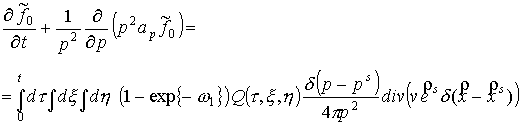 .
(34) .
(34)
Уравнение (4)
учитывает ионизационные столкновения в приближении малых потерь энергии,
действие электромагнитного поля и упругие столкновения электронов с
нейтральными молекулами.
Конечная сумма (21)
является решением уравнения (4) при любом числе слагаемых, если выполнено
условие
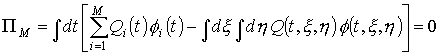 . (35) . (35)
Условие (35) всегда
можно выполнить, если источник электронов задается как результат измерений.
Построенная функция распределения дает возможность [8] использовать для
расчета ее моментов метод крупных частиц при условии
правильного представления источника электронов.
Рассмотрим условие,
ограничивающее применимость представленной модели. Концентрация нейтральных
молекул N при
дифференцировании функции распределения по пространственным переменным в
подстановке (6) предполагалась постоянной величиной. Такое условие не
ограничивает применимость модели для ряда задач, в том числе, в ограниченной
области. Для моделирования электромагнитных полей можно использовать уравнения
Максвелла с правой частью, представляющей собой плотность электрического тока,
а не плотность заряда. Применимость данной модели для случая переменной
концентрации рассевающих центров должна исследоваться отдельно.
ЛИТЕРАТУРА
1. Чепмен С.,
Каулинг Т.Дж. Математическая теория неоднородных газов. – М.:ИЛ, 1960.
2. Ландау Л.Д., Лифшиц
Е.М. Физическая кинетика. – М.:"Наука", 1979.
3. Hockney
R.W., Eastwood J.W. Computer Simulation Using Particles.– McGraw-Hill, New
York, 1981.
4. Гайтлер В. Квантовая
теория излучения. – М.:ИЛ, 1956.
5. А.В. Березин и др. О математических моделях вторичной
ионизации. – препринт ИПМ им. М.В.Келдыша РАН, №29, 2002.
6. Ландау Л.Д., Лифшиц
Е.М. Квантовая электродинамика. – М.: "Наука", 1979.
7. Кейс К., Цвайфель Р.
Линейная теория переноса. – М.: "МИР", 1967.
8. Климонтович Ю.Л.
Кинетическая теория неидеального газа и неидеальной плазмы. – М.:
"Наука", 1975.
9.
Жуковский М.Е. Самосогласованная квазитрехмерная модель радиационного
возбуждения электромагнитных полей. – М.: "Математическое моделирование",
т.8, № 4, 1996.
|