Аннотация
В настоящей работе представлен метод расчетов распространения лазерного излучения в неустойчивых
резонаторах с лазерными зеркалами, произвольной формы. Предлагаемый метод основан на переходе к
неортогональной системе криволинейных координат, позволяющей адекватно сводить полную волновую
краевую задачу к системе эволюционных задач типа нестационарных уравнений Шредингера.
Отличительная особенность предлагаемого метода – отказ от преобразования Сигмена-Синклаша.
Вследствие этого отпадает необходимость в интерполяции поля на малом зеркале на более подробную
сетку, что принципиально необходимо для решения уравнения, описывающего распространение
излучения после отражения поля от малого зеркала. В предлагаемой работе для численного решения
краевых задач использованы спектральные методы и итерационные процессы. Основные особенности
расчетов неустойчивых резонаторов продемонстрированы на примере телескопического резонатора
с цилиндрическими зеркалами, заполненного насыщающейся активной средой.
Abstract
The mathematical modeling of the laser beam propagation in the unstable resonator with the
mirrors of the arbitrary form is represented in the article. The method considered is based
on using the non-orthogonal coordinate systems, which allows the adequate reduction of full
wave boundary problem to the system of the evolution Shredinger’s equations.
The features of the method described are neglecting from the Siegman-Siclash transformations.
As a result it doesn’t need to interpolate the field near the back mirror on the detailed grid,
that is necessary generally for the solution of the equation, describing the radiation
propagation after the field reflection from the back mirror. The spectral methods and
iterations have been used for the numerical solution of the boundary problems. The telescope
resonator with the cylindrical mirrors has demonstrated the features of the unstable resonator
calculations when the active medium has been saturated.
Проблеме
распространения лазерного излучения в открытых неустойчивых резонаторах,
начиная со статьи Сигмена [1],
посвящено большое количество теоретических и экспериментальных работ,
основные результаты которых подытожены в известных монографиях [2,3].
Математические модели и основные численные методы изложены в работах [4,5].
В настоящей работе представлен метод расчетов распространения
лазерного излучения в неустойчивых резонаторах с отражающими зеркалами, вообще
говоря, произвольной формы. Предлагаемый метод основан на переходе к
неортогональной системе криволинейных координат, позволяющей адекватно сводить
полную волновую краевую задачу к системе эволюционных задач типа нестационарных
уравнений Шредингера.
В
данной работе проведено четкое разделение особенностей двумерных и трехмерных
задач, получаемых из соответствующих уравнений Гельмгольца [6,7]. Важной
особенностью полученных эволюционных уравнений является наличие в них членов,
характерных для уравнений переноса. Так, в частном, но важном случае
телескопического резонатора в уравнении, описывающем распространение излучения
от малого зеркала к большому, появляется член переносного типа.
Одна
из особенностей предлагаемого метода – отказ от преобразования Сигмена-Сиклаша.
Вследствие этого отпадает необходимость в интерполяции поля
на малом зеркале на более подробную сетку, что принципиально необходимо для решения уравнения,
описывающего распространение излучения после отражения поля от малого зеркала.
Поскольку время, затрачиваемое только на интерполяцию, вносит существенный
вклад в общее время решения всей задачи, отказ от использования преобразования
Сигмена-Сиклаша позволяет существенно увеличить эффективность численного
решения.
В
предлагаемой работе для численного решения краевых задач использованы
спектральные методы [8,9] и итерационные
процессы. При численном решении наличие достаточно резких изменений поля
в резонаторе приводит к необходимости использования достаточно подробных сеток
и проведения значительного числа итераций. Это, в свою очередь, приводит к
необходимости точного учета кривизны зеркал.
Основные
особенности расчетов неустойчивых резонаторов продемонстрированы на примере
телескопического резонатора с цилиндрическими зеркалами, заполненного
насыщающейся активной (усиливающей) средой.
Особый
интерес представляет численное исследование поля в резонаторе в трехмерном
случае. Решение такой задачи требует больших вычислительных ресурсов, которыми
обладают многопроцессорные ЭВМ.
1. Рассмотрим открытый
оптический резонатор с зеркалами произвольной формы. Поверхности зеркал в
декартовой системе координат 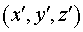 описываются
соответственно гладкими функциями описываются
соответственно гладкими функциями
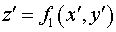 и и 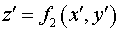 , имеющими ограниченные вторые частные производные. , имеющими ограниченные вторые частные производные.
Во внутренней области
резонатора электрическое поле удовлетворяет уравнению Гельмгольца:
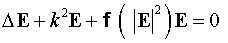 , , 
где 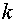 - волновой вектор в среде с показателем преломления - волновой вектор в среде с показателем преломления 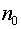 , , 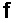 -известная функция. Будем рассматривать задачу в специально
выбранных неортогональных криволинейных
системах координат -известная функция. Будем рассматривать задачу в специально
выбранных неортогональных криволинейных
системах координат 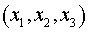 , позволяющих адекватно описывать распространение лазерного
излучения в резонаторе. , позволяющих адекватно описывать распространение лазерного
излучения в резонаторе.
В произвольной системе координат
уравнение (1) принимает вид:
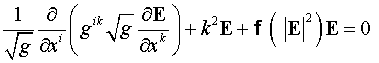 . .
Здесь 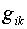 - метрический тензор, - метрический тензор,  , , 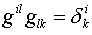 . По повторяющимся индексам
подразумевается суммирование. . По повторяющимся индексам
подразумевается суммирование.
Перейдем от
уравнения Гельмгольца к системе
эволюционных уравнений типа уравнения Шредингера для медленно меняющихся
комплексных амплитуд. Представим поле в виде 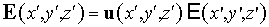 . Здесь
быстроменяющаяся функция . Здесь
быстроменяющаяся функция 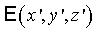 - либо фундаментальное решение оператора Гельмгольца, либо решение,
адекватно отражающее физический процесс распространения излучения. Тогда из
уравнения (2) следует: - либо фундаментальное решение оператора Гельмгольца, либо решение,
адекватно отражающее физический процесс распространения излучения. Тогда из
уравнения (2) следует:
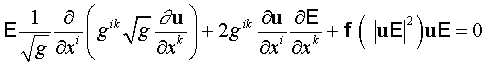 . .
или
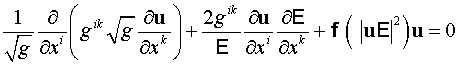 . .
Для удобства перепишем
(3) следующим образом:
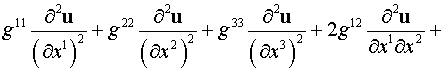
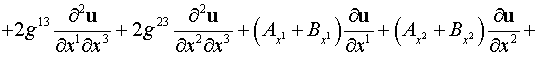
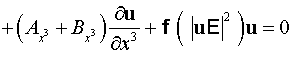 . .
Здесь
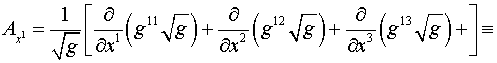
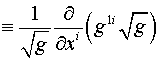 , ,
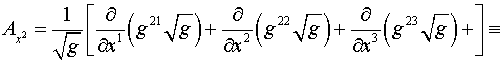
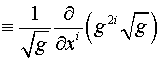 , ,
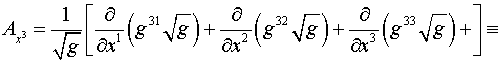
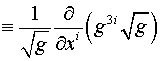 , ,
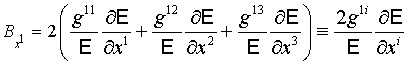 , ,
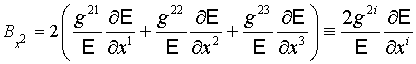 , ,
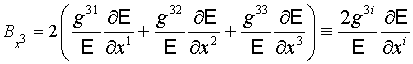 . .
2. Выпишем
условия отражения излучения на зеркалах
резонатора, т.е. найдем связь между фазой и амплитудой падающей волны и волны отраженной. Полагаем, что
поверхность 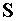 является гладкой и идеально проводящей. Тогда суммарное электрическое поле является гладкой и идеально проводящей. Тогда суммарное электрическое поле 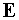 удовлетворяет на
поверхности условию для тангенциальных составляющих: удовлетворяет на
поверхности условию для тангенциальных составляющих: 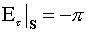 . Опуская постоянный скачок фазы, получаем соотношение,
связывающее падающую . Опуская постоянный скачок фазы, получаем соотношение,
связывающее падающую 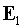 и отраженную и отраженную 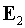 волны: волны:

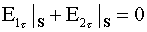 . .
Пусть электрическое
поле 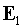 излучения, падающего
на отражающую поверхность излучения, падающего
на отражающую поверхность 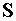 , описывается в координатах , описывается в координатах 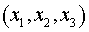 . Тогда: . Тогда:
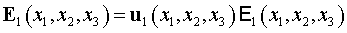 . .
Здесь 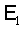 - либо
фундаментальное решение уравнения Гельмгольца, описывающее падающую на
поверхность - либо
фундаментальное решение уравнения Гельмгольца, описывающее падающую на
поверхность 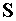 волну, либо решение,
адекватно отражающее физический процесс распространения излучения. волну, либо решение,
адекватно отражающее физический процесс распространения излучения.
Электрическое поле 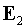 излучения,
отраженного от поверхности зеркала, описывается в других координатах, а именно излучения,
отраженного от поверхности зеркала, описывается в других координатах, а именно 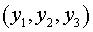 имеет вид: имеет вид:
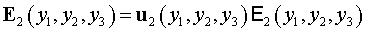 . .
Здесь 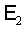 - либо
фундаментальное решение уравнения Гельмгольца, описывающее отраженную от
поверхности - либо
фундаментальное решение уравнения Гельмгольца, описывающее отраженную от
поверхности 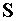 волну, либо решение,
адекватно отражающее физический процесс. волну, либо решение,
адекватно отражающее физический процесс.
Тогда из соотношения (6)
следует:
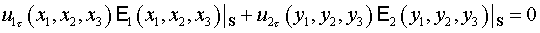 . .
Окончательно:
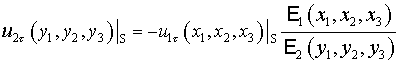 . . 
3. Продемонстрируем
предлагаемый подход на примере пустого
(т.е. 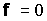 ) открытого конфокального (телескопического) неустойчивого
резонатора со сферическими зеркалами квадратной формы, работающего в режиме
лазерного генератора. Радиус малого зеркала равен ) открытого конфокального (телескопического) неустойчивого
резонатора со сферическими зеркалами квадратной формы, работающего в режиме
лазерного генератора. Радиус малого зеркала равен 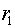 , радиус большого зеркала равен , радиус большого зеркала равен 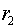 . Фокусное расстояние малого зеркала равно . Фокусное расстояние малого зеркала равно 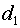 , фокусное расстояние большого зеркала равно , фокусное расстояние большого зеркала равно 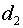 . Расстояние между зеркалами равно . Расстояние между зеркалами равно 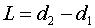 . Сторона квадрата малого зеркала равна . Сторона квадрата малого зеркала равна 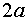 . Считаем сторону квадрата большого зеркала достаточно
большой, чтобы не учитывать ее размеры. . Считаем сторону квадрата большого зеркала достаточно
большой, чтобы не учитывать ее размеры.
Выберем
начало координат в точке фокуса зеркал конфокального неустойчивого резонатора.
Примем за ось 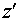 оптическую ось резонатора.
Положительное направление оси оптическую ось резонатора.
Положительное направление оси 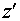 - направление от малого зеркала к большому
зеркалу. - направление от малого зеркала к большому
зеркалу.
В процессе численного исследования
распространения лазерных пучков в открытом неустойчивом резонаторе мы
рассматриваем задачу, естественно, в ограниченной области, как по оси 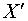 : :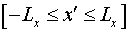 , так и по оси , так и по оси 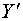 : :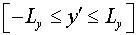 . Достаточно большие размеры большого зеркала резонатора
позволяют, существенно не усложняя математическую постановку задачи, поставить
граничные условия именно там, где это необходимо для адекватного описания
физического процесса распространения излучения в резонаторе. . Достаточно большие размеры большого зеркала резонатора
позволяют, существенно не усложняя математическую постановку задачи, поставить
граничные условия именно там, где это необходимо для адекватного описания
физического процесса распространения излучения в резонаторе.
В системе декартовых координат
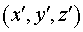 , функция , функция 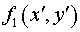 , определенная в области , определенная в области 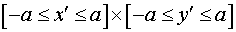 и описывающая
сферическую поверхность малого зеркала имеет вид: и описывающая
сферическую поверхность малого зеркала имеет вид:
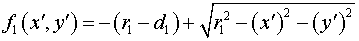 . .
Используя это
определение, продолжим функцию 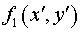 на область на область 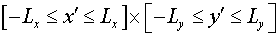 . Поскольку резонатор
телескопический, функция . Поскольку резонатор
телескопический, функция 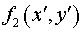 , описывающая поверхность большого зеркала имеет вид: , описывающая поверхность большого зеркала имеет вид:
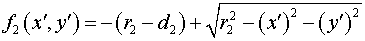 . .
Выберем такую систему криволинейных координат 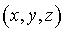 , в которой функция , в которой функция 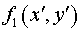 переходит в
плоскость переходит в
плоскость 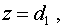 а функция а функция 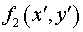 в плоскость в плоскость 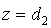 . Искомой системой криволинейных координат является: . Искомой системой криволинейных координат является:
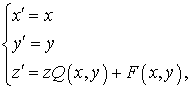
где 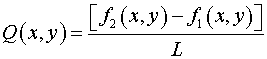 , , 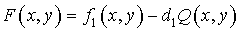 . .
Поле 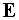 в резонаторе
представим в виде: в резонаторе
представим в виде:
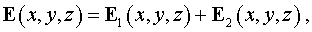
где поле 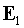 - распространяется от малого зеркала к большому зеркалу
(нечетный проход излучения в резонаторе), а - распространяется от малого зеркала к большому зеркалу
(нечетный проход излучения в резонаторе), а 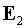 - от большого зеркала
к малому (четный проход излучения в резонаторе). Построим решения уравнения
Гельмгольца для четного и нечетного проходов излучения независимо. - от большого зеркала
к малому (четный проход излучения в резонаторе). Построим решения уравнения
Гельмгольца для четного и нечетного проходов излучения независимо.
3.1 Нечетные проходы.
Пусть источник отраженной от малого зеркала сферической волны находится в
начале координат. Представим поле 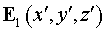 в виде: в виде: 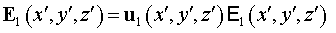 , где , где 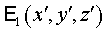 - фундаментальное
решение оператора Гельмгольца [6,7]: - фундаментальное
решение оператора Гельмгольца [6,7]:
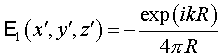 . .
Здесь 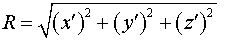 . .
Компоненты тензора 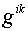 в координатах в координатах 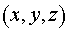 равны: равны:
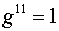 , , 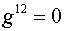 , , 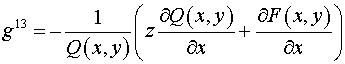 , ,
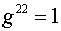 , , 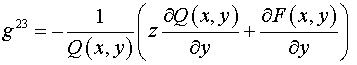 , ,
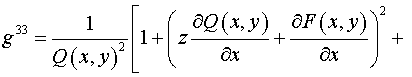
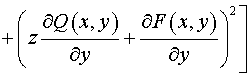 . .
 Определитель Определитель 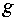 матрицы метрического
тензора матрицы метрического
тензора 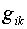 : : 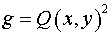 . Следовательно, согласно (5) имеем: . Следовательно, согласно (5) имеем: 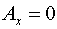 , , 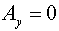 , ,

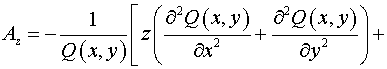
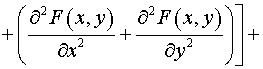
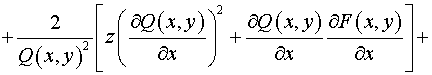
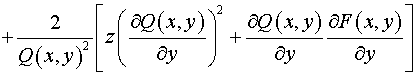 , ,
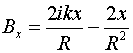 , , 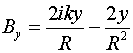 , ,
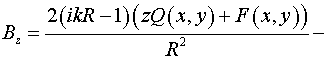
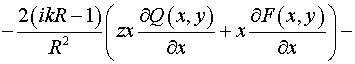
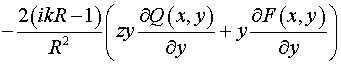 . .
Таким образом, в выбранной системе криволинейных координат 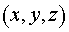 уравнение (4)
принимает вид: уравнение (4)
принимает вид:
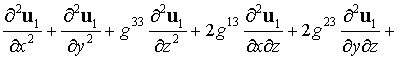
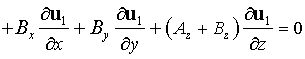 . .
Выбор
краевых условий зависит от специфики задачи. Среди возможных краевых условий
следует отметить условия излучения, условие равенства нулю поля 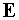 на достаточно больших
расстояниях от оптической оси резонатора: на достаточно больших
расстояниях от оптической оси резонатора:
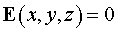 , при , при 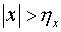 , , 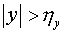 . .
Иногда выбор конкретного краевого условия
является разумным компромиссом между условиями, навязываемыми, с одной стороны
физической постановкой задачи, с другой стороны – методом ее численного
решения. К таким граничным условиям можно отнести периодические граничные
условия, довольно часто возникающие при использовании спектральных методов для
построения алгоритмов численного решения задачи.
Начальное
условие получаем из граничных соотношений (7):
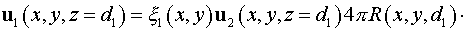
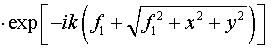 . .
Здесь 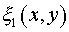 - коэффициент отражения от малого зеркала. - коэффициент отражения от малого зеркала.
В
довольно широком классе задач расчета распространения излучения в неустойчивых
резонаторах выполняются условия квазиоптического приближения:
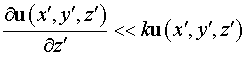 , , 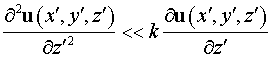 , ,
или в криволинейной системе координат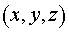 : :
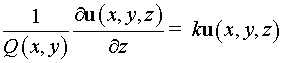 , , 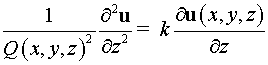 . .
Следовательно, учитывая условие (9), переходим от уравнения (8) к
уравнению:
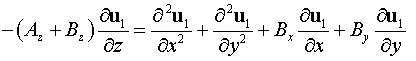 . .
3.2 Четные проходы.
Поскольку резонатор
телескопический, т.е. волна, отраженная от большого зеркала близка к плоской
волне, естественно использовать решение оператора Гельмгольца в виде [6]:
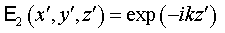 . .
Тогда, согласно (5) имеем: 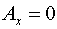 , , 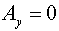 , ,
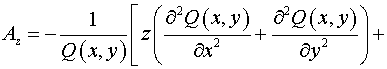
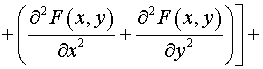
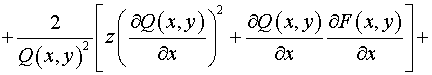
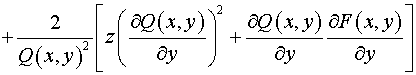 , ,
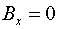 , , 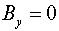 , , 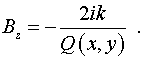
Таким
образом, в выбранной системе криволинейных координат уравнение (4) принимает
вид:
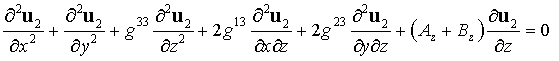 . .
Если
выполняются условия (9), переходим в уравнении (11) к квазиоптическому
приближению:
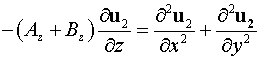 . .
Обсуждение краевых условий приведено выше. Начальное условие:
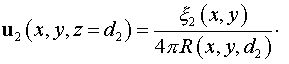
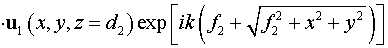 . .
Здесь 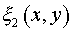 - коэффициент отражения от большого зеркала. - коэффициент отражения от большого зеркала.
4. Перейдем к
рассмотрению двумерной задачи. Постановка двумерной задачи имеет ряд
отличительных особенностей. Переход от трехмерного к двумерному случаю
предполагает, что в трехмерном
случае зеркала резонатора есть
бесконечные цилиндрические поверхности с образующими, параллельными оси 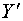 : : 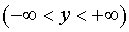 . Поэтому зеркала резонатора в двумерном случае есть
сечения бесконечных цилиндрических
поверхностей произвольной плоскостью . Поэтому зеркала резонатора в двумерном случае есть
сечения бесконечных цилиндрических
поверхностей произвольной плоскостью 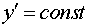 . На секущей плоскости . На секущей плоскости
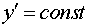 выберем систему координат.
Поскольку резонатор телескопический удобно выбрать начало координат в точке
фокуса зеркал резонатора. Примем за ось выберем систему координат.
Поскольку резонатор телескопический удобно выбрать начало координат в точке
фокуса зеркал резонатора. Примем за ось 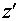 оптическую ось
резонатора. Положительное направление оси оптическую ось
резонатора. Положительное направление оси 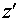 - направление от малого
зеркала к большому зеркалу. - направление от малого
зеркала к большому зеркалу.
При
численном исследовании распространения лазерных пучков в открытом неустойчивом резонаторе мы
рассматриваем задачу, естественно, в ограниченной области по оси 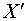 : : 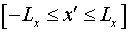 . Достаточно большие размеры большого зеркала резонатора
позволяют поставить граничные условия именно там, где это необходимо для
адекватного описания физического
процесса распространения излучения в резонаторе. . Достаточно большие размеры большого зеркала резонатора
позволяют поставить граничные условия именно там, где это необходимо для
адекватного описания физического
процесса распространения излучения в резонаторе.
В системе декартовых координат 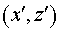 , функция , функция 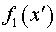 , определенная в области , определенная в области 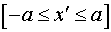 и описывающая поверхность малого зеркала имеет вид: и описывающая поверхность малого зеркала имеет вид:
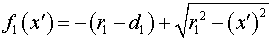 . .
Используя это
выражение, продолжим функцию 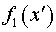 на область на область 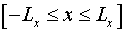 . Поскольку резонатор
телескопический, функция . Поскольку резонатор
телескопический, функция 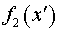 , описывающая поверхность большого зеркала имеет вид: , описывающая поверхность большого зеркала имеет вид:
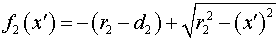 . .
Выберем такую систему криволинейных
координат 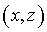 , в которой функция , в которой функция 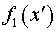 переходит в
плоскость переходит в
плоскость 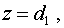 а функция а функция 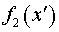 в плоскость в плоскость 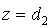 . Искомой системой криволинейных координат является: . Искомой системой криволинейных координат является:
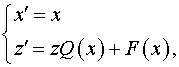
где 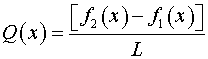 , , 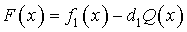 . .
Аналогично методу, изложенному для
трехмерного случая, поле в резонаторе
представим в виде:
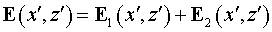 . .
Здесь поле 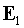 распространяется от
малого зеркала к большому зеркалу (нечетный поход), а распространяется от
малого зеркала к большому зеркалу (нечетный поход), а 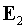 - от большого зеркала
к малому (четный проход). - от большого зеркала
к малому (четный проход).
4.1 Нечетные проходы.
Источник
цилиндрической волны, отраженной от малого зеркала представляет собой
однородный линейный источник, простирающийся от 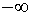 до до 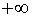 вдоль оси вдоль оси 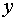 . .
Представим 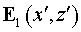 в виде в виде 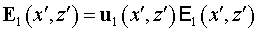 , где , где 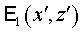 - фундаментальное
решение двумерного оператора Гельмгольца [6]: - фундаментальное
решение двумерного оператора Гельмгольца [6]:
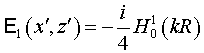 . .
Здесь 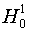 - функция Ханкеля первого рода, - функция Ханкеля первого рода, 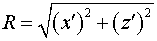 . .
Компоненты тензора 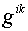 в координатах в координатах 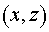 равны: равны:
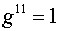 , , 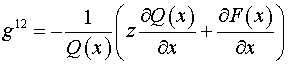 , ,
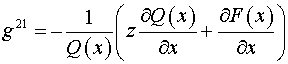 , ,
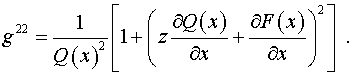
Определитель 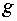 матрицы метрического
тензора матрицы метрического
тензора 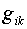 : : 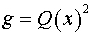 . Следовательно, согласно (5) имеем: . Следовательно, согласно (5) имеем: 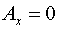 , ,
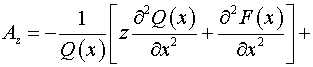
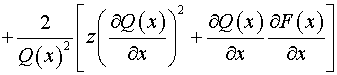 , ,
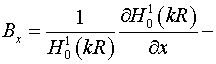
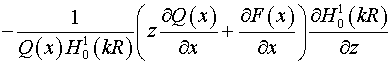 , ,
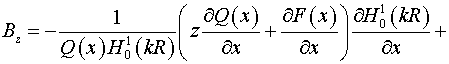
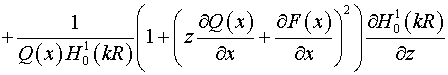 . .
Таким
образом, в выбранной системе криволинейных координат уравнение (4) принимает
вид:
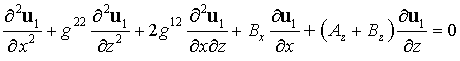 . .
Так как переменные 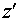 и и 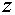 связаны соотношением связаны соотношением 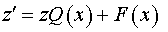 , необходимо выразить функции , необходимо выразить функции  и и  только в переменных только в переменных 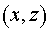 . .
Переходя к
квазиоптическому приближению в уравнении
(15) получаем:
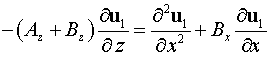 . .
Выбор
краевых условий обсужден выше. Начальное условие получаем из соотношений типа
(7):
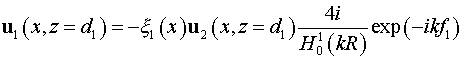 . .
Здесь 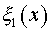 - коэффициент отражения от малого зеркала. - коэффициент отражения от малого зеркала.
4.2 Четные проходы.
Поскольку резонатор
телескопический, т.е. волна, отраженная от большого зеркала близка к плоской
волне, простирающейся вдоль оси 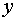 от от 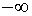 до до 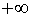 , естественно использовать решение оператора Гельмгольца в виде: , естественно использовать решение оператора Гельмгольца в виде:
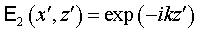 . .
Следовательно,
согласно (5) имеем: 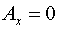 , ,
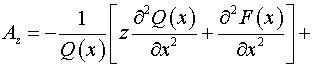
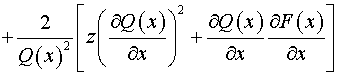 , ,
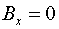 , , 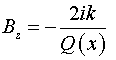 . .
Таким
образом, в выбранной системе координат уравнение (4) имеет вид:
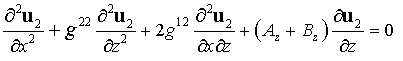 . .
Переход
в уравнении (17) к квазиоптическому приближению приводит к уравнению:
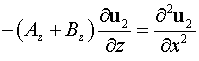 . .
Выбор краевых условий обсужден выше.
Начальное условие:
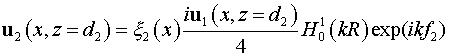 . .
Здесь 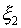 - коэффициент отражения от большого зеркала. - коэффициент отражения от большого зеркала.
5. Рассмотрим математическую модель
распространения лазерного излучения в генераторе на базе неустойчивого
телескопического резонатора, заполненного активной нелинейной средой.
Используем широко известную модель Ригрода [10] для описания усиливающей
(активной) среды. Эффективный коэффициент усиления 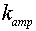 в этой модели
представляется в виде: в этой модели
представляется в виде:
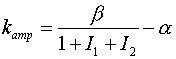 , ,
где 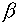 - коэффициент
усиления слабого поля, - коэффициент
усиления слабого поля, 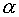 - коэффициент
линейных потерь, - коэффициент
линейных потерь, 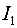 - приведенная
интенсивность поля нечетного прохода, - приведенная
интенсивность поля нечетного прохода, 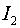 - приведенная
интенсивность поля четного прохода. - приведенная
интенсивность поля четного прохода.
Тогда процесс распространения лазерного излучения
описывается системой нелинейных уравнений для медленно меняющихся комплексных
амплитуд 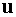 и и 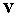 : : 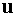 - нечетный проход излучения, - нечетный проход излучения, 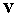 - четный проход излучения. - четный проход излучения.
5.1 В трехмерном случае с учетом эффективного
коэффициента усиления активной среды имеем систему уравнений:
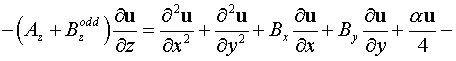
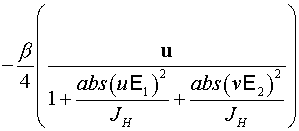 , ,
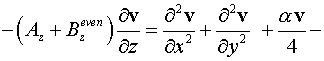
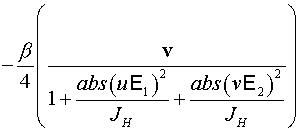 . .
Условие отражения от малого зеркала:
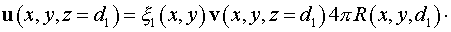
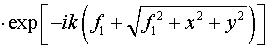 . .
Условие отражения от
большого зеркала:
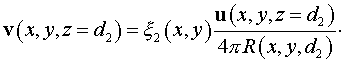
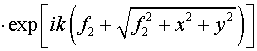 . .
Здесь 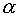 - коэффициент
поглощения, - коэффициент
поглощения, 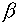 - коэффициент
усиления слабого поля, - коэффициент
усиления слабого поля, 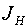 - интенсивность насыщения. - интенсивность насыщения.
5.2 В двумерном случае имеем систему уравнений:
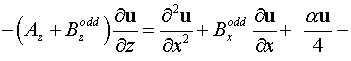
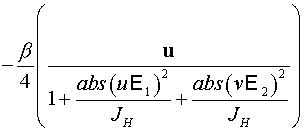 , ,
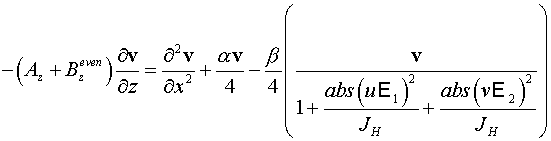 . .
Условие отражения от малого зеркала:
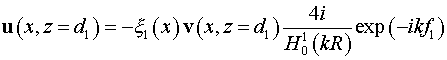 . .
Условие отражения от большого зеркала:
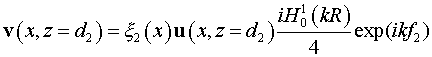 . .
6. Рассмотрим подробнее двумерный случай. Коэффициенты 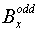 и и 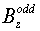 в уравнении (15)
зависят согласно (13), (14) как от функции Ханкеля, так и от ее производных, что создает
определенные неудобства при численном исследовании задачи распространения
лазерного излучения в резонаторе. Воспользуемся приближенной формулой [11]: в уравнении (15)
зависят согласно (13), (14) как от функции Ханкеля, так и от ее производных, что создает
определенные неудобства при численном исследовании задачи распространения
лазерного излучения в резонаторе. Воспользуемся приближенной формулой [11]:
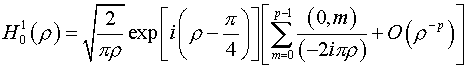 , ,
где :
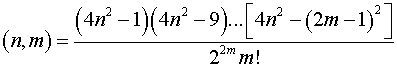 . .
Ограничимся
тремя членами в разложении (21):
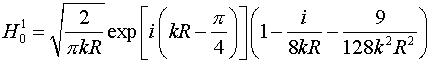 . .
Подставляя (22) в выражения для коэффициентов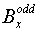 и и 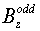 , получаем: , получаем:
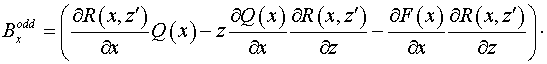
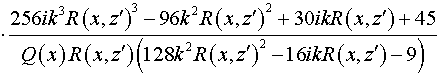 , ,
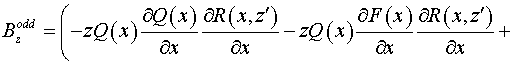
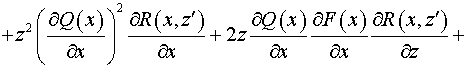
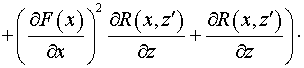
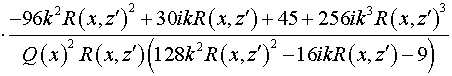 . .
Представим уравнения (19) и (20) в виде, удобном для численного решения. Поскольку
справедливы соотношения:
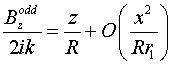 , , 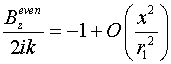 , ,
после
тождественных преобразований уравнения (19), (20) перепишем следующим образом:
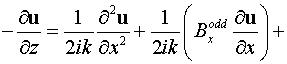
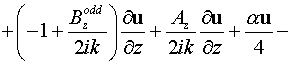 
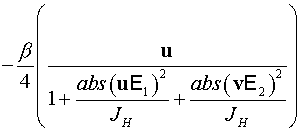 , ,
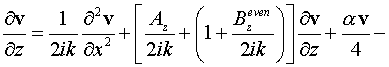
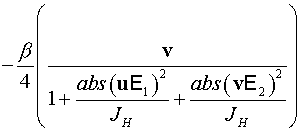 . .
Введем безразмерные переменные:  , , 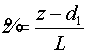 . .
В переменных 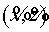 уравнение для
нечетного прохода: уравнение для
нечетного прохода:
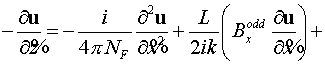
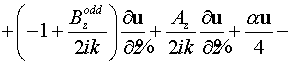
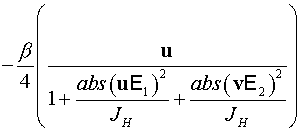 . .
Уравнение для четного прохода:
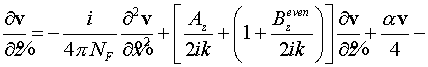
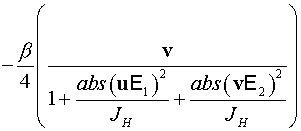 . .
По
переменной  применяем
преобразование Фурье. Для нечетного прохода получаем: применяем
преобразование Фурье. Для нечетного прохода получаем:
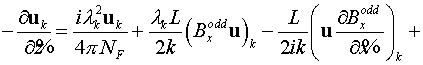
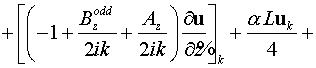
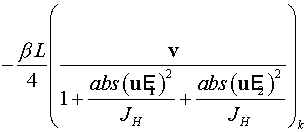 . .
Для четного прохода имеем:
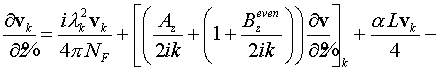 
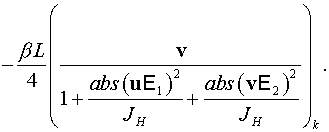
Здесь нижним индексом 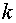 обозначены
соответствующие Фурье компоненты функций, например, обозначены
соответствующие Фурье компоненты функций, например, 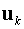 , , 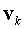 , , 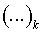 и т.д. и т.д.
По переменной 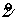 применяем схему
Кранка-Николсона [12] с итерациями. Для нечетного прохода: применяем схему
Кранка-Николсона [12] с итерациями. Для нечетного прохода:
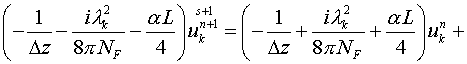
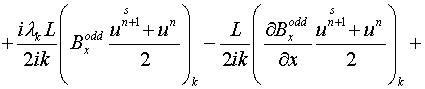
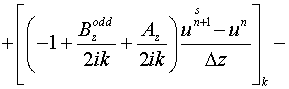
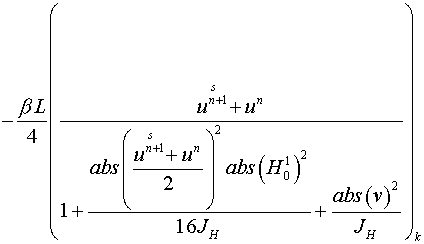 . .
Для четного прохода:
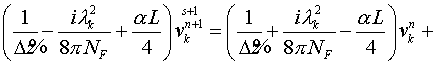
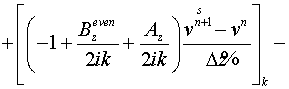
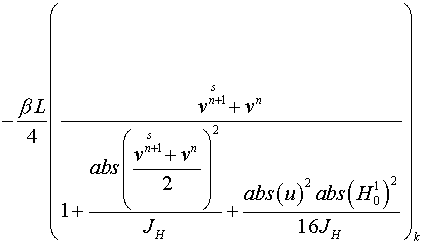 . .
Уравнения
(23)-(24), условия отражения на зеркалах резонатора:
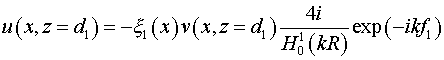 , ,
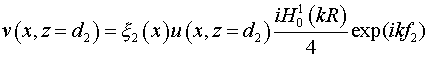 . .
и краевые условия: 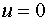 , , 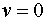 при при 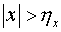 позволяют определить,
как минимум, несколько наиболее добротных мод и соответствующих им собственных
значений генератора, опираясь, например, на методики, предложенные в [5, 15]. позволяют определить,
как минимум, несколько наиболее добротных мод и соответствующих им собственных
значений генератора, опираясь, например, на методики, предложенные в [5, 15].
7. Несомненно, практический интерес
представляет распределение поля на выходе генератора не в криволинейных
координатах 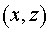 , а в декартовых координатах на плоскости , а в декартовых координатах на плоскости 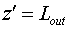 (так называемая
ближняя зона). Переход к специально выбранной неортогональной системе координат (так называемая
ближняя зона). Переход к специально выбранной неортогональной системе координат
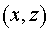 позволяет решить и эту
задачу. Действительно, пусть мы имеем в криволинейных координатах позволяет решить и эту
задачу. Действительно, пусть мы имеем в криволинейных координатах 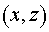 установившееся
распределение поля установившееся
распределение поля 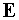 на плоскости на плоскости 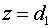 . В декартовой системе координат плоскость . В декартовой системе координат плоскость 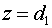 есть поверхность малого зеркала есть поверхность малого зеркала 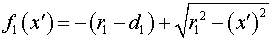 . Излучение распространяется от поверхности . Излучение распространяется от поверхности 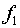 до плоскости до плоскости 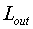 , расположенной вне
активной среды. Выбираем такую систему криволинейных координат , расположенной вне
активной среды. Выбираем такую систему криволинейных координат 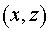 , в которой поверхность, описываемая функцией , в которой поверхность, описываемая функцией 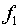 , переходит в плоскость , переходит в плоскость 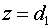 , а плоскость , а плоскость 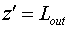 переходит в себя переходит в себя 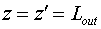 : :
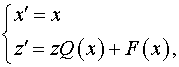
где 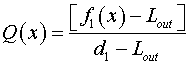 , , 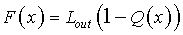 . .
Компоненты тензора 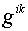 в координатах в координатах 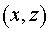 равны: равны:
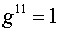 , , 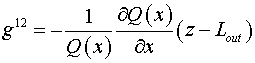 , ,
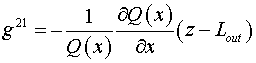 , ,
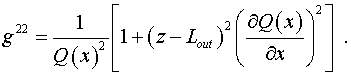
Определитель 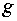 матрицы метрического
тензора матрицы метрического
тензора 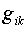 : : 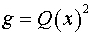 . Следовательно, имеем: . Следовательно, имеем: 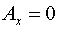 , ,
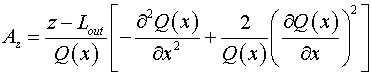 , ,
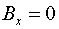 , , 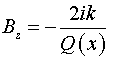 . .
Таким
образом, в выбранной системе координат уравнение (4) имеет вид:
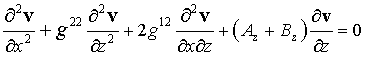 . .
Переходим
в уравнении (25) к квазиоптическому приближению:
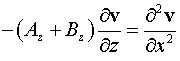 . .
Выбор
краевых условий обсужден выше. Начальное условие с учетом апертуры малого
зеркала:
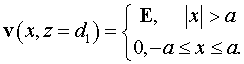
Поскольку поле 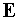 распространяется от
поверхности распространяется от
поверхности 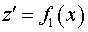 до плоскости до плоскости 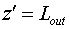 вне активной среды,
согласно (23) имеем: вне активной среды,
согласно (23) имеем:
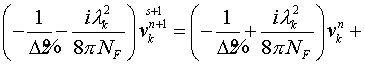
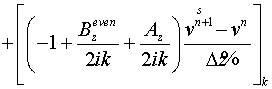 . .
Решая уравнение (26) получаем установившееся значение
поля на произвольной плоскости  в декартовой системе
координат. в декартовой системе
координат.
Предложенный подход к
расчету распространения излучения в лазерных
генераторах применен к известной модельной задаче [3,5] определения наиболее
добротных мод и соответствующих им собственных чисел резонатора. в лазерных
генераторах применен к известной модельной задаче [3,5] определения наиболее
добротных мод и соответствующих им собственных чисел резонатора.
Приведены результаты расчета
поля в неустойчивом телескопическом резонаторе, имеющем следующие геометрические
характеристики: радиус  малого зеркала равен 1120мм. Радиус малого зеркала равен 1120мм. Радиус  большого зеркала
равен 3360мм. Длина волны затравочного излучения в генераторе – 10.7мкм. Расчет
наиболее добротных мод и соответствующих им собственных значений проведен для
диапазона изменения чисел Френеля большого зеркала
равен 3360мм. Длина волны затравочного излучения в генераторе – 10.7мкм. Расчет
наиболее добротных мод и соответствующих им собственных значений проведен для
диапазона изменения чисел Френеля 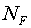 от 0.5 до 5.0. от 0.5 до 5.0.
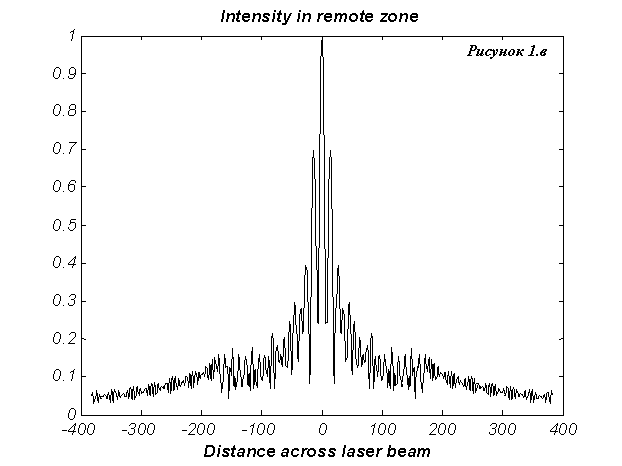
На Рис.1а изображено поле
основной моды в относительных единицах для 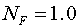 и коэффициента
усиления и коэффициента
усиления 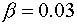 см.–1 в криволинейных координатах см.–1 в криволинейных координатах 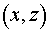 на плоскости на плоскости 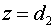 , совпадающей с плоскостью малого зеркала (см. стр.23).
Отметим, что особенности поведения поля в затемненной прямоугольной зоне могут
определяться как наличием эффекта Гиббса, так наличием периодических условий на
границе расчетной области. , совпадающей с плоскостью малого зеркала (см. стр.23).
Отметим, что особенности поведения поля в затемненной прямоугольной зоне могут
определяться как наличием эффекта Гиббса, так наличием периодических условий на
границе расчетной области.
На Рис.1.б изображено поле основной моды в
ближней зоне в декартовой системе координат 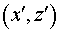 . .
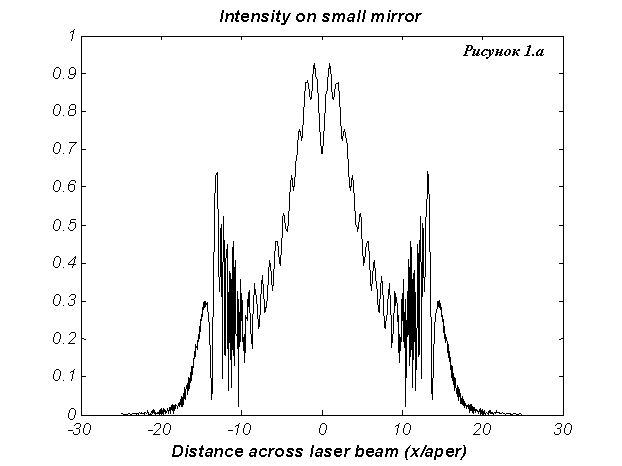
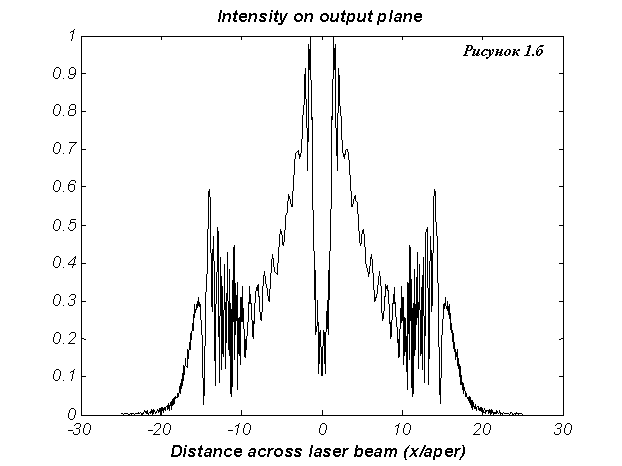
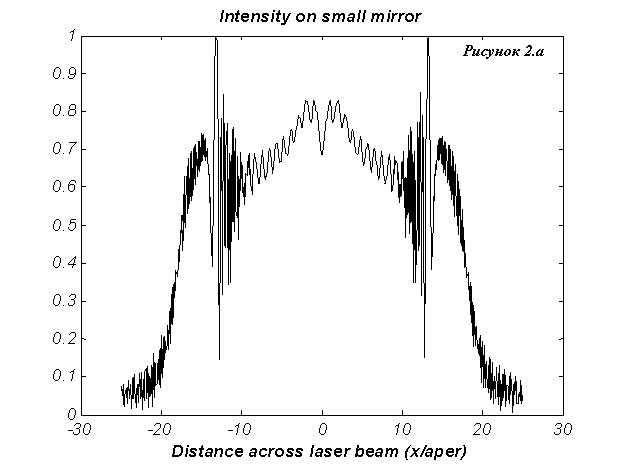
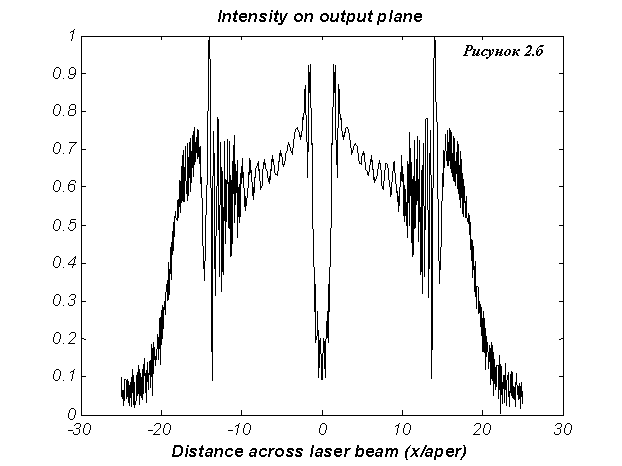
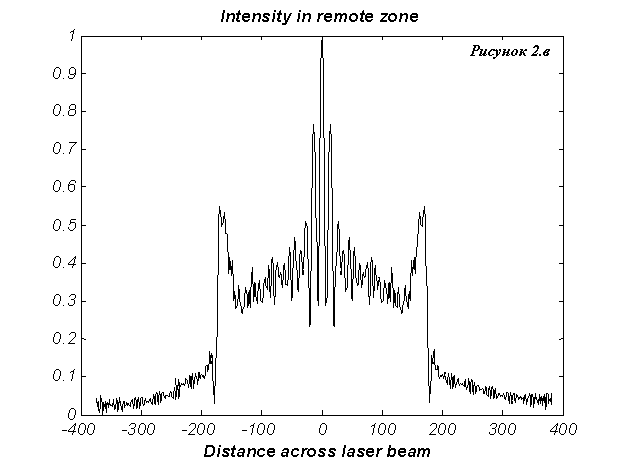
На Рис.2а изображено поле
основной моды в относительных единицах для 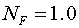 и коэффициента
усиления и коэффициента
усиления 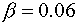 см.–1 в криволинейных координатах см.–1 в криволинейных координатах 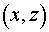 на плоскости,
совпадающей с плоскостью малого зеркала. На Рис.2.б изображено поле основной
моды в ближней зоне в декартовой системе координат на плоскости,
совпадающей с плоскостью малого зеркала. На Рис.2.б изображено поле основной
моды в ближней зоне в декартовой системе координат 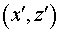 . .
 


ЛИТЕРАТУРА
1.
Siegman A.E. Proc. IEEE, 1965, v. 53, p. 277.
2.
Ананьев Ю.А. Оптические резонаторы и проблемы расходимости лазерного
излучения. – М.: Наука, 1979.
3.
Ананьев Ю.А. Оптические резонаторы и лазерные пучки. – М.: Наука, 1990.
4.
Карамзин Ю.Н., Конев Ю.Б. Численные методы исследования работы
неустойчивых телескопических резонаторов с учетом дифракции и эффекта насыщения
в активной среде. – Препринт ИПМ им.М.В.Келдыша АН СССР, 1974, № 57.
5.
Елкин Н.Н., Напартович А.П. Прикладная оптика лазеров. – М.:ЦНИИатоминформ,
1989.
6.
Владимиров В.С. Уравнения математической физики. - М.: Наука, 1971.
7.
Тихонов А.Н., Самарский А.А. Уравнения Математической физики. – М.:
Наука, 1972.
8.
Карамзин Ю.Н., Цветкова И.Л. Спектральный метод решения нелинейных
квазиоптических задач. – Препринт ИПМ им.М.В.Келдыша АН СССР, 1979, № 115.
9.
Карамзин Ю.Н., Цветкова И.Л. О сходимости спектрального метода решения
одной задачи нелинейной оптики. – ЖВМ и МФ, 1982, т.22, с. 235-240.
10.
Rigrod W. Gain saturation and output power of optical
mazers. – J. Appl. Phys., 1963, v. 34, p. 2602.
11.
Ватсон Г.Н. Теория бесселевых функций, часть первая. – М.: Из-во
Иностранной литературы, 1949.
12.
Самарский А.А. Теория разностных схем. – М.: Наука, 1977.
13.
Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. –
М.-Л.: ГИФМЛ, 1963.
14.
Уилкинсон Дж. Х. Алгебраическая проблема собственных значений. – М.:
Наука, ГИФМЛ., 1970.
15.
Siegman A.E., Miller H.Y. Unstable Optical Loss
Calculations Using the Prony Method. – Applied
Optics, 1970, v. 9, № 12, p. 2729.
|