Аннотация
Работа посвящена получению решения нелинейной монотонизированной разностной схемы К.И.Бабенко
('квадрат') для одномерного уравнения переноса со знакопеременной скоростью. Показано, что
решение нелинейных уравнений, определяющих неизвестные на верхнем временном слое, существует
и единственно. Получены точные выражения для решений.
Abstract
The paper is dedicated to construction of the solution of the nonlinear monotonized K.I.Babenko
difference scheme for 1D advection equation with sign-alternative velocity. The analysis
has shown that the solution exists and is unique. The formula of the exact solution has been
obtained.
1.
Постановка задачи
Для определения решения 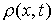 смешанной задачи на
отрезке смешанной задачи на
отрезке 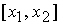
для одномерного уравнения переноса со
знакопеременной ограниченной скоростью 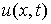 , , 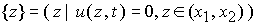 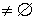 , с начальным условием , с начальным условием 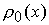 и граничными
условиями и граничными
условиями  , , 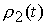
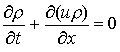 , (1) , (1)
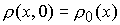 , , 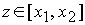 , ,
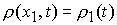 , при , при 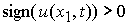 , , 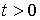 , ,
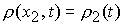 , при , при 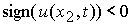 , , 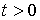
в [1]
предложена нелинейная монотонизированная разностная схема К. И. Бабенко («квадрат») [2].
Особенность схемы заключается в различии нелинейных разностных уравнений на
участках знакопостоянства скорости и в окрестностях точек перемены ее знака.
Уравнения имеют следующий вид.
1. При 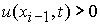 , , 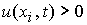 , , 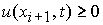 : :
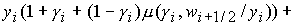
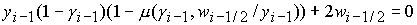 . (2) . (2)
2. При 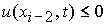 , , 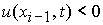 , , 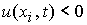 : :
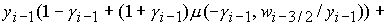
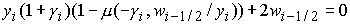 .
(3) .
(3)
3. При 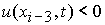 , , 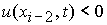 , , 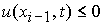 , , 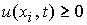 , , 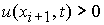 , , 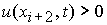 (перемена знака
скорости типа (–, +)): (перемена знака
скорости типа (–, +)):
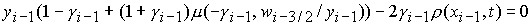 , ,
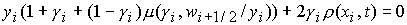 . (4) . (4)
4. При 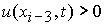 , , 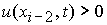 , , 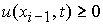 , , 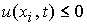 , , 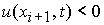 , ,  (перемена знака
скорости типа (+, –)): (перемена знака
скорости типа (+, –)):
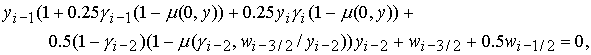 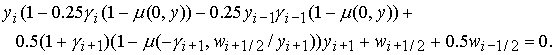 (5) (5)
где 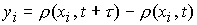 , , 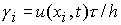 , , 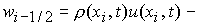 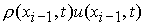 , , 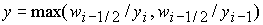 , , 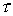 , , 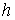 – соответственно временной и пространственный шаг разностной
сетки, а функция – соответственно временной и пространственный шаг разностной
сетки, а функция 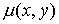 определена в [1] и
имеет вид определена в [1] и
имеет вид
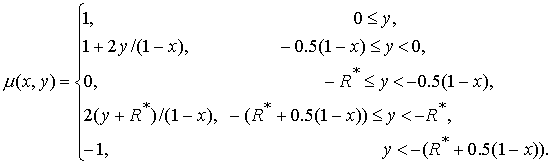

В
первых двух случаях неизвестной является соответственно либо 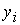 , либо , либо 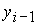 , а в последних двух случаях обе неизвестные , а в последних двух случаях обе неизвестные 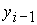 и и 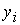 подлежат
определению. Окончательно, подлежат
определению. Окончательно, 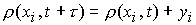 , , 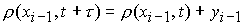 . .
Представляет интерес найти расчетные
формулы для точного решения нелинейной разностной схемы. Альтернативой
рассматриваемого ниже прямого метода является итерационный метод.
2.
Разностное решение при сохранении знака скорости
2.1.
В случае 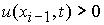 , , 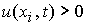 , , 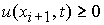 неизвестная величина неизвестная величина 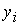 удовлетворяет
нелинейному уравнению удовлетворяет
нелинейному уравнению
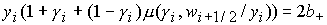 , ,
где 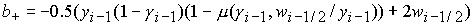 – известное значение.
Уравнение является дробно-рациональным и имеет решение следующего вида: – известное значение.
Уравнение является дробно-рациональным и имеет решение следующего вида:
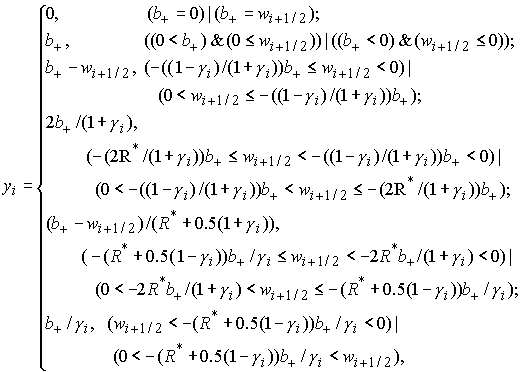
где
& – логическое «и», | – логическое «или». Очевидно, что решение 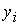 существует и единственно
для любых значений известных величин существует и единственно
для любых значений известных величин  и и 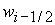 . .
2.2.
В случае 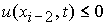 , , 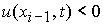 , , 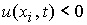 неизвестная величина неизвестная величина 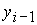 удовлетворяет
нелинейному уравнению удовлетворяет
нелинейному уравнению
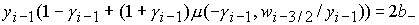 , ,
где 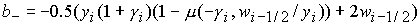 , ,
Уравнение
имеет решение следующего вида:
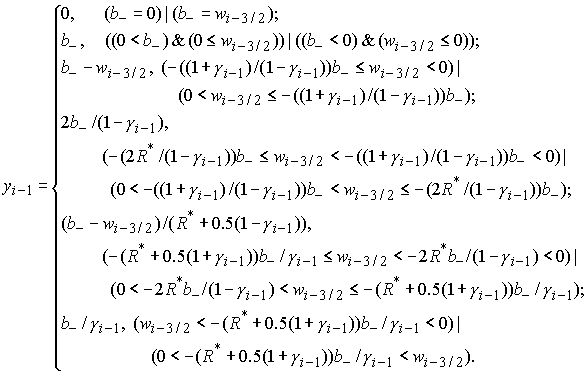
Решение
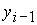 существует и
единственно для любых значений известных величин существует и
единственно для любых значений известных величин 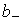 и и 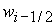 . .
3.
Решение задачи в окрестности точки перемены знака скорости типа (–, +)
В случае 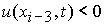 , , 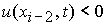 , , 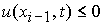 , , 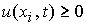 , , 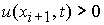 , , 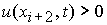 необходимо определить
неизвестные величины необходимо определить
неизвестные величины 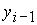 и и 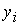 из независимых
нелинейных уравнений из независимых
нелинейных уравнений
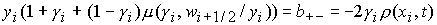 , ,
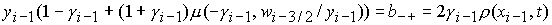 , ,
которые
всегда имеют единственное решение вида:
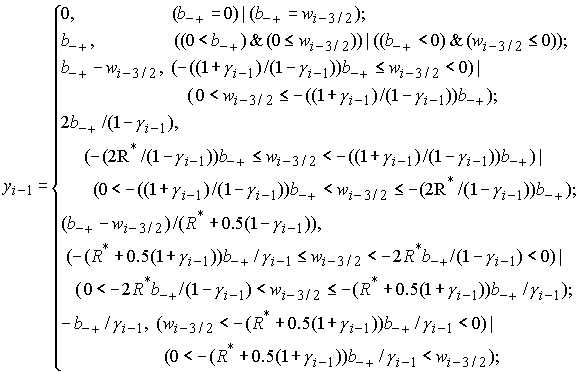

Отметим, что при 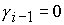 неизвестная неизвестная 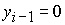 , а при , а при 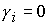 величина величина 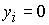 . .
4.
Точное решение в окрестности точки перемены знака скорости типа (+, –)
В окрестности точки типа (+, –)
неизвестные величины 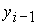 , , 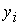 удовлетворяют
следующей системе нелинейных уравнений удовлетворяют
следующей системе нелинейных уравнений
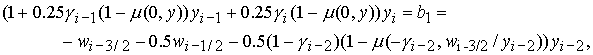 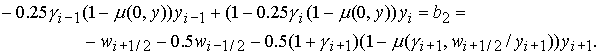 Величина Величина 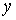 определяется
нелинейной функцией определяется
нелинейной функцией
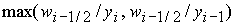 , а значение , а значение 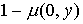 вычисляется по
формуле вычисляется по
формуле
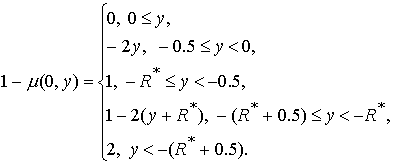
Из уравнений вытекает следствие
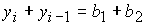 .
(6) .
(6)
Поэтому
ниже будем искать лишь неизвестную 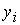 , которую обозначим через , которую обозначим через 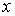 . Поиск точного решения системы нелинейных уравнений
выполняется по следующей схеме. . Поиск точного решения системы нелинейных уравнений
выполняется по следующей схеме.
1.
Определение функции 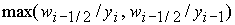 . .
2.
Приведение исходной системы к уравнению для
неизвестной 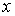 . .
3.
Выполнение отбора решений нелинейных уравнений.
4.
Нахождение области существования различных ветвей
решения.
5.
Получение окончательного выражения для решения в
окрестности точки перемены знака скорости типа (+, –).
4.1. Функция 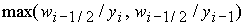
Согласно
(6), 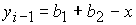 , поэтому , поэтому
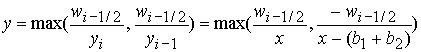 и и
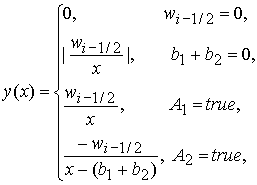 (7) (7)
где
булевы переменные 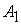 и и 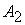 имеют
следующий вид: имеют
следующий вид:
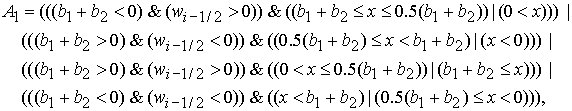
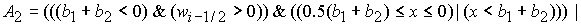 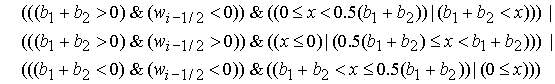 (8) (8)
Графики
качественно различных зависимостей 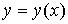 представлены на рис. 1: а) представлены на рис. 1: а) 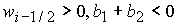 ; b) ; b) 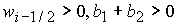 ; c) ; c) 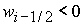 , , 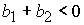 ; d) ; d) 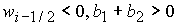 ; e) ; e) 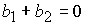 ; f) ; f) 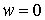 . .
Отметим, что 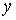 может быть
отрицательным лишь при выполнении неравенства может быть
отрицательным лишь при выполнении неравенства
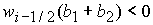 . (9) . (9)
При
выполнении этого неравенства отрицательная ветвь зависимости 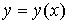 существует
при существует
при 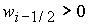 ( (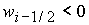 ) на отрезке ) на отрезке  ( (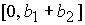 ). На этих отрезках ). На этих отрезках 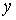 имеет
максимальное значение имеет
максимальное значение 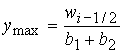 и
минимальное значение и
минимальное значение 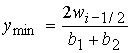 . Минимум достигается в центре указанного отрезка . Минимум достигается в центре указанного отрезка 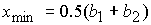 . Максимум достигается на концах отрезка . Максимум достигается на концах отрезка 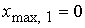 и и 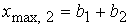 . На отрезке . На отрезке
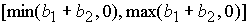 при
выполнении условия (9) функция при
выполнении условия (9) функция 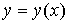 может быть
определена более просто (следует из (7)) может быть
определена более просто (следует из (7))
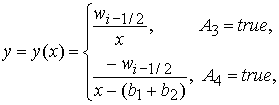 (10) (10)
где 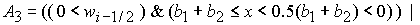

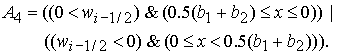 (11) (11)
4.2. Частные случаи
1.
Пусть 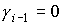 , , 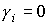 . Тогда решение системы (5) имеет следующий вид: . Тогда решение системы (5) имеет следующий вид:
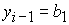 , , 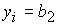 . (12) . (12)
2.
Пусть 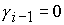 , , 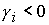 . Тогда решение . Тогда решение 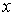 удовлетворяет одному из пяти уравнений: удовлетворяет одному из пяти уравнений:
1) 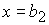 , при , при 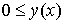 ; ;
2) 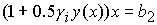 , при , при 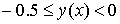 ; ;
3) 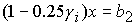 , при , при 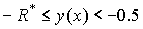 ; ;
4) 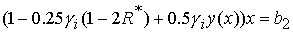 , при , при 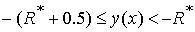 ; ;
5) 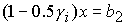 , при , при 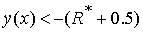 . .
Найдем
в 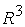 ( ( 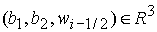 ) области 1, 2, 3, 4, 5, в которых решение
исходной задачи определяется соответственно одним из перечисленных уравнений 1)
– 5). ) области 1, 2, 3, 4, 5, в которых решение
исходной задачи определяется соответственно одним из перечисленных уравнений 1)
– 5).
Область 1. Анализ свойств функции 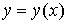 показывает, что неравенство показывает, что неравенство 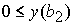 справедливо при выполнении условия справедливо при выполнении условия
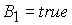 , (13) , (13)
где 
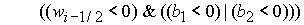 . .
При
выполнении условия (13) решение системы (5) имеет вид (12).
Области
2 – 5 существует либо при 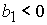 , , 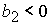 , либо при , либо при 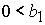 , , 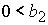 . .
Область 3. В этой области 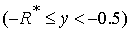 решение решение 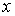 находится
по формуле находится
по формуле
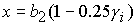 . (14) . (14)
Для
определения области 3 необходимо решить следующие системы неравенств 1) – 4):
1) 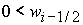 , , 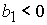 , , 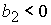 , , 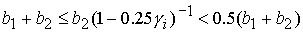 , ,
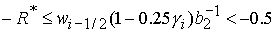 ; ;
2) 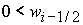 , , 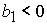 , , 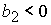 , , 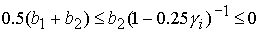 , ,
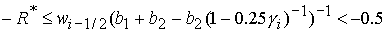 ; ;
3) 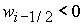 , , 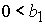 , , 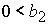 , , 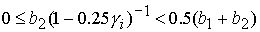 , ,
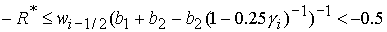 ; ;
4) 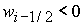 , , 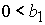 , , 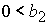 , , 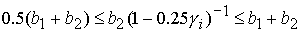 , ,
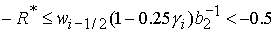 . .
Граница
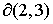 областей 2
и 3 областей 2
и 3 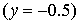 в в 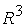 представляет собой фрагменты плоскостей представляет собой фрагменты плоскостей 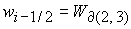 : :
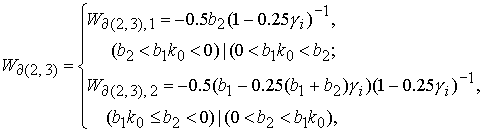 (15) (15)
где 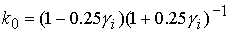 . .
Граница
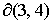 областей 3
и 4 областей 3
и 4 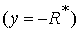 в в 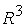 представляет собой фрагменты плоскостей представляет собой фрагменты плоскостей 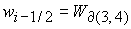 : :
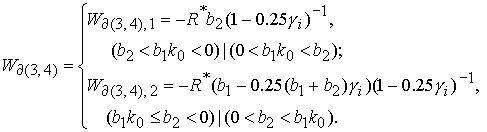 (16) (16)
Решение
неравенств 1) – 4) определяет область 3:
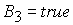 , (17) , (17)
где 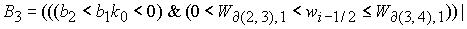
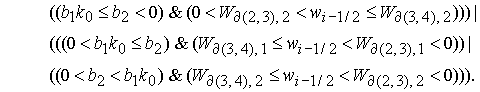
Область 5. В этой области 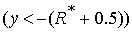 решение решение 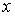 находится
по формуле находится
по формуле
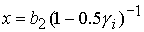 . (18) . (18)
Для
определения области 5 необходимо решить следующие системы неравенств 1) – 4):
1) 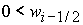 , , 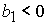 , , 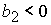 , , 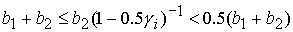 , ,
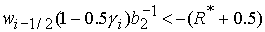 ; ;
2) 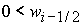 , , 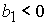 , ,  , , 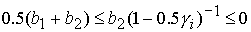 , ,
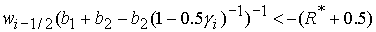 ; ;
3) 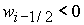 , , 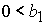 , ,  , , 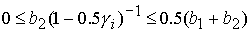 , ,
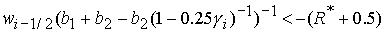 ; ;
4) 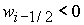 , , 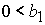 , , 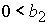 , , 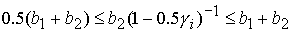 , ,
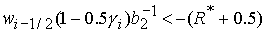 . .
Граница
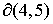 областей 4
и 5 областей 4
и 5 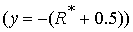 в в 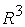 представляет собой фрагменты плоскостей представляет собой фрагменты плоскостей 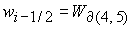 : :
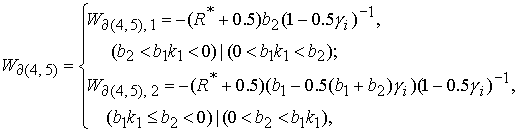 (19) (19)
где 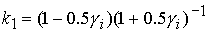 . .
Решение
неравенств 1) – 4) определяет область 5
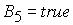 , (20) , (20)
где 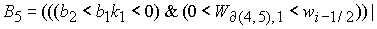
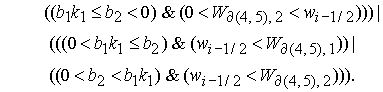
Область 2 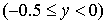 определяется условием определяется условием
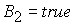 , (21) , (21)
где 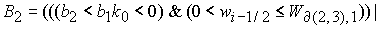
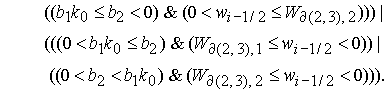
В
области 2 существуют три подобласти 21/3, 22, 24, в которых решение находится
различным образом.
Соотношение
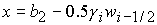 (22) (22)
определяет
решение в области 21/3. Эта область определяется решением неравенств
1) 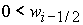 , , 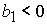 , , 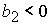 , , 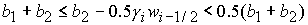 , ,
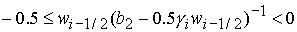 ; ;
2) 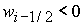 , , 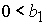 , , 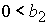 , , 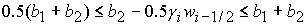 , ,
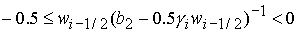 . .
Точка 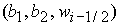 принадлежит этой области, если выполняется условие принадлежит этой области, если выполняется условие
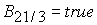 , (23) , (23)
где 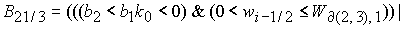
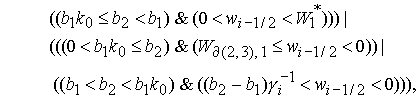
где 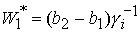 . .
При
выполнении неравенств
1) 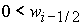 , , 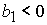 , , 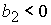 , , 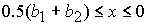 , ,
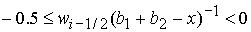 ; ;
2) 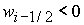 , , 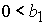 , , 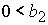 , , 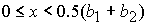 , ,
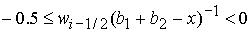
неизвестная
величина 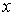 удовлетворяет уравнению удовлетворяет уравнению
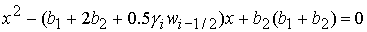 с корнями с корнями
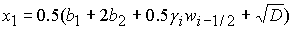 , (24.1) , (24.1)
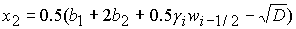 , (24.2) , (24.2)
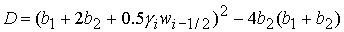 . (24.3) . (24.3)
Корень 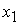 дает
решение задачи в области 22, которая определяется неравенствами дает
решение задачи в области 22, которая определяется неравенствами
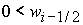 , , 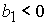 , , 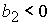 , , 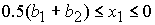 , ,
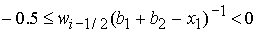 . .
Решение
этой группы неравенств определяет область 22. Точка 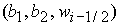 принадлежит этой области, если выполнено условие принадлежит этой области, если выполнено условие
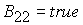 , (25) , (25)
где 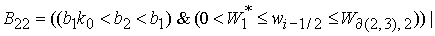
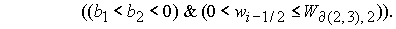
Корень 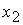 дает
решение задачи в области 24, определяемой неравенствами дает
решение задачи в области 24, определяемой неравенствами
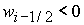 , , 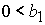 , , 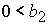 , , 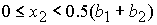 , ,
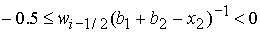 . .
Точка 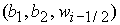 принадлежит области
24 при выполнении условия принадлежит области
24 при выполнении условия
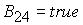 , (26) , (26)
где 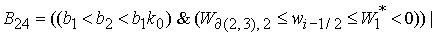
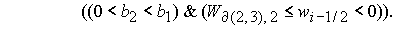
Область 4. Область 4 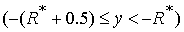 определяется условием определяется условием
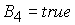 , (27) , (27)
где 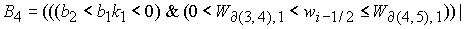
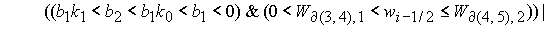
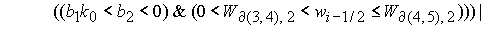
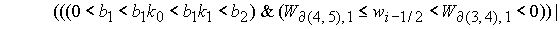
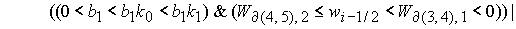
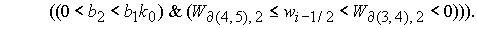
В
области 4 существуют подобласти 46/8, 47, 49, в которых решения находятся с
помощью разных выражений.
Соотношение
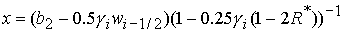 (28) (28)
определяет
решение в области 46/8. Область 46/8 определяется решением неравенств:
1) 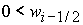 , , 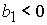 , , 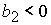 , ,
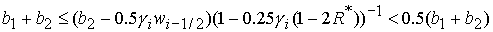 , ,
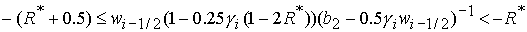 ; ;
2)  , , 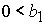 , , 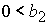 , ,
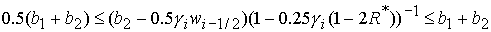 , ,
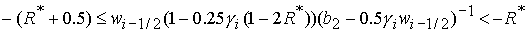 . .
Точка  принадлежит области
46/8 при выполнении условия принадлежит области
46/8 при выполнении условия
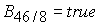 , (29) , (29)
где 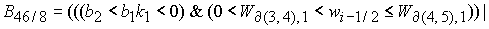
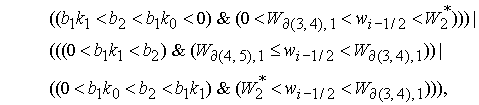
где 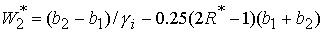 . .
При
выполнении неравенств:
1) 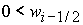 , , 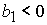 , , 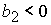 , , 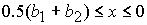 , ,
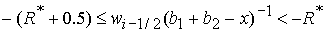 ; ;
2) 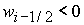 , , 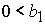 , , 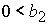 , , 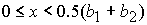 , ,
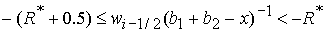
неизвестная
величина 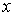 удовлетворяет уравнению удовлетворяет уравнению
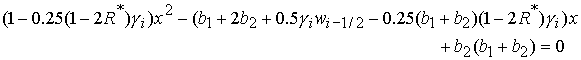
с
корнями
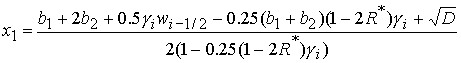 , (30.1) , (30.1)
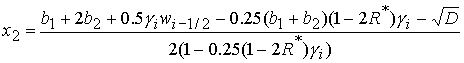 , (30.2) , (30.2)
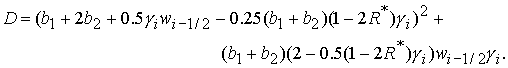 (30.3) (30.3)
Корень 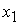 дает
решение задачи в области 47 дает
решение задачи в области 47
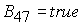 , (31) , (31)
где 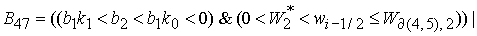
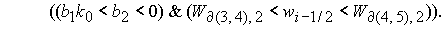
Корень 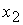 дает
решение задачи в области 49 дает
решение задачи в области 49
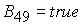 , (32) , (32)
где 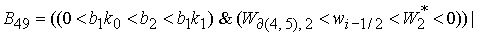
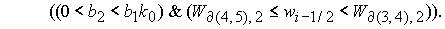
На рис.
2 схематически представлены области применимости формул (14), (18), (22),
(24.1), (24.2), (30.1), (30.2) в 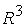 в частном случае в частном случае 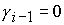 , , 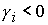 . .
3.
Аналогично определяется решение для частного случая 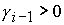 , , 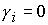 . .
4.3. Редукция исходной системы уравнений
Пусть 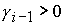 , , 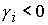 . В зависимости от . В зависимости от  значение значение 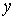 принадлежит одной из пяти областей: 1) принадлежит одной из пяти областей: 1) 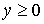 ; 2) ; 2) 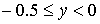 ; 3) ; 3) 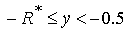 ; 4) ; 4)  ; 5) ; 5) 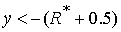 . В каждой из областей исходная система уравнений
принимает специфический вид. Так, в областях 1, 3, 5 система (5) является
линейной (не зависит от . В каждой из областей исходная система уравнений
принимает специфический вид. Так, в областях 1, 3, 5 система (5) является
линейной (не зависит от 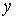 ), а в областях 2 и 4 сводится к квадратному
уравнению относительно ), а в областях 2 и 4 сводится к квадратному
уравнению относительно 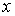 . .
Область 1. В этом случае (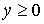 ): ):
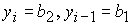 . .
Область 2. В этой области система принимает вид:
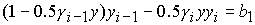 , ,
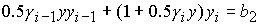 , ,
и дает
следующее нелинейное уравнение для 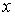
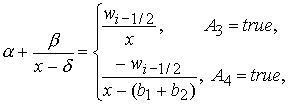 (33) (33)
где 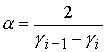 , , 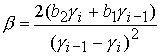 , , 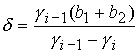 . .
При
выполнении условия 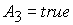 (33)
сводится к квадратному уравнению (33)
сводится к квадратному уравнению  с
коэффициентами с
коэффициентами
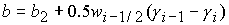 , , 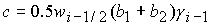 . (34) . (34)
Дискриминант
уравнения 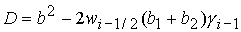 положителен в рассматриваемой области, так как положителен в рассматриваемой области, так как 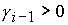 и и 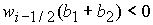 . .
Корни
уравнения имеют следующий вид
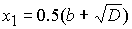 , (35.1) , (35.1)
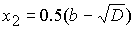 . (35.2) . (35.2)
При 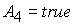 коэффициенты квадратного уравнения имеют вид: коэффициенты квадратного уравнения имеют вид:
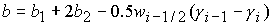 , , 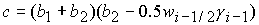 . (36) . (36)
Его
дискриминант 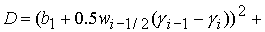 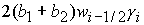 положителен в рассматриваемой области, так как положителен в рассматриваемой области, так как 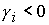 и и 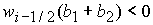 . Корни вычисляются по формуле (35) с
использованием (36). . Корни вычисляются по формуле (35) с
использованием (36).
Область 3. При 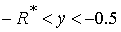 система (5) имеет
вид: система (5) имеет
вид:
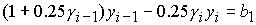 , ,
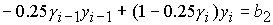
и дает
единственное решение:
Ф5: 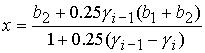 . (37) . (37)
Область 4. В этой области исходные уравнения имеют вид:
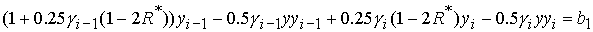 , ,
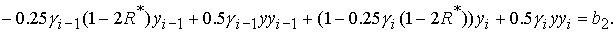 Разрешая эту систему относительно Разрешая эту систему относительно 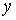 , получаем аналог уравнения (33) со следующими
коэффициентами , получаем аналог уравнения (33) со следующими
коэффициентами
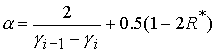 , , 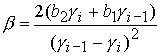 , , 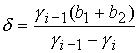 . .
При
условии 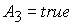 это
уравнение сводится к виду это
уравнение сводится к виду
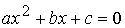 с
коэффициентами: (38) с
коэффициентами: (38)
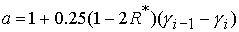 , ,
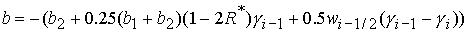 , , 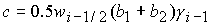 . (39) . (39)
Дискриминант
уравнения (38)
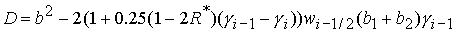 положителен в положителен в
рассматриваемой
области при выполнении условия
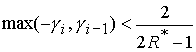 , (40) , (40)
и
уравнение (39) имеет действительные корни
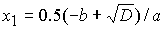 , (41.1) , (41.1)
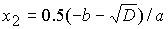 . (41.2) . (41.2)
При
условии 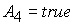 коэффициенты квадратного уравнения (38) вычисляются по формулам: коэффициенты квадратного уравнения (38) вычисляются по формулам:
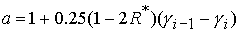 , ,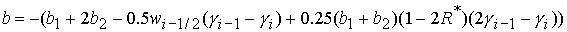 , , 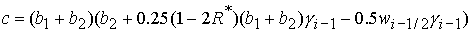 . (42) . (42)
Дискриминант
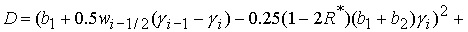
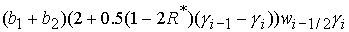 положителен в положителен в
рассматриваемой
области при выполнении условия (40). Корни уравнения имеют вид (41) с
коэффициентами (42).
Область 5. В этой области исходные уравнения принимают вид:
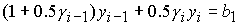 , ,
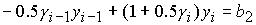 , ,
и дают
единственное решение
Ф10: 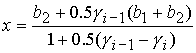 . (43) . (43)
Редукция
исходной системы завершена. Предстоит отобрать подходящие корни квадратных
уравнений в областях 2 и 4.
4.4. Отбор корней
нелинейных уравнений
Отбор
корней в областях 2 и 4 выполним, исходя из требования непрерывности решений
системы (5) на границах областей 2, 3, 4, 5.
Область 2. На границе 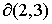 областей 2
и 3 значение неизвестной областей 2
и 3 значение неизвестной 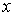 равно равно 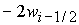 ( ( 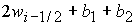 ) при
выполнении условия ) при
выполнении условия 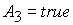 ( (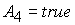 ). Поэтому из требования непрерывности решение
(34), (35) ((35), (36)) должно принимать значение ). Поэтому из требования непрерывности решение
(34), (35) ((35), (36)) должно принимать значение 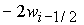 ( ( 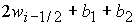 ) при
условии ) при
условии 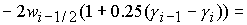 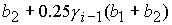
( 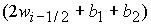 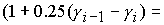 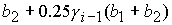 ). ).
Анализ
показывает, что при выполнении 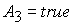 ( (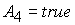 ) этому условию удовлетворяет корень ) этому условию удовлетворяет корень 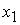 при при  и и 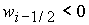 ( ( 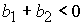 и и 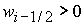 ) или корень ) или корень 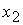 при при 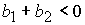 и и 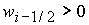 ( (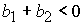 и и 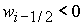 ). Таким образом, решение ). Таким образом, решение  в области
2 имеет вид: в области
2 имеет вид:
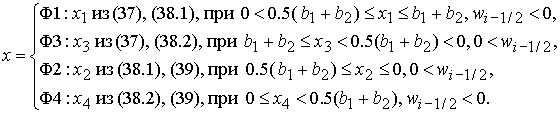 (44) (44)
Область 4. На границе 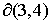 областей 3
и 4 значение неизвестной областей 3
и 4 значение неизвестной 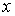 равно равно 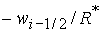 ( ( 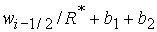 ) при ) при 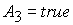 ( (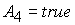 ). Поэтому решение (39), (41) ((41), (42)) должно
принимать то же значение при условии ). Поэтому решение (39), (41) ((41), (42)) должно
принимать то же значение при условии
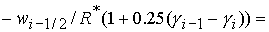 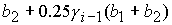
( 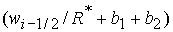 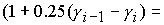 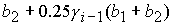 ). Анализ
показывает, что при ). Анализ
показывает, что при 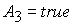 ( (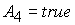 ) в области 4 следует выбрать корень ) в области 4 следует выбрать корень 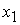 при при 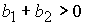 и и 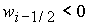 ( (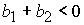 и и 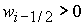 ) или корень ) или корень 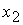 при при  и и  ( (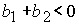 и и 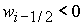 ). ).
На границе 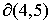 областей 4
и 5 значение областей 4
и 5 значение 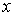 равно равно 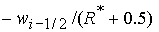 ( ( 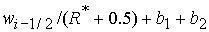 ) при ) при 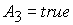 ( (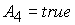 ). Описанный выше выбор корней в области 4
обеспечивает непрерывность решения на этой границе. Поэтому решение ). Описанный выше выбор корней в области 4
обеспечивает непрерывность решения на этой границе. Поэтому решение  в области
4 имеет вид: в области
4 имеет вид:
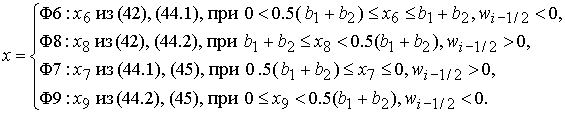 (45) (45)
4.5. Точные выражения
для решения и области их применимости
До сих пор границы областей 1 – 5 определялись в терминах
величины 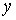 . Для определения зависимости решения системы (5)
от параметров . Для определения зависимости решения системы (5)
от параметров 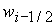 , , 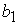 , , 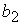 , , 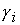 , , 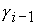 следует
выразить границы областей 1 – 5 в
терминах следует
выразить границы областей 1 – 5 в
терминах 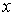 , а затем, воспользовавшись решением, найти
границы в терминах параметров задачи. , а затем, воспользовавшись решением, найти
границы в терминах параметров задачи.
1. Из (7), (8) следует, что величина 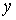 неотрицательна при выполнении условия неотрицательна при выполнении условия 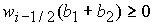 для любого
действительного для любого
действительного 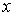 . Она положительна при . Она положительна при 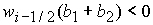 для любого для любого
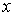 , не принадлежащего отрезку , не принадлежащего отрезку 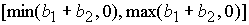 . Поэтому система (5) имеет единственное решение
вида (12) . Поэтому система (5) имеет единственное решение
вида (12)
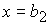
при выполнении следующих условий:
либо 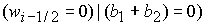 , (46.1) , (46.1)
либо 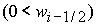 & ( & (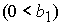 | | 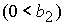 ), (46.2) ), (46.2)
либо 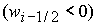 & ( & (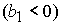 | | 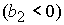 ). (46.3) ). (46.3)
Условия (46) определяют область 1 в 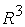 , , 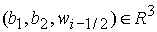 (см. рис. 3). (см. рис. 3).
2. Решение системы (5) принадлежит области 2 и определяется по
формулам Ф1, Ф2, Ф3, Ф4, если, соответственно, выполнены неравенства:
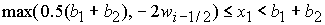 , , 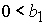 , , 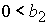 , (47.1) , (47.1)
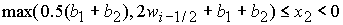 , , 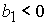 , , 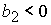 , (47.2) , (47.2)
 , , 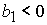 , , 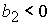 , (47.3) , (47.3)
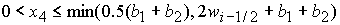 , , 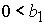 , , 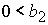 . (47.4) . (47.4)
Граница 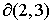 между областями 2 и 3
определяется одним из следующих уравнений при соответствующих условиях: между областями 2 и 3
определяется одним из следующих уравнений при соответствующих условиях:
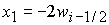 , при , при 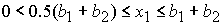 , , 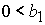 , , 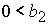 , (48) , (48)
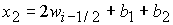 , при , при 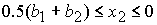 , , 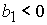 , , 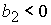 , (49) , (49)
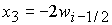 , при , при 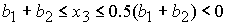 , , 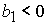 , , 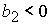 , (50) , (50)
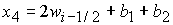 , при , при 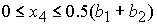 , , 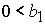 , , 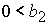 . (51) . (51)
Решения уравнений (48) – (51) относительно 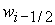 дают следующее
значение дают следующее
значение 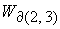 , определяющее границу , определяющее границу 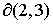 : :
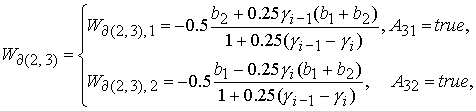 (52) (52)
где 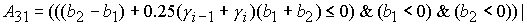
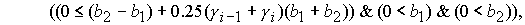
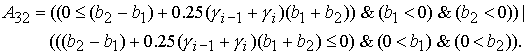
Значение 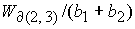 принадлежит интервалу принадлежит интервалу
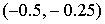 . .
3. Решение системы (5) принадлежит области 3 и определяется по
формуле Ф5:
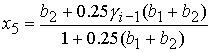 , ,
если выполнены неравенства
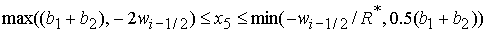 , , 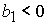 , , 
(53.1)
или
 , , 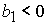 , , 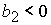 , (53.2) , (53.2)
или
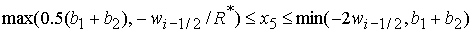 , , 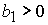 , , 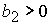 , ,
(53.3)
или
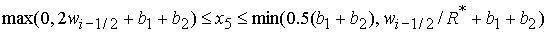 , , 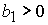 , , 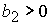 . (53.4) . (53.4)
Граница 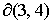 между областями 3 и 4
определяется следующими равенствами: между областями 3 и 4
определяется следующими равенствами:
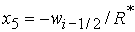 , (54) , (54)
при  , , 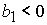 , , 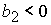 , ,
либо при 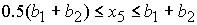 , , 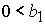 , , 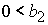 , ,
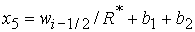 , (55) , (55)
при 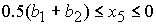 , , 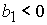 , , 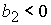 , ,
либо при 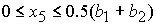 , , 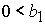 , , 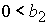 . .
Решения уравнений (54), (55) относительно 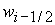 дают значение дают значение 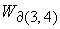 , определяющее границу , определяющее границу 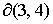 : :
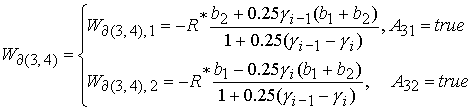 (56) (56)
Значение 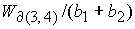 принадлежит интервалу принадлежит интервалу
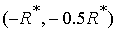 . .
4. Решение системы (5) принадлежит области 4 и определяется по
формулам Ф6, Ф7, Ф8, Ф9, если, соответственно, выполнены неравенства:
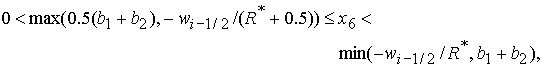 (57.1) (57.1)
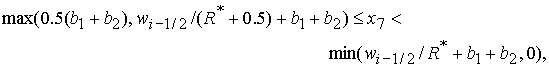 (57.2) (57.2)
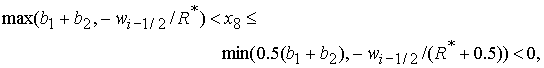 (57.3) (57.3)
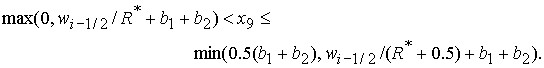 (57.4) (57.4)
Граница 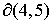 между областями 4 и 5
определяется одним из следующих уравнений: между областями 4 и 5
определяется одним из следующих уравнений:
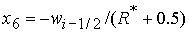 при при  , , 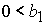 , , 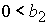 , (58) , (58)
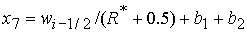 при при 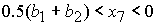 , , 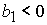 , , 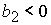 , (59) , (59)
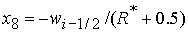 при при 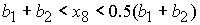 , , 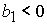 , , 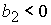 , (60) , (60)
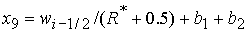 при при 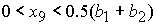 , , 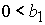 , , 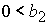 . (61) . (61)
Решение уравнений (58) – (61) относительно 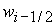 дает значение дает значение 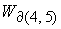 , определяющее границу , определяющее границу 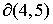 : :
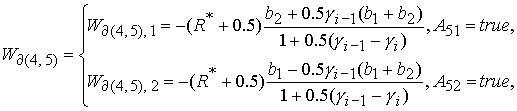 (62) (62)
где 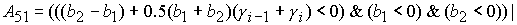
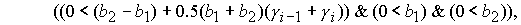
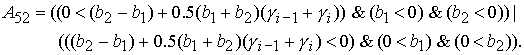
Значение 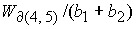 принадлежит интервалу принадлежит интервалу
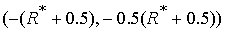 . .
5. Решение системы (5) принадлежит области 5 и вычисляется по
формуле Ф10:
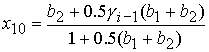 , ,
если 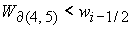 ( (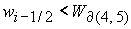 ) при ) при  , , 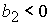 ( (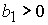 , , 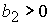 ). ).
6. Области 21, 22, 23, 24 применимости формул Ф1 – Ф4 определяются решением
неравенств (47). Решение этих неравенств дает следующие результаты.
6.1.
Решение системы (5) находится по формуле Ф1, если 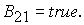 Здесь Здесь
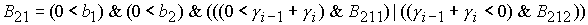 , ,
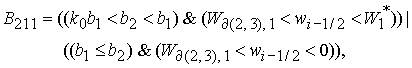
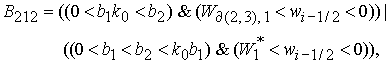
где 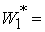 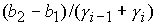 , , 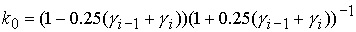 . .
6.2.
Решение системы (5) вычисляется по формуле Ф2, если 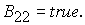 Здесь Здесь
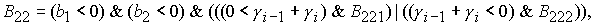 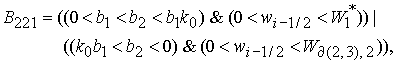
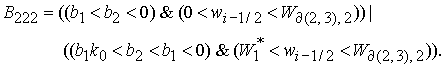
6.3.
Решение системы (5) определяется по формуле Ф3, если 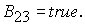 Здесь Здесь
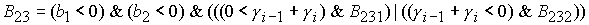 , ,
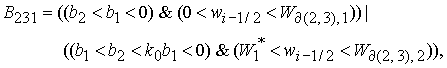
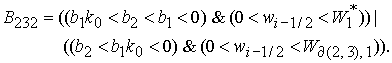
6.4.
Решение системы (5) находится по формуле Ф4, если 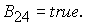 Здесь Здесь
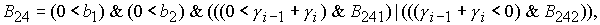 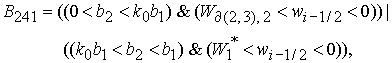
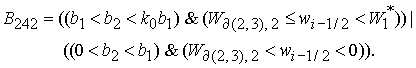
7. Область применимости формул Ф5 определяется неравенствами (53). Решение
этих неравенств дает следующий результат. Формула Ф5 используется, если
либо 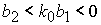 и и 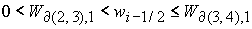 , ,
либо 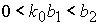 и и 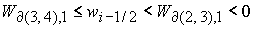 , ,
либо 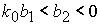 и и  , ,
либо 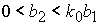 и и 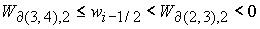 . .
8. Область применимости формул Ф6 – Ф9 определяется решениями неравенств
(57). Решение этих неравенств дает следующие результаты.
8.1. Решение системы (5)
находится по формуле Ф6, если 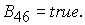 Здесь Здесь
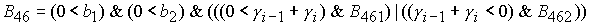 , ,
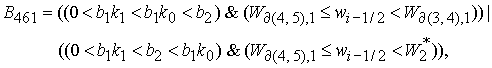
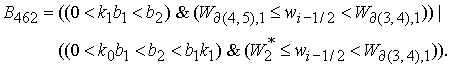
8.2. Решение системы (5)
вычисляется по формуле Ф7, если 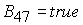 . Здесь . Здесь
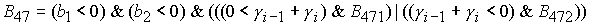 , ,
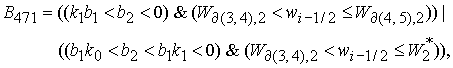
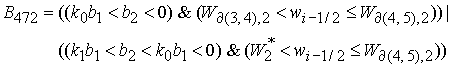
8.3.
Решение системы (5) определяется по формуле Ф8, если 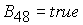 . Здесь . Здесь
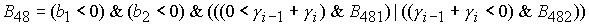 , ,
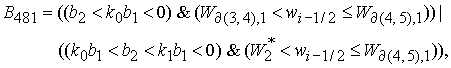
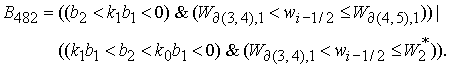
8.4.
Решение системы (5) находится по формуле Ф9, если 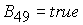 . Здесь . Здесь
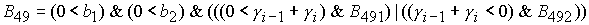 , ,
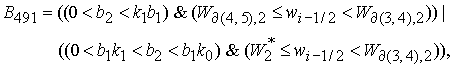
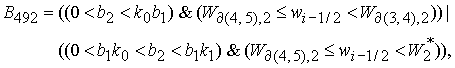
где 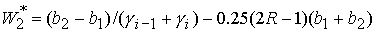 , ,
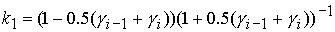 . .
8.5.
Решение системы (5) находится по формуле Ф10, если
либо 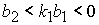 и и 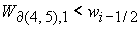 , ,
либо 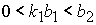 и и 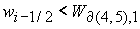 , ,
либо 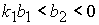 и и  , ,
либо 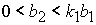 и и 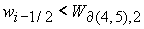 . .
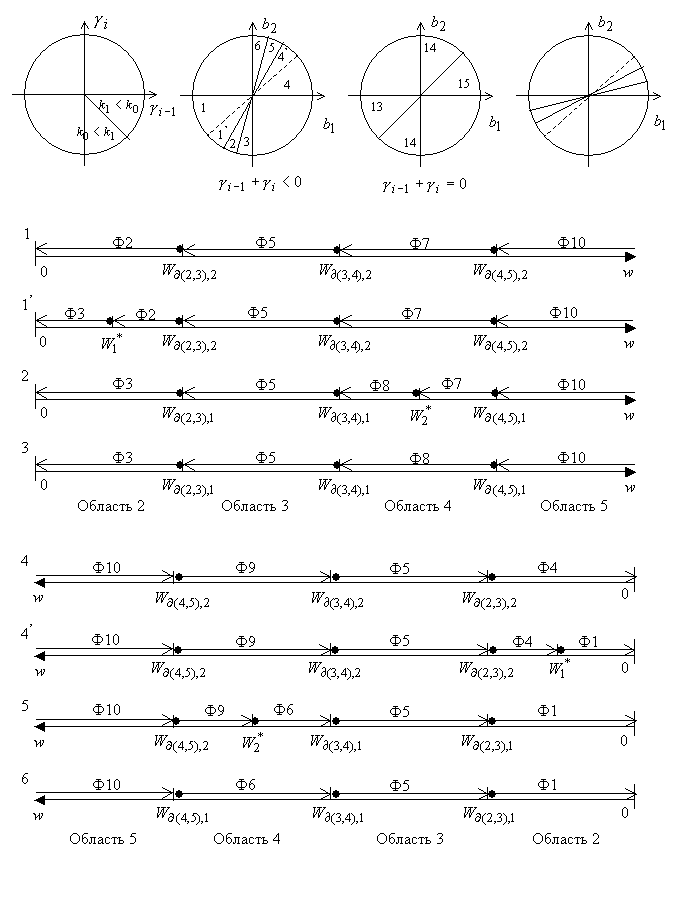
На рис.
4 схематически изображены области формул Ф1 – Ф10 в 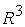 для случаев для случаев 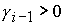 , , 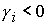 . .
Отметим, что при 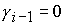 формулы (22), (24.1),
(24.2), (14), (28), (30.1), (30.2), (18) являются частными случаями формул Ф1,
Ф2, Ф4, Ф5, Ф6, Ф7, Ф9, Ф10 соответственно. формулы (22), (24.1),
(24.2), (14), (28), (30.1), (30.2), (18) являются частными случаями формул Ф1,
Ф2, Ф4, Ф5, Ф6, Ф7, Ф9, Ф10 соответственно.
Анализ построенных точных решений и условий
их применимости показывает, что для любых значений 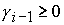 , , 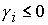 и любой точки и любой точки 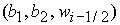 в в 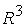 построено
единственное решение системы уравнений (5). Это решение определяется с помощью
соответствующих формул. построено
единственное решение системы уравнений (5). Это решение определяется с помощью
соответствующих формул.
Заключение
В
работе показано, что нелинейная монотонизованная разностная схема Бабенко имеет
единственное решение. Найдены формулы, определяющие это решение и области их
применимости.
Считаю
своим приятным долгом выразить благодарность М.П. Галанину за многочисленные полезные советы и
обсуждения.
Литература
1. М. П. Галанин, Т. Г. Еленина. Нелинейная монотонизация схемы К. И. Бабенко («квадрат») для уравнения
переноса. Препринт ИПМ им. М. В. Келдыша РАН, № 4, 2002, 26 с.
2. К. И. Бабенко, Г. П.
Воскресенский. Численный метод расчета пространственного
обтекания тел сверхзвуковым потоком газа.// ЖВМиМФ, 1961, т. 1, № 6, с. 1051 -
1060.
Приложение
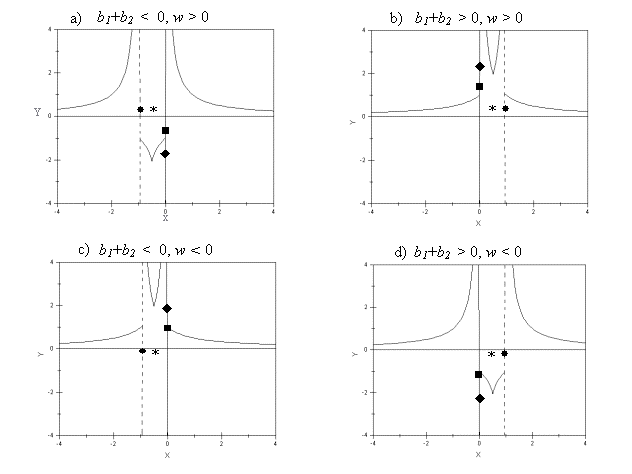
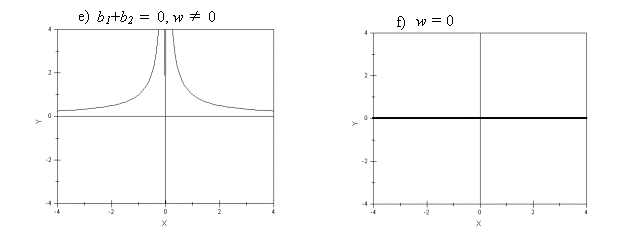
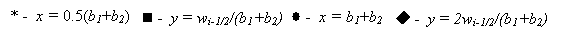
Рис. 1.
Зависимость 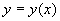 для различных
значений параметров для различных
значений параметров 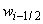 и и 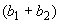 . .
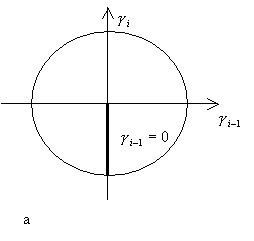


Рис. 2. Номера формул решения (указаны в скобках) в подобластях
областей 2 – 5 в 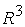 при при 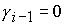 . .
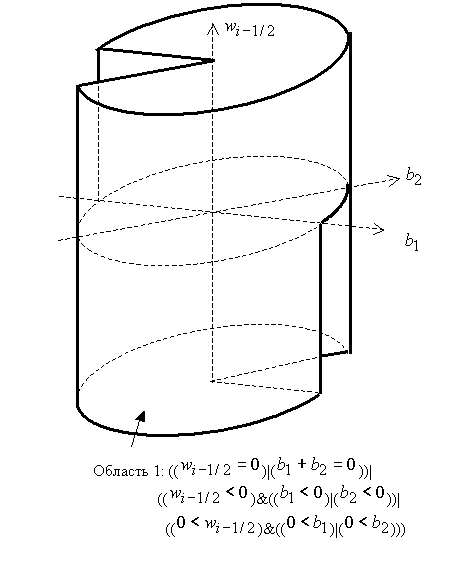
Рис.
3. Область 1 в 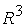 . Вырезанные полуцилиндрические секторы . Вырезанные полуцилиндрические секторы
содержат области 2, 3, 4, 5.

|