Аннотация
Исследуется уравнения переноса нейтронов, в котором учитывается как изменение фазового
объема системы вследствие движения среды, так и зависимость сечений взаимодействия
нейтронов со средой от относительной скорости сталкивающихся частиц. В качестве иллюстрации
влияния движения среды на перенос нейтронов рассматривается изменение спектра деления
Уатта для заданного изэнтропического течения газа. Строятся также другие точные решения
симметричного изэнтропического течения.
Abstract
The neutron transport equation in the case of moving medium is investigated. In the derivation
of transport equation the phase volume evolution and cross-sections relative velocity
dependence are taking into account. The model of isentropic spherical medium motion is
considered for illustration of medium motion effects in the transport processes.
СОДЕРЖАНИЕ
1. Постановка задачи
2. Качественный анализ влияния движения среды на примере изэнтропийного
сферически симметричного сжатия шара
3. Точные решения симметричных изэнтропических течений
4. Построение новых изэнтропических решений
Литература
1. Постановка задачи.
Система уравнений для описания
развития цепной ядерной реакции в среде, испытывающей сжатие, состоит из
уравнения переноса нейтронов в движущейся среде, уравнений гидродинамики,
описывающих процесс движения среды с учетом выделения энергии в ядерных
реакциях, и уравнения состояния вещества. Движение среды существенно влияет на
достижение критичности при высоких скоростях сжатия, когда атомы вещества имеют
скорости порядка 108 см/с, поскольку сдвиг спектра нейтронов деления
приводит к заметному изменению средних значений сечений деления и поглощения.
Ранее в работе [1] было проведено
исследование вкладов от движения среды в уравнение переноса. Там же было
получено многогрупповое уравнения переноса нейтронов в движущейся среде и в
движущейся системе отсчета, которое используется при его численной реализации.
Здесь будет использована методология, развитая в [1], для описания теста,
учитывающего влияние движения среды на процесс размножения нейтронов. Следуя
[1], введем функцию распределения 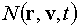 нейтронов по
координатам нейтронов по
координатам 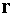 и скоростям и скоростям 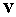 в момент времени в момент времени 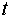 . Обозначим через . Обозначим через 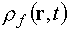 ядерную плотность
среды (какого-либо делящегося вещества), а через ядерную плотность
среды (какого-либо делящегося вещества), а через 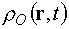 – ядерную плотность
обобщенного осколка деления. Будем для простоты считать, что вся среда движется
с единой скоростью – ядерную плотность
обобщенного осколка деления. Будем для простоты считать, что вся среда движется
с единой скоростью 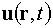 и имеет общее
уравнение состояния и имеет общее
уравнение состояния 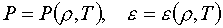 , где , где 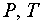 – локально-равновесные
значения давления и температуры, – локально-равновесные
значения давления и температуры, 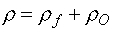 и и 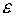 – локальные плотности
ядер и внутренней энергии. Например, для адиабатном сжатии идеального газа – локальные плотности
ядер и внутренней энергии. Например, для адиабатном сжатии идеального газа
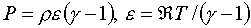 (1.1)
(1.1)
где 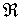 – газовая постоянная, – газовая постоянная,
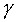 – показатель
адиабаты. Обозначим – показатель
адиабаты. Обозначим 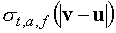 соответственно полное
сечение, сечение поглощения и сечение деления, зависящие от относительной
скорости нейтронов и атомов среды, соответственно полное
сечение, сечение поглощения и сечение деления, зависящие от относительной
скорости нейтронов и атомов среды, 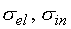 – микросечения
упругого и неупругого рассеяния ( – микросечения
упругого и неупругого рассеяния (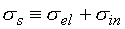 ), ), 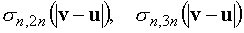 – сечения нейтронных
реакций – сечения нейтронных
реакций 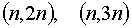 , а также , а также 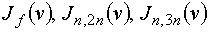 – спектры нейтронов в
соответствующих процессах. Будем считать, что в среде нет другого источника
нейтронов, кроме спонтанного деления с постоянной – спектры нейтронов в
соответствующих процессах. Будем считать, что в среде нет другого источника
нейтронов, кроме спонтанного деления с постоянной 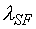 и числом нейтронов
деления и числом нейтронов
деления 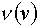 . Эмиссию и рассеяние нейтронов во всех процессах считаем
изотропными. Тогда уравнение нейтронного баланса записывается в виде: . Эмиссию и рассеяние нейтронов во всех процессах считаем
изотропными. Тогда уравнение нейтронного баланса записывается в виде:
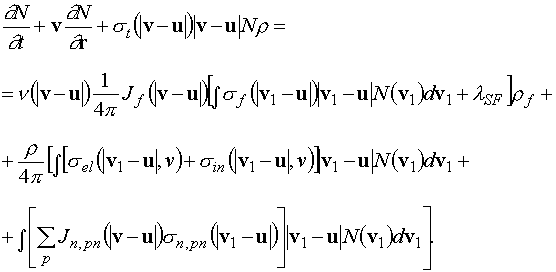 (1.2)
(1.2)
Начальное и граничное условия для уравнения (1.2)
примем в виде
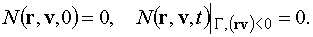 (1.3) (1.3)
Уравнение (1.2) следует из уравнения Больцмана,
записанного для функции распределения нейтронов, взаимодействующих со средой
[9]:
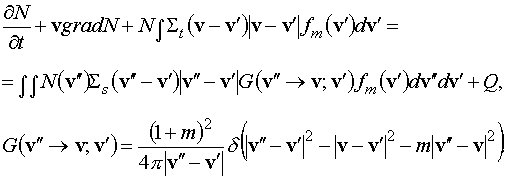
Здесь 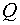 - источник нейтронов, - источник нейтронов,
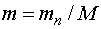 - отношение массы нейтрона к массе атома среды-рассеивателя, - отношение массы нейтрона к массе атома среды-рассеивателя, 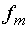 - функция
распределения атомов среды по скоростям. Рассеяние предполагается изотропным. В
приближении, когда нейтроны не взаимодействуют друг с другом, а среда
описывается функцией распределения - функция
распределения атомов среды по скоростям. Рассеяние предполагается изотропным. В
приближении, когда нейтроны не взаимодействуют друг с другом, а среда
описывается функцией распределения 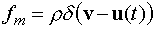 , получаем (1.2). , получаем (1.2).
Запишем уравнение неразрывности для двухкомпонентной
среды
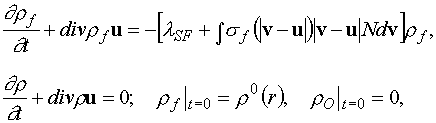 (1.4)
(1.4)
а также уравнение движения вязкой жидкости:
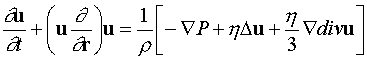 (1.5)
(1.5)
где 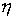 – коэффициент
сдвиговой вязкости. Уравнение изменения внутренней энергии с учетом
теплопроводности имеет вид – коэффициент
сдвиговой вязкости. Уравнение изменения внутренней энергии с учетом
теплопроводности имеет вид
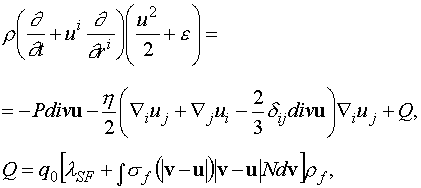 (1.6)
(1.6)
где 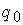 – энергия,
освобождаемая при одном делении (порядка 170 МэВ). – энергия,
освобождаемая при одном делении (порядка 170 МэВ).
В начальный момент нейтроны в
среде отсутствуют, среда однородна и находится в тепловом равновесии. В
заданную область среды вносится тепловая энергия по заданному закону во
времени. При этих предположениях требуется решить систему уравнений (1.1)-(1.6)
и определить момент наступления критичности (коэффициент воспроизводства
нейтронов в среде равен единице), а также долю вещества, распавшегося в течение
процесса сжатия среды.
2. Качественный анализ влияния
движения среды на примере изэнтропийного сферически симметричного сжатия шара.
Проведем
качественный анализ рассматриваемого процесса на примере известных точных
решений уравнений гидродинамики для случая центральной симметрии, который и
будет исследоваться далее. В частности, простейшим является изэнтропийное
сферически-симметричное течение идеального одноатомного газа:
 (2.1)
(2.1)
Здесь 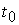 – постоянная,
характеризующая скорость изэнтропического сжатия. Если – постоянная,
характеризующая скорость изэнтропического сжатия. Если 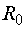 – начальный радиус
сжимающегося шара, то скорость движения его границы есть – начальный радиус
сжимающегося шара, то скорость движения его границы есть 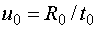 . Оценим плотность вещества, однородно распределенного в
шаре, необходимую для наступления критичности для данной массы делящегося
материала . Оценим плотность вещества, однородно распределенного в
шаре, необходимую для наступления критичности для данной массы делящегося
материала 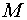 . В случае, если сжатие происходит квазистатически, условие
критичности означает равенство среднего расстояния, проходимого нейтроном от
произвольной точки внутри шара до его поверхности, и средней длины пробега, на
которой после деления и поглощения остается ровно один нейтрон. Вероятность
столкновения нейтрона, изотропно испущенного в объеме . В случае, если сжатие происходит квазистатически, условие
критичности означает равенство среднего расстояния, проходимого нейтроном от
произвольной точки внутри шара до его поверхности, и средней длины пробега, на
которой после деления и поглощения остается ровно один нейтрон. Вероятность
столкновения нейтрона, изотропно испущенного в объеме 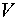 , равна , равна
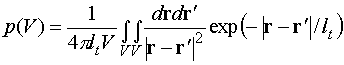 (2.2)
(2.2)
Здесь 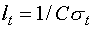 – длина свободного
пробега, – длина свободного
пробега, 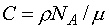 – ядерная
концентрация, – ядерная
концентрация, 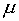 – молярная масса, – молярная масса, 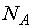 – число Авогадро. – число Авогадро.
Тогда оценка условия критичности
системы запишется в виде
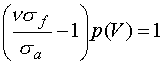 (2.3)
(2.3)
Для шара радиуса  величина величина  равна равна
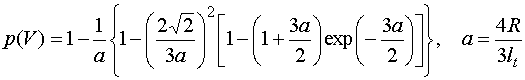 (2.4)
(2.4)
Подстановка (2.3) в (2.2) дает уравнение для
определения критического радиуса сферы.
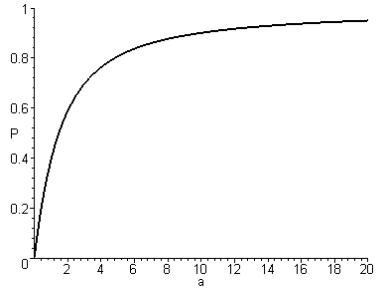
Рис. 2.1. Вероятность столкновения для сферы.
Обозначим

Для нейтронов в тепловой области
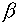 = 14, в среднем по спектру деления Уатта
– 1.28, в быстрой области (при энергиях нейтронов выше 10MeV) – приблизительно 3.
= 14, в среднем по спектру деления Уатта
– 1.28, в быстрой области (при энергиях нейтронов выше 10MeV) – приблизительно 3.
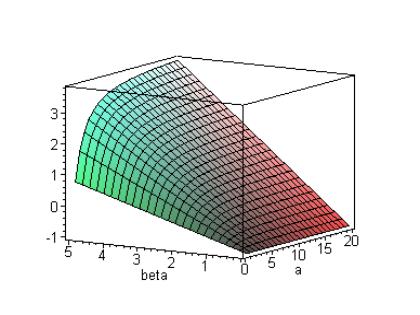
Рис. 2.2. Вид поверхности, определяемой уравнением
(2.3).
Рис. 2.3. Определение критического значения 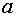 . Верхняя кривая отвечает тепловой области, средняя –
быстрой, нижняя – в среднем по спектру деления. . Верхняя кривая отвечает тепловой области, средняя –
быстрой, нижняя – в среднем по спектру деления.
На этих рисунках приведено графическое решение уравнения (2.3)
относительно значений параметра 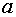 для значений для значений  в основных
энергетических областях. Решение – точка пересечения графика с осью абсцисс. в основных
энергетических областях. Решение – точка пересечения графика с осью абсцисс.
В диффузионном приближении
получается более простая оценка. Ослабление потока нейтронов при прохождении
через среду толщины 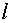 оценивается как оценивается как 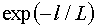 , где , где 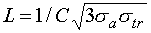 – длина диффузии, а – длина диффузии, а 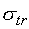 – транспортное сечение, приближенно равное – транспортное сечение, приближенно равное 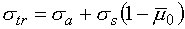 , где , где 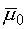 – средний косинус угла рассеяния. Тогда вместо (2.3) имеем – средний косинус угла рассеяния. Тогда вместо (2.3) имеем
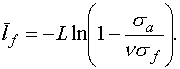 (2.5)
(2.5)
Если теперь вместо интеграла (2.2) ограничиться более
простой оценкой 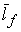 как среднего
расстояния от данной точки, находящейся на расстоянии как среднего
расстояния от данной точки, находящейся на расстоянии  от поверхности шара, от поверхности шара,
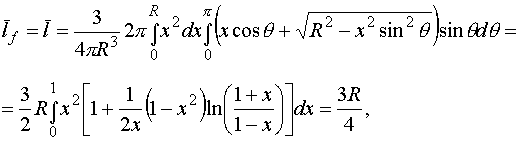 (2.6)
(2.6)
то получаем
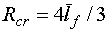 .
(2.7) .
(2.7)
Эта качественная оценка приводит к
тому, что для данных масс отношение соответствующих критических плотностей
обратно пропорционально отношению радиусов критических сфер (и, соответственно,
обратно пропорционально квадратному корню из отношения масс):
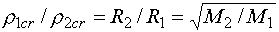 . (2.8) . (2.8)
Оценим получающиеся значения. Если
взять средние значения сечений [барн] по спектру деления равными соответственно
 = 1.24, = 1.24, 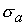 = 1.34, = 1.34, 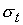 = 2.2, а среднее число вторичных нейтронов равно = 2.2, а среднее число вторичных нейтронов равно 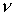 =2.5, то значение
параметра столкновений =2.5, то значение
параметра столкновений 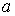 из (2.3)-(2.4)
получается равным примерно 1.18, так что для плотности из (2.3)-(2.4)
получается равным примерно 1.18, так что для плотности  18,7 г/см3 получаем 18,7 г/см3 получаем
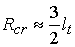 = 8.4 см.
= 8.4 см.
Более грубая оценка (2.7) приводит к значению 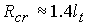 = 7.8 см. Критическая
масса составляет около 48 кг (по второй оценке – 38 кг). Для 100 мг того же
вещества критический радиус в 680 раз меньше (т.е. 0,012 см), а соответствующая
плотность в 680 раз больше (около 13 кг/см3). = 7.8 см. Критическая
масса составляет около 48 кг (по второй оценке – 38 кг). Для 100 мг того же
вещества критический радиус в 680 раз меньше (т.е. 0,012 см), а соответствующая
плотность в 680 раз больше (около 13 кг/см3).
Учтем
теперь движение вещества в рамках модели (2.1). В этом случае параметр
столкновения в (2.4) является функцией времени, поскольку радиус сферы меняется
по закону
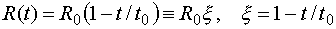 . (2.9) . (2.9)
Учитывая изменение плотности (2.1), получаем, что при
сжатии параметр столкновений меняется по закону
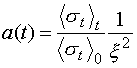 (2.10)
(2.10)
где угловыми скобками обозначено усреднение сечения по
спектру деления (в начальный момент и в момент времени 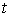 ). Кроме того, сечения поглощения и деления также зависят от
текущего спектра нейтронов. ). Кроме того, сечения поглощения и деления также зависят от
текущего спектра нейтронов.
В неподвижной среде спектр деления
возьмем в виде модифицированного спектра Уатта (энергия измеряется в MэВ):
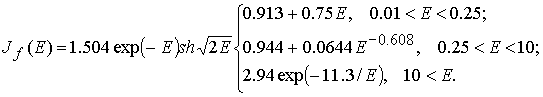 (2.11)
(2.11)
В максвелловском приближении средняя энергия спектра
равна 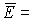 2,0266 MэВ, чему
отвечает температура 2,0266 MэВ, чему
отвечает температура 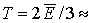 1,35 MэВ. Средняя скорость нейтронов деления по спектру
(2.11) равна 1,35 MэВ. Средняя скорость нейтронов деления по спектру
(2.11) равна
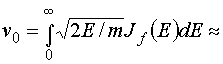 1.8×109 см/с.
1.8×109 см/с.
Пусть нейтрон испускается в точке 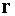 со скоростью со скоростью 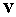 относительно ядра, а
поглощается в точке относительно ядра, а
поглощается в точке 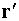 . Тогда, согласно закону движения среды (2.1), относительная
скорость нейтрона и ядра в точке поглощения равна . Тогда, согласно закону движения среды (2.1), относительная
скорость нейтрона и ядра в точке поглощения равна
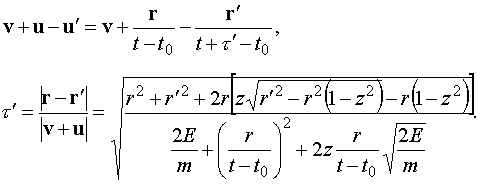
Поскольку же
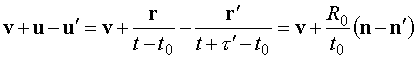
то при усреднении сечения по углам и положениям внутри
шара можно перейти к интегрированию по относительным положениям, что дает
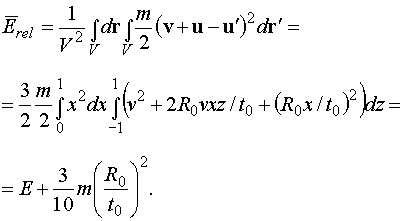 (2.12)
(2.12)
Таким образом, движение среды в среднем проявляется в
сечениях как сдвиг их энергетической зависимости на постоянную величину,
определяемую интенсивностью сжатия:
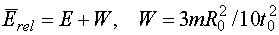 (2.13)
(2.13)
Тогда среднее значение сечения по текущему спектру
определяется по формуле
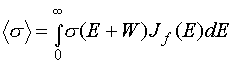 (2.14)
(2.14)
С увеличением энергии 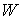 , затрачиваемой на сжатие среды, средние значения сечений
меняются незначительно. Например, среднее сечение деления сначала убывает от
1.245 до 1.04, что связано с выходом основной массы нейтронов из тепловой
области, достигают минимума в области , затрачиваемой на сжатие среды, средние значения сечений
меняются незначительно. Например, среднее сечение деления сначала убывает от
1.245 до 1.04, что связано с выходом основной массы нейтронов из тепловой
области, достигают минимума в области 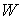 =1.5 MэВ, а затем растут до значений, характерных для быстрой
области спектра (около 2.21 барн). Поэтому для оценки момента достижения
критичности по формуле (2.3) с учетом (2.10) имеем соотношение =1.5 MэВ, а затем растут до значений, характерных для быстрой
области спектра (около 2.21 барн). Поэтому для оценки момента достижения
критичности по формуле (2.3) с учетом (2.10) имеем соотношение
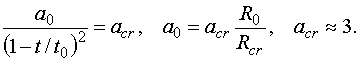 (2.15)
(2.15)
Тогда для заданной массы шара 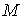 [кг] с начальной плотностью [кг] с начальной плотностью  =18.7 г/см3 момент наступления критичности при
сжатии его по закону (2.1) определяется из равенства =18.7 г/см3 момент наступления критичности при
сжатии его по закону (2.1) определяется из равенства
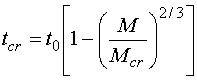 (2.16)
(2.16)
В движущейся среде спектр
нейтронов деления существенно отличается от максвелловского (т.е. от спектра
Уатта):
Доля нейтронов
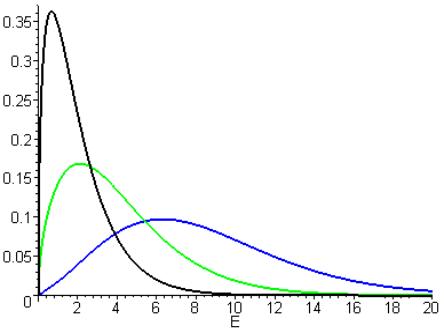 MэВ MэВ
Рис. 2.4. Спектр деления для
скоростей среды  0, 0.06 и 0.1 . 0, 0.06 и 0.1 .
На Рис.
2.4 спектр деления в неподвижной среде показан на первой кривой (имеющей самый
высокий максимум). Влияние движения среды приводит к снижению максимума кривой
спектра деления и одновременно к смещению его в сторону больших энергий, что
означает увеличение доли нейтронов в быстрой области спектра.
Ниже рассмотрены некоторые другие
варианты режимов сжатия.
3. Точные решения
симметричных изэнтропических течений.
Проблема
нахождения точных решений уравнений газовой динамики широко исследована в
литературе (см. фундаментальные работы [2-6]). Известны точные решения для
различных типов газовых течений. В частности, класс автомодельных
адиабатических течений для случая центральной симметрии был построен Седовым [2].
Они характерны тем, что описывают движения типа слета и разлета без образования
вакуума в окрестности центра симметрии. Эти решения, определяющие зависимость
плотности среды и скорости потока как функций расстояния от центра симметрии и
времени, записываются в параметрическом виде через функцию 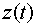 , которая является решением следующего обыкновенного
дифференциального уравнения: , которая является решением следующего обыкновенного
дифференциального уравнения:
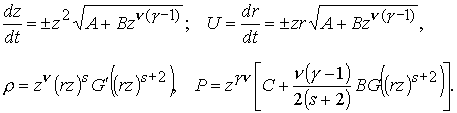 (3.1)
(3.1)
Здесь 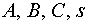 – произвольные
постоянные, – произвольные
постоянные, 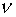 – размерность
пространства, – размерность
пространства, 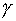 – показатель
адиабаты, – показатель
адиабаты, 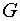 – произвольная
функция, – произвольная
функция,  – соответственно
скорость, плотность и давление газа. – соответственно
скорость, плотность и давление газа.
Изэнтропическое течение в трехмерном случае 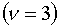 получается из формул
(3.1) при следующем выборе постоянной получается из формул
(3.1) при следующем выборе постоянной 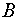 и функции и функции  : :
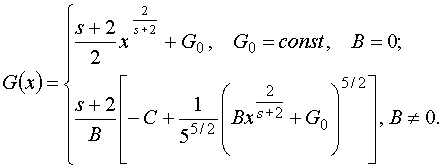 (3.2)
(3.2)
Соответствующие выражения
для плотности и скорости газа имеют вид:
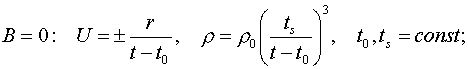 (3.3)
(3.3)
при 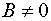 получаем, в
частности, для получаем, в
частности, для 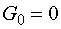 : :
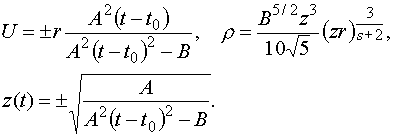 (3.4)
(3.4)
В
настоящей работе строится новое частное решение для центрально-симметричного
изэнтропического течения идеального газа. Оно содержит в себе частный случай
одного из автомодельных решений в качестве особого.
Рассматривается
классическая система уравнений гидродинамики без вязкости и теплопроводности с
заданным уравнением состояния вещества:
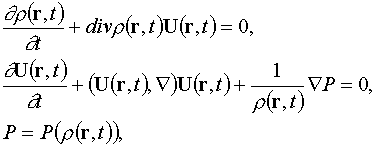 (3.5)
(3.5)
Требуется найти все частные
решения системы (3.5), содержащие центрально-симметричные движения среды со
скоростью, задаваемой соотношением
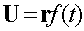 (3.6)
(3.6)
для уравнения состояния 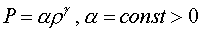 . Ниже будет показано, что решения вида (3.3) и (3.4) не
исчерпывают все возможности реализации изэнтропических сферически-симметричных
течений. . Ниже будет показано, что решения вида (3.3) и (3.4) не
исчерпывают все возможности реализации изэнтропических сферически-симметричных
течений.
4. Построение новых
изэнтропических решений.
Введем
для краткости обозначение
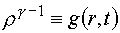 .
(4.1) .
(4.1)
После подстановки (3.6),
(3.7) в систему (3.5), получаем систему уравнений относительно функций 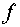 и и 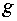 : :
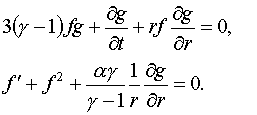 (4.2)
(4.2)
Второе уравнение полученной
системы (4.2) можно явно проинтегрировать по пространственной координате,
определив тем самым зависимость функции 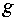 от от 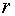 : :
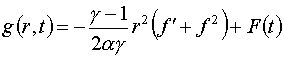 (4.3)
(4.3)
где 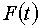 есть некоторая
произвольная функция времени. Подставляя (4.3) в первое уравнение системы
(4.2), получаем уравнение, связывающее функции есть некоторая
произвольная функция времени. Подставляя (4.3) в первое уравнение системы
(4.2), получаем уравнение, связывающее функции 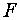 и и 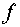 : :
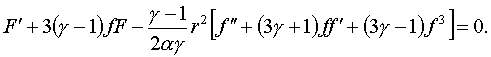 (4.4)
(4.4)
Поскольку равенство (4.4)
должно выполняться при всех значениях 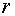 , то, приравнивая в нем коэффициенты при одинаковых степенях , то, приравнивая в нем коэффициенты при одинаковых степенях 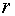 к нулю, получаем, что к нулю, получаем, что 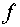 удовлетворяет
нелинейному уравнению удовлетворяет
нелинейному уравнению
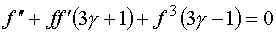 (4.5)
(4.5)
а функция 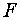 выражается через
решение этого уравнения как выражается через
решение этого уравнения как
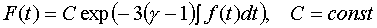 (4.6)
(4.6)
Делая в (4.5) подстановку
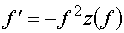 ,
(4.7) ,
(4.7)
получаем уравнение с
разделяющимися переменными:
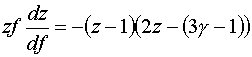 .
(4.8) .
(4.8)
Видно, что случаи 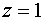 и и 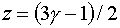 являются особыми решениями
уравнения (4.8). Первое из них отвечает автомодельному решению (3.3), а второе
является новым, не содержащимся среди решений (3.3), (3.4): являются особыми решениями
уравнения (4.8). Первое из них отвечает автомодельному решению (3.3), а второе
является новым, не содержащимся среди решений (3.3), (3.4):
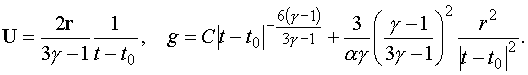 (4.9)
(4.9)
Решая
уравнение (4.8) в неособом случае, получаем его интеграл в виде
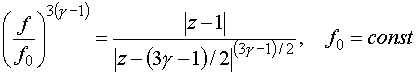 (4.10)
(4.10)
Таким образом, дальнейшее
определение 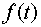 с помощью (4.7),
(4.10) сводится к квадратуре: с помощью (4.7),
(4.10) сводится к квадратуре:
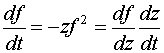 . .
Решение (4.10) также не содержится среди классических
изэнтропических течений, определяемых системой (3.1).
Далее для простоты
рассматривается идеальный одноатомный газ с показателем адиабаты 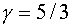 . Тогда (4.10) принимает вид . Тогда (4.10) принимает вид
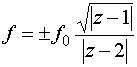 . (4.11) . (4.11)
Для определенности выберем в
(4.11) знак «плюс», чему отвечает разлет среды со скоростью, определяемой по
формуле (3.6). Зависимость 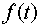 находится посредством
цепочки соотношений находится посредством
цепочки соотношений
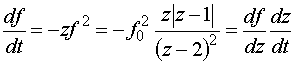 , ,
где 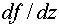 определяется из
(4.11), откуда следует, что определяется из
(4.11), откуда следует, что 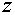 как функция как функция 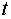 удовлетворяет
уравнению удовлетворяет
уравнению 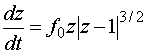 , общее решение которого есть , общее решение которого есть
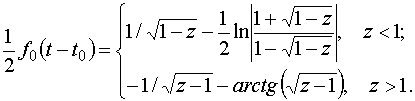 (4.12)
(4.12)
Выражение (4.12) в неявной
форме определяет зависимость 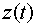 и, согласно (4.11), также и и, согласно (4.11), также и 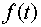 . Соответствующее выражение для . Соответствующее выражение для 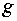 имеет вид имеет вид
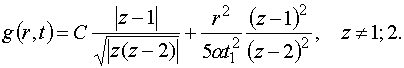 (4.13)
(4.13)
Таким образом,
построены два новых решения изэнтропического течения среды в
центрально-симметричном случае. Первое определяется формулами (4.1) и (4.9), а
второе – совокупностью (3.6), (4.1), (4.11), (4.12) и (4.13).
Основное
отличие решения (4.12) от (3.3), (3.4) состоит в более раннем моменте
наступления обострения при слете и разлете. Особое решение (4.9) для скорости
ведет себя практически так же, как и классическое решение (3.3), а соответствующая
ему зависимость для плотности – аналогично другому классическому решению (3.4).
В отличие от них решение (4.12) имеет два характерных момента обострения, когда
скорость сжатия (разлета) среды стремится в бесконечность.
Для
качественного сравнения новых и известных классических решений движения среды
положим в соответствующих выражениях
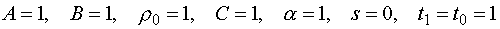 . .
Для этих значений
параметров моментами обострения решения (4.12) являются точки
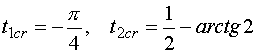 . .
Первому
критическому времени отвечает момент сжатия среды в центре симметрии, а второму
– разлет в бесконечность (при этом плотность в центре отлична от нуля).
Значения 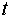 , большие чем , большие чем  , недостижимы.
Зависимость плотности от времени в центре симметрии и на некотором
расстоянии от него аналогична скорости. Существенным, однако, является то, что
темп увеличения плотности на периферии для решения (4.12) значительно выше, чем
для классических решений. Это может оказаться важным при моделировании
изэнтропийного сжатия делящегося радиоактивного вещества, поскольку критичность
системы будет достигаться в более короткие сроки. , недостижимы.
Зависимость плотности от времени в центре симметрии и на некотором
расстоянии от него аналогична скорости. Существенным, однако, является то, что
темп увеличения плотности на периферии для решения (4.12) значительно выше, чем
для классических решений. Это может оказаться важным при моделировании
изэнтропийного сжатия делящегося радиоактивного вещества, поскольку критичность
системы будет достигаться в более короткие сроки.
Литература
1. Воронков А.В., Орлов Ю.Н., Сычугова Е.П. Уравнение переноса
нейтронов в движущейся среде. Препринт ИПМ РАН, № 91, 2001.
2. Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1981.
3. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.VI. Гидродинамика. М.: Наука, 1988.
4. Станюкович К.П. Неустановившиеся движения сплошной среды. М.: ГИТТЛ,
1955.
5. Никольский А.А. Теоретические исследования по механике жидкости и
газа. М.: ЦАГИ, 1981.
6. Христианович С.А. Механика сплошной среды. М.: Наука, 1981.
7. Баренблатт Г.И. Подобие, автомодельность, промежуточная асимптотика.
Л.: Гидрометеоиздат, 1978.
8. Гухман А.А., Зайцев А.А. Обобщенный анализ. М.: Факториал, 1998.
9. Кострица А.А. Теория переноса нейтронов в движущейся среде. М.:
Энергоиздат, 1981.
10. Биркгоф Г. Гидродинамика. М.: ИЛ, 1963.
|