Динамика и устойчивость одномерных задач горения

( Dynamics and Stability of One-Dimensional Combustion Problems
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Заславский М.Ю., Пергамент А.Х., Плющенков Б.Д.
(M.Yu.Zaslavsky, A.Kh. Pergament, B.D.Plushchenkov)

ИПМ им. М.В.Келдыша РАН

Москва, 2002

Аннотация

Рассмотрена система уравнений, включающая уравнения движения газовой смеси и уравнения химической кинетики. Система описывает горение газовой смеси. Цель работы – определение области значений параметров, при которых возможен режим устойчивого ламинарного горения, и определение для такого режима величин ширины и скорости фронта горения. При построении алгоритмов был использован принцип разделения по процессам: газодинамика и конвекция с одной стороны и диффузия и теплопроводность с другой. Для газовой динамики была построена явная TVD схема порядка O(τ+h2), а для диффузионых процессов неявная также порядка O(τ+h2). В результате расчетов установлено наличие термодиффузионных неустойчивостей при заметном различии коэффициентов температуропроводности и диффузии и наличие устойчивого режима при условии Le ∝ 1 , где Le - число Льюиса, что является первым вычислительным подтверждением известных результатов Я.Б.Зельдовича и Г.И.Баренблатта.

Abstract

The governing system including equations of gas mixture motion and an equation of a chemical kinetics is considered. The system describes combustion of gas mixture. The purpose of given work is a definition of parameters values, if the modes of stable combustion is possible, and definition of combustion front width and speed values for such mode. Under the construction of algorithms the principle of separating up processes was used: gas dynamics and convection on the one hand and diffusion and heat conduction on the other hand. For gas dynamics the explicit TVD scheme of order O(τ+h2) and for thermodiffusive processes implicit scheme also of order O(τ+h2) were constructed. As a result of calculations the thermodiffusive instabilities are established under evident difference of coefficients of thermal conduction and diffusion and availability of a stable mode under condition of Le ∝ 1, where Le is Lewis number, that is the first computational endorsement of known outcomes of Ya.B. Zeldovich and G.I. Barenblatt.

 

Содержание

 

1.Введение................................ 3

2.Постановка задачи

и основные уравнения.................... 6

3.Разностная аппроксимация системы:

разделение по процессам................. 8

4.Аппроксимация параболической части...... 10

5.Аппроксимация гиперболической части.... 12

6.Обезразмеривание задачи................ 15

7.Результаты расчета..................... 17

Использованная литература ............... 21

 

Введение

 

В общем случае для определения режима горения необходимо совместное решение системы уравнений, включающей в себя как уравнения химической кинетики, так и уравнения движения газовой смеси.

Характерный пространственный масштаб задачи – ширина фронта горения , где  - температуропроводность газа,  - характерное время реакции, зависящее от термодинамического состояния газа. Если актуальный масштаб задачи , то можно пренебречь толщиной зоны горения и рассматривать ее просто как поверхность, разделяющую зону горения и несгоревший газ. На этой поверхности (фронт пламени) состояние газа испытывает скачок, т.е. она представляет собой поверхность разрыва. Скорость  перемещения этого фронта разрыва относительно газа называют скоростью пламени

Температуропроводность газа по порядку величины есть , где  - длина свободного пробега,  - средняя тепловая скорость молекул газа, которая по порядку величины совпадает со скоростью звука , длина свободного пробега , где  - время свободного пробега. Тогда получаем отношение . Поскольку в реакцию вступает незначительная часть сталкивающихся молекул, то , т.е. скорость распространения пламени много меньше скорости звука.

Известны работы, исследующие одномерный режим медленного горения (Ландау и Лившиц, Зельдович и Франк-Каменецкий). Последние рассмотрели одномерную тепловую задачу и установили формулу, связывающую скорость фронта пламени  с термодинамическими характеристиками газа и параметрами химической реакции. В рассматриваемом случае предполагается, что скорость реакции определяется законом Аррениуса. В этот закон входит малое время . Ширина фронта реакции , т.к. температура горения смеси , где  - энергия активации реакции. Учет конечности  позволяет рассмотреть структуру фронта пламени, что проделано различными авторами, использовавшими асимптотическое разложение оп малому параметру .

Когда топливо представляет собой одну фазу, подразумевается, что все компоненты, необходимые для реакции, присутствуют в топливной смеси с самого начала, и для начала реакции необходимо лишь нагреть смесь. В этом случае скорость горения не определяется процессом диффузии, однако даже здесь диффузия топлива (вместе с теплопроводностью) - важный фактор распространения пламени и им нельзя пренебречь. В частности, когда диффузия топлива сильнее, чем теплопроводность, тогда может развиваться термодиффузионная неустойчивость плоского стационарного пламени (Barenblatt и другие., 1962). В противоположном случае малой диффузии (который не свойственен газовому топливу) скорость движения фронта заметно уменьшается: преобладание теплопроводности по сравнению с диффузией ведет к пульсациям в зоне реакции (Zeldovich и другие., 1985). Обе эти неустойчивости имеют диффузионную природу и сильно зависят от особенностей химической реакции.

Хотя турбулентные режимы горения встречаются чаще других в промышленных приложениях, теория турбулентных течений наименее развита из-за ее сложности. В некотором смысле, теория ламинарного пламени должна быть естественной основой для изучения теории турбулентного пламени с целью избежать необоснованных предположений о свойствах турбулентного пламени. Фактически слова “турбулентное пламя” означают большое количество различных режимов горения от почти ламинарных до реакций в хорошо промешанном топливе. Различные режимы характеризуются различными скоростями и различными линейными масштабами турбулентного пламени и  соответственно, отнесенными к ламинарной скорости пламени  и толщине ламинарного пламени . Очевидно, турбулентность не может существовать при малых числах Рейнольдса , где  - кинематическая вязкость. Т.к. толщина пламени и скорость должны удовлетворять по порядку величин соотношению , то условие  эквивалентно . Выполнение этого условия соответствует угасанию турбулентности в течении. Для другого состояние - слабой турбулентности  - характерно слабое или даже пренебрежимо малое влияние турбулентного течения на динамику пламени. В этом случае пламя может быть описано как ламинарное или квази-ламинарное искривление фронта. В противоположном случае очень сильной турбулентности, когда характерное время турбулентности -  много меньше времени реакции , зоной реакции становится весь поток. Этот режим турбулентного горения называется режимом реакций в хорошо промешанном топливе. Промежуточные режимы между режимами очень слабой и очень сильной турбулентности - режимы флеймлетов и толстого пламени. Чтобы разделить эти два режима, нужно сравнить скорость пламени и скорость турбулентных пульсаций  при линейном масштабе, равном толщине пламени,  для . Как известно, при хорошо развитой (Колмогоровской) турбулентности пульсации скорости зависит от линейного масштаба пульсаций как  (Ландау и Лифшиц, 1987). Значит, скорость пульсации при линейном масштабе, равном толщине пламени, равна 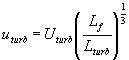. Для скоростей, больших 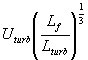, пульсации потока проникают внутри пламени и влияют на внутреннюю структуру пламени. В этом режиме, называемом режимом толстого пламени, фронт реакции распространяется благодаря турбулентной теплопроводности. Для скоростей в режиме флеймлета внешний поток достаточно силен, чтобы сильно изогнуть фронт пламени и сделать его волнистым, но поток слишком слаб, чтобы изменить внутреннюю структуру пламени.

Как было показано, основными параметрами, определяющими режим распространения пламени, являются ламинарная скорость пламени  и толщина ламинарного пламени , которые могут быть определены из одномерного расчета, являющегося целью настоящей работы. Помимо этого будут исследованы режимы для различных соотношений диффузии и температуропроводности для того, чтобы определить режимы, не осложненные диффузионными эффектами.

 

Постановка задачи

и основные уравнения

 

Система, описывающая процесс горения, состоит из 4-х уравнений конвекции-диффузии: неразрывности, Навье-Стокса и уравнений для энергии и концентрации топлива. Она в консервативной форме имеет следующий вид:

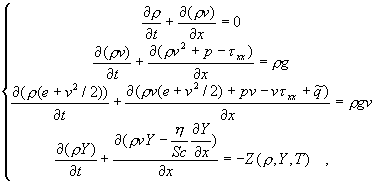         (2.1),

где:  - плотность,;

* - скорость,;

* - давление,;

* - ускорение свободного падения,;

* - внутренняя энергия на единицу массы,;

* - тензор вязких напряжений,

, -тепловой поток;

* - концентрация топлива, часть элементарного объема, занятого им,;

* - скорость реакции;

* - температура,;

* - 1-ая вязкость.

Для замыкания системы необходимо написать определяющие соотношения для :.

 

пПусть рассматриваемая смесь есть совершенный вязкий газ, и скорость реакции дается законом Аррениуса порядка . Таким образом,

 - уравнение состояния совершенного газа,

 - тензор вязких напряжений,

,

 - закон Аррениуса.

Здесь:

 - универсальная газовая постоянная,;

* - молярная масса смеси,;

* - 2-я вязкость (равна 0 для одноатомного газа),;

* - теплотворная способность топлива,;

* и  - теплоемкости при постоянном объеме и давлении соответственно,;

* и  - числа Прандтля и Шмидта,;

* - энергия активации,;

* и  - константы реакции.

 

Из консервативной формы (2.1) следует квазилинейная форма:

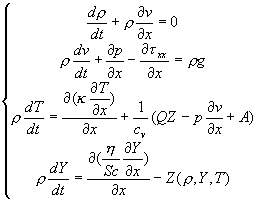                    (2.2).

Здесь  - полная производная по времени,

, , , .

 

Для постановки граничных условий будем рассматривать закрытую трубу:

                                 (2.3).

Для  положим

                           (2.4), т.е. мы ограничимся рассмотрением настолько длинной трубы, что волна горения не успеет дойти до правой ее границы на рассматриваемом промежутке времени.

Разностная аппроксимация системы: разделение по процессам

 

Систему (2.1) можно переписать в следующем виде:

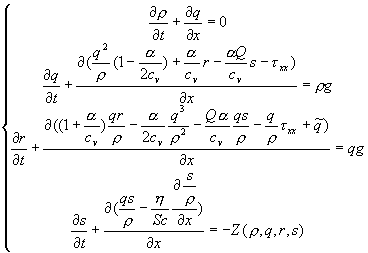          (3.1),

где .

В принятыхданных обозначениях имеем:

.

“Векторная форма” (3.1) имеет вид

,                           (3.2)

где:

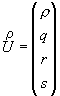 - вектор неизвестных,

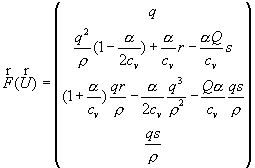 -                  (3.3)

аналог выражения потока в газовой динамике,

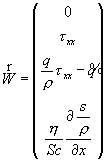 - аналог теплового потока,      (3.3’)

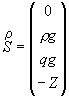 - источник.                         (3.3’’)

Необходимо заметить, что  не есть вектора в обычном понимании этого слова, т.к. они преобразуются при переходе от одной системы координат к другой не по векторном закону; эти записи надо понимать лишь как наборы из четырех функций.

Обозначим значения сеточных функций  на -ом временном слое через , а на -ом – через , и введем обозначение  для вектора неизвестных на вспомогательном временном слое , где  и  - -ый и -ый моменты времени ().

Предлагается следующая схема расщепления по процессам:

,                                (3.4)

,                                (3.5)

где  - разностная аппроксимация , зависящая от  на явном и вспомогательном временном слое; а  - разностная аппроксимация , зависящая лишь от  на .

Таким образом, (3.4) аппроксимирует параболическую часть (3.1), т.е. процесс диффузии, а (3.4) – гиперболическую, т.е. конвекцию.

Заметим, что сложением (3.4) и (3.5) доказывается аппроксимация исходного уравнения.

Основанием для выбранного способа расщепления по процессам является то, что при  (отсутствие вязкости, а, значит, и отсутствие температуропроводности) вектор  обращается в , а система имеет ненулевое решение при ненулевых начальных данных.

Аппроксимация параболической части

 

Для параболической части напишем схему с весом .

Введем оператор, действующий на сеточную функцию , определенную на сетке 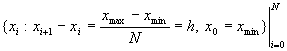 . Очевидно, что данный оператор аппроксимирует дифференциальный оператор . Обозначим  и . Тогда (3.3) примет вид

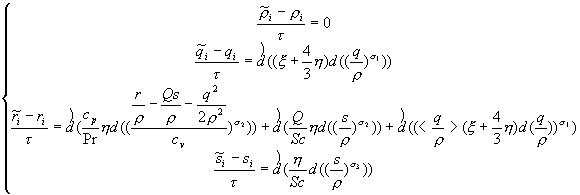(4.1)

Раскрывая скобки в каждом из уравнений (4.1) (кроме первого, которое решается автоматически), мы получим уравнения относительно неизвестных на вспомогательном временном слое вида

,                       (4.2)

где  - неизвестные.

Т.к. нам заданы граничные условия, то будем решать (4.2) методом прогонки. Пусть

                                   (4.3).

Подставляя данное выражение в (4.2), имеем .

 Т.е.

                      (4.4).

Далее рассмотрим уравнения по отдельности. Для второго уравнения (4.1) в силу граничных условий (2.3) и определения  и  (4.3) получаем . Тогда с помощью формул прямой прогонки (4.4) мы можем найти , а затем по формулам (4.3) с использованием граничного условия  (т.е. ) мы находим . Четвертое уравнение рассматривается аналогично, но граничные условия (2.4) дают  и  (т.к. ). Рассмотрим третье уравнение. Для прямой прогонки граничные условия (2.3) и (2.4) дают

  

(это следует из аппроксимации граничных условий  и выражения  через ).

Чтобы найти  для начального условия в обратной прогонке, необходимо решить систему

,

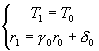где  и  выражены через ., Тт.е. решить систему

,

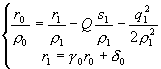из которой следует уравнение

.

Отсюда окончательно получаем, что

.

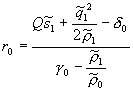Очевидно, что предъявленный оператор аппроксимирует параболическую часть (3.1) с 1-ым порядком по  и 2-ым по . Каждое из уравнений (4.1) (кроме первого) является неявной схемой для уравнения теплопроводности. При  она безусловно устойчива.

Аппроксимация гиперболической части

 

Для аппроксимации (3.4) будем использовать явную схему типа TVD, основанную на методах Ю.Б. Радвогина, которая устойчива при выполнении условия Куранта на шаг по времени и имеет порядок аппроксимации .

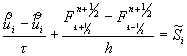Перейдем к описанию самой схемы. Напомним, что нам необходимо предъявить аппроксимацию  дифференциального оператора . Согласно схеме Ю.Б. Радвогина уравнение (3.4) переписывается для -го узла сетки в виде , где . И мы имеем явный алгоритм нахождения : , где .

Теперь необходимо определить потоки . Обозначим . Заметим, что . Т.е. вектор  - является однородным первой степени. Это очень важное свойство, которое существенно используется при конструкции разностной схемы. В нашем случае .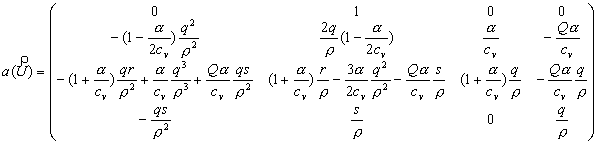

Вычислим собственные значения матрицы :

,

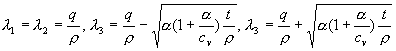где .

Матрица, по строкам которой стоят левые собственные вектора матрицы  (-ая строка – вектор, соответствующий ), имеет вид:

.

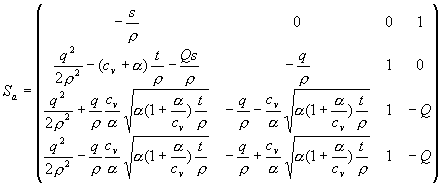
Нам еще понадобится матрица . Ее столбцы равны:

,

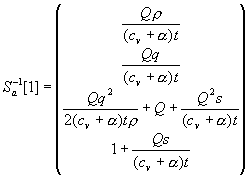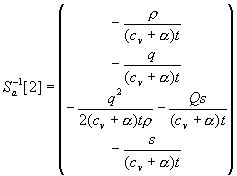
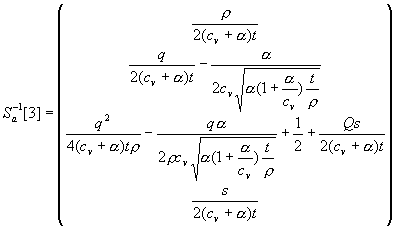
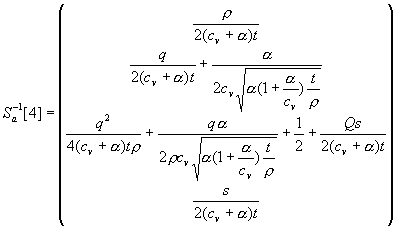
Введем матрицы ,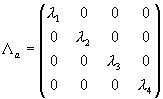

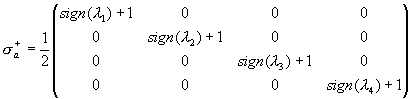, , ,  (равенства справедливы в силу того, что ). Здесь  - единичная матрица. Таким образом  - это диагональная матрица, у которой в -ой строке стоит 1, если , и 0, если . Нулевые значения  можно относить к любой области, положительной или отрицательной. Важно только чтобы . Тогда

,                                (5.1)

,               (5.2)

.                              (5.3)

В формуле (5.2) первое слагаемое в случае линейной системы уравнений с постоянными коэффициентами в точности соответствует схеме Годунова. Второе слагаемое обеспечивает второй порядок аппроксимации. Третье же необходимо для аппроксимации со вторым порядком правой части.

Оператор  принято называть «лимитером» потока. Он определяется покомпонентно: -ой компонентой результата применения оператора должна быть величина, аппроксимирующая выражение , где  - -ая строка матрицы . Простейшим вариантом оператора  является оператор :

,     (5.4)

где ., т.е.На словах оператор  равен меньшему по модулю из двух своих аргументов, если они одного знака, и равен нулю, если знаки разные.

Необходимо выбратьзаметить, в каких точках надо брать члены формул (5.2)-(5.4). В них матрицы , векторы  и собственные числа  надо вычислять в точках . Существенной разницы между усреднением полусуммой вектора неизвестных и самих матриц, векторов и собственных значений, а также усреднением по Роу замечено не было.

Обезразмеривание задачи

 

Введем константы , на которые будем обезразмеривать  соответственно. Обезразмеренные величины будем обозначать теми же символами, но с чертой сверху. Рассмотрим по отдельности каждое уравнение системы (2.1).

Первое уравнение нам даст

.

Таким образом, для избавления от ненужных констант целесообразно будет связать масштабы по времени, скорости и длине соотношением

.                                     (6.1)

В этом случае исходное и обезразмеренное уравнения будут совпадать с точностью до обозначений.

Из второго уравнения имеем

 

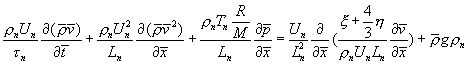
или в силу (6.1)

.

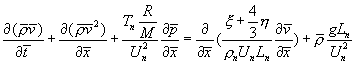Положив с той же целью

,                                   (6.2)

мы получим то же уравнение, что было изначально, но с вязкостями

,                          (6.3)

ускорением свободного падения

                                     (6.4)

и коэффициентом

.                                      (6.5)

С помощью четвертого уравнения нетрудно получить ,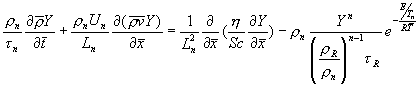

что эквивалентно в силу (6.1), (6.3)

.

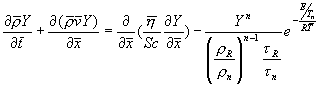 Значит, полученное четвертое уравнение совпадает с исходным, если положить

 и .                      (6.6)

Наконец, третье уравнение, расписав обозначения , эквивалентно

Тогда из него получаеммы получим: .

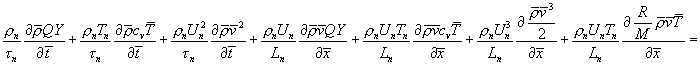
Поделив обе части данного уравнения на  и учтя соотношения (6.1)-(6.5), имеем то же третье уравнение, но с

.                       (6.7)

Из проведенного исследования, можно сделать вывод, что введяпри введении масштабыов по длине, скорости, плотности, температуре и времени , согласованные условиями (6.1) и (6.2), обезразмеренные уравнения имеют тот же вид, что и исходные, но с параметрами, полученными в формулах (6.3)-(6.7).

Естественно использовать в качестве характерного масштаба длины ширину фронта . Если  - температуре топлива перед фронтом, то  есть , где  - скорость звука. В таких единицах скорость фронта . Характерное время  - это время, необходимое акустической волне, чтобы преодолеть ширину фронта, т.е. малая величина ( в рассматриваемом случае ). Однако время , характеризующее реакцию горения, – величина, существенно меньшая, чем .

Результаты расчета

 

 

Для расчета брались характерные величины  , Ммолярная масса . Тогда согласно формулам (6.1) и (6.2) получаем  . Рассматривался порядок реакции  и движения вне поля силы тяжести . Константы . Таким образом, масштаб времени  много больше, чем величина , входящая в выражение для скорости реакции, т.е.  - это малый параметр. Для простоты брался одноатомный газ с  и . 1-аяой вязкостью .

 





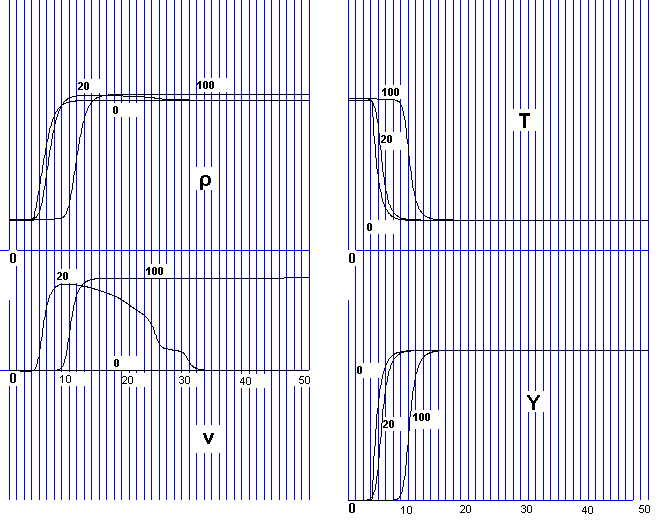
Рис.1

 

Далее рассматривалась обезразмеренная задача при постоянном начальном давлении. Предполагалось, что скорость топлива вначале равна 0, а температура, плотность и концентрация описываются фронтом Франка-Каменецкого., Тт.е. до некоего  (у нас ) , где  - коэффициент расширения, который полагался равным 5. При :

.

.Расчет производился при принятых параметрах ,  и шаге . Шаг по времени брался в соответствии с условием Куранта.

На рис.1 представлены графики основных параметров топливной смеси в моменты времени  и  соответственно.

Решение описывается тремя фронтами, в общем случае не совпадающими друг с другом: скачок плотности (ударная волна), тепловой фронт (фронт горения) и скачок концентрации. Т.к. источник в (3.3) при отсутствии гравитации один и равен , где  - скорость реакции в уравнении для концентрации топлива, то существует решение в виде фронта пламени, распространяющегося с постоянной скоростью. Я.Б. Зельдович и Д.А. Франк-Каменецкий (1938) при рассмотрении стационарного фронта ламинарного пламени получили выражения для скорости установившегося плоского фронта:

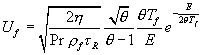.                        (7.1) При этом получено пространственное распределение температуры. Оно имеет следующий вид:

,

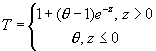где  - координата точки максимума величины, характеризующей скорость реакции, т.е. выражения , которые в единицах  для температуры может быть представлено в виде . График данной величины представлен на рис.2.

Очевидно, из соотношения (2.21) (V.V. Bychkov, M.A. Liberman, 2000) можно получить выражения для скорости фронта горения :

.

Сопоставляя это значение со значением, полученным из вышеуказанной формулы, легко убедиться, что они близки друг к другу.

Результат сравнения вычисленных значений температуры с формулой Зельдовича и Франк-Каменецкого приведен на рис.3. За фронтом наблюдается подъем температуры по сравнению с начальной . Отличие также наблюдается в незначительной области вблизи максимума. В работах P. Clavin и F.A. Williams (1979, 1981, 1982),профиль температуры получен путем асимптотического разложения по малому параметру . В этом случае наблюдается сглаживание температурного профиля вблизи максимума, что соответствует вычислительному результату.





 

 

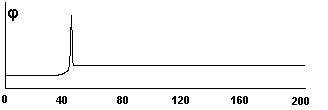
Рис.2

Рис.3

В устойчивых режимах , т.е. коэффициенты температуропроводности и диффузии совпадают или близки друг к другу. В противном случае возможны различные типы неустойчивости.

Если , т.е. скачок концентрации движется много быстрее фронта температуропроводности, может произойти срыв горения. На рис.4 изображена эволюция функции . Видно, что в какие-то моменты реакция затухает, поскольку не хватает топлива. В противоположном случае  скорость фронта горения очень мала и неустойчивость горения на фронте также имеет место, т.к. топливо не успевает прогорать. Рассмотрены два случая с одним и тем же коэффициентом теплопроводности, т.е. значения  остаются без изменения и тем самым сохраняется временной масштаб, но с разными значениями чисел Шмидта. На рис.5-6 представлены пространственные распределения концентрации топлива  для момента времени . Во втором случае число Шмидта на несколько порядков больше, чем в первом, т.е. коэффициент диффузии на несколько порядков меньше. Сопоставление результатов расчета показывает, что скорость пламени уменьшилась.

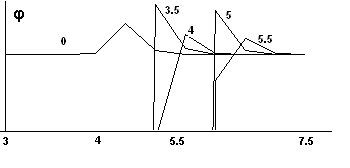
Рис.4





 

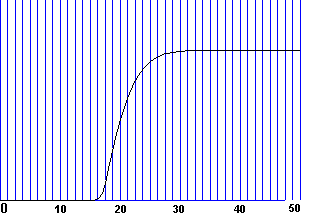
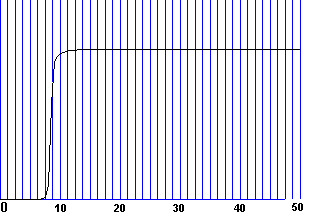
Рис.5                           Рис.6


 

Таким образом, одномерные расчеты подтверждают корректность определения характерных значений ширины фронта пламени  и скорости стационарного плоского фронта . Кроме того, подтверждено существование различных термодиффузионных неустойчивостей в том случае, когда  заметно отличается от 1. В целом это подтверждает эффективность предложенного метода численного решения, т.е. расщепления по процессам и выбора явных схем высокого разрешения(TVD схемы) для расчета гиперболических систем. Помимо прочего, приведенный анализ одномерных задач позволяет утверждать, что при исследовании гидродинамических свойств пламени, следует ограничиться значениями , чтобы избежать осложнений, вызванных диффузионными эффектами.

 

 

 

Использованная литература

 

 

1.           Bychkov V.V., Liberman M.A. Dynamics and stability of premixed flames. Physics reports. Volume 325, numbers 4-5, March 2000.

2.           Радвогин Ю.Б. О квазимонотонных  разностных схемах второго порядка. Препринт Института прикладной математики им. М.В. Келдыша АН СССР, 1991, № 9

3.           Radvogin Yu.B., Zaitsev N.A. Multidimensional minimal stencil supported second order accurate upwind schemes for solving hyperbolic and Euler systems. Preprint, Keldysh Institute Applied Mathematics, Russian Academy of Science, 1996,
№ 22

4.           Zeldovich Ya.B., Barenblatt G.I., Librovich V.B., Makhviladze G.M. The mathematical theory of combustion and explosion. Consultants bureau, New York, 1985

5.           Zeldovich Ya.B., Frank-Kamenetski D.A. Acta Physicochimica. URSS 9,341, 1985

6.           Landau L.D., Lifshitz E.M. Fluid mechanics. Pergamon press, Oxford,1987

7.           Clavin P., Williams F.A. Premixed flames in turbulence. Journal of fluid mechanics, 1982, vol.116, pp.251-282

8.           Clavin P., Williams F.A. Theory of premixed flame propagation in large-scale turbulence. Journal of fluid mechanics, 1979, 90, 589-604.

9.           Clavin P., Williams F.A. Effects of Lewis number on propagation of wrinkled flames in turbulent flow. In combustion in reactive systems. Prog. Aeronautics Astronautics 76,403-411.