НЕСТАЦИОНАРНАЯ МЕТОДИКА ДЛЯ РАСЧЕТА
МНОГОГРУППОВЫХ ДВУМЕРНЫХ КИНЕТИЧЕСКИХ УРАВНЕНИЙ
НА СЕТКАХ, СОСТОЯЩИХ ИЗ ПРОИЗВОЛЬНЫХ ЧЕТЫРЕХУГОЛЬНИКОВ
|
|
|
- единичный вектор в
направлении полета частиц, |
|
|
- полное число
энергетических групп частиц, |
|
|
- плотность потока
частиц в точке |
|
|
- скалярный поток
частиц в точке |
|
|
- макроскопическое
сечение рассеяния частиц из группы |
|
|
- минимальный номер
группы, из которой частицы рассеиваются в группу |
|
|
- максимальный номер
группы, из которой частицы рассеиваются в группу |
|
|
- полное
макроскопическое сечение взаимодействия, |
|
|
- макроскопическое
сечение деления, |
|
|
- число вторичных
частиц, возникающих при одном акте деления, |
|
|
- спектр деления, |
|
|
- функция распределения
внутренних источников в точке |
На границе пространственной области ![]() задаются
значения углового потока входящего внутрь этой области:
задаются
значения углового потока входящего внутрь этой области:
![]() (4)
(4)
где
![]() - внешняя нормаль к
границе.
- внешняя нормаль к
границе.
В начальный момент времени ![]() угловой поток задается
для всех групп
угловой поток задается
для всех групп ![]() :
:
![]() (5)
(5)
Система уравнений (1) - (2) описывает нестационарный
перенос частиц под действием процессов деления.
Если в правой части (2) отсутствует компонента с делением
(![]() ), то система уравнений (1) - (5) описывает
поведение потоков во времени в зависимости от заданных внутренних и граничных
источников.
), то система уравнений (1) - (5) описывает
поведение потоков во времени в зависимости от заданных внутренних и граничных
источников.
Если в уравнении (1) отсутствует производная по времени, а
в правой части (2) при компоненте с делением стоит множитель ![]() и источник
и источник ![]() для всех групп, если,
кроме того, значения углового потока входящего внутрь области для всех групп
равны нулю, то имеем задачу на
для всех групп, если,
кроме того, значения углового потока входящего внутрь области для всех групп
равны нулю, то имеем задачу на ![]() (однородная
задача).
(однородная
задача).
Предполагается, что макроскопическое сечение рассеяния ![]() задается в виде ряда
по полиномам Лежандра
задается в виде ряда
по полиномам Лежандра ![]() степени
степени ![]() (в
(в ![]() приближении,
приближении, ![]() ):
):
 (6)
(6)
с условиями нормировки:
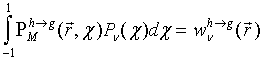
(7)
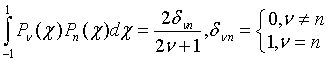
Для упрощения выражения (6) используется теорема сложения
полиномов Лежандра: Пусть ![]() и
и ![]() - два единичных
вектора со сферическими координатами
- два единичных
вектора со сферическими координатами ![]() и
и ![]() соответственно, и
пусть
соответственно, и
пусть ![]() ,
, ![]() ,
, ![]() . Тогда следующие формулы справедливы:
. Тогда следующие формулы справедливы:
![]() ,
,
(8)
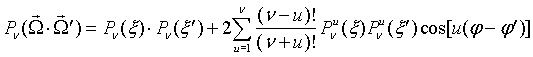 ,
,
где
![]() - присоединенные
функции Лежандра первого рода с нормировкой:
- присоединенные
функции Лежандра первого рода с нормировкой:
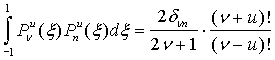 (9)
(9)
На практике обычно используются нормированные функции ![]() , которые определяются через функции
, которые определяются через функции ![]() следующим образом:
следующим образом:
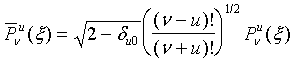 (10)
(10)
Для
этих функций имеем:
![]() ,
,  (11)
(11)
В случае
аксиально-симметричной двумерной R-Z геометрии (Рис.1) решение
уравнения переноса (1) обладает свойством симметрии:

Рис. 1.
Система координат для уравнения переноса в R-Z геометрии.
Система
уравнений (13) решается в пространственной области ![]() , которая заключена между внешней образующей тела вращения и
осью симметрии Z и
представляет собой сечение тела вращения плоскостью, проходящей через ось Z (Рис. 2).
, которая заключена между внешней образующей тела вращения и
осью симметрии Z и
представляет собой сечение тела вращения плоскостью, проходящей через ось Z (Рис. 2).
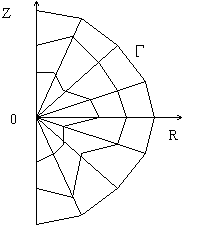
Рис. 2.
Область D и четырехугольная пространственная сетка.
Подставляя
(6) с использованием (8) в интеграл рассеяния, входящий в правую часть
уравнения (1) для частиц группы ![]() , получим выражение для источника рассеяния:
, получим выражение для источника рассеяния:
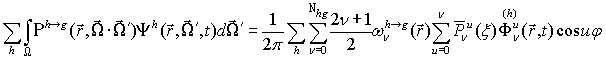 (14)
(14)
В (14) используются
нормированные функции Лежандра (10) и угловые моменты ![]() решения
уравнения переноса (13) в группе
решения
уравнения переноса (13) в группе ![]() , определяемые по формуле:
, определяемые по формуле:
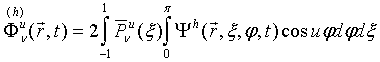 (15)
(15)
Выражение (14) получено с
использованием формулы:
![]()
и свойства четности
функции ![]() по углу
по углу ![]() , а именно:
, а именно:
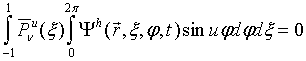
Запишем
правую часть уравнения (13) в случае аксиально-симметричной двумерной R-Z
геометрии с учетом (14) и (15):
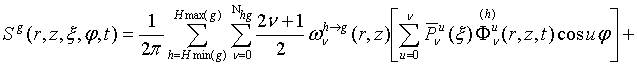
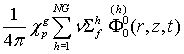
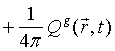 (16)
(16)
Граничное условие на
внешней поверхности задается в виде потока частиц, входящих внутрь области ![]() :
:
![]() ,
, ![]() (17)
(17)
Кроме
того, используются дополнительные граничные условия, которые вытекают из
уравнения (13). При ![]() , имеем
, имеем ![]() . В расчетах это условие используется в следующем
виде:
. В расчетах это условие используется в следующем
виде:
![]() (18)
(18)
Для ![]() , имеем граничное условие:
, имеем граничное условие:
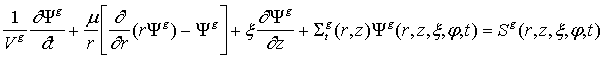 (19)
(19)
Задаются также начальные условия:
![]()
![]() (20)
(20)
3. Конечно-разностная аппроксимация
уравнений.
Для получения
консервативной конечно-разностной схемы в двумерной аксиальной геометрии на
сетке, состоящей из произвольных выпуклых четырехугольников, используются
интегро-интерполяционный метод.
Угловая
сетка задается ![]() квадратурой, которая разбивает полусферу направлений на сектора.
Каждому узлу
квадратурой, которая разбивает полусферу направлений на сектора.
Каждому узлу ![]() ,
, ![]() из интервала
из интервала ![]() соответствует набор
интервалов
соответствует набор
интервалов ![]() ,
, ![]() области изменения
угла
области изменения
угла ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ,
, ![]() . Построенное таким образом разбиение верхней части
полусферы (
. Построенное таким образом разбиение верхней части
полусферы (![]() ) единичного радиуса симметрично отображается на нижнюю часть
полусферы (
) единичного радиуса симметрично отображается на нижнюю часть
полусферы (![]() ). В результате, площадь поверхности полусферы разбивается на
сектора с весами
). В результате, площадь поверхности полусферы разбивается на
сектора с весами ![]() ,
, ![]() .
.
Введем
интервал времени ![]() и рассмотрим
пространственную область
и рассмотрим
пространственную область ![]() , покрытую регулярной сеткой, состоящей из выпуклых
четырехугольников. Обозначим значения функции
, покрытую регулярной сеткой, состоящей из выпуклых
четырехугольников. Обозначим значения функции ![]() на интервале
на интервале ![]() для фиксированного
направления
для фиксированного
направления ![]() на сторонах четырехугольника
через
на сторонах четырехугольника
через ![]()
![]() и в центре
четырехугольника -
и в центре
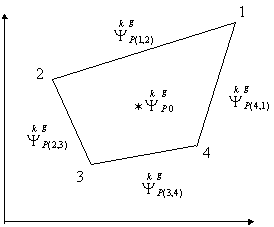
четырехугольника - ![]() (Рис. 3).
(Рис. 3).
Z
R
Рис. 3.
Значения функции ![]() в четырехугольной
пространственной ячейке.
в четырехугольной
пространственной ячейке.
Интегрируя
уравнение (13) с весом ![]() по
четырехугольнику с координатами вершин
по
четырехугольнику с координатами вершин ![]() в пределах
разностной угловой ячейки
в пределах
разностной угловой ячейки ![]()
![]()
![]() площадью
площадью ![]() и по интервалу
и по интервалу ![]() , применяя
формулу Гаусса - Остроградского и сокращая на
, применяя
формулу Гаусса - Остроградского и сокращая на ![]() , получим следующее балансное уравнение, где индекс группы
, получим следующее балансное уравнение, где индекс группы ![]() опущен:
опущен:
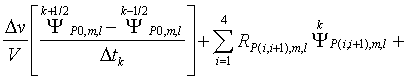
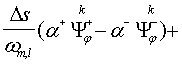
(21)
![]() ,
,
где
![]() (22)
(22)
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Параметры ![]() для фиксированного
значения
для фиксированного
значения ![]() и для всех
и для всех ![]() вычисляются из
дополнительного соотношения:
вычисляются из
дополнительного соотношения:
![]() ,
,![]() (23)
(23)
Площадь  четырехугольной пространственной ячейки в плоскости R-Z
вычисляется через координаты вершин по формуле:
четырехугольной пространственной ячейки в плоскости R-Z
вычисляется через координаты вершин по формуле:
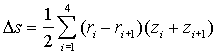 (24)
(24)
Объем ![]() области,
образованной вращением этой ячейки вокруг оси симметрии Z, вычисляется по формуле:
области,
образованной вращением этой ячейки вокруг оси симметрии Z, вычисляется по формуле:
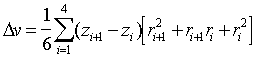 (25)
(25)
Для
замыкания системы (21) - (25) вводятся дополнительные “алмазные” соотношения по
угловой переменной ![]() и по времени
и по времени ![]() :
:
![]() (26)
(26)
![]() (27)
(27)
где ![]() и
и ![]() - весовые параметры
из интервала
- весовые параметры
из интервала ![]() .
.
Дополнительные
соотношения по пространственным переменным должны быть такими, чтобы для любых
направлений полета частиц ![]() они
приводили к невырожденной системе сеточных уравнений. Количество дополнительных
соотношений и их вид определяются освещенностью сторон четырехугольной ячейки.
Возможные варианты освещенности и соответствующие дополнительные соотношения
рассматриваются ниже более подробно.
они
приводили к невырожденной системе сеточных уравнений. Количество дополнительных
соотношений и их вид определяются освещенностью сторон четырехугольной ячейки.
Возможные варианты освещенности и соответствующие дополнительные соотношения
рассматриваются ниже более подробно.
Граничные
условия (17) задаются на внешней границе для тех сторон четырехугольной ячейки,
для которых ![]() , что эквивалентно условию
, что эквивалентно условию ![]() . Чтобы аппроксимировать граничное условие (18) на
примыкающих к оси Z сторонах четырехугольников и в центре координат, это
условие заменяется соотношением:
. Чтобы аппроксимировать граничное условие (18) на
примыкающих к оси Z сторонах четырехугольников и в центре координат, это
условие заменяется соотношением:
![]() (28)
(28)
Для
аппроксимации граничного условия (19) при ![]() используется следующее балансное уравнение:
используется следующее балансное уравнение:
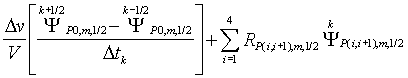
![]()
![]() , (29)
, (29)
где ![]() .
.
Дополнительные
соотношения по пространственным переменным для направлений ![]() задаются также в
зависимости от освещенности ячейки.
задаются также в
зависимости от освещенности ячейки.
Алгоритм
решения системы сеточных уравнений с заданной правой частью на интервале ![]() следующий.
следующий.
Для
фиксированного значения ![]() сначала решается
уравнение (29) для направления
сначала решается
уравнение (29) для направления ![]() снаружи
пространственной области
снаружи
пространственной области ![]() во внутрь (
во внутрь (![]() ) с учетом граничных условий (17) и начальных условий (20), а
также дополнительных соотношений по пространственным переменным. Полученное во
всех пространственных ячейках решение
) с учетом граничных условий (17) и начальных условий (20), а
также дополнительных соотношений по пространственным переменным. Полученное во
всех пространственных ячейках решение ![]() , используется затем в качестве граничного значения для
направления
, используется затем в качестве граничного значения для
направления ![]() . Сеточные уравнения системы (21) - (27) решаются
последовательно для каждого значения
. Сеточные уравнения системы (21) - (27) решаются
последовательно для каждого значения ![]() ,
, ![]() , используя начальные условия (20) и граничные условия (17),
а также условия (18) для направлений изнутри области
, используя начальные условия (20) и граничные условия (17),
а также условия (18) для направлений изнутри области ![]() наружу (
наружу (![]() ).
).
Возможны
три различных типа освещенности ячейки. Им соответствуют три различных способа
задания дополнительных соотношений в зависимости от выбранного направления ![]() . Дополнительные соотношения строятся, использую средние
значения функции
. Дополнительные соотношения строятся, использую средние
значения функции ![]() на сторонах и в
центре пространственной ячейки с общим весовым параметром
на сторонах и в
центре пространственной ячейки с общим весовым параметром ![]() ,
, ![]() .
Построенные дополнительные соотношения обеспечивают либо первый, либо второй
порядок аппроксимации, в зависимости от числа освещенных сторон.
.
Построенные дополнительные соотношения обеспечивают либо первый, либо второй
порядок аппроксимации, в зависимости от числа освещенных сторон.
Тип
освещенности ячейки определяется количеством сторон, у которых ![]() . Если на стороне
. Если на стороне ![]() ячейки
ячейки ![]() (Рис. 4) величина
(Рис. 4) величина ![]() , то частицы входят в ячейку. Если
, то частицы входят в ячейку. Если ![]() , то частицы выходят из ячейки. Если
, то частицы выходят из ячейки. Если ![]() , частицы летят вдоль этой стороны, и соответствующее
слагаемое в уравнении (21) отсутствует. Поэтому такой случай не требует
дополнительного рассмотрения. Рассмотрим три типа освещенности ячейки.
, частицы летят вдоль этой стороны, и соответствующее
слагаемое в уравнении (21) отсутствует. Поэтому такой случай не требует
дополнительного рассмотрения. Рассмотрим три типа освещенности ячейки.
Тип 1.
Освещена
одна сторона, например, AB (Рис. 4). В этом случае
значение ![]() известно, значения
известно, значения ![]() ,
, ![]() ,
, ![]() и
и ![]() не известны.
не известны.
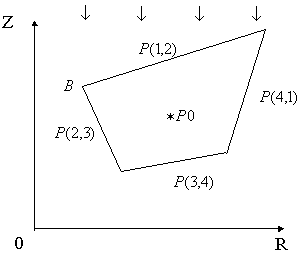
Рис. 4.
Освещена одна сторона четырехугольной ячейки.
Используется
дополнительное соотношение:
![]() (30)
(30)
и два соотношения одного
из двух вариантов:
1)
![]() ,
, ![]() (31а)
(31а)
2)
![]() ,
, ![]() (31б)
(31б)
Соотношения (31) понижают
порядок аппроксимации схемы в целом. Подставляя (26), (27), (30) и (31а) в
балансное уравнение (21), получим формулу для вычисления ![]() :
:
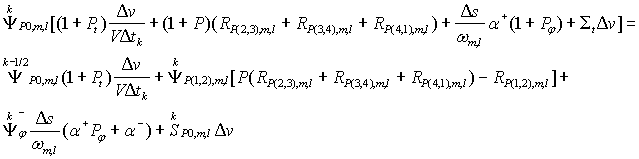
Тип 2.
Освещены
две стороны, например, AB и AD (Рис. 5). В этом случае
значения ![]() и
и ![]() известны, значения
известны, значения ![]() ,
, ![]() и
и ![]() не известны.
не известны.
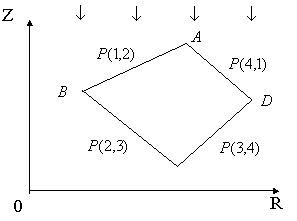
Рис. 5.
Освещены две стороны четырехугольной ячейки.
Используются следующие
дополнительные соотношения:
![]() (32)
(32)
![]() (33)
(33)
Подставляя (26), (27),
(32), (33) в (21), получим формулу для вычисления ![]() :
:
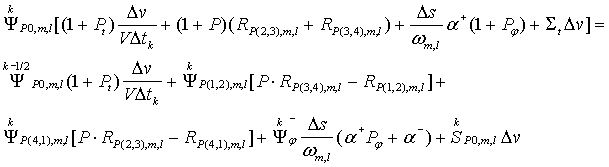
Тип 3.
Освещены
три стороны, например, AB, BC и AD (Рис. 6). В этом случае
известны следующие значения: ![]() ,
, ![]() ,
, ![]() . Значения
. Значения ![]() и
и ![]() не известны.
не известны.
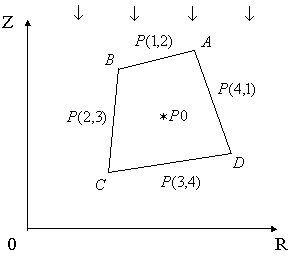
Рис. 6.
Освещены три стороны четырехугольной ячейки.
Используется
следующее дополнительное соотношение:
![]() (34)
(34)
Подставляя (26), (27), и
(34) в (21), получим формулу для вычисления ![]() :
:
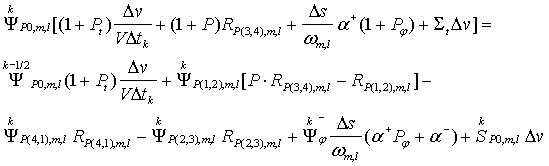
Скалярный
поток частиц вычисляется по формуле:
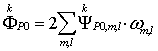 (35)
(35)
4. Численный алгоритм решения нестационарной задачи.
4.1. Внешние итерации.
Система
уравнений (13) с правой частью (16) может быть записана в следующем операторном
виде (![]() ):
):
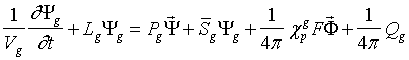 (36)
(36)
где
![]() - оператор
переноса,
- оператор
переноса,
![]() - оператор рассеяния из верхних групп,
- оператор рассеяния из верхних групп,
![]() - оператор рассеяния внутри группы
- оператор рассеяния внутри группы ![]() ,
,
![]() - оператор размножения частиц,
- оператор размножения частиц,
![]() - оператор возникновения частиц от внутреннего
источника,
- оператор возникновения частиц от внутреннего
источника,
![]() - вектор скалярных потоков частиц, состоящий из
нулевых моментов углового потока для всех групп (
- вектор скалярных потоков частиц, состоящий из
нулевых моментов углового потока для всех групп (![]() ),
),
![]() - вектор угловых потоков частиц,
- вектор угловых потоков частиц, ![]() .
.
Специфика
рассматриваемой задачи состоит в том, что система нестационарных уравнений (36)
принадлежит к классу "жестких" систем. Это означает, что в ее решении
присутствуют как быстроизменяющиеся компоненты, так и сравнительно медленные,
определяющие характер поведения решения через большие промежутки времени.
Известно, что явные методы для решения таких систем требуют очень малых шагов
по времени. Неявные методы позволяют выполнять численное интегрирование с более
крупными шагами.
Рассмотрим
уравнение переноса в конечно-разностном виде с учетом разбиения по временным
слоям:
 (37)
(37)
На
каждом временном интервале ![]() в уравнении
(37) операторы размножения и внутренних источников берутся на нижнем слое
в уравнении
(37) операторы размножения и внутренних источников берутся на нижнем слое ![]() , а операторы рассеяния берутся на промежуточном
временном слое
, а операторы рассеяния берутся на промежуточном
временном слое ![]() . Возникает необходимость в проведении
итерационного процесса (внешние
итерации).
. Возникает необходимость в проведении
итерационного процесса (внешние
итерации).
Перед
началом итераций необходимо иметь начальное приближение угловых моментов потока
![]() (
(![]() - номер внешней итерации) в каждой группе на
промежуточном временном слое
- номер внешней итерации) в каждой группе на
промежуточном временном слое ![]() . Эти значения берутся с нижнего слоя
. Эти значения берутся с нижнего слоя ![]() . Кратко алгоритм решения нестационарной системы
уравнений переноса (36) можно описать следующим образом:
. Кратко алгоритм решения нестационарной системы
уравнений переноса (36) можно описать следующим образом:
1. Вычисляется
количество частиц, возникающих от источника размножения:
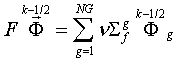 (38)
(38)
2. Затем
последовательно решается каждое конечно-разностное уравнение (37), начиная с
уравнения с самой высокой энергией (![]() ) и заканчивая уравнением с самой низкой энергией (
) и заканчивая уравнением с самой низкой энергией (![]() ):
):
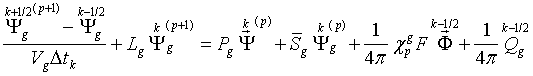
3. Внешний
итерационный процесс заканчивается, если скалярные потоки изменяются в пределах
заданной точности, либо если выполнено заданное количество внешних итераций. На
каждом слое ![]() проверяется критерий
окончания внешних итераций:
проверяется критерий
окончания внешних итераций:
 (39)
(39)
где
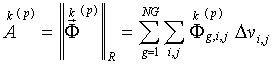 (40)
(40)
Если
критерий не выполняется, переходим к пункту 2 (![]() ).
).
4. В
противном случае переходим к расчету на следующем временном интервале ![]() .
.
4.2. Внутренние итерации.
Рассмотрим
конечно-разностное уравнение переноса в энергетической группе ![]() (
(![]() ) на интервале времени
) на интервале времени ![]() . Уравнение записывается в операторном виде:
. Уравнение записывается в операторном виде:
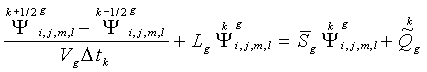 , (41)
, (41)
![]()
Для решения этого
уравнения используется дополнительное линейное соотношение по времени:
![]()
![]() (42)
(42)
Подставляя это
соотношение в уравнение (37), получим:
![]() (43)
(43)
где
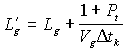 ,
, 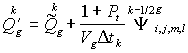 (44)
(44)
Уравнение
(43) решается методом итерации источника рассеяния (внутренние итерации).
Опуская индекс номера группы ![]() , можно записать итерационный процесс на
промежуточном временном слое
, можно записать итерационный процесс на
промежуточном временном слое ![]() (
(![]() - номер внутренней итерации):
- номер внутренней итерации):
![]() (45)
(45)
Итерационный
процесс (45) выполняется следующим образом.
Для
каждого фиксированного направления ![]() в пространственной
области
в пространственной
области ![]() проводится анализ
освещенности каждой четырехугольной ячейки. Если для расчета углового потока в
ячейке имеется необходимая информация, то:
проводится анализ
освещенности каждой четырехугольной ячейки. Если для расчета углового потока в
ячейке имеется необходимая информация, то:
1. По
угловым моментам потока ![]() вычисляется
правая часть уравнения (45).
вычисляется
правая часть уравнения (45).
2. Вычисляется
угловой поток ![]() по формулам
конечно-разностной схемы.
по формулам
конечно-разностной схемы.
После вычисления потока ![]() во всей
пространственной области для всех направлений вычисляются угловые моменты
во всей
пространственной области для всех направлений вычисляются угловые моменты ![]() для расчета
правой части (45) на следующей итерации. Процесс внутренних итераций
заканчивается, если потоки внутри группы изменяются в пределах заданной
точности, либо если выполнено заданное количество внутренних итераций. На
каждом слое
для расчета
правой части (45) на следующей итерации. Процесс внутренних итераций
заканчивается, если потоки внутри группы изменяются в пределах заданной
точности, либо если выполнено заданное количество внутренних итераций. На
каждом слое ![]() проверяются два
критерия окончания внутренних итераций:
проверяются два
критерия окончания внутренних итераций:
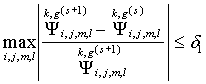 (46)
(46)
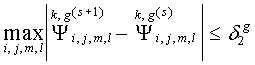 (47)
(47)
Если эти критерии не
выполняются, переходим к пункту 1 (![]() ). В противном случае переходим к расчету потоков
следующей группы
). В противном случае переходим к расчету потоков
следующей группы ![]() на интервале времени
на интервале времени ![]() .
.
4.3. Решение задачи на собственное значение.
Иногда
требуется решать задачу на ![]() путем
использования алгоритма для решения нестационарной системы уравнений переноса.
Значение
путем
использования алгоритма для решения нестационарной системы уравнений переноса.
Значение ![]() удовлетворяет решению квазикритической задачи, которая в
операторной форме имеет вид:
удовлетворяет решению квазикритической задачи, которая в
операторной форме имеет вид:
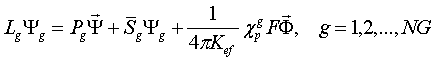 (48)
(48)
Задача
вычисления ![]() решается
методом установления. Алгоритм решения описывается ниже по шагам:
решается
методом установления. Алгоритм решения описывается ниже по шагам:
1. Задается
начальное значение параметра ![]() , равное единице. Задаются начальные значения
скалярных потоков и угловых моментов на слое
, равное единице. Задаются начальные значения
скалярных потоков и угловых моментов на слое ![]() , угловые потоки на слое
, угловые потоки на слое ![]() во всех
пространственных точках и для всех угловых направлений (
во всех
пространственных точках и для всех угловых направлений (![]() ):
):
![]() ,
, ![]() ,
, ![]()
2. Вычисляются
функция источника размножения и величина ![]() на слое
на слое ![]() по формуле:
по формуле:
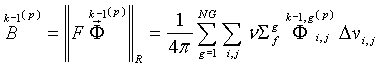
3. Решается
нестационарное уравнение переноса с коэффициентом ![]() для всех
групп
для всех
групп ![]() . Результатом являются значения потока:
. Результатом являются значения потока:
![]() ,
, ![]() ,
, ![]()
4. Вычисляются
функция источника размножения и величина ![]() на слое
на слое ![]() по формуле:
по формуле:
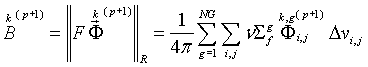
5. Новое
собственное значение ![]() вычисляется
по формуле:
вычисляется
по формуле:
![]()
6. Внешние
итерации заканчиваются, если значение ![]() на соседних
итерациях изменяется в пределах заданной точности, либо если максимальное
количество внешних итераций достигнуто. Критерием является условие:
на соседних
итерациях изменяется в пределах заданной точности, либо если максимальное
количество внешних итераций достигнуто. Критерием является условие:
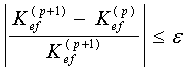 (49)
(49)
7. Если
оба критерия не выполняются, то новые значения потоков
![]() ,
, ![]() ,
, 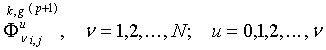
делятся
на величину ![]() и
осуществляется переход к пункту 3 для расчета следующей внешней итерации на
следующем временном слое (
и
осуществляется переход к пункту 3 для расчета следующей внешней итерации на
следующем временном слое (![]() ).
).
5.
Тестирование
алгоритма.
5.1. Аналитическое решение
нестационарной задачи в одномерной геометрии в диффузионном приближении.
Задача
пространственной кинетики в одномерной пространственной области в диффузионном
приближении записывается в виде:
 (50)
(50)
![]()
Здесь приняты следующие
обозначения:
![]() -
групповые нейтронные потоки;
-
групповые нейтронные потоки;
![]() -
групповые коэффициенты диффузии;
-
групповые коэффициенты диффузии;
![]() -
групповые макросечения утечки;
-
групповые макросечения утечки;
![]() -
групповые макросечения деления;
-
групповые макросечения деления;
![]() -
макросечения перехода из группы
-
макросечения перехода из группы ![]() в группу
в группу ![]() ;
;
![]() -
групповой спектр мгновенных нейтронов деления;
-
групповой спектр мгновенных нейтронов деления;
![]() -
усредненные групповые скорости нейтронов;
-
усредненные групповые скорости нейтронов;
![]() - число энергетических групп нейтронов.
- число энергетических групп нейтронов.
На внешней границе области
заданы нулевые значения потоков: ![]() .
.
После
процедуры дискретизации по пространству эта задача может быть записана в
операторном виде, описывающем эволюционную систему уравнений:
![]() ,
, ![]() (51)
(51)
где
![]() - вектор групповых нейтронных
потоков,
- вектор групповых нейтронных
потоков,
![]() -
матрицы операторов исходной системы уравнений (50).
-
матрицы операторов исходной системы уравнений (50).
Эволюционной системе (50) соответствует
квазикритическая задача на ![]() , которая записывается в следующем виде:
, которая записывается в следующем виде:
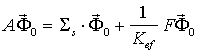 (52)
(52)
Нейтронные потоки ![]() будут в дальнейшем
использоваться в качестве начальных значений для эволюционной системы (50).
будут в дальнейшем
использоваться в качестве начальных значений для эволюционной системы (50).
Для
однородного бесконечного цилиндра ![]() решение системы (51)
можно представить в виде произведения двух функций, одна из которых зависит
только от времени (амплитудная функция), а другая только от пространства:
решение системы (51)
можно представить в виде произведения двух функций, одна из которых зависит
только от времени (амплитудная функция), а другая только от пространства:
![]() (53)
(53)
где ![]() - функция Бесселя
первого рода,
- функция Бесселя
первого рода, ![]() - ее первый корень,
- ее первый корень, ![]() . После подстановки (53)
в (51) и сокращения функций Бесселя
получается система уравнений относительно функций
. После подстановки (53)
в (51) и сокращения функций Бесселя
получается система уравнений относительно функций ![]() с матрицей
с матрицей ![]() следующего вида:
следующего вида:
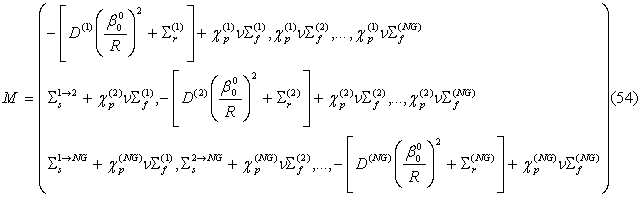
Точное
решение упрощенной системы уравнений для амплитудного вектора ![]() может быть
представлено в виде:
может быть
представлено в виде:
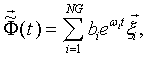 (55)
(55)
где
![]() - система собственных векторов матрицы
- система собственных векторов матрицы ![]() ,
,
![]() - система собственных
чисел матрицы
- система собственных
чисел матрицы ![]() , которые определяются из системы уравнений
, которые определяются из системы уравнений ![]() ,
,
![]() - коэффициенты разложения начального
приближения
- коэффициенты разложения начального
приближения ![]() по системе
по системе ![]() .
.
5.2. Описание тестовой задачи.
Для
проведения расчетов была взята тестовая модель однородной цилиндрической зоны с
набором макроконстант, характерных для тепловых систем [3]. Исходные 4х-групповые
макроконстанты и средние скорости нейтронов для рассматриваемой задачи
приведены в Таблице 1.
Таблица
1. Макроконстанты для диффузионного приближения.
|
№ группы |
|
|
|
|
|
|
|
1 |
1. |
|
1.80125 |
0.024880 |
1®2 |
0.018832 |
|
2 |
0. |
|
0.715137 |
0.114846 |
1®3 |
0.000016 |
|
3 |
0. |
|
0.662379 |
0.470175 |
2®3 |
0.017480 |
|
4 |
0. |
|
0.310534 |
0.431861 |
1®4 |
0.000031 |
|
|
|
|
|
|
2®4 |
0.032791 |
|
|
|
|
|
|
3®4 |
0.355210 |
Радиус
пространственной области R=81.35
см. Начальные условия для нестационарной задачи берутся из решения
квазикритической задачи (52), нормированного таким образом, чтобы удовлетворить
условию:
 (56)
(56)
Изменение
реактивности моделировалось изменением сечений деления. В Таблице 2 приведены
значения ![]() для
различных сечений деления. Исследовалась эволюция собственных чисел
для
различных сечений деления. Исследовалась эволюция собственных чисел ![]() матрицы
матрицы ![]() при
изменении реактивности
при
изменении реактивности ![]() , определяемой по формуле:
, определяемой по формуле:
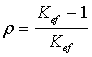 (57)
(57)
Значения
собственных чисел ![]() матрицы
матрицы ![]() в
зависимости от величины
в
зависимости от величины ![]() приведены в
Таблице 3. Из Таблицы 3 видно, что решение на асимптотике определяется ведущим
собственным числом
приведены в
Таблице 3. Из Таблицы 3 видно, что решение на асимптотике определяется ведущим
собственным числом ![]() , которое для
, которое для ![]() отрицательно, для
отрицательно, для ![]() равно нулю и для
равно нулю и для ![]() положительно. Для
тестирования использовался вариант с
положительно. Для
тестирования использовался вариант с ![]() = 0.96809.
Собственные векторы матрицы
= 0.96809.
Собственные векторы матрицы ![]() и
коэффициенты разложения по системе
и
коэффициенты разложения по системе ![]() начального
приближения
начального
приближения ![]() представлены в
Таблице 4 для вычисления аналитического решения.
представлены в
Таблице 4 для вычисления аналитического решения.
Таблица
2. Макросечения ![]() .
.
|
№ группы |
1.0000 |
0.968098 |
0.99356 |
1.00322 |
1.00644 |
|
1 |
0.0061648 |
0.0059692 |
0.0061263 |
0.00618585 |
0.0062057 |
|
2 |
0.063237 |
0.061219 |
0.0628297 |
0.0634406 |
0.0636442 |
|
3 |
0.151951 |
0.147104 |
0.150974 |
0.152442 |
0.152932 |
|
4 |
0.518583 |
0.502034 |
0.515243 |
0.520253 |
0.521923 |
Таблица
3. Собственные числа ![]() матрицы
матрицы ![]() .
.
|
I |
0.96809 |
0.99356 |
1.00000 |
1.00322 |
1.00644 |
|
1 |
-2.7625+07 |
-2.7625+07 |
-2.7631+07 |
-2.7633+07 |
-2.7635+07 |
|
2 |
-4.6486+06 |
-4.4845+06 |
-4.4228+06 |
-4.4228+06 |
-4.4022+06 |
|
3 |
-2.0383+04 |
-4.2183+03 |
0. |
2.1802+03 |
4.3487+03 |
|
4 |
-6.4034+05 |
-6.4233+05 |
-6.4284+05 |
-6.4310+05 |
-6.4336+05 |
Таблица
4. Собственные векторы ![]() и коэффициенты
и коэффициенты ![]() (
(![]() = 0.96809).
= 0.96809).
|
i |
|
|
|
|
|
|
1 |
-7.52370 |
5.3853 |
-2.97160 |
0.74950 |
-0.2547 |
|
2 |
0.88240 |
1.4701 |
-0.48550 |
0.12940 |
0.8725 |
|
3 |
-0.00071 |
-0.00796 |
-0.01878 |
-0.05616 |
-28.759 |
|
4 |
-0.00071 |
-0.00705 |
-0.05644 |
0.03030 |
-0.4570 |
5.3. Численные результаты.
Описанная
выше тестовая одномерная задача в диффузионном четырех групповом приближении
была использована для тестирования нестационарной программы NPTQT для решения многогруппового
уравнения переноса в аксиально-симметричной R-Z геометрии на регулярной сетке,
образованной произвольными выпуклыми четырехугольниками.
Ставилась
задача исследования качественного поведения по времени решения уравнения
переноса на примере нейтронного потока в первой группе. Кроме того, требовалось
вычислить декремент затухания,
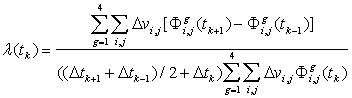 (58)
(58)
который совпадает с ведущим
собственным числом ![]() на асимптотике.
на асимптотике.
Соответствующие
четырех групповые макроконстанты и средние скорости нейтронов для
рассматриваемой задачи приведены в Таблице 5. Значения полного сечения и
сечения рассеяния вычислялись по формулам:
![]() ,
, ![]()
Решения кинетического и
диффузионного уравнений совпадают при таких значениях макросечений, если
ограничиться разложением индикатрисы рассеяния только до первого момента.
Таблица
5. Макроконстанты для кинетического приближения.
|
№ группы |
|
|
|
|
|
|
|
1 |
1. |
|
0.185056 |
0.160176 |
1®2 |
0.018832 |
|
2 |
0. |
|
0.466111 |
0.351264 |
1®3 |
0.000016 |
|
3 |
0. |
|
0.503236 |
0.033061 |
2®3 |
0.017480 |
|
4 |
0. |
|
1.073419 |
0.641557 |
1®4 |
0.000031 |
|
|
|
|
|
|
2®4 |
0.032791 |
|
|
|
|
|
|
3®4 |
0.355210 |
Сечения
деления подбирались таким образом, чтобы при решении квазикритической задачи
значение ![]() было равно
0.96809. Приведем используемые значения сечений деления:
было равно
0.96809. Приведем используемые значения сечений деления:
![]()
Бесконечный
цилиндр моделировался заданием условий отражения на торцевых поверхностях
цилиндра с высотой Z=104.7
см. На боковой границе задавалось нулевое значение входящего потока.
Решение
многогруппового уравнения переноса получается наиболее близким к решению
диффузионного, когда используется минимальное количество угловых направлений.
Поэтому расчеты проводились в ![]() приближении метода
дискретных ординат. Решалась квазикритическая задача (48) на
приближении метода
дискретных ординат. Решалась квазикритическая задача (48) на ![]() для задания начальных скалярных
потоков. Эти потоки нормировались так, чтобы значение скалярного потока в
первой группе
для задания начальных скалярных
потоков. Эти потоки нормировались так, чтобы значение скалярного потока в
первой группе ![]() в точке с
координатами
в точке с
координатами ![]() ,
, ![]() совпало со значением
потока
совпало со значением
потока ![]() в первой группе в
диффузионном приближении. Следующие значения потоков были получены в
диффузионном и кинетическом приближениях соответственно:
в первой группе в
диффузионном приближении. Следующие значения потоков были получены в
диффузионном и кинетическом приближениях соответственно:
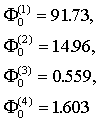

Изменение
решения по времени возникало вследствие замены значения ![]() с 0.96809
на 1.
с 0.96809
на 1.
Четырехугольная
пространственная сетка строилась заданием числа интервалов по радиусу ![]() и заданием числа
секторов по углу
и заданием числа
секторов по углу ![]() . На Рис.7 показана пространственная область и
четырехугольная сетка, образованная лучами, выходящими из центра координат. Один
из лучей делит пространственную область пополам. В каждой из двух частей
области строится равномерная по углу сетка.
. На Рис.7 показана пространственная область и
четырехугольная сетка, образованная лучами, выходящими из центра координат. Один
из лучей делит пространственную область пополам. В каждой из двух частей
области строится равномерная по углу сетка.
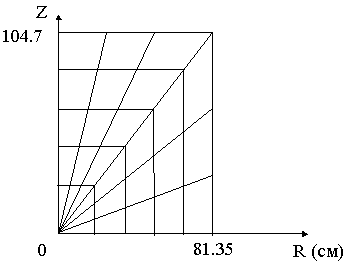
Рис. 7.
Четырехугольная пространственная сетка в R-Z геометрии.
Результаты
численных расчетов по времени представлены в Таблице 6. Здесь приведены
значения потока нейтронов в центре области в первой энергетической группе,
полученные по программе расчета аналитического диффузионного решения в
одномерной цилиндрической геометрии, а так же по программе NPTQT расчета конечно-разностного
кинетического решения на четырехугольной сетке с 50 точками по радиусу и 6
секторами по углу в двумерной R-Z геометрии. Кроме того, в
Таблице 6 приводятся значения декремента затухания, вычисленные по программе NPTQT.
Таблица 6. Поток нейтронов в первой энергетической группе
и декремент затухания ![]() в различные моменты
времени, вычисленные с шагом
в различные моменты
времени, вычисленные с шагом ![]() с.
с.
|
Время (с) |
Аналитическое решение одномерной диффузионной
задачи |
Численное решение двумерной кинетической задачи
по программе NPTQT |
Декремент затухания |
|
0. |
91,73 |
91,73 |
|
|
10-8 |
91,04 |
91,04 |
-0,3170*106 |
|
10-7 |
88,03 |
88,06 |
-0,2374*106 |
|
10-6 |
83,60 |
83,53 |
-0,2223*105 |
|
3.0*10-6 |
80,34 |
80,28 |
-0,1994*105 |
|
5.0*10-6 |
77,16 |
77,12 |
-0,2022*105 |
|
7.0*10-6 |
74,09 |
74,05 |
-0,2030*105 |
|
9.0*10-6 |
71,13 |
71,10 |
-0,2032*105 |
|
10-5 |
69,70 |
69,67 |
-0,2032*105 |
|
3.0*10-5 |
46,36 |
46,39 |
-0,2033*105 |
|
5.0*10-5 |
30,84 |
30,89 |
-0,2033*105 |
|
7.0*10-5 |
20,51 |
20,57 |
-0,2033*105 |
|
9.0*10-5 |
13,64 |
13,69 |
-0,2033*105 |
|
10-4 |
11,13 |
11,17 |
-0,2033*105 |
|
3.0*10-4 |
0,18 |
0,19 |
-0,2033*105 |
|
5.0*10-4 |
0,0032 |
0,0033 |
-0,2033*105 |
Из
приведенной таблицы видно, что численное решение по времени двумерной
кинетической задачи близко к аналитическому решению одномерной диффузионной
задачи в центре цилиндра, декремент затухания ![]() на асимптотике близок
к ведущему собственному числу
на асимптотике близок
к ведущему собственному числу ![]() аналитического
решения. Тем самым подтверждается предположение о совпадении этих решений,
вытекающее из теории.
аналитического
решения. Тем самым подтверждается предположение о совпадении этих решений,
вытекающее из теории.
Полученные
незначительные различия предполагается устранить путем повышения порядка
аппроксимации дополнительных пространственных соотношений в конечно-разностной
схеме на сетке из произвольных выпуклых четырехугольников, а также путем
использования более подходящего граничного условия (например, условия Маршака,
или же нулевого условия на экстраполированной границе) для одномерного
диффузионного уравнения.
6. Заключение
Результаты
тестирования предложенной методики демонстрируют высокую эффективность метода.
Дальнейшие исследования предполагается направить на повышение порядка точности
используемых схем и увеличение размерности геометрии.
7. Литература
1. А.В.
Воронков, Е.П. Сычугова. «Алгоритм решения многогруппового стационарного
уравнения переноса нейтронов и гамма - квантов на сетках, согласованных со
структурой расчетной области», Препринт ИПМ им. М.В. Келдыша, 2000 г.
2. A.
Voronkov, E. Zemskov, A. Ionkin, L. Strakhovskaya, E. Sychugova, R. Fedorenko,
A. Churbanov. «Simulation of neutron physical and thermal hydraulic processes
in nuclear reactors», Proceedings International Conference on the Physics of
Nuclear Science and Technology, October 5-8, 1998, New York, Vol. 1, p. 604 -
611.
3. Е.А.
Земсков. «Некоторые алгоритмы пространственной кинетики ядерного реактора в ( r ) - геометрии. Программа
расчета нестационарной системы диффузионных уравнений RKIN. Отчет ФЭИ, №5803, г. Обнинск,
1989 г.
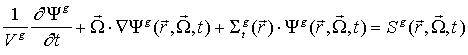
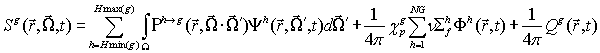 (2)
(2)