Низкий штабель
Высокий штабель
Представлен метод преодоления шестиногим роботом (ШР) препятствия в виде штабеля из трех цилиндров разного радиуса, два из которых лежат на горизонтальной плоскости, а третий цилиндр лежит сверху на указанных двух. На цилиндры действуют сила тяжести, сухое трение и трение качения. Найдены условия равновесия системы под действием внешней силы, возникающей из-за опоры ШР на систему цилиндров. С привлечением средств компьютерного моделирования разработан алгоритм преодоления штабеля, не разрушающего структуру препятствия. Приводятся результаты численных экспериментов и соответствующие видеоматериалы.
Ключевые слова: шестиногий робот, штабель, шероховатые цилиндры, преодоление препятствий, компьютерное моделирование
Abstract
Yury Filippovich Golubev, Victor Vladimirovich Koryanov
Overcoming a stack of rough cylinders by a six-legged robot
A method has been developed for overcoming obstacles in the form of a stack of rough cylinders of different radii by a six-legged robot. Two of the cylinders are lying on a horizontal plane and the third one is lying on the two mentioned above. The cylinders are under the influence of gravity, dry friction, and rolling friction. The equilibrium conditions of the system were found when the system is under the influence of a force due to the support of the robot on the system of cylinders. Using computer modeling tools, an algorithm for overcoming the stack that does not destroy the structure of the obstacle was developed. The results of numerical experiments and corresponding video materials are presented.
Key words: six-legged robot, stack, rough cylinders, overcoming obstacles, computer simulation
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (РФФИ: 19-01-00123).
Введение
В работе [] показано, что шагающие машины и, в частности, инсектоморфные роботы, имея достаточно развитую кинематику конечностей относительно корпуса, теоретически могут успешно преодолевать весьма сложные препятствия. Встречающиеся в естественной среде завалы из стволов деревьев бывают очень разнообразны []. Применение для повышения надежности опоры в стопах ног аппарата таких специальных средств, как вакуумные присоски, магнитные контактные устройства и средства химической адгезии [, , ], представляется в рассматриваемом случае нецелесообразным. В наиболее естественном варианте взаимодействия с опорой робот контактирует с ней стопами ног, и в точках контакта возникает сила сухого трения. Особенность преодоления завалов состоит в том, что робот, наступая на отдельные предметы и создавая дополнительную нагрузку на опору, может ее разрушить. Поэтому проблемы выбора опорных точек на бревнах и направлений опорных усилий в процессе преодоления препятствия требуют специального исследования. Часто можно встретить завалы из отдельных стволов деревьев. Простейший вариант этой задачи, когда деревья были представлены круговыми шероховатыми параллельными цилиндрами, причем каждый из них лежит на опорной горизонтальной плоскости, был рассмотрен в [, ].
Более сложные варианты завалов возникают, когда стволы деревьев лежат друг на друге. Один из вариантов получается, когда два цилиндра в произвольном положении лежат на опорной плоскости, а третий цилиндр лежит на них поперек. Если радиусы цилиндров, лежащих на плоскости равны, то такая система цилиндров будет в безразличном равновесии. Исследование ее движения в предположении, что все контакты системы абсолютно шероховаты, известно как задача А.Ю. Ишлинского. Уравнения движения для этой задачи были получены в [] в виде уравнений Лагранжа с множителями. Из них как частный случай можно получить и условия равновесия системы. В [, ] исследованы некоторые свойства движений такой системы. Вместе с тем предположение об абсолютной шероховатости контактов цилиндров является слишком сильным для анализа возможности опоры о препятствие. Кроме того, если радиусы цилиндров, лежащих на плоскости, не равны, то равновесие системы достигается лишь в некоторых отдельных ее конфигурациях. Одна из таких конфигураций образуется тремя параллельными цилиндрами, два из которых лежат на плоскости, а третий лежит на них и образует подобие штабеля.
Равновесие штабеля и возможность его использования в качестве опоры для шагающего робота будут исследоваться в предположении, что сухое трение и трение качения в контактах системы ограничены. Предлагаемый препринт развивает результаты работ [, , , , , , ] и увеличивает набор препятствий, которые инсектоморфный робот теоретически может преодолеть. В препринте рассматривается следующая локомоционная задача. На горизонтальной плоскости лежит штабель из трех параллельных прямых круговых шероховатых цилиндров. Первоначально робот движется в направлении, перпендикулярном осям цилиндров. В общем случае он не видит участок опорной плоскости за препятствием. Если в процессе движения робота будет установлено, что опорная плоскость за препятствием непосредственно по курсу движения робота непригодна для наступания, то робот, находясь на препятствии, должен изменить свое положение на нем, так чтобы спуститься с препятствия в доступном для опоры месте. В статье представлен конструктивно построенный алгоритм решения сформулированной задачи. Этот алгоритм был отработан на программном комплексе «Универсальный механизм» [] с учетом полной динамики системы в целом. Представленные результаты компьютерного моделирования свидетельствуют о принципиальной реализуемости предложенного алгоритма. Полная динамическая модель робота формируется автоматически средствами комплекса «Универсальный механизм» [].
Равновесие штабеля из трех цилиндров
Рассмотрим вариант препятствия, моделирующего совокупность трех бревен, расположенных на горизонтальной плоскости параллельно друг другу так, что одно бревно лежит на двух других. Для простоты пусть это будут однородные шероховатые прямые круговые цилиндры разного радиуса. Вид торцевого сечения такой системы цилиндров вертикальной плоскостью, перпендикулярной осям цилиндров, представлен на рис. . Радиусы цилиндров, лежащих на горизонтальной плоскости, обозначим $r_1$ и $r_2$. Для определенности будем считать, что $r_1\ge r_2$. Радиус цилиндра, лежащего на двух других, обозначим $r_3$. Центры окружностей торцевых сечений цилиндров обозначим $O_1$, $O_2$, $O_3$ соответственно. К некоторой точке $B$ верхнего цилиндра приложим силу $\bf F$. Выберем абсолютную декартову систему координат $A_1\xi\eta\zeta$. Начало координат $A_1$ поместим в точку соприкосновения торцевой окружности радиуса $r_1$ с опорной плоскостью, ось $A_1\eta$ направим в сторону точки $A_2$ соприкосновения торцевой окружности радиуса $r_2$, ось $A_1\zeta$ направим вертикально вверх, ось $A_1\xi$ дополняет систему координат до правоориентированной. Расстояние между точками $A_1$ и $A_2$ обозначим буквой $d$. Расстояние между центрами $O_1$ и $O_2$ окружностей, касающихся оси $A_1\eta$, обозначим буквой $\lambda=\sqrt{d^2+(r_1-r_2)^2}$. Возьмем вспомогательную декартову систему координат $O_1xyz$. Ось $O_1y$ пустим вдоль линии центров от точки $O_1$ к точке $O_2$, ось $O_1z$ направим вверх в вертикальной плоскости. Ось $O_1x$ будет сонаправлена с осью $A_1\xi$ (рис. ).
Точка $O_3$ принадлежит пересечению двух окружностей. Одна из них имеет центр $O_1$ и радиус $R_1=r_1+r_3$, а другая имеет центр $O_2$ и радиус ${R_2=r_2+r_3}$. Найдем координаты $(y_3,z_3)$ точки $O_3$, как решение следующей системы уравнений.
Эта система имеет два решения. Из них следует выбрать решение с положительным значением координаты $z_3$:
В осях $A_1\xi\eta \zeta$ координаты $(\eta_3,\zeta_3)$ точки $O_3$ выражаются следующим образом
Когда нижние цилиндры касаются, имеем $\lambda=r_1+r_2$ и ${d=2\sqrt{r_1r_2}}$, а формулы
Рассмотрим условия равновесия системы. Пусть активная сила ${\bf F}=(F_\eta,F_\zeta)$ приложена к точке верхнего цилиндра, заданной центральным углом $\varphi$, отсчитываемым от вертикального радиуса этого цилиндра, направленного вверх. Координата этой точки вдоль оси $A_1\xi$, так же как и активная составляющая $F_\xi$ силы $\bf F$, для рассматриваемой задачи значения не имеют из-за того, что цилиндры в дальнейшем предполагаются достаточно протяженными.
Рассмотрим случай, когда $d>2\sqrt{r_1r_2}$, то есть нижние цилиндры не находятся в соприкосновении. Обозначим ${\bf N}_1=(N_{1\eta},N_{1\zeta})$, ${\bf N}_2=(N_{2\eta},N_{2\zeta})$ неизвестные реакции опоры в точках $A_1$ и $A_2$ соответственно. Уравнения равновесия системы в целом в осях координат $A_1\eta\zeta$ имеют вид
Первые два уравнения системы
где
суть моменты силы $\bf F$ относительно точек $A_1$ и $A_2$ соответственно.
Для того чтобы найти горизонтальные составляющие, рассмотрим уравнения равновесия нижних цилиндров. Обозначим ${\bf Q}_1=(Q_{1\eta},Q_{1\zeta})$ нормальную составляющую силы, действующей со стороны верхнего цилиндра на первый цилиндр, а ${\bf T}_1=(T_{1\eta},T_{1\zeta})$ $-$ касательную составляющую той же силы:
где $Q_1$ $-$ величина нормальной (со знаком), $T_1$ $-$ величина касательной (со знаком) составляющих силы в точке касания первого и третьего цилиндров. Уравнения равновесия первого цилиндра примут вид
где третье уравнение выражает равенство нулю момента всех сил, действующих на первый цилиндр, относительно его оси. Отсюда находим
где
Напишем условия равновесия второго цилиндра. Пусть ${\bf Q}_2=(Q_{2\eta},Q_{2\zeta})$ $-$ нормальная составляющая силы, действующей со стороны верхнего цилиндра на второй цилиндр, а ${\bf T}_2=(T_{2\eta},T_{2\zeta})$ $-$ касательная составляющая той же силы:
где $Q_2$ $-$ величина нормальной, $T_2$ $-$ величина касательной составляющих силы в точке касания второго и третьего цилиндров. Уравнения равновесия второго цилиндра примут вид
где третье уравнение выражает равенство нулю момента всех сил, действующих на второй цилиндр, относительно его оси. Отсюда
где
Условия, которым должны удовлетворять реакции связей в точках контакта шероховатых односторонних поверхностей, имеют вид
где $k$ $-$ коэффициент сухого кулоновского трения.
Проанализируем сначала формулы
Равновесие должно быть как в случае, когда $M_2=0$ (то есть робот еще не наступил на верхнее бревно), так и в случае, когда $M_2\ne 0$. Поскольку должно быть $Q_1\le 0$, то при указанных условиях равенство
Ограничение по трению на линии контакта первого и третьего цилиндров, а также на линии контакта первого цилиндра с опорной плоскостью приводит к неравенствам
где $k$ $-$ коэффициент сухого кулоновского трения. Приняв во внимание второе неравенство
Аналогично проанализируем формулы
Равновесие должно быть как в случае, когда $M_1=0$ (то есть робот еще не наступил на верхнее бревно), так и в случае, когда $M_1\ne 0$. Поскольку должно быть $Q_2\le 0$, то при указанных условиях равенство
Ограничение по трению на линии контакта второго и третьего цилиндров, а также на линии контакта второго цилиндра с опорной плоскостью приводит к неравенствам
Приняв во внимание второе неравенство
Из неравенств
где $\eta$ $-$ координата точки пересечения линии действия силы $\bf F$ с осью $O\eta$. Поскольку речь идет о возможности опоры шагающего аппарата о верхний цилиндр, следует принять $F_\zeta<0$. Поэтому если
то ограничения на моменты в формуле
Примем во внимание ограничения по трению в точках касания цилиндров друг с другом. Из первых неравенств в формулах
что возможно, лишь если высота препятствия $\zeta_3+r_3\ge d/(2k)$.
Рассмотрим ограничения по трению в точках $A_1$ и $A_2$. Заметим, что при выполнении первого из неравенств
Кроме того, при отсутствии силы $\bf F$ должно быть выполнено $N_{1\eta}=-N_{2\eta}$. Поэтому критичной в смысле нарушения ограничения по трению будет та точка опоры $A_i$, ${i=1,2}$, для которой вертикальная нагрузка окажется меньше.
При действии силы $\bf F$ ограничения по трению примут вид
Поскольку $M_1=F_{\zeta}\eta$, $M_2=F_{\zeta}(\eta-d)$, $0\le\eta\le d$ и $F_\zeta\le 0$, видим, что при действии силы $F_{\zeta}$ левые части неравенств
За счет выбора координаты $\eta$ можно регулировать нагрузку на точки $A_1$ и $A_2$ с тем, чтобы уравнять глубину погружения реакций в соответствующие конусы трения. Для этого достаточно найти решение уравнения
относительно $\eta$. Уравнение
В случае, когда $r_1=r_2$, оказывается, что $a_1=a_2$ и $\eta_3=d/2$, а уравнение
Отсюда при $F_\zeta\ne 0$ с учетом того, что $0\le\eta\le d$, получим
Если при этом окажется, что $m_1=m_2$, то получим $\eta=0.5$. Отсюда ясно, что если цилиндры, лежащие на опорной плоскости, имеют приблизительно равные радиусы и массы, то для сохранения устойчивости опорной конструкции силу в опорной точке следует направить в середину опорного отрезка $[0,d]$.
В качестве итога проведенного исследования можно сформулировать следующие рекомендации, касающиеся поведения робота при преодолении завала из бревен.
1. Препятствие в виде штабеля из трех бревен устойчиво, если высота препятствия больше половины основания, деленного на коэффициент сухого трения (см. формулу
2. Если в основании штабеля лежат приблизительно одинаковые бревна, то линия действия силы в точке опоры робота о верхнее бревно должна проходить приблизительно через середину основания препятствия. При необходимости уменьшения опасности проскальзывания какого-либо нижнего цилиндра силу, действующую со стороны ног на верхний цилиндр, следует направлять ближе к точке опоры другого нижнего цилиндра.
Дополнительно отметим, что система цилиндров, изображенная на рис. , имеет принципиальную возможность катиться без нарушения своей конфигурации вдоль опорной плоскости []. Для этого достаточно выбрать
где $\omega_1$, $\omega_2$, $\omega_3$ $-$ соответственно угловые скорости цилиндров, а $v$ $-$ скорость движения центра масс системы. Если система цилиндров до опоры шагающего аппарата была неподвижной, то при выполнении рассмотренных выше условий равновесия, предполагающих равенство нулю силовых моментов, равновесие при опоре о нее робота не нарушится, и система останется неподвижной. Наличие в точках контакта трения качения создает некоторую дополнительную гарантию надежности опоры.
Механическая модель системы
Конструкция робота совпадает с принятой в []. Твердый корпус робота имеет форму прямоугольного параллелепипеда массы $m$, $a$ $-$ его боковая сторона (длина), $b$ $-$ передний или задний край (ширина), $c$ $-$ высота параллелепипеда. По бокам корпуса симметрично прикреплены шесть одинаковых инсектоморфных ног. Точки прикрепления ног с каждой стороны корпуса расположены на одинаковом расстоянии друг от друга. Отдельная нога состоит из двух твердых звеньев: бедра длины $l_1$, массы $m_1$ и голени длины $l_2$, массы $m_2$. Допускается касание роботом поверхности опоры и окружающих предметов только стопами, ноги робота не должны иметь взаимных пересечений во все время движения.
Программные значения шарнирных углов генерируются алгоритмом управления с учетом информации о реализовавшейся конфигурации робота при его движении. Реализация программных значений шарнирных углов осуществляется так же, как в [], с помощью простейшей модели электроприводов с самоиндукцией. Предполагается, что роботу известны: собственное положение относительно препятствий, несущая способность участков поверхности, выбираемых для опоры, шарнирные углы, скорости перемещения как самого робота, так и объектов, выбираемых для опоры.
Цилиндры, образующие препятствия, могут свободно перекатываться по плоскости и друг по другу. На них действует сухое кулоновское трение и трение качения. Если какие-нибудь реакции выходят за ограничивающие их пределы, то возникает соответствующее проскальзывание.
Траектории переносов ног формируются в виде плоских шаговых циклов [, ], адаптируемых в зависимости от поверхностей препятствий, скорости движения робота, предписанных следовых точек. Движения ног, соответствующие шаговым циклам, сглаживаются, чтобы сохранить непрерывность, как самого движения, так и его скорости [].
Наличие силового момента в опорных точках не предполагается. Реакции в них должны удовлетворять условию малой деформации опорной поверхности и должны принадлежать конусам кулоновского трения с заданным коэффициентом []. Коэффициент трения при контактах стоп ног с цилиндрами предполагается равным единице. Контакты цилиндров друг с другом могут иметь иные характеристики. Программное движение создается в виде последовательности событий, в начале каждого из которых в некоторой абсолютной системе координат $O\xi\eta\zeta$ определяются траектории перемещений стоп и точек их крепления к корпусу.
Постановки задачи
Решаемая задача формулируется следующим образом. Шестиногий робот идет вдоль прямолинейной трассы по горизонтальной плоскости походкой «трешки». Поперек трассы под прямым углом к ней расположены три цилиндра разных радиусов, уложенные в виде штабеля. Расстояния между центрами цилиндров удовлетворяют неравенству треугольника. Штабель устойчивый, так что центр верхнего цилиндра проектируется на горизонтальную плоскость между проекциями центров нижних цилиндров на ту же плоскость. Цилиндры могут свободно катиться по опорной плоскости и при возможности друг по другу. Если нижние цилиндры не соприкасаются, то система цилиндров может свободно перемещаться вдоль опорной плоскости как единое целое, когда угловые скорости нижних и верхнего цилиндров удовлетворяют соотношению
Из-за неустойчивости системы в целом последовательность действий робота будет зависеть от высоты преодолеваемого штабеля. В дальнейшем будут рассмотрены два варианта. В первом из них (низкий штабель) высота препятствия приблизительно совпадает с маршевой высотой робота, а во втором (высокий штабель) она в полтора раза превышает маршевую высоту робота.
Преодоление препятствий
4.1. Задача «Низкий штабель». Все размеры укажем относительно длины корпуса. Радиусы цилиндров имеют следующие размеры:
Расстояние между точками опоры нижних цилиндров равно $d=0.44$, высота всего препятствия составляет $\approx\!0.7$, маршевое расстояние от корпуса до опорной поверхности равно 0.65. С такой высоты робот не видит, что находится непосредственно за препятствием. Опишем основные этапы действий робота.
Этап 4.1.1. Приблизившись к препятствию походкой «трешки», робот перестраивает положение ног для походки «галоп» и готовится к постановке передних ног на верхний цилиндр (рис. , а). На этом рисунке также отмечены оси $O\eta$, $O\zeta$.
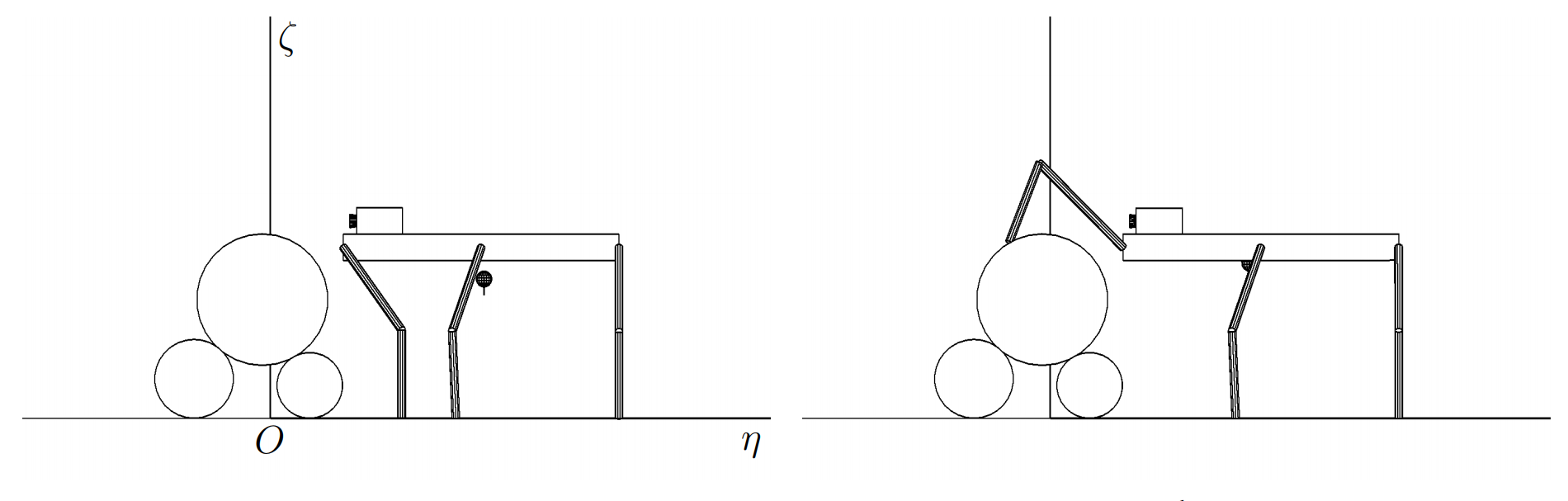
Этап 4.1.2. Передними ногами робот наступает на верхний цилиндр. Точка опоры передних ног расположена за центром верхнего цилиндра (по ходу движения корпуса робота). Такое расположение точки опоры создает силовой момент, направленный против хода часовой стрелки относительно центра верхнего цилиндра, и с учетом соотношения
Этап 4.1.3. Передняя точка корпуса (середина отрезка между точками крепления передних ног) движется по вертикальной окружности с центром на оси верхнего цилиндра и с радиусом $r_3+\sigma$, средняя точка корпуса совершает вынужденное движение по прямой, составляющей с горизонтальной осью $O\eta$ угол $-\varepsilon$ (рис. , а). Значения $\sigma$ и $\varepsilon$ выбираются так, чтобы обеспечить последующий поворот корпуса [, , ].
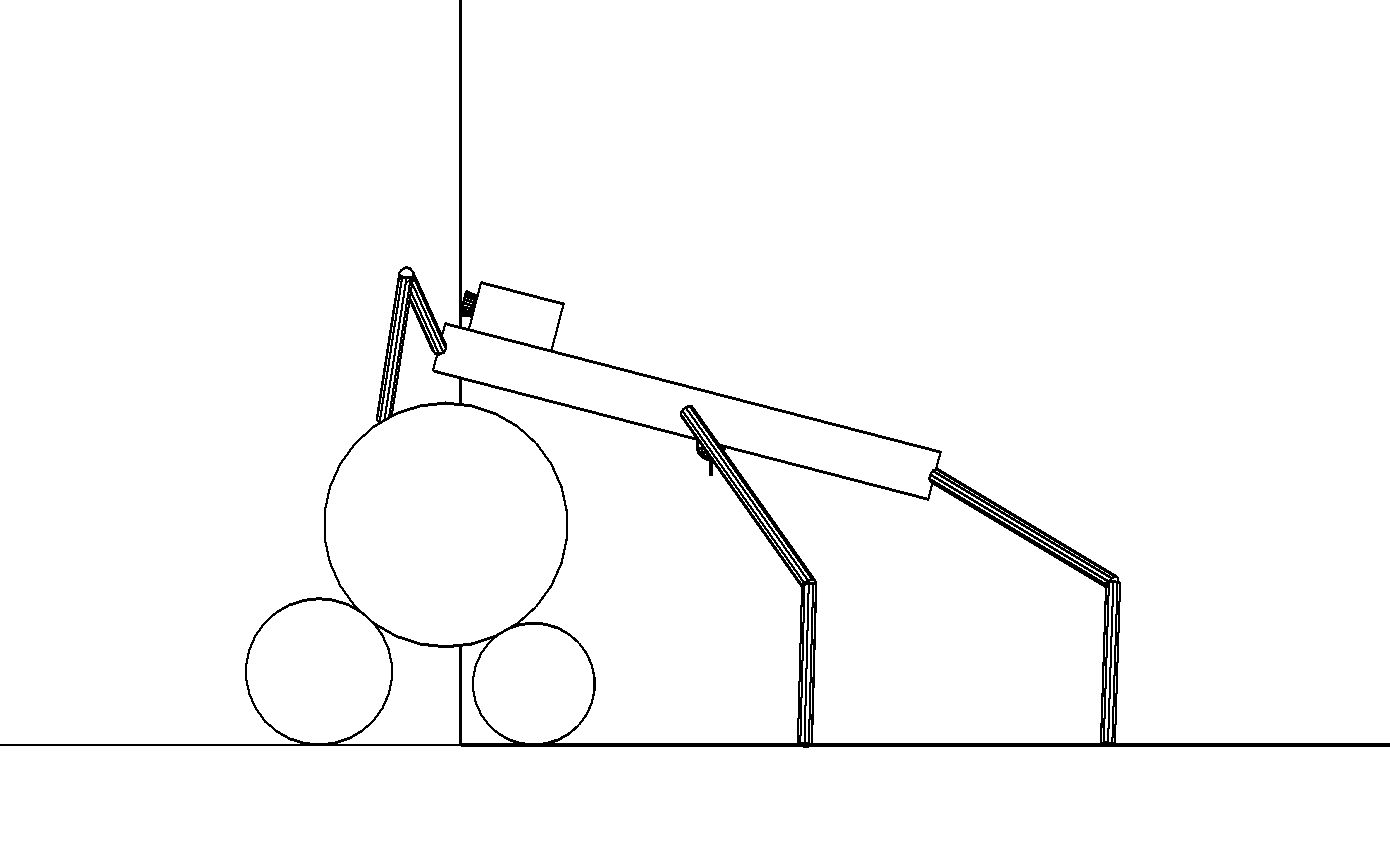
а
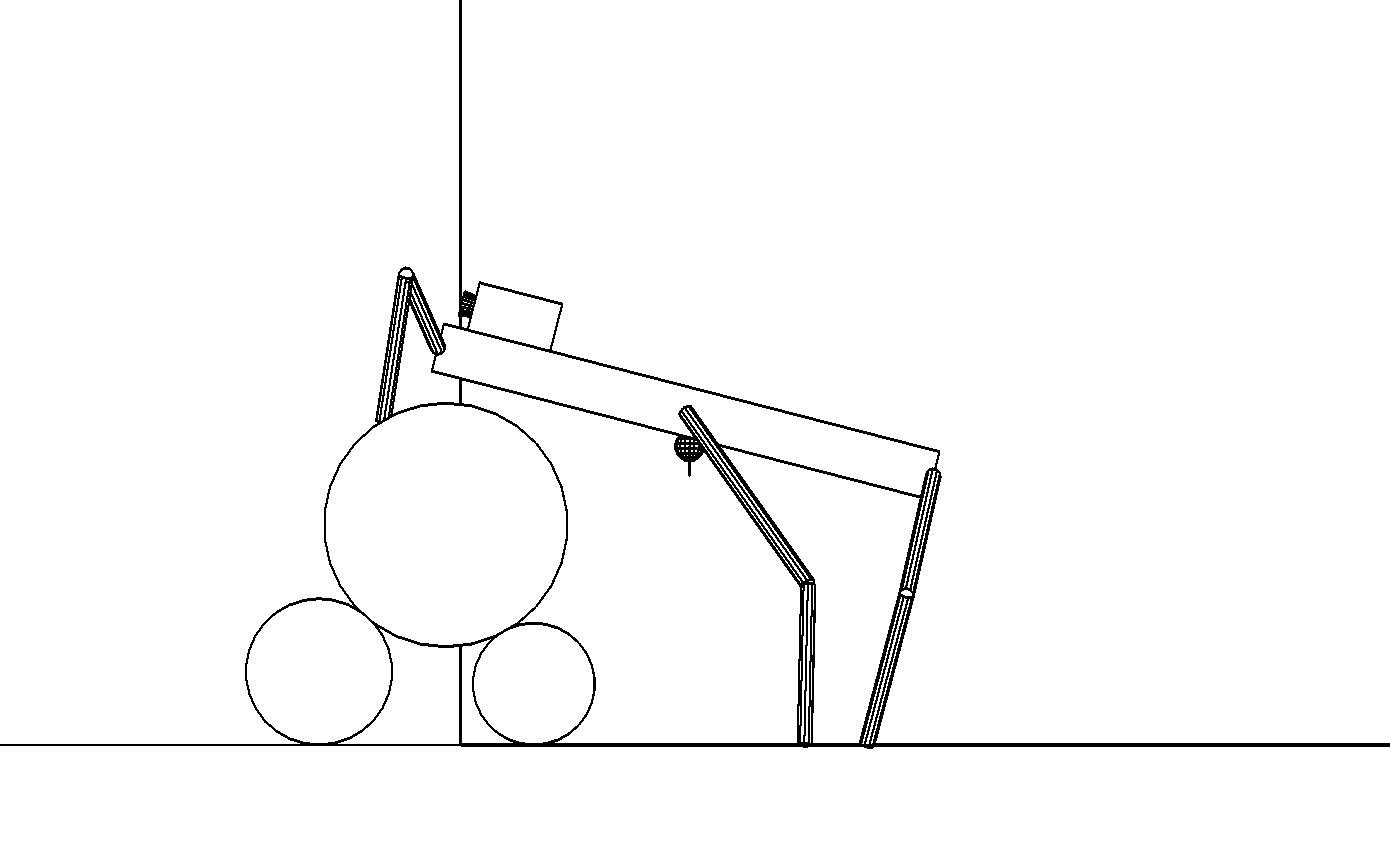
б
Этап 4.1.4. Робот переносит задние ноги в точки опоры, расположенные ближе к препятствию. Готовится перенос средних ног (рис. , б)
Этап 4.1.5. Средние ноги переносятся в точки опоры на цилиндр наименьшего радиуса (рис. , а). На этом цилиндре возможность выбора точек опоры ограничена, так как над ним нависает верхний цилиндр и создает помеху для дальнейшего движения средних ног из-за предстоящего перемещения корпуса робота.
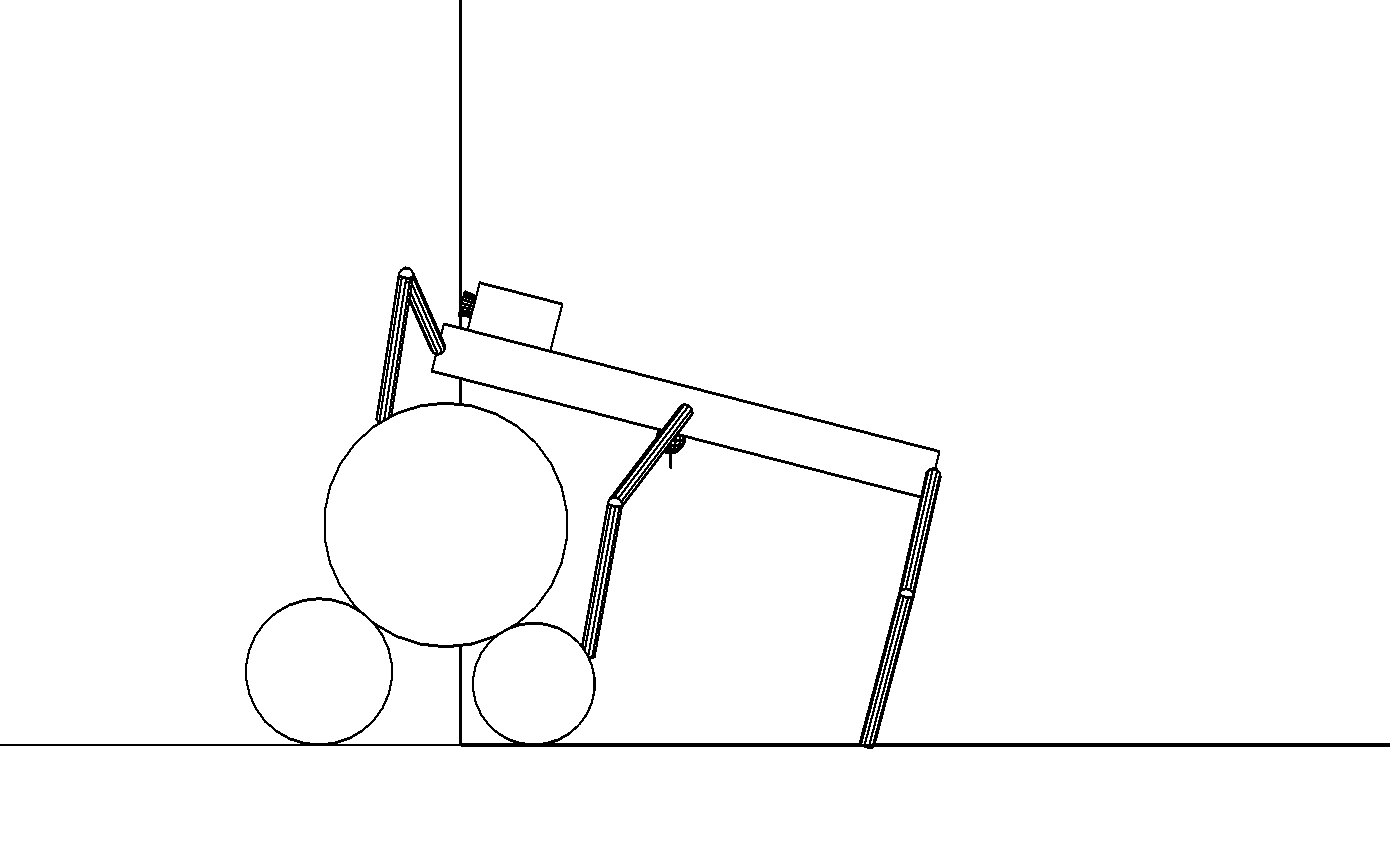
а
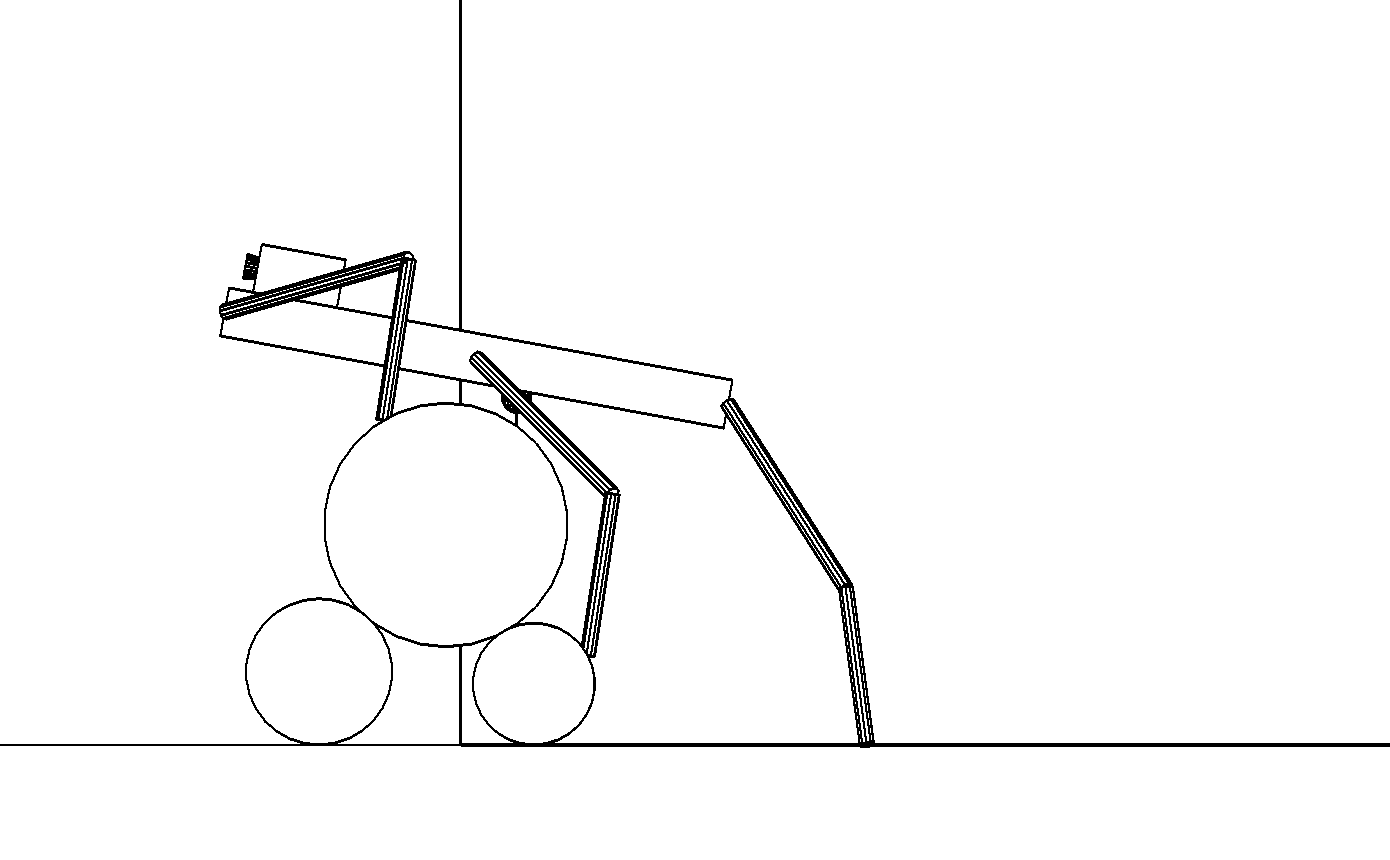
б
Этап 4.1.6. Корпус робота перемещается параллельно его боковой стороне, так чтобы центр масс робота проектировался в опорный четырехугольник, образованный точками опоры передних и средних ног. В результате движения корпуса его центр оказывается на расстоянии $r_3+\sigma$ от верхнего цилиндра, и корпус ориентирован по касательной к нему [, , ]. Готовится перенос задних ног (рис. , б).
Этап 4.1.7. Задние ноги переносятся поближе к препятствию, и осуществляется поворот корпуса против хода часовой стрелки (рис. , а).
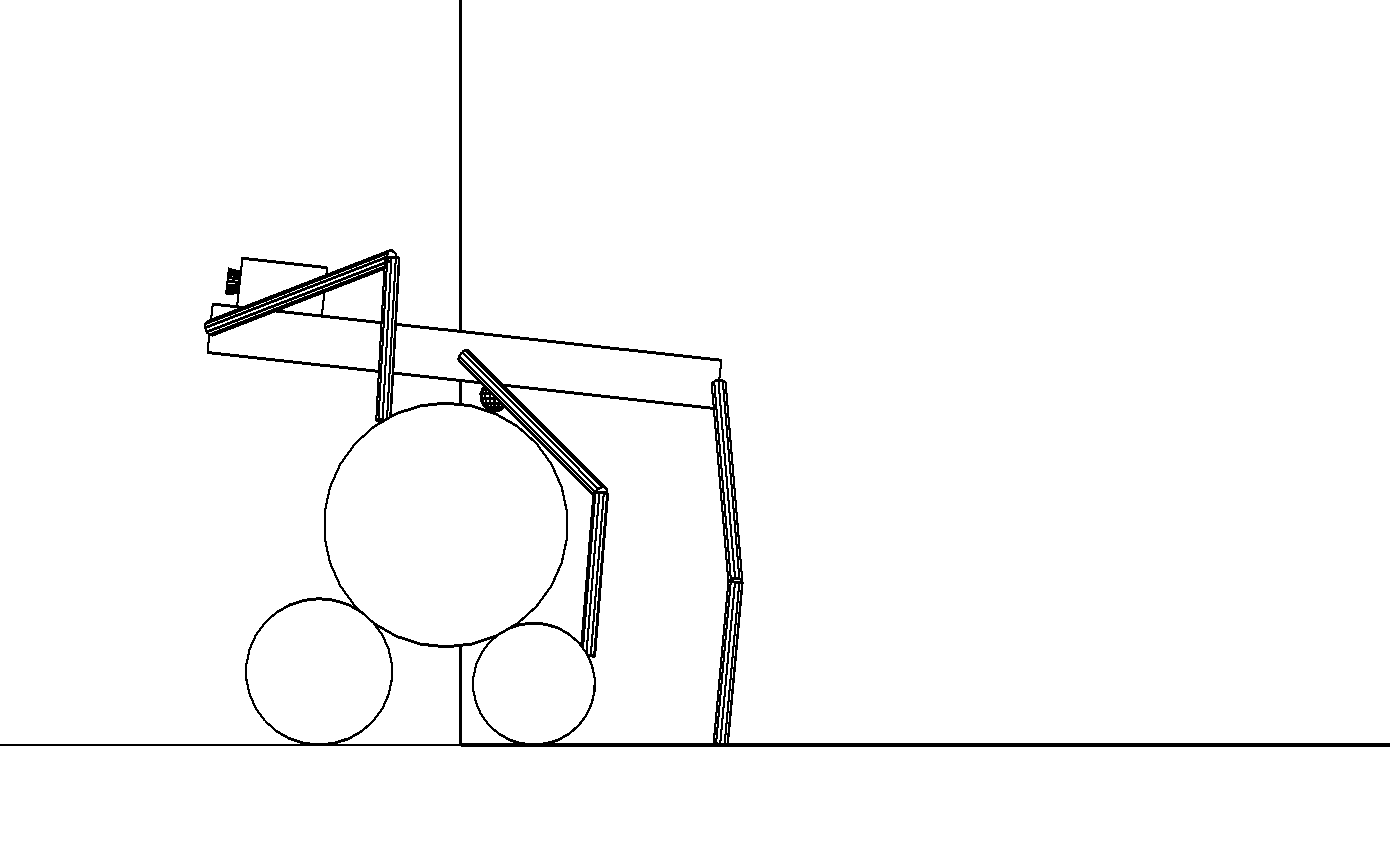
а
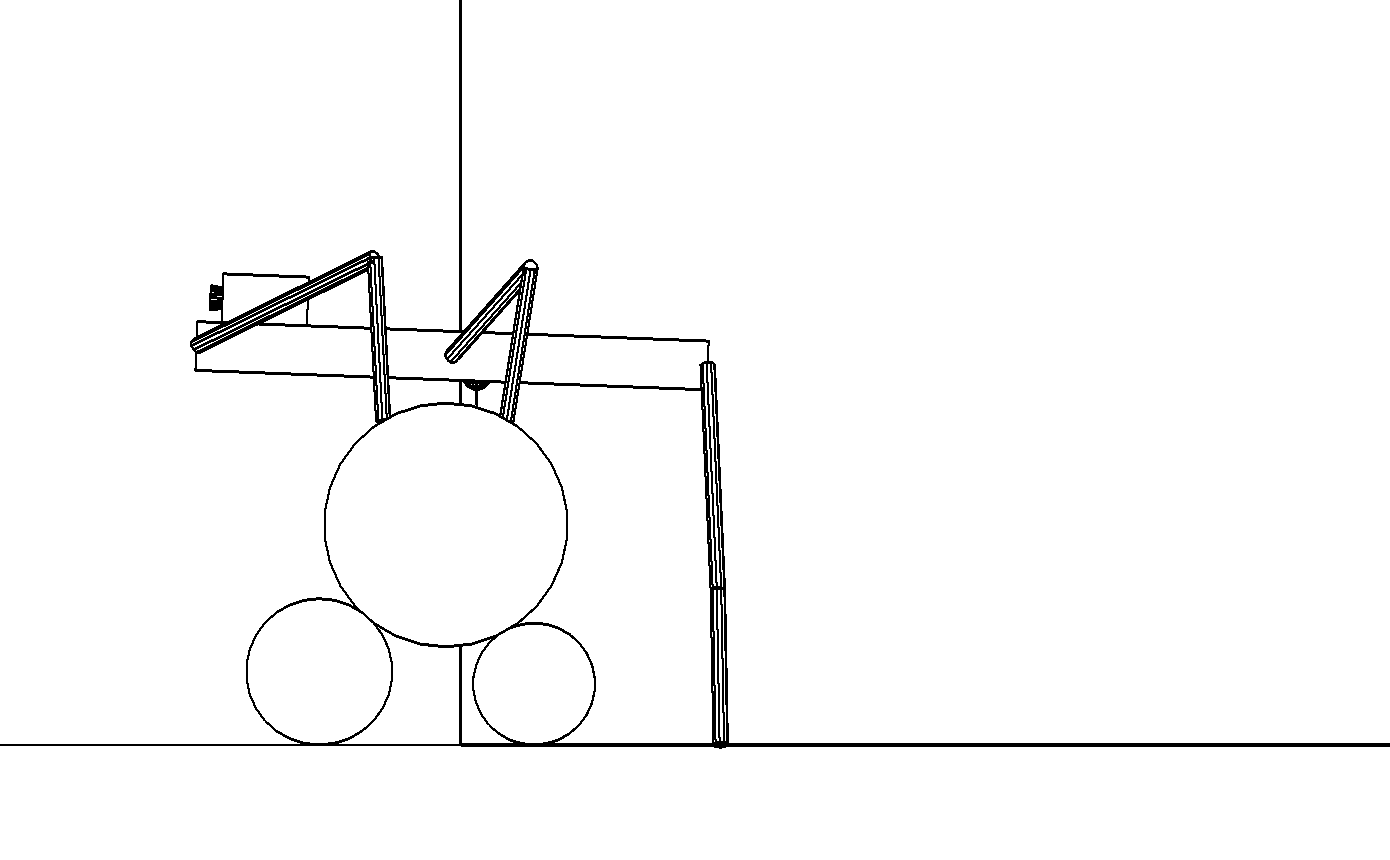
б
Этап 4.1.8. Стопы средних ног переносятся на верхний цилиндр, а корпус продолжает поворачиваться до горизонтального положения. Задние ноги почти предельно распрямлены (рис. , б).
Этап 4.1.9. Задние ноги опираются о верхний цилиндр. Корпус поднимается над препятствием и приводится в горизонтальное положение (рис. , а).

а

б
Этап 4.1.10. Средние ноги переносятся так, чтобы центр масс робота проектировался в опорный многоугольник, образованный стопами средних и задних ног (рис. , б).
Этап 4.1.11. Робот обнаруживает, что в месте предполагаемого спуска со штабеля имеется непроходимая зона. Он начинает движение вдоль штабеля походкой «трешки» (рис. , а).
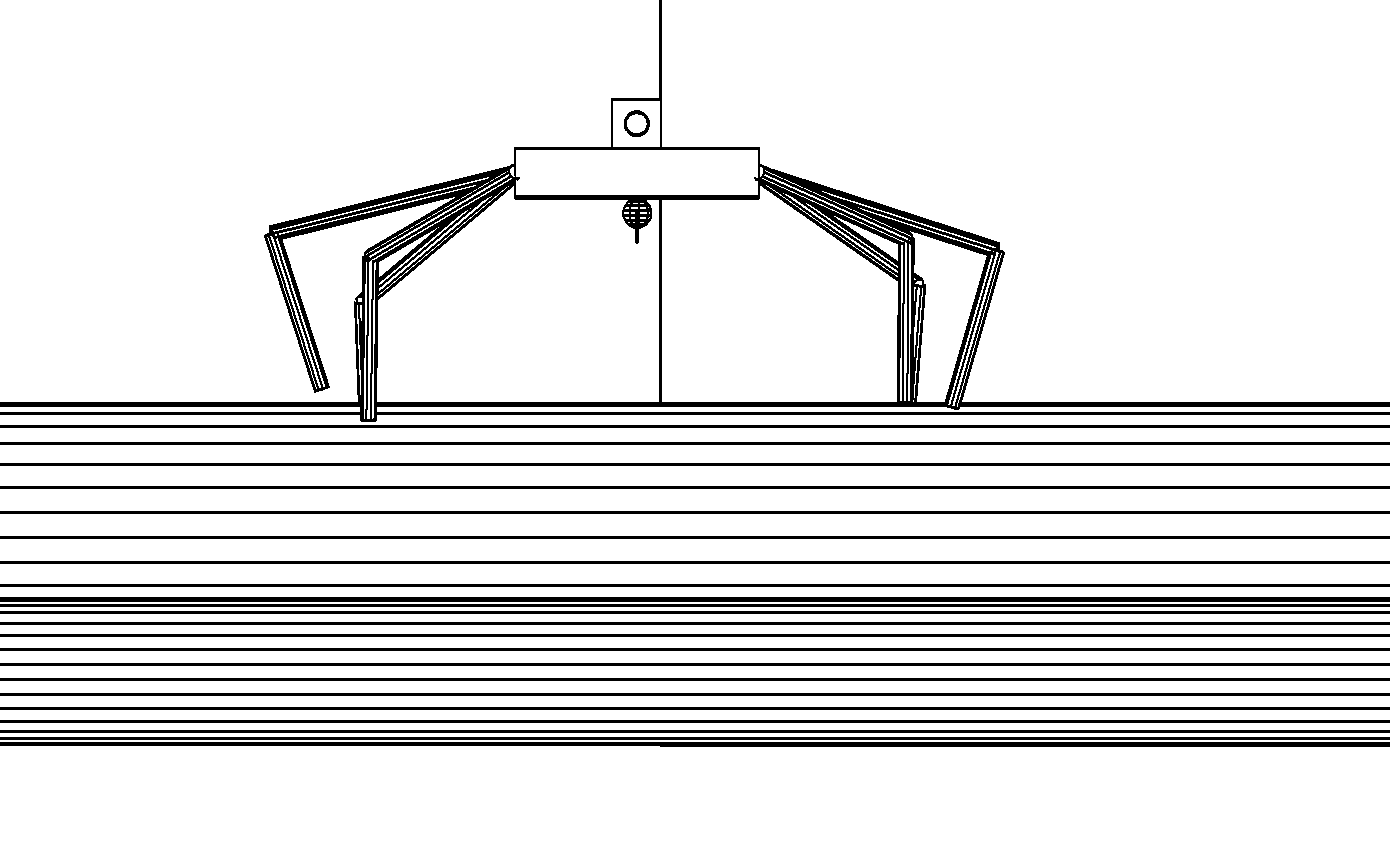
а
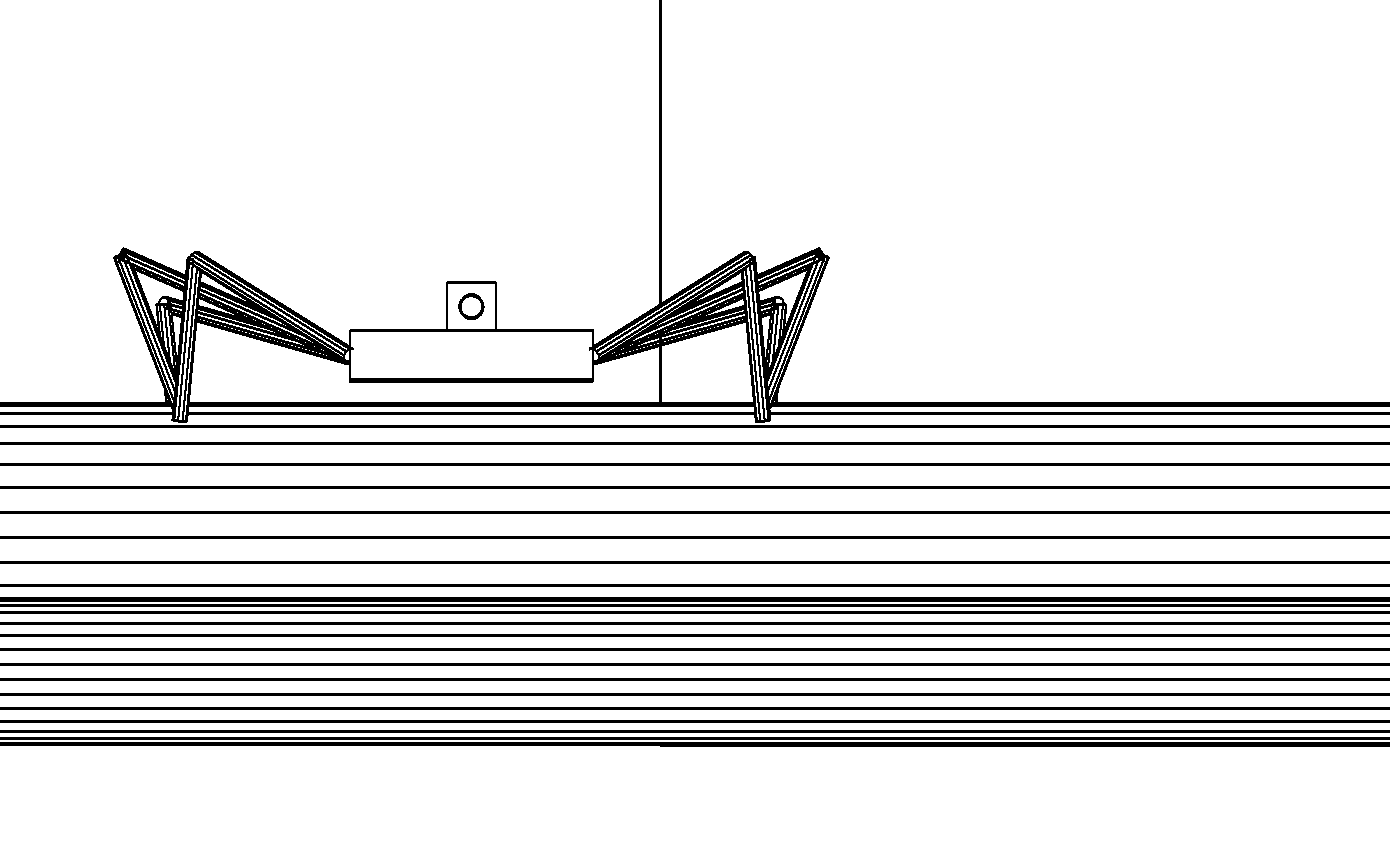
б
Этап 4.1.12. Обход непроходимой зоны закончен. Робот приседает, чтобы начать спуск со штабеля (рис. , б).
Этап 4.1.13. Робот ставит передние ноги на левый нижний цилиндр, одновременно наклоняя корпус и смещая его в направлении движения (рис. , а).
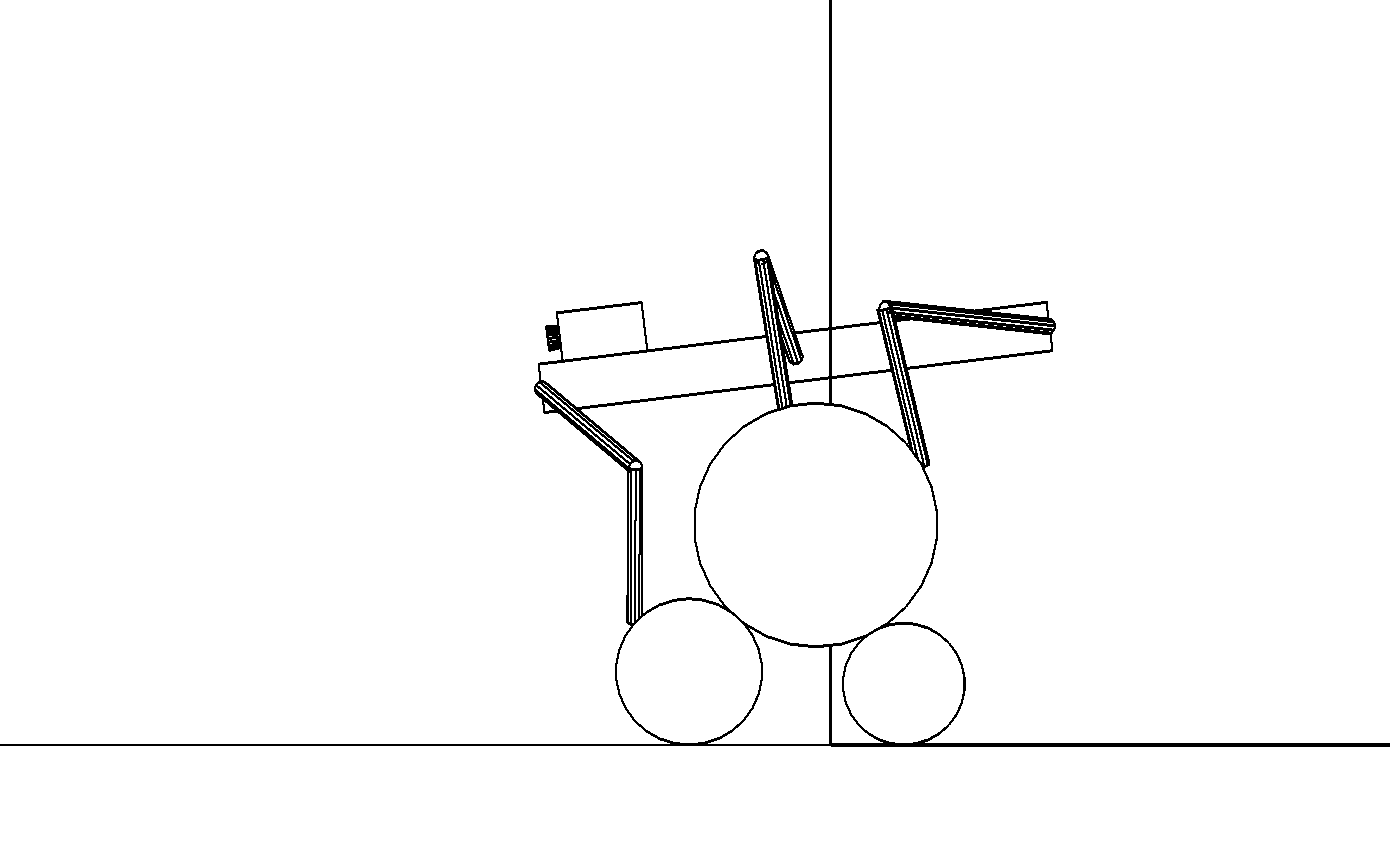
а
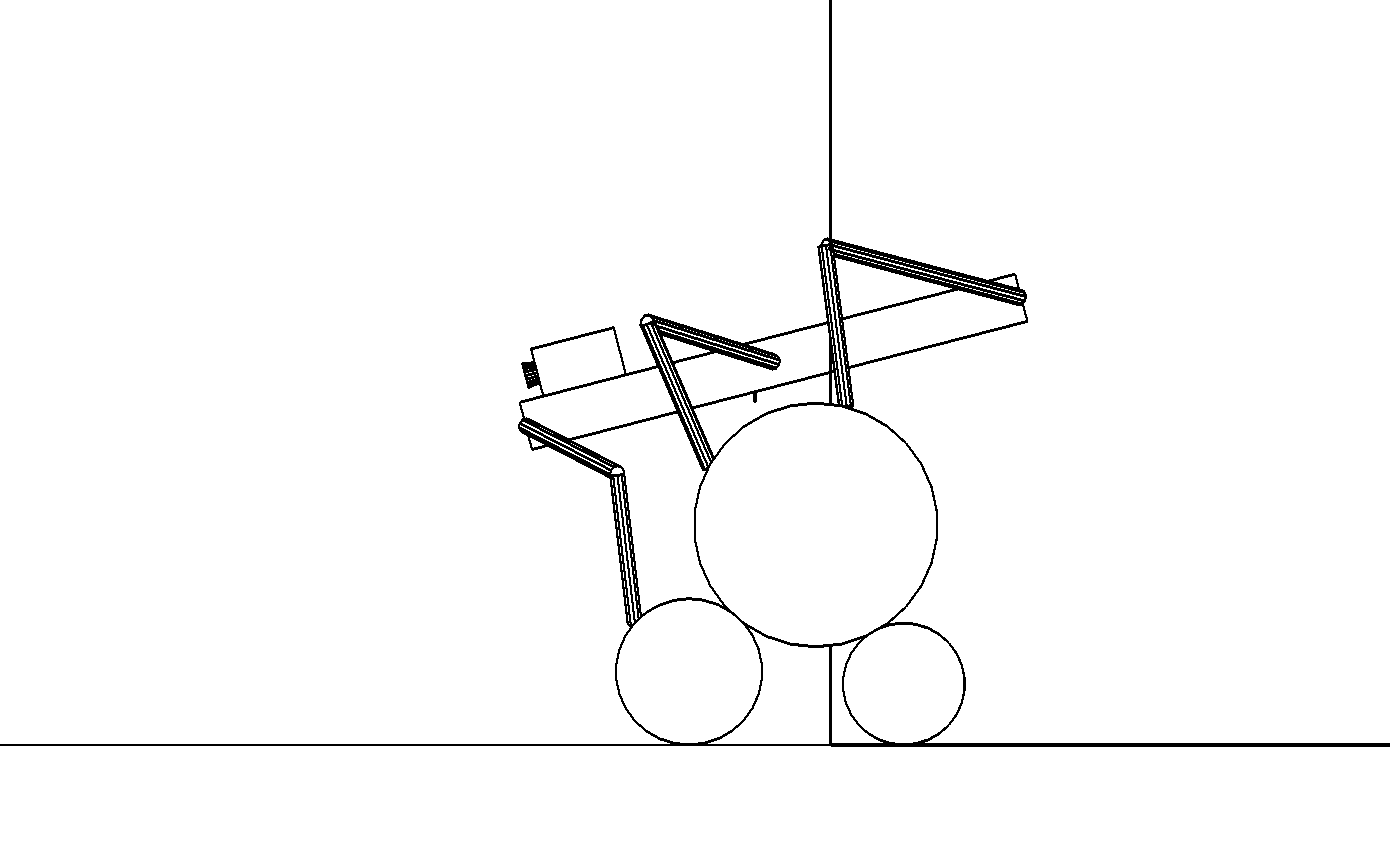
б
Этап 4.1.14. Средние ноги переносятся вперед на верхнем цилиндре с одновременным наклоном и смещением корпуса (рис. , б).
Этап 4.1.15. Передние ноги выполняют полный шаг и ставятся на опорную плоскость, а корпус продвигается вперед параллельно своей боковой стороне (рис. , а).
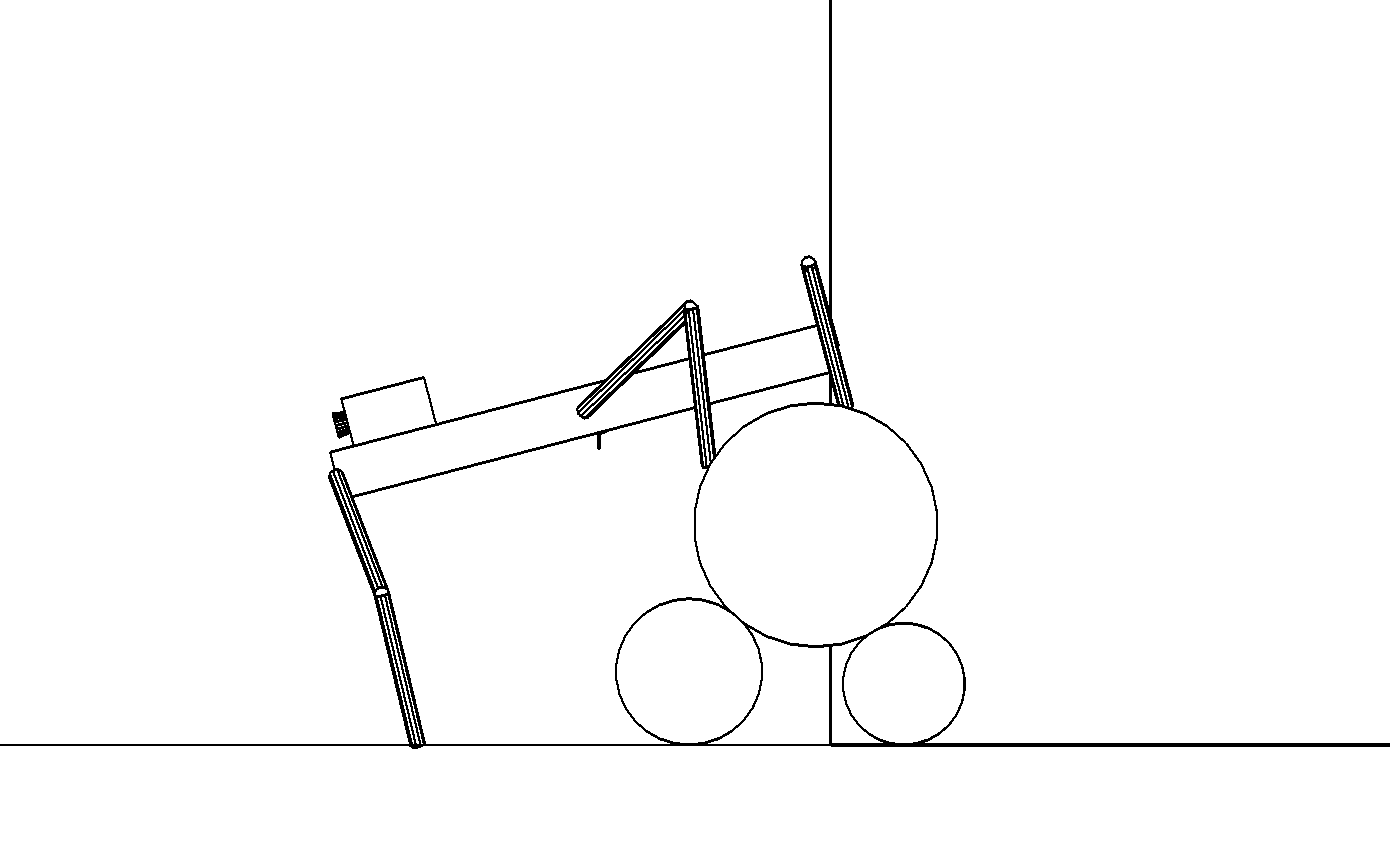
а
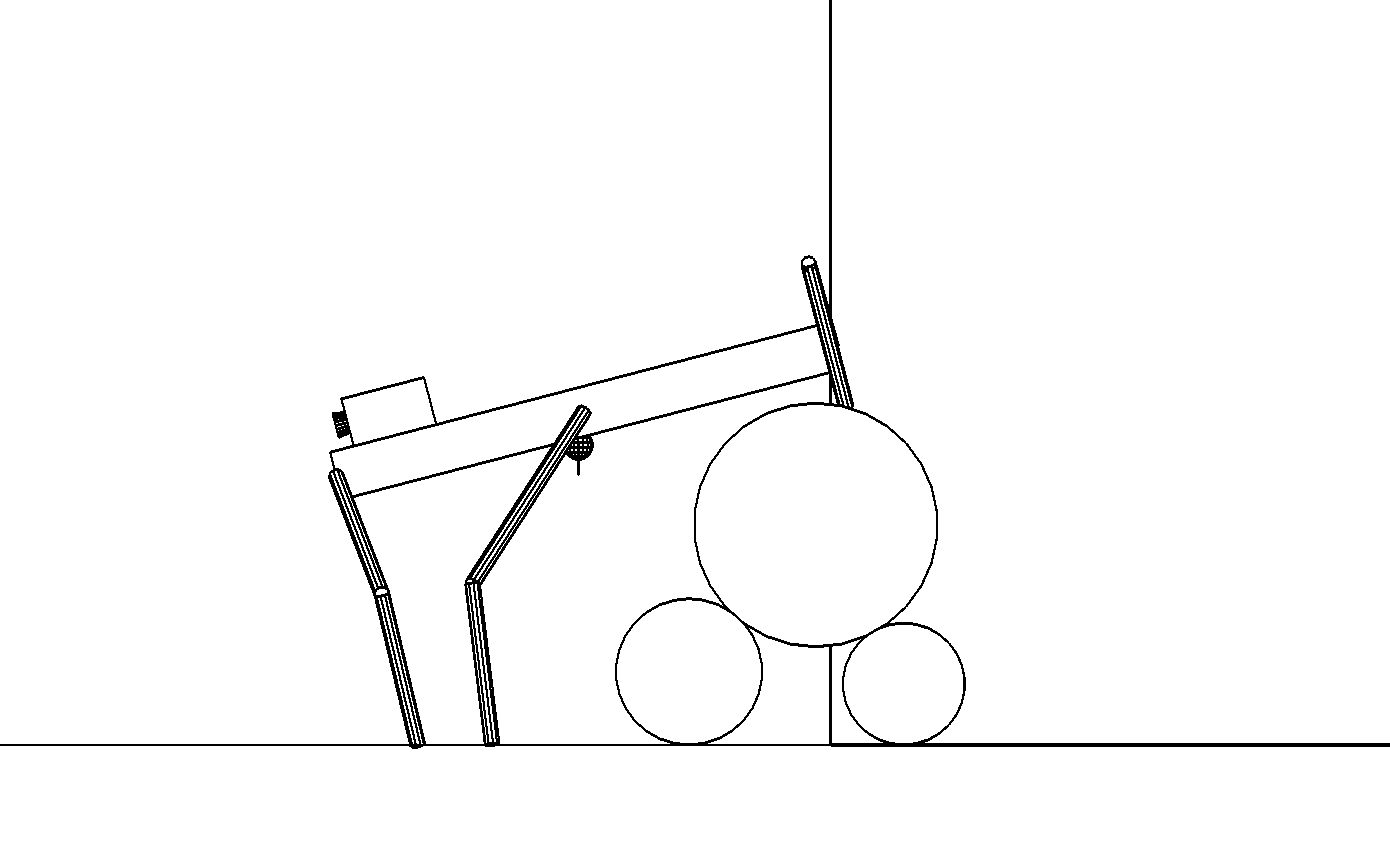
б
Этап 4.1.16. Средние ноги переносятся и ставятся на опорную плоскость вблизи точек опоры передних ног (рис. , б).
Этап 4.1.17. Передние ноги делают шаг вперед, а корпус, продвигаясь вперед, постепенно уменьшает наклон, стремясь к своему нормальному горизонтальному положению (рис. , а). Движение корпуса формируется аналогично тому, как это делалось на этапе 4.1.3 с применением необходимых зеркальных коррекций, соответствующих слезанию.
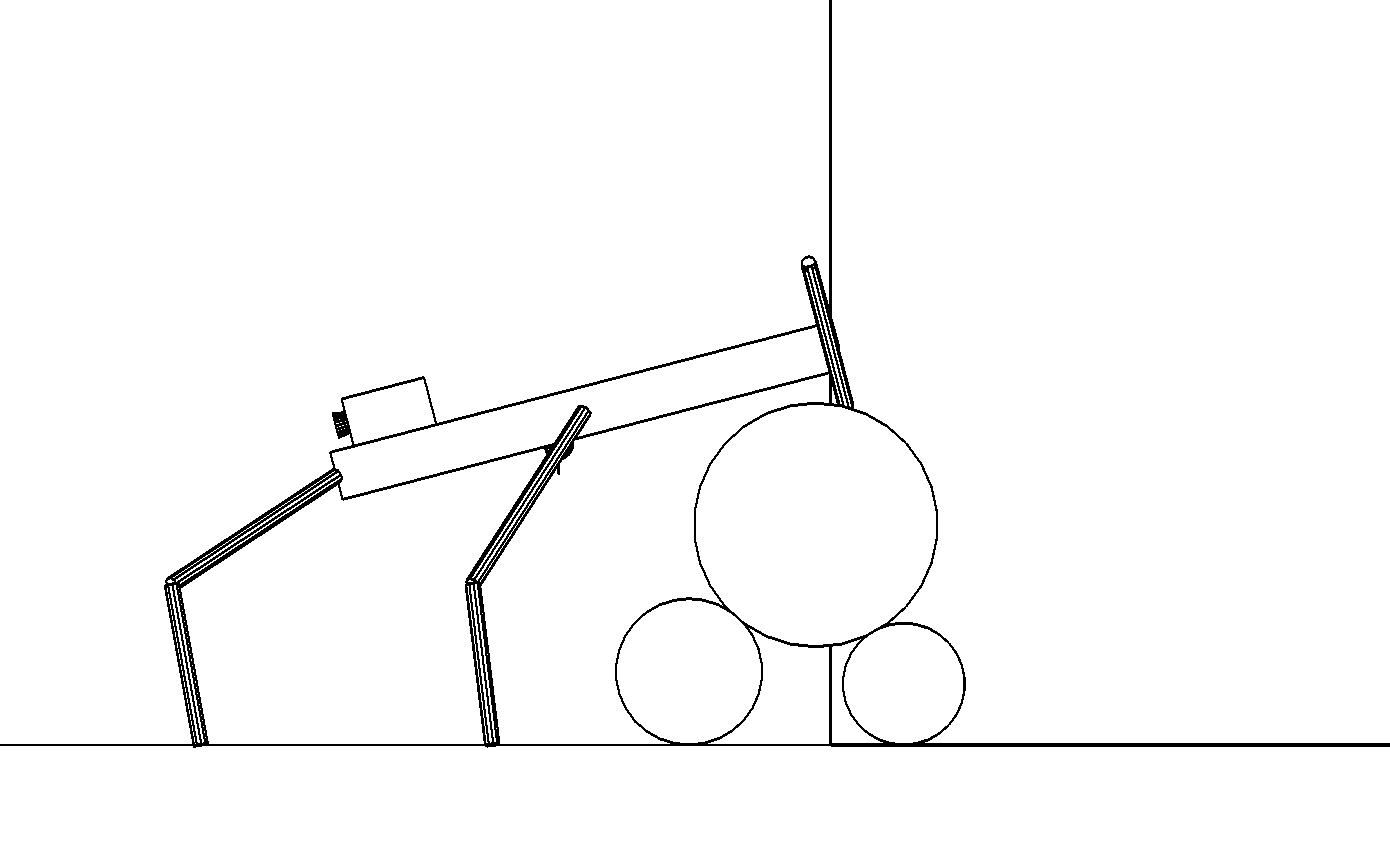
а
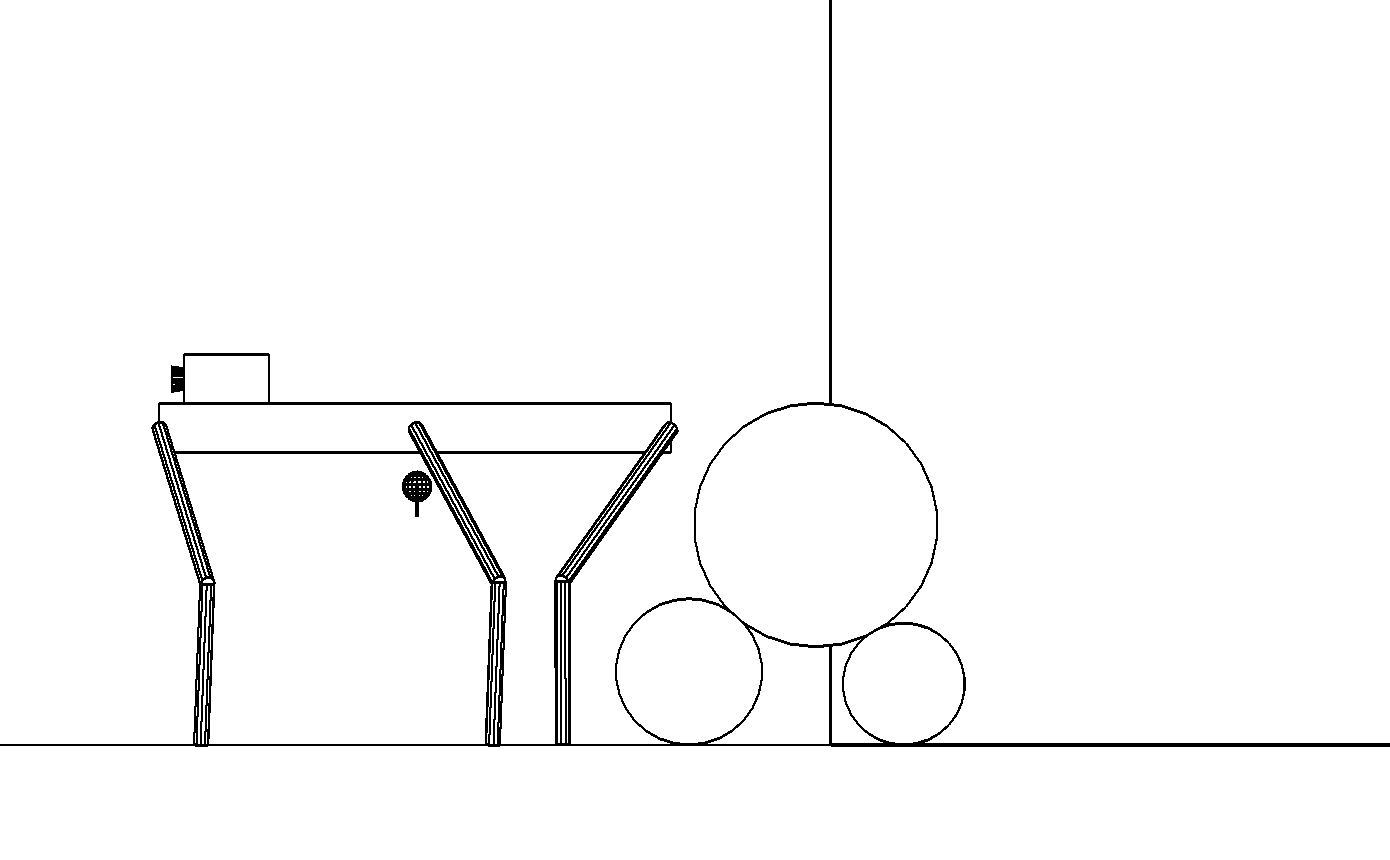
б
Этап 4.1.18. Задние ноги переносятся с верхнего цилиндра на опорную плоскость. Это завершает процесс преодоления препятствия в виде сравнительно невысокого штабеля.
В процессе компьютерного экспериментирования было принято, что коэффициент трения во всех контактах не превосходит 1, а трение качения покоя в контактах между цилиндрами, а также между цилиндрами и плоскостью отсутствует. Тем не менее в процессе маневров штабель остается на месте и представляет собой достаточно надежную опору для робота. В естественных условиях трение качения покоя всегда имеется, и оно будет увеличивать способность робота к преодолению препятствий рассмотренного типа.
4.2. Задача «Высокий штабель». Все размеры по-прежнему указываются относительно длины корпуса. Радиусы цилиндров имеют следующие размеры:
Расстояние между точками опоры нижних цилиндров равно $d=0.66$, высота всего препятствия составляет $\approx 1.05$, а маршевое расстояние от корпуса до опорной поверхности равно 0.65. На рис. ,а показан результат первого этапа преодоления препятствия, обеспечивающий начальную позицию робота, а также отмечены оси $O\eta$, $O\zeta$.
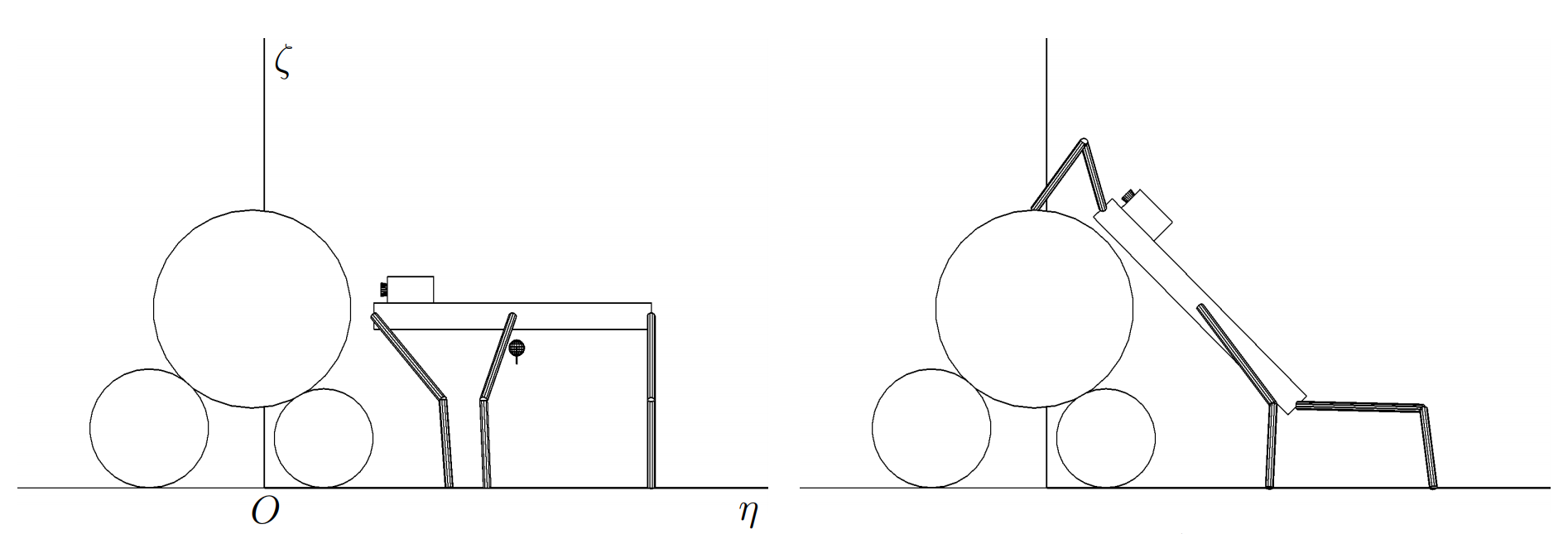
Опишем основные этапы действий робота.
Этап 4.2.2. Робот, сохраняя горизонтальное положение корпуса, ставит передние ноги на вершину штабеля. В данном случае это оказывается почти на пределе возможности робота, когда клиренс его корпуса равен маршевой высоте. Для преодоления более высокого штабеля необходимо будет либо приподнимать передний край корпуса робота, либо увеличивать клиренс. Далее корпус робота при опоре на все ноги поворачивается аналогично тому, как это делалось на этапе 4.1.3 задачи «низкий штабель» (рис. ,б). Передняя точка корпуса движется по вертикальной окружности радиуса $r_3+\sigma_2$, с центром на оси верхнего цилиндра, средняя точка движется по прямой под углом $-\varepsilon$ к оси $O\eta$. В результате корпус приближается к верхнему цилиндру.
Этап 4.2.3. Робот сначала переставляет задние ноги на опорную плоскость поближе к заднему краю корпуса робота. Затем он переносит средние ноги на нижний второй цилиндр (рис. ,а).
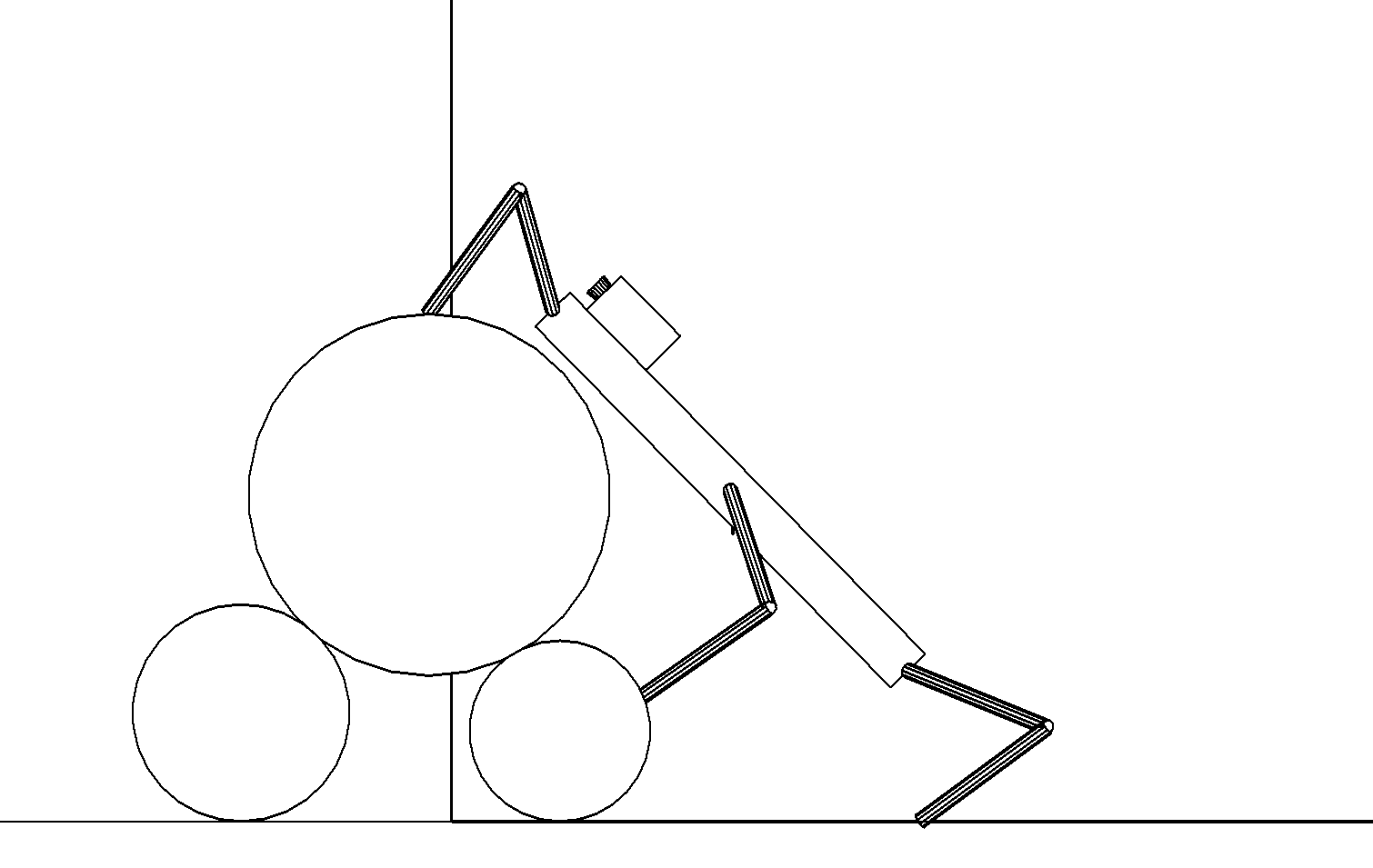
а
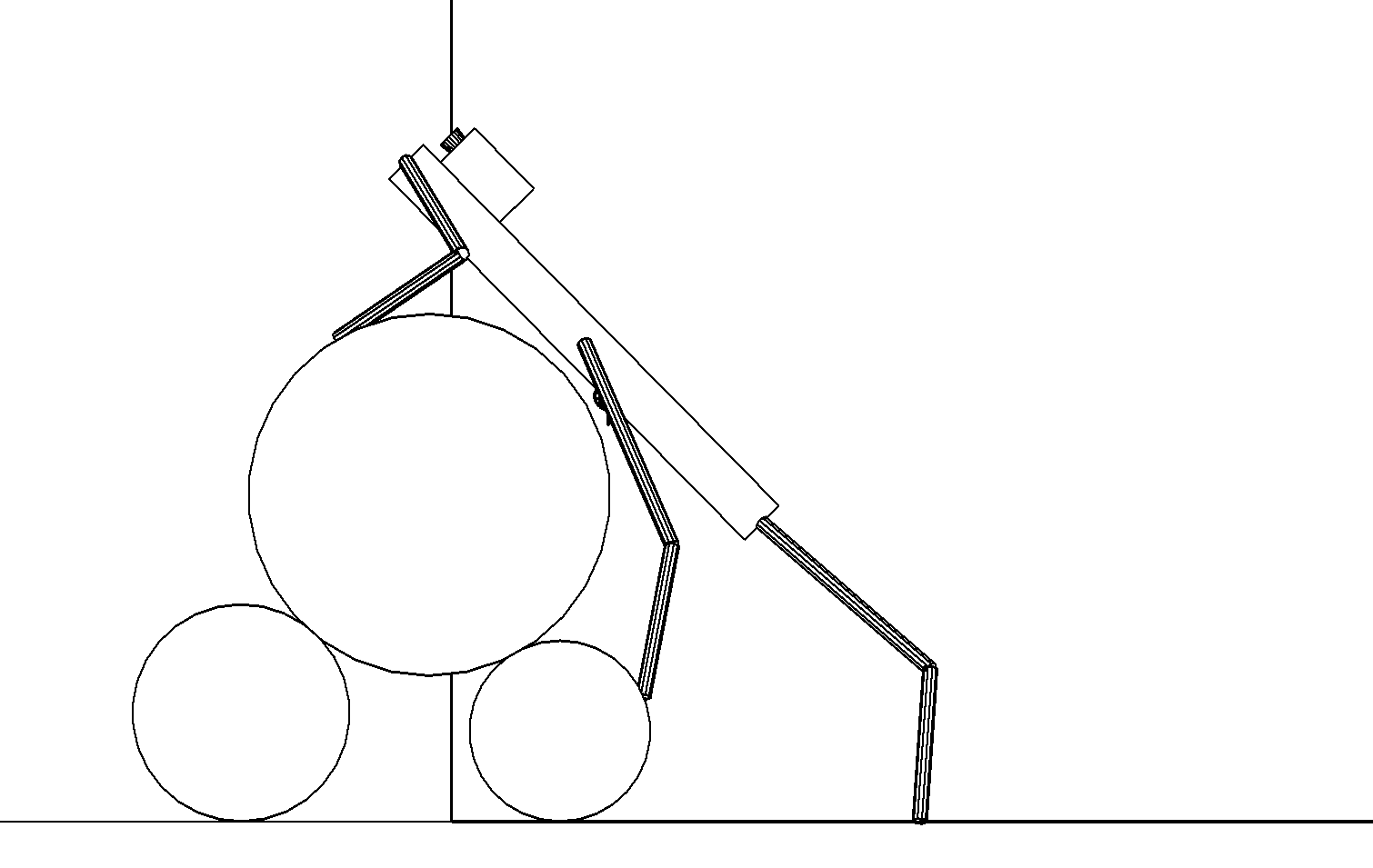
б
Этап 4.2.4. Передние ноги переставляются на верхнем цилиндре для обеспечения возможности опоры на нем других ног. Корпус продвигается вверх параллельно самому себе так, чтобы центр масс проектировался внутрь опорного многоугольника, образованного передними и средними ногами (рис. ,б). В результате движения корпуса его центр оказывается на расстоянии $r_3+\sigma_2$ от верхнего цилиндра, и корпус ориентирован по касательной к нему.
Этап 4.2.5. Задние ноги переставляются ближе к штабелю, чтобы обеспечить надежную опору при подъеме вверх заднего края корпуса робота (рис. ,а).
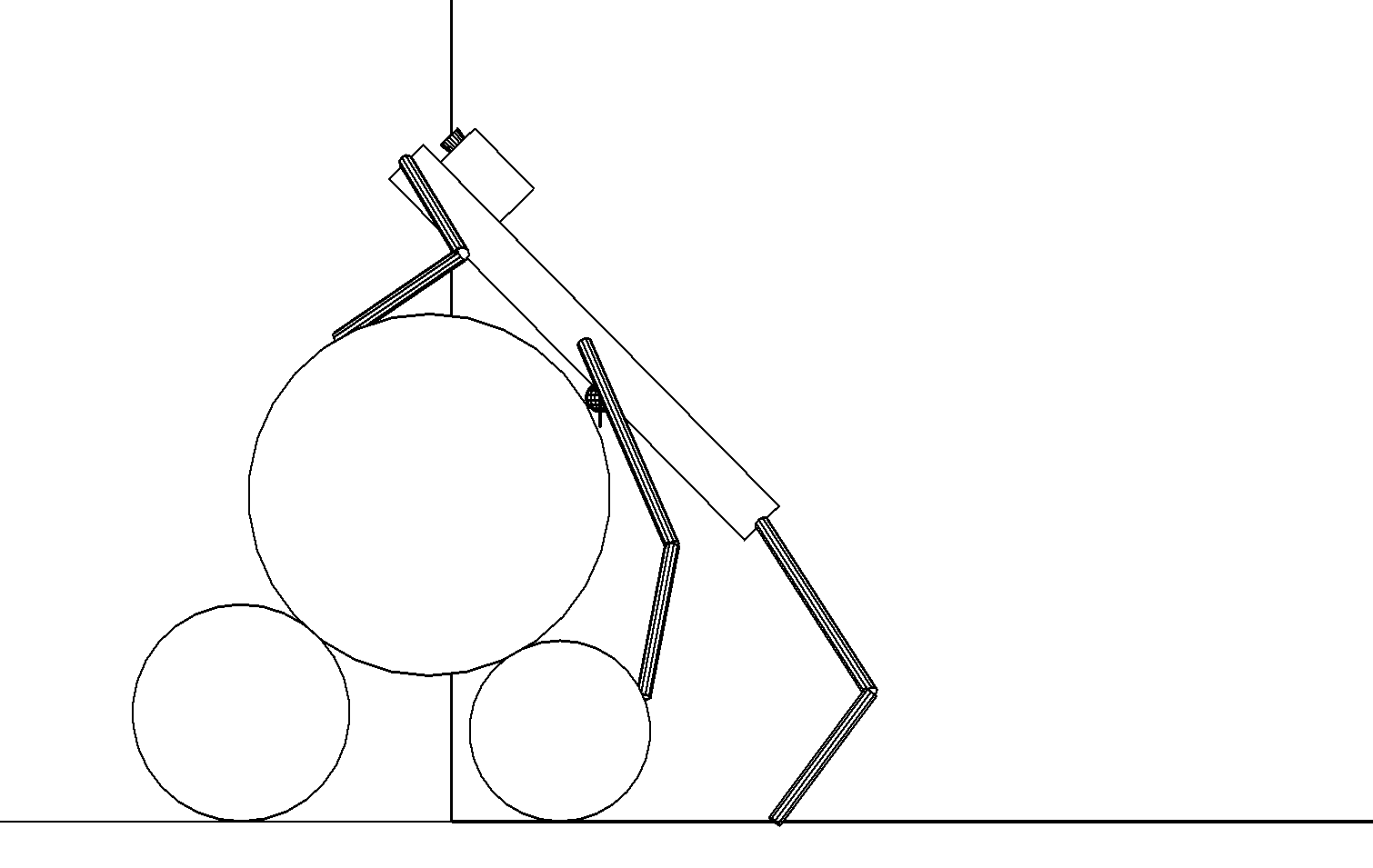
а
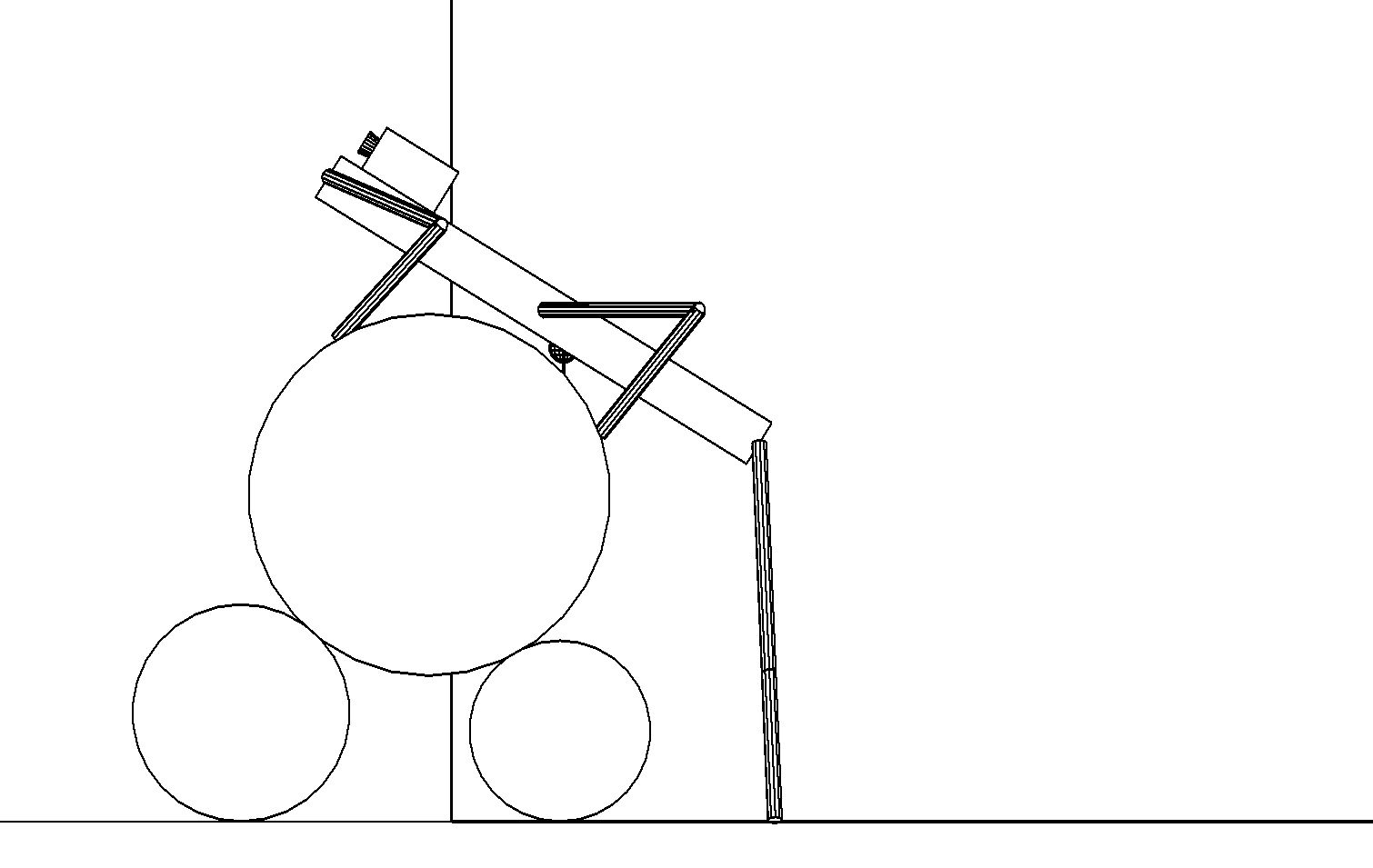
б
Этап 4.2.6. Средние ноги переставляются на верхний цилиндр, а корпус продвигается вверх с одновременным поворотом заднего края до полного распрямления задних ног (рис. ,б).
Этап 4.2.7. Задние ноги переставляются на второй нижний цилиндр, затем средние ноги переставляются на верхнем цилиндре поближе к его вершине. Корпус начинает приподниматься над верхним цилиндром и поворачиваться в горизонтальное положение с одновременным переносом задних ног на верхний цилиндр (рис. ,а).
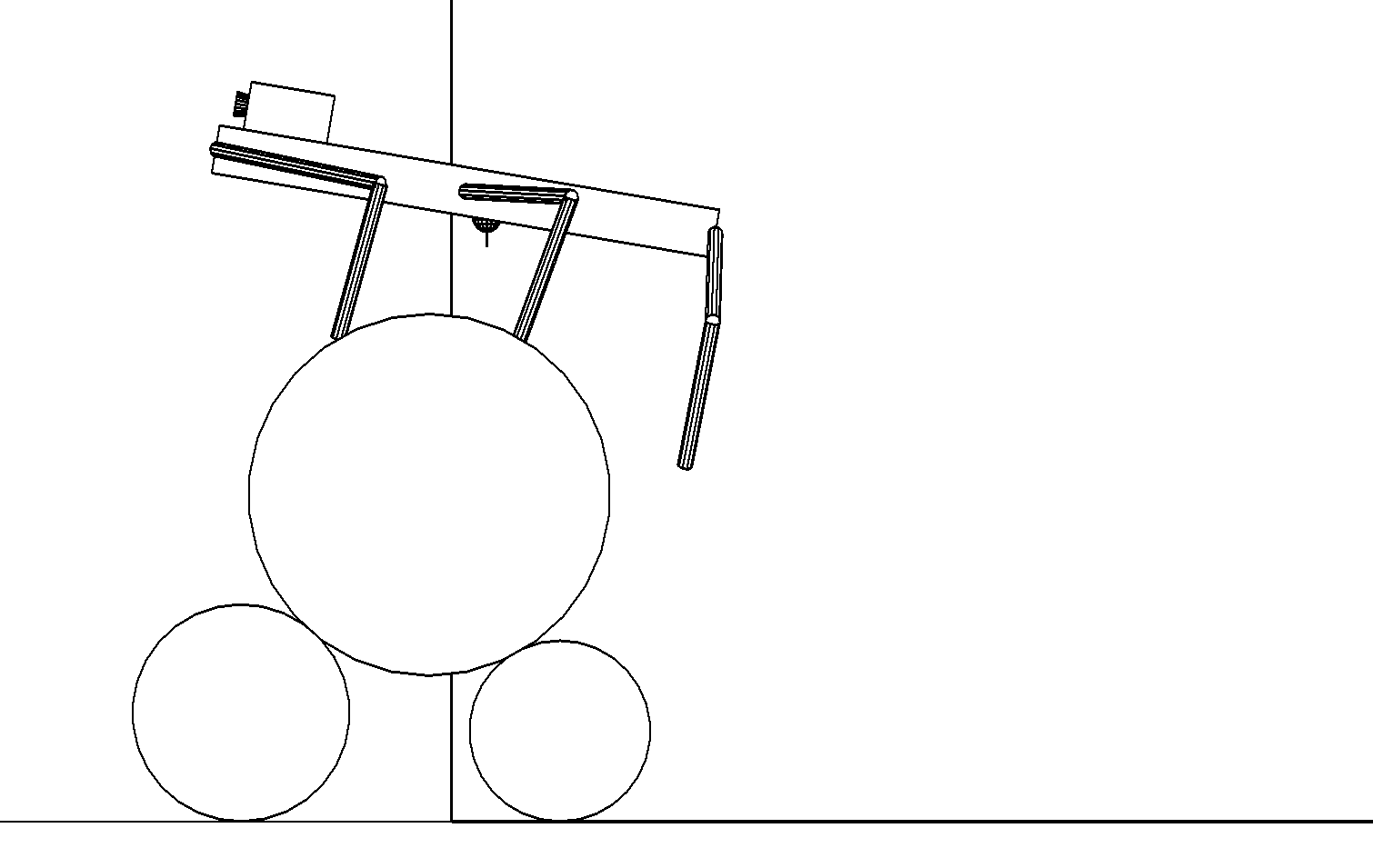
а
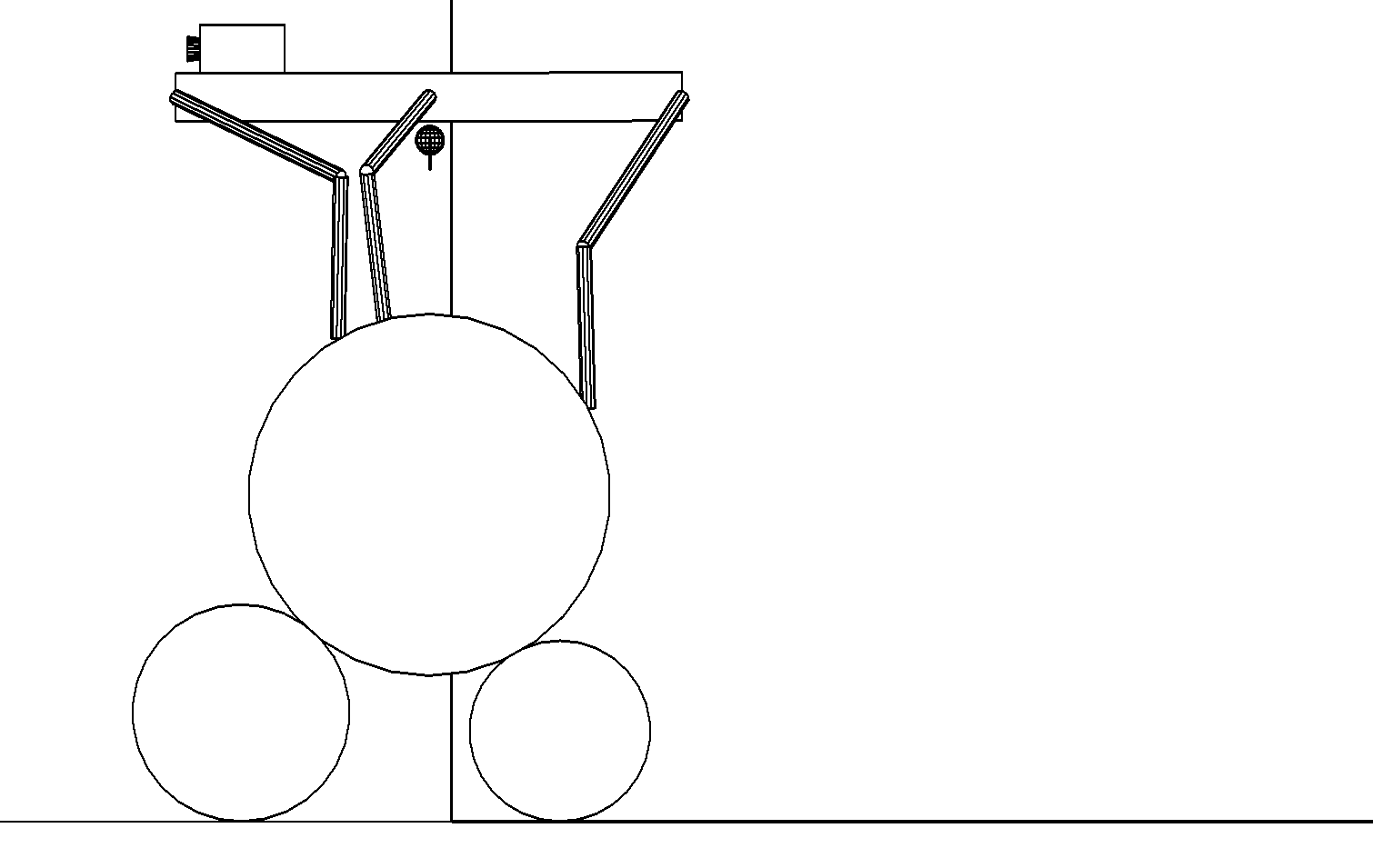
б
Этап 4.2.8. Задние ноги робота поставлены на верхний цилиндр, корпус приведен в горизонтальное положение, центр масс робота расположен над вершиной верхнего цилиндра, а средние ноги перенесены вперед поближе к передним ногам. Залезание робота на штабель закончено. Робот видит перед собой непроходимый участок и начинает подготовку к боковому маневру (рис. ,б), который будет осуществляться походкой «трешки».
Этап 4.2.9. Робот переместился вбок на достаточное расстояние и начинает подготовку к спуску со штабеля (рис. ,а).
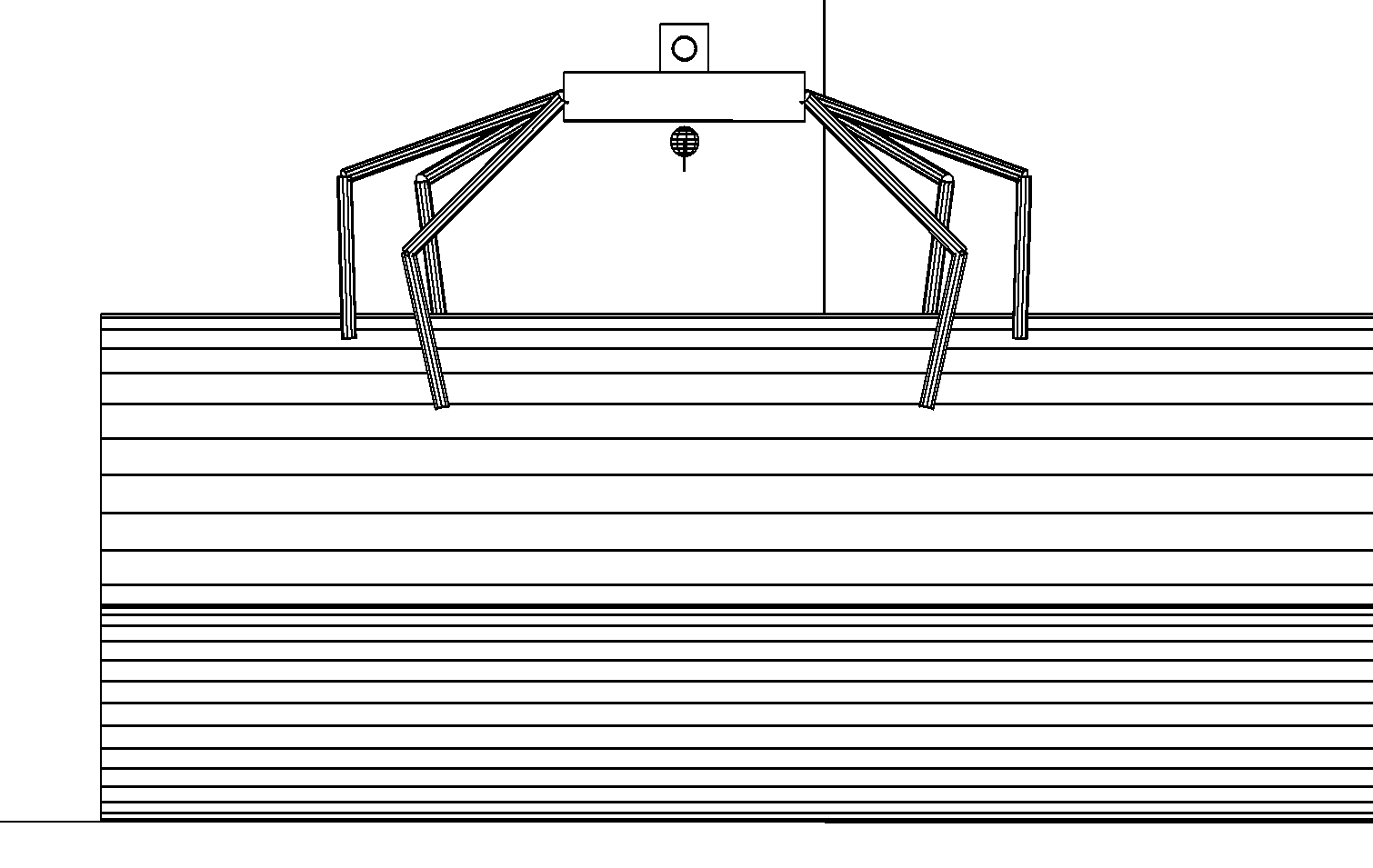
а
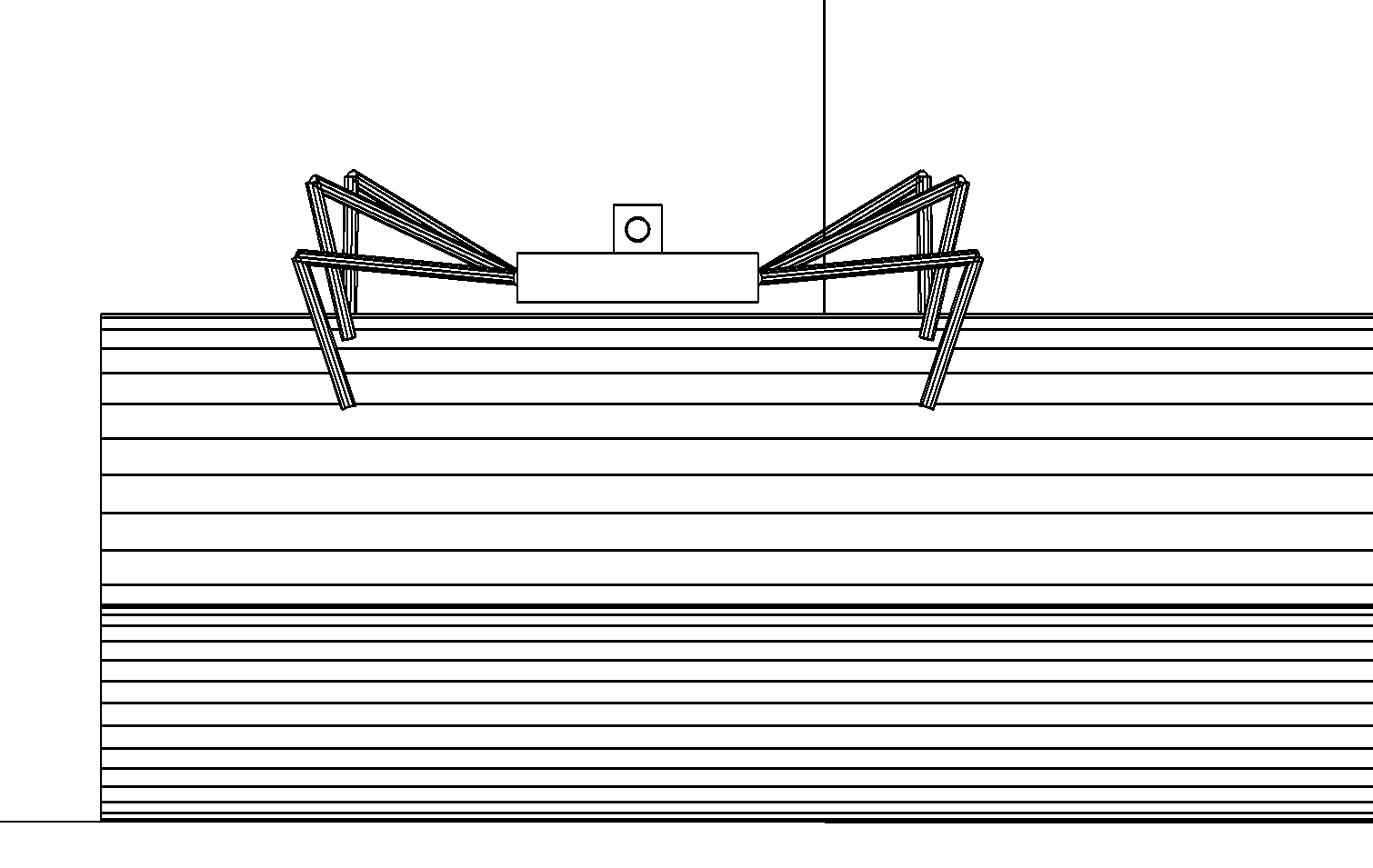
б
Этап 4.2.10. Робот перестраивает свою конфигурацию для продолжения движения походкой «галоп» и приседает, чтобы обеспечить себе возможность дотягивания до необходимых точек опоры (рис. ,б).
Этап 4.2.11. Робот начинает наклонять корпус вперед с одновременным смещением его вдоль поверхности верхнего цилиндра и переносит передние ноги на первый нижний цилиндр. Проекция центра масс робота находится внутри опорного многоугольника средних и задних ног (рис. ,а).
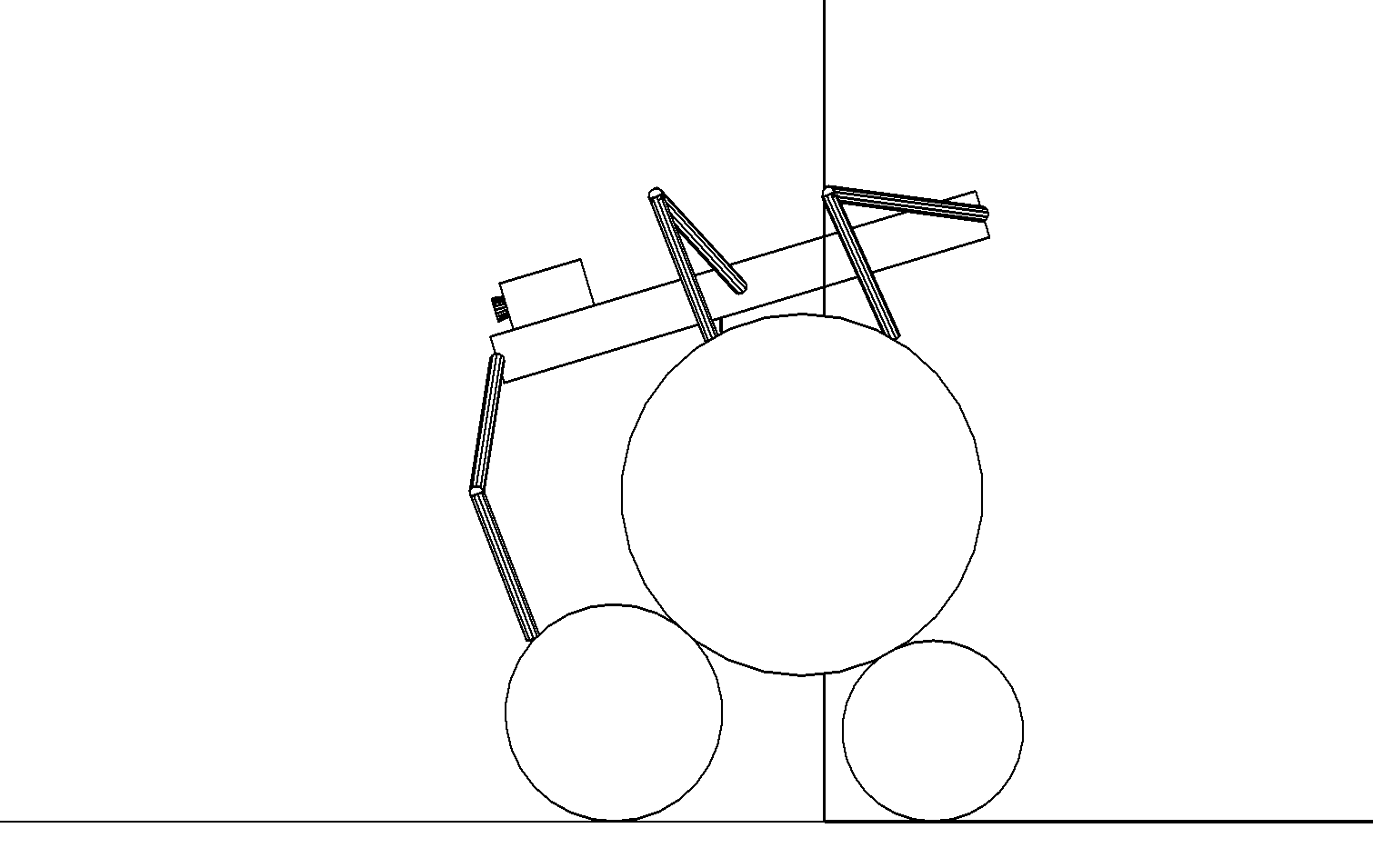
а
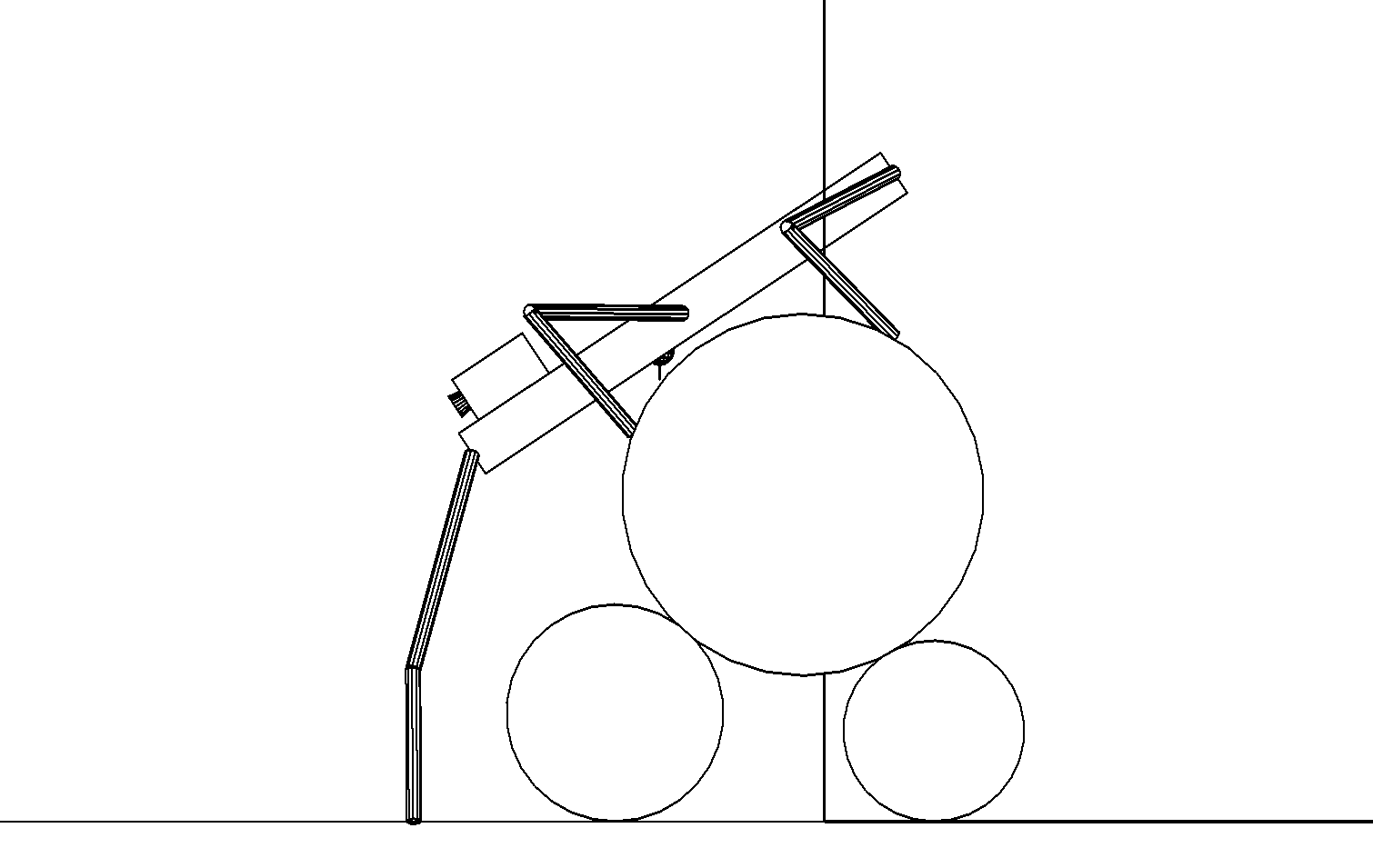
б
Этап 4.2.12. Робот переносит средние ноги вперед в новые точки опоры на верхнем цилиндре и продолжает наклон корпуса вперед с одновременным смещением его вдоль поверхности верхнего цилиндра до возможности постановки передних ног на опорную плоскость (рис. ,б). Этот маневр необходим из-за того, что на первом нижнем цилиндре не хватает места для точек опоры средних ног.
Этап 4.2.13. Корпус робота вращается вокруг верхнего цилиндра до тех пор, пока задние ноги едва не начнут касаться боковой стороной голени поверхности верхнего цилиндра, затем средние ноги ставятся на правый нижний цилиндр (рис. ,а).
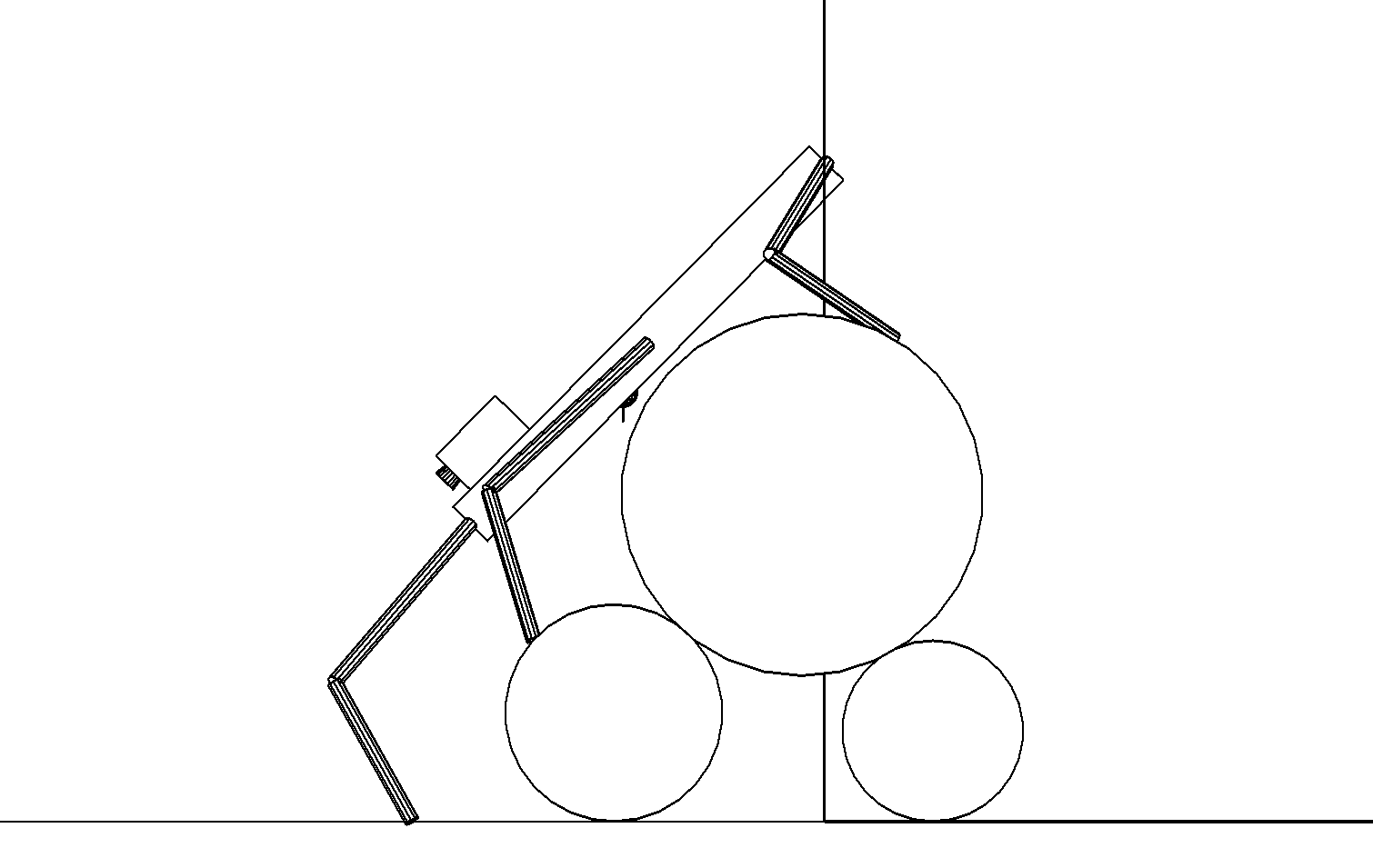
а
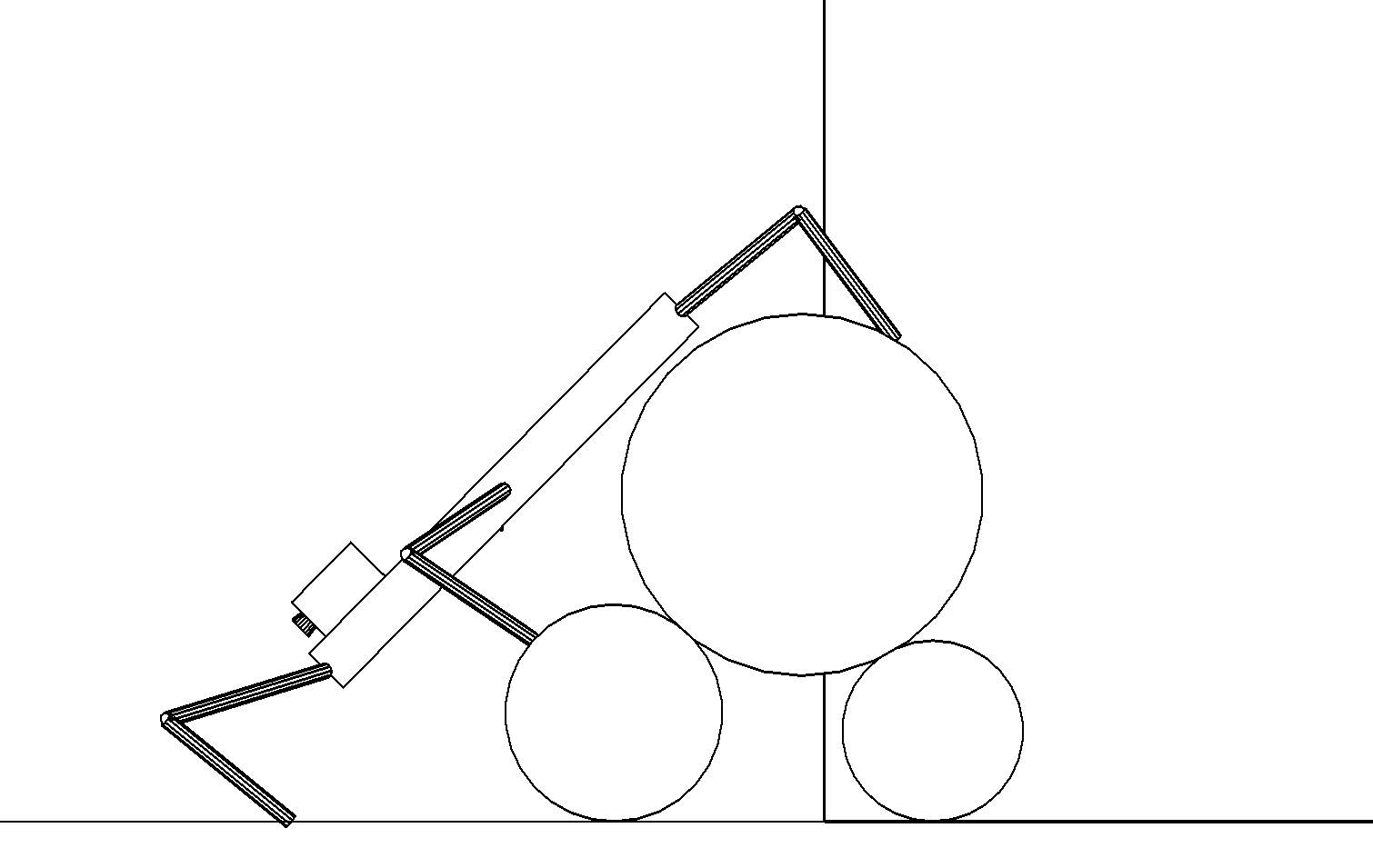
б
Этап 4.2.14. Передние ноги переносятся на плоскости вперед, затем, используя опору на них, робот продолжает движение корпуса вперед и вниз (рис. ,б).
Этап 4.2.15. Робот переносит задние ноги на поверхность верхнего цилиндра, а затем он переносит средние ноги на опорную плоскость (рис. ,а).
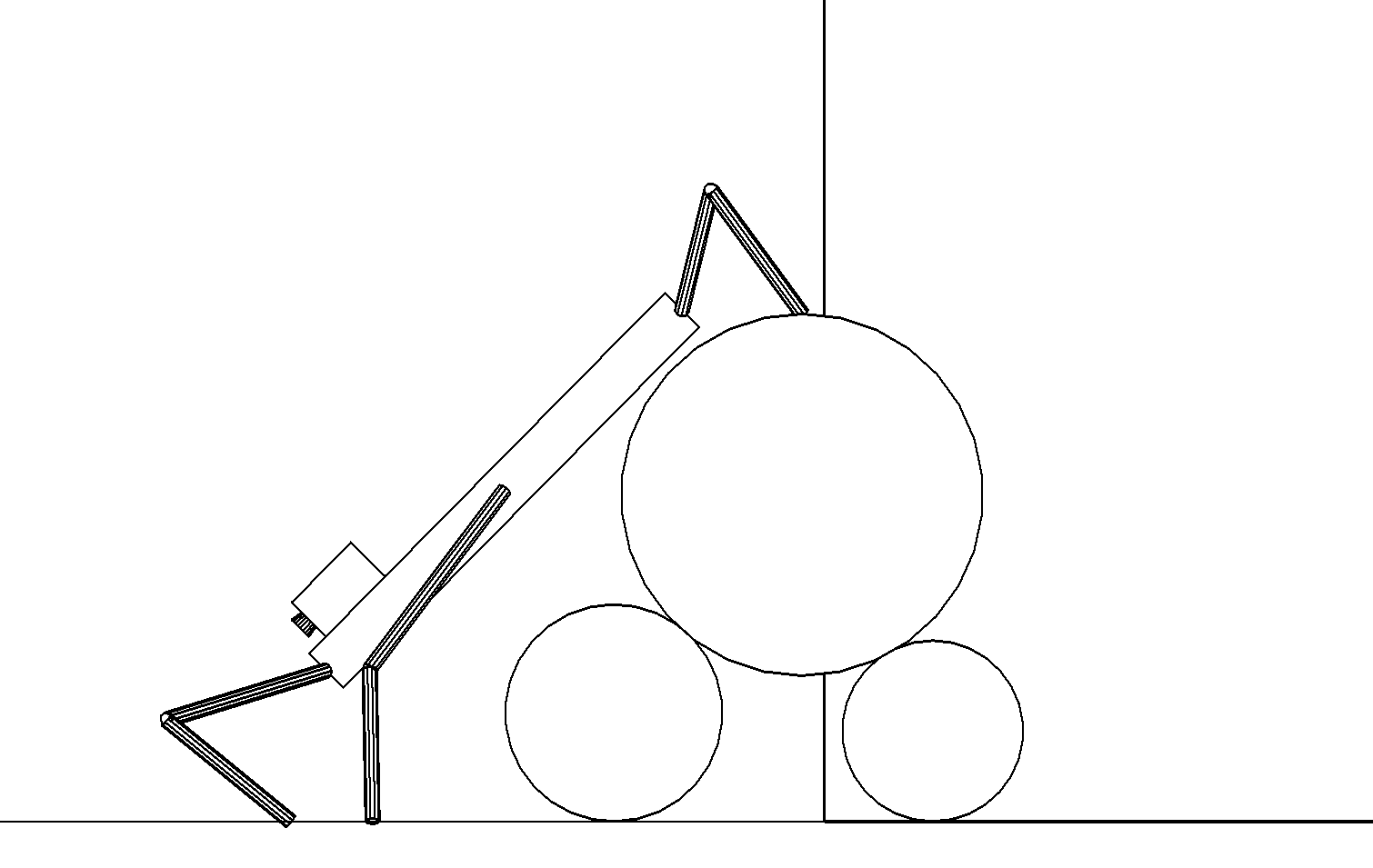
а
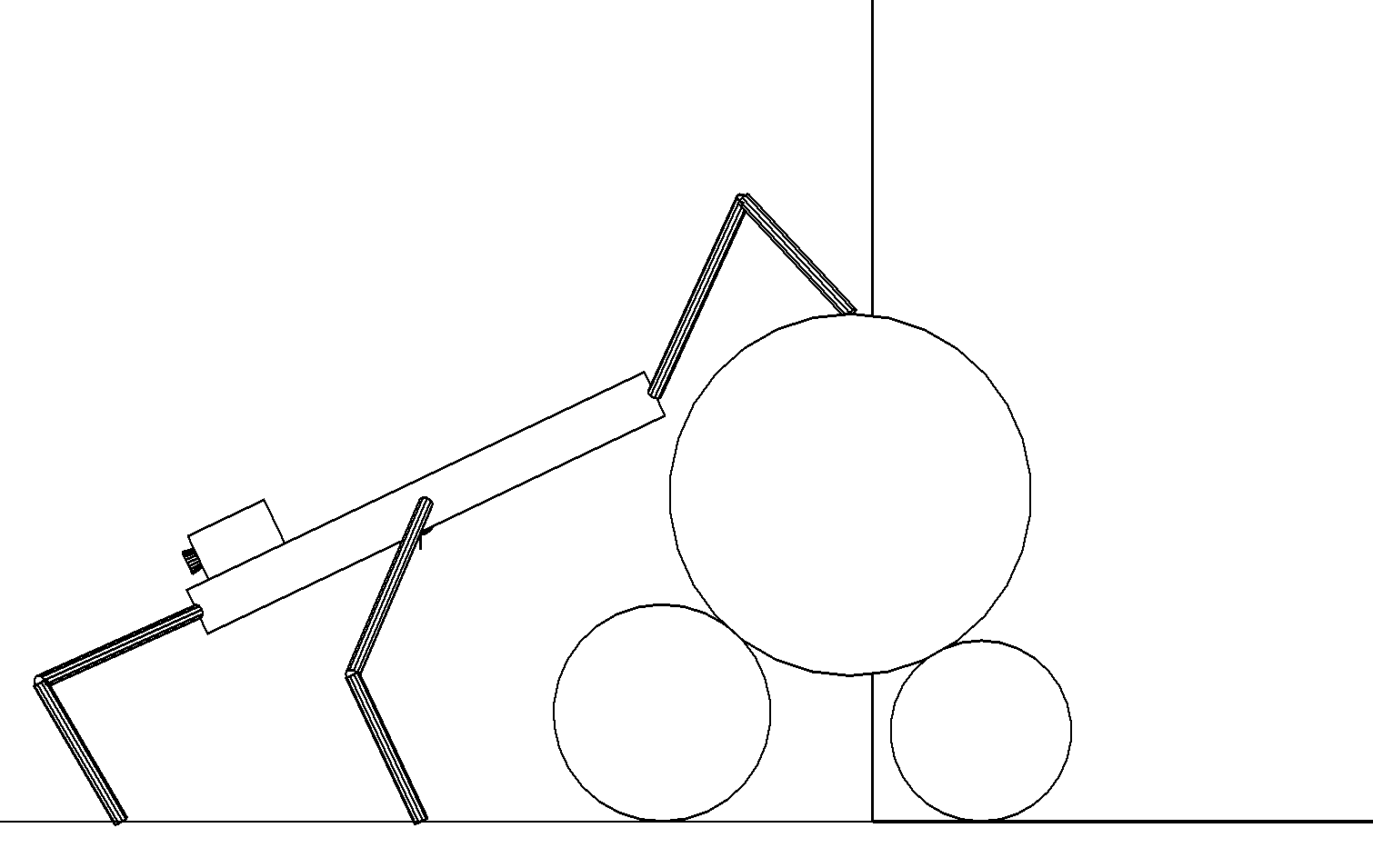
б
Этап 4.2.16. Робот переносит передние ноги и поворачивает корпус с одновременным перемещением его вперед так, чтобы центр масс робота попал внутрь опорного многоугольника передних и средних ног (рис. ,б). Движение корпуса формируется аналогично тому, как это делалось на этапе 4.2.2 с применением необходимых зеркальных коррекций, соответствующих слезанию. Это движение можно делать до тех пор, пока задние ноги не касаются каким-либо своим звеном верхнего цилиндра (рис. ,а).
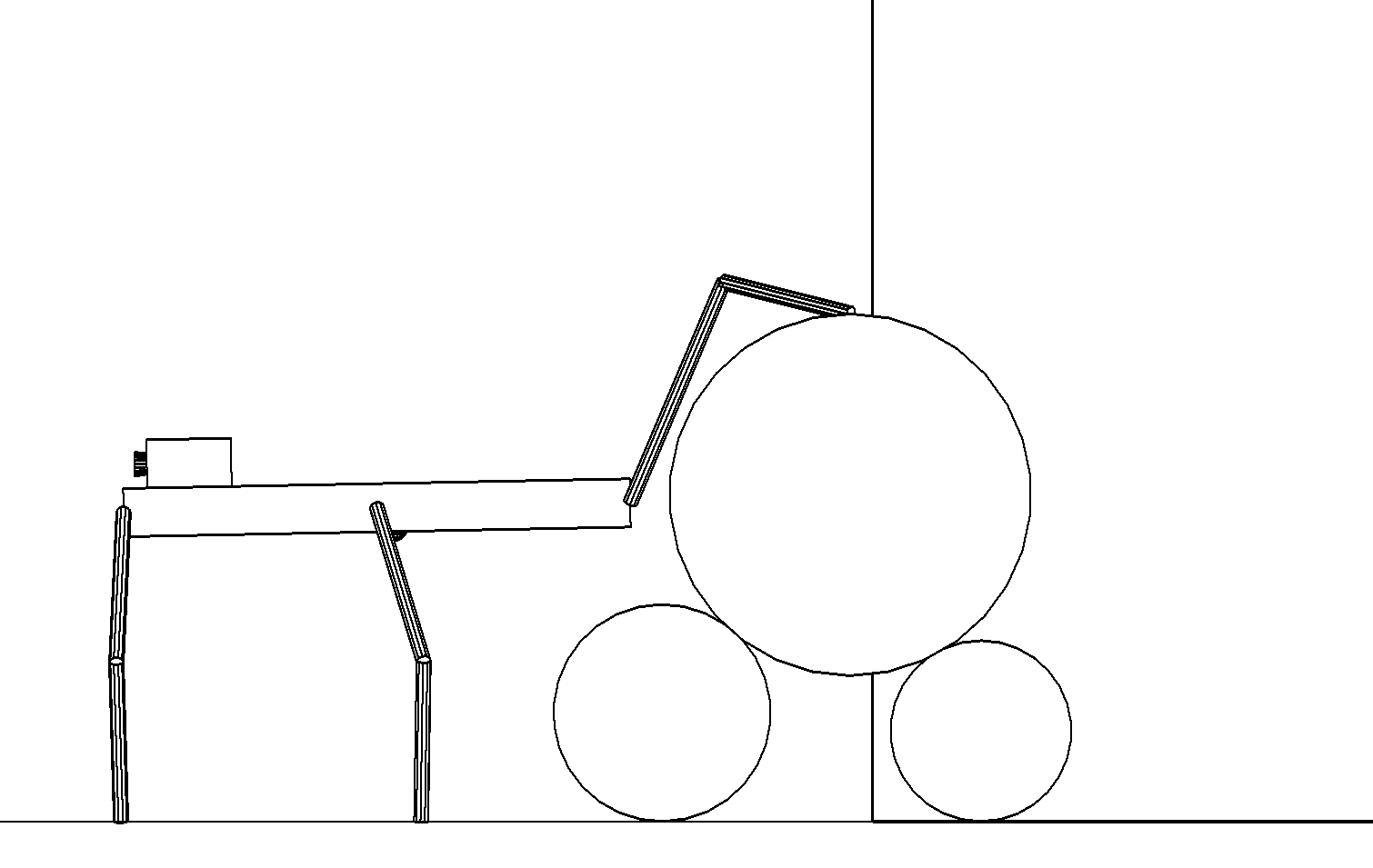
а
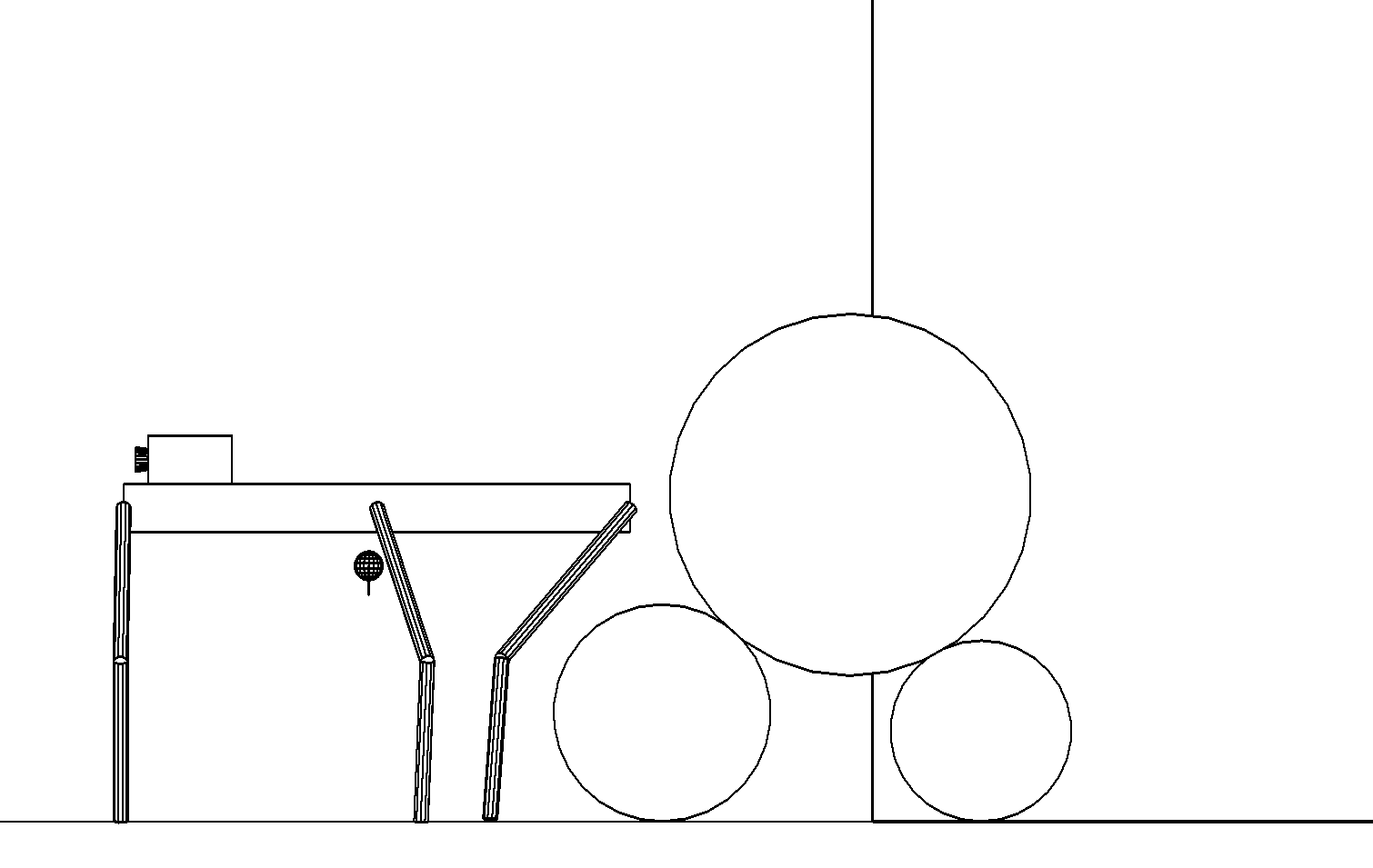
б
Этап 4.2.17. Задние ноги переносятся сразу на опорную плоскость. Преодоление препятствия завершено (рис. ,б).
Компьютерное моделирование
Компьютерное моделирование осуществлялось аналогично тому, как это было описано в [, , ]. Управление роботом, закон взаимодействия корпуса и стоп ног с опорой реализованы в виде DLL-библиотеки, подключенной к программному комплексу «Универсальный механизм» []. Тем самым создается виртуальная среда обитания робота. Неподвижная опорная поверхность в ней представлена горизонтальной плоскостью. Опорная плоскость, корпус и ноги робота взаимодействуют друг с другом согласно модели трения, основанной на вязко-упругом взаимодействии тел в точках контакта. Управление движением реализуется посредством компьютерного моделирования работы электромеханических приводов шарнирных углов. Выполнение требуемого движения робота осуществляется, как и в реальности, лишь в результате подачи значения управляющего электрического напряжения на модели электромеханических приводов. Соотношение размеров корпуса и звеньев ног имеет вид
Массы корпуса робота и звеньев ног относятся как
Представление о движении корпуса робота и его ног возникает в результате численного интегрирования дифференциальных уравнений полной трехмерной динамики робота и элементов окружающей среды. Поскольку в точках контакта объектов предполагается силовое взаимодействие, соответствующая механическая система имеет 42 степени свободы. Уравнения динамики синтезируются автоматически []. Результаты компьютерного моделирования отображаются на экране монитора в виде движения геометрических образов исследуемых материальных объектов.
На рис. , представлены графики изменения по времени вертикальных координат нечетных стоп $\zeta_1$, $\zeta_3$, $\zeta_5$, а также передней и задней точек корпуса $\zeta_f$, $\zeta_r$ для задач 4.1 и 4.2. На рис. дополнительно нанесен модуль линейной скорости верхнего цилиндра $v_3$. Все величины даны в абсолютной системе координат $O\xi\eta\zeta$. По графикам можно подробно отследить все подробности выполнения вышеописанных этапов выполнения задач. Напомним, что уровень 0.65 м соответствует маршевой высоте корпуса над опорной плоскостью. Уровень 0.7 м соответствует высоте низкого штабеля, а уровень 1.05 м соответствует высоте высокого штабеля. В середине процесса преодоления препятствия видны характерные для походки «трешки» волнообразные зависимости высот стоп от времени.
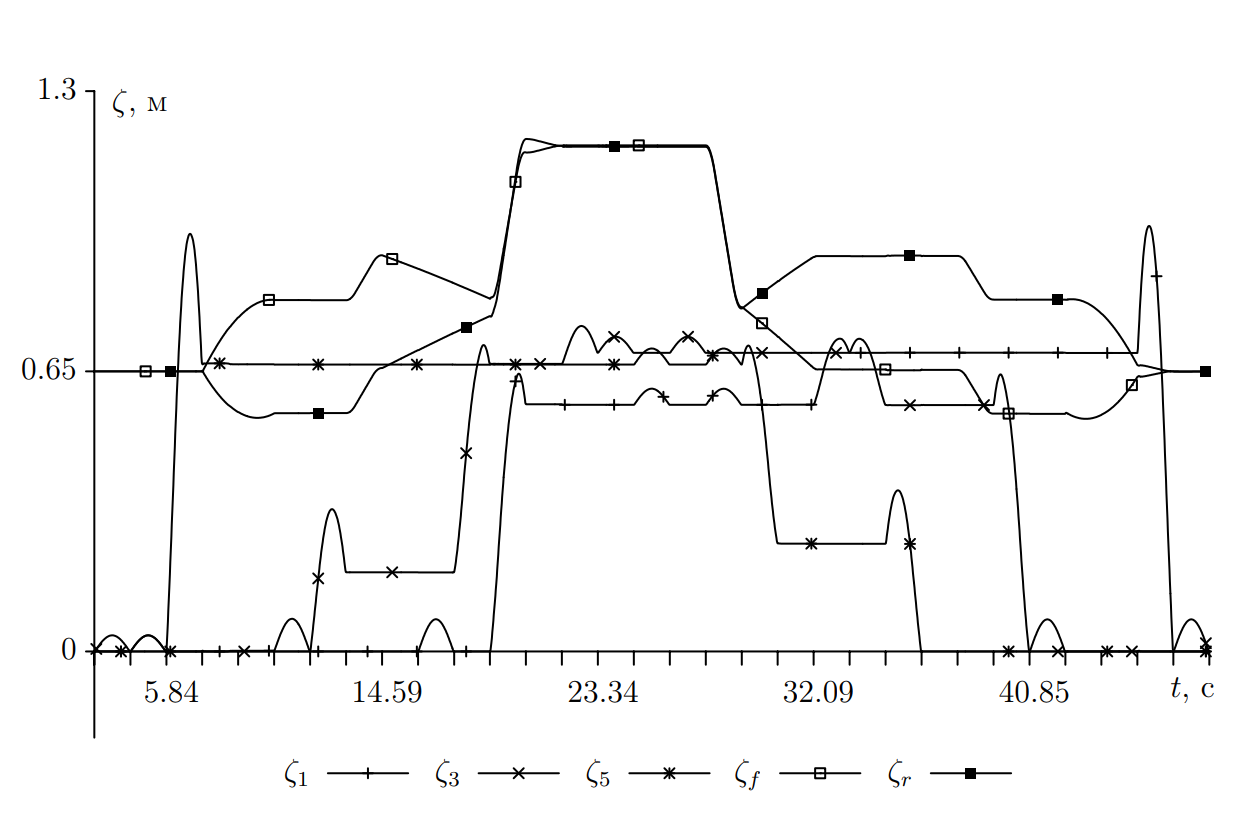

На рис. небольшие колебания $v_3$ видны между отметками времени $31.44$ и $40.19$. Максимальное значение $v_3$ на графике $\approx0.023$ м/с. Небольшие колебания не мешали движению, то есть подсистема отслеживания реальных положений стоп робота справлялась с такими помехами.
Управляющие шарнирные моменты были ограничены по модулю величинами 30 Н$\cdot$м и 60 Н$\cdot$м для задач 4.1 и 4.2 соответственно.
Ролики с компьютерной 3D анимацией полученных решений в реальном масштабе времени представлены на рис. , для задач 4.1, 4.2 соответственно. По ним можно наглядно и детально представить себе, как происходит движение робота при решении этих задач.
Эти ролики также доступны по адресам
https://keldysh.ru/e-biblio/golubev/cyl-pyramid.mp4
https://keldysh.ru/e-biblio/golubev/cyl-bigger-pyramid.mp4
Заключение
Исследована новая задача о преодолении инсектоморфным роботом препятствий в виде штабеля из параллельных бревен разного радиуса. Установлена принципиальная возможность преодоления препятствий указанного типа, имеющих высоту, существенно превосходящую характерные размеры робота.
Аналитически получены условия устойчивости штабеля при действии на него ограниченных сил сухого трения и трения качения, а также активной равнодействующей сил, возникающих из-за опоры робота на штабель. Сформулированы простые правила, руководствуясь которыми робот может качественно определять возможность опоры о препятствие без его разрушения, а также выбирать надежные точки опоры на препятствии и направления действия сил в точках опоры для сохранения равновесия системы.
Конструктивно построены алгоритмы залезания робота на штабели разной высоты. Специфика алгоритмов существенно зависит от высоты препятствия из-за возникающих потребностей дотягивания до надежных точек опоры, тесноты областей, пригодных для опоры, и других геометрических ограничений.
Предложенные алгоритмы формирования движения робота при преодолении указанных препятствий были отработаны средствами компьютерного моделирования в программной среде, реализующей расчет взаимодействия трехмерной полной динамической модели робота и окружающих его объектов с учетом сил кулоновского трения, трения качения и моделей электромеханических приводов в шарнирах робота. Показано, что предложенные программные движения реализуемы при коэффициенте трения, не превышающем единицы. Возникающие в шарнирных углах переходные процессы не разрушают требуемое программное движение робота на всех этапах движения системы. Представлены видеоролики, которые наглядно демонстрируют подробности преодоления рассматриваемых препятствий.
Список литературы
-
Голубев Ю.Ф., Корянов В.В.
Экстремальные локомоционные возможности инсектоморфных роботов
М: ИПМ им. М.В. Келдыша, 2018. 212 с.
ISBN 978-5-98354-040-8
https://doi.org/10.20948/mono-2018-golubev -
Завал
Википедия
https://ru.wikipedia.org/wiki/Завал -
Сырых Н.В., Чащухин В.Г.
Роботы вертикального перемещения с контактными устройствами но основе постоянных магнитов: конструкции и принципы управления контактными устройствами
Известия РАН. Теория и системы управления, 2019, № 5, с. 163-173
https://doi.org/10.1134/S0002338819050135
Syrykh N.V., Chashchukhin V.G.
Wall-Climbing Robots with Permanent-Magnet Contact Devices: Design and Control Concept of the Contact Devices
Journal of Computer and Systems Sciences International, 2019. Vol. 58, No. 5, p. 818-827
https://doi.org/10.1134/S1064230719050137 -
Градецкий В.Г., Князьков М.М., Кравчук Л.Н., Крюкова А. А., Семенов Е.А., Суханов А.Н., Чащухин В.Г.
Управляемое формирование вакуума в устройствах сцепления с поверхностями при движении мобильных роботов с аэродинамическим прижимом
Мехатроника, автоматизация, управление. 2017, том 18, № 7, с. 447-452
https://doi.org/10.17587/mau.18.447-452 -
Longo D., Muscato G.
Adhesion techniques for climbing robots: State of the art and experimental considerations
Proc. 11-th Internat. Conf. CLAWAR-2008. Coimbra, Portugal: World Scientific Publishing Co. Pte. Ltd, 2008. P. 6-28 -
Голубев Ю.Ф., Корянов В.В.
Преодоление шестиногим роботом изолированных цилиндрических препятствий
Препринты ИПМ им. М.В.Келдыша. 2020. № 65. 34 с.
https://doi.org/10.20948/prepr-2020-65 -
Голубев Ю.Ф., Корянов В.В.
Преодоление инсектоморфным роботом завалов в виде изолированных цилиндров
Известия РАН. Теория и системы управления, 2021, № 2, с. 156-176
https://doi.org/10.31857/S0002338821020050
Golubev Yu.F., Koryanov V.V.
An Insectomorphic Robot Overcoming Obstructions Formed by Isolated Cylinders
Journal of Computer and Systems Sciences International, 2021. Vol. 60, No. 2, pp. 333-352
https://doi.org/10.1134/S1064230721020052 -
Неймарк Ю.И., Фуфаев Н.А.
Динамика неголономных систем
М.: Наука. 1967. 519 с. -
Rabier P.J., Rheinboldt W.C.
Nonholonomic motion of rigid mechanical systems from a DAE viewpoint
Philadelphia: Society for Industrial and Applied Mathematics. 2000. 140 p. -
Кулешов А.С., Рыбин В.В.
Об управляемости системы А.Ю. Ишлинского
Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 2014. Т. 1(59). Вып. 2. С. 98-103 -
Охоцимский Д.Е., Голубев Ю.Ф.
Механика и управление движением автоматического шагающего аппарата
М.: Наука. Глав. ред. физ.-мат. лит., 1984. 312 с. -
Голубев Ю.Ф., Корянов В.В.
Преодоление небольшой водной преграды инсектоморфным роботом на плоту
Известия РАН. Теория и системы управления, 2017, № 6, с. 141-162
https://doi.org/10.7868/S0002338817060117
Golubev Yu.F., Koryanov V.V.
Crossing a Small Body of Water by an Insectomorphic Robot on a Raft
Journal of Computer and Systems Sciences International, 2017. Vol. 56, No. 6, pp. 1037-1058. © Pleiades Publishing, Ltd., 2017
https://doi.org/10.1134/S1064230717050045 -
Голубев Ю.Ф., Корянов В.В.
Транспортировка груза на плоту инсектоморфным роботом
Известия РАН. Теория и системы управления, ISSN: 0002-3388, 2018, №5, с. 136-146
https://doi.org/10.31857/S000233880002853-7
Golubev Yu.F., Koryanov V.V. Shipping Cargo on a Raft by an Insectomorphic Robot
Journal of Computer and Systems Sciences International, ISSN 1064-2307, 2018. Vol. 57, No. 5, pp. 813-821. © Pleiades Publishing, Ltd., 2018
https://doi.org/10.1134/S1064230718050052 -
Голубев Ю.Ф., Корянов В.В., Мелкумова Е.В.
Приведение инсектоморфного робота в рабочее состояние из аварийного положения «вверх ногами»
Известия РАН. Теория и системы управления, ISSN: 0002-3388, 2019, № 6, С. 163-176
https://doi.org/10.1134/S0002338819060052
Golubev Yu.F., Koryanov V.V., Melkumova E.V.
Bringing an Insectomorphic Robot to a Normal Position from an Abnormal Upside Down Position
Journal of Computer and Systems Sciences International, ISSN PRINT 1064-2307, 2019. Vol. 58, No. 6, pp. 987-999. © Pleiades Publishing, Ltd., 2019
https://doi.org/10.1134/S1064230719060054 -
Универсальный механизм. Моделирование динамики механических систем
http://www.umlab.ru -
Голубев Ю.Ф., Корянов В.В.
Залезание инсектоморфного робота на свободно катающийся шар
Известия РАН. Теория и системы управления, ISSN: 0002-3388, 2010, № 6, С. 182-192
Golubev Yu.F., Koryanov V.V.
Insectomorphic Robot Climbing a Freely Rolling Ball
Journal of Computer and Systems Sciences International, ISSN PRINT 1064-2307, 2010. Vol. 49, No. 6, pp. 1009-1019. © Pleiades Publishing, Ltd., 2010
https://doi.org/10.1134/S1064230710060195
